圆管水力计算(面积湿周Q)
雨水管道水力设计的可靠性计算

雨水管道水力设计的可靠性计算张子贤王瑞恩提要:雨水管道水力设计中,由于各水力因子的不确定性,管道的过水能力是一随机变量。
文中分析了各水力因子的不确定性,并通过一次二阶矩法求过水能力的统计参数,给出了过水能力的均值、变差系数的计算式以及管道水力设计可靠度的计算式和计算方法。
算例说明,现行的水力计算方法,水力设计的可靠度较低。
0引言城市雨水管道设计中,一般只考虑水文因素造成的不确定性,即考虑雨水流量的不确定性,首先通过拟定雨水排除设计标准,确定雨水设计流量,然后按此进展雨水管道的水力计算,认为雨水管道一经确定,其排水能力是确定的。
事实上,由于各种不确定性因素的影响,管道的过水能力不是与设计流量一致确实定量,而是随机变量,这就是水力不确定性。
由于这种不确定性的存在,管道能通过设计流量的可靠程度应能在工程设计中给予足够的重视,以便使工程设计可靠合理。
本文运用概率统计方法对此问题进展研究,给出了计算公式和计算方法。
1雨水管道水力设计可靠性的度量所谓可靠性是指产品在规定的时间内,在规定的条件下,完成规定功能的能力[1]。
当使用概率来度量这一能力时,就是可靠度,即可靠度是可靠性的概率度量。
在可靠性定义中,论述的对象泛指产品,本文中可靠性问题的对象是指雨水管道。
设计条件下雨水管道的水力计算,常按满管无压均匀流计算,计算公式为:V=(1/n)R2/3I1/2(1)Q=ω·(1/n)R2/3I1/2(2)式中V--管道流速,m/s;Q--管道的过水流量,雨水管道水力计算时即是管道的过水能力,m3/s;ω--过水断面面积,m2;n--管壁粗糙率;R--水力半径(过水断面面积与湿周之比),m;I--水力坡度。
雨水管道中常用的断面形式大多为圆形,以此种情况为例进展讨论,式(2)中ω、R均可由管径反映,此时式(2)变为Q=0.311685D8/3(1/n)I1/2=Q(D,n,I)(3)式中D--圆管直径,m。
水力计算时,设计流量为,设为Q0,通常在选定管材之后,粗糙率为数值,设为n0,利用式(1)、式(3)可计算出既符合水力计算根本技术规定,又满足Q0要求的流速V0、管径D0和水力坡度I0。
(整理)第三章给水排水管道系统水力计算基础

第三章给水排水管道系统水力计算基础本章内容:1、水头损失计算2、无压圆管的水力计算3、水力等效简化本章难点:无压圆管的水力计算第一节基本概念一、管道内水流特征进行水力计算前首先要进行流态的判别。
判别流态的标准采用临界雷诺数Re k,临界雷诺数大都稳定在2000左右,当计算出的雷诺数Re小于2000时,一般为层流,当Re大于4000时,一般为紊流,当Re介于2000到4000之间时,水流状态不稳定,属于过渡流态。
对给水排水管道进行水力计算时,管道内流体流态均按紊流考虑紊流流态又分为三个阻力特征区:紊流光滑区、紊流过渡区及紊流粗糙管区。
二、有压流与无压流水体沿流程整个周界与固体壁面接触,而无自由液面,这种流动称为有压流或压力流。
水体沿流程一部分周界与固体壁面接触,另一部分与空气接触,具有自由液面,这种流动称为无压流或重力流给水管道基本上采用有压流输水方式,而排水管道大都采用无压流输水方式。
从水流断面形式看,在给水排水管道中采用圆管最多三、恒定流与非恒定流给水排水管道中水流的运动,由于用水量和排水量的经常性变化,均处于非恒定流状态,但是,非恒定流的水力计算特别复杂,在设计时,一般也只能按恒定流(又称稳定流)计算。
四、均匀流与非均匀流液体质点流速的大小和方向沿流程不变的流动,称为均匀流;反之,液体质点流速的大小和方向沿流程变化的流动,称为非均匀流。
从总体上看,给水排水管道中的水流不但多为非恒定流,且常为非均匀流,即水流参数往往随时间和空间变化。
对于满管流动,如果管道截面在一段距离内不变且不发生转弯,则管内流动为均匀流;而当管道在局部有交汇、转弯与变截面时,管内流动为非均匀流。
均匀流的管道对水流的阻力沿程不变,水流的水头损失可以采用沿程水头损失公式进行计算;满管流的非均匀流动距离一般较短,采用局部水头损失公式进行计算。
对于非满管流或明渠流,只要长距离截面不变,也没有转弯或交汇时,也可以近似为均匀流,按沿程水头损失公式进行水力计算,对于短距离或特殊情况下的非均匀流动则运用水力学理论按缓流或急流计算。
过水断面面积

(Н·Н·Павловский) 等公式,其中,国内常用的是舍维列夫公式和巴甫洛夫
斯基公式。
(1)舍维列夫公式
舍维列夫公式根据他对旧铸铁管和旧钢管的水力实验(水温 10℃),提出了计算紊流过
渡区的经验公式。
当 v≥1.2 m/s 时
0.00214
g D0.3
(3-3)
当 v 1.2 m/s 时
0.001824
速,g 为重力加速度)。 位置水头和压力水头属于势能,它们二者的和称为测压管水头,流速水头属于动能。流
体在流动过程中,三种形式的水头 (机械能)总是处于不断转换之中。给水排水管道中的测 压管水头较之流速水头一般大得多,在水力计算中,流速水头往往可以忽略不计。
实际流体存在粘滞性,因此在流动中,流体受固定界面的影响(包括摩擦与限制作用), 导致断面的流速不均匀,相邻流层间产生切应力,即流动阻力。流体克服阻力所消耗的机械 能,称为水头损失。当流体受固定边界限制做均匀流动(如断面大小,流动方向沿流程不变 的流动)时,流动阻力中只有沿程不变的切应力,称沿程阻力。由沿程阻力所引起的水头损 失称为沿程水头损失。当流体的固定边界发生突然变化,引起流速分布或方向发生变化,从 而集中发生在较短范围的阻力称为局部阻力。由局部阻力所引起的水头损失称为局部水头损 失。
在给水排水管道中,由于管道长度较大,沿程水头损失一般远远大于局部水头损失, 所以在进行管道水力计算时,一般忽略局部水头损失,或将局部阻力转换成等效长度的管道 沿程水头损失进行计算。
第二节 管渠水头损失计算
一、沿程水头损失计算
管渠的沿程水头损失常用谢才公式计算,其形式为:
hf
v2 C2R
l
(m)
式中 hf — 沿程水头损失,m; v — 过水断面平均流速,m/s; C — 谢才系数;
流体力学作业3 答案

作业3 答案 (第5章、第6章)第5章一、选择题1. 管道中液体的雷诺数与( D )无关。
A. 温度B. 管径C. 流速D. 管长2. 某圆管直径d=30mm ,其中液体平均流速为20cm/s 。
液体粘滞系数为0.0114cm 3/s ,则此管中液体流态为( B )。
A. 层流B. 层流向紊流过渡C.紊流3.等直径圆管中紊流的过流断面流速分布是 ( D )A 呈抛物线分布 B. 呈对数线分布C.呈椭圆曲线分布D. 呈双曲线分布4.等直径圆管中的层流,其过流断面平均流速是圆管中最大流速的( C )A 1.0倍 B.1/3倍 C. 1/4倍D. 1/2倍5.圆管中的层流的沿程损失与管中平均流速的( B )成正比.A. 一次方B. 二次方C. 三次方D. 四次方6.圆管的水力半径是 ( A )A. d/2B. d/3C.d/4D. d/5.7、 谢才公式中谢才系数的单位是( C )A. 无量纲B.s m 21C. s m 23D. s m 28. 判断层流和紊流的临界雷诺数是 ( C )A.上临界雷诺数B.下临界雷诺数C.上下临界雷诺数代数平均D.上下临界雷诺数几何平均二、判断题1. 层流的沿程水头损失系数仅与雷诺数有关。
( 正确 )2.壁面光滑的管道一定是水力光滑管。
( 错误 )3.在过流断面突变处一般发生局部水头损失。
( 正确 )4. 等直径圆管中的层流,其过流断面平均流速是圆管中最大流速的1/2倍(正确 ) 5.流体内切应力方向与流体运动方向相同。
( 错误 )6.阻力平方区内阻力系数与雷诺数无关。
( 正确 )三、简答题1. 圆管中层流与紊流,其流速分布有什么不同?答: 层流为抛物线分布,紊流为对数曲线分布.(也可以画图)2. 简述尼古拉兹实验中沿程阻力系数λ的变化规律。
答: 尼古拉兹实验揭示了沿程阻力系数λ的变化规律,文字表述或数学公式表述.层流:(Re)f =λ;水力光滑区: (Re)f =λ;过渡粗糙区: )(Re,d K f =λ 粗糙区(阻力平方区) : )(dK f =λ . 3.写出管流和明渠水流雷诺数的表达式,并说明其层流、紊流的判别标准?答: 管流:νvd=Re 2000Re <(层流) 2000Re > (紊流)明渠水流: νvR =Re 500Re <(层流) 500Re > (紊流)4.雷诺数Re 的物理意义?它为什么能用来判别流态?答: 雷诺数实质是反映粘性力与惯性力之比。
水力学常用计算公式

水力学常用计算公式水力学是研究液体流动的力学学科,其中包含了一系列常用的计算公式。
以下是一些水力学常用计算公式的介绍:1.流速计算:流速是流体通过一个截面的体积流量与该截面的面积之比。
常用的流速计算公式有:-海明公式:V=K*R^2/3*S^1/2,其中V表示流速,K为常数,R为液体通过管道、河道等的湿周长度,S为这段的坡度。
-曼宁公式:V=K*R^(2/3)*S^(1/2),其中V表示流速,K为摩擦系数,R为水流断面湿周和湿径的比值,S为水流的坡度。
2.流量计算:流量指的是单位时间内流经其中一截面的液体体积,常用的流量计算公式有:-面积乘以流速:Q=A*V,其中Q表示流量,A为液体流动截面的面积,V为流速。
-引伯定理:Q=Cd*A*dH^1/2,其中Q表示流量,Cd为管道或孔洞的流量系数,A为流动截面的面积,dH为压力差。
3.湿周计算:湿周是液体通过管道、河道等截面时湿润的周边长度,常用的湿周计算公式有:-圆形截面的湿周:P=π*D,其中P表示湿周,π为圆周率,D为圆的直径。
-矩形截面的湿周:P=2*(L+H),其中P表示湿周,L为矩形的长,H 为矩形的高。
-圆形管道的湿周:P=π*D,其中P表示湿周,π为圆周率,D为管道的直径。
4.重力控制流量计算:重力控制流量是指由重力作用下,液体流经管道、河道等截面时的流量。
-拉金方程:v=C*(2g*H)^1/2,其中v表示流速,C为拉金系数,g为重力加速度,H为压力头。
5.水头计算:水头是流体流动过程中的压力能。
常用的水头计算公式有:-静水头:H=h+P/ρg+V^2/2g,其中H表示总水头,h为液面高度,P 为压力,ρ为液体密度,g为重力加速度,V为速度。
-压力头:P/ρg,其中P为压力,ρ为液体密度,g为重力加速度。
-速度头:V^2/2g,其中V为速度,g为重力加速度。
以上只是水力学中一些常用的计算公式,还有很多其他的公式在不同的具体问题中也会使用到。
钢筋混凝土管满流非满流的管道水力计算表

项目
换算结果
单位
计算公式或者依据
计算值
取值
=⋅
1
v = ⋅ 2/3 ⋅ ⅈ1/2
=
= − sⅈn ⋅ cos ⋅ 2
流量
Q
(m3/s)
流速
v
(m/s)
水力半径
R
(m)
水流断面
A
(m2)
湿周
ρ
1.8
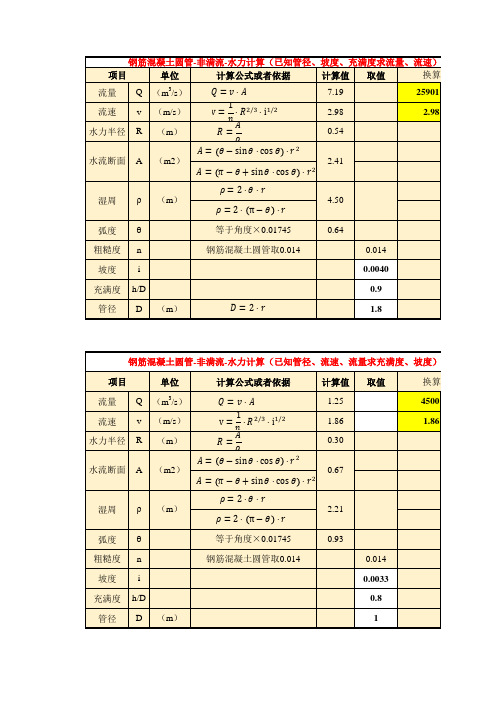
钢筋混凝土圆管-非满流-水力计算(已知管径、流速、流量求充满度、坡度)
项目
单位
流量
Q
(m3/s)
流速
v
(m/s)
水力半径
R
(m)
水流断面
A
(m2)
计算公式或者依据
计算值
=⋅
1
v = ⋅ 2/3 ⋅ ⅈ1/2
=
= − sⅈn ⋅ cos ⋅ 2
= − + sⅈn ⋅ cos ⋅
2
0.06
=2⋅⋅
湿周
ρ
弧度
θ
等于角度×0.01745
粗糙度
n
钢筋混凝土圆管取0.014
坡度
i
充满度
h/D
管径
D
(m)
=2⋅ π− ⋅
0.66
0.93
0.014
0.0002
0.8
(m)
0.3
满度求坡度、流速)
换算结果
4500 m3/h
1.86 m/s
3.30 ‰
满度求坡度、流量)
钢筋混凝土管满流非满流的管道水力计算表
计算值 0.01
取值
0.2 0.09
水力半径 R
������=������/������ ������=(������−sin ������⋅cos ������ )⋅������^2
水流断面 A
(m2) ������=(������−������+sin ������⋅cos ������ )⋅度 充满度 管径
θ n i h/D D (m)
等于角度×0.01745 钢筋混凝土圆管取0.014
0.93 0.014 0.0033 0.8 1
满度、坡度) 换算结果 m3/h m/s
钢筋混凝土圆管-非满流-水力计算(已知管径、流速、充满度求坡度、流量) 项目 流量 流速 Q v 单位 (m3/s) (m/s) (m) 计算公式或者依据
3.30 ‰
充满度求坡度、流量) 换算结果 44 m3/h 0.20 m/s
0.19 ‰
������=2⋅������⋅������
0.06
湿周
ρ
(m)
0.66 ������=2⋅(π−������)⋅������ 等于角度×0.01745 钢筋混凝土圆管取0.014 0.93 0.014
弧度 粗糙度
θ n
坡度 充满度 管径
i h/D D (m)
0.0002 0.8 0.3
充满度求坡度、流速) 换算结果 4500 m3/h 1.86 m/s
水力半径 R
弧度 粗糙度
θ n
坡度 充满度 管径
i h/D D (m)
0.0033 0.8 1
流量、流速) 换算结果 m /h m/s
给水排水管道系统水力计算

e ( mm )
平均 0.003 0.03 0.06 0.15 0.3 0.6 3 15 150
( 4 )巴甫洛夫斯基公式 巴甫洛夫斯基公式适用于明渠流和非满流管道的计算,公式为:
C
R
y
nb 0.10
3-3 。
( 3-11 )
式中: y
2.5 nb
0.13 0.75 R
nb
nb — 巴甫洛夫斯基公式粗糙系数,见表
2
A 和水力半径 R 的值 (表中 d 以 m 计) 充满度 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 过水断面积 A ( m 2) 0.4426 d 0.4920 d 0.5404 d 0.5872 d 0.6319 d 0.6736 d 0.7115 d 0.7445 d 0.7707 d 0.7845 d
图 3-1 无压圆管均匀流的过水 断面
3-1 所示。设其 , 称为充满度,
h d
sin
2
4
所对应的圆心角 素之间的关系为:
称为充满角。由几何关系可得各水力要
过水断面面积:
A
湿周:
d
2
8
sin
( 3-16 )
d 2
水力半径:
( 3-17 )
R
所以
d 4
1
sin
( 3-18 )
2
v
2
1 d n 4 sin
将( 3-11 )式代入( 3-2 )式得:
hf
nb v R
2
2
2y 1
l
( 3-12 )
常用管渠材料粗糙系数
nb 值
管渠材料
