工程力学 第二版 (范钦珊 唐静静 著) 高等教育出版社 课后答案 第11章 压杆的稳定性问题
力学(第二版)课后答案-高等教育出版社
力学习题剖析目录第01 章物理学、力学、数学 (01)第02 章质点运动学 (05)第03 章动量定理及其守恒定律 (15)第04 章动能和势能 (28)第05 章角动量及其规律 (38)第06 章万有引力定律 (42)第07 章刚体力学 (45)第08 章弹性体的应力和应变 (56)第09 章振动 (60)第10 章波动 (68)第11 章流体力学 (75)大学物理学院1 + x 2xx3 x xa ∫ a dx 3 2 ∫ 2 (x 3 − 3x +1)dx = x 3dx − 3 dx = 1 x 4 − 3 2+ x + c 1+ x 21+ x 21+ x 2dh = d (102 −10− 4 x 2 + 5 ×10−7 x 4 ) = 2 ×10−6 x 3 − 2 ×10−4 x dx =1 (ax + b ) −1 /2 d (ax + b ) = 2 x x ∫ 2x x 2 2 41. 求下列函数的导数⑴y = 3x 2− 4x + 10⑵ y = 1/+ 7 s in x + 8 c os x −100⑴ ∫( x 3− 3x +1)dx⑵∫ (2x+ x 2 )dx⑶∫ ( 3 + 2e x− 1 )dx⑷∫ (sin x − cos x )dx⑶ y = (ax + b ) /( a + bx ) ⑷ y = sin ⑸ x 21+ x ⑹ ∫ sin( ax + b )dx⑸ y = e sin x⑹ y = e− x+ 100x⑺∫e − 2 x dx 2 ⑻ ⑼ ∫ sin x cos xdx ⑽ ∫ xe dx 解：⑴ y ' = 6x − 4(11) ∫ cos 2xdx(12)∫ ln x dx⑵ y ' = −1/( 2x x ) + 7 cosx − 8 sin x 解：⑶ y ' = (a 2 − b 2 ) /( a + bx ) 2⑷ y ' = cos(1+ x 2 )1/ 2· 1(1+ x 2 )−1 / 2· 2x∫ ∫ ∫ ∫ 4 2 2= x c os /⑵ ∫ (2x + x 2 )dx = ∫ 2xdx + ∫x 2 dx = 2xln 2 + 1 x 3+ c ⑸ y ' = e sin x cos x⑶ ∫ ( 3 + 2e x − 1 dx = 3∫ dx+ 2∫ e xdx − ∫ x − 3/ 2 dx ⑹ y ' = e − x (−1) + 100 = 100 − e − x= 3ln x + 2e x c⑷ ∫(sin x − cos x )dx = ∫sin xdx − ∫ cos xdx = − c os x − sin x + c 2.已知某地段地形的海拔高度 h 因水平坐标 x 而变，h=100-⑸ ∫ x 2 dx = ∫ 1+ x2−1dx = ∫ dx − ∫dx = x − arctgx + c 0.0001x 2(1-0.005x 2)，度量x 和 h 的单位为米。
范钦珊《工程力学》习题解答
2F ⋅
（2） （3）
1 3 tan θ = sin θ = F cos θ 3 ， θ = 30° 2 ，
代入（3） ，得
F1 = F2 = F3 =
W 2
8 如图所示，试求 F 对点 A 的力矩。 解： M A ( F ) = r AB × F
M2 d 由（1） 、 （2） ，得 M1 = M2
′ = FD
（2）
' FD
习题 14 图
A
D
B
M1
M
2
FA
FD
(a) (b)
15 试求图示两外伸梁的约束反力 FRA、FRB，其中（a）M = 60kN·m，FP = 20 kN； （b）FP = 10 kN，FP1 = 20 kN，q = 20kN/m，d = 0.8m。 解：图（a-1） ∑ Fx = 0 ，F = 0
F − FRA ⋅
(c)
FRC
FR D
2 2 − FRE ⋅ =0 2 2
（1） （2）
2 2 ∑ Fy = 0 ， FRE ⋅ 2 − FRA ⋅ 2 = 0 由（2） FRE = FRA
代入（1） ，得
FRE =
2 F 2 ； 2 F 2
（3）
3．由图（b） ： ∑ Fx = 0 ，
′E = FRA = FR
10 图示电动机固定在支架上，它受到自重 160N、轴上的力 120N 以及力偶矩为 25N·m 的力偶的作 用。试求此力系向点 A 简化的结果。
z
75
z
F1
范钦珊《工程力学》习题解答
rAB
9 齿轮箱有三个轴，其中 A 轴水平，B 和 C 轴位于 yz 铅垂平面内，轴上作用的力偶如图所示。试求合力 偶。 解：MA =（1, 0, 0）MA =3.6（1, 0, 0）kN·m MB =（0, sin40°,cos40°）MB =6（0, sin40°,cos40°）kN·m MC =（0, sin40°,-cos40°）MC =6（0, sin40°,-cos40°）kN·m ∴ M = ΣMi = MA+ MB + MC =（3.6, 12sin40°, 0）kN·m
即 ∴
2 FR·MO = − FO （l3 + l1 + l2）= 0 l1 + l2 + l3 = 0
12 齿轮箱两个外伸轴上作用的力偶如图所示。为保持齿轮箱平衡，试求螺栓 A、B 处所提供的约束 力的铅垂分力。
FBy
FAy
解：ΣMi = 0， −500 + 125 + FAy × 0.5 = 0 FAy = 750N（↓） FBy = 750N（↑） （本题中 FAx ，FBx 等值反向，对力偶系合成结果无贡献。 ） 13 试求图示结构中杆 1、2、3 所受的力。 解：3 杆为二力杆 图（a） ：ΣM = 0， F3 ⋅ d − M = 0
10 图示电动机固定在支架上，它受到自重 160N、轴上的力 120N 以及力偶矩为 25N·m 的力偶的作 用。试求此力系向点 A 简化的结果。
z
75
z
F1
A
r
75 25 200 75
y
x
F2
习题 10 图
M
(a)
解：由已知 F1 =160N，F2 =120N，F3 =25N·m F1 =（0, 0, -160）N F2 =（-120, 0, 0）N M =（25, 0, 0）N·m r =（0.075, 0.2, 0.025）m 向 A 点简化，得 FR = F1 + F2 =（-120, 0, -160）N M A = M + r × F1 + r × F2
工程力学(工程静力学与材料力学)第二版答案
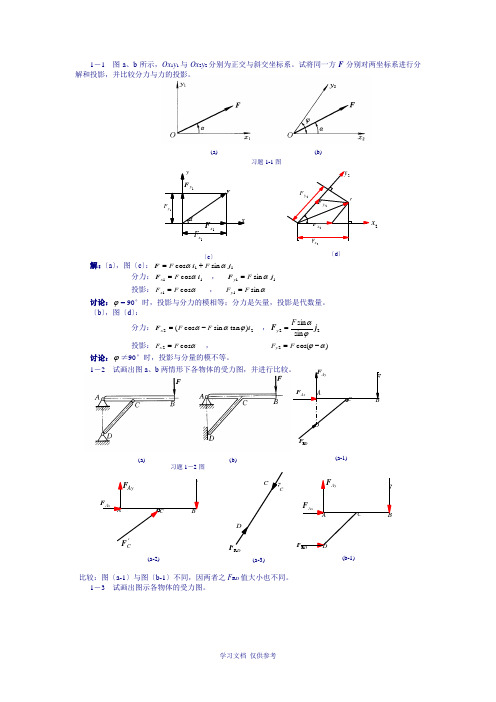
(a) (b) 习题1-1图 (a) (b) 习题1－2图FD R F AC BD Ax F AyF(a-1) Ay F F B C A AxF 'F C (a-2)C D C F D R(a-3)AxF D R F FA C BD Ay F(b-1) 1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解和投影，并比较分力与力的投影。
解：〔a 〕，图〔c 〕：11 sin cos j i F ααF F += 分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
〔b 〕，图〔d 〕：分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y =投影：αcos 2F F x = ， )cos(2αϕ-=F F y 讨论：ϕ≠90°时，投影与分量的模不等。
1－2 试画出图a 、b 两情形下各物体的受力图，并进行比较。
比较：图〔a-1〕与图〔b-1〕不同，因两者之F R D 值大小也不同。
1－3 试画出图示各物体的受力图。
1y F x 1x F 1y F α1x F y F 〔c 〕2F 2y F 2y 2x 2x F 2y F F 〔d 〕习题1－4图习题1－3图1－4 图a 所示为三角架结构。
力F 1作用在B 铰上。
杆AB 不计自重，杆BD 杆自重为W 。
试画出图b 、c 、d 所示的隔离体的受力图，并加以讨论。
F AxF AyF D C B A B F 或(a-2) F B B AF D C A (a-1) B F AxF A Ay F B C(b-1)W F B DC Ay F AxF (c-1) F A F C BBF A或(b-2) αD A F A B CB FC F C AA F (e-1) Ax F A Ay F D F D C αF或(d-2)B F FCD B OOx F OyF W 1O F A(f-1)FA F D C AB B F (e-3) F AO Ox F OyF AW (f-2) A F 1O F A 1O (f-3) c F F A F D F B F A F AAx F C 'Cx F 'BF B AyF 'F Cy A(b-3)E F D F E D (a-3) CF F CE 'F E(a-2) 习题1－5图E EF B B F (b-2)CxF C CyF W T(b-1) B F B C 'C F D 'D F Ax F Ay F A (a-1)1－5 试画出图示结构中各杆的受力图。
工程力学 第二版 (范钦珊 唐静静 著) 高等教育出版社 课后答案 第10章 组合受力与变形杆件的强度计算
网
FP a2
ww w
5
.k hd
b
m
上表面
∴
σa 4 = σb 3
习题 10－7 图
和 ε 2 。证明偏心距 e与 ε1 、 ε 2 之间满足下列关系：
FP
网
ww w
e=
ε1 − ε 2 h × ε1 + ε 2 6
课
后 答
案
FP
M = FP e
习题 10－8 图
解：1，2 两处均为单向应力状态，其正应力分别为： 1 处：
第10章
组合变形与变形杆件的强度计算
10－1 根据杆件横截面正应力分析过程， 中性轴在什么情形下才会通过截面形心？试分析 下列答案中哪一个是正确的。 （A）My = 0 或 Mz = 0， FN ≠ 0 ； （B）My = Mz = 0， FN ≠ 0 ； （C）My = 0，Mz = 0， FN ≠ 0 ； （D） M y ≠ 0 或 M z ≠ 0 ， FN = 0 。 正确答案是 D 。 解：只要轴力 FN x ≠ 0 ， 则截面形心处其拉压正应力一定不为零， 而其弯曲正应力一定为零， 这样使其合正应力一定不为零，所以其中性轴一定不通过截面形心，所以答案选（D） 。 关于中性轴位置，有以下几种论述，试判断哪一种是正确的。 （A）中性轴不一定在截面内，但如果在截面内它一定通过形心； （B）中性轴只能在截面内并且必须通过截面形心； （C）中性轴只能在截面内，但不一定通过截面形心； （D）中性轴不一定在截面内，而且也不一定通过截面形心。 正确答案是 D 。 解：中性轴上正应力必须为零。由上题结论中性轴不一定过截面形心；另外当轴力引起的 拉（压）应力的绝对值大于弯矩引起的最大压（拉）应力的绝对值时，中性轴均不在截面内， 所以答案选（D） 。 并且垂 10－3 图示悬臂梁中， 集中力 FP1 和 FP2 分别作用在铅垂对称面和水平对称面内， 直于梁的轴线，如图所示。已知 FP1＝1.6 kN，FP2＝800 N，l＝1 m，许用应力 σ ＝160 MPa。 试确定以下两种情形下梁的横截面尺寸： 1．截面为矩形，h＝2b； 2．截面为圆形。
工程力学习题答案-范钦珊-蔡新着-工程静力学与材料力学-第二版
(a) (b) 习题1-1图 (a) (b) 习题1－2图FD R F ACBDAx F AyF(a-1) Ay F F B C A Ax F 'F C(a-2)C D F D R F(a-3)AxF F FA C BD Ay F(b-1) 1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解和投影，并比较分力与力的投影。
解：（a ），图（c ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ），图（d ）：分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y =投影：αcos 2F F x = ， )cos(2αϕ-=F F y 讨论：ϕ≠90°时，投影与分量的模不等。
1－2 试画出图a 、b 两情形下各物体的受力图，并进行比较。
比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。
1－3 试画出图示各物体的受力图。
1y F x 1F 1y F α1x F y F （c ）x F 2y F 2y 2x 2x F 2y F F （d ）习题1－3图1－4 图a 所示为三角架结构。
力F 1作用在B 铰上。
杆AB 不计自重，杆BD 杆自重为W 。
试画出图b 、c 、d 所示的隔离体的受力图，并加以讨论。
F Ax F AyF D C B A B F 或(a-2) F B F A F D C A (a-1) B F AxF AAy F C(b-1)W F B DC Ay F F (c-1) FF C B B F A或(b-2) αD A F A BCBFC F C A A F (e-1) Ax F A Ay FD F D C αF或(d-2)BF F C D B OOx F OyF W 1O F A(f-1)FA F D C AB B F 'F A O Ox F OyF AW (f-2) A 1F A 1O (f-3) c F F A F D F B F AF AAx F C 'CxF 'B F B Ay F 'F CyA (b-3)EF D F E D (a-3) C F F CE 'F E (a-2) 习题1－5图E EF B B F(b-2)Cx F C CyF W T(b-1) AyF Ax F 'BF 'C F C 'D F A D D F E F 'E F E BBF C F C D(c) F A G B F B C 'CF D 'D F Ax F AyF A1－5 试画出图示结构中各杆的受力图。
材料力学习题详解(范钦珊)第11章
在第 2 力系作用下，圆柱体上的任意点都处于三向等压应力状态σ1 = σ 2 = σ3 = −q 。因 此圆柱体两端面的相对线位移
3
Δ(q)
=
εx
×l
=
1 E
⎡⎣−q
−ν
(−q
1 2
⋅
l 4
⋅l ⎟⎞⎥⎤ ⎠⎦
=
ql 4 32EI
（↓）
习题 11－7a 图
题（b） 解： 1、画载荷引起的弯矩图 载荷引起的弯矩图，如图 11－7b（a）所示。
习题 11－7b 图 9
2、根据所要求的位移性质，建立单位载荷系统，画出单位载荷引起的弯矩图
确定θA 、ΔCy 的单位载荷引起的弯矩图分别如图 11－7b（b）、（c）所示。 3、弯矩图互乘
（2）
S 表面
S表面
于是，应用功的互等定理，有
由此解得
qΔV ( F ) = FΔ (q) = 1− 2ν Fql
E
ΔV ( F ) = 1− 2ν Fl
E
x
p
p
pz
（a）
(b)
习题 11－2 图
yp
习题 11－2 的解
11－3 具有中间铰的线弹性材料梁，受力如图 a 所示，两段梁的弯曲刚度均为 EI。用 莫尔法确定中间铰两侧截面的相对转角有下列四种分段方法，试判断哪一种是正确的。
⎟⎞ ⎠
+
⎜⎜⎝⎛
2⋅ 3
ql 2 8
⋅
l 2
⎟⎟⎠⎞⎥⎦⎤
=
5ql 4 384 EI
（↓）
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 .
eBook工程力学（静力学与材料力学）习题详细解答（教师用书）(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7－1 直径为d的圆截面梁，两端在对称面内承受力偶矩为M的力偶作用，如图所示。
若已知变形后中性层的曲率半径为ρ；材料的弹性模量为E。
根据d、ρ、E可以求得梁所承受的力偶矩M。
现在有4种答案，请判断哪一种是正确的。
习题7－1图(A) M＝Eπd 64ρ64ρ (B) M＝Eπd4Eπd3(C) M＝32ρ32ρ (D) M＝Eπd34 正确答案是。
7－2 关于平面弯曲正应力公式的应用条件，有以下4种答案，请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载；(B) 弹性范围内加载、载荷加在对称面或主轴平面内；(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内；(D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7－3 长度相同、承受同样的均布载荷q作用的梁，有图中所示的4种支承方式，如果从梁的强度考虑，请判断哪一种支承方式最合理。
l 5习题7－3图正确答案是7－4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm。
求：梁的1－1截面上A、 2B两点的正应力。
习题7－4图解：1. 计算梁的1－1截面上的弯矩：M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1－1截面上A、B两点的正应力：A点：⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点：⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127－5 简支梁如图所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
角钢(连结成一整体)。试确定梁与柱的工作安全因 数。
解：1．查型钢表得
习题 11－12 图
No.16aI：Iz = 1130cm4，Wz = 141cm3 2No. 63×63×5： A = 2 × 6.143 = 12.286 cm2
i y = 1.94cm I y = 2 × 23.17 = 46.34 cm
采用，欧拉公式计算临界力
FPcr = σ cr A =
轴的工作安全因数
2 π E
λ2
=
所以，轴不安全。
11－11 图示正方形桁架结构，由五根圆截面钢杆组成，
连接处均为铰链，各杆直径均为 d＝40 mm，a＝1 m。材料 均为 Q235 钢，E＝200 GPa，[n]st＝1.8。试；
网
ww w
.k hd 案
μ =1
co
界力。
m
11－5
图示 a、b、c、d 四桁架的几何尺寸、圆杆的横截面直径、材料、加力点及加力
方向均相同。关于四桁架所能承受的最大外力 FPmax 有如下四种结论，试判断哪一种是正确 的。 （A）FPmax(a)=FPmax(c)<FPmax(b)=FPmax(d)； （B）FPmax(a)=FPmax(c)=FPmax(b)=FPmax(d)； （C）FPmax(a)=FPmax(d)<FPmax(b)=FPmax(c)；
案
对于 A3 钢， λ P = 102,
λs = 61.6 。因此，第一杆为大柔度杆，第二杆为中柔度杆，
网
i μl λ2 = 2 i μl λ3 = 3 i
λ1 =
=
ww w
FPcr = ( a − bλ ) A = (304 − 1.12 × 62.5) × 10 3 ×
第三杆的临界力
.k hd
π × 160 Байду номын сангаас × 10 −6
m
-F P
2 FP
FP
案
FP
0
0
0
0
0
-F P -F P
0
11－6
（A）减小杆长，减小长度系数，使压杆沿横截面两形心主轴方向的长细比相等； （B）增加横截面面积，减小杆长； （C）增加惯性矩，减小杆长； （D）采用高强度钢。 解：由细长杆临界力公式： FPcr = 差别不大。正确答案是 A 。 正确答案是
4
2．梁为静不定问题，由变形谐调条件，得：
课
q=24 kN/m。竖杆为两根 63 mm×63 mm×5 mm 等边
后 答
*11－12 图示结构中，梁与柱的材料均为 Q235
案
网
1 π3 E 1 × × × 402 × 10 −6 1.8 141.42 4 = 68.9 × 10−3 MN = 68.9 kN
2．校核托架是否安全
当已知工作载荷为 70kN 时 由（1） ， FAB =
nw =
6 7 FP = 158.7 kN
3．横梁为 No.18 普通热轧工字钢，[σ]＝160Mpa，计算托架所能承受的最大载荷
条件 [σ ] = 160MPa 意谓着既要保证 CD 强度，又要保证 AB 杆稳定。
CD 梁中：
第 11 章
压杆的稳定性问题
11－1 关于钢制细长压杆承受轴向压力达到临界载荷之后， 还能不能继续承载有如下四 种答案，试判断哪一种是正确的。 （A）不能。因为载荷达到临界值时屈曲位移将无限制地增加； （B）能。因为压杆一直到折断时为止都有承载能力； （C）能。只要横截面上的最大正应力不超过比例极限；
co
m
所以， σ cr
− A 不存在线性关系， [ FP ] = σ cr A 与面积 A 之间为非线性关系。所以，正确
[ n]st
2．若已知工作载荷 FP＝70 kN，并要求杆 AB 的稳定安全因数[n]st=2.0，校核托架是否 安全。 3．若横梁为 No.18 普通热轧工字钢，[σ]＝160Mpa，则托架所能承受的最大载荷有没 有变化？
0.3FP 185 × 10 −8
FP ≤ 73.5kN<FPcr = 118kN
所以，托架所能承受的最大载荷为 73.5kN。
11－10 长 l＝50 mm，直径 d＝6 mm 的 40 Cr 钢制微型圆轴，在温度为 t1＝－60º C 时
安装，这时轴既不能沿轴向移动，又不承受轴向载荷，温度升高时，轴和架身将同时因热膨
课
FPcr =
7 × 267.4 kN = 118kN 6
267.4 = 1.685 < [ n ]st ，不安全。 158.7
M max = M B = 0.3FP ，
6
后 答
2 π = 212.8 × × 40 ×10−3 4 = 0.2674MN = 267.4 kN
(
案
网
)
ww w
σ cr = 304 − 1.14 λ = 304 − 1.14 × 80
(
3．确定工作安全因数
F 462.7 nw = Pcr = = 2.77 167 FP
.k hd
)
2
aw .
习题 11－8 图 5 习题 11－9 图
答案是 D 。
11－9 图示托架中杆 AB 的直径 d＝40 mm。长度 l＝
800 mm。两端可视为球铰链约束，材料为 Q235 钢。试： 1．求托架的临界载荷。
课
提高钢制细长压杆承载能力有如下方法．试判断哪一种是最正确的。
后 答
习题 11-5 解图
A
。
π 2 EI min
(μl )2
中各量可知；另外各种钢的弹性模量 E 值
4
11－7 根据压杆稳定设计准则，压杆的许可载荷 [FP ] =σcr A 。当横截面面积 A 增加一倍
[n]st
时，试分析压杆的许可载荷将按下列四种规律中的哪一种变化？ （A）增加 1 倍； （B）增加 2 倍； （C）增加 l／2 倍； （D）压杆的许可载荷随着 A 的增加呈非线性变化。 解：由于 i =
co
m
正确答案是
C
。
5l i 4.9l （b） λb = i 4.5l （c） λc = i
（a） λ a = （d） λ d =
( μ = 1)
( μ = 0.7) ( μ = 0.5)
4l i
( μ = 2)
可见 λ a > λb > λc > λ d ，故（a）最容易失稳， （d）最不容易失稳。
40Cr 钢的σp＝300 MPa，E＝210 GPa。若规定轴的稳定工作安全因数[n]st＝2.0，并且忽略架
后 答
案
网
解：温升时， α 1 > α 2 使轴受压力 FN。这是轴向载荷作用下的静不定问题。
变形谐调条件为：
课
α 1 (t 2 − t1 )l −
FN l = α 2 (t 2 − t1 )l EA
对于 AB 等压杆，需进行稳定计算：
λ=
则
8
课
μl 1× 1000 = = 100 < λp = 101 40 i 4
后 答
aw .
π2 = 1.645 < [ n ]st = 2 1002 × 0.5 ×10 −5 × 120
co
nw =
FPcr π 2 EA = 2 FN λ ( α1 − α2 )( t2 − t1 ) EA
.k hd
d = 10 mm 4 μl 1 × 800 λ= = = 80 < λ P ，中长杆 i 10 i=
aw .
co
m
(a)
FNx = FAB cos θ =
3 cot θ ⋅ FP ， 2
FQ = FP
σ max =
M B FNx + ≤ [σ ] ， W A
3 cot θ ⋅ FP ≤ 160 × 10 6 ， + 2 30.6 × 10 − 4
11－4
三根圆截面压杆的直径均为 d=160mm，材料均为 A3 钢，E＝200GPa，σs＝
240MPa。已知杆的两端均为铰支，长度分别为 l1、l2 及 l3，且 l1=2l2=4l3=5m。试求各杆的临
第三杆为小柔度杆。
于是，第一杆的临界力
课
FPcr = σ cr A =
第二杆的临界力
后 答
π 2 E πd 2 π 3 × 200 × 10 6 × 160 2 × 10 −6 = 2540 kN = 125 2 × 4 λ2 4
2 ， 解：只有当二压杆的柔度 λ ≥ λP 时，才有题中结论。这是因为，欧拉公式 FPcr = π EI ( μl ) 2
2
kh
11－2 今有两根材料、 横截面尺寸及支承情况均相同的压杆． 仅知长压杆的长度是短压 杆的长度的两倍。试问在什么条件下短压杆临界力是长压杆临界力的 4 倍?为什么?
da
w.
m
π FABcr = ( a − bλ ) A = ( 304 − 1.14 × 100 ) × × 402 × 10 4
−6
= 0.2387 MN = 238.7 kN
FPcr = 2 FAB = 2 × 238.7kN = 337.6 kN
[ FP ] =
FPcr 337.6 = = 187.6 kN [ n]st 1.8
习题 11－11 图
l．求结构的许可载荷；
2．若 FP 力的方向与 1 中相反，问：许可载荷是否改变，若有改变应为多少？
解：
（1）由静力平衡得到： 1．
F AB = F AD = FBC = FCD = 2 FP （压） 2
FDB = FP（拉）
（2）对于拉杆 BC，由强度条件，有