《工程力学》课后习题解答
(完整版)工程力学课后详细答案
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故：22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+= 方向沿OB 。
2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。
（a ） 由平衡方程有：0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=（拉力）1.155AC F W=（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=（拉力）0.364AC F W=（压力）（c ） 由平衡方程有：0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=（压力）（d ） 由平衡方程有：0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解：（a ）受力分析如图所示：由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解：受力分析如图所示：由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式，得：22.410RA RB F KN F KN==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力）列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得： 5RD F Q =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。
大学《工程力学》课后习题解答-精品
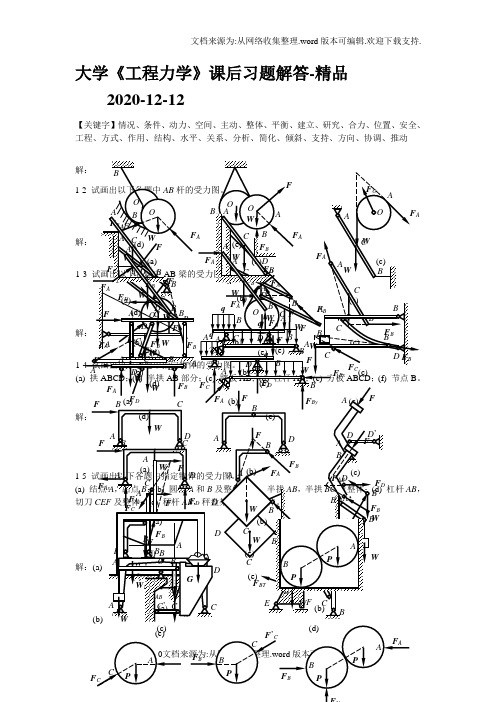
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。
解：(1) 取整体(2) 2-4 在简支梁，力的大小等于20KN ，如图所示。
若解：(1)(2)求出约束反力：2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计，图中的长度单位为cm 。
已知F =200 N ，试求支座A 和E 的约束力。
解：(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解：（1）取铰链B (2) 取铰链C 由前二式可得：F FF ADF2-9 三根不计重量的杆AB，AC，AD在A点用铰链连接，各杆与水平面的夹角分别为450，，450和600，如图所示。
试求在与O D平行的力F作用下，各杆所受的力。
已知F=0.6 kN。
解：(1)间汇交力系；(2)解得：AB、AC3-1 已知梁AB 上作用一力偶，力偶矩为M ，梁长为l ，梁重不计。
求在图a ，b ，c 三种情况下，支座A 和B 的约束力解：(a) (b) (c) 3-2 M ，试求A 和C解：(1) 取 (2) 取 3-3 Nm ，M 2解：(1)(2) 3-5 大小为AB 。
各杆 解：(1)(2)可知：(3) 研究OA 杆，受力分析，画受力图：列平衡方程：AB A3-7 O1和O2圆盘与水平轴AB固连，O1盘垂直z轴，O2盘垂直x轴，盘面上分别作用力偶（F1，F’1），（F2，F’2）如题图所示。
《工程力学》课后习题与答案全集
由 ，作出速度平行四边形，如图示：
即：
7．图示平行连杆机构中， mm, 。曲柄 以匀角速度 2rad/s绕 轴转动，通过连杆AB上的套筒C带动杆CD沿垂直于 的导轨运动。试示当 时杆CD的速度和加速度。
解：取CD杆上的点C为动点，AB杆为动系。对动点作速度分析和加速度分析，如图（a）、（b）所示。图中：
解：设该力系主矢为 ，其在两坐标轴上的投影分别为 、 。由合力投影定理有：
=-1.5kN
kN
kN
；
由合力矩定理可求出主矩：
合力大小为： kN，方向
位置： m cm，位于O点的右侧。
2．火箭沿与水平面成 角的方向作匀速直线运动，如图所示。火箭的推力 kN与运动方向成 角。如火箭重 kN，求空气动力 和它与飞行方向的交角 。
(d)由于不计杆重，杆AB在A、C两处受绳索作用的拉力 和 ，在B点受到支座反力 。 和 相交于O点，
根据三力平衡汇交定理，
可以判断 必沿通过
B、O两点的连线。
见图(d).
第二章力系的简化与平衡
思考题：1.√;2.×;3.×;4.×;5.√;6.×;7.×;8.×;9.√.
1．平面力系由三个力和两个力偶组成，它们的大小和作用位置如图示，长度单位为cm，求此力系向O点简化的结果，并确定其合力位置。
则
（mm/s）
故 =100（mm/s）
又有： ，因
故：
即：
第四章刚体的平面运动
思考题
1．×；2.√; 3.√;4.√;5.×.
习题四
1．图示自行车的车速 m/s,此瞬时后轮角速度 rad/s,车轮接触点A打滑，试求点A的速度。
工程力学课后习题答案解析
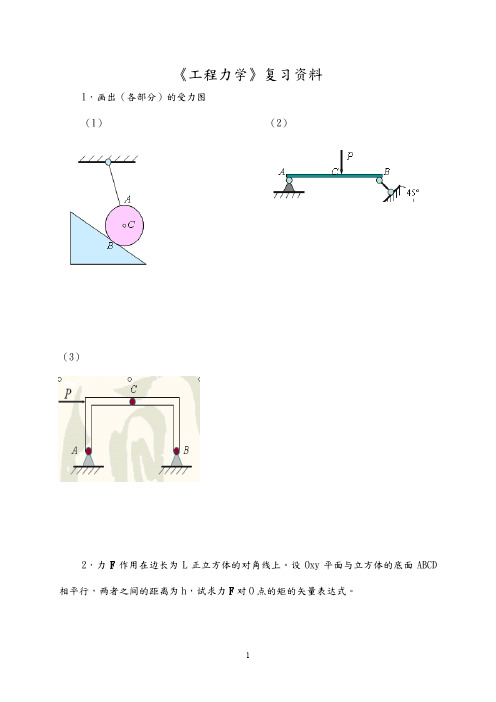
《工程力学》复习资料1．画出（各部分）的受力图（1）（2）（3）2．力F作用在边长为L正立方体的对角线上。
设Oxy平面与立方体的底面ABCD 相平行，两者之间的距离为h，试求力F对O点的矩的矢量表达式。
解：依题意可得：ϕθcos cos ⋅⋅=F F xϕθsin cos ⋅⋅=F F y θsin ⋅=F F z 其中33sin =θ 36cos =θ 45=ϕ 点坐标为：()h l l ,, 则()3)()(3333333j i h l F k F j F i F F M +⋅+=-+-= 3．如图所示力系由F 1，F 2，F 3，F 4和F 5组成，其作用线分别沿六面体棱边。
已知：的F 1=F 3=F 4=F 5=5kN, F 2=10 kN ，OA=OC/2=1.2m 。
试求力系的简化结果。
解：各力向O 点简化 0.0.0.523143=-==-==+-=C O F A O F M C B F A O F M C O F C O F M Z Y X 即主矩的三个分量 kN F F Rx 55==kN F F Ry 102==kN F F F F RZ 5431=+-=即主矢量为: k j i 5105++合力的作用线方程 Z y X ==24．多跨梁如图所示。
已知：q=5kN ，L=2m 。
试求A 、B 、D 处的约束力。
取CD 段0=∑ci M 0212=-⋅ql l F D 解得 kN F D 5=取整体来研究，0=∑iy F02=+⋅-+D B Ay F l q F F 0=∑ix F 0=Ax F0=∑iAM 032=⋅+⋅-⋅l F l ql l F D B 联合以上各式，解得 kN F F Ay A 10-== kN F B 25=5．多跨梁如图所示。
已知：q=5kN ，L=2m ，ψ=30°。
试求A 、C 处的约束力。
（5+5=10分）取BC 段0=∑iy F0cos 2=⋅+⋅-ϕC B F l q F 0=∑ix F 0sin =⋅-ϕC Bx F F0=∑icM 022=⋅⋅+⋅-l l q l F By联合以上各式，解得 kN F Bx 77.5= kN F By 10= kN F C 574.11=取整体研究0=∑ix F0sin =⋅-ϕC Ax F F 0=∑iy F 0cos 2=⋅+⋅-ϕC Ay F l q F0=∑iAM 04cos 32=⋅⋅+⋅⋅-l F l l q M C A ϕ 联合以上各式，解得 kN F Ax 774.5= kN F Ay 10= m kN M A ⋅=406．如图无底的圆柱形容器空筒放在光滑的固定地面上，内放两个重球。
(完整版)工程力学课后详细答案
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故：22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+= 方向沿OB 。
2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。
（a ） 由平衡方程有：0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=（拉力）1.155AC F W=（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=（拉力）0.364AC F W=（压力）（c ） 由平衡方程有：0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=（压力）（d ） 由平衡方程有：0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解：（a ）受力分析如图所示：由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解：受力分析如图所示：由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式，得：22.410RA RB F KN F KN==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力）列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得： 5RD F Q =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。
工程力学课后习题解答
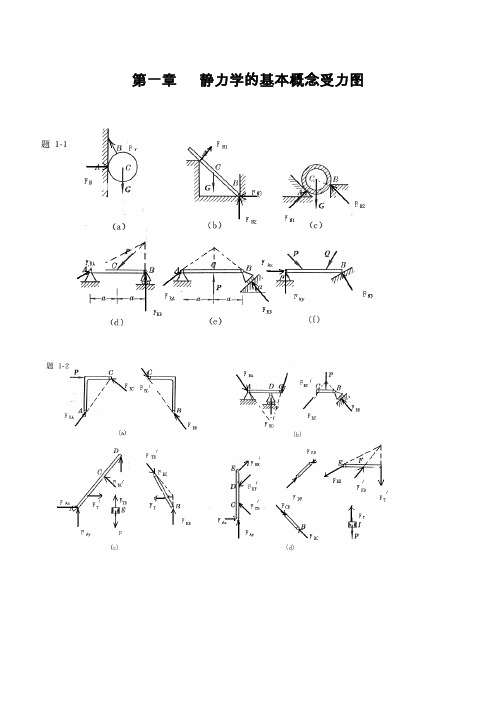
1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)BA(a)(b) A(c)A(d)A(e)B(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。
(d)(e)B(a)B(b)(c)F BF(a)W (c)AF (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。
解：(a)AF (b)WA (c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b) CB(c)BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。
解：(a)(d)F CD(e)WB(f)F ABF BC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)FCAAC’CDDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点，如图所示。
如不计刚架重量，试求支座A 和D 处的约束力。
解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.1222D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。
(完整版)工程力学课后习题答案
工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
（a）（b）（c）2 第一章静力学基础（d）（e）（f）（g）第一章静力学基础 3 1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计，各物自重除图中已画出的外均不计。
（a）第一章静力学基础 5 （b）（c）（d）6 第一章静力学基础（e）第一章静力学基础7 （f）（g）8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。
梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如第二章 平面力系 9图所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。
电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。
大学《工程力学》课后习题解答
1-1试画出以下各题中圆柱或圆盘的受力图,与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。
解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b) CB(c)BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。
解：(a)(d) FC(e)WB (f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点，如图所示。
如不计刚架重量，试求支座A 和D 处的约束力。
解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.1222D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。
《工程力学》详细版习题参考答案
∑ Fx
=FAx
+
FBx
+
FCx
=− 1 2
F
+
F
−
1 2
F
=0
∑ Fy
= FAy
+
FBy
+
FCy
= − 3 2
F
+
3 F = 0 2
∑ M B= FBy ⋅ l=
3 Fl 2
因此，该力系的简化结果为一个力偶矩 M = 3Fl / 2 ，逆时针方向。
题 2-2 如图 2-19（a）所示，在钢架的 B 点作用有水平力 F，钢架重力忽 略不计。试求支座 A，D 的约束反力。
（a）
（b）
图 2-18
解：（1）如图 2-18（b）所示，建立直角坐标系 xBy。 （2）分别求出 A，B，C 各点处受力在 x，y 轴上的分力
思考题与练习题答案
FAx
= − 12 F ，FAy
= − 3 F 2
= FBx F= ，FBy 0
FCx
= − 12 F ，FCy
= 3 F 2
（3）求出各分力在 B 点处的合力和合力偶
（3）根据力偶系平衡条件列出方程，并求解未知量
∑ M =0 − aF + 2aFD =0
《工程力学》
可解得 F=Ay F=D F /2 。求得结果为正，说明 FAy 和 FD 的方向与假设方向相同。 题 2-3 如 图 2-20 （ a ） 所 示 ， 水 平 梁 上 作 用 有 两 个 力 偶 ， 分 别 为
3-4 什么是超静定问题？如何判断问题是静定还是超静定？请说明图 3-12 中哪些是静定问题，哪些是超静定问题？
（a）
(完整word版)《工程力学》课后习题解答
1—1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)(e)A(a)(b) A(c)A(d)(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。
解:(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)FWA1—4 试画出以下各题中指定物体的受力图。
（a) 拱ABCD ；(b) 半拱AB 部分；(c ） 踏板AB;(d) 杠杆AB;（e ） 方板ABCD;（f ） 节点B 。
解：(d)D(e)F Bx(a)(b)(c)(d)(e)W(f)(a)D(b) CB(c)BF DF CBF F BC1-5 试画出以下各题中指定物体的受力图。
（a) 结点A ，结点B ；（b) 圆柱A 和B 及整体；（c) 半拱AB ，半拱BC 及整体；（d ） 杠杆AB ,切刀CEF 及整体；(e ） 秤杆AB ，秤盘架BCD 及整体。
解：（a ）（b ）(c ）(c)(d)ATFBAF(b)D(e)(d ）（e)’CB2—2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接,如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解:（1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，（2） 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2—3 水平力F 作用在刚架的B 点，如图所示.如不计刚架重量，试求支座A 和D 处的约束力。
解：(1) 取整体ABCD 为研究对象，受力分析如图,画封闭的力三角形：(2）F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o的力F ，力的大小等于20KN ，如图所示。
工程力学课后习题答案(-章 版本2)
3.3 图3.3所示钢架的点B 作用一个水平力F ，钢架重量忽略不计。
求支座A 、D 的约束力。
解：由图3.3可以确定D 点受力的方向，这里将A 点的力分解为x 、y 方向，如图3.3.1根据力与矩平衡有0)2(:)(0:)(0:)(=-=-=-∑∑∑FL L F A M F F y F F F x F Dy D x （1）解上面三个方程得到)(2),(2),(↑=↓=←=F F F F F F D y x3.5如图3.5铰链四杆机构ABCD 的CD 边固定，在铰链A 、B 处有力F1、F2作用，如图所示。
该机构在图示位置平衡，杆重忽略不计。
求力F1和力F2的关系。
解：（1）对A 点分析，如图3.5.1，设AB 杆的内力为T ，则将力投影到垂直于AC 方向的AM 上有0)15cos()30cos(:)(1=︒-︒∑T F AM F ① 图3.5（2）对B 点分析，如图3.5.2，将力投影到垂直于BD 方向的BN 有0)30cos()60cos(:)B N (2=︒-︒∑T F F ②由①、②可得22108593790.64395055332F F F ≈+=3.8如图3.8有5根杆件组成的结构在A 、B 点受力，且CA 平行于DB ，CA DE BE DB ===。
F=20kN,P=12kN 。
求BE 杆的受力。
解：（1）对A 点受力分析，将力投影到垂直于AC 方向的AN 上有 060sin :)(=-︒∑F F AN F AB ①（2）对B 点受力分析，如图3.8.2.将力投影到垂直于BD 方向的BM 上有060cos 60sin 30cos :)B M (=︒-︒-︒∑P F F F BE AB ②由①、②可得373095kN 16.1658075kN 328≈=BE F （方向斜向上）3.9如图（见书上）所示3根杆均长2.5m ，其上端铰结于K 处，下端A 、B 、C 分别与地基铰结，且分布在半径r=1.5m 的圆周上，A 、B 、C 的相对位置如图所示。
工程力学课后答案
工程力学课后答案第一题题目：一辆汽车以60km/h的速度在平直的公路上匀速行驶，车辆的质量是1000kg。
求汽车行驶过程中受到的摩擦力是多少？答案：根据牛顿第二定律，我们知道力的大小等于质量乘以加速度。
由于汽车匀速行驶，所以加速度为零。
因此，汽车行驶过程中受到的摩擦力也必须为零。
第二题题目：一根长为3m、截面积为4平方米的杆子，顶端受力5N，底端受力3N。
求杆子的弯曲应力。
根据力的定义，力等于压力乘以面积。
所以，杆子顶端的压力是5N/4平方米，底端的压力是3N/4平方米。
由于杆子是一维杆，所以弯曲应力等于顶端的压力减去底端的压力，即5N/4平方米 - 3N/4平方米 = 2N/4平方米 = 0.5N/平方米。
第三题题目：一个质量为2kg的物体从高度为10m的地方自由下落，求物体下落的速度。
答案：根据重力势能转化为动能的定律，我们知道物体的重力势能等于物体的质量乘以重力加速度乘以物体的高度，即mgh。
在物体自由下落的过程中，重力势能转化为动能，所以mgh = 1/2mv²，其中v是物体下落的速度。
解这个方程，我们可以得到v = √(2gh) = √(2 × 9.8 × 10) ≈ 14m/s。
题目：一个质量为0.5kg的物体水平受到一个10N的力，物体的初始速度是4m/s，求物体行驶了多长时间之后速度变成6m/s。
答案：根据牛顿第二定律，我们知道力等于质量乘以加速度。
所以，加速度等于10N/0.5kg = 20m/s²。
我们可以使用加速度的定义来求解这个问题：a = (v - u) / t，其中v是物体的最终速度，u是物体的初始速度，t是时间。
将已知条件代入方程，我们可以得到20m/s² = (6m/s - 4m/s) / t。
解这个方程，我们可以得到t = (6m/s - 4m/s) / 20m/s² = 0.1秒。
第五题题目：一个质量为10kg的物体放在一个倾斜角度为30度的斜面上，斜面的摩擦系数为0.2。
工程力学课后答案
工程力学课后答案篇一：工程力学习题解答(详解版)工程力学答案详解1-1试画出来以下各题中圆柱或圆盘的受到力图。
与其它物体碰触处的摩擦力均省略。
b(a)(b)a(d)(e)解：aa(a)(b)a(d)(e)1-2试画出来以下各题中ab杆的受到力图。
(a)(b)(c)a(c)(c)(d)解：b(a)(b)(c)bb(e)1-3试画出来以下各题中ab梁的受到力图。
f(a)(b)(c)(d)(e)求解：d(d)(a)(b)fw(c)fbx(e)1-4试画出来以下各题中选定物体的受到力图。
(a)拱abcd；(b)半拱ab部分；(c)踏板ab；(d)杠杆ab；(e)方板abcd；(f)节点b。
解：(a)(b)(c)bfdb(d)(e)(f)(a)dw(b)(c)1-5试画出来以下各题中选定物体的受到力图。
(a)结点a，结点b；(b)圆柱a和b及整体；(c)半拱ab，半拱bc及整体；(d)杠杆ab，切刀cef及整体；(e)秤杆ab，秤盘架bcd及整体。
(b)(c)(e)解：(a)atfc(d)(e)fbc(f)w(d)ffba(b)(c)ac(d)’c(e)dbacdc’篇二：工程力学课后习题答案工程力学学学专学教姓习册校院业号师名练第一章静力学基础1-1画出下列各图中物体a，构件ab，bc或abc的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
（a）（b）（c）（d）（e）（f）（g）1-2试画出图示各题中ac杆（带销钉）和bc杆的受力图（a）（b）（c）（a）1-3图画Theil中选定物体的受到力图。
所有摩擦均数等，各物蔡国用除图中已图画出来的外均数等。
（a）篇三：工程力学习题及答案1.力在平面上的投影（矢量）与力在坐标轴上的投影(代数量)均为代数量。
正确2.力对物体的促进作用就是不能在产生外效应的同时产生内效应。
错误3.在静力学中，将受力物体视为刚体（d）a.没特别必要的理由b.是因为物体本身就是刚体c.是因为自然界中的物体都是刚体d.是为了简化以便研究分析。
(完整版)工程力学课后习题答案
工程力学练习册学校 ______________学院 _______________专业 ______________学号 _______________教师 _______________姓名 ______________第一章静力学基础1-1画出下列各图中物体A,构件AB, BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
1-3画出图中指定物体的受力图。
所有摩擦均不计，各物自重除图中已画出的外均不计。
(1 J AB杆(2)CTJff(3)整体(1 ) K段槊(2) CD段梁r 3)鹫佐t 1)滑轮日⑵ABff(3) DF 样C I 】CDW⑵曲杵⑶CA杵(e)t 1，直(并tlikkiv t n OA IT(g)第二章平面力系2-1电动机重P=5000N,放在水平梁AC的中央，如图所示。
梁的A端以皎链固定，另一端以撑杆BC支持，撑杆与水平梁的夹角为30 °。
如忽略撑杆与梁的重量，求绞支座A、B处的约束反力。
F x0, F B CO S30F A COS300F y0, F A sin30F B sin30P解得：F A F B P5000N2-2 物体重P=20kN，用绳子挂在支架的滑轮B上，绳子的另一端接在绞车D上，如图所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为皎链连接。
当物体处于平衡状态时，求拉杆 AB 和支杆BC 所受的力。
2-3如图所示，输电线 ACB 架在两电线杆之间，形成一下垂线，下垂距离 CD=f=1m, 两电线杆间距离 AB=40m 。
电线ACB 段重P=400N,可近视认为沿 AB 直线均匀分布，求电 线的中点和两端的拉力。
F x0, F AB F BC F y0, F BC sin 30 解得：F BC 3.732P F AB 2.732Pcos30 Psin30 0 Pcos30 P 0F x 0,F A COS F C,F y 0, F A Sin F Gtan 1/10解得：F A 201NF C 2000 N2-4 图示为一拔桩装置。
工程力学课后习题答案(单辉祖著)
工程力学课后习题答案(单辉祖著)工程力学课后习题答案(单辉祖著)在工程力学课程中，习题是提高学生运用理论知识解决实际问题的有效途径。
然而，在自学过程中，学生常常会遇到一些困难和疑惑。
为了帮助同学们更好地掌握工程力学的知识，我将为大家提供工程力学课后习题的答案和详细解析，希望能够对大家的学习有所帮助。
1. 第一章：静力学1.1 问题1：答案：根据平面力系统的平衡条件，可以将每个力分解为水平力和垂直力的分量，然后通过求和计算每个方向上的合力和力矩。
使用力学平衡方程，可以解得所需的未知量。
1.2 问题2：答案：该问题是一个平面力系统的静力平衡问题。
通过绘制自由体图，在各个方向上应用平衡条件，计算出所需的未知量。
2. 第二章：静力学2.1 问题1：答案：根据刚体受力平衡的条件，可以通过求和计算每个力的合力和力矩，并解得所需的未知量。
2.2 问题2：答案：该问题是一个刚体受力平衡的问题。
通过绘制刚体的自由体图，在各个方向上应用平衡条件，计算出所需的未知量。
3. 第三章：运动学3.1 问题1：答案：根据物体的运动规律，可以利用位置、速度和加速度之间的关系，通过计算得到所需的未知量。
3.2 问题2：答案：该问题是一个物体运动规律的问题。
根据已知条件，计算物体的加速度、速度和位置等参数。
4. 第四章：动力学4.1 问题1：答案：根据牛顿第二定律和动量定理，利用所给条件计算物体的加速度、速度和位置等参数。
4.2 问题2：答案：该问题是一个物体的动力学问题。
根据已知条件，应用动力学定律，计算所需的未知量。
5. 总结与展望通过解答上述习题，我们可以更深入地理解和应用工程力学的知识。
在解题过程中，我们不仅要熟练掌握理论知识，还需要运用数学工具进行计算和分析。
希望同学们在学习过程中能够勤思考、勤问问题，并结合实际进行练习，以提高解决实际问题的能力。
通过学习工程力学，在实际工程中可以更好地应用科学知识，并解决现实生活中的问题。
完整版工程力学课后习题答案主编佘斌
4-1试求题4-1图所示各梁支座的约束力.设力的单位为kN,力偶矩的单位为 kN m,长度 单位为m,分布载荷集度为kN/m.(提示：计算非均布载荷的投影和与力矩和时需应用积分).M= 3A A ^解:(b): (1)整体受力分析,画出受悖20 (平面任意力系)；20」y n 1M =8口' M A (F )=0:-2 0.8 0.5 1.6 0.4 0.7 F B2 = 0F B=0.26 kN“ F y =0： F Ay -2 0.5 F B =0F Ay =1.24 kNXM B (F )=0:-F Ay 3-3 q 2 dx X = 0F Ay = 0.33 kN(c)30o(2)3A「J 0.80I8F A y选坐标系Axy ,列出平衡方斗.0.8 F X= 0:-F A X0.4 =0F A X=0.4 kN(60.8FB0.4q =2AF AX约束力的方向如下列图.(c): (1)研究AB 杆,受力分析,画出受力图 (平面任意力系);(2)选坐标系x(2)C选坐标系Cxy,列出平衡方程；F eR I 才x dxM e (F ) =0:aOq dx x MF D=5 kNa£ F y =0: F e - 0oqMdx-F D =0F e = 25 kN研究ABC 杆,受力分析,画出受力图(平面平行力系); AF A,y qdxjita qlx2“ F y =0: F Ay - o 2 dx F Bcos30o =0F B= 4.24 kN'、：F x =0：F AX - F B sin30o=0F Ax =2.12 kN约束力的方向如下列图.(e): (1)研究CABD 杆,受力分析,画出受力图 (平面任意力系);20Mdx y" F x =0:F AX =00.8% M A(F ) -0:0 20 dx x 8 F B1.6-202.4-0F B=21 kN0.8“ F y =0:- o 20 dx F Ay F B -20 =0F Ay =15 kN约束力的方向如下列图.4-16由AC 和CD 构成的复合梁通过钱链 C 连接,它的支承和受力如题 4-16图所示. 均布载荷集度q=10 kN/m ,力偶M=40 kN m, a=2 m ,不计梁重,试求支座 A 、B 、D 的约 束力和钱链C 所受的力."yqdx q --1 r J(2) q =20 C dx选坐标系Axy ,列出平衡方旭3M =8I [F AX r20x0.8F A y0.8二B D0.8 f F B0.8解: (1)研究CD 杆,受力分析-画出义力图(平面平行力票*T ； FF A=35 kNa’F y =0:-F A - 0 q dx F B -F C =0F B=80 kN约束力的方向如下列图.4-17刚架ABC 和刚架CD 通过钱链C 连接,并与地面通过钱链 A 、B 、D 连接,如题4-17M A (F )=0:-100 6-,〔q dx x F B 6=0F B=120 kN5F y =0:fy - 1 q dx F B =0F Ay = 80 kN约束力的方向如下列图.(b): (1)研究CD 杆,受力分析,画出受力图 (平面任意力系);(4) 选坐标系Bxy,列出平衡方程;aM B (F )=0: F A a-° q dx x - F C a = 0图所示,载荷如图,试求刚架的支座约束力 (尺寸单位为m,力的单位为 kN , 载荷集度单位为 kN/m).解:(a)： (2)脸q =103y F =50喧Dlf t=FD=0 ;(1)研究苗杆7十日⑶Z例眄引艮那 D 点的约k 性质,gr 知:(2)选C 点为矩心,列出平衡方程;3M C (F )=0:- Q q dx x F D 3=0“ F x =0： F AX -50-0F Ax =50 kN3% M B(F )=0:-F Ay 6- o q dx x F D 3 50 3 = 0F Ay = 25 kN3Z F y =0: F Ay - j 0 qMdx-F B +F D =0F B=10 kN约束力的方向如下列图.8-5图示阶梯形圆截面杆,承受轴向载荷 F1=50 kN 与F2作用,AB 与BC 段的直径分别为 d1=20 mm 和d2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷350 10 =159.2 MPa 12研究整体, F D=15 kN 受力分析,|画出受力图(平面维聿相人(4) 选坐标系 Bxy ,列出平衡方程;F2之值.解: F N I(1)用截面法求出1-1、2-2截面的轴力;=F IF N 2 =F I F 2(2)求 1-1、2-2截面的正应力,利用正应力相同;一二0.02450 103 F 2-1 =159.2 MPa 12—二0.0324= 62.5 kN8-15图示桁架,杆1为圆截面钢杆,杆2为方截面木杆,在节点 A 处承受铅直方向的载荷解：(1)对节点A 受力分析,求出 AB 和AC 两杆所受的力;F AC= 2F =70.7kN F AB=F =50kN(2)运用强度条件,分别对两杆进行强度计算;50 10 —t S 160MPa 12 一d4 所以可以确定钢杆的直径为20 mm,木杆的边宽为 84 mm.11-6图示悬臂梁,横截面为矩形,承受载荷F1与F2作用,且F1=2F2=5 kN ,试计算梁内 的最大弯曲正应力,及该应力所在截面上K 点处的弯曲正应力.F 作用,试确定钢卞f 的直径d 与木杆截面的边宽 b.载荷F=50 kN,钢的许用应力[d S]=160d 一 20.0mmABACFACA 270.7 103bk W I 10MPa b _ 84.1mmMPa,木的许用应力[y边的纵向正应变 £ =3.0 X 钝,试计算梁内的最大弯曲正应力,钢的弹性模量 E=200 Gpa,(1)求支反力3… — _qa R B 4(2)画内力图maxW ZMmaxbh 67.5 1062 =176 MPa 40 80K 点的应力:MmaxMmax ybh 3 7.5 1 063040 803二 132 MPa11-8图示简支梁,由 1212No28工字钢制成,在集度为 q 的均布载荷作用下,测得横截面 C 底 a=1 m.解: R A解：(1)画梁的弯矩图Mmax(3)由胡克定律求得截面 C下边缘点的拉应力为:4-9_= 3.0 10 — 200 10 =60 MPa 也可以表达为:CJmax M cW2qa4W z(4) 梁内的最大弯曲正应力:--maxc 29qaMmax 329 .= T「c max =67.5 MPa811-14图示槽形截面悬臂梁,F=10 kN , Me=70 kNm ,［司=120 MPa ,试校核梁的强度.许用拉应力［(H=35 MPa,许用压应力100 253m50MSj_z c解: (1)截面形心位置及惯性矩:200y cA1y l A2 y2 (150 250) 125 (-100 200) 150A i A2 (150 250) (-100 200)=96 mmI zC150 50312225 2003(150 50) (yc-25)2 2 12(25 200) (150- y C )2= 1.02 108mm4(2)画出梁的弯矩图(3)计算应力A+截面下边缘点处的拉应力及上边缘点处的压应力分别为:A-截面下边缘点处的压应力为可见梁内最大拉应力超过许用拉应力,梁不平安.9.16图示圆越面轴-3与丑C 段的直径分别为由与刈,且由=4比W,试求轴内的最大切应力与截面C 的转角,并画出轴外表母线的位移情况,材料的切变模量为G.解:(11画轴的扭矩图:(2)求最大切应力!九 2"工W _115M比较得.M A. <250- y c )A =C40 106 (250 -96)1.02 108= 60.4 MPaCT n = AI zCM A y c 40 106 961.02 108= 37.6MPaM A_(250-y c )c30 106(250-96)1.02 108= 45.3 MPa(3)求C截面的转角；M M MT“C L3 g" (〃m3-1图示硬铝试样,厚度<5=2mm, 的作用下,测得试验段伸长△/=0.l5mm, 泊松比〃•16M'皿莉X2A/Z Ml 16.6 Ml"GL半f G 1 ".娘32 I 3 J 32试验段板宽/>=20mm,标即/=7(hnm°在轴向拉户=6kN 板宽缩短AA0.014mni,试计算帙铝的弹性模量E与/ .g_4L- bA/ = —得5 解：由胡克定律EA Ukb〃 =——=—=0 327 7丛£ a—=70 GPa* —A1返回3,2(3・5)。
工程力学(静力学和材料力学)课后习题答案
工程力学（静力学与材料力学）习题详细解答(第1章)(a) (b) 习题1－1图第1章 静力学基础1一1 图a 和b 所示分别为正交坐标系11y Ox 与斜交坐标系22y Ox 。
试将同一个力F 分别在两中坐标系中分解和投影，比较两种情形下所得的分力与投影。
解：图（a ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
图（b ）： 分力：22)tan sin cos (i F ϕααF F x −= ， 22sin sin j F ϕαF y =投影：αcos 2F F x = ， )cos(2αϕ−=F F y讨论：ϕ≠90°时，投影与分量的模不等。
1一2 试画出图a 和b 两种情形下各构件的受力图，并加以比较。
比较：解a 图与解b 图，两种情形下受力不同，二者的F R D 值大小也不同。
DR习题1－2b 解图DR习题1－2a 解2图C习题1－2a 解1图(a) (b)习题1－2图1一3 试画出图示各构件的受力图。
习题1－3图B F 习题1－3a 解2图 B习题1－3a 解1图习题1－3b 解1图F Ay Ax 习题1－3c 解图 A习题1－3b 解2图习题1－3d 解1图习题1－3e 解1图习题1－3e 解2图1－4 图a 所示为三角架结构。
荷载F 1作用在B 铰上。
AB 杆不计自重，BD 杆自重为W ，作用在杆的中点。
试画出图b 、c 、d 所示的隔离体的受力图，并加以讨论。
习题1－4图1习题1－3f 解1图F习题1－3e 解3图'A习题1－3f 解2图1O 习题1－3f 解3图F F'F 1习题1－4d 解2图F y B 21习题1－4c 解1图 AA B 1B FDx y2B 习题1－4b 解2图 1习题1－4b 解3图 F y B 2习题1－4c 解2图 F A B1B FAxF'习题1－5b 解3图E D(a-3)E B F习题1－5b 解2图习题1－5b 解1图'AxFF B习题1－5c 解图1一5 试画出图示结构中各杆的受力图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4日1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)98 解：1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。
解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点，如图所示。
如不计刚架重量，试求支座A 和D 处的约束力。
(d) FC(e)WB (f)F F BCF 1F解：(1) 取整体ABCD为研究对象，受力分析如图，画封闭的力三角形：(2)2111.122D A DD AF F FF FBC AB ACF FF F F=====∴===2-4 在简支梁AB的中点C作用一个倾斜45o的力F，力的大小等于20KN，如图所示。
若梁的自重不计，试求两支座的约束力。
解：(1)研究AB，受力分析并画受力图：(2) 画封闭的力三角形：相似关系：B AF FFCDE cdeCD CE ED∆≈∆∴==Q几何尺寸：1122CE BD CD ED=====求出约束反力：FDFF AF DFF BF A dce12010 22010.4 45arctan 18.4B A o oCE F F kNCDED F F kN CDCECD α=⨯=⨯==⨯===-=2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计，图中的长度单位为cm 。
已知F =200 N ，试求支座A 和E 的约束力。
解：(1) 取DE 为研究对象，DE 为二力杆；F D = F E(2) 取ABC 为研究对象，受力分析并画受力图；画封闭的力三角形：'15166.7 23A D E F F F F N ===⨯=F A F3-1 已知梁AB 上作用一力偶，力偶矩为M ，梁长为l ，梁重不计。
求在图a ，b ，c 三种情况下，支座A 和B 的约束力解：(a) 受力分析，画受力图；A 、B 处的约束力组成一个力偶；列平衡方程：0 0 B B A B M M F l M F lMF F l=⨯-==∴==∑(b) 受力分析，画受力图；A 、B 处的约束力组成一个力偶；列平衡方程：0 0 BB A B M M Fl M F lM F F l=⨯-==∴==∑(c) 受力分析，画受力图；A 、B 处的约束力组成一个力偶；(a)(b)(c)BBF列平衡方程：0 cos 0 cos cos B B A B M M F l M F l M F F l θθθ=⨯⨯-==∴==∑3-3 齿轮箱的两个轴上作用的力偶如题图所示，它们的力偶矩的大小分别为M 1=500 Nm ，M 2 =125 Nm 。
求两螺栓处的铅垂约束力。
图中长度单位为cm 。
解：(1) 取整体为研究对象，受力分析，A 、B 的约束力组成一个力偶，画受力图；(2) 列平衡方程：12125001250 0 750 50750 B B A B M M M F l M M F Nl F F N--=⨯-+====∴==∑ 3-5 四连杆机构在图示位置平衡。
已知OA=60cm ，BC=40cm ，作用BC 上的力偶的力偶矩大小为M 2=1N.m ，试求作用在OA 上力偶的力偶矩大小M 1和AB 所受的力F AB 。
各杆重量不计。
解：(1) 研究BC 杆，受力分析，画受力图：列平衡方程：BF B220 sin 30015 0.4sin 30sin 30oBB oo M FBC M M F NBC =⨯-====⨯∑ (2) 研究AB （二力杆），受力如图：可知：''5 A B B F F F N ===(3) 研究OA 杆，受力分析，画受力图：列平衡方程：110 050.6 3 AA M FOA M M F OA Nm=-⨯+=∴=⨯=⨯=∑A BAF4-1 试求题4-1图所示各梁支座的约束力。
设力的单位为kN ，力偶矩的单位为kN ⋅m ，长度单位为m ，分布载荷集度为kN/m 。
(提示：计算非均布载荷的投影和与力矩和时需应用积分)。
解：(b)：(1) 整体受力分析，画出受力图(平面任意力系)；(2) 选坐标系Axy ，列出平衡方程；0: 0.400.4 kNxAx Ax FF F =-+==∑()0: 20.80.5 1.60.40.7200.26 kNAB B MF F F =-⨯+⨯+⨯+⨯==∑0: 20.501.24 kNyAy B Ay FF F F =-++==∑约束力的方向如图所示。
(b)(e)F(c)：(1) 研究AB 杆，受力分析，画出受力图(平面任意力系)；(2) 选坐标系Axy ，列出平衡方程；2()0: 33200.33 kNBAy Ay MF F dx x F =-⨯-+⨯⨯==∑⎰20: 2cos3004.24 kNo yAy B B FF dx F F =-⨯+==∑⎰0: sin 3002.12 kNo xAx B Ax FF F F =-==∑约束力的方向如图所示。
(e)：(1) 研究C ABD 杆，受力分析，画出受力图(平面任意力系)；(2) 选坐标系Axy ，列出平衡方程；0: 0xAx FF ==∑0.8()0: 208 1.620 2.4021 kNAB B MF dx x F F =⨯⨯++⨯-⨯==∑⎰0.80: 2020015 kNy Ay B Ay F dx F F F =-⨯++-==∑⎰约束力的方向如图所示。
4-13 活动梯子置于光滑水平面上，并在铅垂面内，梯子两部分AC 和A B 各重为Q ，重心在A 点，彼此用铰链A 和绳子DE 连接。
一人重为P 立于F 处，试求绳子DE 的拉力和B 、C 两点的约束力。
Fxq x解：(1)：研究整体，受力分析，画出受力图(平面平行力系)；(2) 选坐标系Bxy ，列出平衡方程；()3()0: -cos cos 2cos 2cos 02212BC C l lM F Q Q P l a F l a F Q Pl αααα=⨯-⨯-⨯-+⨯=⎛⎫=+- ⎪⎝⎭∑0: 202yB C B FF F Q P aF Q Pl=+--==+∑(3) 研究AB ，受力分析，画出受力图(平面任意力系)；(4) 选A 点为矩心，列出平衡方程；()0: -cos cos 02cos 2A BD D lM F F l Q F h a l F Q P l h ααα=⨯+⨯+⨯=⎛⎫=+ ⎪⎝⎭∑4-16 由AC 和CD 构成的复合梁通过铰链C 连接，它的支承和受力如题4-16图所示。
已知均布载荷集度q =10 kN/m ，力偶M =40 kN ⋅m ，a =2 m ，不计梁重，试求支座A 、B 、D 的约束力和铰链C 所受的力。
x解：(1) 研究CD 杆，受力分析，画出受力图(平面平行力系)；(2) 选坐标系Cxy ，列出平衡方程；()0: -205 kNaC D D M F q dx x M F a F =⨯⨯+-⨯==∑⎰0: 025 kNayC D C FF q dx F F =-⨯-==∑⎰(3) 研究ABC 杆，受力分析，画出受力图(平面平行力系)；(4) 选坐标系Bxy ，列出平衡方程；'0()0: 035 kNaB AC A M F F a q dx x F a F =⨯-⨯⨯-⨯==∑⎰'00: 080 kNayA B C B FF q dx F F F =--⨯+-==∑⎰约束力的方向如图所示。
4-17 刚架ABC 和刚架CD 通过铰链C 连接，并与地面通过铰链A 、B 、D 连接，如题4-17图所示，载荷如图，试求刚架的支座约束力(尺寸单位为m ，力的单位为 kN ，载荷集度单位为 kN/m)。
=50q Fx解：(a)：(1) 研究CD 杆，它是二力杆，又根据D 点的约束性质，可知：F C =F D =0；(2) 研究整体，受力分析，画出受力图(平面任意力系)；(3) 选坐标系Axy ，列出平衡方程；0: 1000100 kNxAx Ax FF F =-+==∑51()0: 100660120 kNAB B MF q dx x F F =-⨯-⨯⨯+⨯==∑⎰510: 080 kNy Ay B Ay F F q dx F F =--⨯+==∑⎰约束力的方向如图所示。
(b)：(1) 研究CD 杆，受力分析，画出受力图(平面任意力系)；(2) 选C 点为矩心，列出平衡方程；3()0: 3015 kNC D D M F q dx x F F =-⨯⨯+⨯==∑⎰(3) 研究整体，受力分析，画出受力图(平面任意力系)；=50(4) 选坐标系Bxy ，列出平衡方程；0: 50050 kNxAx Ax FF F =-==∑3()0: 63503025 kNB Ay D Ay M F F q dx x F F =-⨯-⨯⨯+⨯+⨯==∑⎰30: 010 kNyAy B D B FF q dx F F F =-⨯-+==∑⎰约束力的方向如图所示。
x5-5 作用于半径为120 mm 的齿轮上的啮合力F 推动皮带绕水平轴AB 作匀速转动。
已知皮带紧边拉力为200 N ，松边拉力为100 N ，尺寸如题5-5图所示。
试求力F 的大小以及轴承A 、B解: (1) 研究整体，受力分析，画出受力图(空间任意力系)；8-2 试画出8-1所示各杆的轴力图。
解：(a)(b)(c) (d)8-14 图示桁架，杆1与杆2的横截面均为圆形，直径分别为d 1=30 mm 与d 2=20 mm ，两杆材料相同，许用应力[σ]=160 MPa 。
该桁架在节点A 处承受铅直方向的载荷F =80 kN 作用，试校核桁架的强度。