材料力学课件:第7章 应力状态分析
合集下载
材料力学第7章应力状态

y
2
2 xy
m m
ax in
m
ax
2
m
in
极值切应力等于极值正应力差的一半。
§7.2 平面应力状态分析的解析法
三、极值切应力和主平面夹角
注意到 则 所以
tan
2 0
2 xy x
y
tan
21
x 2 xy
y
tan
20
1
tan 21
§7.2 平面应力状态分析的解析法
7.2.3 极值切应力及其作用面 一、极值切应力方位角
d 0 d
( x y ) cos 2 2 xy sin 2 0
得
tan
21
x 2 xy
y
二、最大、最小切应力
m m
ax
in
x
2
x
y
2
sin 2
xy cos 2
§7.2 平面应力状态分析的解析法
7.2.2 主应力 主方向 一、主应力
正应力是求极值
d d
x
y
2
(2sin 2 ) xy(2cos2 ) 0
得极值条件为
x
2
y
sin
2
xy
cos
2
0
(1) 极值正应力所在的斜面,恰好是切应力等于零的
平面,即主平面。
(2) 极值正应力就是主应力。
§7.2 平面应力状态分析的解析法
材料力学:第七章 应力、应变状态分析(上)

s
N1
s3
ON 2
t
tan 300
t
cos 300
11.6 Mpa
A
由于ACN1=1200,所以,s1的主平面法
线与A面的夹角为a0= 600。于是,A面的 法线逆时针旋转600可得到s1的主平面法
t
线,从而确定s1的主平面的位置。确定 s1的主平面的位置后,可确定s3的主平
s3
t
面的位置,而s2的主平面为单元体的前
平面应力状态分析的图解法
主应力及最大、最小切应力
– 应力圆与s 轴的两个交点N1,
N2
N2的横坐标,对应于单元的主
应力s1,s2。弧DN1所对应的圆
N1
心角2a0,就是x面的外法线与
s1所在的主平面的外法线的夹
角的两倍
显然
ON1 ON 2
sx
s
2
y
s x
s y
2
2
t xy 2
s s
max min
tan
2a 0
s
2t xy x s
y
平面应力状态分析的图解法
– 应力圆的垂直半径CG1和CG2分
别等于最大、最小切应力,即
G1
CG1 CG2
s
x
s
2
y
2
t
2 xy
s max
s min
2
t t
max min
N2 N1
G2
在应力圆上,由N1到G1和G2的 圆心角分别为900,因此,主 平面法线与剪应力极值所在平 面的法线的夹角为450。
大的一个靠得近些(夹角<45。)
平面应力状态分析的图解法
前面导出了平面应力状态 的解析计算公式
材料力学第七章应力状态和强度理论

2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y
x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2
x
y
2
4 2 xy
x
yx xy x
y
R c
x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2
40
x y
2 0.431MPa
sin( 80 ) xy cos(80 )
C
C
C
例题3:已知梁上的M、Q,试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q = 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y
x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2
x
y
2
4 2 xy
x
yx xy x
y
R c
x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2
40
x y
2 0.431MPa
sin( 80 ) xy cos(80 )
C
C
C
例题3:已知梁上的M、Q,试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q = 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa
材料力学课件第七章变曲应力(机械专业)
A ydA M
yC ydA A ቤተ መጻሕፍቲ ባይዱ A
(c)
(a)(b)
A ydA 0
E
中性轴通过横截面形心
(a)(c)
A
y 2dA M
M EI z 1
Iz
A
y2dA-惯性矩
(d)
(d)(a)
( y )
My Iz
max
M Wz
max
Mymax Iz
静力学方面:
( y)
( y)d d y d
y
(a)
物理方面:
( y) E ( y)
dA0 (b) Fx 0, A M z 0, A ydA M (c)
第七章
弯曲应力
正应力分布
第七章
E
y
弯曲应力
(b)
(a)
dA 0 A
A
F
z
1)画弯矩图 跨中截面 C 为危险截面 危险截面上的最大弯矩
M max 1 Fl 280 kN m 4
M /kN m
C 8m
a
B
y
F
A
C
B
8m
280
x
第七章
2)计算正应力
弯曲应力
查型钢表,No. 50a 工字钢的惯性矩 Iz = 46500 cm4 ,抗弯截面 系数 Wz = 1860 cm3 危险截面 C 上的最大正应力
第七章
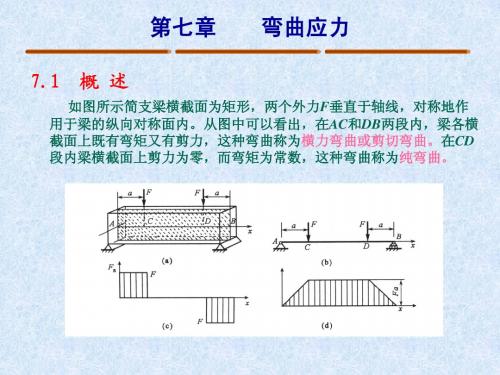
7.1 概 述
弯曲应力
如图所示简支梁横截面为矩形,两个外力F垂直于轴线,对称地作 用于梁的纵向对称面内。从图中可以看出,在AC和DB两段内,梁各横 截面上既有弯矩又有剪力,这种弯曲称为横力弯曲或剪切弯曲。在CD 段内梁横截面上剪力为零,而弯矩为常数,这种弯曲称为纯弯曲。
材料力学第七章 应力状态

主平面的方位:
tan
2a0
2 xy x
y
主应力与主平面的对应关系: max 与切应力的交点同象限
例题:一点处的平面应力状态如图所示。
已知 x 60MPa, xy 30MPa, y 40MPa, a 30。
试求(1)a 斜面上的应力; (2)主应力、主平面; (3)绘出主应力单元体。
x y cos 2a
2
x sin 2a
x
a
x y sin 2a
2
x cos 2a
300
10 30 2
10 30 cos 60020sin 600
2
2.32 MPa
300
10 30 sin 600 2
20cos 600
1.33 MPa
a
20 MPa
c
30 MPa
b
n1
y xy
a x
解:(1)a 斜面上的应力
y xy
a
x
2
y
x
2
y
cos 2a
xy
sin 2a
60 40 60 40 cos(60 ) 30sin(60 )
2
2
a x 9.02MPa
a
x
y
2
sin
2a
xy
cos
2a
60 40 sin(60 ) 30cos(60 ) 2
58.3MPa
2
1.33 MPa
300 600 x y 40 MPa
在二向应力状态下,任意两个垂直面上,其σ的和为一常数。
在二向应力状态下,任意两个垂直面上,其σ 的和为
一常数。
证明: a
x y
材料力学——应力分析【可修改】.ppt

(2)主平面的位置
tg
2α 0
σ
2τ xy
x σ
y
α1 α 2 α1 900
} σ max
σ min
σx σy 2
(σ
x σ 2
y
2
)
τ
2 xy
以1代表max作用面的方位角, 2代表min作用面的方位角。
精选
σ x σ y ,则 α1 450 (α1在 900 范围内取值)
若 σ x σ y ,则 α1 450
x
在坐标系内画出点A( x,
xy)和B(y,yx)
2a C
A(
x
,
a
xy)
AB与a 轴的交点C便是
圆心。
O
以C为圆心,以AC为
B( y ,yx)
半径画圆——应力圆;
精选
y
n 三、单元体与应力圆的对应关系
面上的应力( , )
a xy x 应力圆上一点( , )
y
面的法线 应力圆的半径
Oa n D(xa , a)
所在的平面)垂直的
1
斜截面上的应力。
3
精选
2
3
1
2
用截面法,沿求应力的截 面将单元体截为两部分, 取左下部分为研究对象。
2
3
3
1
1
1
3
2
3
2
精选
主应力 3 所在的两平面上是一对
自相平衡的力, 因而该斜面上的
3
应力, 与 3无关, 只由主应力
1
1 , 2 决定。
3 2
与3所在的面垂直的斜截面上的应力可由
精选
应力的点的概念与面的概念
材料力学-应力状态分析
+
σ x σ y
2
cos 2α τ x sin 2α
sin 2α + τ x cos 2α
注意: 的正负号, 注意:1)σx 、σy 、τx 和 α的正负号, 2) 公式中的切应力是τx ,而非τy, 而非 的正负号。 3) 计算出的σα和τα 的正负号。
τα τ α>0
τα τ α<0
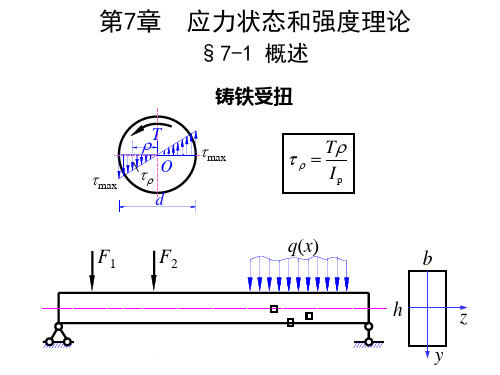
图示圆轴中, 已知圆轴直径d=100mm, 轴向拉 例 : 图示圆轴中 , 已知圆轴直径 , 力 F=500kN,外力矩Me=7kNm。求 C点α = 30°截 , 外力矩 。 点 ° 面上的应力。 面上的应力。 y
σy
τ
D
x
τx τy
σx
o A2
C
A1
σ
D
y
σ1 =
σ x +σ y
2
σ x +σ y + 2
2 +τ x
2
2
σ2 =
σ x +σ y
2
σ x +σ y 2 +τ x 2
σy
τ
D
x
τx τy
σx
o A2
2α0
C
A1
σ
D
y
2τ x 2α 0 = arctan σ x σ y
σ x σ y R= 2
+τ x2
2
σ x +σ y σ α 2
σy
σ x σ y 2 2 + τα = +τ x 2 τ
2 2
D
x
τx τy
σx
o
C D
y
σ
50MPa
材料力学课件:第7章 应力状态分析

示。
显然,用主应力表示的应力状态要比用一般 应力分量表示的应力状态简单。用主应力表 示一点处的应力状态可以说明某些应力状态 表面上是不同的,但实质是相同的,即其主 应力和主方向都相同。
纯剪切状态的最大应力
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
平面应力状态有两个不等于零主应力,这两个 不等于零的主应力以及上述平面应力状态固有的等于 零的主应力,分别用表示 :
根据主应力的大小与方向可以确定材料何时发生 失效或破坏,确定失效或破坏的形式。因此,可以说 主应力是反映应力状态本质内涵的特征量。
TSINGHUA UNIVERSITY
根据上述分析结果,原来用x、y、xy 和yx表示的应力状态,现在可以用主应力表
( x y ) sin 20 2 xy cos 20 0
2
(
σx
σy 2
) s
i
n
2α0
τx
yc
o
s
2α0
2τα0
0
即α=α0 时,切应力为零
y
2 xy x
2 0
tan
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
1 2
(
x
y)
1 2
( x
y ) cos 2
xy
sin
2
1 2
( x
y ) sin
2
xy
cos 2
法二: 解析法
1 2
(
x
y)
1 2
(
x
显然,用主应力表示的应力状态要比用一般 应力分量表示的应力状态简单。用主应力表 示一点处的应力状态可以说明某些应力状态 表面上是不同的,但实质是相同的,即其主 应力和主方向都相同。
纯剪切状态的最大应力
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
平面应力状态有两个不等于零主应力,这两个 不等于零的主应力以及上述平面应力状态固有的等于 零的主应力,分别用表示 :
根据主应力的大小与方向可以确定材料何时发生 失效或破坏,确定失效或破坏的形式。因此,可以说 主应力是反映应力状态本质内涵的特征量。
TSINGHUA UNIVERSITY
根据上述分析结果,原来用x、y、xy 和yx表示的应力状态,现在可以用主应力表
( x y ) sin 20 2 xy cos 20 0
2
(
σx
σy 2
) s
i
n
2α0
τx
yc
o
s
2α0
2τα0
0
即α=α0 时,切应力为零
y
2 xy x
2 0
tan
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
1 2
(
x
y)
1 2
( x
y ) cos 2
xy
sin
2
1 2
( x
y ) sin
2
xy
cos 2
法二: 解析法
1 2
(
x
y)
1 2
(
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
①主平面:单元体上剪应力为零的面;
根据剪应力成对定理,当一对方向面为主平面
时,另一对与之垂直的方向面(=P+π/2),其上
之剪应力也等于零,因而也是主平面,其上之正应力 也是主应力。
需要指出的是,对于平面应力状态,平行于xy
示。
显然,用主应力表示的应力状态要比用一般 应力分量表示的应力状态简单。用主应力表 示一点处的应力状态可以说明某些应力状态 表面上是不同的,但实质是相同的,即其主 应力和主方向都相同。
纯剪切状态的最大应力
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
平面应力状态的极值剪应力 同理:
1 2
(
x
y ) sin
2
xy
cos 2
取导
d d
( x y ) cos 2 2 xy sin
2
设α=α1 时,上式值为零,即
( x y ) cos 21 2 xy sin 21 0
求得
tan
21
x 2 xy
y
max
x
y
2
2
2 xy
平面应力状态有两个不等于零主应力,这两个 不等于零的主应力以及上述平面应力状态固有的等于 零的主应力,分别用表示 :
根据主应力的大小与方向可以确定材料何时发生 失效或破坏,确定失效或破坏的形式。因此,可以说 主应力是反映应力状态本质内涵的特征量。
TSINGHUA UNIVERSITY
根据上述分析结果,原来用x、y、xy 和yx表示的应力状态,现在可以用主应力表
坐标面的平面,其上既没有正应力、也没有剪应力作 用,这种平面也是主平面。这一主平面上的主应力等 于零。
TSINGHUA UNIVERSITY
②主平面微体: 由三对互垂主平面所 构成的微体。
③主应力:主平面上的正应力,用1、 2、3表示, 有1≥2≥3。
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
二 、最大应力
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
( x y ) sin 20 2 xy cos 20 0
2
(
σx
σy 2
) s
i
n
2α0
τx
yc
o
s
2α0
2τα0
0
即α=α0 时,切应力为零
y
2 xy x
2 0
tan
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
Байду номын сангаас
1 2
max min
TSINGHUA UNIVERSITY
min
x
y
2
2
2 xy
1 2
max min
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
主平面、主应力与主方向 平面应力状态的三个主应力 纯剪切的最大应力
主平面、主应力与主方向
1 2
(
x
y)
1 2
( x
y ) cos 2
xy
sin
2
1 2
( x
y ) sin
2
xy
cos 2
法二: 解析法
1 2
(
x
y)
1 2
(
x
y ) cos 2
xy sin
2
d d
( x
y ) sin
2
2 xy cos 2
设α=α0 时,上式值为零,即
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
返回总目录
返回
TSINGHUA UNIVERSITY
第7章 应力状态分析
7-3 极值应力与主应力
一、平面应力状态的极值应力 法一: 应力圆法
TSINGHUA UNIVERSITY
max
x
y
2
1 2
x y
2
4
2 xy
min
x
y
2
1 2
x
y
2
4
2 xy
回顾平面应力状态斜截面应力:
TSINGHUA UNIVERSITY
