数学建模之管道包扎
管道包扎问题的数学模型论文

管道包扎问题的数学模型论文管道包扎问题的数学模型摘要: 本篇论文讨论管道的包扎问题.是一个三维空间的问题我采用剪切的方法把空间问题转化为平面问题建立刚好全部包扎所用带子最短模型和管道包扎出现接缝处重叠模型然后利用数学软件Matlab 求解.在图1 中,求得最短带子包扎的通用表达式并代入题目给出的数据得到第一个问题的最短长度为50.4 米。
在图2 和图3 中,采用近似的处理方法求出管道包扎接缝处重叠带子宽度的表达式代入第二个问题的数据得到带子的重叠宽度为0.004 米.论文的最后对临界角0 和截面是正多边形的管道的情况作进一步的讨论并得到更一般的模型.关键词: 临界角临界点临界长度等量关系1 问题的提出用宽度为0.3m 的带子缠绕包扎圆柱型管道,管道长30m,截面周长为0.5m. 1 如果用带子全部包住管道,最少要用多长的带子,请你给出计算这个最小长度的公式,并且依次计算出所需长度数值. 2 现有一条长度为51m 的带子,想将这条带子全部用于缠绕包扎这个管道,可以使带子的接缝处重叠瘩接.请你给出用这条带子缠绕包扎这个管道的方案.(计算结果精确到0.001m)3 如果管道截面是正三边形正四边形或边数更多的正多边形.2 问题的分析生活的经验告诉我们在包扎圆形管道的过程中如果开始包扎时带子边缘所在的直线与管道母线的夹角过小就可能出现不能把管道全部包扎的现象如果夹角过大就可能出现包扎带子在接缝处重叠的现象. 所以随着夹角的增大总会出现在接缝处恰好接合而没有重叠的情况.这种特殊的情况就是第一问的求解问题称此时包扎带子的长度为临界长度带子边缘所在的直线与管道母线的夹角为临界角管道任一端的带子截口所在边与管道截面的交点称为临界点.如果给定一段带子的长度大于临界长度则总能找到一种包扎方案使得整条带子全都包扎完其中接缝处有重叠. 当管道的截面为正多边形时我们把正多边形的直棱柱管道看作圆形管道的变形来处理即正多边形的直棱柱管道的平面展开图与圆形管道的平面展开图是同样的.3 模型的假设1 管道没有厚度即把管道剪开图看成平面不考虑空间结构2 管道是刚性物体带子也不具备弹性 3 管道截面是圆形或正多边形整条管道粗细均匀 4 包扎过程中带子的宽度不变,带子也不能切断 5 带子没有厚度且两端截口垂直于它的边.即把带子看成一个长方形不考虑空间结构4 符号的约定1)a -----带子的宽度2)b -----管道的长度;3 c -----管道截面的周长4)l ----- 带子的长度5 θ--- 带子截口所在的直线与管道母线的夹角 6 S1 ----- 直角三角形AED 的面积7 S 2 ----- 直角三角形OBF 的面积8 S 3 ---- 四边形COHG 的面积9 x ---- 带子重叠部分的宽度10 y --- 重叠部分的带子长度11 m---- 截面正多边形的边长12 n ---- 截面正多边形的边数.5 模型的建立和求解5.1 刚好全部包扎所用带子最短模型经过临界点沿着管道的母线切开得到矩形ABCD如下图1: 图1 其中矩形ABCD 为管道的侧面展开图三角形AED 为直角三角形四边形OHGC.定理1 直角三角形AED 的面积等于直角三角形OBF 和四边形OHGC 之和. 证明线段BF 和线段CG在空间图形中是重合的故这两线段相等. 把直角三角形OBF 向右移动使BF 与CG 重合则构成直角三角形O HO . 又EDOH OBOCAD 故AED O HO 即定理成立.推论1 沿着管道任一母线剪开得到的平面展开图中管道截面界线的两端分别能组成两个直角三角形且这两个直角三角形的面积相等.由上面的定理 1 和推论可以得出刚好包扎管道所用带子最短的模型: al S1 S 2 S 3 bc 1 S1 a c a 2 2 2 S1 S 2 S 3 求得一般表达式为: bc l c2 a2 a把题目中给出的数据代入一般表达式求得第一问题的临界长度为: 30 0.5 l 0 .5 2 0 .3 2 50.4 米0 .35.2 管道包扎出现接缝处重叠的模型按图1的剪开方法得到管道平面展开图如图2: 图2 其中阴影为带子重叠部分. 命题1 在带子宽度不变的条件下带子相接处重叠的宽度一定相等即图 2 中阴影部分的平行四边形的宽度不改变.5.2.1 求阴影部分的带子的长度. 命题 2 阴影部分的长度比整条包扎带子的长度短线段AE 的长度. 证明由推论 2 阴影部分的宽度相等故可以过图2 的 A 点垂直AE 剪切再把剪切的左边部分图形补到右边如下图3: 图3由图3 可以看出y l AE l c cos5.2.2 利用阴影部分的面积相等得到模型: xy al bc a x c 2 a x 2 y l c cos c 2 a x 2 cos c化简此方程组得: 2 x a c 2 a x 2 xl al bc 0 1利用Matlab 解方程1得到的结果过繁所以为了得到一个比较简单而又接近实际的答案我们作以下处理: 在生活和工作中为了节省材料包扎管道的带子一般不会比临界长度长太多所以可用 c 2 a 2 近似代替c 2 a x 2 求得结果为: a c 2 a 2 bc al x 2 2 c2 a2 l 把第二问题的数据代入方程1得: x 1 0.00357把第二问题的数据代入方程2得: x 2 0.0036由以上计算得到的结果可以看出当带子的长度不太长时用 a c 2 a 2 bc al x 2 c2 a2 l代替这个模型的结果是可以的.且取得第二问题的结果为: x0.004米5.3 截面为正多边形的直棱柱管道模型推理1 对于任何正多边直棱柱的包扎面从临界点沿棱柱的母线剪开得到的剪开平面如图 1 所示包扎方案为临界时如果有带子重合的情形如图 2.类似以上图 1 圆柱管道包扎方案的方法建立模型如下: 5.3.1 包扎正多边直棱柱的临界模型: al S1 S 2 S 3 bmn 1 S1 a mn a 2 2 2 S1 S 2 S 3 解得: mnb l mn 2 a 2 a 5.3.1 包扎正多边直棱柱的有重叠的模型: xy al mnb a x mn 2 a x 2 y l mn cos mn 2 a x 2 cos mn 以mn 2 a 2 代替mn 2 a x 2 解得a mn 2 a 2 mnb al x 2 mn 2 a 2 l6 模型的分析6.1 临界角的讨论 a 临界角0 arcsin 3 c 6.1.1 当0 时带子不能全部包扎整条管道.如果要在角增大即临界角增大的情况下实现全部包扎由3 式可以看出应加大带子的宽度或减小管道截面的周长. 6.1.2 当0 时带子在包扎过程中出现接缝处重叠.如果要在角减小即临界角减小的情况下实现全部包扎由3 式可以看出应减小带子的宽度或增加管道截面的周长.故有以下推理:推理 2 包扎管道的临界角0 随带子宽度的增大而增大管道截面周长的减小而增大随带子宽度的减小而减小管道截面周长的增大而减小.6.2 管道的讨论由推论1、命题1 和推理1可知无论求解模型是圆柱模型或是截面为正多边形的直棱柱其求解过程都是相同的故有以下推理.推理3 管道的包扎方案与管道截面是凸多边形不限边数不限每边的长度或连续的凸封闭曲线无关只与管道截面的周长C、管道长度l 和给定的带子的长度有关.参考文献:1 吕林根. 解析几何〔M〕. 北京:高等教育出版社,2000.2 刘来福. 数学模型与数学建模〔M 北京:北京师范大学出版社20023.姜启源等编.《数学模型》(第三版).北京:高等教育出版社.2003. 》4.姜启源等编.《数学模型(第三版)习题参考解答. 北京:高等教育出版社.2003.5.刘来福,曾文艺.数学模型与数学建模.北京:北京师范大学出版社,19976.杨启帆,边馥萍.数学模型.杭州:浙江大学出版社,19907.叶其孝.中学数学建模M.长沙:湖南出版社.1998.9-108.冯跃峰.对数学教育若干问题的认识J.数学教育学报.1992(1):64-659.卜月华.中学数学建模教与学M.东南大学出版社,2002,310.荆新大.足球中的数学J.数学教学,1993(3)11.廖运章.强调数学理解建模灵活开放.数学通报,2000,12 The study of pipeline bind up’s problem YE Feiwu(Department of mathematics 2000 grade Class Shaoguan College Shaoguan512005Guangdong)Abstract: we will discuss the bind up problems of pipeline in this paper. This problem is athree- figure problem. We can cut the pipeline open and change these plane problems intothree-figure problems. We set up the best of all shot model which use band shot of all and happen tobind up the pipeline entirely and set up the repeated model of which the joint locate appear repeatedthen take the mathematics software to work out the problem. In the fig1 we work out the currencyexpression of best of all bands and make use of the data of subject and gained the answer of thefirst problem is 50.4 meter. In the fig2 and fig3 adopt approximate method to seek out theexpression of the band’s width superposed and make use of the data of subject and gained theanswer of the second problem is 0.004 meter. At the end of the paper we will discuss the critical angle 0 and pipeline of which section ispositive polygon and gained the even more model.Key words: critical angle critical point critical length grade measure relation。
数学建模之钢管下料问题案例分析

钢管下料问题某钢管零售商从钢管厂进货,将钢管按照顾客的要求切割后售出,从钢管厂进货时得到的原料钢管都是 19m。
(1)现在一客户需要50 根 4m、 20 根 6m 和 15 根 8m 的钢管。
应如何下料最节省?(2)零售商如果采用的不同切割模式太多,将会导致生产过程的复杂化,从而增加生产和管理成本,所以该零售商规定采用的不同切割模式不能超过 3 种。
此外,该客户除需要( 1)中的三种钢管外,还需要10 根 5m 的钢管。
应如何下料最节省。
问题( 1)分析与模型建立首先分析 1 根 19m 的钢管切割为 4m、6m、8m 的钢管的模式,所有模式相当于求解不等式方程:4k16k28k319的整数解。
但要求剩余材料 r 19 (4 k1 6k2 8k3 ) 4 。
容易得到所有模式见表1。
表 1钢管切割模式模式4m6m8m余料 (m)14003231013201340023503016111171203决策变量用 x i表示按照第i 种模式 (i=1,2, , 7)切割的原料钢管的根数。
以切割原料钢管的总根数最少为目标,则有min z x1 x2x3 x4 x5 x6x7约束条件为满足客户的需求, 4 米长的钢管至少50 根,有4x13x22x3x6x7 506 米长的钢管至少20 根,有x23x5x62x7208 米长的钢管至少15 根,有x32x4x615因此模型为:min z x1 x2 x3 x4x5x6 x74x13x2 2 x3x6x750x23x5x62x720st..x32x4x615x i取整 , i1,2,L ,7解得:x1 0, x212, x30, x40, x50, x6 15, x70目标值 z=27。
即 12 根钢管采用切割模式2: 3 根 4m, 1 根 6m,余料 1m。
15 根钢管采用切割模式6: 1 根 4m, 1 根 6m,1 根 8m,余料 1m。
切割模式只采用了 2 种,余料为 27m,使用钢管27 根。
入门级数学建模练习题

入门级数学建模练习题2. 假设在一所大学中,一位普通教授以每天一本的速度开始从图书馆借出书。
再设图书馆平均一周收回借出书的1/10,若在充分长的时间内,一位普通教授大约借出多少年本书?3. 一人早上6:00从山脚A上山,晚18:00到山顶B;第二天,早6:00从B下山,晚18:00到A。
问是否有一个时刻t,这两天都在这一时刻到达同一地点?4. 如何将一个不规则的蛋糕I平均分成两部分?5. 兄妹二人沿某街分别在离家3公里与2公里处同向散步回家,家中的狗一直在二人之间来回奔跑。
已知哥哥的速度为3公里/小时,妹妹的速度为2公里/小时,狗的速度为5公里/小时。
分析半小时后,狗在何处?6. 甲乙两人约定中午12:00至13:00在市中心某地见面,并事先约定先到者在那等待10分钟,若另一个人十分钟内没有到达,先到者将离去。
用图解法计算,甲乙两人见面的可能性有多大?7. 设有n个人参加某一宴会,已知没有人认识所有的人,证明:至少存在两人他们认识的人一样多。
8. 一角度为60度的圆锥形漏斗装着10端小孔的面积为0.59. 假设在一个刹车交叉口,所有车辆都是由东驶上一个1/100的斜坡,计算这种情下的刹车距离。
如果汽车由西驶来,刹车距离又是多少?10. 水管或煤气管经常需要从外部包扎以便对管道起保护作用。
包扎时用很长的带子缠绕在管道外部。
为了节省材料,如何进行包扎才能使带子全部包住管道而且带子也没有发生重叠。
:顶=1:a:b,选坐v>0,而设语雨速L,v≤x vv+1),v>x.解:由于教授每天借一本书,即一周借七本书,而图书馆平均每周收回书的1/10,设教授已借出书的册数是时间t的函数小x的函数,则它应满足其中初始条件表示开始时教授借出数的册数为0。
解该线性问题得X=70[1-e?t]由于当∞时,其极限值为70,故在充分长的时间内,一位普通教授大约已借出70本书。
3.解:我们从山脚A点为始点记路程,设从A到B路程函数为f,即t时刻走的距离为f;同样设从B点到A点的路程为函数g。
2021数学建模C题获奖论文2——输油管的布置

2021高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名号为(如果赛区设置报名号的话):1328303所属学校(请填写完整的全名):武汉职业技术学院参赛队员(打印并签名):1. XXX2. XXX3. X X指导教师或指导教师组负责人(打印并签名):数模指导组编号专用页输油管的布置摘要本文对输油管线的布置主要从建设费用最省的角度进行研究。
首先,对问题一,我们按照共用管线与非共用管线铺设费用相同或不相同,进行分类讨论。
为了更好的说明,我们根据共用管线与非共用管线铺设费用相同或不同及两炼油厂连线与铁路线垂直或不垂直分成四类讨论。
其次,对问题二,由于需要考虑在城区中铺设管线,涉及到拆迁补偿费等。
通过对三个公司的估算费用加权,求得期望值021.5P (万元)。
并利用建立的规划模型②求得管道建设的最省费用为282.70万元。
其中共用管线长度为1.85千米,炼油厂B在城区铺设的管道线对城郊分界线的射影为0.63千米。
最后,对问题三,由于炼油厂A和B的输油管线铺设费用不同,所以最短管道长度和未必能保证铺设总费用最省,因而我们又建立了规划模型③,通过LINGO软件求得管道建设的最省费用为251.97万元,三种管道的结合点O到炼油厂A与铁路垂线的距离为6.13千米,结合点O到铁路的距离为0.14千米,炼油厂B在城区铺设的管道线对城郊分界线的射影为0.72千米。
关键词:管线铺设平面镜成像光的反射规划1.问题重述1.1.某油田计划在铁路线一侧建造两家炼油厂,同时在铁路线上增建一个车站,用来运送成品油。
由于这种模式具有一定的普遍性,油田设计院希望建立管线建设费用最省的一般数学模型与方法。
1.2.需要解决的问题1.2.1.问题一针对两炼油厂到铁路线距离和两炼油厂间距离的各种不同情形,提出自己的设计方案。
数学建模-历年考题cumcm2000b
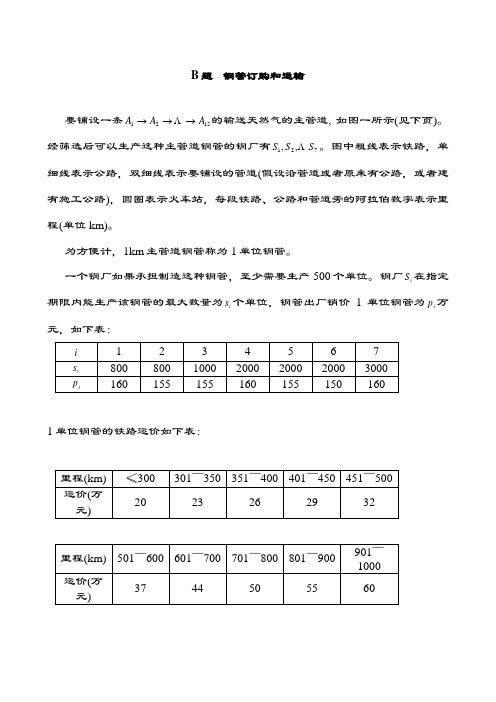
B 题 钢管订购和运输
要铺设一条1521A A A →→→ 的输送天然气的主管道, 如图一所示(见下页)。
经筛选后可以生产这种主管道钢管的钢厂有721,,S S S 。
图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。
为方便计,1km 主管道钢管称为1单位钢管。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限内能生产该钢管的最大数量为i s 个单位,钢管出厂销价1单位钢管为i p 万元,如下表:
1单位钢管的铁路运价如下表:
1000km 以上每增加1至100km 运价增加5
公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算)。
钢管可由铁路、公路运往铺设地点(不只是运到点1521,,,A A A ,而是管道全线)。
(1)请制定一个主管道钢管的订购和运输计划,使总费用最小(给出总费用)。
(2)请就(1)的模型分析:哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并给出相应的数字结果。
(3)如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,请就这种更一般的情形给出一种解决办法,并对图二按(1)的要求给出模型和结果。
7
7。
管道包扎

管道包扎一、摘要家庭中的煤气管道或暖气管道以及化工厂中大量的管道在室外的部分经常需要从外部用很长的带子缠绕包扎,从而对管道加以保护。
在包扎过程中总会考虑到材料最省时需要带子的总量,以及在材料稍微多余的情况下如何包扎才能将材料全部用完的问题。
在这里,我们将建立简单的数学模型并借助数学软件MATLAB求解,利用一些参数可以算出所需最短带子的长度为50.400m,这就解决了第一个问题。
在第二个问题中,带子总长M=51.000m,由此我们算出包扎时每次重叠0.004m 就能刚好把带子用完。
二、问题已知直圆管道的长度,用缠绕的方法包扎管道,需用多长的带子?1、设管道长L = 30m , 圆管截面周长C = 50cm, 带子宽W = 30cm,则最少要用多长M的带子才能将管道缠绕包扎上?2、现有带长M=51m,计划将这条带子全部用来缠绕包扎上面的管道。
缠绕时允许带子互相重叠一部分。
应该如何包扎这个管道?(计算结果精确到0.001)三、问题的分析这是一个很实际化、很生活化的问题,但是题目给得很粗糙,在建立数学模型时为了能顺利解决问题,我们需要作出一些假设,如假设管道是直圆管、带子无弹性等。
根据生活经验,我们需要将带子斜着缠绕在管道上,于是为了使带子全部包住管道而且带子间互不重叠就必须得选择一个适当的角度,为此我们将建立一个简单的数学模型来解决这个问题。
但是,实际生活我们又会遇到这样一个问题,买来的带子通常要稍微多于实际所需要的,这时,我们就得另外建立一个模型,来考虑如何将买来的材料用完并且包扎得比较完美的问题。
四、假设1). 管道是直圆管,粗细一致;2). 带子等宽,无弹性,并且带宽要小于圆管截面周长;3). 为保持包扎过程的连续性以减少劳动量,在包扎过程中昼不将带子剪短;4).针对问题1,假设在包扎过程中带子包住管道且带子互不重叠、边缘衔接处没有空隙:5).针对问题2,假设包扎时带子每次重叠的部分相等;6).为表达更加方便,我们假设一些符号表示——W:带宽,C:截面周长, :倾斜角,W*:问题2中模型上的带宽,L:管长,M:带长五、模型的建立及求解1、问题1模型我们设想将带子已经缠绕在管道上使它包住管道且带子互不重叠、边缘衔接处没有空隙,并且从带子一角的A 点沿圆管母线的方向画一条辅助线l ,再在辅助线与带子边缘的交点处画出圆管的横截面的切口线c ,将画有辅助线的带子剪下一段展开。
2000年数学建模B题钢管订购和运输

钢管订购和运输摘要本文根据问题的条件和要求,建立两个模型,两个模型均为单目标非线性规划模型,并通过求解这两个模型,完整地解决了问题。
由于铁路运输费用函数具有不可加性,不能直接应用现有的最短路算法来求解铁路和公路交通网中任意两点间最小费用路问题。
本文采用了一种分步递推算法,巧妙解决了这一问题。
1278632万元。
.15A →(假1单位钢管的铁路运价如下表:1000km 以上每增加1至100km 运价增加5公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算)。
钢管可由铁路、公路运往铺设地点(不只是运到点,而是管道全线)。
(1)请制定一个主管道钢管的订购和运输计划,使总费用最小(给出总费用)。
(2)请就(1)的模型分析:哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并给出相应的数字结果。
(315A ,的每单i ,j V 的任意两点ik C =运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大。
问题三,利用同问题一一样的方法,从而可求出某钢厂到某某铺设点运输单位钢管的最少运输费用。
(具体算法及程序见附录)模型的假设与符号说明1) 基本假设:○1要铺设的管道侧有公路,可运送所需钢管。
1521,,,A A A○2钢管在运输中由铁路运转为公路运时不计中转(换车)费用; ○3所需钢管均由)7,...,1(=i S i 钢厂提供; ④假设运送的钢管路途中没有损耗。
2) 符号说明:iS : 钢厂i S 的最大生产能力;ip : 钢厂iS 的出厂钢管单位价格(单位: 万元) ;d e ijc jb ijx y j jZ i t W 费用,具体数据如下表1:表1 单位钢管从iS 运输到jA 的最小运输费用(单位:万元)对表1的数据进行分析,我们得到一个非线性规划模型:目标函数是总费用W , 它包含三项: 钢管出厂总价Q , 运输费P , 及铺设费T. 即 W = Q + P + T其中iji j i x p Q ∙=∑∑==71151 ,iji j ij x c P ∙=∑∑==71151,铺设费T 可以如下来确定:jA 开始从左右两个方向铺设,j y 与z j 单位长钢管的费用为(1)12 (2)j jj y y d d d y d++++=与(1)2j jz z d +故 ()()1511122j j j j j y y z z T d =⎡⎤++=+⎢⎥⎢⎥⎣⎦∑目标函数为: 约束条件为:① ② ③④ ⑤0,0,0j ij j x y z ≥≥≥, )15,...,1,7,...,1(==j i i t =0或1 (i=1,..,7)d=0.05;根据模型二编写Lingo 程序,程序运行后,得到最优最小费用为1282142W =万元。
数学建模管道铺设3

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):滨州学院参赛队员(打印并签名) :1:李沙沙2:周洪磊3:杨栓柱指导教师或指导教师组负责人(打印并签名):高合理日期: 2010年 9 月 13 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号)输油管的布置摘要本文讨论了输油管线最佳布置方案及最少费用问题,即最优化问题。
通过分类讨论、图形求解,以及构建非线性规划的目标函数和约束条件,编写程序,然后借助lingo软件,分别给出了三个问题的解决方案。
建立了三个模型,求出了三种情况下的最优管线铺设方案和最少费用。
针对问题一的情形,我们采用分类讨论的方法,细分了三种情况:没有共用管线、有共用管线且共用管线费用与非共用管线费用相同、有共用管线但共用管线费用与非共用管线费用不同。
没有共用管线时,我们根据初等几何中“求直线上一点,到直线一侧的两定点距离之和最短”的知识,利用图形求解,得到了使得铺设管线费用最少的车站建设点。
对于后两种情况,参考了文献[1]中对“费尔马点”问题的推广,即“求一点,使得它到定直线和直线一侧两定点距离之和最短”问题的讨论,结合具体问题进行改进,得到了使得费用最少的管线铺设方案,并求出了最少费用,具体结果见正文。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模之管道包扎
【摘要】:
本文讨论用带子包扎管道,使带子全部包住管道,且用料最省的问题,即在管长一定,带宽一定,管道底边周长一定的情况下,求解出带子如何包扎才能用料最少并建立具体的模型
首先,取用一张细长的纸条,毫无缝隙的绕在一根适当的圆棍上;
其次,用笔画出缠绕后多出管道边缘的部分,并划出一条母线;
然后,展开纸条;
最后, 综合各种模型的优点和缺点,建立模型。
在本文结尾,对模型进行了进一步的改进和优化,使模型更加贴合实际。
【关键词】:
管道包扎、化三维为二维、勾股定理、平移、相似定理
1 问题的重述与分析
用带子包扎管道,使带子全部包住管道,且用料最省
即(1)求出缠绕时的角度
(2)求出带长
2 问题的假设
(1). 直圆管,粗细一致。
(2). 带子等宽,无弹性。
(3). 带宽小于圆管截面周长。
(4). 为省工, 用缠绕的方法包扎管道
3 模型建立的假设
首先,取用一张细长的纸条,毫无缝隙的绕在一根适当的圆棍上; 其次,用笔画出缠绕后多出管道边缘的部分,并划出一条母线;
然后,展开纸条;
4 符号说明
W----带宽
L----管长 l----母线在纸带上的长度
C----管的底面周长
α----缠绕的角度
5 模型建立与分析求解
(1) 纸带展开模型:
O
D
2 / 2
关键是如何在带子起端减去一个合适的直角三角形,使得斜边的长与管子的周长相等。
过B 点作AD 直线的垂线,且长度为W
∴(倾斜角)sin α=C W
∴ OB=22W C - 即在纸带一端剪去一条直角长度为OB,另一条直角边长度为W,的直角三角形
(2)纸条的平移模型
进一步 如果知道直圆管道的长度,用缠绕的方法包扎管道,需用多长的带子? 根据相似三角形定律;
BF C L W =
BF=W
LC 带长模型:OF=BF+OB OF=22W C W
LC -+ 即截一段长为22W C W LC -+的带子 6 模型检验
模型并不太实用,因为毫无缝隙的缠绕在生活中很难实现
7 模型的进一步讨论展望
讨论:如果缠绕时后带压前带的宽度为d,带宽为W,底面周长为C,管长为L. 数学模型,简单说就是用数学语言描述实际现象的过程.数学模型後两对很重拿来的属性,一是合理性,二揍简易性.建立数学模型的过程
B A E F。
