实验11Lingo中数据的导入与导出课案
实验11 Lingo中数据的导入与导出
B( X2) -0.1121112E-01 0.000000
B( X3) -0.5130743 0.000000
B( X4) 0.7885025E-03 0.000000
B( X5) -0.2779719E-02 0.000000
B( X6) 0.3157047 0.000000
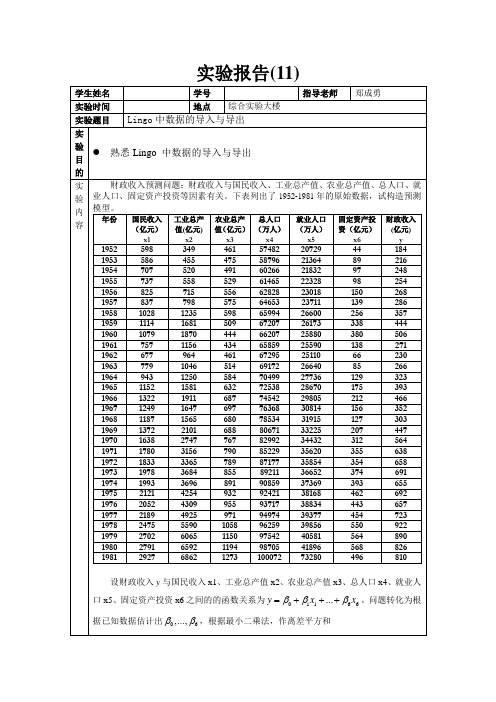
年份国民收入亿元国民收入亿元x1工业总产值工业总产值亿元x2农业总产值亿元农业总产值亿元x3总人口万人总人口万人x4就业人口万人就业人口万人x5固定资产投资亿元固定资产投资亿元x6财政收入亿元y195259834946157482207294418419535864554755879621364892161954707520491602662183297248195573755852961465223289825419568257155566282823018150268195783779857564653237111392861958102812355986599426600256357195911141681509672072617333844419601079187044466207258803805061961757115643465859255901382711962677964461672952511066230196377910465146917226640852661964943125058470499277361293231965115215816327253828670175393196613221911687745422980521246619671249164769776368308141563521968118715656807853431915127303196913722101688806713322520744719701638274776782992344323125641971178031567908522935620355638197218333365789871773585435465819731978368485589211366523746911974199336968919085937369393655197521214254932924213816846269219762052430995593717388344436571977218949259719497439377454723197824755590105896259398565509221979270260651150975424058156489019802791659211949870541896568826198129276862127310007273280496810设财政收入y与国民收入x1工业
Lingo程序设计实验报告

Lingo程序设计实验报告
Lingo程序是一款用于文本编辑和处理的工具程序,它基于Microsoft .NET Framework 开发,支持多种主流的文本编辑操作,例如查找替换、剪切复制、格式调整等,同时还拥
有强大的字符串处理功能,使得用户能够对文本进行更加灵活、便捷的处理。
在Lingo程序设计实验中,我们主要学习了程序的架构、模块设计和代码实现等方面。
首先,我们对程序进行了整体的设计和规划,确定了程序的基本结构和功能模块,并定义
了程序的核心数据结构和算法。
接着,我们使用面向对象的方式,将程序划分为多个不同
的类和对象,为不同的功能模块分别实现了相应的方法和函数。
通过这样的模块化设计,
我们能够更好地管理程序的开发和维护过程,同时也方便了代码的重用和扩展。
在Lingo程序的代码实现过程中,我们首先编写了程序的主体框架和基本输入输出功能,然后分别实现了不同的功能模块,包括字符串查找替换、字符串分割、字符串格式化等。
通过不断的调试和测试,我们最终完成了一个稳定、高效、功能完备的Lingo程序,
它能够满足大多数文本编辑和处理的需求,且易于扩展和修改。
总之,在Lingo程序设计实验中,我们获得了许多宝贵的经验和技能,包括程序分析、设计、编码、测试和调试等方面。
这些经验将有助于我们今后在编写复杂程序时更加自信
和高效,提高我们的专业能力和软件开发水平。
lingo与外部文件间的数据交换

2 5 4ቤተ መጻሕፍቲ ባይዱ2 1 2
5 8 3 7 6 4
9 2 3 1 5 3
MODEL: SETS: WH/@file(my_data.txt)/:AI; VD/@file(my_data.txt)/:DJ; L(WH,VD):C,X; ENDSETS DATA: AI=@file(my_data.txt); DJ=@file(my_data.txt); C=@file(my_data.txt); ENDDATA MIN=@SUM(L(I,J):C(I,J)*X(I,J)); @FOR(WH(I):@SUM(VD(J):X(I,J))<=AI(I)); @FOR(VD(J):@SUM(WH(I):X(I,J))=DJ(J)); END
注意: @OLE只能读一维或二维的Ranges(在单个 的EXCEL工作表(sheet)中),但不能读间 断的或三维的Ranges。Ranges是自左而右、 自上而下来读。
MODEL: SETS: WH//:AI; VD//:DJ; L(WH,VD):C,X; ENDSETS DATA: AI=@ole('my_data.xls','ai'); DJ=@ole('my_data.xls','dj'); C=@ole('my_data.xls','cij'); ENDDATA MIN=@SUM(L(I,J):C(I,J)*X(I,J)); @FOR(WH(I):@SUM(VD(J):X(I,J))<=AI(I)); @FOR(VD(J):@SUM(WH(I):X(I,J))=DJ(J)); END
二、lingo将数据输出到文本文件
函数@text(‘filename ’); 该函数被用在数据部分用来把解输出至文本文件中, 它可以输出集合成员和集合属性值。 这里filename是文件名,可以采用相对路径和 绝对路径两种表示方式。 @text函数仅能出现在模 型数据部分的一条语句的左边,右边是集名(用来 输出该集的所有成员名)或集属性名(用来输出该 集属性的值)。
Lingo教案

第Ⅱ部分运筹学实验§1 LINGO快速入门一、LINDO/LINGO软件简介LINDO和LINGO是美国LINDO系统公司开发的一套专门用于求解最优化问题的软件,这源于芝加哥大学的Linus Schrage教授于1980年前后开发的一套专门用于求解最优化问题的软件包.LINDO用于求解线性规划和二次规划.目前LINGO除了具有LINDO的全部功能外,还可以用于求解非线性规划,也可以用于一些线性和非线性方程组的求解以及代数方程求根等.LINDO和LINGO软件的最大特色是可以求解决策变量为整数的优化问题,而且执行速度很快. LINGO实际上是一种最优化问题的建模语言,简单易学、包括许多常用的函数可调用,并提供与其它数据文件的接口,易于输入、求解和分析大规模最优化问题. 由于这些特点,LINDO和LINGO软件在教学、科研、工业、商业和服务等领域得到广泛应用.本章着重在Microsoft Windows系统下,介绍lingo9.0在运筹学中的使用和课本中相关问题求解的LINGO实现.二、LINGO软件的安装LINGO软件的安装非常简单,在Windows系统下双击运行安装光盘(或其它源)中的安装程序setup.exe,接受安装协议,选择安装目录,选择默认的LINGO 语法(recommended),最后完成(finish)安装.安装完成后,第一次运行LINGO软件,这时提示要输入密码,输入正版的密码输入,即可以使用LINGO软件;当然可以选择测试/试用(demo)版本,这时求解变量不能超过300个.运行成功后得到如下窗口:图1.1图1.1中:File(文件)、Edit(编辑)、LINGO、Window(窗口)和Help为下拉菜单项,下面一行为菜单项中的一些快捷工具按钮.主窗口LINGO Model为输入模型的窗口,在没有命名保存(save)模型时,LINGO自动命名为LINGO1,LINGO2等.点击help菜单的About LINGO 可以获得版本的相关信息,如约束(constrain)、变量(variable)、整数变量(integer variable)、非线性变量(nonlinear variable)的限定个数,可用内存(generator memory)使用等.§2求解规划问题一、LINGO 求解LP 问题下面就用简单的例子来说明LINGO 中线性规划问题的求解. 例2.1求如下线性规划问题:2132min x x z +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥≥+0,600210035026..2121121x x x x x x x t s 在LINGO 模型窗口中图2.1输入:图2.1学习要点:(1) 输入max ,min 后LINGO 就会识别优化类型;数学运算符“乘号,除号,乘方”分别输入“*,/,^”; 关系运算符“≥,≤”分别输入“>=,<=” 来表示; 每行命令结束用“;”来表示.(2)算术运算符按优先级从高到低排序为:-(负号);^;*,/;+,-(减号) (3)关系运算符按优先级从高到低排序为:<,=,>. 输入完毕后,点击求解按钮(或依次点击菜单LINGO/Solve ,或按Ctrl+S),求解状态窗口(LINGO Solve Status )被激活,如图2.2:图2.2此窗口显示:当前的求解状态,包括模型的类型(Model ),解的状态类型(State ),目标值(objective )等,如果模型由于陷入循环等一时无法得到解,可以点击中断求解按钮(Interrupt Solver ).学习要点:(1)LINGO 默认所有变量非负.(2)LINGO 关于求解的种类一般有如下几种(在asibility 处显示):0 全局最优(Global Optimum ) 1 不可行(Infeasible ) 2 无界(Unbounded )3 不确定(Undetermined )4 可行(Feasible )5 可行或者无界(Infeasible or Unbounded )6 局部最优(Local Optimum )7 局部不可行(Locally Infeasible ) 8 目标函数的截断值被达到(Cutoff ) 9 算术运算错误而停止(Numeric Error )当关闭(Close )求解状态窗口时,求解报告窗口(Solution Report )被激活,如图2.3:图2.3求解报告显示:求解所需的迭代次数(iteration )(线性规划默认单纯形法);变量的值(value );及变量变化一个单位时,目标值发生的变化量(Reduced Cost );以及松弛或剩余变量(Slack or Surplus ,按模型输入行的顺序显示)的值和对偶价格(Dual Price ).二、LINGO 求解ILP 问题例2.2 求如下整数规划问题:2123max x x z +=⎪⎩⎪⎨⎧≥≤+≤+且为整数0,14325.45.0..212121x x x x x x t s 在LINGO 模型窗口中按如图2.4输入:图2.4点击求解按钮,就会得到:求解状态窗口显示为纯整数规划(PILP ),全局最优解得到.求解报告窗口显示最优解为x1=4,x2=1,最优值为14. 学习要点:(1)“!”后面可添加为注释语句(注释以英文标识下“;” 结束); “title ” 命令可以添加文档的标题和注释,在解的报告里会显示; LINGO 只有在“!”和“title ” 命令后才可以使用中文字符. (2)LINGO 不区分大小写;(3)LINGO 模型的目标、约束和约束之间的顺序可以颠倒; (4)变量界定函数:@gin(x) :限制x 为整数. @bin(x) : 限制x 为0或1; @bnd(L,x,U) : 限制L ≤ x ≤ U ;@free(x) : 取消对变量x 的默认下界为0的限制,即x 可以为任意 实数;其中符号“@”表示调用函数;三、LINGO 求解非线性规划(NLP)问题例2.3 求如下非线性规划问题:322312119210max x x x x x z -+-+= ⎩⎨⎧≥≤+0,5..2121x x x x t s在模型窗口中输入:max=10*x1+2*x1^2-*x1^3+9*x2-x2^3;x1+x2<=5;运行结果为:x1=2.61,x2=1.73,z=32.33.§3 灵敏度分析对模型的目标函数的系数,约束右端项进行灵敏度分析,首先要激活灵敏度分析.依次点击菜单LINGO|Option|General Solver Tab ,在Dual Computations 列表框中,选择Prices and Ranges 选项.当求解模型时,也作出了灵敏度分析,可以点击菜单LINGO 中的Range (Ctrl+R )来查看.例2.4 对例1.1的线性规划模型,按照上述步骤作灵敏度分析,打开灵敏度分析报告(Range Report )显示如图3.1:图3.1灵敏度分析报告中显示,当前模型中的目标系数(Current Coefficient),约束右端项( Current RHS), 对应参数在其它条件不变的情况下,可允许的增加量和减少量(Allowable Increase, Allowable Decrease),INFINITY 表示无穷.本例显示在其它参数不变的情况下,参数在下列变化范围内,最优基保持不变:目标函数中1x 的系数为2,其允许变化范围为)0,()22,(-∞=--∞,2x 的系数为3,其允许变化范围为)0,()33,(-∞=--∞;第一个约束右端项为350,其允许变化范围为)600,()250350,(-∞=+-∞,第二个右端项为100,其可变化范围为)300,3333.58()200100,6667.41100(=+-,第三个右端项600,其可变化范围为),200(),400600(+∞=+∞-.§4 LINGO中集合的定义与操作当模型的变量、数据较多时,按照前面按照模型逐个输入的办法,就显得力不从心了.LINGO是一种建模语言,使用LINGO语言可以通过输入简单的文字而代替大规模变量和约束,处理大型问题就得心应手.理解LINGO语言,最重要的是理解集合(sets)和属性(atrribute)的概念.下面我们从简单例子出发来说明这些问题.一、定义一个基本集(原始集)基本集的格式为:集合名/成员1,成员2,…/:属性1,属性2,…;例 4.1 产生表示价格的向量x=[35 26 45 78 69 66]:在模型窗口中输入如图4.1:图4.1运行得到:Variable ValueX(1) 35.00000X(2) 26.00000X(3) 45.00000X(4) 78.00000X(5) 69.00000X(6) 66.00000例 4.2 定义一个名为产品的的基本集(可记为products),包括三种产品A,B和C(即它具有成员A,B和C),现在想研究它们对应的单位价格120、100和80以及对应的质量等级1、2和3(即属性可以记为price, quality)在模型窗口中输入如图4.2:图4.2运行结果为:Variable ValuePRICE(A) 120.0000PRICE(B) 100.0000 PRICE(C) 80.00000 QUALITY(A) 1.000000 QUALITY(B) 2.000000 QUALITY(C) 3.000000学习要点:(1)定义一个基本集:集合名/集合的成员/:属性,属性,…,属性; (2)集合要夹在sets 和endsets 之间;(3)连续可编号的n 个成员可以使用1..n 或用带字母的编号表示如w1..wn 来输入,也可以直接以逗号间隔,将n 个成员输入为w1,…,wn ;(4)数据部分要夹在data 和enddata 之间; (5)成员可以当作数据输入.二、定义一个派生集派生集的基本格式:派生集名(基本集1,基本集2,…):属性1,属性2,…;例4.3 导入矩阵⎥⎦⎤⎢⎣⎡=645241A . 在模型窗口中输入如图4.3:图4.3运行结果为:Variable Value A(1,1) 1.000000 A(1,2) 2.000000 A(1,3) 4.000000 A(2,1) 4.000000 A(2,2) 5.000000 A(2,3) 6.000000例4.4 产生矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=314022221221B ,其中“-”表示对应位置没有数据. 在模型窗口中输入如图4.4:图4.4运行结果为:Variable ValueB(1,1) 21.00000B(1,3) 40.00000B(2,1) 12.00000B(2,2) 22.00000B(3,2) 22.00000B(3,3) 31.00000例4.5 在模型窗口中输入:sets:product/1..2/;quality/1..2/;cost/1..2/;links(product,quality,cost):x;endsets运行后会发现:派生集合links产生八个成员:(1,1,1), (1,1,2),(1,2,1),(1,2,2) ,(2,1,1),(2,1,2),(2,2,1),(2,2,2).学习要点:(1)派生集的基本格式为:派生集名(基本集1,基本集2):属性1,属性2,…,属性n;利用派生集可以产生多维数组,它是基本集合成员的所有可能组合;(2)对于派生集,可以定义其具体的成员,其格式与基本集的格式类似:派生集名(基本集1,基本集2)/成员/:属性1,属性2,…,属性n;(3)在例4.4中只取了派生集links中的一些元素,也称为稀疏集.三、集循环函数集循环函数是指对集合的元素进行循环操作的函数,其格式为:@函数名(集合(指标)|过滤条件:表达式)函数有for,max,min,prod,sum五种,分别表示对集合满足过滤条件的每一元素:独立生成表达式,求最大元素,求最小元素,计算乘积,求和.下面以简单例子来介绍@for和@sum函数的使用:1、@for例4.6 产生序列{4 9 16 25 36 49}.在模型窗口中输入:model:sets:number/1..7/:x;endsets@for(number(i)|i#ge#2:x(i)=i^2);end运行结果为:X(2) 4.000000X(3) 9.000000X(4) 16.00000X(5) 25.00000X(6) 36.00000X(7) 49.000002)@sum 求和例4.7 对数列1 2 5 4 6求和.在模型窗口中输入:model:sets:number/1..5/:x;endsetsS=@sum(number(I):x(I));data:x=1 2 5 4 6 ;enddataend运行结果为:Variable ValueS 18.00000X(1) 1.000000X(2) 2.000000X(3) 5.000000X(4) 4.000000X(5) 6.000000学习要点:(1)一个模型可写在model和end之间,这是为了表示一个完整的模型,不至于与模型窗口中的其它模型混淆;(2)集合中使用符号“|”表示其后为过滤条件,只有集合中满足条件的指标才执行其后的表达式;(3)如使用循环函数时,其中number(i) 表示集合number中的第i个元素,循环函数就会遍历number中满足条件的每个元素,执行其后所有表达式;(4)“ge”为逻辑符号,表示“大于等于”,逻辑运算符使用时要夹在“#”之间;所有逻辑运算符按优先级顺序由高到低排序为:not(非);eq(等于),ne(不等于),gt(大于),lt(小于);ge(大于等于),le(小于等于);and(与),or(或).§5 求解运输问题学习了LINGO的集合操作之后,运输问题就可以编写成简单的LINGO程序来求解.例5.1计算有5个产地A1—A5,8个销地B1-B8的运输问题的最优调运方案.分析:六个产地的总产量和为160,8个销售地的销量和为264,故产销不平衡,销大于产.定义集合workshop为有六个成员的产地,shop为有八个成员的销地,a为产量,b为销量,c为单位运价,x为待求调运量,编写程序如图5.1:图5.1运行部分结果为:Objective value: 272.0000X(W1,V1) 0.000000X(W1,V2) 0.000000X(W1,V3) 8.000000X(W1,V4) 0.000000X(W1,V5) 12.00000. . . . . . . .X(W5,V5) 0.000000X(W5,V6) 0.000000X(W5,V7) 0.000000X(W5,V8) 0.000000学习要点:(1)当销大于产时,对任意的销地j,从各个产地调往j的调运量之和不大于b(j),即有需求约束中为小于等于号;若产大于销,则产量约束中为小于等于号;(2)目标函数可以进一步简化为:min=@sum(links: c*x)不影响结果.§6求解网络问题一、最短路问题例6.1 用LINGO 求解图论中§6.3中例6.3.1所示的图6.3.1中从始点1到终点8的最短路问题的求解.分析:图中有8个顶点,需求出从结点1到结点8的最短路;设决策变量⎩⎨⎧=其它,的最短路上到于结点)(当081位,弧,1j i x ij 可把最短问题转化成一个规划问题,∑∈=Ej i ijijxw z ),(min⎪⎪⎩⎪⎪⎨⎧∈≥⎪⎩⎪⎨⎧-=-∑∑∈=∈=E j i x i ,i ,i ,x x ijEi j j ji Ej i j ij ),(,008111s.t.8),(18),(1为中间点为终点为始点 其中ij w 为弧),(j i 上的权(即结点i 与结点j 之间的距离) 在模型窗口中编写程序如图6.1:图6.1运行后部分结果为:Objective value: 12.00000Variable ValueX(1,6) 1.000000 X(5,8) 1.000000 X(6,7) 1.000000 X(7,5) 1.000000这表明路线85761→→→→为从始点1到终点8的最短路,长度为12.学习要点:(1)对无向图要把始点出发的弧和到达终点的弧当作单向弧,其余的等价为双向弧;(2)终点约束与其余约束线性相关可以省略;二、最大流问题例6.2下面介绍运用LINGO 求解§6.4中例6.4.1中图6.4.1所示的从始点s 到终点t 的最大流问题的求解.分析:根据最大流问题的要求和平衡条件,用flow 表示可行流量,可以把它转化成一个规划问题,flow max⎪⎪⎩⎪⎪⎨⎧∈≤≤⎪⎩⎪⎨⎧-=-∑∑∈∈∈∈Aj i c f i ,ti flow ,s i flow ,f f ij ij Ai j V i ji Aj i V j ij ),(,00s.t.),(),(为中间点为终点为始点 在模型窗口中编写程序如图6.2:图6.2运行得到一种最大流方案为:FLOW 22.00000F(S,4) 8.000000 F(2,3) 4.000000F(2,5) 10.00000 F(3,T) 4.000000 F(4,5) 8.000000 F(5,3) 0.000000 F(5,T) 18.00000三、最小费用最大流问题例6.3用LINGO 求解书中§6.5中图6.5.1所示的从始点s 到终点t 的最小费用最大流问题的求解.分析:根据最大流问题的要求和平衡条件,用F 表最大流量,可以把它转化成一个规划问题,∑∈Aj i ij ijf b),(min⎪⎪⎩⎪⎪⎨⎧∈≤≤⎪⎩⎪⎨⎧-=-∑∑∈∈∈∈Aj i c f i ,ti F ,s i F ,f f ij ij Ai j V i ji A j i V j ij ),(,00s.t.),(),(为中间点为终点为始点 根据最大流的求法可求得此网络的最大流量Q=15,编写程序如图6.3:图6.3运行得到一种最小费用最大流方案为:Objective value: 69.00000 F(S,2) 8.000000 F(S,3) 7.000000 F(2,3) 0.000000F(3,4) 7.000000F(4,2) 1.000000F(4,T) 6.000000这与增广链和最短路标号法求得的结果一致.§7 LINGO中外部数据文件的调用一、LINGO中调用文本文件数据调用文本数据函数@file(‘filename’)用于将文本文件中的数据调入LINGO 模型中,可以写相对和绝对路径,文件中的每组数据之间用符号“~”间隔,LINGO 将按照此函数在模型中出现的顺序依次读取每组数据.下面以简例说明之.例7.1 对x=[2 5 8]求和,对y=[3 6 1 4]取其最小元.按如图7.1在模型窗口中编写程序:图7.1其中data1.txt文件与此模型放在同一目录下,内容编写如图7.2:图7.2运行结果可得:S 15.00000,P 1.000000二、LINGO中调用excel数据电子表格数据调用函数@ole(‘filename’)用于将excel表中的数据导入LINGO,文件路径设置与@file函数一致,例7.2 对例7.1,可编程如图7.3:图7.3其中data2.xls文件与模型放在同一目录,编辑如图7.4:图7.4其中要定义单元格A3:A5为集合的名称price,B3:B5定义为x,C3:C6定义为y.定义单元格名称的方法是:选定要定义的单元格,依次打开菜单插入|名称|定义,输入想要定义的名称即可.学习要点:(1)@file和@ole函数可以在模型的集合段,数据段和开始段使用,其他段落不能使用.(2)@ole函数的完整格式为:@ole(‘filename.xls’,[rangelist]),其中rangelist为包含数据的单元范围(与excel表格中的记法一致)(3)这两个函数在集合段可以直接采用@file(‘filename’)和@ole(‘filename’)的形式,而在数据段要采用x=@file(‘filename’)或@ole(‘filename’)格式.。
lingo实验报告

lingo实验报告《lingo 实验报告》一、实验目的本次 lingo 实验旨在深入了解和掌握 Lingo 软件在优化问题求解中的应用,通过实际操作和案例分析,提高对数学建模和优化算法的理解与运用能力。
二、实验环境本次实验使用的计算机配置为:处理器_____,内存_____,操作系统_____。
Lingo 软件版本为_____。
三、实验内容(一)线性规划问题1、问题描述考虑一个生产计划问题,某工厂生产两种产品 A 和 B,生产 A 产品每个需要消耗 2 个单位的原材料和 3 个单位的工时,生产 B 产品每个需要消耗 3 个单位的原材料和 2 个单位的工时。
工厂现有原材料 100 个单位,工时 80 个单位。
A 产品的单位利润为 5 元,B 产品的单位利润为 4 元。
求如何安排生产计划,使得总利润最大。
2、数学模型设生产 A 产品 x 个,生产 B 产品 y 个,则目标函数为:Max Z =5x + 4y约束条件为:2x + 3y <= 1003x + 2y <= 80x >= 0y >= 03、 Lingo 代码及求解结果```lingomodel:max = 5x + 4y;2x + 3y <= 100;3x + 2y <= 80;x >= 0;y >= 0;end```求解结果为:x = 20,y = 20,最大利润为 180 元。
(二)整数规划问题1、问题描述某物流公司需要安排车辆运输货物,有两种车型可供选择,大型车每辆可载货10 吨,小型车每辆可载货5 吨。
共有货物80 吨需要运输,且大型车的数量不能超过 8 辆,小型车的数量不能超过 12 辆。
大型车每辆的运输成本为 100 元,小型车每辆的运输成本为 60 元。
求如何安排车辆,使得运输成本最低。
2、数学模型设安排大型车 x 辆,小型车 y 辆,则目标函数为:Min C = 100x +60y约束条件为:10x + 5y >= 80x <= 8y <= 12x >= 0 且为整数y >= 0 且为整数3、 Lingo 代码及求解结果```lingomodel:min = 100x + 60y;10x + 5y >= 80;x <= 8;y <= 12;@gin(x);@gin(y);end```求解结果为:x = 6,y = 4,最低运输成本为 840 元。
LINGO教程(数据输入输出)

14
例:
LLIINNGGOO 教 程
首先,建立相应的EXCEL数据文件 mydata.xls ,并定义相应的数据单元
B4:B7单元 C4:C7单D元4:D7单元E4:E7单元 F4:F7单元 命名为 CITIES 命名为 CO命S名T 为 NEE命D 名为SUPP命LY名为SOLUTION
用于输出结果
已经存在,则覆盖原文件
11
例:
Lingo程序exam0403.LG4(部分) :
输出表头, 并换行
LLIINNGGOO 教 程
@TEXT('exam0403.txt')=@write(4*' ','Value',12*' ','Dual',13*' ', 输出变量Ordered
'Decrease',8*' ','Increase',@newline(2)); @TEXT('exam0403.txt')=@write('Variables:',@newline(2));
• 打开EXCEL文件 • 菜单命令“插入|对象” • 选择“新建|LINDO
Document”,建立一个空的 LINGO文件对象,且在EXCEL 中出现LINGO菜单 • 输入LINGO 程序内容,即可在 EXCEL中运行LINGO程序 •虽然在EXCEL文件中嵌入了LINGO对象,但需要人工干预才能运行这个对象。 •若希望在EXCEL中自动运行一个LINGO程序 ,则需要将LINGO程序用命令脚 本进行描述,并需要用EXCEL的宏命令进行调用。
数据单元定义方法:选择EXCEL的菜单命令“插入|名称|定义” ,才谈出对话框中输入单元名称
lingo上机实验报告

lingo上机实验报告重庆交通大学学生实验报告实验课程名称专业综合实验Ⅰ开课实验室交通运输工程实验教学中心学院交通运输年级二年级专业班交通运输1班学生姓名学号631205020开课时间2013 至2014 学年第 2 学期总评成绩教师签名实验名称运筹学上机实验(一)实验类型上机实验实验时间2014.5.9—6.16 实验地点BO1机房实验目的:了解LINGO软件的基本入门知识,学习使用LINGO软件对线性规划问题进行灵敏度分析。
仪器、设备名称:LINGO9.0软件实验要求及注意事项:1.写出数学模型;2.在Lingo中输入求解的程序;3.求解得到解报告;4.写出最优解和最优值。
实验内容、操作步骤:一、数学模型:求解线性规划问题max=5*x1+4*x2+3*x3x1+x2+2*x3<=452*x1+x2+x3<=80 S.tx1+3*x2+x3<=90x1,x2,x3>=0并进行灵敏度分析。
二、模型求解:1、在lingo中输入模型如下:2、得出求解报告:(4)选择Dual Computation: Prices & Range;(5)点击OK退出;(6)在键盘上按下ctrl + R。
如图所示:2、灵敏度分析结果如下:Current coefficient—目标函数中变量系数Allowable Increase—允许增加量Allowable Decrease—允许减少量Current RHS—对偶问题系数实验结果分析(含数据、图表整理):结论:(1)该线性规划问题的最优解为:X*=(35,10,0),最优值为Z*=215.(2) c1=5c1在(4,8)内原最优解不变,但最优值是要变的c2=4c2在(2.7,5)内原最优解不变,但最优值是要变的c3=3c3在(-∞,7)内原最优解,最优值都是不变的b1=45b1在(45,50)内原最优基不变,但最优解和最优值是要变的b2=80b2在(67.5,90)内原最优基不变,但最优解和最优值是要变的b3=90b3在(65,∞)内原最优基不变,但最优解和最优值是要变的实验收获、心得及建议:通过对lingo软件的学习和使用,使我初步掌握了用lingo求解最优问题和灵敏度分析的基本方法。
lingo总结

lingo总结集(set)定义原始集的语法规则:集的名字[/集的成员/][:集成员的属性];注意:用“[]”表示该部分内容可选。
显式的:1.sets:students(集的名字)/John ,Jill,Rose ,Mike(集的成员)/:sex,age(集成员的属性);(成员也可以用空格隔开)Endsets (记得这儿是不用分号的)2.集成员不放在集定义中,而在随后的数据部分来定义:sets:students:sex,age;endsetsdata:students,sex,age= John 1 16Jill 0 14Rose 0 17Mike 1 13;enddata隐式sets:students(集的名字)/1..19(集的成员)/:sex,age(集成员的属性);(成员也可以用空格隔开)Endsets(不用一一列出所有的成员)注释是以!开头,以;结束。
有时在定义集时,不写成员,成员在后面再列明。
for example:max z=3*x1+5*x2s.t. x1<42*x2<123*x1+2*x2<=18一维:c1*x1+c2*x2+..+cN*xNsets:decision/1..n/:c,x;endsets@sum(decision(j):c(j)*x(j))多维:a11*x1+a12*x2+...+a1n*xn<=b1 ..am1*x1+am2*x2+...+amn*xn<=bm decision/1..n/:C,x;constraint/1..m/:B;matrix(constraint,decision):A;C=3 5;B=4 12 18;A=1 00 23 2;lingo是不区分大小写的数据的定义:sets:decision/1 2/:C,X;constraint/1..3/:B;Matrix (constraint,decision):A; endsets;max=@sum(decision(i):c(i)*x(i));@for(constraint(i):@sum(decision(j)):a(i,j)*x(j))<b(i));< p="">Data:c=3,5;B=4 12 18;A=1 00 23 2;注意项:(1)将目标函数的表示方式从“min”变成了“min=”(2)“ST”在LINGO 模型中不再需要,所以被删除了(3)每个系数与变量间增加了运算符“*”(即乘号不能省略)(4)每行(目标、约束和说明语句)后面均增加了一个分号“;”(5)模型结束标志“END”也被删除了(LINGO 中只有当模型以“MODEL:”开始时才能以“END”结束)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)@ole('文件名','数据块名称1','数据块名称2')=变量名1,变量名2;
将两个变量的内容分别写入指定文件的两个预先已经定义了名称的数据块,数据块的长度(大小)不应小于变量所包含的数据,如果数据块原来有数据,则@ole写入语句运行后原来的数据将被新的数据覆盖。
年份
国民收入(亿元)
x1
工业总产值(亿元)
x2
农业总产值(亿元)
x3
总人口(万人)
x4
就业人口(万人)
x5
固定资产投资(亿元)
x6
财政收入(亿元)
y
1952
598
349
461
57482
20729
44
184
1953
586
455
475
58796
21364
89
216
1954
707
520
491
60266
21832
选择 使Q达到最小,即可求得财政收入的预测模型。
请用lingo求解 。要求:分别使用@file函数和@ole函数实现数据的导入,并将结果 用@text导出到result.txt文件中。
实验指导
1、文件输入输出函数
输入:@file('filename')
输出:@text('filename')
2、Lingo中的变量默认都是非负的,使用@free(x)可取消x的非负限制。
(2)变量名1,变量名2=@ole('文件名','数据块名称');
左边的两个变量必须定义在同一个集合中,@ole的参数仅指定一个数据块名称,该数据块应当包含类型相同的两列数据,第1列赋值给变量1,第2列赋值给变量2。
(3)变量名1,变量名2=@ole('文件名');
没有指定数据块名称,默认使用Excel文件中与变量名同名的数据块。4.将计算结果导出到Excel文件中
enddata
min=@sum(yearset(i):(y(i)-b0-@sum(ItemSet(k):b(k)*X(i,k)))^2);
(2)@ole('文件名','数据块名称')=变量名1,变量名2;
两个变量的数据写入同一数据块(不止1列),先写变量1,变量2写入另外1列。
(3)@ole('文件名')=变量名1,变量名2;
不指定数据块的名称,默认使用Excel文件中与变量名同名的数据块。
实验结果与分析
首先将上面的原始数据复制到表格中并命名为data存放至c盘中
444
1960
1079
1870
444
66207
25880
380
506
1961
757
1156
434
65859
25590
138
271
1962
677
964
461
67295
25110
66
230
1963
779
1046
514
69172
26640
85
266
1964
943
1250
584
70499
27736
129
323
447
1970
1638
2747
767
82992
34432
312
564
1971
1780
3156
790
85229
35620
355
638
1972
1833
3365
789
87177
35854
354
658
1973
1978
3684
855
89211
36652
374
691
1974
1993
3696
891
90859
37369
3、从Excel文件中导入数据
@ole函数只能用在模型的集合定义段、数据段和初始段,使用格式可以分成以下几种类型:
(1)变量名1,变量名2=@ole('文件名','数据块名称1','数据块名称2');
从指定的Excel文件读取数据,文件名可以包括扩展名(.xls),还可以包含完整的路径目录名称,如果没有指定路径,则默认路径是LINGO的当前工作目录。
代码:1.sets:
yearSet/@ole('c:\data.xls','years')/:y;
ItemSet/x1..x6/:b;
link(yearset,Itemset):X;
endsets
data:
y=@ole('c:\data.xls','incoming');
X=@ole('c:\data.xls','data');
40581
564
890
1980
2791
6592
1194
98705
41896
568
826
1981
2927
6862
1273
100072
73280
496
810
设财政收入y与国民收入x1、工业总产值x2、农业总产值x3、总人口x4、就业人口x5、固定资产投资x6之间的的函数关系为 。问题转化为根据已知数据估计出 ,根据最小二乘法,作离差平方和
实验报告(11)
学生姓名
学号
指导老师
郑成勇
实验时间
地点
综合实验大楼
实验题目
Lingo中数据的导入与导出
实验目的
熟悉Lingo中数据的导入与导出
实验内容
财政收入预测问题:财政收入与国民收入、工业总产值、农业总产值、总人口、就业人口、固定资产投资等因素有关。下表列出了1952-1981年的原始数据,试构造预测模型。
1965
1152
1581
632
72538
28670
175
393
1966
1322
1911
687
74542
29805
212
466
1967
1249
1647
697
76368
30814
156
352
1968
1187
1565
680
78534
31915
127
303
1969
1372
2101
688
80671
33225
207
393
655
1975
2121
4254
932
92421
38168
462
692
1976
2052
4309
955
93717
38834
443
657
1977
2189
4925
971
94974
39377
454
723
1978
2475
5590
1058
96259
39856
550
922
1979
2702
6065
1150
97542
该文件中定义了两个数据块,其中的数据分别用来对变量1和变量2初始化。如果变量名是集合,则对应数据块应该是文本格式表示的集合成员名,如果变量名是集合的属性,则对应数据块应该是一系列数字,并且,若变量是初始集合的属性,则对应的数据块应当是一列数据,若变量是二维衍生集合的属性,则对应数据块应当是二维矩形数据区域。@ole函数无法读取三维数据区域。
97
248
1955
737
558
529
61465
22328
98
254
1956
825
715
556
62828
23018
150
268
1957
837Biblioteka 79857564653
23711
139
286
1958
1028
1235
598
65994
26600
256
357
1959
1114
1681
509
67207
26173
338
