响应面试验设计与分析报告
DesignExpert响应面分析实验的设计案例分析
1.比较分析
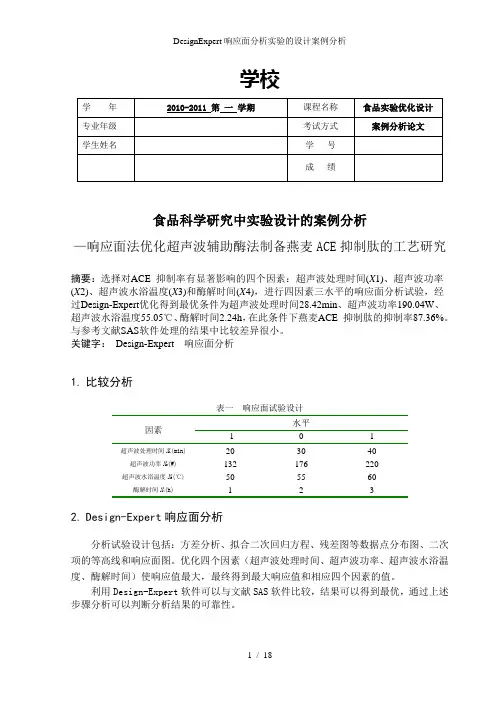
表一响应面试验设计
因素
水平
-1
0
1ห้องสมุดไป่ตู้
超声波处理时间X1(min)
20
30
40
超声波功率X2(W)
132
176
220
超声波水浴温度X3(℃)
50
55
60
酶解时间X4(h)
1
2
3
2.Design-Expert响应面分析
分析试验设计包括：方差分析、拟合二次回归方程、残差图等数据点分布图、二次项的等高线和响应面图。优化四个因素（超声波处理时间、超声波功率、超声波水浴温度、酶解时间）使响应值最大，最终得到最大响应值和相应四个因素的值。
190.08W
55.05℃
2.25h
87.50%
Design-Expert
28.42min
190.04W
55.05℃
2.24h
87.36%
根据两个软件处理结果的数据比较可知各因素最佳工艺条件差异小。
4.案例实验设计和统计分析过程评价
案例中通过Design-Expert软件操作和截下重要的步骤的数据处理的过程的图片，这样可以方便分析和描述，Design-Expert软件能够用清晰和直观的图表表示结果，利于分析，并能够很好的对照和检验文献的数据处理的结果存在的问题和差异。Design-Expert在响应面分析有很强大的功能，能够与文献中SAS软件计算的数据进行比较，SAS软件在计算最大响应面值优于Design-Expert软件，从“ACE抑制率”的比较可知，但差异不大。所以文献中数据没有问题，从分析的结果可知。
图12A及B对ACE抑制率影响的响应面
响应面优化实验
响应面优化实验实验步骤1.输入三因素及其水平,设计响应面实验。
２、应变量3.输入实验数据4.试验方案形成5.实验数据分析利用系统软件SAS8、０对表5实验数据进行二次多项回归拟合,通过RＥSEG(响应面回归)过程进行数据分析，建立二次响应面回归模型,并寻求最优相应因子水平,得到回归方程:Y=2、13６667+0、44６2５X１+0、0４5X2-0、01375X３-0、4４５83Ｘ12-0、1３833X22-０、0908３X32-0、11７5Ｘ1X２＋0、０1５X1Ｘ３－0、07２5X２X3模型得F检验值在α=０、0５时远大于F(9,5）=4、7７，说明方程有很高得显著性。
Ｒ2=0、99７３,表明方程模型与实验数据有9９、73%得符合度,调整后得Ｒ２adj=0、9925,表明方程模型有很高得可信度。
6.正态分布图7.Ｒesｉduaｌs vｓ Prediｃｔeｄ图8.Predｉcｔｅd vs Actuａl 图9.实验实际值与方程预测值10.等高线图11.三维相应曲面图ABAＣBC在获得非线性回归模型与响应面之后,为了求得培养基最佳浓度,对所得得回归拟与方程分别对各自得变量求一阶偏导数，并令其为得到三元一次方程组,求解此方程组可以得到最大多糖量时得最佳条件: X1=0、５066(2、2533%) ,Ｘ2=-0、0488(0、9７56%） , X3＝０、01４4（０、０993%），Y=2、248７g/L。
所以产多糖最高时得培养基组成为:葡萄糖2、2５33%,鱼粉0、97５6%,ＶB1 0、0０3%,NaCｌ０、8%,ＭgSＯ4·7Ｈ2Ｏ0、1%,FeSO4·7H ２O 0、04%,KH2ＰO4 0、0993％，初始ｐH值5、５。
12、用RＳM预测最优值根据最优培养基配方对模型进行验证,香菇菌丝体产粗多糖为2、33g/L,实际值与预测值得误差为+3、６1％。
初始培养基条件下总多糖产量为0、80g/L，优化后提高了１、９１倍。
响应面分析方面
1.Scope of software(4part)
1.1 Response Surface Methods (RSM)
Central Composite 中心组合设计 Box-Behnken 设计 One Factor 单因子设计 Miscellaneous 混杂设计 Optimal 最优设计 User –Defined 用户自定义 Historical Data 历史数据
Optimal 最优设计 User –Defined 用户自定义
Hale Waihona Puke 2. Response Surface Design
响应曲面法( response surface methodology) 是 20 世纪90 年代初西方所兴起的一种试验统计方 法。响应曲面分析法是通过对响应面等值线的分 析寻求最优工艺参数，采用多元二次回归方程来 拟合因素与响应值之间函数关系的一种统计方法。 它囊括了试验设计、建模、检验模型的合适性、 寻求最佳组合条件等众多试验和统计技术。通过 对过程的回归拟合和响应曲面、等值线的绘制, 可方便地求出相应于各因素水平的响应值。 Central Composite Design (CCD)、BoxBehnken Design(BBD)是最常用的实验设计方法。
3.Box-Behnken （BBD）
3.1 进入界面 ：File → New Design(or Open Design)
3.2 选择 Response Surface → Box-Behnken,并选择因素个数
3.3 上图界面完成后，点Continue 进 入下面界面，确定响应（指标）数量
1.2.Factorial Designs
CCD响应面实验案例分析
实验数据分析——方差分析
11
此模型中 因子的主 效应和交 互作用的 显著性 失拟不显著
实验数据分析
12
实验数据分析——响应面分析
13
（a）显示AB25染料浓度和盐度对 P. indicus shell生物质的染料去除 效率的同时影响。随着AB25染料浓度 从90增加到120mg/L，盐度从10增加 到30g/L，AB25染料去除效率增加， 然后保持大致恒定。
实验数据分析——响应面分析
15
AB25染料的去除效率随着虾壳生物量的增加而略有增加，染料去除 达到最佳吸附点后，染料吸附缓慢下降。
实验数据分析——响应面分析
16
显示接触时间对生物吸附剂在染料溶液中对AB25染料去除效率的影 响。随着反应时间的增加，去除效率降低。这些结果表明AB25染料的生 物吸附对时间是有依赖性的。经短时间反应后，大量染料被吸附到生物 质表面上，其中在实验的前25分钟内为吸附速率较快，此后，吸附速率 下降，吸附约在40分钟内达到平衡。
利用虾壳生物质优化酸性蓝25染料的
中心复合设计
Central composite design optimization of Acid Blue 25 dye biosorption using shrimp shell biomass
实验背景
5
除了水生环境中的其他有毒无 机物和有机溶解固体外，合成 染料被认为是最具危害性的水 污染物之一，含有合成染料分 子的废水很难处理。
当pH降低时，生物吸 附效率增加，并且在 pH=2时获得66.67％ 的最大染料去除效率。
中心复合试验
使用P.indicus shell生物量的实际值的中心复合基
响应面试验设计及design-expert实现
响应面试验设计与分析及Design-Expert软件实现
第一部分
响应面试验设计与分析
在响应分析中，观察值y可以表述为：
y f(x1，x2，，xl )
其中 f(x1，x2，，xl )是自变量x1，x2，，xl的函数，是误差项。
在响应面分析中，首先要得到回归方程，然后通过对自变 量 x1，x2，，xl 的合理取值，求得使 yˆ f(x1，x2，，xl )最优 的值，这就是响应面设计试验的目的。
响应面试验设计与分析
立方体
立方点，也称立方体点、角点，即2水平对 应的“-1”和“+1”点。各点坐标皆为+1或-1 。在k个因素的情况下，共有2k个立方点
响应面试验设计与分析及Design-Expert软件实现
第一部分
响应面试验设计与分析
轴向点(axial point)
轴向点，又称始点、星号点，分布在轴向
第一部分
响应面试验设计与分析
响应面方法分类方 法分类
➢中心复合试验设计
(Central Composite Design，CCD)；
➢Box-Behnken试验设计。
响应面试验设计与分析及Design-Expert软件实现
第一部分
响应面试验设计与分析
一般步骤
1. 确定因素及水平，注意水平数为2，因素数一般 不超过4个，因素均为计量值数据；
响应面试验设计与分析及Design-Expert软件实现
第一部分
响应面试验设计与分析
适用范围
➢确信或怀疑因素对指标存在非线性影响； ➢因素个数2-7个，一般不超过4个； ➢所有因素均为计量值数据； ➢试验区域已接近最优区域； ➢基于2水平的全因子正交试验。
DesignExpert响应面法实验设计与案例分析
DesignExpert响应⾯法实验设计与案例分析⾷品科学研究中实验设计的案例分析—响应⾯法优化超声波辅助酶法制备燕麦ACE抑制肽的⼯艺研究摘要：选择对ACE 抑制率有显著影响的四个因素：超声波处理时间(X1)、超声波功率(X2)、超声波⽔浴温度(X3)和酶解时间(X4)，进⾏四因素三⽔平的响应⾯分析试验，经过Design-Expert优化得到最优条件为超声波处理时间28.42min、超声波功率190.04W、超声波⽔浴温度55.05℃、酶解时间2.24h，在此条件下燕麦ACE 抑制肽的抑制率87.36%。
与参考⽂献SAS软件处理的结果中⽐较差异很⼩。
关键字： Design-Expert 响应⾯分析1.⽐较分析表⼀响应⾯试验设计⽔平因素-1 0 1 超声波处理时间X1(min) 20 30 40超声波功率X2(W) 132 176 220超声波⽔浴温度X3(℃) 50 55 60 酶解时间X4(h) 1 2 3 2.Design-Expert响应⾯分析分析试验设计包括：⽅差分析、拟合⼆次回归⽅程、残差图等数据点分布图、⼆次项的等⾼线和响应⾯图。
优化四个因素（超声波处理时间、超声波功率、超声波⽔浴温度、酶解时间）使响应值最⼤，最终得到最⼤响应值和相应四个因素的值。
利⽤Design-Expert软件可以与⽂献SAS软件⽐较，结果可以得到最优，通过上述步骤分析可以判断分析结果的可靠性。
2.1 数据的输⼊图 1 2.2 Box-Behnken响应⾯试验设计与结果图 2 2.3 选择模型图 32.4 ⽅差分析图 4在本例中，模型显著性检验p<0.05，表明该模型具有统计学意义。
由图4知其⾃变量⼀次项A，B，D，⼆次项AC,A2,B2,C2,D2显著(p<0.05)。
失拟项⽤来表⽰所⽤模型与实验拟合的程度，即⼆者差异的程度。
本例P值为0.0861>0.05，对模型是有利的，⽆失拟因素存在，因此可⽤该回归⽅程代替试验真实点对实验结果进⾏分析。
响应面设计
响应面分析在多因素数量处理试验的分析中，可以分析试验指标(依变量)与多个试验因素(自变量)间的回归关系，这种回归可能是曲线或曲面的关系，因而称为响应面分析。
例如农作物产量与N 、P 、K 的施肥量有关，可以通过回归分析建立产量与施肥要素间的回归关系，从而求得最佳施肥配方。
在回归分析中，观察值y 可以表述为：ε+=)，，，(l x x x f y 21其中)，，，(l x x x f 21是自变量l x x x ，，， 21的函数，ε是误差项。
在响应面分析中，首先要得到回归方程)，，，(l x x x f y 21ˆ=，然后通过对自变量l x x x ，，， 21的合理取值，求得使)，，，(l x x x f y 21ˆ=最优的值，这就是响应面分析的目的。
[例13.15] 有一个大麦氮磷肥配比试验，施氮肥量为每亩尿素0，3，6，9，12，15，18kg 7个水平，施磷肥量为每亩过磷酸钙0，7，14，21，28，35，42kg 7个水平，共49个处理组合，试验结果列于表13.66，试作产量对于氮、磷施肥量的响应面分析。
18 0 270.3 9 0274.79 42 278 0 42 88.7 9 21 336.3 921 336.318 42 281.2 18 21 382.2 0 086.90 21 162.5表13.66 大麦氮磷肥配比试验结果 磷 肥 氮 肥 0 3 6 9 12 15 18 0 86.9 162.5 216.4 274.7 274.3 301.4 270.3 7 110.4 204.4 276.7 342.8 343.4 368.4 335.1 14 134.3 238.9 295.9 363.3 361.7 345.4 351.5 21 162.5 275.1 325.3 336.3 381.0 362.4 382.2 28 158.2 237.9 320.5 353.7 369.5 388.2 355.3 35 144.3 204.5 286.9 322.5 345.9 344.6 353.5 4288.7192.5219.9278.0319.1290.5281.2对于表13.66的数据可以采用二元二次多项式拟合，那么产量可表示为：ijj i j i j i ij P b N b P N b P b N b b y ε++++++=25243210其中N i 、P j 、εij 分别表示N 、P 施用量和误差，按此模型的方差分析见表13.67。
DesignExpert响应面分析实验的设计案例分析
学校食品科学研究中实验设计的案例分析—响应面法优化超声波辅助酶法制备燕麦ACE抑制肽的工艺研究摘要：选择对ACE 抑制率有显著影响的四个因素：超声波处理时间(X1)、超声波功率(X2)、超声波水浴温度(X3)和酶解时间(X4)，进行四因素三水平的响应面分析试验，经过Design-Expert优化得到最优条件为超声波处理时间28.42min、超声波功率190.04W、超声波水浴温度55.05℃、酶解时间2.24h，在此条件下燕麦ACE 抑制肽的抑制率87.36%。
与参考文献SAS软件处理的结果中比较差异很小。
关键字：Design-Expert 响应面分析1.比较分析表一响应面试验设计因素水平-1 0 1超声波处理时间X1(min) 20 30 40超声波功率X2(W) 132 176 220超声波水浴温度X3(℃) 50 55 60酶解时间X4(h) 1 2 32.Design-Expert响应面分析分析试验设计包括：方差分析、拟合二次回归方程、残差图等数据点分布图、二次项的等高线和响应面图。
优化四个因素（超声波处理时间、超声波功率、超声波水浴温度、酶解时间）使响应值最大，最终得到最大响应值和相应四个因素的值。
利用Design-Expert软件可以与文献SAS软件比较，结果可以得到最优，通过上述步骤分析可以判断分析结果的可靠性。
2.1 数据的输入图 1 2.2 Box-Behnken响应面试验设计与结果图 22.3 选择模型图 3 2.4 方差分析图 4在本例中，模型显著性检验p<0.05，表明该模型具有统计学意义。
由图4知其自变量一次项A，B，D，二次项AC,A2,B2,C2,D2显著(p<0.05)。
失拟项用来表示所用模型与实验拟合的程度，即二者差异的程度。
本例P值为0.0861>0.05，对模型是有利的，无失拟因素存在，因此可用该回归方程代替试验真实点对实验结果进行分析。
图 5由图5可知：校正决定系数R2(adj)(0.9788>0.80)和变异系数（CV）为0.51%，说明该模型只有2.12%的变异，能由该模型解释。
高老师讲座实验设计与优化-响应面分析
第一部分 影响因素的筛选
每个因子取高、低两个水平（-1和+1），通常， 低水平为原始条件，高水平约取低水平的1.25~1.5 倍左右，一般不超过2倍。 但对某些因子，高低水平的差值不能过大，以防 掩盖了其它因子的重要性，应依据实验条件而定。 当缺乏可参考的数据时，对需结果进行研判，对 负显著和不显著的因素需考虑是否是因为设计不合 理造成，负显著则需减小水平值，不显著可能的原 因是取值过低或取值在B段。
高云涛制作
第二部分 响应面分析
Box-Behnken设计(BBD)和均匀外壳设计， •Box和Behnken设计(1960)将一水平因析设计与平 衡的和不平衡的不完全区组设计结合在一起发展了 一类二水平的_阶设计。 • BBD设计的优点是每个因素只有三水平，所以因 素少。k=3的BBD设计是十分经济的，因此当k>5时， 推荐一般不再采用BBD设计。 •均匀外壳设计？？
高云涛制作
第二部分 响应面分析
星点 设计
建模：因素 与响应值多 元回归分析 模型统方 差分析可 视化 优化
星点设计：因素水平表 星点设计 实验 回归与方差分析 优化
高云涛制作
第二部分 响应面分析
案例 星点设计-效应面法优选灯盏花乙素超声提取
•实验设计--星点设计 因素水平表 通常实验表是以代码的 形式编排的，实验时再转 化为实际操作值，一取值 为 0，±l，±α……。0： 零水平（中央点） ；上 下水平：±l ；上下星号 臂 ±α 。 α=1.414 ， 或 1.732，2.00
高云涛制作
第二部分 响应面优化
•响应法（Response Surface Methodology，RSM）结 合了特定数学与统计方法之集合所衍生出的方法论， 其目的在协助研究人员对科学系统或工业制程中最 佳产品设计、制程改善、系统最佳化等问题提供一 套分析、求解程序，尤其是当系统特性受大量非线 性变量影响，解决多变量问题的一种可视化统计方 法。
DesignExpert响应面分析实验设计案例分析和CCD设计详细教程
DesignExpert响应⾯分析实验设计案例分析和CCD设计详细教程⾷品科学研究中实验设计的案例分析—响应⾯法优化超声波辅助酶法制备燕麦ACE抑制肽的⼯艺研究摘要：选择对ACE 抑制率有显著影响的四个因素：超声波处理时间(X1)、超声波功率(X2)、超声波⽔浴温度(X3)和酶解时间(X4)，进⾏四因素三⽔平的响应⾯分析试验，经过Design-Expert优化得到最优条件为超声波处理时间28.42min、超声波功率190.04W、超声波⽔浴温度55.05℃、酶解时间2.24h，在此条件下燕麦ACE 抑制肽的抑制率87.36%。
与参考⽂献SAS软件处理的结果中⽐较差异很⼩。
关键字：Design-Expert 响应⾯分析1.⽐较分析表⼀响应⾯试验设计因素⽔平-1 0 1超声波处理时间X1(min) 20 30 40超声波功率X2(W) 132 176 220超声波⽔浴温度X3(℃) 50 55 60酶解时间X4(h)2.Design-Expert响应⾯分析分析试验设计包括：⽅差分析、拟合⼆次回归⽅程、残差图等数据点分布图、⼆次项的等⾼线和响应⾯图。
优化四个因素（超声波处理时间、超声波功率、超声波⽔浴温度、酶解时间）使响应值最⼤，最终得到最⼤响应值和相应四个因素的值。
利⽤Design-Expert软件可以与⽂献SAS软件⽐较，结果可以得到最优，通过上述步骤分析可以判断分析结果的可靠性。
2.1 数据的输⼊2.2 Box-Behnken响应⾯试验设计与结果2.3 选择模型2.4 ⽅差分析在本例中，模型显著性检验p<0.05，表明该模型具有统计学意义。
由图4知其⾃变量⼀次项A，B，D，⼆次项AC,A2,B2,C2,D2显著(p<0.05)。
失拟项⽤来表⽰所⽤模型与实验拟合的程度，即⼆者差异的程度。
本例P值为0.0861>0.05，对模型是有利的，⽆失拟因素存在，因此可⽤该回归⽅程代替试验真实点对实验结果进⾏分析。
响应曲面设计与分析
例子：此试验的目标是找出预定控制因子设置，它可在最大化附着 性（脱拉力）的同时最小化尼龙管的组装成本。
因子名称 类型 水平 注释
干扰
控制 3 管道和连接器干扰
壁厚
控制 3 连接器的壁厚度
深度
控制 3 将管道插入至连接器的深度
粘度
控制 3 粘度百分比
时间
噪声 2 处理时间
温度
噪声 2 温度
湿度
噪声 2 相对湿度
20
响应面响应
21
22
交互作用分析
▽\Prediction profiler\Interaction profiler
23
预测刻画器
600 550 500 450 400 350 300 250
预测结果
拉伸 603.75 ±6.0359 66
1
0.5
意愿 0.9987 65
0
0.8 1
1.2 1.4 1.6
High Cur Low
Composite Desirability
1.0000
弹度-1 Maximum y = 603.750 d = 1.0000
硅_1 1.70 [0.70] 0.70
硫_1 2.80 [1.80] 1.80
硅烷_1 60.0 [40.0] 40.0
Percent
Frequency
自定义设计 因子设计 响应面设计
全因子设计,因子个数少,需要考 查交互项
稳健设计 混料设计
预确定设计
5
Minitab软件中DOE的基本类型:
> 因子 > 响应曲面 > 混合 > 田口
6
复习： 中心点center point设计和最大倾斜法
响应面实验设计实例
响应面实验设计实例简介响应面实验设计是一种统计试验设计方法，用于优化和改进多变量系统的性能。
通过系统地探索自变量的不同取值组合，响应面实验设计可以确定最佳的自变量取值，以最大程度地提高系统的性能。
在本文档中，我们将介绍一个响应面实验设计的实例，以展示该方法的应用和效果。
实例背景假设我们是一家生产食品的公司，我们的生产线上有多个工艺参数，包括温度、压力和时间等。
我们希望通过优化这些参数，提高我们产品的质量。
为了实现这个目标，我们决定使用响应面实验设计来找到最佳的工艺参数组合。
设计过程步骤1：确定响应变量首先，我们需要确定一个响应变量来评估我们系统的性能。
在这个实例中，我们选择产品的口感评分作为响应变量，因为我们认为口感是评估产品质量的重要指标。
步骤2：选择自变量接下来，我们需要选择用于优化的自变量。
在这个实例中，我们选择温度、压力和时间作为自变量，因为它们是生产线上的关键工艺参数。
步骤3：确定因子水平对于每个自变量，我们需要确定几个不同的因子水平。
因子水平表示自变量的取值范围。
在这个实例中，我们选择了3个因子水平来测试每个自变量。
因此，总共有3个因子水平的温度、压力和时间。
步骤4：设计实验在这个实例中，我们采用了Box-Behnken设计，这是一种常用的响应面实验设计方法。
Box-Behnken设计是一种中心组合设计，它通过在因子水平的内部和边界上选择试验点，来确定一系列试验点的组合。
该设计方法的特点是需要较少的试验点数，同时可以获得响应变量在因子水平区域内的变化情况。
步骤5：进行实验根据设计，我们进行了一系列实验，记录了每个实验点的温度、压力、时间和口感评分。
这些数据将用于建立响应面模型。
步骤6：建立响应面模型使用实验数据，我们可以建立一个响应面模型。
响应面模型是一个数学模型，可以预测响应变量在不同自变量取值下的值。
在这个实例中，我们选择了二阶多项式模型来描述响应变量（口感评分）与温度、压力和时间之间的关系。
响应面试验方法
响应面试验方法响应面试验方法：带你轻松玩转科学实验嗨，亲爱的小伙伴们！今天我要和你们分享一个超级厉害的科学实验方法——响应面试验方法。
这可是个能让你的实验变得超级有趣又高效的秘籍哦！咱们先来搞清楚啥是响应面试验方法。
简单来说，就像是你要找到一个宝藏，但是这个宝藏的位置不是那么容易确定，响应面试验方法就是帮你在一大片区域里快速缩小范围，找到最有可能藏着宝藏的那个点。
那怎么开始呢？第一步，确定因素和水平。
这就好比你要出门旅游，得先决定去哪个城市，待几天。
比如说你要研究做蛋糕时糖、面粉和鸡蛋的用量对蛋糕口感的影响，那糖、面粉、鸡蛋就是你的因素，而你准备尝试的不同用量就是水平。
我跟你们说，我之前有次做这个，把糖的水平设得太高了，结果做出来的蛋糕甜得能把人齁死，我朋友吃了一口，那表情，就像是被蜜蜂蜇了舌头一样，哈哈哈！第二步，设计实验。
这一步就像是搭积木，你得把各种因素和水平组合好。
常用的有中心组合设计、Box-Behnken 设计等等。
别被这些名字吓到，其实就是给你的实验排个“阵容”。
我有一次设计实验的时候，脑子一抽，把顺序弄乱了，结果做实验的时候那叫一个混乱，感觉自己就像个没头的苍蝇到处乱撞。
第三步，进行实验并收集数据。
这时候可别偷懒，认认真真地按照设计好的方案做实验，把每一次的结果都像宝贝一样记录下来。
第四步，建立模型和分析数据。
这一步就像是给你的实验结果“算总账”，看看哪个因素最重要，它们之间是怎么相互影响的。
我记得我第一次分析数据的时候，看着那些密密麻麻的数字和图表，头都大了，感觉自己像是掉进了数字的迷宫里。
第五步，验证模型。
用新的实验来验证你建立的模型准不准，要是不准，那就得重新回去调整啦。
最后，根据分析结果找到最优的条件。
这就是你最终找到的“宝藏”啦，比如说做蛋糕的最佳配方。
小伙伴们，响应面试验方法其实没有那么难，只要咱们一步一步来，细心点儿，耐心点儿，肯定能玩转它！加油哦，相信你们都能成为实验小能手！好啦，今天的分享就到这里啦，快去试试这个神奇的方法吧！。
响应面试验设计与分析共33页
ห้องสมุดไป่ตู้END
响应面试验设计与分析
36、“不可能”这个字(法语是一个字 )，只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气，不要看破要突 破，不 要嫉妒 要欣赏 ，不要 托延要 积极， 不要心 动要行 动。 38、勤奋，机会，乐观是成功的三要 素。(注 意：传 统观念 认为勤 奋和机 会是成 功的要 素，但 是经过 统计学 和成功 人士的 分析得 出，乐 观是成 功的第 三要素 。
39、没有不老的誓言，没有不变的承 诺，踏 上旅途 ，义无 反顾。 40、对时间的价值没有没有深切认识 的人， 决不会 坚韧勤 勉。
16、业余生活要有意义，不要越轨。——华盛顿 17、一个人即使已登上顶峰，也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人，而用人最大的突破在于信任人。——马云 19、自己活着，就是为了使别人过得更美好。——雷锋 20、要掌握书，莫被书掌握；要为生而读，莫为读而生。——布尔沃
分析响应面实验
• 气体体积（标准条件下气体的摩尔数/泡沫的克数） …对于R141泡沫的压缩强度（psi）的影响。
该实验由Miles负责督导。应用科技实验室报告AT-94-129
1.3
GE Appliances Copyright 1999
Six Sigma Introduction
如果模型中的一个变量以平方项或交互项的形式出现那么该模型中也应包含线通过观察rsqadj残差标准变差残差图以及匹配不足来检查模型的正确性
Six Sigma Introduction
Rev. 10 December 18, 1998
第十节:
分析响应面 实验
1.1
GE Appliances Copyright 1999
1.7
GE Appliances Copyright 1999
Six Sigma Introduction
Rev. 10 December 18, 1998
主要效果图
Stat>ANOVA>Main Effects Plot…
1.8
GE Appliances Copyright 1999
Six Sigma Introduction
•只选择“成分”、 “体积”、“体积 2”项。
•使用左箭头键将选 中的项从“选择”框
外移到“可用”框中 。
在主对话框中，点击“Graphs”。
1.12
GE Appliances Copyright 1999
Six Sigma Introduction
Rev. 10 December 18, 1998
附加残差图
残差正常概率图 （响应变量为强度）
响应面分析方面
Box-Behnken设计方案及平菇多糖得率结果 Run Factor x1 Factor x2 Factor x3 得率/% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 0.00 1.00 0.00 1.00 0.00 0.00 1.00 0.00 -1.00 -1.00 0.00 0.00 0.00 -1.00 1.00 0.00 -1.00 0.00 0.00 0.00 -1.00 -1.00 1.00 1.00 0.00 -1.00 1.00 0.00 1.00 0.00 0.00 0.00 -1.00 0.00 0.00 1.00 0.00 0.00 1.00 1.00 0.00 0.00 0.00 0.00 0.00 -1.00 0.00 1.00 -1.00 -1.00 -1.00
多糖 9.1 8.95 9.13 8.3 8.37 8.53 8.45 9.06 8.13 8.56 9.16 8.41 9.06 8.8 8.86 8.24 8.63
9.1 8.95 9.13 8.3 8.37 8.53 8.45 9.06 8.13 8.56 9.16 8.41 9.06 8.8 8.86 8.24 8.63
Design-Expert是全球顶尖级 的实验设计软件。 DesignExpert 是最容易使用、功能最 完整、界面最具亲和力的软件。 在已经发表的有关响应曲面 （RSM）优化试验的论文中， Design-Expert软件使用最广泛。
How
to start the software File → New Design, File → Open Design: open an existing design