高中数学新课程精品限时训练(16)
高中数学新课程精品限时训练(50)

限时训练(五十)
一、选择题
答案部分
题号
1 2 3 4 5 6 7 89
10Biblioteka 1112答案
BCAACACBB
A
D
D
二、填空题
2
13.
5
14. 3
15. x2 y2 1 y 0
16. 2017
25 16
2018
解析部分
1.解析 由题可得 z 2 i 2 i1 i 1 3 i ,所以 z 1 3 i .故选 B.
6.
若实数
x,y
满足
x
5
y
3
0 ,则 z 2x y 的最小值(
).
x 3y 3 0
A. 3
B.1
C. 6
D. 6
7. 有六名同学参加演讲比赛,编号分别为 1,2,3,4,5,6,比赛结果设特等奖一名,A,B,C,D
四名同学对于谁获得特等奖进行预测. A 说:不是 1 号就是 2 号获得特等奖; B 说:3 号不可能获得
i 3, S 1, A 2 i 4, S 2, A 1 i 5, S 1, A 1 i 6, S 1, A 2 ,由此可得 2
S 的值以 6 为周期循环,循环体为1, 2,1, 1, 2, 1 .因为 i 的初始值为 0 , i 2016 时结束循环,且
2017=6 336 1 ,所以 S 1 .故选 B.
D. 3 1 i 22
2. 已知全集U 1,2,3,4,5 ,集合 A 1,2,5, ðU B 1,3,5 ,则 A B 为( ).
A.2
B.5
C. 1,2,4,5
D. 3,4,5
3. 已知实数 1,x,y,z, 4 成等比数列,则 xyz ( ).
高中数学新课程精品限时训练(26)

限时训练(二十六)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数113i z =-,21i z =-,则12z z +在复平面内对应的点在( ). A .第一象限B .第二象限C .第三象限D .第四象限2.设全集是实数集R ,{}22,M x x x =><-或{}2430N x x x =-+>,则图中阴影部分所表示的集合 是( ).A. {}21x x -< B .{}22x x - C .{}12x x <D .{}2x x <3.已知平面向量()2,1=a ,(),2x =-b ,若//a b ,则a +b 等于( ). A .()2,1-- B .()2,1C .()3,1-D .()3,1-4.定义某种运算S a b =⊗,运算原理如图所示,则式子15π12tan ln e lg10043-⎛⎫⎛⎫⊗+⊗ ⎪ ⎪⎝⎭⎝⎭的值为( ).A .4B .8C .11D .135.把边长为1的正方形ABCD 沿对角线BD 折起,使得平面⊥ABD 平面CBD ,形成三棱锥ABD C -的正视图与俯视图如图所示,则侧视图的面积为 ( ).UA.21 B.41C.42D.226. 已知函数()y f x =()x ∈R 满足()()22f x f x +=,且[]1,1x ∈-时,()1f x x =-+, 则当[]10,10x ∈-时,()y f x =与()4log g x x =的图像的交点个数为( ). A.13B.12C.11D.107.如图所示, 点,A F 分别是双曲线()2222:1,0x y C a b a b-=>的左顶点、右焦点,过点F 的直线l 与C 的一条渐近线垂直且与另一条渐近线和y 轴分别交于,P Q 两点.若AP AQ ⊥,则双曲线C 的离心率是( ).ABC.14+ D.148.在三棱锥P ABC -中,PA 垂直于底面ABC ,90ACB ∠=︒,AE PB ⊥于E ,AF PC ⊥于F ,若2PA AB ==,BPC θ∠=,则当AEF △的面积最大时,tan θ的值为( ).A .2B .12CD.2二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中的横线上.9.已知函数()3log ,02,0x x x f x x >⎧=⎨⎩,则()()19f f=.10.如图所示,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为375颗,以此实验数据为依据可以估计出该不规则图形的ABCDDC B A俯视图正视图1111面积为 平方米(用分数作答).11.在二项式521x x ⎛⎫- ⎪⎝⎭的展开式中,含4x 的项的系数是 .12.已知π02α<<,π3cos 65α⎛⎫ ⎪⎝⎭+=,则cos α= . 13.已知数列{}n a 为等差数列,若23a =,1612a a +=,则789a a a ++= . 14.如图所示, AB MN ∥,且2OA OM =,若OP xOA yOB =+(其中,x y ∈R ),则终点P 落在阴影部分(含边界)时,21y x x +++的取值范围是 .限时训练(二十六)答案部分一、选择题二、填空题 9.14 10. 8311. 10 12. 13. 45 14.4,43⎡⎤⎢⎥⎣⎦解析部分1.解析 因为()()1213i 1i 24i z z +=-+-=-,所以12z z +在复平面上对应的点在第四象限.故选D.2.解析 由图可知,阴影部分表示的集合为UN M ,{}31N x x x =><或,}{22U M x x=-,所以{}21UNM x x =-<.故选A.3.解析 已知()2,1=a ,(),2x =-b ,因为∥a b ,所以212x =-,解得4x =-,所以()4,2=--b ,()+2,1=--a b .故选A.4.解析 15π12tan ln e lg10021+2343-⎛⎫⎛⎫⊗+⊗=⊗⊗ ⎪ ⎪⎝⎭⎝⎭.根据新定义的计算原理,可得()212114⊗=⨯+=,()233219⊗=⨯+=.所以原式21234+9=13=⊗+⊗=.故选D.5.解析 如图所示,在折起形成的三棱锥中,取BD 中点E ,连接CE ,AE .因为DBC △与DAB △分别为等腰直角三角形,所以CE DB ⊥,AE DB ⊥.又因为CE ,AE ⊂平面CAE ,所以DB ⊥平面CAE .所以三棱锥的侧视图为CAE △.又因为平面ABD ⊥平面CBD ,平面ABD 平面CBD BD =,且CE DB ⊥,CE ⊂平面CBD ,所以CE ⊥平面ABD .又因为AE ⊂平面ABD ,所以CE AE ⊥.因为DBC △与DAB △都是等腰直角三角形且腰长为1,所以2CE AE ==,所以1222CEA S =⨯=△14.故选B.6. 解析 由题意,函数()y f x =在区间[]10,10-和()4log g x x =的图像如图所示.观察图像可知,在y 轴右侧,两图像在区间[][][][]1,3,3,5,5,7,7,9各有2个交点,在区间[]9,10有一个交点,在y 轴左侧,两图像在区间[]3,1--上有2个交点,所以共有241+2=11⨯+个交点.故选C.7. 解析 渐近线1:0x y l a b -=,其斜率为ba.因为1PQ l ⊥且直线PQ F 过点(),0c ,所以PQ 的直线方程为()ay x c b=--. 由()0a y x c b x y a b ⎧=--⎪⎪⎨⎪+=⎪⎩,得22222a c x a b abc y a b ⎧=⎪⎪-⎨-⎪=⎪-⎩,即22222,a c abc P a b a b ⎛⎫- ⎪--⎝⎭. 由()a y x c b =--,令0x =,得ac y b =,即0,ac Q b ⎛⎫ ⎪⎝⎭,所以22222,a c abc AP a a b a b ⎛⎫-=+ ⎪--⎝⎭, ,ac AQ a b ⎛⎫= ⎪⎝⎭.因为AP AQ ⊥,所以0AP AQ ⋅=,即222220a c ac abc a a a b b a b ⎛⎫+-⋅= ⎪--⎝⎭,EADCB化简得222c ac a b =+-,由222b c a =-,得22220c ac a --=,得2220e e --=,解得114e +=214e =.故选D. 8. 解析 如图所示,连接EF .因为PA ⊥平面,ABC BC ⊂平面ABC ,所以PA BC ⊥.又因为BC AC ⊥,且=PA AC A ,所以BC ⊥平面PAC .又AF ⊂平面PAC ,所以AF BC ⊥.又因为AF PC ⊥,且PCBC C =,所以AF ⊥平面PBC .又因为EF ⊂平面PBC ,所以AF EF ⊥,故AEF △为直角三角形.可求得AE =()22111242AEF S AF EF AF EF =+=△≤,当且仅当=AF EF 时取等号,此时=1EF .因为AF ⊥平面PBC ,PB ⊂平面PBC ,所以AF PB ⊥.又AE PB ⊥,AF AE A =,所以PB ⊥平面AEF .又因为EF ⊂平面PEF ,所以PB EF ⊥,所以在Rt PEF △中,tan =2EF PE θ==.故选D.9. 解析 因为109>,所以311=log 299f ⎛⎫=- ⎪⎝⎭.因为20-<,所以()212=24f --=,即11=94f f ⎡⎤⎛⎫ ⎪⎢⎥⎝⎭⎣⎦. 10. 解析 设不规则图形的面积为S .根据题意得13751000S =,解得83S =. 11. 解析 521x x ⎛⎫- ⎪⎝⎭展开式的通项为()()()52103+155=1C 1C r r r r r r rr T x x x ----=-,令1034r -=, F EPCBA得2r =,所以4x 的系数为()2251C 10-=.12. 解析 因为π02α<<,所以ππ2π663α<+<,又π3cos 65α⎛⎫+= ⎪⎝⎭,所以π4sin 65α⎛⎫+= ⎪⎝⎭,所以ππππcos cos cos cos6666ααα⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ππ341sin sin 665252α⎛⎫++=+⨯⎪⎝⎭10=. 13. 解析 因为16222+=4=2312a a a d a d a d -+++=,且23a =,所以2d =,所以()()78982336336245a a a a a d ++==+=⨯+⨯=.14. 解析 由OP xOA yOB =+,若点P 在线段AB 上,即,,A B P 三点共线,则有1x y +=. 当点P 在线段MN 上时,2x y +=.所以当点P 落在阴影部分(含边界)时,,x y 需满足的不等式组为120202x y x y +⎧⎪⎨⎪⎩,在平面上画出可行域如图所示.又21111y x y x x +++=+++,11y x ++可看作可行域中的点(),P x y 与定点()1,1C --连线的斜率.结合图可知11BCAC y k k x ++,即11331y x ++,所以42431y x x +++.即21y x x +++的取值范围是4,43⎡⎤⎢⎥⎣⎦.。
2024-2025学年高中数学人教B版必修三课时作业16:两角和与差的正弦

2024-2025学年高中数学人教B 版必修三课时作业(十六)两角和与差的正弦一、选择题1.sin 20°cos 10°-cos 160°sin 10°=()A .-32B .32C .-12D .122.在△ABC 中,若sin B =2sin A cos C ,那么△ABC 一定是()A .等腰直角三角形B .等腰三角形C .直角三角形D .等边三角形3.已知π4<β<π2,sin β=223,则sin (β+π3)=()A .1B .2C .22+36D .22-364.函数f (x )=sin x -cos (x +π6)的值域为()A .[-2,2]B .[-3,3]C .[-1,1]D .[-32,32]二、填空题5.函数y =sin (x +π4)+cos (π4-x )的最大值为________.6.函数f (x )=3sin x +sin (π2+x )的最大值是________.7.函数f (x )=sin (2x -π3)+sin (2x +π3)的最小正周期为________.三、解答题8.已知α,β均为锐角,sin α=55,cos β=1010,求α-β.9.已知函数f (x )=cos 2x +sin (2x -π6).(1)求函数f (x )的最小正周期;(2)若α∈(0,π2),f (α)=13,求cos 2α.[尖子生题库]10.若函数f (x )=(1+3tan x )cos x ,0≤x <π2.(1)把f (x )化成A sin (ωx +φ)的形式;(2)判断f (x )在0上的单调性,并求f (x )的最大值.答案解析1.解析:sin 20°cos 10°-cos 160°sin 10°=sin 20°cos 10°+cos 20°sin 10°=sin (20°+10°)=sin 30°=12,故选D 项.答案:D2.解析:在△ABC 中,因为sin B =sin [π-(A +C )]=sin (A +C )=sin A cos C +cos A sin C =2sin A cos C ,所以sin A cos C -cos A sin C =0,即sin (A -C )=0,因为0<A <π,0<C <π,所以-π<A -C <π,所以A -C =0,即A =C ,所以△ABC 一定是等腰三角形,故选B 项.答案:B3.解析:∵π4<β<π2,∴cos β=1-sin 2β=13,∴sin =12sin β+32cos β=12×223+32×13=22+36.答案:C4.解析:因为f (x )=sin x -cos (x +π6)=sin x -(32cos x -12sin x )=32sin x -32cos x =3(32sin x -12cos x )=3sin (x -π6),所以-3≤f (x )≤3,即函数f (x )=sin x -cos (x +π6)的值域为[-3,3].答案:B5.解析:y =sin (x +π4)+cos (π4-x )=22sin x +22cos x +22cos x +22sin x =2(sin x +cos x )=2sin (x +π4).因为-1≤sin (x +π4)≤1,所以-2≤2sin (x +π4)≤2,故函数的最大值为2.答案:26.解析:因为f (x )=3sin x +cos x =2sin ,所以f (x )的最大值为2.答案:27.解析:由题意,函数f (x )=sin (2x -π3)+sin (2x +π3)=12sin 2x -32cos 2x +12sin 2x +32cos 2x =sin 2x ,所以函数的最小正周期为2π2=π.答案:π8.解析:∵α,β均为锐角,sin α=55,cos β=1010,∴sin β=31010,cos α=255.∵sin α<sin β,∴α<β,∴-π2<α-β<0,∴sin (α-β)=sin αcos β-cos αsin β=55×1010-255×31010=-22,∴α-β=-π4.9.解析:(1)因为f (x )=cos2x +32sin 2x -12cos 2x =32sin 2x +12cos 2x =sin (2x +π6),所以函数f (x )的最小正周期为T =π.(2)由f (α)=13可得,sin (2α+π6)=13.因为α∈(0,π2),所以2α+π6∈(π6,7π6).又因为0<sin (2α+π6)=13<12,所以2α+π6∈(5π6,π),所以cos (2α+π6)=-223,所以cos 2α=cos [(2α+π6)-π6]=cos (2α+π6)cos π6+sin (2α+π6)sin π6=1-266.10.解析:(1)f (x )=(1+3tan x )cos x =cos x +3·sin x cos x·cos x =cos x +3sin x=x +32sin=π6cos x +cos π6sin=2sin ≤x .(2)∵0≤x <π2,∴f (x )在0,π3上是单调减函数.∴当x =π3时,f (x )有最大值为2.。
高中数学新课程精品限时训练(38)

限时训练(三十八)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)已知集合413A x x ⎧⎫=-⎨⎬-⎩⎭…,(){}2log 21B x x =-<,则A B =I ( ).(A )()1,4- (B )()1,3- (C ) ()2,3 (D )()3,4(2)复数z 满足()12i 3i z +=+,则复数z =( ).(A )1i + (B )1i - (C )1i -+ (D )1i -- (3)已知函数()22f x x mx =+-,在区间[]2,4-上随机取一个实数x ,若事件“()0f x '<”发生的概率为23,则m 的值为( ). (A )2(B )2-(C )4(D )4-(4)在ABC △中,三个内角A ,B ,C 所对的边为a ,b ,c ,若cos cos 2cos a B b A c C +=,6a b +=且ABC S =△,则c =( ). (A) (B) (C )3 (D)(5)数列{}n a 满足11=a ,且11n n a a n +=++,对任意的*n ∈N 恒成立,则122017111a a a +++=L ( ). (A )20151008 (B )20171009 (C )40342017 (D )20152018(6)下列命题正确的个数是( ). ①“1x ≠”是“0232≠+-x x”的充分不必要条件② 若()()sin 2f x x θ=+,则“()f x 的图像关于π3x =对称”是“π6θ=-”的必要不充分条件 ③()0,0x ∃∈-∞,使0034xx <成立④命题“角α的终边在第一象限,则α是锐角”的逆否命题为真命题 (A )4 (B )3 (C )2 (D )1(7)过双曲线()222210,0x y a b a b -=>>的右焦点F 作直线by x a=-的垂线,垂足为A 交双曲线左支于B 点,若12OAF OBF S S =△△,则该双曲线的离心率为( ). (A(B )2 (C )(D(8)已知Rt AOB △的面积为1,O 为直角顶点.设向量OAOA=uu r uu r a ,OB OB=uuruur b ,2OP =+uura b ,则PA PB -uu r uu r 的最小值为( ). (A )1(B )2(C)(D )4(9)某三棱锥的三视图如图所示,该三棱锥的外接球半径是( ). (A(B(C(D(10)阅读如图所示的程序框图,运行相应的程序,输出的结果S =( ).(A )20172018 (B )20162017 (C )40332018 (D )40332017俯视图(11)已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示,则π6y f x ⎛⎫=- ⎪⎝⎭图的单调递增区间为( ).(A )πππ,π,44k k k ⎡⎤-+∈⎢⎥⎣⎦Z (B )ππ2π,2π,44k k k ⎡⎤-+∈⎢⎥⎣⎦Z (C )πππ,π,36k k k ⎡⎤-+∈⎢⎥⎣⎦Z (D ) ππ2π,2π,36k k k ⎡⎤-+∈⎢⎥⎣⎦Z (12)设函数()e xxf x =,关于的方程()()210f x mf x +-=⎡⎤⎣⎦有三个不同的实数解,则实数m 的取值范围是( ).(A )1,e e ⎛⎫-∞- ⎪⎝⎭ (B )1e ,e⎛⎫-+∞ ⎪⎝⎭(C )()0,e (D )()1,e 二、填空题:本题共4小题,每小题5分.(13)若变量x ,y 满足约束条件200220x y x y x y +⎧⎪-⎨⎪-+⎩…„…,则2z x y =-的取值范围是________.(14)已知cos 212sin 2αα+=,()tan 2αβ+=,则tan =β .(15)设定义在R 的偶函数()y f x =,满足对任意x R ∈都有()()2f t f t +=-,且(]0,1x ∈时,()1xf x x =+.若20153a f ⎛⎫= ⎪⎝⎭,20165b f ⎛⎫= ⎪⎝⎭,20177c f ⎛⎫= ⎪⎝⎭,则 .(16)过抛物线22y x =的焦点F 的直线分别交抛物线于,A B 两点,交直线12x =-于点P ,若PA mAF =u u u r u u u r ,(),PB nBF m n =∈R u u u r u u u r,则m n +=____________.限时训练(三十八)答案部分一、选择题二、填空题13. []1,2- 14.3415. c b a << 16. 0 解析部分(1)解析 因为{}13A x x =-<„,()()2log 21022242,4x x x B -<⇒<-<⇒<<⇒=, 所以()2,3A B =I.故选C .(2)解析 根据题意可知()()3i 12i 3i 55i1i12i 55z +-+-====-+,所以1i z =+.故选A. (3)解析()20f x x m '=+<,2m x <-,22m -=,4m =-.故选D.(4)解析 由正弦定理得sin cos sin cos 2sin cos A B B A C C +=,()sin 2sin cos A B C C +=⋅,sin 2sin cos C C C =⋅, 因为sin 0C ≠,所以1cos 2C =. ()0,πC ∈,π3C =,又ABC S =△,则1sin 2ab C = 所以8ab =,又因为6a b +=,所以()()2222222cos 2363812c a b ab C a b ab ab a b ab =+-=+--=+-=-⨯=. 所以c =.故选B.(5)解析 因为11n n a a n +=++,所以1n n a a n -=+,即1nn a a n --=,121n n a a n ---=-,…,()2122a a n -=….以上1n -个等式分别相加得()()()11222n n n a a n -+-=….所以()()212122nn n n na -++=+=,所以2121121n a n n n n ⎛⎫==- ⎪++⎝⎭. 所以12201711111111201721223201720181009a a a ⎛⎫+++=-+-++-= ⎪⎝⎭L L .故选B.(6)解析 对于①1x ≠推不出2320x x -+≠,因为22320x x x =⇒-+=,但2320x x -+≠,可得1x ≠且2x ≠,故为必要不充分条件,①为假命题.对于②充分性明显不成立,对于π6θ=-时, ()sin 26f x x π⎛⎫=- ⎪⎝⎭,又sin 21336f πππ⎛⎫⎛⎫=⨯-= ⎪ ⎪⎝⎭⎝⎭,故π3x =是()f x 的对称轴,必要性成立,故②为真命题.对于③()003,0,14x x ⎛⎫∀∈-∞> ⎪⎝⎭,故③为假命题.对于④第一象限角不一定是锐角,原名题为假命题,则其逆否命题为假命题,故选D.(7)解析 设(),0F c ,则直线AB 的方程为()a y x c b =-代入双曲线渐近线方程by x a =-得2,a ab M cc ⎛⎫- ⎪⎝⎭,由2FB FA =u u u r u u u r ,可得2222,33c a ab B c c ⎛⎫+-- ⎪⎝⎭,把B 点坐标代入双曲线方程22221x y a b -=,即()222222224199c a a c a c +-=,整理可得c =即离心率ce a==.故选C. (8)解析 以O 为原点,直线OA 为x 轴建立直角坐标系.由已知2OA OB ⋅=,设()0OA t t =>,则点(),0A t ,20,B t ⎛⎫⎪⎝⎭,()1,0=a ,()0,1=b ,()1,2OP =u u u r . 从而()1,2PA t =--u u u r ,21,2PB t ⎛⎫=-- ⎪⎝⎭u u u r .2,PA PB t t ⎛⎫-=- ⎪⎝⎭u uu r u u u r所以PA PB -u u u r u u u r =2t =时取等号;所以PA PB ⋅u u u r u u u r的最小值为故选A . (9)解析 根据题意,可得出如图所示的三棱锥A BCD -,底面Rt BCD △中,BC CD ⊥,且5BC =,4CD =,侧面ABC △中,高AE BC ⊥于E ,且4AE =,2BE =,3CE =,侧面ACD △中,5AC =.因为平面ABC ⊥平面BCD ,平面ABC I 平面BCD BC =,AE BC ⊥,所以AE ⊥平面BCD ,结合CD ⊆平面BCD ,得AE CD ⊥,因为BC CD ⊥,AE BC E =I , 所以CD ⊥平面ABC ,结合AC ⊆平面ABC ,得AC CD ⊥,所以在ADB △中,AB ==BD ==AD ==设ABC △外心为O ,如图设G 为AB 中点, H 为BC 中点.过1O 的垂线与过CD 中点F 且平行1C C 的直线相交于O ,则O 为外接球球心.则1Rt RtCHO AEB△△:,故1O C HCAB AE=,故14O C=.所以R==.故选D.(10)解析由程序框图知,S可看成一个数列{}n a的前2017项和,其中()()*1,12017nannnn∈=+N„,所以1111111112017112122017201822320172018201820118 S⎛⎫⎛⎫++⋯+++⋯+-⎪ ⎪⎝⎛⎫==---==⎭⎪⎝⎭⎭⨯⨯⨯⎝.故输出的是20172018.故选A.(11)解析由图可知2A=,ππ4π312T⎛⎫=-=⎪⎝⎭,所以2π2πω==.因为由图可得点π,212⎛⎫⎪⎝⎭在函数图像上,可得:π2sin2212ϕ⎛⎫⨯+=⎪⎝⎭,解得ππ22π,122k kϕ⨯+=+∈Z,所以由π2ϕ<,可得π3ϕ=.所以()π2sin23f x x⎛⎫=+⎪⎝⎭.因为若将()y f x=的图像向右平移π6个单位后,得到的函数解析式为()ππ2sin22sin263g x x x⎡⎤⎛⎫=-+=⎪⎢⎥⎝⎭⎣⎦.所以由ππ2π22π,22k x k k-+∈Z剟,可得ππππ,44k x k k-+∈Z剟,所以函数()g x的单调增区间为πππ,π,44k k k⎡⎤-+∈⎢⎥⎣⎦Z.故选A.(12)解析11()()01e ex xx xf x f x x--'=⇒==⇒=,因此当1x„时,()1ef x„;当1x>时()1ef x<<,因此2()10g t t mt=+-=有两个根,其中110,et⎛⎫∈ ⎪⎝⎭,(]21,0et⎧⎫∈-∞⎨⎬⎩⎭U,因为()01g=-,所以110ee eg m⎛⎫>⇒>-⎪⎝⎭.故选B.(13)解析如图所示,2y x z=-,当2y x z=-过()0,1A时,z-取得最大值,此时z取得最小值;当2y x z=-过点()2,2B时,z-取得最小值,此时z取得最大值.故min max1,2z z=-=,故z的范围是[]1,2-.=0评注 2z x y =-的范围呢?这是基本类型,希望同学们滚瓜烂熟!(14)解析 依题意22cos 22sin cos ααα=,故1tan 2α=,故()()()tan tan 3tan tan 1tan tan 4αβαβαβααβα+-=+-==⎡⎤⎣⎦++.(15)解析 ()()()2f t f t f t +=-=,故()y f x =是周期为2的偶函数.()y f x =在(]0,1上为增函数,20151116723333a f f f f ⎛⎫⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,201644140515555b f f f f ⎛⎫⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,201711288777c f f f ⎛⎫⎛⎫⎛⎫==+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,因为111753<<,所以c b a <<. 评注 在研究函数性质特别是奇偶性、周期、对称性、单调性、最值、零点时,要注意用好条件的相互关系,结合特征进行等价转化研究.如奇偶性可实现自变量正负转化,周期可实现自变量大小转化,单调性可实现去“f ”,把函数值的大小转化自变量大小关系.(16)解析 直线1x =-是抛物线的准线,如图设,A B 在直线上的射影分别是,M N ,AM AF =,BN BF =,PA PA AF AM =,PB PB BF BN=,因为//AM BN ,所以PA PBAF BF =,m n =, 又0,0m n <>,所以0m n +=.评注 抛物线问题中抛物线的定义在解题中常常用到.抛物线上点到焦点距离与点到准线的距离常用定义相互转化.利用定义还可得出与焦点弦有关的一些常用结论:(以下图为依据)(1)212y y p =-,1224x x p =;(2)1222sin AB x x p pθ=++=(θ为AB 的倾斜角); (3)11AF BF +为定值2p; (4)以AB 为直径的圆与准线相切; (5)以AF 或BF 为直径的圆与y 轴相切.。
高中数学新课程精品限时训练(14)

高考数学选择题、填空题限时训练理科(十四)一、 选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有 一项是符合题目要求的.1.已知{}2450A x x x =--=,{}21B x x ==,则AB =( ).A. {}1B. {}1,1,5-C. {}1-D. {}1,1,5-- 2.设条件:0p a;条件2:0q a a+,那么p 是q 的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知双曲线()222210,0x y a b a b -=>>).A .2y x =± B.y = C.2y x =±D .12y x =± 4. 已知某四棱台的三视图如图所示,则该四棱台的体积是( ). A .163 B .4 C .143D .65.已知函数()21,0cos ,0x x f x x x ⎧+>=⎨⎩则下列结论正确的是( ).A .()f x 是偶函数 B. ()f x 的值域为[)1,-+∞ C. ()f x 是周期函数 D. ()f x 是增函数6.在ABC △中,2AB=,3AC =,1AB BC ⋅=,则BC =( ).正视图侧视图俯视图C. 7. 设1F ,2F 是双曲线()222210,0x y a b a b-=>>的左、右两个焦点,若双曲线右支上存在一点P ,使()220OP OF F P +⋅=(O 为坐标原点),且12PF =,则双曲线的离心率为( ).A .212+ B.12+C . 213+ D. 13+8.定义在[)1,+∞上的函数()f x 满足:①()()2f x cf x =(c 为正常数);②当24x 时,()()231f x x =-+,若函数()f x 的图像上所有极小值对应的点均在同一条直线上,则=( ).A. 1B. 2C. 1或2D. 2或4 二、填空题(本大题共6小题,每小题5分,共30分) 9. 复数12i1i+-的值是 . 10.若数列{}n a 满足:11a =,()*112n n a a n +=∈N ,其前n 项和为n S ,则44Sa = .11. 在平面直角坐标系下,曲线122:x t a C y t =+⎧⎨=-⎩ (t 为参数),曲线22cos :22sin x C y θθ=⎧⎨=+⎩(θ为参数).若曲线1C ,2C 有公共点,则实数a 的取值范围____________.12. 已知不等式组022020x x y kx y ⎧⎪+-⎨⎪-+⎩,所表示的平面区域的面积为4,则k 的值为__________.13.将A ,B ,C ,D ,E ,F 六个字母排成一排,且A ,B 均在C 的同侧,则不同的排法共有______种(用数字作答). 14. 已知数列:A 123,,,,n a a a a ()*3nn ∈N ,中,令{}*|,1,,A i j T x x a a i j n i j ==+<∈N ,()A card T 表示集合A T 中元素的个数.若1i i a a c +-=(c 为常数,且0c ≠,11in -)则()A card T = .c限时训练(十四)理科参考答案一、选择题二、填空题9.13i2-+ 10. 15 11. 2⎡+⎣ 12. 113. 480 14. ()*223,n nn -∈N解析部分1. 解析 由题意得{}1,5A =-,{}1,1B =-,所以{}1A B =-.故选C.2. 解析 由20a a+解得0a 或1a -,所以p 是q 的充分不必要条件.故选A.3. 解析 由题意得双曲线的渐近线方程为b y x a=±.由2c a =,得22232a b a +=,解得2b a =.故选C. 4. 解析 由四棱台的三视图,还原其立体图形,并构造四棱锥如图所示.所以四棱台的体积1114224112333V =⨯⨯⨯-⨯⨯⨯=.故选C.5. 解析 由函数解析式,画出其图像如图所示,由图可知,()f x 的值域为[)1,-+∞. 故选B.6. 解析 依题意,()21AB BC AB AC AB AB AC AB ⋅=⋅-=⋅-=,且2AB =,3AC =,则6cos 41A -=,5cos 6A =,所以2222cos BC AB AC AB AC A =+-⋅=2223+-2⨯52336⨯⨯=,得3BC =.故选A.7. 解析 由()220OP OF F P +⋅=,得()22OP OF F P +⊥.设2F P 的中点为Q ,连接OQ ,则22OP OF OQ +=,所以2OQ F P ⊥,又1//OQ F P ,因此12PF F △为直角三角形,1290F PF ∠=.依题意,设21PF =,13PF =,122F F =,则离心率12122123F F c c e a a PF PF =====-.故选D.8. 解析 由②可知()f x 在24x上的极小值点为()3,1A .由①得()()12f x f x c=,可得()f x 在[]1,2上极小值点31,2B c ⎛⎫⎪⎝⎭,在[]4,8上的极小值点为()6,C c .又()f x 图像上所有极小值对应的点均在一条直线上,故//ABBC ,又31,12AB c ⎛⎫=--⎪⎝⎭,91,2BC c c ⎛⎫=- ⎪⎝⎭,所以9131122c c c ⎛⎫⎛⎫-=-- ⎪ ⎪⎝⎭⎝⎭,解得1c =或2c =.故选C.9. 解析()()()()12i 1i 12i 13i 1i 1i 1i 2+++-+==--+ . 10. 解析 由112n n a a +=,*n ∈N ,得{}n a 是首项为1,公比为12的等比数列. 所以()()41443341111151a q Sq q a a q q q ---===-. 11. 解析 曲线1C 的直角坐标方程为220x y a +-=,曲线2C 的直角坐标方程为()2224x y +-=.由1C 与2C 有公共点,可得圆心()0,2到直线220x y a +-=的距离2d,即2d =.解得225a+,即22a ⎡∈+⎣.12. 解析 由不等式组,画出可行域,如图所示阴影部分.可得()0,2A ,()2,0C ,联立220x kx y =⎧⎨-+=⎩,得()2,22B k +.由4ABCS =△.即1242BC ⨯⋅=,亦即224k +=,得 1k =.13. 解析 六个字母全排列有66A 720=(种),其中A ,B ,C 三者的位置关系有六种,且A ,B 均在C 的同侧有4种,故六个字母全排列中,A ,B 均在C 同侧有47204806⨯=(种). 14. 解析 由1i i a a c +-=(c 为常数,且0c ≠,11in -),可得数列{}n a 为公差为c 的等差数列.所以()11i a a i c =+-,()11j a a j c =+-,()*,i j ∈N,则()122i j a a a i j c +=++-.由1i j n <,得321i j n +-,所以()()*2131233,A Card T n n n n =--+=-∈N .。
高中数学新课程精品限时训练(10)

限时训练(十) 文科参考答案与解析
一、选择题
题号
1
2
3
4
5
6
7
8
答案
A
B
D
D
B
B
D
D
二、填空题
9. 5 3 8 ; 4 11 5
10.① 0或 2;② 2
11. 9 2
12. 2, 2 2 2
13. 1
53
14.
9
解析部分
1. 解析
1
ai2
i
2
i
2ai
a
,由题意得
2 a 0 1 2a 0
e
3 8
,
4 9
,则双曲线
C2
的离心率取值范围是(
).
A.
5 4
,
5 3
B.
3 2
,
C. 1, 4
D.
3 2
,
4
二、填空题:本大题共 6 小题,每小题 5 分,共 30 分. 把答案填在题中的横线上.
9.
已知 tan
2 ,那么 tan
π 3
________, sin 2
________.
14. 如图所示,某人在垂直于水平地面 ABC 的墙面角的点 A 处进行射击训练,已知点 A 到墙面的距 离为 AB ,某目标点 P 沿墙面上的射线 CM 移动,此人为了准确瞄准目标点 P ,需计算由点 A 观察 点 P 的仰角 的大小(仰角 为直线 AP 与平面 ABC 所成角).
若 AB 15m , AC 25m , BCM 30 ,则 tan 的最大值是________.
综上可知,由①不一定能推出②.由②一定可以推出①.所以①是②的必要不充分条件.故选 B.
高中数学新课程精品限时训练(20)
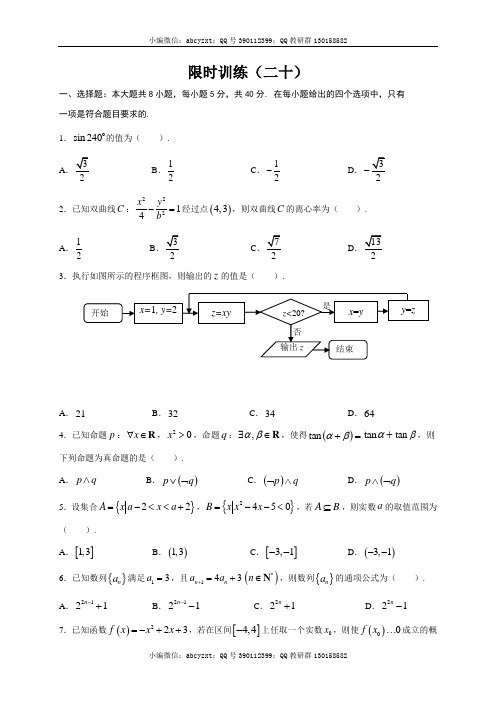
限时训练(二十)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有 一项是符合题目要求的. 1.sin 240o的值为( ).AB .12C .12- D.- 2.已知双曲线C :22214x y b -=经过点()4,3,则双曲线C 的离心率为( ). A .12B.2 C.2 D.23.执行如图所示的程序框图,则输出的z 的值是( ).A .21B .32C .34D .644.已知命题p :x ∀∈R ,20x >,命题q :,αβ∃∈R ,使得()tan αβ+=tan α+tan β,则下列命题为真命题的是( ). A .p q ∧ B .()p q ∨⌝ C .()p q ⌝∧ D .()p q ∧⌝5.设集合{}22A x a x a =-<<+,{}2450B x x x =--<,若A B ⊆,则实数a 的取值范围为( ).A .[]1,3B .()1,3C .[]3,1--D .()3,1-- 6.已知数列{}n a 满足13a =,且143n n a a +=+()*n ∈N ,则数列{}na 的通项公式为( ).A .2121n -+ B .2121n -- C .221n + D .221n -7.已知函数()223f x x x =-++,若在区间[]4,4-上任取一个实数0x ,则使()00f x …成立的概率为( ). A .425B .12C .23D .18.设函数()3233f x x ax bx =++有两个极值点1x ,2x ,且[]11,0x ∈-,[]21,2x ∈,则点(),a b 在平面aOb 上所构成区域的面积为( ). A .14 B .12 C .34D .1二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中的横线上. 9.已知i 为虚数单位,复数1iiz -=,则z = . 10.已知向量(),1x =a ,()2,y =b ,若()1,1=-a +b ,则x y += .11.某种型号的汽车紧急刹车后滑行的距离y km 与刹车时的速度x km /h 的关系可以 用2y ax =来描述,已知这种型号的汽车在速度为60km/h 时,紧急刹车后滑行的距离 为b km .一辆这种型号的汽车紧急刹车后滑行的距离为3b km ,则这辆车的行驶速度12.在平面直角坐标系中,已知曲线1C 和2C 的方程分别为3212x ty t =-⎧⎨=-⎩(t 为参数)和242x ty t=⎧⎨=⎩(t 为参数),则曲线1C 和2C 的交点有 个. 13. 一个几何体的三视图如图所示,图中直角三角形的直角边长均为1,则该几何体体积为 .14.设点()0,1M x ,若在圆O :221x y +=上存在点N ,使得45OMN ∠=o,则0x 的取值范围是 .限时训练(二十)答案部分一、选择题二、填空题9.10. 3- 11.12. 1 13.1614. []1,1- 解析部分1. 解析 ()sin 240sin 18060sin 602=+=-=-o o o o .故选D. 2. 解析 由题可得216914b -=,解得23b =,所以2227c a b =+=,所以2c e a ==. 故选C.3. 解析 1x =,2y =,220z =<→2x =,2y =,420z =<→2x =,4y =,820z =<→4x =,8y =,3220z =>→输出32z =.故选B.4. 解析 因为x ∈R 时,20x …,所以命题p 是假命题;当tan 0α=或tan 0β=时,都有()tan tan tan αβαβ+=+,所以命题q 是真命题,所以()p q ⌝∧是真命题.故选C.5. 解析 由题可得{}15B x x =-<< ,若A B ⊆,则有2125a a --⎧⎨+⎩……,解得13a剟.故选A.6. 解析 因为143n n a a +=+,所以()1141n n a a ++=+.又因为14n a +=,所以{}1n a +是以4为首项,4为公比的等比数列,所以1214442n n n n a -+=⨯==,所以221n n a =-.故选D.7. 解析 令()0f x …,得2230x x -++…,解得1x -…或13x-剟,所以当[]01,3x ∈-时,()00f x …,根据几何概型知成立的概率()()311442P --==--. 故选B.8. 解析 由()3233f x x ax bx =++可得()2363f x x ax b '=++.因为()f x 有两个极值点1x ,2x ,所以()0f x '=有两个根1x ,2x ,且[]11,0x ∈-,[]21,2x ∈.又因为()f x '的图像开口向上,所以有()()()()10001020f f f f '-⎧⎪'⎪⎨'⎪⎪'⎩…………,即2102144a b b a b a b -⎧⎪⎪⎨+-⎪⎪+-⎩…………,对应的可行域如图阴影部分所示,所以点(),a b 在平面aOb 上所构成区域的面积111111121121222222S =⨯-⨯⨯-⨯⨯-⨯⨯=.故选D.9. 解析 221i i i 1i i iz --===--,所以z 10. 解析 ()()2,11,1x y +=++=-a b ,所以2111x y +=⎧⎨+=-⎩,解得12x y =-⎧⎨=-⎩,所以3x y +=-.11. 解析 由题意可得3600b a =,所以33360010800b a a =⨯=,所以这辆车的行驶速度/h x ==.12. 解析 曲线1C 和2C 的直角坐标系方程分别为20x y --=和28x y =,联立方程2208x y x y--=⎧⎨=⎩,消去y ,整理得28160x x -+=,解得4x =,所以1C 和2C 的交点只有1个. 13. 解析 由三视图可知该几何体是底面为直角三角形,高为1的倒置的三棱锥,将其放入正方体中如图所示,所以111111326V ⎛⎫=⨯⨯⨯⨯= ⎪⎝⎭.414. 解析 解法一:如图所示,在圆O 上任取一点N ,连接ON ,在OMN △中,由正弦定理得sin sin ON OMOMN ONM =∠∠,即sin sin ON ONM OM ONM OMN∠==∠∠.又因为3π0,4ONM ⎛⎫∠∈ ⎪⎝⎭,所以(]sin 0,1ONM ∠∈,故(OM ∈,即2012x +…,得011x -剟,所以0x 的取值范围是[]1,1-.解法二:过点M 作圆O 的切线,切点为Q ,连接OQ ,如图所示,则)45,90OMQ ⎡∠∈⎣o o,所以sin sin 452OMQ ∠=o…又在Rt OMQ △中,1sin OQ OMQ OM OM ∠==,所以12OM …,即OM …11x -剟,即0x 的取值范围是[]1,1-.1CA。
高中数学新课程精品限时训练(3)

y x 1
14.设
x,
y
满足约束条件:
y
2
,则 z x y 的最大值_______.
2x y 7
15.已知 a (1,1),OA a b,OB a b .若 △OAB 是以 O 为直角顶点的等腰直角三角形,则
△OAB 的面积是_______.
16.椭圆
x2 a2
y2 b2
1a Βιβλιοθήκη S△PAC1 1 2
5
5 2
, S△PBC
1 2 2
5
5,
因此三棱锥的表面积为 S△PAB S△PAC S△ABC S△PBC
5 2
5 2 2
52 52.
故选 C.
9. 解析 依题意,从10 个球中任取一球,已知它不是白球的情形下,
3 则它是黑球的概率为 .故选 D.
5
10. 解析 依题意,当 i 6 时输出 S的值.
A.若 // , m , n ,则 m//n
B.若 m, n , m// , n// ,则 //
C. m, n 是异面直线,若 m// , m// , n// , n// ,则 //
D. 若 // , m// ,则 m//
6.过点 2, 3 的直线 l 与圆 C : x2 y2 4x 3 0 交于 A, B 两点,当弦 AB 取最大值时,直线
F1Q//l
,
所以直线
F1Q
的斜率为
b c
,可得直角顶点
Q
0,
b
,
且 FQO π ,故 b c . 4
所以椭圆的离心率 e c
c
2
.
a b2 c2 2
b
0 的右焦点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学选择题、填空题限时训练理科(十六)
一、 选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.集合{}|ln ,1A y y x x =∈=>R ,{}2,1,1,3B =--则下列结论正确的是( ). A . {}2,1A B =--
B . ()(),0A B =-∞R
C . [0,)A
B =+∞
D .
(
){}2,1A B =--R
2.已知复数满足(i 1)2z -=,则z 为( ).
A . 1i +
B .1i - C
D. 2 3.下列四个函数中,在闭区间]1,1[-上单调递增的函数是
A .2
x y =
B .x
y 2=
C .x y 2log =
D .x y 2sin =
4.若向量||a
=,||b 2=,(),a b a -⊥则a ,b 的夹角是( ).
A .
5π12 B .π3 C .π6 D .π
4
5.已知变量,x y 满足20
25020
x y x y y --⎧⎪
+-⎨⎪-
⎩
,则31x y u x +=+的取值范围是( ).
A .514,
25⎡⎤⎢⎥⎣⎦ B .11,25⎡⎤
--⎢⎥⎣⎦ C .15,22⎡⎤-
⎢⎥⎣⎦ D .514,25⎡⎤
-⎢⎥⎣⎦
6.如图所示,在执行程序框图所示的算法时, 若输入3a ,2a ,1a ,0a 的值依次是1,3-,
3,1-,则输出v 的值为( ).
A .2-
B .2
C .8-
D .8
z
7.某人根据自己爱好,希望从{},,,O P Q S 中选2个不同字母,从{}0,2,6,8中选3 个不同数字编拟车牌号,要求前3位是数字,后两位是字母,且数字2不能排在首位,字母Q 和数字2不能相邻,那么满足要求的车牌号有( ).
A .198个
B .180个
C .216个 D.234个
8.已知抛物线:C 的焦点为F ,过点F 的直线l 与抛物线C 在第一、四象限分别交于A ,B
两点,
||
3||
AF BF =,则直线l 倾斜角为( ). A .15 B . 30 C . 45 D.60 二、填空题(本大题共6小题,每小题5分,共30分)
9.在ABC △中,三个内角A ,B ,C 所对的边分别是a ,b ,c ,已知2c=,π
3
C =,ABC △,则a b +=________. 10.若x ,y 均为正数,且13
x y =-
,则32
x y +的最小值是 .
11.设P ,Q 分别为直线⎪⎩
⎪⎨⎧
+=+=t
y t
x 53
1541(t 为参数)和曲线π:4C ρθ⎛
⎫=+ ⎪⎝
⎭上的点,
则PQ 的最小值为 .
12.设数列{}n a 是由正数组成的等比数列,n S 为其前n 项和,已知151a a =,37S =, 则5S = .
13.已知函数()3
221(1)3
f x x a x b x =
--+,其中a ,b 为常数,任取[]0,4a ∈,[]0,3b ∈函数()f x 在R 上是增函数的概率为 .
14.长方体1111D C B A ABCD -的底面是边长为a 的正方形,若在侧棱1AA 上至少存在一点E ,使得
︒=∠901EB C ,则侧棱1AA 的长的最小值为 .
)0(22
>=p px y
限时训练(十六) 理科参考答案
一、选择题
二、填空题
9.
4 10. 8 11.
910- 12. 31
4
13.
7
12
14. 2a 解析部分
1. 解析 由题意可得{}
0A y y =>,则
{}
0A y y =R
.所以
(
){}2,1A B =--R
.
故选D.
2. 解析 由题意可得()()()
2i 12i 1i 1i 1i 1z +=
==----+,所以z ==故选C.
3. 解析 函数2
y x =在(),0-∞上单调递减,在()0,+∞上单调递增;函数2log y x =的定义域为
()0,+∞,且在()0,+∞上单调递增;函数sin 2y x =为周期函数,在[]1,1-上不具有单调性;函数
2x y =在R 上单调递增.故选B.
4. 解析 因为()-⊥a b a ,所以()0-⋅a b a =,即2
0-⋅a a b =, 2
=⋅a a b ,又a ,2=b ,
所以cos ,
2⋅===⋅a b a b a b ,故π,4=a b 或7π
,4=a b ,故选D. 5. 解析 x ,y 对应的可行域如图阴影部分所示.
()313333111x y x y y u x x x ++-+-=
==++++,31
y x -+可看作点()1,3P -与可行域内的点的连线的斜率,由图可得3
1
PB PA y k k x -+,12PB k =-,15PA k =-,所以
5
14
2
5
u
.故选A.
6. 解析 由程序框图可知,第一次循环为:31a =,0311v =⨯+=,312i =-=;第二次循环:
23a =-,()1330v =⨯+-=,
211i =-=;第三次循环为:13a =,0333v =⨯+=,110i =-=;第四次循环为:01a =-,()3318v =⨯+-=,011i =-=-.此时循环结束.输出v 的值为8.故选D.
7. 解析 不选2时,有3234A A 72=种; 选2,不选Q 时,有2122
3223C C A A 72=种;选2,选Q 时,
2在数字的中间,有211323A C C 36=种,当2在数字的第三位时,21
33A A 18=种,根据分类计数原理,共有72723618198+++=.故选A.
8. 解析 由题意作图,如图所示.由抛物线的第二定义得,AD AF =,BF BN =.由
3AF
BF
=,得3AD
BN
=.令BF k =,可得2AE k =,4AB k =,则30EBA ∠=,所以直线l 的倾斜角为60.故选D.
9. 解析
由条件知,1π
sin 23
ab =4ab =,因为22π4cos 32a b ab +-=,
所以2
2
8a b +=,所以()2
22
28816a b a b ab +=++=+=,所以4a b +=.
10. 解析 因为213
x
y =-
,所以233x y +=, 则
()321321942312833y x x y x y x y x y ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭
.
当且仅当2294233y x x y ⎧=⎨+=⎩,即34
1
2
x y ⎧
=⎪⎪⎨⎪=⎪⎩时等号成立,所以32x y +的最小值为8.
11. 解析 把直线方程化为:3410l x y -+=,把曲线方程化为
2
2
111:222C x y ⎛
⎫⎛⎫-++= ⎪ ⎪⎝
⎭⎝⎭.所以C
的圆心到直线的距离9
10
d =
=
,
所以min 9910210
PQ d r -=-=
-=. 12. 解析 设此数列的公比为()0q q >,由已知151a a =,得2
31a =所以31a =,由37S =,知
33327a a a q q +
+=,即2610q q --=,解得1
2
q =,进而14a =, 所以55
1412311412
S ⎡⎤
⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦==-. 13.解析 ()()2
2
21f x x a x b '=--+,
若函数()f x 在R 上是增函数,则对于任意x ∈R ,()0f x '恒成立.
所以()2
2
4140a b
∆=--,即()()
110a b a b +---,
设“在()f x 在R 上是增函数”为事件A ,则事件A 对应的区域为()()(){},|110a b a b a b +---,
全部试验结果构成的区域{}(,)|0
4,03a b a b
Ω=,
所以()11
3411337223412
A S P A S Ω⨯-⨯⨯-⨯⨯===⨯. 故函数在R 上是增函数的概率为
7
12
. 14.解析 如图所示,在长方体1111ABCD A B C D -中,若190C EB ∠=,则1C E EB ⊥,且11B C ⊥平面11ABB A ,故11B C BE ⊥,又1111C E
B C C =,1C E ,11B C ⊂平面11B C E ,因此BE ⊥平面11B C E ,
得1BE B E ⊥.在矩形11ABB A 中,由1BE B E ⊥,得11A B E AEB △∽△,即
111A B AE
A E AB
=,设1A E =ka ,则
a AE ka a =
,得a
AE k
=,0k >. 因此1122a
a
AA A E AE ka ka a k
k
=+=+
⋅
=,当且仅当1k =时取“=”.故1AA 长的最小值为2a .
D 1
B 1
C 1
A 1E
D C B
A。
