现代控制理论MATLAB算法
现代控制理论-MATLAB

建模
0 x1 x 0 2 x3 0 x4 0 1 0 mg 0 M 0 0 ( M m) g 0 Ml 0 0 x1 1 0 x2 M u 1 x3 0 x4 1 0 Ml
if rank(ob)==n
disp('系统可观') elseif rank(ob)<n disp('系统不可观') end
%判断可观性%
现代控制理论
状态反馈控制器设计
HPole = [-10,-10,-2-2*sqrt(3)*j,-2+2*sqrt(3)*j];%期望极点 K = acker(A,B,HPole) A0=A-B*K; %极点配置后的系统矩阵 eig(A0) %显示极点配置后的特征根
现代控制理论
状态观测器的设计
%设计一个状态观测器使其极点为-50 -50 -50 -50 op=[-50 -50 -50 -50]; L=(acker(A',C',op))' A2=[A -B*K; L*C A-L*C-B*K]
现代控制理论
y 1
0
0
x1 x 0 2 x3 x4
M=1;m=0.1;l=1
现代控制理论
建模
A = [0 0 0 1 0 0 0 -m*g/M 0 0; 0; 1;
0
B=[ 0; 1/M; 0;
0
g*(M+m)/(M*l)
二次型最优控制器的设计
Klqr = lqr(A,B,Q,R);
现代控制理论MATLAB上机实验指导1

《现代控制理论》MATLAB实践指导书刘红军编写《现代控制理论》MATLAB实践指导书1 MA TLAB概述MA TLAB是MA Trix LABoratory的缩写,早期主要用于现代控制中复杂的矩阵、向量的各种运算。
由于MA TLAB提供了强大的矩阵处理和绘图功能,很多专家因此在自己擅长的领域用它编写了许多专门的MA TLAB工具包(toolbox),如控制系统工具包(control systems toolbox);系统辨识工具包(system identification toolbox);信号处理工具包(signal processing toolbox);鲁棒控制工具包(robust control toolbox);最优化工具包(optimization toolbox)等等。
由于MA TLAB功能的不断扩展,所以现在的MA TLAB已不仅仅局限与现代控制系统分析和综合应用,它已是一种包罗众多学科的功能强大的“技术计算语言(The Language of Technical Computing)”。
MathWorks 公司于1992 年推出了具有划时代意义的MA TLAB 4.0 版本,并推出了交互式模型输入与仿真系统SIMULINK,它使得控制系统的仿真与CAD应用更加方便、快捷,用户可以方便地在计算机上建模和仿真实验。
1997 年MathWorks推出的MA TLAB 5.0 版允许了更多的数据结构,1999 年初推出的MA TLAB 5.3 版在很多方面又进一步改进了MA TLAB 语言的功能。
2000 年底推出的MA TLAB 6.0。
最新版本是MA TLAB7.0。
MA TLAB以矩阵作为基本编程单元,它提供了各种矩阵的运算与操作,并有较强的绘图功能。
MA TLAB集科学计算、图像处理、声音处理于一身,是一个高度的集成系统,有良好的用户界面,并有良好的帮助功能。
MA TLAB不仅流行于控制界,在机械工程、生物工程、语音处理、图像处理、信号分析、计算机技术等各行各业中都有极广泛的应用。
现代控制理论的MATLAB实现

现代控制理论的MATLAB实现现代控制理论是控制工程中一门重要的学科,它研究如何设计和分析控制系统以满足一定的性能指标。
MATLAB是一种功能强大的科学计算和工程仿真软件,广泛应用于控制系统设计与分析。
本文将介绍现代控制理论的一些常见方法在MATLAB中的实现。
1.线性系统的状态空间表示线性系统的状态空间表示是现代控制理论的核心内容之一、在MATLAB中,可以使用`ss`命令创建线性系统的状态空间模型。
例如,假设存在一个二阶线性时不变系统,其传递函数为:可以使用以下代码将其转换为状态空间模型:```matlabnum = [1];den = [1, 1, 1];sys = tf(num, den);ss_sys = ss(sys);```2.线性系统的传递函数表示传递函数是描述线性系统输入输出关系的一种常用表示方法。
在MATLAB中,可以使用`tf`命令创建线性系统的传递函数模型。
例如,假设存在一个二阶线性时不变系统,其状态空间描述为:```matlabA=[0,1;-1,-1];B=[0;1];C=[1,0];D=0;ss_sys = ss(A, B, C, D);```可以使用以下代码将其转换为传递函数模型:```matlabtf_sys = tf(ss_sys);```3.常见控制器的设计与分析现代控制理论中常用的控制器设计方法包括PID控制器、根轨迹法、频率域分析等。
在MATLAB中,可以使用`pid`命令创建PID控制器,并使用`rlocus`命令绘制根轨迹图。
例如,创建一个PID控制器:```matlabKp=1;Kd=0.1;pid_controller = pid(Kp, Ki, Kd);```绘制根轨迹图:```matlabsys = tf([1], [1, 1, 1]);rlocus(sys);```4.系统的频率响应分析频率响应分析是现代控制理论中常用的系统性能评估方法之一、在MATLAB中,可以使用`bode`命令绘制系统的频率响应曲线。
现代控制理论MATLAB算法
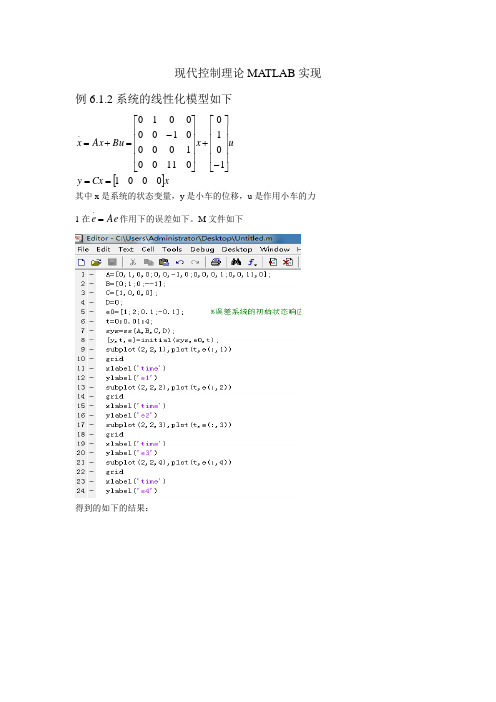
现代控制理论MATLAB 实现例6.1.2系统的线性化模型如下[]xCx y ux Bu Ax x 0001101001100100001000010.==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=+=其中x 是系统的状态变量,y 是小车的位移,u 是作用小车的力 1在Ae e =.作用下的误差如下。
M 文件如下得到的如下的结果:设计一个状态观测器,使得观测器极点是10,10,322,3224321-=-=+-=+-=u u j u j u解 观测器模型如下Ly Bu x LC A x++-=~.)(~运行如下m 文件状态估计的误差状态方程为:e LC A e )(.-=以下进一步通过仿真来检验观测器的效果,取初始误差向量为[]Te 1.01.021)0(-=执行如下m 文件状态估计的误差曲线如下降维观测器的题:例6,3,2考虑系统Cxy Bu Ax x =+=.其中,[]001,100,6116100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=C B A 设计一个具有极点u1=-10,u2=-10,的降维的观测器。
因此降阶观测器的增益矩阵是L=[]T514,具有期望极点的降阶观测器为u y w w ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡---=10260191616114~.~跟踪控制器的设计例5.4.1已知被控对象的状态空间模型为[]xy u x x 21104310.=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--= 设计状态反馈控制器,使得闭环极点为-4和-5,和跟踪控制器。
并讨论闭环系统的稳态性能。
可以知道能稳定跟踪先判断是否能稳定跟踪可以得到如下的结果00.511.522.530.20.40.60.811.21.4time(sec)O u t p u t最优控制的习题例7.2.2考虑以下状态空间模型的描述的系统:其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=100,92735100010B A系统的性能指标J 定义为 ⎰∞+=)(t T T d Ru u Qx x J其中,[]1,100010001=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=R Q 设计最优状态反馈控制器,并检验最优闭环系统对初始状态[]Tx 001)0(=的响应。
现代控制理论MATLAB编程

现代控制理论实验报告姓名:班级:学号:目录一.实验设备二.实验目的三.实验步骤一、实验设备PC计算机1台,MATLAB软件1套。
二、实验目的1。
学习系统状态空间表达式的建立方法、了解系统状态空间表达式与传递函数相互转换的方法;2。
通过编程、上机调试、掌握系统状态空间表达式与传递函数相互转换方法;3。
学习MATLAB的使用方法。
三、实验步骤1、根据所给系统的结构图写出死循环系统的传递函数,若K=10,T=0。
1时阶跃输出下的系统输出响应,并采用MATLAB编程.2、在MATLAB接口下调试程序,并检查是否运行正确.3、给出定二阶系统结构图:图为二阶系统结构图(1)求二阶系统的闭环循环传递函数ɸ(s )=)(1)(s G s G +=K S TS K++2(2)若K=10,T=0。
1,仿真给出阶跃下的系统输出响应把K T 代入方程得Φ(S)= =1)MATLAB 命令得出的系统响应曲线在MATLAB 上输入下列指令:〉> num=[100];>> den=[1,10,100];>> step (num,den)程序运行后显示的时域动态响应曲线(如图2)图为 时域动态响应曲线2)、用进行Simulink 进行仿真启动Simulink并打开一个空白的模块编辑窗口,画出所需模块,并给出正确参数,将画出的所有模块链接起来(如图1),构成一个原系统的框图描述(如图3).选择仿真控制参数,启动仿真过程。
仿真结果示波器显示如图4。
图3二阶系统的Simulink(仿真)图4仿真结果示波器显示(仿真输出)(3) 调整比例系数K,使之从零开始增加。
同时,观察仿真曲线的变化,并给出过阻尼、临界、欠阻尼的条件。
当K=0时的仿真曲线当K=1时的仿真曲线当K=2.5时的仿真曲线当K=3。
5时的仿真曲线当K=4时的仿真曲线根据调整比例系数K,使之从零开始增加,同时观察仿真曲线的变化,得出以下结论;过阻尼的条件:K>2.5时;临界阻尼条件:K=2.5时;欠阻尼的条件:K<2。
现代控制理论Matlab实验报告

现代控制理论第一次Matlab 实验报告一、实验目的:1、学习系统状态空间模型的建立方法、了解状态空间模型与传递函数、零极点模型之间相互转换的方法;2、通过编程、上机调试,掌握系统状态空间模型与传递函数相互转换的方法。
3、通过编程、上机调试,掌握系统模型的联结方法。
二、实验过程实验题目1:(1)在运行以上例程序的基础上,应用MATLAB 求下面传递函数阵的状态空间实现232252()234s s s G s s s s +⎡⎤⎢⎥++⎣⎦=+++ 提示:num =[0 0 1 2;0 1 5 3](2)Matlab 源程序num=[0 0 1 2;0 1 5 3];den=[1 2 3 4];[A ,B ,C ,D ]=tf2ss (num,den);(3)实验结果 A =—2 —3 -4 1 0 00 1 0B =1C =0 1 21 5 3D =实验题目2:(1)一个双输入双输出系统112233412311022711353x x x x u x x -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦11223120011x y x y x ⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦求出此模型的能控标准型和能观标准型.提示:写出两个子系统的传递函数模型,进而求出这两个传递函数模型的能控标准型实现或能观标准型实现,讨论是否能通过子系统的能控标准型实现或能观标准型实现求出原来系统的能控标准型和能观标准型。
(2)Matlab 源程序A=[4 1 -2;1 0 2;1 -1 3];B=[3 1;2 7;5 3];C=[1 2 0;0 1 1];D=[0 0;0 0];[num1,den1]=ss2tf (A,B ,C ,D,1);[num2,den2]=ss2tf(A ,B,C,D,2);(3)实验结果:num1 =0 7。
0000 -19。
0000 —36。
现代控制理论习题与解答MATLAB验证

1 0 2 0 1 1 0 2
解法二 (拉普拉斯变换法)
( sI A) 1
s 0 0 1 1 0 1 1 0 0 s 0 0 0 s 0 0 1
6 / 10
p11 解方程组可得 p12
7 p12 4 p22 5 8
5 8 9 24 7 p12 4 p22 5 8 5 8 9 24
p11 根据矩阵正定性判别的塞尔维斯特方法,对 p12
解以上线性方程组可得
0 (t ) 1
1 (t ) 2et e 2t
1 3 2 2 1 1 2 (t ) et e 2t 2 2
At
所以, e
0 (t ) I 1 (t ) A 2 (t ) A2
1 3 1 1 I (2et e 2t ) A (et e 2t ) A2 2 2 2 2 1 1 1 3 ( A2 2 A)et ( A2 A)e 2t ( A2 A I ) 2 2 2 2
0 s 1 1 1 s 1 0 0 s 1 0
1
1
s 1 s ( s 2) 1 s ( s 2) 0
1 s ( s 2) s 1 s ( s 2) 0
0 0 1 s 1
Gs C sI A B D
1
2 4 s 4 1 2 2 4 s 3 3 1 s2 s 4 14s 6 s 2 15s 10 2 1 2 s s4 s s4
MATLAB 验证: >> A=[3 2;-4 -4]; >>B=[4;3]; >>C=[2 2]; >>D=[1]; >>[num,den]=ss2tf(A,B,C,D) num = 1.0000 den = 1.0000
Matlab程序解现代控制理论与工程中的状态方程.docx

用矩阵指数法解状态方程的MATLAB函数vslovel:函数vslovel:求解线性定常连续系统状态方程的解function [Phit z PhitBu]=vsolvesl(A,B,ut)%vsolvesl求线性连续系统状态方程X^AX+Bu的解%[Phit,phitBu]=vsolvesl(A,B,ut)%A,B系数矩阵%ut控制输入,必须为时域信号的符号表达式,符号变量为t%Phit——输出Phi(t)%P hitBu ------ 输出phi (t-tao)*B*u(tao)在区间(0, t)的积分syms t ta o %定义符号变量t,taoPhit=expm(A*t);%求矩阵指数exp(At)if (B==0)B=zeros(size(A J)J);%重构系数矩阵Bendphi=s ub(Phit/t7t-tao z);%求e xp[A(t-tao)]PhitBu=int(p hi*B*ut/tao 求exp[A(t -tao)]*B*u(t ao)在0~t 区间的积分用拉氏变换法解状态方程的MATLAB函数vslo ve2:函数vslove 2:求解线性定常连续系统状态方程的解functi on [sl_A,sl_ABu]=vsolves l(A,B,us)%vs olves2求线性连续系统状态方程X^AX+B u的解%[sl_A,sl _ABu]=vsolve sl(A,B,ut)%A,B系数矩阵%us控制输入,必须为拉氏变换后的符号表达式,符号变量为s%sl_A——输出矩阵(s l-A)A(-l)拉式反变换的结果%sl_ABu——输出(sl-A)"-l)*B*u(s)拉式反变换后的结果syms s %定义符号变量t,taoAA=s*eye(siz e(A))-A;%求sl-AinvAA=inv(AA );%求(sl-A )矩阵的逆intAAtA A=ilaplace(i ntAA) ;%求intA A 的拉氏反变换sl_A=simplify;%简化拉式反变换的结果if (B==0)B=zeros(siz e(A,l)J);%重构系数矩阵BendtAB=ilaplace(int AA*B*us) ;%求intAA *B*us 的拉氏反变换s l_ABu=simpli fy(tAB);%化简拉式反变换的结果求解时变系统状态方程的MATLAB函数tslove:函数ts love:求解线性时变连续系统状态方程的解fun ction [Phi,P hiBu]=tsolve s(A z B,u,x z a,n)%tsolves求吋变系统状态方程%[Phi ,phiBu]=vsol vesl(A,B,u z x ,a,n)%A,B时变系数矩阵%Phi——状态转移矩阵计算结果%PhiB u——受控解分量%u——控制输入向量,吋域形式%x一一符号变量,指明矩阵A中的时变参数,通常为时间t%a一一积分下限%n ——时变状态转移矩阵屮计算重积分的最大项数,n=0时无重积分项% n=l时包含二重积分项,.....Phi=trans mtx(A,x,a,n);%计算状态转移矩阵P hitao=subs(P hi,x,'tao');%求Phi(tao)讦(B==0)Bt ao=zeros(siz e(AJ),l);%求B(tao)endutao=subs(u,x/ta o');%求u(ta o)PhiBu=simp le(int(Phita o*Btao*utao/taoSa,x));%计算受控分量求解时变系统转移矩阵的MA TLAB函数transm tx:函数transmt x:求解线性时变系统状态转移矩阵function Phi=transmt x(A,x,a,n)%t ransmtx计算时变系统状态转移矩阵%Phi=transmtx(A,x ,a z n)%Phi一一状态转移矩阵计算结果%A时变系数矩阵%x——符号变量,指明矩阵A屮的时变参数,通常为时间t%a ——积分下限%n——吋变状态转移矩阵中计算重积分的最大项数,n=0吋无重积分项 % 时包含二重积分项,••…P hi=eye(size(A));%初始化Phi=lfor Io p=0:nAA=A;for i=l:lop讦(AA==0)break;endAtemp=subs(A A,x,'taoi');AA=sim plify(A*int(Atemp/tao\a,x));endif (AA==O)break;endAte mp=subs(AA,x /taoi');AA=simplif y(A*int(Atem p,'tao',a,x)); %计算重积分Phi=sim plify(Phi+AA );%修正Phiend求解线性定常离散系统状态方程的MA TLAB函数disolv e:函数disolve:求解线性定常离散系统状态方程的解function [Ak,AkBu]=d isolve(A,B,u z)%disolve求线性离散系统状态方程x(k+l)=Ax(k)+B u(k)的解%[Ak,A kBu]=disolve (A,B,uz)%A,B系数矩阵%uz控制输入,必须为Z变换后的符号表达式,符号变量为z%A k——输出矩阵[((zl -A)A(-l)z]Z反变换后的结果%AkBu——输出矩阵[((zl-A )A(_I)*B*U(Z )]Z反变换后的结果sy ms z %定义符号变量zA A=z*eye(size (A))-A;%求zl-Ai nvAA=inv(AA);%求(zl-A)矩阵的逆intAAtAA =iztrans(int AA*z) ;%求intAA *z 的Z 反变换Ak=si mple(tAA);%简化Z反变换的结果if (B==0)B二zeros⑸ze(AJ)J);%重构系数矩阵BendtAB=izt rans(intAA*B *uz) ;%求intAA*B*u z 的Z 反变换AkBu=s imple(tAB);%化简Z反变换的结果求解线性时变离散系统状态方程的MATLAB函数tds olve:函数tdsol ve:求解线性时变离散系统状态方程的解funct ion xk=tsol ve(Ak,Bk,uk,xO,kstart,ke nd)%tdsolve求线性时变离散系统状态方程x(k+l)=A(k)x(k)+B(k)u(k啲解%xk=tsolv e(Ak,Bk,uk,x O,kstart,ken d)%Ak,Bk系数矩阵%uk控制输入,必须为时域符号表达式,符号变量为k%x0初始状态%kstart——初始时刻%kend——终止吋刻%xk一一输出结果,矩阵每一列分别对应x(k 0+l),x(k0+2)….syms k %定义符号变量kif (B k==0)Bk=z eros(size(AJ)J);%重构系数矩阵Bendxk=[];for kk=kst art+1: kendAA=ey e(size(k));for i=kstart:kk-1 %计算A (k-l)A(k-2)....A(kO+l)A(kO)A=subs (Ak/k'J);AA=A*AA;en dAAB=eye(siz e(Ak));BB=ze ros(size(Bk));for i=kk-l :-l:kk+l %计算A(k-l)A(k-2)....A(j+l)B(j)u(j)的累加和A=subs(Ak,‘k;i);AAB=AAB*A;B =subs(Bk/k\kk-l+i+ksta rt);u=subs (uk/k^kk-l +i+kstart);BB=BB+AAB*B *u;endB=subs(Bk/k\kk-l);u=su bs(uk,'k:kk -1);BB=BB+B*u;xk=[xk AA*xO+BB];%计算x(k)end连续系统状态方程离散化的MAT LAB符号函数sc2d:函数sc2d:线性连续系统状态方程的离散化f unction [Ak,Bk]=sc2d(A,B )%sc2d离散化线性连续系统状态方程X^AX+Bu%sysd=s c2d(A,B)%A,B——连续系统的系数矩阵%Ak,Bk ——离散系统系数符号矩阵%离散状态方程为:x(k+l)=Ak*x(k)+Bk*u(k)%Ak,Bk中变量T为采样周期syms t T %定义符号变量tTPhit=expm(A*t);%求矩阵指数exp(At)if (B==0)B=zeros(s ize(AJ)J);%重构系数矩阵BendPhi tB=int(Phit*B;t:O,T); %求e xp(At)*B 在0~T 区间的积分Ak=si mple(subs(Ph it,'t:T));Bk=simple(P hitB);线性时变系统离散化的MATLAB函数tc2d:函数tc2d :线性吋变系统的离散化function [Ak ,Bk]=tc2d(A,B,x,n)%tc2d线性时变系统的离散化%[Ak,Bk]=tc2d (A z B z x,n)%A,B——连续系统的系数矩阵%Ak ——离散化后的系数矩阵A(kt)%B k 一一离散化后的系数矩阵B(kt)%x 一一符号变量,指明矩阵A \B中的时变参数,通常为时间t%n ——时变状态转移矩阵中计算重积分的最大项数,n=0时无重积分项, %n=l时包含二重积分项,.....syms t TPhit=tra nsmtx(A,x,k*T,n);%计算时变系统的状态转移矩阵Ak=simpli fy(subs(Phi,x,(k+l)*T));%计算离散化后的系数矩阵A(kT)Phitao =subs(Phi,x/tao,);%求Phi(t ao)if (B==0)Btao=zero s(size(AJ),l);elseBtao =subs(B,x/t ao');%求B(tao)e ndPhitB=simp le(int(Phita o*Btao/tao,k*7;x,));%计算受控分量Bk=simplify (subs(PhiB,x ,(k+l)*T));%计算离散化后的系数矩阵B(kT)定常系统可控规范I型变换函数ccano nl:函数ccanonl :求线性定常系统的町控规范I型形式functi on [Abar.Bba r,Cbar,T]=cc anonl(A,B,C)%ccanonl求系统X^AX+Bu, y=Cx的可控规范I型系数矩阵%Abar/Bbar,Cbar/——变换后的可控规范I型系数矩阵%T 一一相似变换矩阵n=len gth(A);Co=ct rb(A,B);if (rank(Co)~=n),%判断系统可控性errorC系统不可控!J;endR s=sym(polymt x(A));%计算R矩阵并转变为符号矩阵Rs形式As=sym(A);%讲矩阵A 转变为符号矩阵AsBs=s ym⑻;%讲矩阵B转变为符号矩阵BsTs=Bs;fo r i=l:n-l zTs=[As A i*BsTs];endTs =Ts*Rs;%计算相似变换符号矩阵TsAbar=n umeric(inv(T s)*As*Ts);%实现矩阵A的相似变换并转变为数值形式Bbar=numeric(i nv(Ts)*Bs);%实现矩阵B的相似变换并转变为数值形式Cbar=numer ic(inv(C)*Ts ); %实现矩阵C的相似变换并转变为数值形式T=nume ric(Tc);%相似变换矩阵T转变为数值形式求系统相似变换的R矩阵函数polymt x:函数polymtx:求系统相似矩阵变换的R矩阵function R =polymtx(A)%R=polymtx(A) ------- A 须为方针%[10 0 0]% [a(n-l) 10 0]% R= [a(n-2) a(n-l) 0 0][•・♦••••.. •••]% [a (2) a(3)l 0]% [a(l ) a(2)a(n-l) 1]%英中a(i)(i=l z...n-l)^J矩阵A的特征多项式%|s*l-A|=s A n+a(n-1 )*s A(n-l)+...+a(l)*s+a(0)%的各项系数d=siz e(A);if (len gth(d)~=2),%判断系统可控性errorf错误:非二维矩阵!9;endif (d(l)-=d (2)),%判断系统可控性error (,错误:A非方针!endn=d(l);A s=sym(A);p=s ym2poly(poly (As));R=[];f or i=l:nR=[R P(l:nH;P=[o p(l:n)[;en dR二numeric(R );线性定常系统可控分解函数cdecomp:函数cdecomp:线性定常系统的可控性分解fun ction [Abar/Bbar z Cbar,P]=cdecomp(A,B ,C)%cdecomp可控性分解%[Abar,Bbar/Cbar,P]=cdecomp(A z B ,C)%若系统不完全可控,则存在相似变换矩阵P,使得% -1 ・:!%Abar=P*A*P/Bbar=P*B, Cb ar=C*P%其中%Ab ar=|Ac A121 ,Bbar= | Be |z Cbar= |Cc Cu c||0 Auc| |0|%(Ac,Bc)构成系统的可控子空间As =sym(A); %转变为符号矩阵求解Bs=sym(B);Cs=sym(C);nA=size(A s,l);Ms=sym(ctrb(As,Bs));%求可控性矩阵Mn二nume ric(rank(IVIs));P二[];%系统不可控,计算变换矩阵Pi=l;while nume ric (rank(P)%取M的n个线性无关列矢量至P矩阵P=[P Ms (:J)]; if (numeric(e(P,2)),P (:,size (P,2))=[];endi=i+l;endE=s ym(eye(size(A)));i=l;w hile numeric A,%収某一单位向量至P阵使P满秩P=[P E(:,i)];if (n umeric(rank()),P (:,size(P,2))=[];e ndi=i+l;endelseP =ey&size(A));%若系统可控,取P=1endAbar=num enc(inv(P)*A*P);%转变为数值矩阵输岀Bbar =numeric(inv (P)*B);Cbar二nume ric(inv(C*P));P 二numeric(P);线性定常系统可观分解函数odecomp:函数odecomp:线性定常系统的可观性分解f unction [Aba r,Bbar,Cbar/P]=odecomp(A ,B,C)%odecom p可控性分解%[Abar,Bbar,Cbar,P ]=odecomp(A,B,C)%若系统不完全可观,则存在相似变换矩阵P,使得%-1 J%Abar=P*A*P,Bbar=P*B z C bar=C*P%其中%A bar=|Ao 0| /Bbar=|B o |,Cbar=|Co 0|| A 21 Ano||Bno|%(A o,Bo)构成系统的可观子空间%根据对偶原理,应用可控性分解函数cdec omp实现可观性分解[a bar,bbar,cba r,P]二cdecomp (A:B'C);A bar=abar,;B bar=cbar';C bar=bbar z;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
现代控制理论MATLAB 实现
例6.1.2系统的线性化模型如下
[]x
Cx y u
x Bu Ax x 00
01101001100
1000010000
1
0.
==⎥
⎥⎥⎥⎦⎤
⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢
⎢⎣⎡-=+=
其中x 是系统的状态变量,y 是小车的位移,u 是作用小车的力 1在Ae e =.
作用下的误差如下。
M 文件如下
得到的如下的结果:
设计一个状态观测器,使得观测器极点是
10,10,322,3224321-=-=+-=+-=u u j u j u
解 观测器模型如下
Ly Bu x LC A x
++-=~
.
)(~
运行如下m 文件
状态估计的误差状态方程为:
e LC A e )(.
-=
以下进一步通过仿真来检验观测器的效果,取初始误差向量为
[]T
e 1.01.021)0(-=
执行如下m 文件
状态估计的误差曲线如下
降维观测器的题:例6,3,2考虑系统
Cx
y Bu Ax x =+=.
其中,[]001,100,6116100010=⎥⎥
⎥⎦
⎤
⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=C B A 设计一个具有极点u1=-10,u2=-10,的降维的观测器。
因此降阶观测器的增益矩阵是L=[]T
514,具有期望极点的降阶观测器为
u y w w ⎥
⎦
⎤
⎢⎣⎡+⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡---=10260191616114~.~
跟踪控制器的设计例5.4.1已知被控对象的状态空间模型为
[]x
y u x x 21104310
.
=⎥⎦⎤⎢⎣⎡+⎥
⎦⎤⎢⎣⎡--= 设计状态反馈控制器,使得闭环极点为-4和-5,和跟踪控制器。
并讨论闭环系统
的稳态性能。
可以知道能稳定跟踪
先判断是否能稳定跟踪
可以得到如下的结果
00.51
1.52
2.53
0.2
0.4
0.6
0.8
1
1.2
1.4
time(sec)
O u t p u t
最优控制的习题例7.2.2考虑以下状态空间模型的描述的系统:
其中⎥⎥
⎥⎦
⎤
⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=100,92735100010B A
系统的性能指标J 定义为 ⎰
∞
+=
)(t T T d Ru u Qx x J
其中,[]1,100010001=⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡=R Q 设计最优状态反馈控制器,并检验最优闭环系统对初始状态[]T
x 00
1)0(=的响应。
2
46
8
-0.5
00.5
1
t(sec)
x 2
02
468
-1.5
-1-0.50
0.5t(sec)
x 3。
