公交车调度方案的优化模型
可变线路式公交车辆调度优化模型

i ∈S
( ) 1
. t . s
∑x ∑x
, i j
/ { } S 1 = 1, j∈S / { S S} = 1, j∈S
( ) 2 ( ) 3 ( ) 4 ( ) 5 ( ) 6 ( ) 7 ( ) 8 ( ) 9 ( ) 1 0
, i j
T S S i∈ S i >A i +T s, e Pk ≤l k ∈ N1 ∪ N3 k ≤T k, T Pk < T Dk , k∈ N T Pk ≥ T Rk , k ∈ N1 ∪ N3 ) ≤C NB( t∈ ( 0, T) t B ,
0 引 言
随着经济的发 展 和 机 动 化 水 平 的 提 高 , 城市 交通拥堵问题也不断加剧 。 公共交通在道路交通 资源的充分利用上具有私人交通无法比拟的优越 性, 已经成为缓解道路交通拥堵的 1 条重要途径 。 ) 可变线路 式 公 交 ( 作为1种新 f l e x r o u t e t r a n s i t - 融合了常规公交运营模式 型公 交 运 营 模 式 , ( 的高成本效益以及需求响应式公交系统 F R T) ( ) 能够提供门到门的公交运输 D R T 的机动灵活 , 是解决城郊 地 区 公 交 服 务 问 题 的 1 条 重 要 服务 , 途径 。 可变线路式公 交 可 以 描 述 为 : 车辆在一定的 服务区域内围绕 基 准 线 路 运 行 , 并在松弛时间内 偏离基准路线行 驶 , 在乘客要求的地点停车上下 客 。 车辆行驶过 程 中 满 足 一 定 的 时 空 限 制 , 即车 辆驶离基 准 路 线 为 乘 客 提 供 站 外 上 下 车 服 务 之 需要返回基准线路继续行驶 , 并且满足线路上 后, 固定站点的时间约束 。 根据可变线路式公交乘客 的上下车位置可 以 将 其 分 为 4 类 : 站外上车站外 、 、 下车 ( 站内 上 车 站 外 下 车 ( 站外上车 I类 ) I I类 ) 。 站内下车 ( 和站内上车站内下车( I I I类 ) I V 类) 其运行模式见图 1, 其中 1 和s 为公交线路的首末 站。
公交线路发车频率优化的双层规划模型及其解法_于滨

主要研究更具普遍意义的第二种优化方法 。在发 车频率制定的过程中 , 存在着供给 (公交企业 )和 需求 (乘客 )两个主体 , 供 、需双方是相互作用 、 相互影响的 , 即供给方依据线路的客流量制定发 车频率 , 而需求方调整自己的行为来适应这个频
收稿日期 :2005-12-01. 基金项目 :国家自然科学基金资助项目 (50479055). 作者简介 :于滨 (1977 - ), 男 , 博士研究生. 研究方向 :网格 , 智能公交. E-ma il:m in lfish@ yahoo. com. cn 通讯联系人 :程春田 (1965 - ), 男 , 教授 , 博士生导师. 研究方向 :电力系统优化 , 防汛减灾.
m k n =Umk +1
Sk - 1 m
- (n
-
1) /rk ) +Rmk
f)
M o 分为三部分 :①等待车辆费用 τw 是在车
辆到站前 , 站台上的乘客 (不包括上趟车 留剩的
乘客 )等待的时间费用 ;②等待上车费用 τμ是车 辆到站后 , 在站台停车期间乘客在车外等待上车
的时间费用 ;③额外费用 τφ是留剩乘客 (受车容 量限制被留剩在站台上的乘客 )等待当前车辆和
吉 林 大 学 学 报 (工 学 版 )
Journa l o f Jilin U niversity (Enginee ring and T echno logy Ed ition)
V o.l 36 N o. 5 S ep.t 2006
文章编号 :1671 - 5497(2006)05 - 0664 - 05
第 36卷
辆车在第 k 站的停车时间 , Smk
=m
ax(uU
k m
车辆调度和路线优化的设计方案

车辆调度和路线优化的设计方案在现代物流和交通运输中,车辆调度和路线优化被广泛应用。
它们不仅可以提高资源利用率和运输效率,还可以减少成本和时间,提高用户体验和服务质量。
在本文中,我们将讨论车辆调度和路线优化的设计方案,介绍其实现原理和技术工具,探讨其应用场景和效果评估。
背景介绍车辆调度和路线优化是指在一定的运输条件下,根据货物、车辆、路况等因素,合理安排车辆的数量、位置、时间和路线,满足客户需求,并保证运营效率和质量。
在实际应用中,车辆调度和路线优化具有广泛的应用场景和优势,如:•物流配送调度:在优化仓库、配送中心、配送线路、配送车辆等资源分配的同时,满足客户的货物送达时间和安全性要求。
•出租车调度:在考虑司机、车辆、客户、路况等因素的基础上,实现高效的订单分配和服务质量保障。
•公交车调度:在满足日常运营需求的同时,优化车辆数量、线路规划和公共交通出行体验。
由此可见,车辆调度和路线优化在交通运输和物流管理中具有重要的作用和意义。
实现原理车辆调度和路线优化的核心是数据分析和算法模型。
我们需要根据不同的应用场景和业务需求,采集配送、出行、客户等数据,以实现决策的科学性和准确性。
具体而言,实现车辆调度和路线优化的步骤如下:1.数据预处理和建模:对采集的数据进行清洗、分类、聚合等处理,以建立符合实际情况的数学模型和数据库。
2.算法设计和测试:选取合适的数据挖掘、优化算法和模拟仿真方法,进行任务分配、路径规划、调度优化等方面的设计和测试。
3.系统集成和应用:将算法模型和数据库集成为车辆调度和路线优化系统,提供用户界面、数据交互和决策支持功能。
在实现车辆调度和路线优化的过程中,算法模型的选择和优化是非常关键的因素。
通常采用的算法模型包括数学规划、图论、遗传算法、模拟退火等等。
这些算法模型可以根据数据量、实时性、处理效率和质量等要求,灵活地进行组合和应用。
技术工具车辆调度和路线优化的设计方案需要使用多种技术工具。
公交车调度的优化模型

种 较 好 的解 决方 法 。本 文 以公 交公 司运 营 的 总 车 辆数 最 小 为 目标, 运 营 过 程 中满 足 各 方 需 求 的 车 辆 数 为 约 束 务 件 建 立 了优 化 模 型 模 型 实 以 现 了 对 线路 运 营 进 行 评 估 和 优 化 公 交 车 配 置 、 考 虑 了 乘 客 等 车 的 社 会 成 本 又 兼顾 了公 交 公 司 的 利 益, 法 易 于操 作 , 有 较 大 的 实 际 应 用 价 既 方 具
善城市交 通环境 、 改进市 民出行 状况 、 高公交公 司的经济 和社会 效 提 益, 都具有重要意义 。 下面考虑一条公 交线路上公 交车的调度问题 , 其 数 据 来 自我 国 一 座 特 大 城 市某 条公 交 线 路 的 客 流 调 查 和 运 营 资 料 。 该 条 公 交 线 路 上 行 方 向共 l 4站 , 行 方 向 共 l 下 3站 。 3 4页 给 第 - 出的是典型 的~个工 作 日两个运 行方 向各 站上下车 的乘 客数量统计 ( 数据从略) 。公交公司配给该线路同一型号的大客车 ,每辆标准载客 10人 , 0 据统计 客车在该线路上运行 的平均速度 为 2 0公里 、 运 营 时。 调度要求 , 客候 车时间一般不要超过 1 乘 0分钟 , 早高 峰时一 般不要超 过 5分钟 , 车辆满载率不应超过 10 一般也不要低 于 5 %。 2 %, 0 试根据这些 资料和要求 , 为该线路设计 一个便于 操作 的全天 ( 工 作 日) 的公 交 车 调 度 方 案 , 括 两 个 起 点 站 的 发 车 时 刻 表 : 共 需 要 多 包 一 少 辆 车 ;这 个 方 案 以 怎 样 的程 度 照 顾 封 了乘 客 和 公 交 公 司 双 方 的利 益: 等. 等 . 如何 将 这 个 调 度 问题 抽 象 成 一 个 明 确 、 整 的 数 学 模 型 。 出 求 完 指 解模 型的方法 ; 根据 实际问题 的要求 , 如果要设 计更 好的调度方案 , 应 如何 采集 运 营数 据 。
数学建模-公交车调度问题
第三篇公交车调度方案得优化模型2001年 B题公交车调度Array公共交通就是城市交通得重要组成部分,作好公交车得调度对于完善城市交通环境、改进市民出行状况、提高公交公司得经济与社会效益,都具有重要意义。
下面考虑一条公交线路上公交车得调度问题,其数据来自我国一座特大城市某条公交线路得客流调查与运营资料。
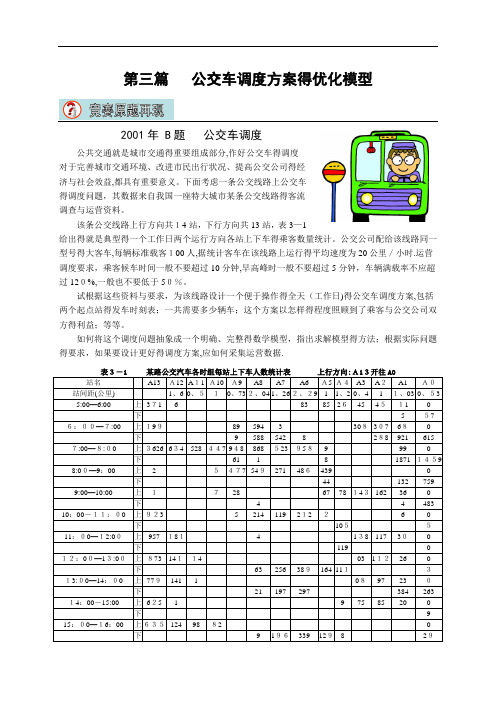
该条公交线路上行方向共14站,下行方向共13站,表3—1给出得就是典型得一个工作日两个运行方向各站上下车得乘客数量统计。
公交公司配给该线路同一型号得大客车,每辆标准载客100人,据统计客车在该线路上运行得平均速度为20公里/小时.运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过120%,一般也不要低于50%。
试根据这些资料与要求,为该线路设计一个便于操作得全天(工作日)得公交车调度方案,包括两个起点站得发车时刻表;一共需要多少辆车;这个方案以怎样得程度照顾到了乘客与公交公司双方得利益;等等。
如何将这个调度问题抽象成一个明确、完整得数学模型,指出求解模型得方法;根据实际问题得要求,如果要设计更好得调度方案,应如何采集运营数据.公交车调度方案得优化模型*摘要:本文建立了公交车调度方案得优化模型,使公交公司在满足一定得社会效益与获得最大经济效益得前提下,给出了理想发车时刻表与最少车辆数。
并提供了关于采集运营数据得较好建议。
在模型Ⅰ中,对问题1建立了求最大客容量、车次数、发车时间间隔等模型,运用决策方法给出了各时段最大客容量数,再与车辆最大载客量比较,得出载完该时组乘客得最少车次数462次,从便于操作与发车密度考虑,给出了整分发车时刻表与需要得最少车辆数61辆。
模型Ⅱ建立模糊分析模型,结合层次分析求得模型Ⅰ带给公司与乘客双方日满意度为(0、941,0、811)根据双方满意度范围与程度,找出同时达到双方最优日满意度(0、8807,0、8807),且此时结果为474次50辆;从日共需车辆最少考虑,结果为484次45辆。
公交车调度优化模型

公交车调度优化模型
何宝泉;吴斯浩;陆文辉;罗世庄
【期刊名称】《暨南大学学报(自然科学与医学版)》
【年(卷),期】2003(024)005
【摘要】提出了制定一条公交线路车辆调度方案的优化数学模型.该模型计算了乘客在车站等候的时间内所可能创造的财富--社会效益,并将乘客因候车而丧失创造该财富的机会看成一种社会成本.对车辆调度方案的评估时,不仅考虑了公司运营成本,而且考虑了相应的社会成本.因此,该模型制定的调度方案兼顾了公司利益和社会效益.最后将实际的统计数据带入模型,给出一个车辆调度发车时刻表的优化方案.【总页数】6页(P65-70)
【作者】何宝泉;吴斯浩;陆文辉;罗世庄
【作者单位】暨南大学统计系,广东,广州,510632;暨南大学统计系,广东,广
州,510632;暨南大学统计系,广东,广州,510632;暨南大学数学系,广东,广州,510632【正文语种】中文
【中图分类】O224
【相关文献】
1.公交车调度的优化模型 [J], 李传伟;叶红
2.基于候车与乘车满意度的公交车调度优化模型 [J], 姜少毅;王博;闫哲
3.公交车调度优化模型 [J], 李成功;脱小伟;郭尚彬;祁忠斌
4.可变线路式公交车辆调度优化模型 [J], 林叶倩;李文权;邱丰;丁钰玲
5.基于NSGA算法的公交车辆调度优化模型 [J], 宋晓鹏;韩印;姚佼
因版权原因,仅展示原文概要,查看原文内容请购买。
公交运营调度优化的评价指标模型研究

项 目( 0 7 A1 Z 0 ) 2 0 A 12 1 、
全 面 、 理 的特 点 。 由于公 共交 通涉 及 的 目标 、 合 因素 很 多 , 要对所 有 因素进行 有效 筛选 , 用定 性 与定 需 利 量 相结合 的方 法建 立一套 完整 的评 价 指标 体 系 。因
1 评价指标的确立的原则和方法
1 1 确 立的原 则 .
行 评价 , 仅 以乘 客 等待 时间为 依据 , 于 片面 。本 但 过
公交 运 营调度 优化 的评价 指标 的构 建是 以乘客
出行利益 并兼 顾公 交企业 效益 最大 为 目标 而建 立 的
线 网优化 模型 。评 价指标 模型 应该 具有 简 单 、 学 、 科
第1 0卷
第 1 期
21 00年 1月
科
学
技
术
与
工
程
Vo. 0 No 1 J n 2 1 11 . a . 0 0
@ 2 0 S i T c . g g 01 c. e h En n .
l 7 — l 1 ( 0 0 10 2 - 6 l 8 5 2 1 ) -3 4 6 0
文献标志码
公共 交通对 于一个 城市 的发展 起 着举 足轻 重 的
文 旨在研 究 出一种 公 交 调 度优 化效 果 的模 型 , 模 该 型将 集合 各种影 响调 度效 果 的因素 , 面 、 观地 对 全 客 优化 效果 进行评 价 。 建立 一套科 学 、 系统 、 有效 的评 价指标 体 系不 仅
作用 , 而公 交运 营调度 是通 过合理 的资 源配置 , 效 有 地 管理 车辆资源 , 使供 需矛 盾得 到解 决 。现 阶段 , 对
公交调度中的数学模型

公交调度 中的数 学模型
武 斌 ( 中国石油大学胜利学院 山东 东营 270) 5 0 0 摘要:建立合理有效 的数 学模 型来模 拟公 交运 营是优 化公交调度 、改善公 交服 务的关键 ,在分析现有模型 的基础 上,建立 以乘客
费用 最 小 ,公 交企 业 运 营 利 润 最 大化 的 多 目标 规 划模 型 。
l. 为第f h} —— 个小时时 间内。以^ 车时间 为发 间隔的 到达
第七站前的公交车已有的乘客数;
— —
公交车的最大载客量;
—
—
第1 个小时时间内在 车站下车的乘客总人数; 第f 个小时时问内到达 车站的乘客总人数; 根据客流量划分的时间段:
—
—
—
—
将 教育 理论知 识具体 应用到 教学 实践 中 去, 新教师在 岗前 培训 中亲 的总 成绩 记入 人事 档案 。 使 身体验 教 学的 各个环 节 ,掌握 教 学 的方 法和 艺术 ,尽快 适应 教 学的 青 年教师从毕业 到走上工 作岗位真正适应 教师角色需 要一个长期 过 程 。 的过程 ,把培训工作作为教师成长和教师队伍建设的重要环节,从 5 .建立有效考核体系 青年教 师 的需要 入手 ,促进 高 校教 师 岗前培 训 向专 业化 、科 学化 发 严格考核是检查督促岗前培训工作的有效手段, 但在授课后即以 展 ,以切 实提 高 青年 教 师 岗前 培 训 的效果 。 闭卷形 式考核却 不利 于新教 师对 所学 理论 的融会 贯通 。 青年 教师 岗前 培训体 系的建立 应本着 科学 性和 可操 作性 的原则 。 闭卷 考试 可用来 考 参考 文献: 察高 等教 育学 、高等 心理 学等 课 堂讲 授 内容 的记 忆情 况 ,督促 受训 【】 海高校教师岗前培训述评 【】 山东省青年管理干部学 1 J. 教师 强化 记忆 , 以指 导 实际教 学 工 作 。同时 ,青年 教 师听 取专题 讲 院学报 ,2 0 , 1 O 3 () 座 、典 型 报 告 、参 加 教 学观 摩 、 交流 讨 论 、参 观访 问和 提 交 论 文 [】赵志鲲 ,陶 勤. 高校青年教师岗前培训制度研究 【】 2 J. 的情况 也都要 以学分 形式记 入 岗前培 训档案 。 在使 用期结束 后 、 并 转 黑龙 江 高教研 究, 2 0 , 1) 7 (0 口 0 正之前 由专家 小组对 教学实 践能 力进 行考核 , 计总分 作为 岗前培 训 合
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三篇公交车调度方案的优化模型2001年 B题公交车调度Array公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益,都具有重要意义。
下面考虑一条公交线路上公交车的调度问题,其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站,下行方向共13站,表3-1给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车,每辆标准载客100人,据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过120%,一般也不要低于50%。
试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益;等等。
如何将这个调度问题抽象成一个明确、完整的数学模型,指出求解模型的方法;根据实际问题的要求,如果要设计更好的调度方案,应如何采集运营数据。
23 / 14公交车调度方案的优化模型*摘要:本文建立了公交车调度方案的优化模型,使公交公司在满足一定的社会效益和获得最大经济效益的前提下,给出了理想发车时刻表和最少车辆数。
并提供了关于采集运营数据的较好建议。
在模型Ⅰ中,对问题1建立了求最大客容量、车次数、发车时间间隔等模型,运用决策方法给出了各时段最大客容量数,再与车辆最大载客量比较,得出载完该时组乘客的最少车次数462次,从便于操作和发车密度考虑,给出了整分发车时刻表和需要的最少车辆数61辆。
模型Ⅱ建立模糊分析模型,结合层次分析求得模型Ⅰ带给公司和乘客双方日满意度为(0.941,0.811)根据双方满意度范围和程度,找出同时达到双方最优日满意度(0.8807,0.8807),且此时结果为474次50辆;从日共需车辆最少考虑,结果为484次45辆。
对问题2,建立了综合效益目标模型及线性规划法求解。
对问题3,数据采集方法是遵照前门进中门出的规律,运用两个自动记录机对上下车乘客数记录和自动报站机(加报时间信息)作录音结合,给出准确的各项数据,返站后结合日期储存到公司总调度室。
关键词:公交调度;模糊优化法;层次分析;满意度3.1 问题的重述3.1.1 问题的基本背景公交公司制定公交车调度方案,要考虑公交车、车站和乘客三方面因素。
我国某特大城市某条公交线路情况,一个工作日两个运营方向各个站上下车的乘客数量统计见表3-1。
3.1.2 运营及调度要求⑴公交线路上行方向共14站,下行方向共13站;⑵公交公司配给该线路同一型号的大客车,每辆标准载客100人,据统计客车在该线路上运营的平均速度为20公里/小时。
车辆满载率不应超过120%,一般也不低于50%;⑶乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟。
3.1.3 要求的具体问题⑴试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益,等等;⑵如何将这个调度问题抽象成一个明确完整的数学模型,并指出求解方法;⑶据实际问题的要求,如果要设计好更好的调度方案,应如何采集运营数据。
3.2 问题的分析本问题的难点是同时考虑到完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益等诸多因素。
如果仅考虑提高公交公司的经济效益,则只要提高公交车的满载率,运用数据分析法可方便地给出它的最佳调度方案;如果仅考虑方便乘客出行,只要增加车辆数的次数,运用统计方法同样可以方便地给出它的最佳调度方案,显然这两种方案是对立的。
于是我们将此题分成两个方面,分别考虑到:⑴公交公司的经济效益,记为公司的满意度;⑵乘客的等待时间和乘车的舒适度,记为乘客的满意度。
显然公交公司的满意度取决于每一趟车的满载率,且满载率越高,公交公司的满意度越高;乘客的满意度取决于乘客等待的时间和乘车的舒适度,而乘客等待时间取决于车辆的班次,班次越多等待时间越少,满意度越高;乘客的舒适度取决于是否超载,超载人数越少,乘客越满意。
很明显可以知道公交公司的满意度与乘客的满意度相互矛盾,所以我们需要在这两个因素中找出一个合理的匹配关系,使得双方的满意度达到最好。
3.3 模型的假设⑴道路:交通情况、路面状况良好,无交通堵塞和车辆损坏等意外情况;⑵公交车:发车间隔取整分钟,行进中彼此赶不上且不超车,到达终点站后调头变为始发车;⑶乘客:在每时段内到达车站的人数可看作是负指数分布,乘客乘车是按照排队的先后有序原则乘车,且不用在两辆车的间隔内等待太久;⑷数据:“人数统计表”中的数据来源准确、可信、稳定、科学;⑸票价:乘车票价为定值,不因乘车远近而改变。
3.4 定义与符号说明序号符号意义1a上或下行第j时段第k站上车人数;ijk2b上或下行第j时段第k站下车人数;ijk3l上或下行第j时段最大客容量;ij4k上或下行时第j时段平均载客量;ij5 C日所需总车次;6c上或下行第j时段的车次;ij7s上或下行第j时段平均发车时差;ij8p上或下行第j时段平均载客量;ij9t上或下行的平均发车时间间隔;ij10m上或下行时公交公司日平均满意度;gi11m上或下行时乘客整体日平均满意度;ci12m上或下行时公交公司各时段的满意度;gij13m上或下行时乘客各时段的满意度;cij14 Q日所需车辆数。
*本文获2001年全国一等奖。
队员:叶云,周迎春,齐欢,指导教师:朱家明等。
25 / 14注:1=i (表示上行运动(14,,3,2,1 =k ),2=i 表示下行运动(13,,3,2,1 =k ),18,3,2,1 ,=j 。
3.5 模型的建立与求解3.5.1 模型Ⅰ:相关量及车辆数的确定模型对问题1为设计便于操作的公交车调度方案,根据表3-1给出的一个工作日两个运营方向各个站上下车的乘客数量统计,假设各时段车辆平均足够载完在相等时间内到达的乘客,乘客也只能乘坐该路车而没有太大的不满,我们要设计两个起点站的发车时刻表,计算需要的车辆数,首先可建立以下各模型来求相关量。
⑴相关量①上下行各时间段内最大客容量:建立模型如下{}{}⎪⎪⎩⎪⎪⎨⎧==-==-=∑∑==13,2,12max 14,2,11max11 ,,n i b a m i b a l nk ijk ijk m k ijk ijk ij运用模型和表3-1中的上下车乘客数,算出上下行各时间段内最大客容量如下:图3-1 (1)上行各时间段内最大客容量 图3-1 (2)下行各时间段内最大客容量②车次数:因为座位数为100的客车满载率在50%和120%之间,即12050≤≤ij k ,在满足客车满载率和载完各时段所有乘客前提下,由模型:∑∑===21181i j ij c C ,⎪⎪⎪⎩⎪⎪⎪⎨⎧∈∉+⎥⎦⎤⎢⎣⎡=++Z l l Z l l c ij ijij ij ij 1201201201120(其中Z +是正整数)可计算每个时段的详细车次数如下:上行:6,25,42,23,13,10,12,10,9,8,8,18,24,8,4,4,3,4 下行:3,9,23,27,16,10,9,7,8,9,11,19,31,21,10,7,7,4求和可得出全工作日可行的最少车次总数:462231231=+=C 。
③安排发车时间间隔:用每个时段60分钟除以车次数,即:ij ij c s /60=,经计算可得出该时段平均发车时间间隔依次如下:上行:10,2.4,1.4,2.6,4.6,6,5,6,6.7,7.5,7.5,3.3,2.5,7.5,15,15,20,20; 下行:20,6.7,2.6,2.2,3.8,6,6.7,8.6,7.5,6.7,5.5,3.1,1.9,2.8,6,8.6,20。
27 / 14由ij s 的值有分数出现,而现实中列车、客车等时刻表的最小单位为分钟,故间隔应取整数。
当ij s 取整数时,可直接安排等时间发车ij c 次。
当某个ij s 取小数时,不妨设][ij s F 和][ij s C 是与ij s 相邻的两个连续整数且][][ij ij ij s C s s F ≤≤,由模型:)18,,2,1;2,1(60][][ ==⎪⎩⎪⎨⎧=+=⨯+⨯j i c n m s C n s F m ijij ij ij ij ij ij可求出以][ij s F 为间隔的班次ij m 和以][ij s C 为间隔的班次ij n ,再分别以发车间隔;为][ij s F 和][ij s C ,兼顾发车密度,将此时间段进行适当划分。
将上述各ij c 与ij s 值代入方程组,可相应地求出具体的发车间隔的次数ij ij n m ,,考虑到公交车调度方案的可操作性和公交公司的利益所在,在同时段线路上的车辆不宜过多,我们对结果进行了分析比较,将相邻时间段内发车间隔相等的班次尽量安排在一起,并且对高峰时期发车的先后顺序作了调整,得出了全天(一个工作日)内的公交车调度方案,见表3-5。
⑵日所需车辆数由汽车平均速度20千米/小时和A0-A13的距离61.14千米、A13-A0的距离58.14千米,可求得车辆从起点站到终点站的时间约为44分钟;又由假设可知车辆到达终点站后立即调头往回开且不跑空车,由于早高峰乘客数最多,故此时车辆实际占用数也应是当日的上限,考虑到8:00之前从A13发出的车次每个时段都多于A0发出的车次,且最大逆差数为3819163)(3121=++=-∑=i j jc c即从A13多发出38辆车;8:00到9:00虽然从A0发来的车辆多于从A13发出的车辆,但从8:00到8:44仍要从A13发出的15辆车,由假设恰在8:44时对方开来的车辆到站并调头再结合动态车辆有8辆赶不上时差。
故早高峰车辆实际占用为61辆,也即当天共需开动的车辆最少为61辆。
3.5.2 模型Ⅱ 最小车次数线性规划模型问题明显可看作是一个排队随机服务系统,我们把汽车看作是“顾客”,将各个车站看作是“服务台”,则此公交系统可看作是一个顾客不消失的、单通道多级服务台串联的排队系统。
因此,这里所遇到的,主要是排队问题。
归纳起来,需要考虑三种活动:①首站发车活动:根据发车时刻表确定;②到达中途站活动:在中途站主要考虑和计算上下车人数、车上的总人数和上下车时间;③到达终点站调头活动:在终点站根据发车时刻表确定。
我们先考上行时乘客在站的逗留时间,即乘客在k A 1站的等待时间,它包括相邻两趟车到达kA 1站的时间间隔jk q 1即发车间隔和乘客上下车的服务时间jk p 1。
