人教版高中数学必修五第4讲:等差数列的概念、性质(学生版)
高中数学必修五-等差数列

等差数列知识集结知识元等差数列的性质知识讲解1.等差数列的性质【等差数列】如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列.这个常数叫做等差数列的公差,公差常用字母d表示.等差数列的通项公式为:a n=a1+(n﹣1)d;前n项和公式为:S n=na1+n(n﹣1)或S n=(n∈N+),另一重要特征是若p+q=2m,则有2a m=a p+a q(p,q,m都为自然数)例:已知等差数列{a n}中,a1<a2<a3<…<a n且a3,a6为方程x2﹣10x+16=0的两个实根.(1)求此数列{a n}的通项公式;(2)268是不是此数列中的项?若是,是第多少项?若不是,说明理由.解:(1)由已知条件得a3=2,a6=8.又∵{a n}为等差数列,设首项为a1,公差为d,∴a1+2d=2,a1+5d=8,解得a1=﹣2,d=2.∴a n=﹣2+(n﹣1)×2=2n﹣4(n∈N*).∴数列{a n}的通项公式为a n=2n﹣4.(2)令268=2n﹣4(n∈N*),解得n=136.∴268是此数列的第136项.这是一个很典型的等差数列题,第一问告诉你第几项和第几项是多少,然后套用等差数列的通项公式a n=a1+(n﹣1)d,求出首项和公差d,这样等差数列就求出来了.第二问判断某个数是不是等差数列的某一项,其实就是要你检验看符不符合通项公式,带进去检验一下就是的.【等差数列的性质】(1)若公差d>0,则为递增等差数列;若公差d<0,则为递减等差数列;若公差d=0,则为常数列;(2)有穷等差数列中,与首末两端“等距离”的两项和相等,并且等于首末两项之和;(3)m,n∈N+,则a m=a n+(m﹣n)d;(4)若s,t,p,q∈N*,且s+t=p+q,则a s+a t=a p+a q,其中a s,a t,a p,a q是数列中的项,特别地,当s+t=2p时,有a s+a t=2a p;(5)若数列{a n},{b n}均是等差数列,则数列{ma n+kb n}仍为等差数列,其中m,k均为常数.(6)a n,a n﹣1,a n﹣2,…,a2,a1仍为等差数列,公差为﹣d.(7)从第二项开始起,每一项是与它相邻两项的等差中项,也是与它等距离的前后两项的等差中项,即2a n+1=a n+a n+2,2a n=a n﹣m+a n+m,(n≥m+1,n,m∈N+)(8)a m,a m+k,a m+2k,a m+3k,…仍为等差数列,公差为kd(首项不一定选a1).例题精讲等差数列的性质例1.设等差数列{a n}的前n项和为S n,若a2+a8=15-a5,则S9等于()A.18B.36C.45D.60例2.记等差数列{a n}的前n项和为S n.若a5=3,S13=91,则a1+a11=()A.7B.8C.9D.10例3.在等差数列{a n}中,a3+a9=24-a5-a7,则a6=()A.3B.6C.9D.12等差数列的通项公式知识讲解1.等差数列的通项公式【知识点的认识】等差数列是常见数列的一种,数列从第二项起,每一项与它的前一项的差等于同一个常数,已知等差数列的首项a1,公差d,那么第n项为a n=a1+(n﹣1)d,或者已知第m项为a m,则第n项为a n=a m+(n﹣m)d.【例题解析】eg1:已知数列{a n}的前n项和为S n=n2+1,求数列{a n}的通项公式,并判断{a n}是不是等差数列解:当n=1时,a1=S1=12+1=2,当n≥2时,a n=S n﹣S n﹣1=n2+1﹣(n﹣1)2﹣1=2n﹣1,∴a n=,把n=1代入2n﹣1可得1≠2,∴{a n}不是等差数列考察了对概念的理解,除掉第一项这个数列是等差数列,但如果把首项放进去的话就不是等差数列,题中a n的求法是数列当中常用到的方式,大家可以熟记一下.eg2:已知等差数列{a n}的前三项分别为a﹣1,2a+1,a+7则这个数列的通项公式为解:∵等差数列{a n}的前三项分别为a﹣1,2a+1,a+7,∴2(2a+1)=a﹣1+a+7,解得a=2.∴a1=2﹣1=1,a2=2×2+1=5,a3=2+7=9,∴数列a n是以1为首项,4为公差的等差数列,∴a n=1+(n﹣1)×4=4n﹣3.故答案:4n﹣3.这个题很好的考察了的呢公差数列的一个重要性质,即等差中项的特点,通过这个性质然后解方程一样求出首项和公差即可.【考点点评】求等差数列的通项公式是一种很常见的题型,这里面往往用的最多的就是等差中项的性质,这也是学习或者复习时应重点掌握的知识点.例题精讲等差数列的通项公式例1.在等差数列{a n}中,a4,a12是方程x2+3x+1=0的两根,则a8=()A.B.C.D.不能确定例2.在等差数列{a n}中,a2+a10=0,a6+a8=-4,a100=()A.212B.188C.-212D.-188例3.在等差数列{a n}中,若a2=5,a4=3,则a6=()A.-1B.0C.1D.6当堂练习单选题练习1.在等差数列{a n}中,a3+a9=24-a5-a7,则a6=()A.3B.6C.9D.12练习2.等差数列{a n}中,已知a2+a6=4,则a4=()A.1B.2C.3D.4练习3.在等差数列{a n}中,若a3+a9=17,a7=9,则a5=()A.6B.7C.8D.9练习4.《孙子算经》是中国古代重要的数学著作,上面记载了一道有名的“孙子问题”(又称“物不知数题”),后来我国南宋数学家秦九韶在《数书九章∙大衍求一术》中将此问题系统解决.“大衍求一术”是中国古算中最有独创性的成就之一,属现代数论中的一次同余式组问题.后传入西方,被称为“中国剩余定理”.现有一道一次同余式组问题:将正整数中,被3除余2且被5除余1的数,按由小到大的顺序排成一列,则此列数中第10项为()A.116B.131C.146D.161练习5.已知2,b的等差中项为5,则b为()A.B.6C.8D.10练习6.数列{a n}是等差数列,a1=1,公差d∈[1,2],且a4+λa10+a16=15,则实数λ的最大值为()A.B.C.D.练习7.等差数列{a n}中,S n是它的前n项和,a2+a3=10,S6=54,则该数列的公差d为()A.2B.3C.4D.6练习8.等差数列{a n}中,a1+a8=10,a2+a9=18,则数列{a n}的公差为()A.1B.2C.3D.4练习9.在等差数列{a n}中,已知a2+a6=18,则a4=()A.9B.8C.81D.63。
高一数学必修5PPT课件:等差数列的性质
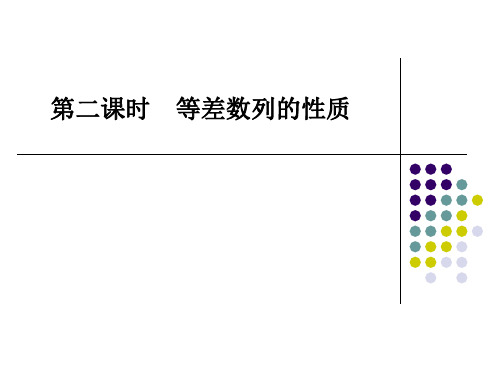
a4= 11 a7= 17
∴d= _2或2, 从而a14= _列的 性质
变 式 1 : 已 知 { a } 为 等 差 数 列 , a a a 高一数学必修5PPT课件:等差数列的性质
n
4
5
6
a7 56,a4a7 187,求a1,d
变式2:已知{an }为等差数列,a2 a5 a8 9, a3a5a7 21,求数列通项公式
解: a3+a11 =a6+a8 =2a7 ,又已知 a3+a11=10, ∴ a6+a7+a8= 23(a3+a11)=15
(解3):已a4+知a5+aa4+6+aa57+=a566+a7=a54+6a,7=a248a7①=187,求a14及公差d.
又 a4a7=187 ② , 解 ①、 ② 得
a4= 17 或 a7= 11
研究性问题
1. 若a12=23,a42=143, an=263,求n. d= 4 n=72
2.已知{an}为等差数列,若a10= 20 ,d= -1 ,求a 3 ?
a 3= a 10 +(3-10)d
a 3=27
3. 三数成等差数列,它们的和为12,首尾二数的
积为12,求此三数. 6,4,2或2,4,6
笔记①: 三个数等差的设法:a-d,a,a+d
练习2、成等差数列的四个数之和为26,第二个 与第三个数之积为40,求这四个数。
笔记:
四个数等差的设法: a-3d,a-d,
a+d,a+3d
公差为2d
性质一、任意两项的关系
在等差数列 an 中,有
an
人教版高中数学必修5《等差数列》PPT课件

等差数列的通项公式中包含四个量: an、a1、n、d
这四个量只需知道其中的三个就可以求出第四个.
例2.在等差数列{an}中, a5=10, (1)若a12=31,求a25 ; (2)若d=2,求a10; 解:(1)依题意得
a1+4d=10 a1+11d=31 解得 a1= - 2 , d = 3 ∴ a25=a1+24d = -2+24×3=70
解:a8=a1+7d=-1+7×4=27
(2)已知a1=15,an=3,d= -3,求n; 解:∵3=15-3(n-1) ∴n=5
(3)已知a1=8,a6=23,求d; 解:∵a6=a1+5d,即23=8+5d ∴ d=3
(4)已知d=2,a7=9,求a1; 解:∵a7=a1+6d 即9=a1+6×2 ∴a1=-3
拓展:在等差数列{an}中, 若a5=10,a12=31,求a25 。 解:设等差数列{an}的公差为d,则依题意有
d a12 a5 3110 3 12 5 7
∴ a25=a5+20d = 10+20×3=70
练习:在下列两个数中间再插入两个数,使这四个数组成 一个等差数列,(1)-1,5; (2)-12,0.
观察并发现:下面数列有什么共同特点?
(1)0,5,10,15,20,25,…
(2)鞋的尺寸,按照国家统一规定,有: 22,22.5,23,23.5,24,24.5,25,25.5,26,… (3)21,19,17,15,…… (4)3,3,3,3,……
(1)从第2项起,每一项与前一项的差都等于 5 (2)从第2项起,每一项与前一项的差都等于 0.5 (3)从第2项起,每一项与前一项的差都等于 -2 (4)从第2项起,每一项与前一项的差都等于 0
等差数列的性质 高中数学必修五课件

巩固练习
3、已知{an}为等差数列 且 a4+a5+a6+a7=56,a4a7=187,求公差d.
4. 三数成等差数列,它们的和为12,首尾二数的
积为12,求此三数. 6,4,2或2,4,6
设这三个数分别为a-d ,a,a+d,则3a=12,a2-d2=12
5. 四个数成等差数列,它们的和为12,首尾二数
…,a-3d,a-d,a+d,a+3d,…
对称项设法的优点:若有n个数构成等差数列.利用对 称项设出这个数列,则其各项和为na.
巩固练习
1. 在数列{an}中a1=1,an= an+1+4,则a10= -35 提示: d=an+1—an=4
2、
已知 a n 中 a 数 1 3 , ,a 1 n 列 a 1 n 1 5 (n 2 )则 ,a n __ .
m n p q , a m a n a p a q .
例题分析
例1 .在等差数列{an}中 (1) 已知 a6+a9+a12+a15=20,求a1+a20
分析:由 a1+a20 =a6+ a15 = a9 +a12 及 a6+a9+a12+a15=20,可得a1+a20=10
(2)已知 a3+a11=10,求 a6+a7+a8
试ap求 q.
解:设 d,则公 因 apa 差 q为 (p 为 q)d, 所d以 apaqqp1. pq pq 从 a p q a p 而 q q d q ( 1 ) 0 . 所a以 pq0.
二、 例:
例: 已知数列{ a n }的通项公式为 an pnq,其
高中数学人教A版必修5《等差数列》PPT课件

一个定义: an-an-1=d(d是常数,n≥2, n∈N*) 一个公式:an=a1+(n-1)d 一种思想:方程思想 一个概念: A=a+b/2
方法二
由递推公式:an-an-1=d (d是常数,n≥2,n∈N*)
可得:
a2-a1=d
a3-a2=d a4-a3=d
……
an-an-1=d
列。 这也是判断,证明一个数列是等差数列的一种方 法。 等差中项法
高中数学人教A版必修5《等差数列》P PT课件
高中数学人教A版必修5《等差数列》P PT课件
5.证明数列为等差数列的方法: (1)定义法: an an1 d (n 2) (2)等差中项法:2an an1 an1(n 2)
解法一
高中数学人教A版必修5《等差数列》P PT课件
高中数学人教A版必修5《等差数列》P PT课件
证明: 1 , 1 , 1 成等差数列 abc
2 11 b ac
bcba bcabac2
ac
a
c
(a b c)(1 1) 2 ac
(a b c) 2 2 b
2(a c) 2b 2 bb
4
4 an1
(n
1)记bn
1 an 2
(1)求证:数列bn 是等差数列;
(2)求数列an 的通项公式
构造法
解:(2)由(1)知,b n
1 2
(n 1)
1 2
n 2
bn
1 an 2
an
1 bn
2
2 n
2
求数列通项公式的方法:
(1)公式法;
(2)累加法;an1 an f (n)
(3)累乘法;an1 f (n)
人教版高三必修五数学知识点:等差数列基本性质

⑴公差為d的等差數列,各項同加一數所得數列仍是等差數列,其公差仍為d.
⑵公差為d的等差數列,各項同乘以常數k所得數列仍是等差數列,其公差為kd.
⑶若{an}{bn}為等差數列,則{an±bn}與{kan+bn}(k、b為非零常數)也是等差數列.
⑷對任何m、n,在等差數列中有:an=am+(n-m)d(m、n∈N+),特別地,當m=1時,便得等差數列的通項公式,此式較等差數列的通項公式更具有一般性.
⑸、一般地,當m+n=p+q(m,n,p,q∈N+)時,am+an=ap+aq.
⑹公差為d的等差數列,從中取出等距離的項,構成一個新數列,此數列仍是等差數列,其公差為kd(k為取出項數之差).
(7)下表成等差數列且公差為m的項ak.ak+m.ak+2m.....(k,m∈N+)組成公差為md的等差數列。
⑻在等差數列中,從第二項起,每一項(有窮數列末項除外)都是它前後兩項的等差中項.
⑼當公差d>0時,等差數列中的數隨項數的增大而增大;當d<0時,等差數列中的數隨項數的減少而減小;d=0時,等差數列中的數等於一個常數.。
高中数学人教版必修5课件:2.2.1等差数列的性质(共14张PPT)

昨日的明天是今天。明天的昨日是今天。为什么要计较于过去呢(先别急着纠正我的错误,你确实可以在评判过去中学到许多)。但是我发现有的人过分地瞻前顾后了。为 何不想想“现在”呢?为何不及时行乐呢?如果你的回答是“不”,那么是时候该重新考虑一下了。成功的最大障碍是惧怕失败。这些句子都教育我们:不要惧怕失败。如 果你失败了他不会坐下来说:“靠,我真失败,我放弃。”并且不是一个婴儿会如此做,他们都会反反复复,一次一次地尝试。如果一条路走不通,那就走走其他途径,不 断尝试。惧怕失败仅仅是社会导致的一种品质,没有人生来害怕失败,记住这一点。宁愿做事而犯错,也不要为了不犯错而什么都不做。不一定要等到时机完全成熟才动手。 开头也许艰难,但是随着时间的流逝,你会渐渐熟悉你的事业。世上往往没有完美的时机,所以当你觉得做某事还不是时候,先做起来再说吧。喜欢追梦的人,切记不要被 梦想主宰;善于谋划的人,切记空想达不到目标;拥有实干精神的人,切记选对方向比努力做事重要。太阳不会因为你的失意,明天不再升起;月亮不会因为你的抱怨,今 晚不再降落。蒙住自己的眼睛,不等于世界就漆黑一团;蒙住别人的眼睛,不等于光明就属于自己!鱼搅不浑大海,雾压不倒高山,雷声叫不倒山岗,扇子驱不散大雾。鹿 的脖子再长,总高不过它的脑袋。人的脚指头再长,也长不过他的脚板。人的行动再快也快不过思想!以前认为水不可能倒流,那是还没有找到发明抽水机的方法;现在认 为太阳不可能从西边出来,这是还没住到太阳从西边出来的星球上。这个世界只有想不到的,没有做不到的!不是井里没有水,而是挖的不够深;不是成功来的慢,而是放 弃速度快。得到一件东西需要智慧,放弃一样东西则需要勇气!终而复始,日月是也。死而复生,四时是也。奇正相生,循环无端,涨跌相生,循环无端,涨跌相生,循环 无穷。机遇孕育着挑战,挑战中孕育着机遇,这是千古验证了的定律!种子放在水泥地板上会被晒死,种子放在水里会被淹死,种子放到肥沃的土壤里就生根发芽结果。选
高中数学人教版必修5PPT课件:等差数列

(3)已知等差数列{an}的首项是a1,公差是d,通项公式 是___________;
方法1:∵由等差数列的定义可得
∴ a2=a1+d a3=a2+d=(a1+d )+d=a1+2d a4=a3+d=(a1+2d )+d=a1+3d ……
an=an-1+d=a1+(n-1)d
不完全归 纳法
又∵当n=1时,上式也成立 ∴an=a1+(n-1)d
思考:上述数列的公差与该数列的类型有关系吗? 已知数列{an}是等差数列,d是公差,则: 当d=0时, {an}为常数列; 当d>0时, {an}为递增数列; 当d<0时, {an}为递减数列;
高中数学人教版必修5PPT课件:等差 数列
高中数学人教版必修5PPT课件:等差 数列
探究
在如下的两个数之间插入一个什么数之后这 三个数会成为一个等差数列。
高中数学人教版必修5PPT课件:等差 数列
问0题, 51,:10观, 1察5,一2下0 上面的这四个数列:①
48, 53, 58, 63
②
18,15.5,13,10.5,8,5.5.
③
10072, 10144, 10216, 10288, 10360 ④
这些数列有什么共同特点呢?
以上四个数列从第2项起,每一项与 前一项的差都等于同一个常数
如果等差数列 的首项是 ,公差是 ,那么根 据等差数列的定义可以得到以下结论:
数列 为等差数列
高中数学人教版必修5PPT课件:等差 数列
练 高中数学人教版必修5PPT课件:等差数列
习
判断下列各组数列中哪些是等差数列,哪些不是? 如果是,写出首项a1和公差d, 如果不是,说明理 由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版高中数学 等差数列的概念、性质__________________________________________________________________________________ __________________________________________________________________________________教学重点: 掌握等差数列的概念、通项公式及性质;求等差中项,判断等差数列及与函数的关系; 教学难点: 通项公式的求解及等差数列的判定。
1. 等差数列的概念一般地,如果一个数列从第二项起,每一项与它的前一项的差都等于___________,那么这个数列就叫做___________,这个常数叫做等差数列的______,公差通常用字母d 来表示。
用递推关系系表示为_________________或()12,n n a a d n n N -+-=≥∈ 2. 等差数列的通项公式若{}n a 为等差数列,首项为1a ,公差为d ,则________________3. 等差中项如果三个数,,x A y 组成等差数列,那么A 叫做x 和y 的等差中项4. 通项公式的变形对任意的,p q N +∈,在等差数列中,有:()11p a a p d =+-()11q a a q d =+- 两式相减,得()p q a a p q d =+- 其中,p q 的关系可以为,,p q p q p q <>=5. 等差数列与函数的关系由等差数列的通项公式()11n a a n d =+-可得()1n a dn a d =+-,这里1,a d 是常数,n 是自变量,n a 是n 的函数,如果设1,,d a a d b =-=则n a an b =+与函数y ax b =+对比,点(),n n a 在函数y ax b =+的图像上。
6. 等差数列的性质及应用(1)12132...n n n a a a a a a --+=+=+=(2)若2,m n p q w +=+=则2m n p q w a a a a a +=+=(,,,,m n p q w 都是正整数)(3)若,,m p n 成等差数列,则,,m p n a a a 也成等差数列(,,m n p 都是正整数)(4)()n m a a n m d =+-(,m n 都是正整数)(5)若数列{}n a 成等差数列,则(),n a pn q p q R =+∈(6)若数列{}n a 成等差数列,则数列{}n a b λ+(,b λ为常数)仍为等差数列(7)若{}n a 和{}n b 均为等差数列,则{}n n a b ±也是等差数列类型一: 等差数列的判定、项及公差的求解、通项公式的求解例1.(2015河北唐山月考)数列{}n a 是首项11a =-,公差3d =的等差数列,若2015,n a = 则n =A.672B.673C.662D.663 练习1. 数列{}n a 是首项11a =-,公差3d =的等差数列,若2003,n a = 则n =A.669B.673C.662D.663 练习2. 数列{}n a 是首项11a =-,公差3d =的等差数列,若2000,n a = 则n =A.669B.668C.662D.663例2.(2015山西太原段考)一个首项为23、公差为整数的等差数列从第7项开始为负数,则其公差d 为()A.-2B.-3C.-4D.-6 练习3. 一个首项为23、公差为整数的等差数列从第6项开始为负数,则其公差d 为()A.-2B.-3C.-4D.-5 练习4.等差数列{a n }中,a 1+a 5=10,a 4=7,则数列{a n }的公差为( )A .1B .2C .3D .4 例3.(2014浙江绍兴一中期中)已知数列{}n a 满足1111,1,4n na a a +==- 其中n N +∈设221n n b a =-(1) 求证:数列{}n b 是等差数列(2) 求数列{}n a 的通项公式练习5.已知数列{}n a 满足()1114,21n n n a a a n a --==≥+令1n nb a = (1) 求证:数列{}n b 是等差数列(2) 求数列{}n b 与{}n a 的通项公式练习6.在等差数列{}n a 中,已知581,2,a a =-= 求1,a d例4.已知数列8,,2,,a b c 是等差数列,则,,a b c 的值分别为____________练习7. 已知数列8,,2,,a b 是等差数列,则,a b 的值分别为____________练习8. 已知数列2,,8,,a b c 是等差数列,则,,a b c 的值分别为____________类型二:等差数列的性质及与函数的关系例5.等差数列{}n a 中,已知100110142015a a +=,则12014a a +=()A.2014B.2015C.2013D.2016练习9.在等差数列{}n a 中,若4681012120,a a a a a ++++=则10122a a -的值为 ()A.24B.22C.20D.18练习10.(2015山东青岛检测)已知等差数列{}n a 中,1007100812015,1,a a a +==-则2014a = _____ 例6.已知数列{}n a 中,220132013,2a a ==且n a 是n 的一次函数,则 2015a =________ 练习11.若,,a b c 成等差数列,则二次函数()22f x ax bx c =-+的零点个数为() A.0 B.1 C.2 D.1或2练习12.已知无穷等差数列{}n a 中,首项13,a = 公差5d =-,依次取出序号被4除余3的项组成数列{}n b(1) 求1b 和2b(2) 求{}n b 的通项公式(3){}n b中的第503项是{}n a的第几项1.在等差数列{a n}中,a1+a9=10,则a5的值为()A.5 B.6 C.8 D.102.在数列{a n}中,a1=2,2a n+1=2a n+1,则a101的值为()A.49 B.50 C.51 D.523. 如果等差数列{a n}中,a3+a4+a5=12,那么a1+a2+…+a7=()A.14 B.21 C.28 D.354. 已知等差数列{a n}满足a1+a2+a3+…+a101=0,则有()A.a1+a101>0 B.a2+a100<0 C.a3+a100≤0 D.a51=0 5. 等差数列{a n}中,a1+a4+a7=39,a2+a5+a8=33,则a3+a6+a9的值为()A.30 B.27 C.24 D.216. 等差数列{a n}中,a5=33,a45=153,则201是该数列的第()项()A.60 B.61 C.62 D.63_________________________________________________________________________________ _________________________________________________________________________________基础巩固1.在等差数列{a n}中,a3=7,a5=a2+6,则a6=()A.11 B.12 C.13 D.142.若数列{a n}是等差数列,且a1+a4=45,a2+a5=39,则a3+a6=()A.24 B.27 C.30 D.333.已知等差数列{a n}中,a7+a9=16,a4=1,则a12等于()A.15 B.30 C.31 D.64 4.等差数列中,若a3+a4+a5+a6+a7+a8+a9=420,则a2+a10等于()A.100 B.120 C.140 D.1605.已知a=13+2,b=13-2,则a,b的等差中项为()A.3B.2C.13D.126. 在等差数列{a n }中,a 3+a 7=37,则a 2+a 4+a 6+a 8=________.7. 等差数列{a n }中,公差为12,且a 1+a 3+a 5+…+a 99=60,则a 2+a 4+a 6+…+a 100=_______. 8. 在等差数列{a n }中,若a 4+a 6+a 8+a 10+a 12=120,则a 9-13a 11的值为( ) A .14 B .15 C .16 D .179. 在等差数列{a n }中,已知a 1=2,a 2+a 3=13,则a 4+a 5+a 6=________.10. 等差数列{a n }的前三项依次为x,2x +1,4x +2,则它的第5项为__________.11. 已知等差数列6,3,0,…,试求此数列的第100项.能力提升12. 等差数列的首项为125,且从第10项开始为比1大的项,则公差d 的取值范围是( ) A .d >875 B .d <325 C.875<d <325 D.875<d ≤32513. 设等差数列{a n }中,已知a 1=13,a 2+a 5=4,a n =33,则n 是( ) A .48 B .49 C .50 D .5114. 已知数列{a n }中,a 3=2,a 7=1,又数列{1a n +1}是等差数列,则a 11等于( ) A .0 B.12 C.23D .-1 15. 若a ≠b ,两个等差数列a ,x 1,x 2,b 与a ,y 1,y 2,y 3,b 的公差分别为d 1、d 2,则d 1d 2等于( ) A.32 B.23 C.43 D.3416. 《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为________升.17. 等差数列{a n }中,a 2+a 5+a 8=9,那么关于x 的方程:x 2+(a 4+a 6)x +10=0( )A .无实根B .有两个相等实根C .有两个不等实根D .不能确定有无实根 18. 在a 和b 之间插入n 个数构成一个等差数列,则其公差为( ) A.b -a n B.a -b n +1 C.b -a n +1 D.b -a n -119. 在等差数列{a n }中,已知a m +n =A ,a m -n =B ,,则a m =__________.20.三个数成等差数列,它们的和等于18,它们的平方和等于116,则这三个数为__________.21. 在等差数列{a n }中,已知a 3+a 8=10,则3a 5+a 7=________.22. 已知数列{a n }是等差数列,且a 1=11,a 2=8.(1)求a 13的值;(2)判断-101是不是数列中的项;(3)从第几项开始出现负数?(4)在区间(-31,0)中有几项?23. 已知等差数列{a n }中,a 15=33,a 61=217,试判断153是不是这个数列的项,如果是,是第几项?24. 已知函数f (x )=3x x +3,数列{x n }的通项由x n =f (x n -1)(n ≥2,且n ∈N *)确定. (1)求证:{1x n}是等差数列; (2)当x 1=12时,求x 100的值. 25. 四个数成等差数列,其平方和为94,第一个数与第四个数的积比第二个数与第三个数的积少18,求此四个数.26. 已知等差数列{a n }中,a 2+a 6+a 10=1,求a 3+a 9.27. 在△ABC 中,若lgsin A ,lgsin B ,lgsin C 成等差数列,且三个内角A ,B ,C 也成等差数列,试判断三角形的形状.。
