大学物理静电场环路定理 电势能及电势
合集下载
静电场—电场力做功和环路定理以及电势
WAB = −( EPB − EPA ) = EPA − EPB = q0 ∫
AB
q0
B
A
K K E ⋅ dl
K E
电荷在电场中一点的电势能与该电荷的电荷量、电荷所 在位置和电势能零点的选择都有关系。电势能的参考零点选 择是任意的。若选择 EPB=0 ，则A点的电势能为：
E PA = q0 ∫
B
A
K K E ⋅ dl
黄山学院教学课件
大学物理学电子教案
电势及其计算
7.4-1、2 静电场的环路定理 电势能 7.4-3 电势
复 习 7.2 电场强度通量 高斯定理
• • • • 电场线 电场强度通量 高斯定理 高斯定理应用举例
7.3 密立根测定电子电荷的实验
7.4 静电场的环路定理 电势能 电势
一、静电场力作功 一、静电场力作功
R
O
σ
x
P
K E (P)
x
均匀带电圆盘在轴线上 x 位置处的场强为 K ⎛ ⎞ K x σ E (P) = 1− ⋅i ⎜ ⎟ 2 2 2ε 0 ⎝ R +x ⎠ 无穷远处电势为零，取正向x轴为积分路径，对 x 作积分 得到 P 点的电势： ∞ σ ⎛ ⎞K K σ x 2 2 1 V (P) = ∫ i dx R x − ⋅ = + −x ⎜ ⎟ 2 2 x 2ε 2 ε 0 ⎝ 0 R +x ⎠
要注意参考点的选择，只有电荷分布在有限的空间时，才 能选无穷远点的电势为零； 积分路径上的电场强度的函数形式要求已知或可求。 步骤： 利用电势的叠加原理 (1) 把带电体→分为无限多dq dq V = (2) 由dq → dV Q 4πε r 0 (3) 由dV → V = ∫ d V 要求电荷的分布区域是已知的； 当电荷分布在有限的区域内，可以选择无穷远点作为电势的 零点；而当激发电场的电荷分布延伸到无穷远时，只能根据具 体问题的性质，在场中人为选择某点为电势的零点。
AB
q0
B
A
K K E ⋅ dl
K E
电荷在电场中一点的电势能与该电荷的电荷量、电荷所 在位置和电势能零点的选择都有关系。电势能的参考零点选 择是任意的。若选择 EPB=0 ，则A点的电势能为：
E PA = q0 ∫
B
A
K K E ⋅ dl
黄山学院教学课件
大学物理学电子教案
电势及其计算
7.4-1、2 静电场的环路定理 电势能 7.4-3 电势
复 习 7.2 电场强度通量 高斯定理
• • • • 电场线 电场强度通量 高斯定理 高斯定理应用举例
7.3 密立根测定电子电荷的实验
7.4 静电场的环路定理 电势能 电势
一、静电场力作功 一、静电场力作功
R
O
σ
x
P
K E (P)
x
均匀带电圆盘在轴线上 x 位置处的场强为 K ⎛ ⎞ K x σ E (P) = 1− ⋅i ⎜ ⎟ 2 2 2ε 0 ⎝ R +x ⎠ 无穷远处电势为零，取正向x轴为积分路径，对 x 作积分 得到 P 点的电势： ∞ σ ⎛ ⎞K K σ x 2 2 1 V (P) = ∫ i dx R x − ⋅ = + −x ⎜ ⎟ 2 2 x 2ε 2 ε 0 ⎝ 0 R +x ⎠
要注意参考点的选择，只有电荷分布在有限的空间时，才 能选无穷远点的电势为零； 积分路径上的电场强度的函数形式要求已知或可求。 步骤： 利用电势的叠加原理 (1) 把带电体→分为无限多dq dq V = (2) 由dq → dV Q 4πε r 0 (3) 由dV → V = ∫ d V 要求电荷的分布区域是已知的； 当电荷分布在有限的区域内，可以选择无穷远点作为电势的 零点；而当激发电场的电荷分布延伸到无穷远时，只能根据具 体问题的性质，在场中人为选择某点为电势的零点。
静电场的环路定理静电场力的功电势能
静电场力的功
02
电场力的定义
电场力是电荷在电场中受到的 力，其大小和方向由电场强度
和电荷的乘积决定。
电场力的大小为 F=qE，其 中 F 是电场力，q 是电荷量，
E 是电场强度。
电场力的方向与电场强度的方 向相同，即由正电荷指向负电
荷。
电场力做功的计算
电场力做功可以通过积分计算，即 W=∫F·dr，其中 W 是电场力做的功， F 是电场力，dr 是位移矢量。
在匀强电场中，电场力做功可以通过 W=qEd计算，其中 W 是电场力做 的功，q 是电荷量，E 是电场强度，d 是位移。
在非匀强电场中，需要计算电场力在路径上的积分来计算电场力做的功。
电场力做功的特点
01
电场力做功与路径无关，只与初末位置的电势差有关。
02
电场力做功是标量，没有方向。
03
电场力做功的过程是能量转化的过程，可以转化为其他形式 的能量。
电势能
03
电势能的定义
电势能是指电荷在电场中由于位置差 异而具有的能量。
电势能是电荷与电场共同具有的能量， 其大小由电场强度和电荷量共同决定。
电势能是相对的，与零电势点的选择 有关。
电势能的变化规律
1
电场力做功与路径无关，只与初末位置有关。
2
电场力做正功，电势能减少；电场力做负功，电 势能增加。
3
静电力做功与电荷的运动路径无关，只与初末位 置有关。
电势能与电场力的关系
01
电场力做功等于电势能的减少量。
02
电势能的变化量等于电场力做的功。
03 电势能与电场力做功的关系是能量守恒定律在静 电场中的具体表现。
THANKS.
静电场的环路定理、静 电场力的功、电势能
大学物理-电势
Va E dl a E dl
讨论
a
a
1)电势零点的选择(参考点)
任意 视分析问题方便而定
参考点不同电势不同
10
通常：
理论计算有限带电体电势时选无限远为参考点
实际应用中或研究电路问题时取大地、仪器外 壳等
2)电势的量纲
SI制：单位 V (伏特)
量纲
V
W q
L2 MT
3I
1
3)电势是一个长程物理量
b b
a
f dl q E dl Wa Wb
a
a
b E dl
Wa
Wb
a
q
q 与试验电荷无关
根据静电场 Wa Wb 的环路定理 q q
E dl Va Vb
a
称 a b两点电势差
若选b点的势能为参考零点 则
a点的电势：
势能零点
势能零点
VA VB
11
rB rA
E
dr
Q 4πε0
rB dr rA r 2
()
4πε0 rA rB
（2）r R
VA VB
rB rA
E
dr
0
o A B A dr B
R
drrA r
r
rB
20
（3）r R 令 rB V 0
Q 1 1
VA VB
（4）r R
()
4πε0
rA R
q
x2 R2
x
R，VP
q 4πε0 x
V
dl
q
q
4πε0 R
4πε0 x2 R2
R
r
xo x
Px
o
x
大学物理课件-静电场的环路定理电势
(
2 0
x2 R2 x)
根据电场与电势的微分关系：
V
x
Ex
x
[1
2 0
] x2 R2
教学基本要求
第六章热力学基础
一 掌握描述静电场的两个 物理量——电场强度 和电势的概念，理解电场强度E 是矢量点函数，而
③电势高低的判断：沿电力线电势降低。
正电荷产生的电场各点的电势为正，∞处最小为0。
负电荷产生的电场各点的电势为负，∞处最大为0。
④电势是标量，单位为伏特。
2、电势差（电压）
第六章热力学基础
电场中两点的电势差：
Vab Va Vb
E
a
dl
E
b
dl
b
E
a
dl
Aab q0
定义：
Vab Va Vb
dalb与nd0夹 n, a角c为 dl
考虑电势沿 dl方向的变化率（
方向导数）
dV dV dn dV cos dV
dl dn dl dn
dn
电势梯度：
dV dn
n0
方向等于电势升高第最六快章的热方力向学。基础
2 场强与电势梯度的关系：
令q0从a b, dAab F dl q0E dl q0Edn dAab q0 (Va Vb ) q0dV E dV (1) dn
Vp
dq
4 0r
①由点电荷电势公式，利用电势叠加原理计算。
dq
V p
4 0r
qi
i 4 0ri
连续带电体 点电荷系
前提条件为有 限大带电体且 选无限远处为 电势零点.
②根据已知的场强分布，按定义计算。 Vp
Edl
电势能 电势
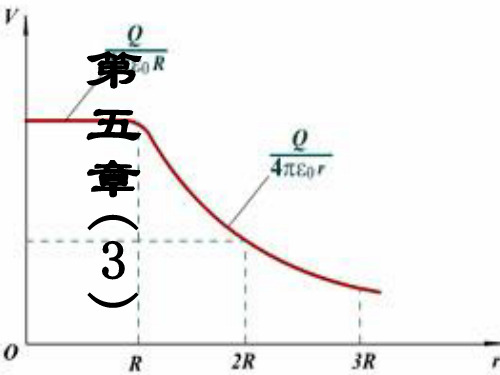
B r R
r
37.
讨论： 讨论：
q
4πε0R 结论 V = q 4πε0r
(r < R)
V
Q 4πε0 R
(r ≥ R) (记住 记住) 记住
Q 4πε 0 r
o a. r < R 等势体 ； r >> R“点电荷” 点电荷”
电势分布？(设V∞= 0 ) 电势分布？ 设 Ⅰ法 叠加法
利用上述结论 V = ∑Vi
v E
v v q0 ( ∫ E ⋅ dl +
ABC
v v v v ∫ E⋅ dl ) = q0 ∫ E⋅ dl =0
L CDA
即
v v v 的环流为零） ∫ E⋅ dl = 0 （ E 的环流为零）
l
说明：静电力 保守力， 说明：静电力——保守力，静电场 保守力 静电场——保守场 保守场
29 .
三. 电势能
q dl 任取点电荷 dq = o 2πR dq dV = 4πε0r 积分中： 与 积分中：r与d q 选取无关 常量
b. 线积分法 利用P.159例1结论 例 结论 利用 积分路径 P
x轴 轴
R
P
x
x
无穷远
35.
讨论 结论
V=
q 4πε0 x + R
2 2
记住） （记住）
q 4 πε0 R
V
q 4πε0 x2 + R2
a. E 的分布函数已知, 用线 积分法较方便
R
rA
r r
rB
b. 选径向为积分路径 v v v v 则 dl = dr er ⋅ dr = dr oA B R r c. 对球面内一点B : 分段积分 dr A v R ∞ v ∞ VB = ∫ E ⋅ dl = ∫ E1 ⋅ dr + ∫ E2 ⋅ dr
r
37.
讨论： 讨论：
q
4πε0R 结论 V = q 4πε0r
(r < R)
V
Q 4πε0 R
(r ≥ R) (记住 记住) 记住
Q 4πε 0 r
o a. r < R 等势体 ； r >> R“点电荷” 点电荷”
电势分布？(设V∞= 0 ) 电势分布？ 设 Ⅰ法 叠加法
利用上述结论 V = ∑Vi
v E
v v q0 ( ∫ E ⋅ dl +
ABC
v v v v ∫ E⋅ dl ) = q0 ∫ E⋅ dl =0
L CDA
即
v v v 的环流为零） ∫ E⋅ dl = 0 （ E 的环流为零）
l
说明：静电力 保守力， 说明：静电力——保守力，静电场 保守力 静电场——保守场 保守场
29 .
三. 电势能
q dl 任取点电荷 dq = o 2πR dq dV = 4πε0r 积分中： 与 积分中：r与d q 选取无关 常量
b. 线积分法 利用P.159例1结论 例 结论 利用 积分路径 P
x轴 轴
R
P
x
x
无穷远
35.
讨论 结论
V=
q 4πε0 x + R
2 2
记住） （记住）
q 4 πε0 R
V
q 4πε0 x2 + R2
a. E 的分布函数已知, 用线 积分法较方便
R
rA
r r
rB
b. 选径向为积分路径 v v v v 则 dl = dr er ⋅ dr = dr oA B R r c. 对球面内一点B : 分段积分 dr A v R ∞ v ∞ VB = ∫ E ⋅ dl = ∫ E1 ⋅ dr + ∫ E2 ⋅ dr
高等物理静电场环路定理
a
a 20
V Edl Edr pp
p
R
z
1q
y
4 0 r
xz
2 ) 定义法:
1
Vp
4 0r
dq
q
qx
x 40(R2x2)3/2dx
q 4
0
1 (R2 x2)1/2
x
o q
4 0 R2 x2
特例:
★若x = 0，
得：Vp
q
40R
W A B q 0 A B E d l E p A E p B ( E p B E p A )
试探电荷q o 在电场中某一点的静电势能在数值上等于 把试探电荷q o 由该点移到零势能点静电力所作的功。 若选 B 点为电势能零点，则
B
E P A q 0A E d l q 0A B E d l
E内 0
p
R
q
z
x
z
4 0 R2 x2
V 0
场强分布
电势分布
q
例题2均匀带电球面内外的电势分布。带电量为Q，球面半径为R
。
解∶由高斯定理得：
p
E外
1 4 0
Q r2
1 V
40
dV
r
1）对球内的一点P，其电势为:
r
r dWFdlq0Edl
Q
p
VEdr drrC
q0Q
1 (1)
20 20
4 0 r ra
2、电势、电势差 ：
V dV （1）、定义：
电势的物理意义：
09-4静电场的环路定理和电势
电子伏特是近代物理学中能量单位
19
19
J
一个电子伏特的能量
9.4 静电场的环路定理和电势
9.4.3 电势的计算
一、点电荷q的电场中任一场点的电势
无穷远处为电势零点
V ( P)
P
E dl E dr P Edr P
q q dr 2 r 4 πε r 4πε 0 r 0
电场指向电势降落方向
沿电场线方向移动正电荷，电场力做正功， 正电荷的电势能减少，故电势减小。
9.4 静电场的环路定理和电势
我们的心脏附近 的等电势线（类似于 电偶极子）
9.4 静电场的环路定理和电势
电势差
9.5.2 电场强度与电势梯度 E
U AB VA VB V
U AB E l El cos
9.4 静电场的环路定理和电势
电势是相对的，电势差是绝对的
电势差 U V V PQ P Q
单位：1V＝1J/C
P
Q
E dl
二、电势零点 1、电荷只分布在有限区域时，电势零点通常选在无 穷远处。 VP E dl 设Q点在无限远，VQ=0
P
2、 电荷分布延伸到无限远；可选取场中任一点， 合理选择电势零点可使问题简化。
y
P( x, y)
p cos V 4 π 0 r 2
在图示的Oxy坐标系中
q
r
O
r
r
q
r x y
2 2
2
l
x
cos
x x2 y 2
px V 2 2 3/ 2 4 π 0 ( x y )
9.4 静电场的环路定理和电势
19
19
J
一个电子伏特的能量
9.4 静电场的环路定理和电势
9.4.3 电势的计算
一、点电荷q的电场中任一场点的电势
无穷远处为电势零点
V ( P)
P
E dl E dr P Edr P
q q dr 2 r 4 πε r 4πε 0 r 0
电场指向电势降落方向
沿电场线方向移动正电荷，电场力做正功， 正电荷的电势能减少，故电势减小。
9.4 静电场的环路定理和电势
我们的心脏附近 的等电势线（类似于 电偶极子）
9.4 静电场的环路定理和电势
电势差
9.5.2 电场强度与电势梯度 E
U AB VA VB V
U AB E l El cos
9.4 静电场的环路定理和电势
电势是相对的，电势差是绝对的
电势差 U V V PQ P Q
单位：1V＝1J/C
P
Q
E dl
二、电势零点 1、电荷只分布在有限区域时，电势零点通常选在无 穷远处。 VP E dl 设Q点在无限远，VQ=0
P
2、 电荷分布延伸到无限远；可选取场中任一点， 合理选择电势零点可使问题简化。
y
P( x, y)
p cos V 4 π 0 r 2
在图示的Oxy坐标系中
q
r
O
r
r
q
r x y
2 2
2
l
x
cos
x x2 y 2
px V 2 2 3/ 2 4 π 0 ( x y )
9.4 静电场的环路定理和电势
【大学物理】静电场的环路定理 电势 等势面 电势梯度
r r r r－ r l cos
r
r
r+
q l
q+
3. 连续分布电荷电场中的电势 利用电势叠加原理：
dV
dq
dq VP 4 π 0 r
r
P
使用此公式的前提条件为有限大带电体且选无限远 处为电势零点；积分是对整个带电体的积分。 E 利用电势定义式： dl “ 0 ” P
qr E1 3 4 π 0 R
r
q E2 2 4 π 0 r
V1 E1dr E 2 dr
r R
R
q R
R
r
qr q dr dr 3 2 R 4 π r 4 π 0 R 0
2
q q q (3 R r ) 2 2 (R r ) 3 8 π 0 R 4 π 0 R 8 π 0 R
与路径无关
a
dr
任意带电体系产生的电场
任意带电体系都可以看成电荷系 q1、q2、…，移动q0， 静电力所作功为: b b q E •b dr W F dr 0
ab
q0 a• q0 ( E1 E 2 E n ) dr a( L) n b q 0 E i d r ＝ qi q0 ( 1 1 ) a( L) i 1 rbi i 4 0 rai
注意：
• 电势能的零点可以任意选取，但是在习惯上， 当场源电荷为有限带电体时，通常把电势能的零 点选取在无穷远处。 这时，空间a点的电势能：
E pa
a
q0 E dl
• 电势能为电场和位于电场中的电荷这个系统所 共有。