极值与凹凸性
曲线的凹凸 极值

曲线的凹凸极值曲线是数学中一个重要的概念,它在自然科学、社会科学和工程技术等领域都有广泛的应用。
曲线的凹凸性和极值是曲线分析的重要内容,它们有助于我们更好地理解和把握曲线的性质和规律。
在之前的文章中,我们讨论了曲线的凹凸性和极值的基本概念,以及如何判断和求解极值问题。
接下来,我们将进一步探讨曲线凹凸性与极值之间的关系,以及如何利用这些概念解决实际问题。
一、曲线凹凸性与极值的关系1.凹凸性的判断曲线的凹凸性可以通过二阶导数来判断。
设曲线方程为y=f(x),则曲线在点x处的凹凸性如下:-当f''(x)>0时,曲线在点x处凸向上;-当f''(x)<0时,曲线在点x处凸向下;-当f''(x)=0时,曲线在点x处可能为极值点或拐点。
2.极值点的判断设f(x)在区间[a, b]上连续,在区间(a, b)内可导,那么极值点满足以下条件:-当f'(x)=0时,x为极值点的必要条件;-当f''(x)<0时,x为极大值点;-当f''(x)>0时,x为极小值点。
二、曲线凹凸性与极值的实际应用1.优化问题在实际问题中,我们常常需要寻找函数的极值点,以求解最优化问题。
例如,在经济学中,我们可能需要求解最大利润或最小成本的问题;在工程学中,我们可能需要求解最小能耗或最大效益的问题。
通过研究曲线的凹凸性和极值,我们可以找到最优解对应的参数值。
2.物理力学在物理力学领域,曲线的凹凸性和极值有着重要的应用。
例如,在弹性力学中,曲线凹凸性对应着物体的应变情况,极值点则对应着应力集中现象。
通过分析曲线的凹凸性和极值,我们可以更好地了解和预测物体的力学性能。
3.经济学与金融学在经济学和金融学领域,曲线凹凸性和极值有助于我们分析和预测市场走势。
例如,在股票市场中,股价走势图可以看作是一条曲线,通过研究曲线的凹凸性和极值,我们可以判断股价的波动趋势,从而为投资决策提供依据。
ch单调性极值凹凸性拐点渐近线实用

(3) 斜渐近线 y=ax+b
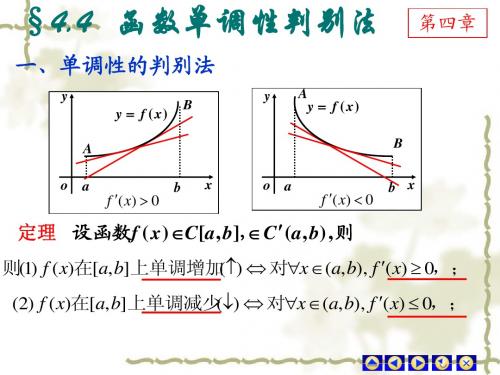
说明:y 0, y不存在的点成为函数单调性可能改变的点. 二、确定函数单调区间的步骤: 1、确定函数定义域. 2、求f ( x) 0及f ( x)不存在的点x0, x1, x2,xn .
3、用xi将D划为几个开子区间(除去xi ).
4、列表判定各子区间内f 的符号,得单调性结论。
第2页/共56页
(1)(2)弯曲方向不同---凹凸性不同
第24页/共56页
ox
曲线的凹凸性 B 曲线的弯曲方向
A
第25页/共56页
一、函数的凹凸性
凸
y
引例
y f1(x)
凹
y f2(x)
oa
b
x
1定义:若在某区间内,曲线 y f (x)上任意一点处切线
都在曲线的上方,则称该曲线是凸;
若曲线 y f (x)上任意一点处切线,都在曲线的下方
第17页/共56页
练 习 :求 下 列 函 数 的 极 值: y x ln(1 x).
解:函数的定义域为(1, )
令 y 1 1 0, 得 驻点x 0, 1 x
又
y
(1
1 x)2
,
y(0)
1
0,
故 函数在x 0处取得极小值 y(0) 0.
第18页/共56页
已知f ( x)连续可导且f "( x0 ) 0,则f ( x0 )() C A一定是极大值;B一定是极小值; C一定不是极大值;D一定不是极小值 注意:若f ”(x0)=0, 此定理失效,用第一充 分条件判断。
第3页/共56页
例、讨论y
x
3
2
x 3的单调性。
2
解:
4.4-5 函数的单调性,极最值,凹凸性,拐点
例4 求下列函数的最值
(1) y 3 ( x 2 2 x ) 2 x 0,3 4( x 1) ( x ) 解 f 33 x 2 2 x 而 令f x) 0,得驻点 x 1, x 0,2是不可导点 ( 由于f (1) 1, f ( 2) 0, f (0) 0, f ( 3) 3 9
内的所有 x 0及f x不存在的点 找出 a, b f (一般有限个) :
x 1 , x 2 , , x k ;在f a , f x 1 , f x 2 , , f x k , f b 中 选取出最大最小 ,
即为f x 在a, b上的M, m.
若 f ( x0 ) f ( x0 ) f ( x0 ) 0,f
( 4)
( x0 ) 0, 则如何?
(1).若 f ( x0 ) f ( x0 ) f ( 2n1) ( x0 ) 0,f
则f ( x)在x0处取极值 .
( 2n)
( x0 ) 0,
x
f (x) f (x)
故
( , 1)
1
0
(1 , 2)
2 0 1
( 2 , )
y
2
(2 , ); 的单调减(单减)区间 为 (1 , 2).
的单调增(单增)区间为 ( , 1) ,
2 1
o
1 2
x
说明:
1) 单调区间的分界点除驻点外,也可是导数不存在的点.
例如,
y y 3 x2
f ( x0 ) f ( x) f ( x0 ) f ( x0 )( x x0 ) ( x x0 ) 2 o ( x x0 ) 2 2!
中值定理、洛必达、函数单调性、极值、最值,凹凸性的应用

所以,由推论 1,
推论 2:若对于
,则
.
四.洛必达法则
我们在第一章曾注意到,考试时考察得最多的求极限问题要么是 型,要么是
。对付这种问题,我们根据具体情形曾给出了因式分解约零因子、根式有理 化约零因子、等价无穷小替换、凑重要极限等方法。现在有一个著名的法则— —洛必达法则,可用一招统一解决大部分的 或 的极限问题。 现在先回顾一下洛必大达法则的条件及结论:
定义:设函数
在区间 内有定义,如果对
,都有:
则称函数
在区间 内为下凸的.
函数凹、凸性的判定
定理:设函数
在区间 内存在二阶导数且
(或
则函数
在区间 内为下凸(或上凸)的.
例 13.确定
的上(下)凸性.
例 14.确定
的上(下)凸性.
拐点的定义:称曲线
上凸与下凸的分界点为其拐点,或变曲点.
拐点的必要条件:如果在 附近 具有连续的二阶导数且
的极值.
解一:(一)
.
(二)
.
(三)令 (四)列表判断:
。无不可导点.
(
解二:(一) (二)
1 0 极大 2 .
3
—
0
极小-2
.
(三)令
.无不可导点.
(四)
.因为,
,所以
为极大值;
又因为 七.最值
第一种情况:设
,所以 在闭区间
为极小值. 上连续,则 在
上必可取到最大
值与最小值.最值的达到只有两种情况:(1) 或 即为最值;
例 15.求曲线
上(下)凸区间及拐点.
解:(一)
;
(二)
,
;
(三)令 (四)列表判断: (
高等数学课件3-7凹凸性

凹凸性研究的重要成果和突破
添加项标题
19世纪初,法国数学家拉格朗日提出了函数的凹凸性概念,为 研究函数的性质提供了新的工具。
添加项标题
19世纪末,德国数学家魏尔斯特拉斯提出了函数的极值定理, 为研究函数的凹凸性提供了理论基础。
添加项标题
20世纪初,英国数学家哈代和波兰数学家莱维提出了函数的凹 凸性判别法,为研究函数的凹凸性提供了新的方法。
化证明过程
举例:利用凸 函数的性质, 可以证明不等 式f(x) > g(x)
凹凸性在优化问题中的应用
凸优化问题:求解凸函数最小值 凹优化问题:求解凹函数最大值 凸优化算法:梯度下降法、牛顿法等
凹优化算法:梯度上升法、牛顿法等
凸优化与凹优化的区别:凸优化问题有 唯一解,凹优化问题可能有多个解
凸优化与凹优化的应用:在机器学习、 图像处理、信号处理等领域有广泛应用
,
汇报人:
目录
凹函数和凸函数的定义
凹函数:对于任意x1,x2∈D, f(x1)+f(x2)≥2f((x1+x2)/2)
凹函数和凸函数的区别在于不等号 的方向不同
添加标题
添加标题
凸函数:对于任意x1,x2∈D, f(x1)+f(x2)≤2f((x1+x2)/2)
添加标题Βιβλιοθήκη 添加标题凹函数和凸函数的定义是判断函数 凹凸性的基础
研究前景:凹凸性研究在许多领域都有广泛的应用前景,如优化问题、图像处理、机 器人控制等
汇报人:
凹凸性的几何意义
凸性:函数在某点处的切线斜 率大于等于该点处的函数值
凹性:函数在某点处的切线斜 率小于等于该点处的函数值
凸性函数:函数图像在定义域 内任意两点之间是凸的
函数的凹凸性与极值点

函数的凹凸性与极值点函数的凹凸性和极值点是微积分中重要的概念。
通过研究函数的凹凸性和极值点,我们可以更加深入地理解函数的性质,进而应用于许多实际问题的求解中。
本文将详细介绍函数的凹凸性和极值点。
一、凹凸性的定义首先我们来定义函数的凹凸性。
假设函数f(x)在区间I上可导,若对于任意的x1、x2∈I且x1<x2,有f'(x1)<f'(x2),则称函数f(x)在区间I上是凹函数;若对于任意的x1、x2∈I且x1<x2,有f'(x1)>f'(x2),则称函数f(x)在区间I上是凸函数。
凹凸函数很类似于水果篮中的凹凸形状,凹函数可以想象成篮子底部向上凹陷,而凸函数则相反,底部向下凸起。
函数凹凸性的变化有助于我们分析函数的增减性、拐点等特性。
二、凹凸性与导数的关系函数的凹凸性与函数的导数密切相关。
如果函数f(x)在区间I上连续,那么f'(x)的正负性与函数的凹凸性有以下关系:1. 如果f'(x)在区间I上单调递增,那么f(x)在区间I上是凹函数;2. 如果f'(x)在区间I上单调递减,那么f(x)在区间I上是凸函数;3. 若f''(x)存在且在区间I上恒大于零,那么f(x)在区间I上是凸函数;4. 若f''(x)存在且在区间I上恒小于零,那么f(x)在区间I上是凹函数。
通过对函数的导数进行研究,我们可以得到函数的凹凸性质。
这为我们进一步分析函数的特点提供了重要的线索。
三、极值点的定义与判定接着我们来回顾一下极值点的定义。
对于函数f(x),如果存在某一点x0,使得在x0的某个邻域内,f(x0)是函数的最大值或最小值,则称x0是函数f(x)的极值点。
对于可导的函数f(x),我们可以通过导数来判断函数的极值点:1. 若f'(x0) = 0,且f''(x0)存在,则x0是函数f(x)的驻点。
2. 若f'(x0) = 0,且f''(x0) > 0,则x0是函数f(x)的极小值点。
高等数学I(软件)D4_4单调性凹凸性极值与最值
例3 确定函数 f (x) (x 5) 3 x2 的单调区间. 2
解 (1) 定义域 ,
(2) f (x) 3 x2 (x 5) 2 1 5 x 1 2 3 3x 3 3x
令 f ( x) 0 , 得 x1 1, 当 x2 0 时, f ( x)不存在,
(3) 列表:
1
因此
从而
证明 目录 上页 下页 返回 结束
* 证明 x tan x 0
令
则
(x) 1 sec2 x
tan2 x 0,
x
(0,
2
)
从而
即
x tan x 0,
x
(0 ,
2
)
例5 证明不等式 2 x 3 1 (x 1)
x
证明 令 f (x) 2 x (3 1)
x
f (x)
1 x
1 x2
1 x2
(x
x 1)
当 x 1 时, f (x) 0 , 即 f (x)在 [1, )上单增,
当 x 1 时, f (x) f (1) 0,
即 x 1时,2 x 3 1 x
例5 证明:方程 xex =2在(0,1)内有且仅有一个实根
证明 设f (x) xex -2,因f (x)在[0,1]上连续, 且f (0) 2 0, f (1) e 2 0.由零值定理,
o
x
y
y x3
o
x
机动 目录 上页 下页 返回 结束
确定函数单调区间的方法和步骤:
(1) 确定函数 y f ( x) 的定义域;
(2) 求 f (x), 找使 f (x) 0 的点(驻点)和 f (x) 不存在的点;
(3) 以(2)中所找点为分界点,将定义域分割成部分区间, 判断在每一区间上导数的符号,由定理得出结论。
函数的凹凸性与极值探讨
函数的凹凸性与极值探讨函数的凹凸性对其极值的存在性、数量以及判断方式都有重要影响。
以下是从几个方面详细分析函数的凹凸性如何影响其极值:1. 极值的存在性●凸函数:对于严格凸函数(即在整个定义域内都保持凸性的函数),如果在某点取得极值,则该极值必然是全局最小值(因为凸函数在任意两点之间的线段上都在函数图像上方或重合,所以在其内部不可能有比该点更低的点)。
同样地,如果函数是凹的,则在该点取得的极值可能是全局最大值。
●非严格凸/凹函数:对于非严格凸函数(即存在直线段与函数图像相切但不相交的凸函数)或非严格凹函数,可能存在多个极值点,但这些极值点可能不是全局最优解,而只是局部最优解。
2. 极值的数量●凸函数:在严格凸函数中,如果函数在某区间内连续可导,且在该区间的端点处函数值趋于无穷大(或满足其他适当的边界条件),则该函数在该区间内至多有一个全局最小值点(没有最大值点,除非定义域有界)。
这是因为凸函数的图像总是在任意两点之间的线段上方或与其重合,所以不可能在同一区间内有两个或更多的全局最小值。
●非凸函数:非凸函数可能具有多个局部极值点(包括局部最小值和局部最大值),这些极值点的数量取决于函数的复杂性和定义域的性质。
3. 极值的判断方式●一阶导数测试:对于可导函数,可以通过检查一阶导数的符号变化来判断极值点。
然而,这种方法在非凸函数上可能不够有效,因为可能存在多个驻点(一阶导数为零的点),其中只有部分是极值点。
●二阶导数测试:在二阶导数存在的情况下,可以利用二阶导数的符号来判断极值点的类型。
对于凸函数,其二阶导数(或海森矩阵对于多元函数)在非极值点处非负;在极小值点处等于零(对于严格凸函数,极小值点处二阶导数严格大于零)。
然而,需要注意的是,并非所有凸函数都是二阶可导的,且二阶导数测试在非凸函数上可能不够可靠。
●凹凸性直接判断:对于凸函数,可以直接利用凸函数的定义来判断极值点。
即,如果函数在某点取得极值,并且该点位于定义域的边界上或其一阶导数在该点附近发生变化(从正变为负或从负变为正),则该点很可能是全局最小值点(对于凹函数,则可能是全局最大值点)。
34 函数的单调性、凹凸性与极值
(2)求拐点的方法
方法: 设函数f ( x )在 x0的邻域内二阶可导, 且 f ′′( x0 ) = 0, 则有:
1) x0 两近旁f ′′( x )变号, 点( x0 , f ( x0 ))为拐点;
2) x0 两近旁f ′′( x )不变号, 点( x0 , f ( x0 ))不是拐点.
例9 求曲线 y = 3 x 4 − 4 x 3 + 1 的拐点及凹、凸的区间. 解 易见函数的定义域为 ( −∞ ,+∞ ),
定理4 (第一充分条件) 设函数 f ( x ) 在点 x0 的某个邻域内连续并且 可导(导数 f ′( x0 ) 也可以不存在), (1)如果在点 x0的左邻域内 f ′( x ) > 0; 在点 x0的右 邻域内 f ′( x ) < 0, 则 f ( x ) 在 x0 处取得极大值 f ( x0 ); (2)如果在点 x0的左邻域内 f ′( x ) < 0; 在点 x0的右 邻域内 f ′( x ) > 0, 则 f ( x ) 在 x0 处取得极小值 f ( x0 ); (3)如果在点 x0的邻域内, 在 x0处没有极值.
例3
2 3 y = x 讨论函数 的单调区间.
解 Q D : ( −∞ ,+∞ ).
y′ = 32 ( x ≠ 0), 3 x 当 x = 0 时, 导数不存在.
当 x < 0时,y′ < 0,
∴ 在 ( −∞ , 0]上单调减少;
当 x > 0时,y′ > 0,
∴ 在 [0, +∞ )上单调增加;
向上凸:图形 上任意弧段位 于所张弦的上 方
定义 设 f ( x ) 在区间 I 内连续,
x1 + x 2 f ( x1 ) + f ( x 2 ) ∀x1 , x2 ∈ I , 恒有 f ( )< , 2 2 则称 f ( x ) 在 I 上的图形是(向上)凹的. x1 + x 2 f ( x1 ) + f ( x 2 ) ∀x1 , x2 ∈ I , 恒有 f ( )> , 2 2
函数的最值及凹凸性
注意:拐点处 =0或者 不存在;
例:求曲线 的凹凸区间与拐点;
令 =0,得 ,
则曲线在 , 为凹的;
曲线在 为凸的;
为拐点;
例2:求曲线 的凹凸性及拐点;
解:求导数
当x=2时, 不存在(也可能是拐点)
则曲线在 为凸的;
曲线在 为凹的;
为拐点;
3.其他例题
例:设曲线 在x=1处取极小值,(0,2)为其拐点试确定常数a,b,c的值
注意:前提是可导的,若不可导,需要另外讨论?
凹凸性如何判断,从图形分析问题。
, 由小变大 由大变小
小, 小 小, 大
单调上升 单调下降
>0 >0
2.曲线凹凸性的判别方法
定理4.7假设函数 在区间 内具有二阶导数,那么
(1)若 ,恒有 >0,则曲线 在区间 内是凹的;
(2)若 ,恒有 <0,则曲线 在区间 内是凸的;
实际问题的最值
(1)建立目标函数;
(2)求最值;
例2:某房地产公司有50套公寓要出租,当租金定为每月180元时,公寓会全部租出去.当租金每月增加10元时,就有一套公寓租不出去,而租出去的房子每月需花费20元的整修维护费.试问房租定为多少可获得最大收入?
解:设房租为每月 元,
租出去的房子有 套,
每月总收入为:
解:(0,2)为曲线拐点,则2=c;
,因为x=1处取极小值,则 ;
,因为(0,2)为拐点,则
则:a=0,b=-3,c=2
小结:
1)凹凸性的定义;
2)凹凸性的判定;
课外作业
教学后记
§4.6曲线的凹凸性及其拐点
1.曲线的凹凸性
