第八章 第八节抛 物 线
【世纪金榜】高考数学(文科,全国通用)一轮总复习练习：8.7抛 物 线(含答案解析)
课时提升作业五十二抛物线(25分钟60分)一、选择题(每小题5分,共25分)1.(2016·聊城模拟)设抛物线y=x2上的一点P到x轴的距离是4,则点P到该抛物线焦点的距离为()A.3B.4C.5D.6 【解题提示】由题意可得点P的纵坐标为4,由抛物线的定义可得点P到该抛物线焦点的距离等于点P到准线y=-1的距离,由此求得结果.【解析】选C.由于抛物线y=x2上的一点P到x轴的距离是4,故点P的纵坐标为4.再由抛物线y=x2的准线为y=-1,结合抛物线的定义可得点P到该抛物线焦点的距离等于点P到准线的距离,故点P到该抛物线焦点的距离是4-(-1)=5.2.(2016·杭州模拟)已知点P是抛物线y2=2x上的动点,点P到准线的距离为d,且点P在y轴上的射影是M,点A,则|PA|+|PM|的最小值是()A. B.4C. D.5【解析】选C.抛物线焦点F,准线x=-,如图,延长PM交准线于点N,由抛物线定义得|PF|=|PN|,因为|PA|+|PM|+|MN|=|PA|+|PN|=|PA|+|PF|≥|AF|=5,而|MN|=,所以|PA|+|PM|≥5-=,当且仅当A,P,F三点共线时,取等号,此时,点P位于抛物线上,所以|PA|+|PM|的最小值为.【加固训练】设F为抛物线y2=4x的焦点,A,B,C为该抛物线上三点,若++=0,则|FA|+|FB|+|FC|等于()A.9B.6C.4D.3【解析】选B.设A(x1,y1),B(x2,y2),C(x3,y3),又F(1,0).由++=0知(x1-1)+(x2-1)+(x3-1)=0,即x1+x2+x3=3,|FA|+|FB|+|FC|=x1+x2+x3+p=6.3.(2016·重庆模拟)O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若|PF|=4,则△POF的面积为()A.2B.2C.2D.4【解析】选C.抛物线C的方程为y2=4x,所以2p=4,可得=,得焦点F(,0).设P(m,n),根据抛物线的定义,得|PF|=m+=4,即m+=4,解得m=3.因为点P在抛物线C上,得n2=4×3=24,所以n=±=±2,因为|OF|=,所以△POF的面积S=|OF|×|n|=××2=2.4.已知抛物线y2=4x的焦点F,A,B是抛物线上横坐标不相等的两点,若AB的垂直平分线与x 轴的交点是(4,0),则|AB|的最大值为()A.2B.4C.6D.10【解题提示】可将|AB|与|AF|,|BF|之间的关系联系起来,再利用抛物线的定义求解.【解析】选C.因为抛物线y2=4x的焦点F(1,0),设A(x1,y1),B(x2,y2),因为线段AB的垂直平分线恰过点M(4,0),所以|MA|2=|MB|2,即(4-x1)2+=(4-x2)2+,又=4x1,=4x2,代入并展开得:16-8x1++4x1=-8x2+16+4x2,即-=4x1-4x2,又x1≠x2,所以x1+x2=4,所以线段AB中点的横坐标为(x1+x2)=2,所以AB≤AF+BF=+=4+2=6(当A,B,F三点共线时取等号),即|AB|的最大值为6.5.(2016·临沂模拟)已知抛物线y2=2px(p>0),过其焦点且斜率为-1的直线交抛物线于A,B两点,若线段AB的中点的纵坐标为-2,则该抛物线的准线方程为()A.x=1B.x=2C.x=-1D.x=-2【解析】选C.由题意可设直线方程为y=-,设A(x1,y1),B(x2,y2),联立方程整理得y2+2py-p2=0,所以y1+y2=-2p.因为线段AB的中点的纵坐标为-2,所以=-2.所以p=2.所以抛物线的准线方程为x=-1.二、填空题(每小题5分,共15分)6.顶点在坐标原点,对称轴是坐标轴,且经过点M(-2,-4)的抛物线方程是.【解析】满足题意的抛物线应有两条,设为y2=ax或x2=by,将点M(-2,-4)的坐标代入求得y2=-8x 或x2=-y.答案:y2=-8x或x2=-y7.抛物线x2=2py(p>0)的焦点为F,其准线与双曲线-=1相交于A,B两点,若△ABF为等边三角形,则p=.【解析】如图,在等边三角形ABF中,DF=p,BD=p,所以B点坐标为.又点B 在双曲线上,故-=1.解得p=6.答案:6【加固训练】已知直线l1:4x-3y+11=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是.【解析】因为x=-1恰为抛物线y2=4x的准线,所以可画图观察.如图,连接PF,过F作FQ⊥l1于点Q,d2=PF,所以d1+d2=d1+PF≥FQ===3.答案:38.已知过点P(4,0)的直线与抛物线y2=4x相交于A(x1,y1),B(x2,y2)两点,则+的最小值是.【解析】当直线的斜率不存在时,直线方程为x=4,代入y2=4x,得交点为(4,4),(4,-4),所以+=16+16=32;当直线的斜率存在时,设直线方程为y=k(x-4),与y2=4x联立,消去x得ky2-4y-16k=0,由题意,知k≠0,则y1+y2=,y1y2=-16.所以+=(y1+y2)2-2y1y2=+32>32.综上知,(+)min=32.答案:32【误区警示】本题易出现最小值不存在的错误结论.其原因是忽略直线的斜率不存在的情况,从而得出错误的结论.三、解答题(每小题10分,共20分)9.(2016·莱芜模拟)已知抛物线C的顶点为坐标原点,焦点F(0,c)(c>0)到直线y=2x的距离是.(1)求抛物线C的方程.(2)若直线y=kx+1(k≠0)与抛物线C交于A,B两点,设线段AB的中垂线与y轴交于点P(0,b),求实数b的取值范围.【解析】(1)由题意,=,故c=.所以抛物线C的方程为x2=2y.(2)设A(x1,y1),B(x2,y2),则由得x2-2kx-2=0.所以Δ=4k2+8>0.所以x1+x2=2k,所以线段AB的中点坐标为(k,k2+1).线段AB的中垂线方程为y=-(x-k)+k2+1,即y=-x+k2+2.令x=0,得b=k2+2.所以b∈(2,+∞).10.(2016·菏泽模拟)如图,曲线C由上半椭圆C1:+=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1,C2的公共点为A,B,其中C1的离心率为.(1)求a,b的值.(2)过点B的直线l与C1,C2分别交于P,Q(均异于点A,B),若AP⊥AQ,求直线l的方程.【解析】(1)在C1,C2的方程中,令y=0,可得b=1,且A(-1,0),B(1,0)是上半椭圆C1的左右顶点. 设C1的半焦距为c,由=及a2-c2=b2=1得a=2.所以a=2,b=1.(2)由(1)知,上半椭圆C1的方程为+x2=1(y≥0).易知,直线l与x轴不重合也不垂直,设其方程为y=k(x-1)(k≠0),代入C1的方程,整理得(k2+4)x2-2k2x+k2-4=0.(*)设点P的坐标为(x P,y P),因为直线l过点B,所以x=1是方程(*)的一个根,由求根公式,得x P=,从而y P=,所以点P的坐标为.同理,由得Q点的坐标为(-k-1,-k2-2k).所以=(k,-4),=-k(1,k+2).因为AP⊥AQ,所以·=0,即[k-4(k+2)]=0,因为k≠0,所以k-4(k+2)=0,解得k=-.经检验,k=-符合题意,故直线l的方程为y=-(x-1).(20分钟40分)1.(5分)(2016·烟台模拟)若抛物线C:y2=2px(p>0)上一点到焦点和x轴的距离分别为5和3,则此抛物线的方程为()A.y2=2xB.y2=(-4)xC.y2=2x或y2=18xD.y2=3x或y2=(-4)x【解析】选C.因为抛物线y2=2px(p>0)上一点到x轴的距离为3,所以设该点为P,则点P的坐标为(x0,±3),因为点P到抛物线的焦点F的距离为5,所以由抛物线的定义,得x0+=5 (1)因为点P是抛物线上的点,所以2px0=9 (2)由(1)(2)联立,解得p=1,x0=或p=9,x0=,则抛物线方程为y2=2x或y2=18x.2.(5分)设O为坐标原点,F为抛物线y2=4x的焦点,A为抛物线上一点,若·=-4,则点A 的坐标为()A.(2,±2)B.(1,±2)C.(1,2)D.(2,2) 【解析】选B.设A(x0,y0),F(1,0),=(x0,y0),=(1-x0,-y0),·=x0(1-x0)-=-4.因为=4x0,所以x0--4x0+4=0⇒+3x0-4=0, x0=1或x0=-4(舍).所以x0=1,y0=±2.3.(5分)(2016·武汉模拟)已知抛物线y2=4x的焦点为F,准线为直线l,过抛物线上一点P作PE ⊥l于点E,若直线EF的倾斜角为150°,则|PF|=.【解析】由抛物线方程y2=4x,可得焦点F(1,0),准线l的方程为:x=-1.因为直线EF的倾斜角为150°,所以k1=tan150°=-.所以直线EF的方程为:y=-(x-1),联立解得y=.所以E.因为PE⊥l于点E,所以y P=,代入抛物线的方程可得=4x P,解得x P=.所以|PF|=|PE|=x P+1=.答案:4.(12分)已知A,B是抛物线W:y=x2上的两个点,点A的坐标为(1,1),直线AB的斜率为k,O为坐标原点.(1)若抛物线W的焦点在直线AB的下方,求k的取值范围.(2)设C为W上一点,且AB⊥AC,过B,C两点分别作W的切线,记两切线的交点为D,求|OD|的最小值.【解析】(1)抛物线y=x2的焦点为.由题意,得直线AB的方程为y-1=k(x-1),令x=0,得y=1-k,即直线AB与y轴相交于点(0,1-k).因为抛物线W的焦点在直线AB的下方,所以1-k>,解得k<.(2)由题意,设B(x1,),C(x2,),D(x3,y3),联立方程消去y,得x2-kx+k-1=0,由根与系数的关系,得1+x1=k,所以x1=k-1.同理,得AC的方程为y-1=-(x-1),x2=--1.对函数y=x2求导,得y′=2x,所以抛物线y=x2在点B处的切线斜率为2x1,所以切线BD的方程为y-=2x1(x-x1),即y=2x1x-.同理,抛物线y=x2在点C处的切线CD的方程为y=2x2x-.联立两条切线的方程解得x3==,y3=x1x2=-k,所以点D的坐标为.因此点D在定直线2x+y+2=0上.因为点O到直线2x+y+2=0的距离d==,所以|OD|≥,当且仅当点D时等号成立.由y3=-k=-,得k=,验证知符合题意.所以当k=时,|OD|有最小值.5.(13分)(2015·福建高考)已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3.(1)求抛物线E的方程.(2)已知点G(-1,0),延长AF交抛物线E于点B,证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.【解析】方法一:(1)由抛物线的定义得=2+,因为=3,即2+=3,解得p=2,所以抛物线E的方程为y2=4x.(2)因为点A(2,m)在抛物线E:y2=4x上,所以m=±2,由抛物线的对称性,不妨设A(2,2).由A(2,2),F(1,0)可得直线AF的方程为y=2(x-1).由得2x2-5x+2=0,解得x=2或x=,从而B.又G(-1,0),所以k GA==,k GB==-,所以k GA+k GB=0,且∠AGF=∠BGF,这表明点F到直线GA,GB的距离相等,故以F为圆心且与直线GA相切的圆必与直线GB相切.方法二:(1)同方法一.(2)设以点F为圆心且与直线GA相切的圆的半径为r.因为点A(2,m)在抛物线E:y2=4x上,所以m=±2,由抛物线的对称性,不妨设A(2,2),由A(2,2),F(1,0)可得直线AF的方程为y=2(x-1).由得2x2-5x+2=0,解得x=2或x=,从而B.又G(-1,0),故直线GA的方程为2x-3y+2=0,从而r==.又直线GB的方程为2x+3y+2=0,所以点F到直线GB的距离d===r. 这表明以点F为圆心且与直线GA相切的圆必与直线GB相切.。
高中数学考点-抛 物 线
9．8抛 物 线1．抛物线的定义平面内与一个定点F 和一条定直线l (F ∉______)距离相等的点的轨迹叫做抛物线．点F 叫做抛物线的________，直线l 叫做抛物线的________． 2．抛物线的标准方程及几何性质标准 方程 y 2＝2px (p ＞0)y 2＝－2px (p ＞0)x 2＝2py (p ＞0)x 2＝－2py (p ＞0)图形性 质焦 点 ① ②⎝⎛⎭⎫－p2，0 ③ ④⎝⎛⎭⎫0，－p 2 准 线 ⑤x ＝－p2⑥ ⑦y ＝－p2⑧ 范 围 ⑨x ≥0， y ∈R⑩⑪⑫y ≤0， x ∈R对 称 轴 ⑬⑭y 轴顶 点 ⑮原点O (0，0)离 心 率 ⑯开 口⑰⑱向左⑲向上⑳自查自纠1．l 焦点 准线2．①⎝⎛⎭⎫p 2，0 ③⎝⎛⎭⎫0，p 2 ⑥x ＝p 2 ⑧y ＝p 2⑩x ≤0，y ∈R ○11y ≥0，x ∈R ○13x 轴 ○16e ＝1 ○17向右 ○20向下抛物线y ＝2x 2的焦点坐标是( )A.⎝⎛⎭⎫18，0B.⎝⎛⎭⎫12，0 C.⎝⎛⎭⎫0，18 D.⎝⎛⎭⎫0，12 解：由抛物线的标准方程为x 2＝12y ，可知p 2＝18，所以焦点坐标是⎝⎛⎭⎫0，18.故选C. A (2，1)为抛物线x 2＝2py (p >0)上一点，则A 到该抛物线的焦点F 的距离为( ) A.32 B.2＋12 C ．2 D.2＋1解：把A (2，1)代入抛物线方程得2＝2p ，得p ＝1，所以A 到焦点的距离为1＋12＝32，则|AF |＝32，故选A.设抛物线y 2＝8x 的准线与x 轴交于点Q ，若过点Q 的直线l 与抛物线有公共点，则直线l 的斜率的取值范围是( )A.⎣⎡⎦⎤－12，12 B ．[－2，2] C ．[－1，1] D ．[－4，4]解：由已知得Q (－2，0)，由题意知直线l 的斜率存在，设直线l 的方程为y ＝k (x ＋2)，代入抛物线方程，消去y 整理得k 2x 2＋(4k 2－8)x ＋4k 2＝0，由Δ＝(4k 2－8)2－4k 2·4k 2＝64(1－k 2)≥0，解得－1≤k ≤1.故选C. 已知直线l 过拋物线C 的焦点，且与C 的对称轴垂直，l 与C 交于A ，B 两点，且|AB |＝12，P 为C 的准线上的一点，则△ABP 的面积为________．解：设抛物线的焦点到准线的距离为p ，则由题意有2p ＝12，即p ＝6，则△ABP 的面积为12×12×6＝36.故填36.(2016·浙江)若抛物线y 2＝4x 上的点M 到焦点的距离为10，则M 到y 轴的距离是____________． 解：由题意可知焦点F 的坐标为(1，0)，则准线方程为x ＝－1，设M (x M ，y M )，则x M ＋1＝10，所以x M ＝9，即M 到y 轴的距离是9.故填9.类型一 抛物线的定义及标准方程(1)已知双曲线C 1：x 2a 2－y 2b 2＝1(a >0，b >0)的离心率为2.若抛物线C 2：x 2＝2py (p >0)的焦点到双曲线C 1的渐近线的距离为2，则抛物线C 2的方程为( ) A ．x 2＝833y B ．x 2＝1633yC ．x 2＝8yD ．x 2＝16y 解：因为x 2a 2－y 2b2＝1的离心率为2，所以c a ＝2，即c 2a 2＝a 2＋b 2a 2＝4，所以b 2a 2＝3，ba＝ 3.x 2＝2py (p >0)的焦点坐标为⎝⎛⎭⎫0，p 2，x 2a 2－y 2b 2＝1的渐近线方程为y ＝±ba x ，即y ＝±3x .由题意得p 21＋（3）2＝2，所以p ＝8.故C 2的方程为x 2＝16y .故选D.(2)已知椭圆x 24＋y 23＝1的右焦点F 为抛物线y 2＝2px (p >0)的焦点，点P 的坐标为(3，2)．若点M 为该抛物线上的动点，则|MP |＋|MF |的最小值为________．解：因为椭圆x 24＋y 23＝1的右焦点F 为(1，0)，所以p2＝1，解得p ＝2，所以抛物线y 2＝4x 的准线方程为x ＝－1，如图所示，过M 作抛物线的准线l 的垂线MA ，垂足为A ，由抛物线的定义有|MA |＝|MF |，所以|MP |＋|MF |＝|MP |＋|MA |， 显然当P ，M ，A 三点共线时，|MP |＋|MF |取得最小值．因为点P 的坐标为(3，2)， 所以|MP |＋|MF |的最小值为3－(－1)＝4.故填4.【点拨】(1)求抛物线的标准方程，若开口未知，则要先判断开口，以便设方程；(2)求最值问题，则常借助抛物线定义及平面几何中三角形两边和大于第三边或两点直线段最短等性质．(1)设抛物线C ：y 2＝2px (p >0)的焦点为F ，点M 在C 上，|MF |＝5.若以MF 为直径的圆过点(0，2)，则C 的方程为( ) A ．y 2＝4x 或y 2＝8x B ．y 2＝2x 或y 2＝8x C ．y 2＝4x 或y 2＝16xD ．y 2＝2x 或y 2＝16x解：因为以MF 为直径的圆过点(0，2)，所以点M 在第一象限．由|MF |＝x M ＋p2＝5得M ⎝⎛⎭⎫5－p 2，2p ⎝⎛⎭⎫5－p 2，从而以MF 为直径的圆的圆心N 的坐标为⎝⎛⎭⎫52，122p ⎝⎛⎭⎫5－p 2. 因为点N 的横坐标恰好等于圆的半径，所以圆与y 轴切于点(0，2)，从而2＝122p ⎝⎛⎭⎫5－p2，即p 2－10p ＋16＝0，解得p ＝2或p ＝8， 所以抛物线方程为y 2＝4x 或y 2＝16x .故选C.(2)设P 是抛物线y 2＝4x 上的一个动点，则点P 到点A (－1，1)的距离与点P 到直线x ＝－1的距离之和的最小值为________． 解：如图，易知抛物线的焦点为F (1，0)，准线是x ＝－1，由抛物线的定义知：点P 到直线x ＝－1的距离等于点P 到F 的距离．于是，问题转化为在抛物线上求一点P ，使点P 到点A (－1，1)的距离与点P 到F (1，0)的距离之和最小， 显然，连接AF 与抛物线相交的点即为满足题意的点， 此时最小值为[1－（－1）]2＋（0－1）2＝ 5.故填 5.类型二 抛物线焦点弦的性质如图，AB 为过抛物线y 2＝2px (p ＞0)焦点F 的弦，点A ，B 在抛物线准线上的射影分别为A 1，B 1，且A (x 1，y 1)，B (x 2，y 2)．求证：(1)||AB ＝x 1＋x 2＋p ；(2)x 1x 2＝p 24，y 1y 2＝－p 2；(3)以AB 为直径的圆与抛物线的准线相切；(4)1||AF ＋1||BF ＝2p. 证明：(1)由抛物线的定义知||AB ＝||AF ＋||BF ＝||AA 1＋||BB 1＝x 1＋x 2＋p .(2)当直线AB 的斜率不存在时，直线AB 的方程为x ＝p 2，x 1x 2＝p 24，y 1y 2＝－2px 1·2px 2＝－p 2；当直线AB 的斜率存在时， 设直线AB 的方程为y ＝k ⎝⎛⎭⎫x －p2， 联立抛物线方程，消x 得y 2－2pk y －p 2＝0， 所以y 1y 2＝－p 2，x 1x 2＝y 212p ·y 222p＝p 24.(3)设AB 的中点为M ，M 到准线的距离为d ，则d ＝||AA 1＋||BB 12＝||AF ＋||BF 2＝||AB 2，所以以AB 为直径的圆与准线相切．(4)当直线AB 的斜率不存在时，1|AF |＋1|BF |＝1|AA 1|＋1|BB 1|＝1x 1＋p 2＋1x 2＋p 2＝1p ＋1p ＝2p；当直线AB 的斜率存在时，因为x 1＋x 2＝⎝⎛⎭⎫y 1k ＋p 2＋⎝⎛⎭⎫y 2k ＋p 2＝y 1＋y 2k ＋p ＝2p k 2＋p ，x 1x 2＝p 24，所以1||AF ＋1||BF ＝1||AA 1＋1||BB 1＝1x 1＋p 2＋1x 2＋p 2＝x 1＋x 2＋p x 1x 2＋p 2（x 1＋x 2）＋p 24＝2pk 2＋2p p 2＋p 2k2＝2p. 【点拨】本题小结了抛物线的焦点弦的有关性质，当抛物线的坐标方程形式发生变化时，性质(3)、(4)不变，性质(1)、(2)略有变化，如对于抛物线x 2＝2py ，性质(1)应为|AB |＝y 1＋y 2＋p ，性质(2)应为x 1x 2＝－p 2，y 1y 2＝p 24，其余情况可自行推导．已知过抛物线y 2＝2px (p >0)的焦点，斜率为22的直线交抛物线于A (x 1，y 1)，B (x 2，y 2)(x 1<x 2)两点，且|AB |＝9.(1)求该抛物线的方程；(2)O 为坐标原点，C 为抛物线上一点，若OC →＝OA →＋λOB →，求λ的值．解：(1)由题意得直线AB 的方程为y ＝22⎝⎛⎭⎫x －p2，与y 2＝2px 联立，消去y 有4x 2－5px ＋p 2＝0，所以x 1＋x 2＝5p4. 由抛物线定义得|AB |＝x 1＋x 2＋p ＝5p4＋p ＝9，所以p ＝4，从而该抛物线的方程为y 2＝8x .(2)由(1)得4x 2－5px ＋p 2＝0，即x 2－5x ＋4＝0，则x 1＝1，x 2＝4，于是y 1＝－22，y 2＝42，从而A (1，－22)，B (4，42)．设C (x 3，y 3)，则OC →＝(x 3，y 3)＝OA →＋λOB →＝(1，－22)＋λ(4，42)＝(4λ＋1，42λ－22)．又y 23＝8x 3，所以[22(2λ－1)]2＝8(4λ＋1)，整理得(2λ－1)2＝4λ＋1，解得λ＝0或λ＝2.1．抛物线的定义、标准方程和性质是解决有关抛物线问题的基础，应当熟练掌握．2．求抛物线的标准方程的常用方法是待定系数法或轨迹法．若抛物线的开口不确定，为避免多种情况分类求解的麻烦，可以设抛物线方程为y 2＝mx 或x 2＝ny (m ≠0，n ≠0)．若m ＞0，开口向右；若m ＜0，开口向左．m 有两解时，则抛物线的标准方程有两个．对n ＞0与n ＜0，有类似的讨论．3．抛物线的离心率e ＝1，体现了抛物线上的点到焦点的距离等于该点到准线的距离．因此，涉及抛物线的焦半径、焦点弦问题时，要看到焦点想准线(看到准线想焦点)，优先考虑利用抛物线的定义，将其转化为点到准线的距离，这样往往可以使问题简单化．4．有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB |＝x 1＋x 2＋p ，若不过焦点，则必须用一般弦长公式． 5．抛物线的几个常用结论(1)抛物线上的点P (x 0，y 0)与焦点F 之间的线段长度(一般叫做抛物线的焦半径)记作r ＝||PF .①y 2＝2px (p ＞0)，r ＝x 0＋p2；②y 2＝－2px (p ＞0)，r ＝－x 0＋p2；③x 2＝2py (p ＞0)，r ＝y 0＋p2；④x 2＝－2py (p ＞0)，r ＝－y 0＋p2.(2)若AB 为抛物线y 2＝2px (p ＞0)的焦点弦，A ，B 两点的坐标分别为(x 1，y 1)，(x 2，y 2)，弦中点M (x 0，y 0)，||AB ＝l .则：①x 1x 2＝p 24；②y 1y 2＝－p 2；③弦长l ＝x 1＋x 2＋p ，因x 1＋x 2≥2x 1x 2＝p ，故当x 1＝x 2时，l 取得最小值，最小值为2p ，此时弦AB 垂直于x 轴，所以抛物线的焦点弦中通径最短(垂直于抛物线对称轴的焦点弦叫做抛物线的通径)．1．(2016·河北唐山一模)已知抛物线的焦点F (a ，0)(a <0)，则抛物线的标准方程为( ) A ．y 2＝2ax B ．y 2＝4ax C ．y 2＝－2ax D ．y 2＝－4ax解：由题意可令抛物线的标准方程为y 2＝－2px (p >0)，由－p2＝a 可知p ＝－2a ，则抛物线的标准方程为y 2＝4ax .故选B.2．(2016·东北三省三校一联)点M (1，1)到抛物线y ＝ax 2准线的距离为2，则a 的值为( ) A.14 B ．－112 C.14或－112 D ．－14或112解：抛物线y ＝ax 2的准线方程为y ＝－14a ，依题意有⎪⎪⎪⎪1＋14a ＝2，解得a ＝14或a ＝－112.故选C. 3．(2016·全国卷Ⅱ)设F 为抛物线C ：y 2＝4x 的焦点，曲线y ＝kx (k >0)与C 交于点P ，PF ⊥x 轴，则k ＝( )A.12 B ．1 C.32D ．2 解：因为y 2＝4x ，所以F (1，0)．又因为曲线y ＝kx (k >0)与C 交于点P ，PF ⊥x 轴，所以P (1，2)．将点P (1，2)的坐标代入y ＝kx(k >0)，得k ＝2.故选D.4．已知椭圆E 的中心在坐标原点，离心率为12，E 的右焦点与抛物线C ：y 2＝8x 的焦点重合，A ，B 是C 的准线与E 的两个交点，则|AB |＝( )A ．3B ．6C ．9D ．12解：因为抛物线y 2＝8x 的焦点为(2，0)，所以椭圆中c ＝2，又c a ＝12，所以a ＝4，b 2＝a 2－c 2＝12，从而椭圆的方程为x 216＋y 212＝1.因为抛物线y 2＝8x 的准线为x ＝－2，所以x A ＝x B ＝－2，将x A ＝－2代入椭圆方程可得|y A |＝3，由图象的对称性可知|AB |＝2|y A |＝6.故选B.5．(2016·运城期末)已知抛物线x 2＝ay 与直线y ＝2x －2相交于M ，N 两点，若MN 中点的横坐标为3，则此抛物线的方程为( )A ．x 2＝32y B ．x 2＝6yC ．x 2＝－3yD ．x 2＝3y 解：设M (x 1，y 1)，N (x 2，y 2)．由⎩⎪⎨⎪⎧x 2＝ay ，y ＝2x －2消去y 得x 2－2ax ＋2a ＝0， 所以x 1＋x 22＝2a 2＝3，即a ＝3，因此所求的抛物线的方程为x 2＝3y .故选D.6．(2016·甘肃模拟)过抛物线y 2＝2px (p >0)的焦点F 且倾斜角为120°的直线l 与抛物线在第一、四象限分别交于A ，B 两点，则|AF ||BF |的值等于( )A.13B.23C.34D.43解：记抛物线y 2＝2px 的准线为l ′，如图，作AA 1⊥l ′，BB 1⊥l ′，AC ⊥BB 1，垂足分别是A 1，B 1，C.则有cos∠ABB 1＝||BC ||AB ＝|BB 1|－|AA 1||AF |＋|BF |＝|BF |－|AF ||AF |＋|BF |，即cos60°＝|BF |－|AF ||AF |＋|BF |＝12，由此得||AF ||BF ＝13.故选A.7．如图是抛物线形拱桥，当水面在l 时，拱顶离水面2m ，水面宽4m ，当水下降1m 后，水面宽为________．解：建立如图所示的直角坐标系，设拱桥抛物线的方程为x 2＝－2py ，因为拱顶离水面2m ，水面宽4m ，所以22＝－2p ·(－2)，得p ＝1.所以抛物线方程为x 2＝－2y ，水面下降1m ，则y ＝－3，代入抛物线方程，得x 2＝－2×(－3)，x ＝±6，这时水面宽为26m.故填26m.8．设F 为抛物线C ：y 2＝3x 的焦点，过F 且倾斜角为30°的直线交C 于A ，B 两点，则|AB |＝________．解：焦点F 的坐标为⎝⎛⎭⎫34，0， 方法一：直线AB 的斜率为33， 所以直线AB 的方程为y ＝33⎝⎛⎭⎫x －34， 即y ＝33x －34，代入y 2＝3x ，得13x 2－72x ＋316＝0. 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝212，所以|AB |＝x 1＋x 2＋p ＝212＋32＝12.方法二：由抛物线焦点弦的性质可得|AB |＝2p sin 2θ＝3sin 230°＝12.故填12.9．已知抛物线C ：y 2＝2px (p >0)的焦点为F ，直线y ＝4与y 轴的交点为P ，与C 的交点为Q ，且|QF |＝54|PQ |，求C 的方程．解：设Q (x 0，4)，代入y 2＝2px 得x 0＝8p ，所以|PQ |＝8p ，所以|QF |＝x 0＋p 2＝8p ＋p2.又因为|QF |＝54|PQ |，所以8p ＋p 2＝54·8p ，解得p ＝2(舍去负值)．所以C 的方程为y 2＝4x .10．已知抛物线y 2＝2px (p >0)的焦点为F ，A 是抛物线上横坐标为4，且位于x 轴上方的点，A 到抛物线准线的距离等于5，过A 作AB 垂直于y 轴，垂足为B ，OB 的中点为M . (1)求抛物线的方程；(2)若过M 作MN ⊥F A ，垂足为N ，求点N 的坐标．解：(1)抛物线y 2＝2px 的准线为x ＝－p 2，于是4＋p2＝5，所以p ＝2，所以抛物线方程为y 2＝4x . (2)由(1)知点A 的坐标是(4，4)， 由题意得B (0，4)，M (0，2)．又因为F (1，0)，所以k F A ＝43.因为MN ⊥F A ，所以k MN ＝－34.所以F A 的方程为y ＝43(x －1)，MN 的方程为y ＝－34x ＋2，联立⎩⎨⎧y ＝43（x －1），y ＝－34x ＋2，解方程组得x ＝85，y ＝45，所以点N 的坐标为⎝⎛⎭⎫85，45.11．已知抛物线y 2＝2px (p >0)，过点C (－2，0)的直线l 交抛物线于A 、B 两点，坐标原点为O ，OA →·OB →＝12. (1)求抛物线的方程；(2)当以AB 为直径的圆与y 轴相切时，求直线l 的方程．解：(1)设直线l ：x ＝my －2，代入y 2＝2px ，得y 2－2pmy ＋4p ＝0.(*)设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝2pm ，y 1y 2＝4p ，则x 1x 2＝y 21y 224p 2＝4.因为OA →·OB →＝12，所以x 1x 2＋y 1y 2＝12，即4＋4p ＝12， 所以p ＝2，所以抛物线的方程为y 2＝4x .(2)(*)化为y 2－4my ＋8＝0，则y 1＋y 2＝4m ，y 1y 2＝8.设AB 的中点为M (x M ，y M )，则|AB |＝2x M ＝x 1＋x 2＝m (y 1＋y 2)－4＝4m 2－4，① 又|AB |＝1＋m 2|y 1－y 2|＝（1＋m 2）（16m 2－32），② 由①②得(1＋m 2)(16m 2－32)＝(4m 2－4)2， 解得m 2＝3，m ＝± 3.所以直线l 的方程为x ＋3y ＋2＝0或x －3y ＋2＝0.(2016·全国卷Ⅲ)已知抛物线C ：y 2＝2x 的焦点为F ，平行于x 轴的两条直线l 1，l 2分别交C 于A ，B 两点，交C 的准线于P ，Q 两点．(1)若F 在线段AB 上，R 是PQ 的中点，证明AR ∥FQ ；(2)若△PQF 的面积是△ABF 的面积的两倍，求AB 中点的轨迹方程．解：由题知F ⎝⎛⎭⎫12，0.设l 1：y ＝a ，l 2：y ＝b ，则ab ≠0，且A ⎝⎛⎭⎫a 22，a ，B ⎝⎛⎭⎫b 22，b ，P ⎝⎛⎭⎫－12，a ，Q ⎝⎛⎭⎫－12，b ，R ⎝⎛⎭⎫－12，a ＋b 2.记过A ，B 两点的直线为l ，则l 的方程为2x －(a ＋b )y ＋ab ＝0. (1)证明：由于F 在线段AB 上，故1＋ab ＝0.记AR 的斜率为k 1，FQ 的斜率为k 2，则k 1＝a －b 1＋a 2＝a －b a 2－ab ＝1a＝－aba ＝－b ＝k 2.所以AR ∥FQ .(2)设l 与x 轴的交点为D (x 1，0)，则S △ABF ＝12|b －a |·|FD |＝12|b －a |⎪⎪⎪⎪x 1－12，S △PQF ＝|a －b |2. 由题设可得|b －a |⎪⎪⎪⎪x 1－12＝|a －b |2，所以x 1＝0(舍去)或x 1＝1. 设满足条件的AB 的中点为E (x ，y )． 当AB 与x 轴不垂直时， 由k AB ＝k DE 可得2a ＋b ＝yx －1(x ≠1)．而a ＋b 2＝y ，所以y 2＝x －1(x ≠1)．当AB 与x 轴垂直时，E 与D 重合． 所以，所求轨迹方程为y 2＝x －1．。
5.4抛体运动的规律(课件)-2022-2023学年高中物理(人教版2019必修第二册)
解析：
设小球被抛出时的高度为h，则h＝ gt2，小球从抛出到落地的水平位移x＝v0t，
两式联立得x＝
v ，根据题意，再次抛小球时，要使小球运动的水平位移x
0
减小，可以采用减小初速度v0或降低抛出点高度h的方法，故A、C两项正确．
【例题】甲、乙两球位于同一竖直直线上的不同位置，甲比乙高出h.将甲、乙两球
(1)一炮弹以初速度v0斜向上方飞出炮筒，初速度与水平方向夹角为θ，请根据下图
求解炮弹在空中的飞行时间、射高和射程.
射高Y
射程X
答案
先建立直角坐标系，将初速度v0分解为：
v0x＝v0cos θ，v0y＝v0sin θ
2v0y 2v0sin θ
飞行时间：t＝
＝
g
g
v0y 2 v02sin2 θ
射高：Y＝ 2g ＝ 2g
vy
由勾股定理可得物体在任意时刻的合速度大小为：
v vx v y
2
v0 2 g 2t 2
故物体在下落过程中合速度越来越大；
vy
gt
合速度的方向：tan
vx v0
随着物体的下落，偏角θ越来越大。
0
t
y 方向：初速度为零，a=g，做自由落体运动。
2
x
v
θ
vx
v
y
速度和它在x、y方向上的分速度
2
2
合速度大小: v v x v y
vy
合速度方向: tan
vx
2
2
合位移大小: s x y
y
合位移方向: tan
x
x
斜抛运动的动态演示
抛体模型的运动学问题与功能动量(解析版)
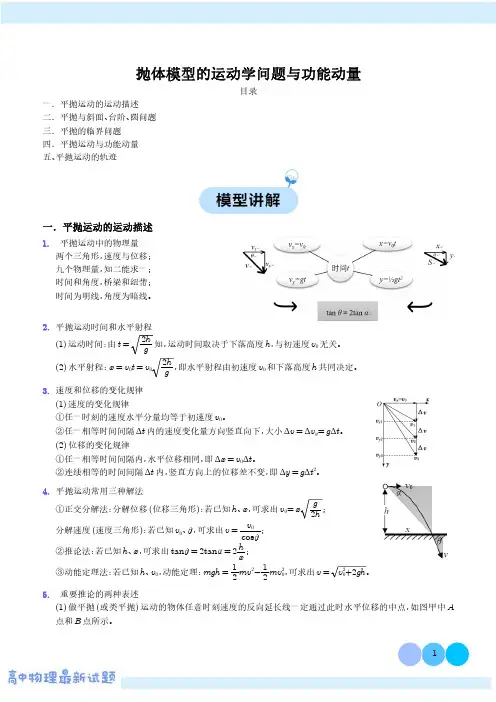
抛体模型的运动学问题与功能动量目录一．平抛运动的运动描述二．平抛与斜面、台阶、圆问题三．平抛的临界问题四．平抛运动与功能动量五、平抛运动的轨迹一．平抛运动的运动描述1.平抛运动中的物理量两个三角形，速度与位移；九个物理量，知二能求一；时间和角度，桥梁和纽带；时间为明线，角度为暗线。
2.平抛运动时间和水平射程(1)运动时间：由t =2h g 知，运动时间取决于下落高度h ，与初速度v 0无关。
(2)水平射程：x =v 0t =v 02h g，即水平射程由初速度v 0和下落高度h 共同决定。
3.速度和位移的变化规律(1)速度的变化规律①任一时刻的速度水平分量均等于初速度v 0。
②任一相等时间间隔Δt 内的速度变化量方向竖直向下，大小Δv =Δv y =g Δt 。
(2)位移的变化规律①任一相等时间间隔内，水平位移相同，即Δx =v 0Δt 。
②连续相等的时间间隔Δt 内，竖直方向上的位移差不变，即Δy =g Δt 2。
4.平抛运动常用三种解法①正交分解法：分解位移(位移三角形)：若已知h 、x ，可求出v 0=x g2h；分解速度(速度三角形)：若已知v 0、θ，可求出v =v 0cos θ；②推论法：若已知h 、x ，可求出tan θ=2tan α=2hx ；③动能定理法：若已知h 、v 0，动能定理：mgh =12mv 2-12mv 20，可求出v =v 20+2gh 。
5.重要推论的两种表述(1)做平抛(或类平抛)运动的物体任意时刻速度的反向延长线一定通过此时水平位移的中点，如图甲中A 点和B 点所示。
(2)做平抛(或类平抛)运动的物体在任一时刻任一位置处，设其速度方向与水平方向的夹角为θ，位移与水平方向的夹角为α，则tan θ=2tan α，如图乙所示。
二．平抛与斜面、台阶、圆问题1.斜面上平抛运动的时间的计算斜面上的平抛(如图)，分解位移(位移三角形)x =v 0t ，y =12gt 2，tan θ=y x ，可求得t =2v 0tan θg。
高考数学 第八章第八节 抛物线课件 新A
∴(y1＋y2)·xy11－－yx22＝a，
∴a＝4×1＝4，∴y2＝4x.
答案：y2＝4x
1．抛物线的定义 平面内与一个定点F和一条定直线l(l不经过点F) 距离相等 的点的轨迹叫做抛物线， 点F 叫做 抛物线的焦点， 直线l 叫做抛物线的准线．
2．抛物线的标准方程和几何性质
B．y2＝－8x D．y2＝－4x
()
解析：设抛物线方程为 y2＝2px(p<0)， 由抛物线定义知，|－p2＋3|＝5，解得 p＝－4， ∴抛物线方程为 y2＝－8x.
答案： B
3．过抛物线y2＝4x的焦点作直线交抛物线于A(x1，y1)，
B(x2，y2)两点，若x1＋x2＝6，那么|AB|等于 ( )
图形
范围
y≥0，x∈R
x2＝－2py(p>0) y≤0，x∈R
对称轴 顶点坐标
焦点坐标
(0，p2)
y轴
原点O(0,0) (0，－p2)
准线方程 离心率 焦半径
y＝－p2
y＝p2 e＝1
|PF|＝y0＋p2
|PF|＝－y0＋p2
考点一 抛物线的定义及应用
设P是抛物线y2＝4x上的一个动点． (1)求点P到点A(－1,1)的距离与点P到直线x＝－1的距离 之和的最小值； (2)若B(3,2)，求|PB|＋|PF|的最小值．
3．直线与抛物线的位置关系 (1)设抛物线方程为y2＝2px(p>0)，直线Ax＋By＋C＝0，将
直线方程与抛物线方程联立，消去x得到关于y的方程my2＋ny＋ q＝0， ①若m≠0，当Δ>0时，直线与抛物线有两个公共点； 当Δ＝0时，直线与抛物线只有一个公共点； 当Δ<0时，直线与抛物线没有公共点． ②若m＝0，直线与抛物线只有一个公共点，此时直线与抛物线 的对称轴平行．
绝密资料高中数学抛 物 线(解析版)
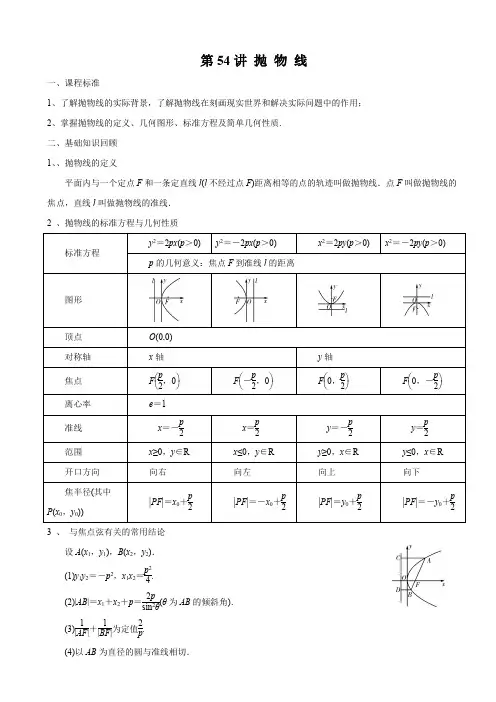
第54讲 抛 物 线一、课程标准1、了解抛物线的实际背景，了解抛物线在刻画现实世界和解决实际问题中的作用；2、掌握抛物线的定义、几何图形、标准方程及简单几何性质. 二、基础知识回顾 1、、抛物线的定义平面内与一个定点F 和一条定直线l (l 不经过点F )距离相等的点的轨迹叫做抛物线．点F 叫做抛物线的焦点，直线l 叫做抛物线的准线． 2 、抛物线的标准方程与几何性质标准方程y 2＝2px (p ＞0)y 2＝－2px (p ＞0)x 2＝2py (p ＞0)x 2＝－2py (p ＞0)p 的几何意义：焦点F 到准线l 的距离图形顶点 O (0,0) 对称轴 x 轴 y 轴 焦点 F ⎝⎛⎭⎫p 2，0 F ⎝⎛⎭⎫－p2，0 F ⎝⎛⎭⎫0，p2 F ⎝⎛⎭⎫0，－p2 离心率 e ＝1 准线 x ＝－p 2x ＝p 2y ＝－p2y ＝p 2范围 x ≥0，y ∈R x ≤0，y ∈R y ≥0，x ∈R y ≤0，x ∈R 开口方向 向右向左向上向下焦半径(其中P (x 0，y 0))||PF ＝x 0＋p2||PF ＝－x 0＋p2||PF ＝y 0＋p2||PF ＝－y 0＋p23 、 与焦点弦有关的常用结论设A (x 1，y 1)，B (x 2，y 2)． (1)y 1y 2＝－p 2，x 1x 2＝p 24. (2)|AB |＝x 1＋x 2＋p ＝2psin 2θ(θ为AB 的倾斜角)．(3)1|AF |＋1|BF |为定值2p. (4)以AB 为直径的圆与准线相切．(5)以AF 或BF 为直径的圆与y 轴相切． 三、自主热身、归纳总结1、抛物线y 2＝4x 的准线方程为( )A. x ＝1B. x ＝－1C. y ＝1D. y ＝－1 【答案】 B【解析】 由题意得抛物线的焦点在x 轴上，且2p ＝4，即p ＝2，所以抛物线的准线方程为直线x ＝－p2＝－1.2、 设抛物线y 2＝8x 上的一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是( )A. 4B. 6C. 8D. 12 【答案】 B【解析】 如图所示，抛物线的准线l 的方程为x ＝－2，F 是抛物线的焦点，过点P 作PA ⊥y 轴，垂足为A ，延长PA 交直线l 于点B ，则AB ＝2.因为点P 到y 轴的距离为4，所以点P 到准线l 的距离PB ＝4＋2＝6，所以点P 到焦点的距离PF ＝PB ＝6.故选B.3、过抛物线y 2＝4x 的焦点的直线l 交抛物线于P (x 1，y 1)，Q (x 2，y 2)两点，如果x 1＋x 2＝6，则|PQ |＝( )A ．9B ．8C ．7D ．6【答案】B【解析】抛物线y 2＝4x 的焦点为F (1,0)，准线方程为x ＝－1.根据题意可得，|PQ |＝|PF |＋|QF |＝x 1＋1＋x 2＋1＝x 1＋x 2＋2＝8.4、拋物线y ＝2ax 2(a ≠0)的焦点是( )A.⎝⎛⎭⎫a 2，0B.⎝⎛⎭⎫a 2，0或⎝⎛⎭⎫－a 2，0C.⎝⎛⎭⎫0，18aD.⎝⎛⎭⎫0，18a 或⎝⎛⎭⎫0，－18a 【答案】C【解析】抛物线的方程化成标准形式为x 2＝12a y (a ≠0)，其焦点在y 轴上，所以焦点坐标为⎝⎛⎭⎫0，18a .故选C. 5、已知抛物线C 与双曲线x 2－y 2＝1有相同的焦点，且顶点在原点，则抛物线C 的方程为________． 【答案】y 2＝±4 2x【解析】：由已知可知双曲线的焦点为(－2，0)，(2，0)．设抛物线方程为y 2＝±2px (p >0)，则p2＝2，所以p ＝2 2，所以抛物线方程为y 2＝±4 2x .6、设抛物线y 2＝8x 的准线与x 轴交于点Q ，若过点Q 的直线l 与抛物线有公共点，则直线l 的斜率的取值范围是________． 【答案】[－1,1]【解析】：Q (－2,0)，当直线l 的斜率不存在时，不满足题意，故设直线l 的方程为y ＝k (x ＋2)，代入抛物线方程，消去y 整理得k 2x 2＋(4k 2－8)x ＋4k 2＝0，当k ＝0时，l 与抛物线有公共点；当k ≠0时，Δ＝64(1－k 2)≥0得－1≤k <0或0<k ≤1.综上，－1≤k ≤1.四、例题选讲考点一 抛物线的定义及其应用例1 (1)已知抛物线定点在原点，对称轴为坐标轴，焦点在直线x －y ＋2＝0上，则抛物线方程为____．(2)动圆过点(1，0)，且与直线x ＝－1相切，则动圆的圆心的轨迹方程为____． 【答案】（1）y 2＝－8x 或x 2＝8y （2）y 2＝4x【解析】 (1)直线x －y ＋2＝0与坐标轴的交点分别为(－2，0)和(0，2)，当焦点为(－2，0)时，抛物线焦点在x 轴负半轴上，且p ＝4，则抛物线方程为y 2＝－8x ；当焦点为(0，2)时，抛物线焦点在y 轴正半轴上且p ＝4，则抛物线方程为x 2＝8y ；故抛物线方程为y 2＝－8x 或x 2＝8y.(2)设动圆的圆心坐标为(x ，y)，则圆心到点(1，0)的距离与到直线x ＝－1的距离相等，根据抛物线的定义易知动圆的圆心的轨迹方程为y 2＝4x.变式1、(1)若抛物线y 2＝4x 上一点P 到其焦点F 的距离为2，O 为坐标原点，则△OFP 的面积为( )A.12 B ．1 C.32D ．2(2)设P 是抛物线y 2＝4x 上的一个动点，若B (3,2)，则|PB |＋|PF |的最小值为________． 【答案】 (1)B (2)4【解析】 (1)设P (x P ，y P )，由题可得抛物线焦点为F (1,0)，准线方程为x ＝－1. 又点P 到焦点F 的距离为2， ∴由定义知点P 到准线的距离为2. ∴x P ＋1＝2，∴x P ＝1. 代入抛物线方程得|y P |＝2，∴△OFP 的面积为S ＝12·|OF |·|y P |＝12×1×2＝1.(2)如图，过点B 作BQ 垂直准线于点Q ，交抛物线于点P 1，则|P 1Q |＝|P 1F |.则有|PB |＋|PF |≥|P 1B |＋|P 1Q |＝|BQ |＝4，即|PB |＋|PF |的最小值为4.变式2、(1)定长为3的线段AB 的两个端点在抛物线y 2＝2x 上移动，M 为AB 的中点，则点M 到y 轴的最短距离为( )A.12 B ．1 C.32D ．2 (2)设P 是抛物线y 2＝4x 上的一个动点，F 为抛物线的焦点，若B (3,2)，则|PB |＋|PF |的最小值为__________． 【答案】(1)B (2)4【解析】 (1)如图所示，抛物线y 2＝2x 的准线为l ：x ＝－12，过A ，B ，M 分别作AA ′，BB ′，MM ′垂直于l ，垂足分别为A ′，B ′，M ′.由抛物线定义知|AA ′|＝|FA |，|BB ′|＝|FB |.又M 为AB 中点，由梯形中位线定理得|MM ′|＝12(|AA ′|＋|BB ′|)＝12(|FA |＋|FB |)≥12|AB |＝12×3＝32，则M 到y 轴的距离d ≥32－12＝1(当且仅当AB 过抛物线的焦点时，等号成立)，所以d min ＝1，即点M 到y 轴的最短距离为1.(2)如图，过点B 作BQ 垂直准线于点Q ，交抛物线于点P 1，则|P 1Q |＝|P 1F |，则|PB |＋|PF |≥|P 1B |＋|P 1Q |＝|BQ |＝4.故|PB |＋|PF |的最小值为4.方法总结：与抛物线有关的最值问题，一般情况下都与抛物线的定义有关，实现由点到点的距离与点到直线的距离的转化．(1)将抛物线上的点到准线的距离转化为该点到焦点的距离，构造出“两点之间线段最短”，使问题得解． (2)将抛物线上的点到焦点的距离转化为到准线的距离，利用“与直线上所有点的连线中垂线段最短”原理解决． 考点二 抛物线的标准方程及其几何性质例2 已知抛物线y 2＝2px(p ＞0)的焦点为F ，过F 的直线l 与抛物线交于A ，B 两点，且|AF|＝4|FB|，O 为坐标原点，若△AOB 的面积为58，求p 的值．【解析】 易知抛物线y 2＝2px 的焦点F 的坐标为⎝⎛⎭⎫p 2，0，准线为x ＝－p 2，不妨设点A 在x 轴上方，如图，过A 、B 作准线的垂线AA′，BB′，垂足分别为A′，B′，过点B 作BH ⊥AA′，交AA′于H ，则|BB′|＝|A′H|，设|FB|＝t ，则|AF|＝|AA′|＝4t ，∴|AH|＝|AA′|－|A′H|＝3t ，又|AB|＝5t ，∴在Rt △ABH 中，cos ∠HAB ＝35，∴tan ∠HAB ＝43，则可得直线AB 的方程为y ＝43⎝⎛⎭⎫x －p 2.由⎩⎪⎨⎪⎧y ＝43⎝⎛⎭⎫x －p 2，y 2＝2px ，得8x 2－17px ＋2p 2＝0， 设A(x 1，y 1)，B(x 2，y 2)，则|AB|＝x 1＋x 2＋p ＝178p ＋p ＝258p ，易知点O 到直线AB 的距离为d ＝25p.∴S △AOB ＝12×258p×25p ＝5p 28＝58，∴p 2＝1，又p ＞0，∴p ＝1.变式1、已知点F 1，F 2分别是双曲线3x 2－y 2＝3a 2(a >0)的左、右焦点，点P 是抛物线y 2＝8ax 与双曲线的一个交点，若||PF 1＋||PF 2＝12，则抛物线的准线方程为__________．【答案】x ＝－2【解析】 将双曲线方程化为标准方程得x 2a 2－y 23a2＝1，抛物线的准线为x ＝－2a ，联立⎩⎪⎨⎪⎧x 2a 2－y 23a 2＝1，y 2＝8ax⇒x＝3a ，即点P 的横坐标为3a .而由⎩⎪⎨⎪⎧|PF 1|＋|PF 2|＝12，|PF 1|－|PF 2|＝2a ⇒|PF 2|＝6－a ，又因为双曲线的右焦点与抛物线的焦点相同，所以|PF 2|＝3a ＋2a ＝6－a ，解得a ＝1，所以抛物线的准线方程为x ＝－2.变式2、（黑龙江省鹤岗一中2019届模拟）顶点在原点，对称轴为坐标轴，且过点P (－4，－2)的抛物线的标准方程是( )A ．y 2＝－x B.x 2＝－8y C ．y 2＝－8x 或x 2＝－y D ．y 2＝－x 或x 2＝－8y【答案】D【解析】设抛物线为y 2＝mx ，代入点P (－4，－2)，解得m ＝－1，则抛物线方程为y 2＝－x ；设抛物线为x 2＝ny ，代入点P (－4，－2)，解得n ＝－8，则抛物线方程为x 2＝－8y .故抛物线方程为y 2＝－x 或x 2＝－8y . 变式3、（山西省临汾一中2019届模拟）直线l 过抛物线y 2＝－2px (p ＞0)的焦点，且与该抛物线交于A ，B 两点，若线段AB 的长是8，AB 的中点到y 轴的距离是2，则此抛物线的方程是( )A ．y 2＝－12xB .y 2＝－8xC ．y 2＝－6xD ．y 2＝－4x 【答案】B【解析】设A (x 1，y 1)，B (x 2，y 2)，根据抛物线的定义可知|AB |＝－(x 1＋x 2)＋p ＝8.又AB 的中点到y 轴的距离为2，∴－x 1＋x 22＝2，∴x 1＋x 2＝－4，∴p ＝4，∴所求抛物线的方程为y 2＝－8x .故选B.方法总结：1．求抛物线标准方程的方法(1)定义法：若题目已给出抛物线的方程(含有未知数p )，那么只需求出p 即可．(2)待定系数法：若题目未给出抛物线的方程，对于焦点在x 轴上的抛物线的标准方程可统一设为y 2＝ax (a ≠0)，a 的正负由题设来定；焦点在y 轴上的抛物线的标准方程可设为x 2＝ay (a ≠0)，这样就减少了不必要的讨论．2．抛物线性质的应用技巧(1)利用抛物线方程确定及应用其焦点、准线时，关键是将抛物线方程化成标准方程． (2)要结合图形分析，灵活运用平面图形的性质简化运算考点三 综合考查直线与抛物线的问题例3、如图，已知抛物线关于y 轴对称，它的顶点在坐标原点，点P(2，1)，A(x 1，y 1)，B(x 2，y 2)均在抛物线上． (1)求抛物线的方程；(2)若∠APB 的平分线垂直于y 轴，求证：直线AB 的斜率为定值．【解析】 (1)由已知条件，可设抛物线的方程为x 2＝2py(p>0)．∵点P(2，1)在抛物线上，∴22＝2p×1，解得p ＝2.故所求抛物线的方程为x 2＝4y.(2)由题意知k AP ＋k BP ＝0，∴y 1－1x 1－2＋y 2－1x 2－2＝0，∴x214－1x1－2＋x224－1x2－2＝0，∴x1＋24＋x2＋24＝0，∴x1＋x2＝－4，∴k AB＝y1－y2x1－x2＝x214－x224x1－x2＝x1＋x24＝－1，∴直线AB的斜率为定值－1.变式1、如图，在平面直角坐标系xOy中，点A(8，－4)，P(2，t)(t<0)在抛物线y2＝2px(p>0)上．(1)求p，t的值；(2)过点P作PM垂直于x轴，M为垂足，直线AM与抛物线的另一交点为B，点C在直线AM上，若PA，PB，PC的斜率分别为k1，k2，k3，且k1＋k2＝2k3，求点C的坐标．【解析】(1)将点A(8，－4)代入y2＝2px，得p＝1.将点P(2，t)代入y2＝2x，得t＝±2.∵t<0，∴t＝－2.(2)由题意知，点M的坐标为(2，0)，直线AM的方程为y＝－23x＋43.联立⎩⎪⎨⎪⎧y＝－23x＋43，y2＝2x，解得B ⎝⎛⎭⎫12，1，∴k1＝－13，k2＝－2，代入k1＋k2＝2k3，得k3＝－76，故直线PC的方程为y＝－76x＋13，联立⎩⎨⎧y＝－23x＋43，y＝－76x＋13，解得C⎝⎛⎭⎫－2，83.变式2、过抛物线y2＝4x的焦点F的直线l与抛物线交于A，B两点，若|AF|＝2|BF|，则|AB|等于() A．4 B.92C．5 D．6【答案】B【解析】易知直线l的斜率存在，设为k，则其方程为y＝k(x－1)．由⎩⎪⎨⎪⎧y＝k x－1，y2＝4x得k2x2－(2k2＋4)x＋k2＝0，得x A·x B＝1，①因为|AF|＝2|BF|，由抛物线的定义得x A ＋1＝2(x B ＋1)， 即x A ＝2x B ＋1，② 由①②解得x A ＝2，x B ＝12，所以|AB |＝|AF |＋|BF |＝x A ＋x B ＋p ＝92.[应用结论] 法一：由对称性不妨设点A 在x 轴的上方，如图，设A ，B 在准线上的射影分别为D ，C ，作BE ⊥AD 于E ，设|BF |＝m ，直线l 的倾斜角为θ，则|AB |＝3m ， 由抛物线的定义知|AD |＝|AF |＝2m ，|BC |＝|BF |＝m ，所以cos θ＝|AE ||AB |＝13，所以tan θ＝22，则sin 2θ＝8cos 2θ，所以sin 2θ＝89.又y 2＝4x ，知2p ＝4，故利用弦长公式|AB |＝2p sin 2θ＝92. 法二：因为|AF |＝2|BF |，1|AF |＋1|BF |＝12|BF |＋1|BF |＝32|BF |＝2p ＝1，解得|BF |＝32，|AF |＝3， 故|AB |＝|AF |＋|BF |＝92.方法总结：(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系．(2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式||AB ＝x 1＋x 2＋p ；若不过焦点，则必须用弦长公式．(3)涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”“整体代入”等解法．涉及弦的中点、斜率时一般用“点差法”求解．五、优化提升与真题演练1、（2020年高考全国Ⅰ卷理数）已知A 为抛物线C :y 2=2px （p >0）上一点，点A 到C 的焦点的距离为12，到y 轴的距离为9，则p =（ ） A ．2 B ．3C ．6D ．9【答案】C【解析】设抛物线的焦点为F ，由抛物线的定义知||122A p AF x =+=，即1292p=+，解得6p.故选：C ．2、（2020年高考全国Ⅰ卷理数）设O 为坐标原点，直线2x =与抛物线C ：22(0)y px p =>交于D ，E 两点，若OD OE ⊥，则C 的焦点坐标为（ ） A ． 1,04⎛⎫ ⎪⎝⎭B ． 1,02⎛⎫ ⎪⎝⎭C ． (1,0)D ． (2,0)【答案】B【解析】因为直线2x =与抛物线22(0)y px p =>交于,E D 两点，且OD OE ⊥， 根据抛物线的对称性可以确定4DOx EOx π∠=∠=，所以()2,2D ，代入抛物线方程44p =，求得1p =，所以其焦点坐标为1(,0)2， 故选：B ．3、（2020年高考北京）设抛物线的顶点为O ，焦点为F ，准线为l ．P 是抛物线上异于O 的一点，过P 作PQ l ⊥于Q ，则线段FQ 的垂直平分线（ ） A ． 经过点O B ． 经过点P C ． 平行于直线OP D ． 垂直于直线OP【答案】B【解析】如图所示：．因为线段FQ 的垂直平分线上的点到,F Q 的距离相等，又点P 在抛物线上，根据定义可知，PQ PF =，所以线段FQ 的垂直平分线经过点P . 故选：B ．4、（2019·全国高考）若抛物线y 2=2px （p >0）的焦点是椭圆2231x y pp+=的一个焦点，则p =（ ）A ．2B ．3C ．4D ．8【答案】D【解析】因为抛物线22(0)y px p =>的焦点(,0)2p 是椭圆2231x y p p +=的一个焦点，所以23()2p p p -=，解得8p =，故选D ．5、(2018·全国卷Ⅰ)设抛物线C ：y 2＝4x 的焦点为F ，过点(－2,0)且斜率为23的直线与C 交于M ，N 两点，则FM →·FN →＝( )A ．5B ．6C ．7D ．8【答案】D【解析】由题意知直线MN 的方程为y ＝23(x ＋2)．联立⎩⎪⎨⎪⎧y ＝23x ＋2，y 2＝4x ，消去y 并整理，得x 2－5x ＋4＝0.解得x N ＝1，x M ＝4.所以y N ＝2，y M ＝4.又抛物线y 2＝4x 的焦点为F (1,0)，所以FM →＝(3,4)，FN →＝(0,2)．所以FM →·FN →＝3×0＋2×4＝8.故选D.6、（2017·全国高考）过抛物线2:4C y x =的焦点F ，3C 于点M （在x 轴上方），l 为C 的准线，点N 在l 上且MN l ⊥，则点M 到直线NF 的距离为（ ）A.3B.335 D.22【答案】A【解析】设直线l 与x 轴相交于点P ，与直线MN 相交于点Q ，(1,0)F ，设||||MN MF m ==，因为||2,30PF NQM =∠=，所以||4,||2QF QM m ==， 所以42m m +=，解得：4m =，设00(,)M x y ，由焦半径公式得：014x +=， 所以03x =，023y =，所以sin sin NP MNF NFP NF ∠=∠===，所以点M 到直线NF 的距离为||sin 42NM MNF ⋅∠=⋅= 7、(2018·全国卷Ⅰ)已知点M (－1,1)和抛物线C ：y 2＝4x ，过C 的焦点且斜率为k 的直线与C 交于A ，B 两点．若∠AMB ＝90°，则k ＝________.【答案】2【解析】解法一：由题意可知C 的焦点坐标为(1,0)，所以过焦点(1,0)，斜率为k 的直线方程为x ＝y k＋1， 设A ⎝⎛⎭⎫y 1k ＋1，y 1，B ⎝⎛⎭⎫y 2k ＋1，y 2， 将直线方程与抛物线方程联立得⎩⎪⎨⎪⎧x ＝y k ＋1，y 2＝4x ，整理得y 2－4ky －4＝0， 从而得y 1＋y 2＝4k，y 1·y 2＝－4. ∵M (－1,1)，∠AMB ＝90°，∴MA →·MB →＝0，即⎝⎛⎭⎫y 1k ＋2·⎝⎛⎭⎫y 2k ＋2＋(y 1－1)(y 2－1)＝0，即k 2－4k ＋4＝0，解得k ＝2.解法二：设A (x 1，y 1)，B (x 2，y 2)，则⎩⎪⎨⎪⎧y 21＝4x 1，①y 22＝4x 2，②②－①得y 22－y 21＝4(x 2－x 1)，从而k ＝y 2－y 1x 2－x 1＝4y 1＋y 2. 设AB 的中点为M ′，如图，连接MM ′.∵直线AB 过抛物线y 2＝4x 的焦点，∴以线段AB 为直径的⊙M ′与准线l ：x ＝－1相切．∵M (－1,1)，∠AMB ＝90°，∴点M 在准线l ：x ＝－1上，同时在⊙M ′上，∴准线l 是⊙M ′的切线，切点为M ，且M ′M ⊥l ，即MM ′与x 轴平行，∴点M ′的纵坐标为1，即y 1＋y 22＝1⇒y 1＋y 2＝2， 故k ＝4y 1＋y 2＝42＝2. 8、（2020届山东省潍坊市高三上期末）已知P 是抛物线24y x =上的动点，点P 在y 轴上的射影是M ，点A的坐标为()2,3，则PA PM +的最小值是__________．1【解析】设抛物线的焦点是()1,0F ， 根据抛物线的定义可知1PM PF =-1PA PM PA PF ∴+=+-，PA PF AF +≥，当,,A P F 三点共线时，等号成立， PA PM ∴+的最小值是1AF ，AF ==PA PM ∴+1.19、（2020届山东省泰安市高三上期末）已知抛物线()220y px p =>的焦点为F (4，0)，过F 作直线l 交抛物线于M ，N 两点，则p =_______，49NF MF-的最小值为______． 【答案】8p = 13【解析】∵ 抛物线()220y px p =>的焦点为F(4，0)，∴ 8p =，∴ 抛物线的方程为216y x =，设直线l 的方程为4x my =+，设()11,M x y ，()22,N x y ，由2164y x x my ⎧=⎨=+⎩得216640y my --=， ∴1216y y m +=，1264y y =-，由抛物线的定义得11MF NF +121144x x =+++()()21124444x x x x +++=++()()211244888my my my my ++++=++()()122121216864m y y m y y m y y ++=+++22216166412864m m m +=-++()()22161641m m +=+14=，∴49NFMF-11494NFNF⎛⎫=--⎪⎪⎝⎭419NFNF=+-1≥13=，当且仅当49NFNF=即6NF=时，等号成立，故答案为：13．。
高中新教材物理课件必修第二册第五章抛体运动抛体运动的规律
在地质勘探中，抛体运动的规律可用于计算地震波的传播和反射。地震波在地层中传播时会发生反射 和折射现象，通过测量反射波或折射波的传播时间和路径，可以推断出地层的结构和性质。了解抛体 运动的规律有助于地质勘探人员更准确地分析和解释地震数据。
实验：探究不同
06 角度下斜抛物体 射程与初速度关
系
实验目的和原理介绍
斜抛运动
物体以一定的初速度斜向射出去， 在空气阻力可以忽略的情况下，物 体所做的这类运动叫做斜抛运动。
抛体运动轨迹与方程
轨迹
抛体运动的轨迹是一条抛物线，其形状和开口方向由初速度和抛出角度决定。
方程
对于不同的抛体运动，其运动方程也有所不同。例如，对于竖直上抛运动，其位 移方程为x=v0t-1/2gt^2；对于平抛运动，其水平位移方程为x=v0t，竖直位移 方程为y=1/2gt^2；对于斜抛运动，其位移方程需要根据具体情况进行推导。
01
结果分析讨论
02
03
04
1. 观察曲线图，分析射程随 抛射角度的变化趋势，并解释
原因。
2. 讨论实验结果与理论预测 的差异，分析可能验结果，总结斜抛 物体射程与初速度、抛射角度 的关系，加深对抛体运动规律
的理解。
THANKS
感谢观看
导弹拦截
导弹拦截系统需要精确计算来袭导弹的飞行轨迹和速度，以便发射拦截导弹进 行准确拦截。了解抛体运动的规律有助于提高导弹拦截系统的精度和效率。
其他领域如建筑、地质勘探等应用
建筑领域
在建筑领域，抛体运动的规律可用于计算建筑物的稳定性和安全性。例如，在设计高层建筑时，需要 考虑风荷载对建筑物的影响，通过计算风荷载下建筑物的振动和变形，可以评估建筑物的稳定性和安 全性。
第八章 第八节 直线与圆锥曲线的位置关系及应用
曲线上一点 P(x0 ， y0) 处 的 切线方程
xa02x＋yb02y＝1
xa02x－yb02y＝1 y0y2＝2p(x＋x0)
教材知识四基导航 考点典例探究领航 创新变化提能返航 课时规范训练
大一轮复习 数学（理）
曲线外一点 P(x0 ， y0) 的 所 引两条切线的 切点弦方程
xa02x＋yb02y＝1
教材知识四基导航 考点典例探究领航 创新变化提能返航 课时规范训练
大一轮复习 数学（理）
2．过抛物线 y2＝4x 的焦点作一条直线与抛物线相交于 A，B
两点，它们到直线 x＝－2 的距离之和等于 5，则这样的直线( )
A．有且仅有一条
B．有且仅有两条
C．有无穷多条
D．不存在
教材知识四基导航 考点典例探究领航 创新变化提能返航 课时规范训练
教材知识四基导航 考点典例探究领航 创新变化提能返航 课时规范训练
大一轮复习 数学（理）
3．过点(0，1)作直线，使它与 y2＝4x 仅有一个公共点，这样
的直线有( )
A．1 条
B．2 条
C．3 条
D．4 条ຫໍສະໝຸດ 答案：C教材知识四基导航 考点典例探究领航 创新变化提能返航 课时规范训练
大一轮复习 数学（理）
大一轮复习 数学（理）
解析：选 D.抛物线 y2＝4x 的焦点坐标为(1，0)，准线方程为 x ＝－1，设 A，B 的坐标分别为(x1，y1)，(x2，y2)，则 A，B 到直线 x＝－1 的距离之和为 x1＋x2＋2.
设直线方程为 x＝my＋1，代入抛物线 y2＝4x， 则 y2＝4(my＋1)，即 y2－4my－4＝0， ∴x1＋x2＝m(y1＋y2)＋2＝4m2＋2. ∴x1＋x2＋2＝4m2＋4≥4. ∴A，B 到直线 x＝－2 的距离之和 x1＋x2＋2＋2≥6＞5. ∴满足题意的直线不存在．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
由Δ=4m-4m2>0可得0<m<1.
令u= m m2 ,0<u≤ ,则S=u(1-2u2), 2 设S(u)=u(1-2u2),0<u≤ 1 ,则S′(u)=1-6u2,
2 1
由S′(u)=0Biblioteka 得u= 6 (0, 1 ) ,6 2
所以S(u)max= S( 6 ) 6 , 故△ABP的面积的最大值为 6 .
(1)求p,t的值.
(2)求△ABP面积的最大值.
【解析】(1)点P(1, 1 )到抛物线C:y2=2px(p>0)的准线的距离 为 5 ，可得准线方程为x= 1 ,所以抛物线C:y2=x,p= 1 .
4 4 2 2
点M(t,1)是C上的点，所以t=1. (2)设动点A(x1,y1),B(x2,y2),直线AB的斜率为k,线段AB的中点 为Q(m,m),
3 于A，B两点，若|AF|＝3，则|BF|＝__________.
想一想：与焦点弦有关的常用结论有哪些？
2
(1)y1y2
=-p2,x
p2 1x2= 4
.
(2)|AB|=x1+x2+p= 2p (θ为AB的倾斜角). 2
(3)S△AOB= p
(4)
1 1 AF | BF |
2
sin
2sin
拓展：点 M x0 , y0 是抛物线
y 2 2 px 上的一定点， 动弦ME，MF分别交x轴于A，B两点,且MA=MB。 证明：直线EF的斜率为定值。
考向 3 直线与抛物线的综合问题
例4.(2012·浙江高考)如图，在直角坐标系xOy中，点 1 5 P(1, )到抛物线C：y2=2px(p>0)的准线的距离为 ， 4 2 点M(t,1)是C上的定点，A，B是C上的两动点，且线段AB 被直线OM平分.
(2)方程y=ax2(a≠0)表示的曲线是焦点在x轴上的抛物
a a 线，且其焦点坐标是( ,0)，准线方程是x= . 4 4
这个结论是否正确？
抛物线的标准方程有几个？如何利用标准方程判断焦点 位置、焦点坐标和准线方程？
练一练：若一抛物线过 点 (3,2)，求其标准方程 .
（3）(2013·新课标)设抛物线C:y2=2px(p>0)的 焦点为F，点M在C上，|MF|=5，若以MF为直径的 圆过点(0，2)，则C的方程为( (A)y2=4x或y2=8x (C)y2=4x或y2=16x
第八节 抛 物 线
考向 1 抛物线的定义和标准方程 【典例1】(1)已知动圆过定点F( p ,0)，且与直线x= p 2 2 y2=2px 相切，其中p>0,则动圆圆心的轨迹E的方程为_______. 平面内与一个定点F和一条定直线l的距离相等的点的轨 迹一定是抛物线.这句话对不对？
抛物线定义： 平面内与一个定点F和一条定直线L(L不经过点F） 的距离相等的点的轨迹叫做抛物线.
C)
(B)y2=2x或y2=8x (D)y2=2x或y2=16x
考向 2 抛物线的性质及其应用 【典例2】(1)已知点P是抛物线y2=2x上的一个动点， 则点P到点(0，2)的距离与点P到该抛物线准线的距离
17 之和的最小值为_________. 2
变式：已知抛物线 y 2 2 x的焦点是F , 点P是抛物线 上的动点 , 又有点A(3,2).求 | PA | | PF | 的最小值 .
已知过抛物线 y 2 px(p 0 )的焦点F的直线l
2
交抛物线于Ax1 , y1 , Bx2 , y2 两点，若CD是 过F的抛物线的另一条弦， 且CD AB.
1 1 1 性质（ 8） AB CD 2p
[例 3](1)A、B 是抛物线 y ＝2px 上的两点，满足 →· → ＝0(O 是原点)．求证：直线 AB 过定点． OA OB
巩固练习1.已知抛物线 y2=8x 的焦点为F， 准线l与x轴的交点为K， C为抛物线上一点. （1）若CA⊥l于点A ，且直线AF的斜率为 3 , 则 |CF|=_______
2.已知抛物线y=x2,动弦AB的长为2，求AB 中点纵坐标的最小值.
【典例2】(2)过抛物线y2=4x的焦点F的直线交该抛物线
(θ为AB倾斜角).
为定值 2 . p (5)以AB为直径的圆与准线相切.
(6)以AF或BF为直径的圆与y轴相切.
(7)∠CFD=90°.
1 2 练一练：已知抛物线C:y= x ，则过其焦点F且斜率 4 1 为 的直线l被抛物线截得的线段长为( C ) 2 17 9 (A) (B) (C)5 (D)4 4 8
2
定点(2p,0)
y
A
O F
.
该结论反之也成立。
M
B
x
若直线l过定点(2p,0)且与抛物线 y2 =2px(p>0) 交于A、B两点，则OA⊥OB.
2 y 2 x 上一定点， (2)已知点 M a,2 是抛物线 直线MP,MQ的倾斜角之和为 ，且分别与抛物线 交于P,Q两点，则直线PQ的斜率为________
9 6 9
所以Δ=4m-4m2>0,y1+y2=2m,y1·y2=2m2-m,
从而|AB|= 1 1 ·|y1-y2| 2
k
= 1 4m2
4m 4m2 ,
设点P到直线AB的距离为d,则 d=
1 2m 2m2 1 4m2
,
设△ABP的面积为S，则
S= 1 | AB | d |1 2m 2m 2 | m m 2 ,
2 y1 x1 , 由 得(y1-y2)(y1+y2)=x1-x2, 2 y2 x 2 ,
所以2km=1.
∴直线AB的方程为y-m= 1 (x m) ,
2m
即x-2my+2m2-m=0,
2 x 2my 2m m 0, 消去x，整理得y2-2my+2m2-m=0. 由 2 y x,