东南大学《工程矩阵理论》06(下)工程矩阵理论统考试卷(A)
东南大学《工程矩阵理论》工程矩阵理论期终考试(A)

12东南大学考试卷(A)Array课程名称工程矩阵理论考试学期08-09-2 得分
适用范围工科硕士研究生考试形式闭卷考试时间长度150分钟
1.地子空间地一组基是;
2.若线性空间地线性变换在基下地矩阵是,则在基下地矩阵是;
3.如果矩阵满足,并且地秩为,则行列式;
4.若矩阵,则矩阵函数地行列式;
5.若是维单位列向量,是正定地,则参数满足条件.
二.(12%)设矩阵.讨论地可能地Jordan标准形.并问:当参数满足什么条件时,矩阵与是相似地.
三.(20%)记,上地变换定义为:对,.
1.证明:是上地线性变换;
2.求在地基下地矩阵;
3.求地特征值及相应地特征子空间地基;
4.问:是否存在地基,使得在这组基下地矩阵是对角阵?如存在,试给出这样地一组基及相应地对角阵;如不存在,请说明理由.
四.(10%)设.试将表示成关于地次数不超过2地多项式.
五.(8%)求地广义逆矩阵.
六.(15%)假设是有限维欧氏空间,是单位向量,上地线性变换定义如下:对任意,.
1.证明:是上地正交变换.
2.在中定义内积:对,.于是,成为欧氏空间.分别求中向量及地长度,并求正实数及单
位向量,使得如上地正交变换将变成.
七.证明题(20%)
1.假设是矩阵,分别是、酉矩阵.证明:.
2.假设是正规矩阵.若地特征值地模都等于1,证明:是酉矩阵.
3.假设是Hermite矩阵,其中,是地子矩阵,并且都是方阵.若是正定地.证明关于行列
式地不等式:.。
3、东南大学工程矩阵模拟题12套

2. 求 n=2 时,f 的所有特征值及相应特征子空间的基。
3. 写出一般 n(n ≥ 3) 时,对应于 1 与 2 的结论。
工程矩阵模拟题 4
一:已知
C
2×2
的子空间:V1
=
{B
|
AB
=
BA,
B
∈
C
2×2 }
则 V1 的标准正交基为______, V2 的标准正交基为______, V1 ∩V2 的标准正交基为
______,V1 + V2 的标准正交基为______。
二:设 f , g 为线性空间V 上的线性变换且 fg = f 。试证: 1.V = k ( f ) + R(g) (V 未必是有限维) 2.若 dim V=n, 则 K ( f ) + R(g ) 为直和的充要条件为 dim R(f)=dim R(g)。
______,V2 的基为______,V1 ∩V2 的基为______,V1 + V2 的基为______。
⎛a 0 b⎞
3.
已知线性变换
f
在基 α1 , α 2
,α3
下的矩阵为
⎜ ⎜
0
c
0
⎟ ⎟
,则
f
在基
α3
,α2
,α1
下的矩阵
⎜⎝ b 0 a ⎟⎠
为______.
4.
设 A ∈ C s×n , B ∈ Ct×n ,又 (r A)=m,(r B)=r,作
2. 若 A 为 Hermite 阵,则 e A 为正定阵。
3. 若 n 阶方阵 A, B 满足: A, A − BH AB 均为正定阵,则 ρ (B) < 1 。
工程矩阵理论东南周建华共351页

9
由此导致的一些问题 • 乘法消去律不成立
对给定 A,当 的 A满矩 足阵 什么A条 BA件 必 C 时 可B, 推 C?由 出
•一些代数恒等式对矩阵不再成立
当 A与 B可交,换 相时 应的二项式 ,即定理成立
ABmAmCm 1Am1BCm 2Am2B2Cm m1AB m1Bm
10
解:
例3
计算下 nn矩 述阵k次 的幂A:
1
1
A I N 且 I 与 N 可交换,
A k (I N ) k (I ) k C k 1 (I ) k 1 N C k 2 (I ) k 2 N 2 C k k 1 (I ) N k 1 C k k N k
C1r C2r
C p1 C p2 C pr
其中,
C ij A i1 B 1 j A i2 B 2 j A iq B q j
12
C i j A i 1 B 1 j A i2 B 2 j A iB q qj
条件:上式有意义
A的列的分 B的 法行 与的分.法一致
13
一些特殊的分块形式
022
1 1 0 0 4 5
初 等 行 变 换000
0 0 0
1 0 0
0 1 0
14 26
11 0
022
23
例6
求齐次线性方程组的基 础解系:
x1 x2 x3 x4 x5 0
32xx11
2x2 3x2
3x3 3x4 x5 x3 2x4 4x5
0 0
x1 x2 4x3 5x4 5x5 0
工程矩阵理论东南周建华
幽默来自智慧,恶语来自无能
工程矩阵理论试题A
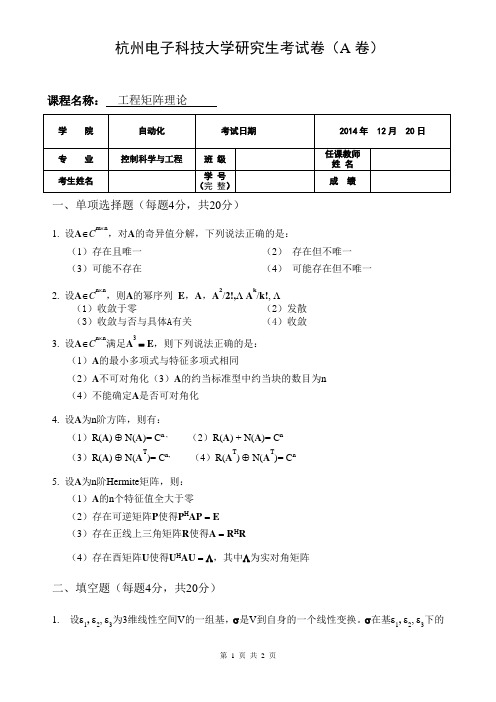
杭州电子科技大学研究生考试卷(A卷)课程名称:工程矩阵理论一、单项选择题(每题4分,共20分)1. 设A∈C m⨯n,对A的奇异值分解,下列说法正确的是:(1)存在且唯一(2)存在但不唯一(3)可能不存在(4)可能存在但不唯一2. 设A∈C n⨯n,则A的幂序列E,A,A2/2!, A k/k!,(1)收敛于零(2)发散(3)收敛与否与具体A有关(4)收敛3. 设A∈C n⨯n满足A3= E,则下列说法正确的是:(1)A的最小多项式与特征多项式相同(2)A不可对角化(3)A的约当标准型中约当块的数目为n(4)不能确定A是否可对角化4. 设A为n阶方阵,则有:(1)R(A) ⊕ N(A)= C n , (2)R(A) + N(A)= C n(3)R(A) ⊕ N(A T)= C n, (4)R(A T) ⊕ N(A T)= C n5. 设A为n阶Hermite矩阵,则:(1)A的n个特征值全大于零(2)存在可逆矩阵P使得P H AP=E(3)存在正线上三角矩阵R使得A=R H R(4)存在酉矩阵U使得U H AU=Λ,其中Λ为实对角矩阵二、填空题(每题4分,共20分)1. 设ε1, ε2, ε3为3维线性空间V的一组基,σ是V到自身的一个线性变换。
σ在基ε1, ε2, ε3下的矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡333231232221131211a a a a a a a a a ,则σ在基ε3, 2ε2, 3ε1下的矩阵为。
2. 设方阵A 满足A 2= 3A, 则sin (3A ) = 。
3.矩阵A = diag 21312,,0203⎛⎫⎡⎤⎡⎤ ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭,则A 的最小多项式为 。
4. 设X = (x 1, x 2, , x n )T 为变向量,α = (a 1, a 2, , a n )T 为常向量,H = (h ij )n ⨯n 为常矩阵,则:,()=HX X XT D D。
5. 设A ∈C n ⨯n 为Hermite 矩阵,X ∈C n ,A 的n 个特征值为λ1,λ2, ,λn ,满足λ1 ≤ λ2 ≤ ≤ λn ,则: XX AXX H X H 0max ≠ =。
矩阵论试卷及答案(2011A)

三(20分)设
(1) 证明: 是 的线性子空间,并求 的基和维数;
(2) 在 中定义变换 ,其中 为 的伴随矩阵, 证明: 为线性变换;
(3) 求 在(1)中所取基下的矩阵表示;
(4) 求(2)中线性变换 的值域 和核 ,并确定它们的维数.
(1)因为 ,则 非空。对任意 都有 则 是 的子空间.
(iii)写出 的Jordan标准形;
(2)设 ,试问A和B是否相似?并说明原因。
(1) , ;………5分
行列式因子
不变因子
初等因子 ……...8分
A的Jordan标准形为 ……..3分
(2)矩阵A,B的行列式因子均为 , A,B相似.
………4分
或A,B 的特征值均为-1和2,有两个互异的特征值,所以A,B均相似于 ,所以,A,B相似。
………3分
共5页第5页
五(20分)(1)设 , .
(i)求A的奇异值分解;
(ii)计算广义逆矩阵 ;
(iii)用广义逆矩阵判定线性方程组 是否相容。若相容,求其通解;若不相容,求其极小最小二乘解;
(2)设 ,判定矩阵级数 是否收敛。若收敛,求其和。
(1)(i) , 的奇异值为 , 对应于特征值3和2的标准正交特征向量为 , 对应于特征值3和2,0的标准正交特征向量分别为 , ,则 的奇异值分解为
Ni南京航空航天大学2010级硕士研究生
共5页第1页
2010~ 2011学年第1学期《矩阵论》课程考试A卷答案
考试日期:2011年1月12日,课程编号:A000003,命题教师:阅卷教师:
学院专业学号姓名成绩
一(20分)(1)设 。
(i)求 的特征多项式和 的全部特征值;
东南大学工程矩阵理论试题及答案

et = f(1) = g(1) = c0(t) + c1(t) + c2(t), (1+t)et = f ¢(1) = g¢(1) = c1(t) + 2c2(t), 由此可得 c0(t) = 0, c1(t) = (1-t)et, c2(t) = tet, 于是有 AeAt = (1-t)etA + tetA2.
0ö æ1 1÷ø çè1
2 2
ö ÷ø
=
æ çè
0 1
0 2
ö ÷ø
=
0E11
+
0E12
+
1E21
+
2E22,
æ1 1 0 0ö
由此可见
f
在
£2´2
的基
E11,
E12,
E21,
E22
下的矩阵
A
=
ç ç ç
2 0
2 0
0 1
0÷
1
÷ ÷
.
è0 0 2 2ø
张小向@seu
2
◆ 工程矩阵理论 ◆ 试题一 ◆ 答案仅供参考 ◆
2 a -1
0
3ö 4 ÷ , r(A-I) = 0 ÷ø
1, 2,
a = 8 / 3; a ¹ 8 / 3,
æ1 0 0 ö
æ1 1 0ö
当 a = 8/3 时, A 的 Jordan 标准形为 ç 0 1 0 ÷ ; 当 a ¹ 8/3 时, A 的 Jordan 标准形为 ç 0 1 0 ÷ .
则 QHQ = I, aHQ = (1, 0, ..., 0), QHa = (1, 0, ..., 0)H,
æ1+ k 0 L 0ö
工程矩阵理论(第6章-矩阵的广义逆)

矩阵的广义逆可以用于求解线性方程组,特别是当系数矩阵奇异或接近奇异时,广义逆提供了有效的 解决方案。
最小二乘解
在最小二乘问题中,广义逆可以找到使得残差平方和最小的解,这在数据分析和统计中非常有用。
在控制论中的应用
系统稳定性分析
在控制系统中,广义逆可以用于分析 系统的稳定性,通过计算系统的极点 来评估系统的动态行为。
04
矩阵的广义逆的存在性条件
存在性条件
矩阵A的秩为n
矩阵A的秩必须等于其维数n,即 $rank(A) = n$,以保证存在一个广义逆 矩阵。
VS
线性方程组有解
矩阵A所对应的线性方程组必须有解,即 系数矩阵A的行列式值不为零,即 $det(A) neq 0$。
唯一性条件
要点一
矩阵A为非奇异矩阵
矩阵A必须是非奇异矩阵,即其行列式值不为零,即 $det(A) neq 0$,以保证广义逆矩阵的唯一性。
程实际需求。
工程实例三:最优化问题求解
总结词
最优化问题求解是矩阵广义逆的一个重要应用方向。
详细描述
在工程领域中,经常需要解决各种最优化问题,如线 性规划、二次规划、非线性规划等。这些问题的数学 模型通常可以转化为矩阵形式。通过利用矩阵的广义 逆,可以高效地求解这些最优化问题,为工程实践提 供更好的解决方案。
最小二乘法的优点是简单易行,适用于大规模数据的计算。 但是,它只能找到一个近似解,而不是精确解。
迭代法
迭代法是一种通过不断迭代来逼近解的方法。在矩阵的广 义逆中,迭代法可以用来求解线性方程组的迭代解。通过 不断迭代更新解向量,最终逼近方程组的解。
迭代法的优点是适用于大规模数据的计算,且可以找到精 确解。但是,迭代法的收敛速度较慢,需要多次迭代才能 得到满意的结果。
工程矩阵理论(第6章-矩阵的广义逆)

第六章 矩阵的广义逆
§6.1 广义逆及其性质
(7) A+ = (AHA)+AH = AH(AAH)+; (8) (UAV)+ = VHA+UH, 其中U, V为酉矩阵; (9) A+AB = A+AC AB = AC. 证明: (7) (AHA)+AH = A+(AH)+AH = A+(A+)HAH = A+(AA+)H = A+AA+ = A+.
D1 O 令G = V O O ns UH,
则可直接验证G为A的广义逆.
第六章 矩阵的广义逆
§6.1 广义逆及其性质
(唯一性) 设X, Y满足 (1) AXA = A = AYA; (2) XAX = X, YAY = Y; (3) (AX)H = AX, (AY)H = AY; (4) (XA)H = XA, (YA)H = YA, 则X = XAX = X(AX)H = XXHAH = XXH(AYA)H = XXHAH(AY)H = X(AX)H(AY)H = XAXAY = XAY = XAYAY = (XA)H(YA)HY = (YAXA)HY = (YA)HY = YAY = Y.
AH(AAH)+ = AH(AH)+A+ = AH(A+)HA+ = …
(8) 利用定理4.2.6 (奇值分解), (9)() A+AB = A+AC AB = AA+AB = AA+AC = AC.
第六章 矩阵的广义逆
§6.1 广义逆及其性质
定理6.1.3 设A (1)
sn,
则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程矩阵理论试卷(A )
2006年10月
系别 学号 姓名 成绩
一. (20%)记22C ⨯为复数域C 上的22⨯矩阵全体在通常的运算下所构成的复数域上的线性空间,矩阵1100A -⎛⎫= ⎪⎝⎭
,{}22|V X C AX XA ⨯=∈=。
1.证明V 是22C ⨯的子空间,并求V 的基和维数;
2.假设22C ⨯的子空间0|,a W a b C a b b ⎧⎫⎛⎫=∀∈⎨⎬ ⎪-⎝⎭⎩⎭
,求W 的基和维数; 3.求,V W V W +⋂的基和维数。
二. (12%)假设矩阵000
0050000310031A ⎛⎫ ⎪ ⎪= ⎪- ⎪-⎝⎭,试求A 的广义逆矩阵A +。
三. (16%)设矩阵101101000A ⎛⎫ ⎪=- ⎪ ⎪⎝⎭。
1. 分别求A 的特征多项式及Jordan 标准型;
2. 写出A 的最小多项式;
3. 将At e 表示成关于A 的次数不超过2的多项式,并求At e 。
四. (20%)记22C ⨯为复数域C 上的22⨯矩阵全体在通常的运算下所构成的复数域上的
线性空间,对固定的矩阵22,A B C ⨯∈,定义22C ⨯上的变换如下:对任意22X C ⨯∈,
()f X AXB =。
1. 证明:对给定的矩阵22,A B C
⨯∈,f 是22C ⨯上的线性变换; 2. 设1011,1000A B ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭。
分别求11122122,,,E E E E 在f 下的像,并求f 在22C ⨯的基11122122,,,E E E E 下的矩阵M ;
3. 假设1011,1000A B ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭
,求f 的值域()R f 及核子空间()K f 的各一组
基及它们的维数;
4. 问:22()()C R f K f ⨯=⊕是否成立?为什么?
五. (12%)设矩阵21000403A x ⎛⎫ ⎪= ⎪ ⎪⎝⎭,32020003y B ⎛⎫ ⎪= ⎪ ⎪⎝⎭。
1. 根据x 的不同的值,讨论矩阵A 的所有可能的Jordan 标准形;
2. 若A 与B 是相似的,问:参数,x y 应满足什么条件?试说明理由。
六. (10%)假设3R 的由12,ξξ 生成的子空间12(,)V L ξξ=,其中
12(0,1,0),(1,0,2)ξξ== 。
设(1,0,1)η=。
在V 中求向量0η,使得
0min V
ξηηηξ∈-=-。
七. (10%)证明题
1. 证明:Hermite 阵和酉矩阵都是正规阵。
试举一例说明存在这样的正规阵,它既不
是Hermite 矩阵,也不是酉矩阵。
2. 若n 维列向量n C α∈的长度小于2,证明:4H I αα-是正定矩阵。
