动态投入产出模型理论及其在经济学中的应用【开题报告】
考虑税收的动态投入产出模型及其系统分析的开题报告

考虑税收的动态投入产出模型及其系统分析的开题报告开题报告题目:考虑税收的动态投入产出模型及其系统分析一、研究背景及意义投入产出模型是宏观经济学的重要工具之一,用于分析不同部门之间的产业关系,可以直观地描述经济系统的结构和运行情况。
在实践中,投入产出模型常常被用于制定宏观经济政策、评估经济政策的效果以及预测经济的发展趋势。
但是,现有的投入产出模型往往忽略了税收对经济的影响,无法准确估计税收对产业发展和经济增长的贡献。
因此,建立考虑税收的动态投入产出模型,有利于更准确地分析税收对经济的影响,为制定更为科学合理的税收政策提供参考。
二、研究内容本研究的主要内容包括:1.建立考虑税收的动态投入产出模型2.利用该模型分析税收对产业发展和经济增长的影响3.开展系统的灵敏度分析,探讨不同因素对模型结果的影响。
三、研究方法本研究主要采用投入产出模型的方法,通过建立数学模型,分析税收对经济增长和产业发展的影响,并进行系统分析和灵敏度分析。
四、预期成果本研究预期能够建立一个考虑税收的动态投入产出模型,深入分析税收对产业发展和经济增长的影响,探讨税收政策对经济的影响机制,为制定更为科学合理的税收政策提供参考。
五、研究计划本研究计划分为以下几个阶段:1.文献调研和理论研究,明确研究目标、研究内容和研究方法。
预计用时1个月。
2.建立基本的投入产出模型,并添加税收因素。
预计用时2个月。
3.利用已有数据估算模型的各项参数,并进行简单的模型验证。
预计用时3个月。
4.利用该模型分析税收对产业发展和经济增长的影响,并进行系统分析和灵敏度分析。
预计用时4个月。
5.撰写论文,准备答辩。
预计用时2个月。
总体研究周期约12个月。
六、参考文献1. Chen, Q., & Yu, J. (2014). Investment and consumption in China:A dynamic panel analysis. Journal of Macroeconomics, 39, 89-100.2. Li, Y., Liu, X., Li, Q., & Li, X. (2013). Tax reform and self-employment in China: Evidence from Chinese individuals’ tax return data. Journal of Comparative Economics, 41(1), 130-148.3. Zhang, Z., & Yuan, X. (2015). The heterogeneous effects of taxes on economic growth in China. Economic Modelling, 50, 308-315.4. Miller, R. E., & Blair, P. D. (2009). Input-output analysis: Foundations and extensions. Prentice Hall.5. Dietzenbacher, E. (2017). The role of accountants and census takers in the creation and early development of the input-output framework. Journal of the History of Economic Thought, 39(2), 163-179.。
投入产出分析在经济分析中的应用

§3.3 投入产出分析在经济分析中的应用——投入产出型价格模型作为投入产出分析在经济系统分析中的应用的一个例子,本节介绍它在价格分析中的应用。
在我国的价格改革过程中,投入产出分析模型曾经发挥重要作用。
国民经济价格体系是一个庞杂的大系统,与其它经济系统的联系错综复杂,就价格体系内部,各种产品、各个部门的价格相互关联,真可谓牵一发而动全身。
而且价格改革或价格调整的不可试验性,更增加了价格定量研究的难度。
经济数学方法的应用,建立价格数学模型,可以模拟价格体系复杂的运动过程,并起到试验的作用。
建立价格数学模型的方法很多,其中投入产出分析由于其描述了每个部门产品的价值形成过程、描述了部门之间、产品之间的联系,以及它描述了社会财富从生产、分配到最终使用各环节之间的数量关系,一直被人们认为是建立价格数学模型的较好方法。
尽管在市场经济条件下,商品的价格是由供求关系决定的,但是投入产出型价格模型在经济分析中仍然具有一定的意义。
本节对在我国的价格改革过程中建立的几个类型的投入产出型价格模型作一简单介绍。
由于模型是在特定的历史条件下建立的,从用语到思路都有那个历史时期的烙印,为了说明它的作用,这里未作修改。
一、理论价格测算模型1. 测算理论价格的意义理论价格是商品价值在人们观念上的货币表现,它不等于实际价格,它产生于人们的计算,所以又称为计算价格。
理论价格并不执行现实价格的职能,但是它对于经济的宏观管理具有重要的作用,概括说来有以下几点:首先,理论价格可作为正确核算和评价经济效益的手段。
因现行价格(包括计划价格和市场价格)与价值的或多或少的偏离,使得用现行价格核算的经济指标,往往不能准确反映微观和宏观的经济效益。
其次,理论价格是用于检验现行价格背离价值和不合理程度的标准,为价格管理决策和自觉利用价格杠杆提供信息。
另外,在正确的理论价格构成理论下测算的理论价格,可以作为价格改革的目标。
合理的价格体系不是一朝一夕就能实现的,理论价格的测算可提供一个理想的目标。
投入产出模型的推广及其应用

投入产出模型的推广及其应用投入产出模型是一种经济分析工具,用于评估一个经济体中不同部门之间的相互依赖关系和资源流动。
它可以帮助政府、企业和研究机构了解各个部门的贡献和影响,从而制定合理的政策和决策。
本文将介绍投入产出模型的基本原理、推广方式以及其在实际应用中的一些案例。
一、投入产出模型的基本原理投入产出模型是由经济学家沃森·勒奇(Wassily Leontief)在20世纪30年代提出的。
它基于一个简化假设,即一个经济体可以被划分为若干个部门,每个部门都需要一定数量的投入才能生产出相应的产出。
这些投入和产出之间存在着复杂的相互依赖关系,通过建立一个输入输出矩阵来描述这种关系。
输入输出矩阵是一个n行n列的方阵,其中n表示经济体中部门的数量。
矩阵中第i行第j列的元素表示第i个部门向第j个部门提供了多少单位的投入。
通过对输入输出矩阵进行数学运算,可以计算出每个部门的产出、就业和价值创造等指标。
二、投入产出模型的推广方式1. 数据收集:投入产出模型需要大量的数据支持,因此在推广应用之前,需要进行全面而准确的数据收集。
这包括各个部门的生产数据、投入数据以及经济体整体的经济指标等。
2. 模型构建:根据收集到的数据,可以构建输入输出矩阵,并计算各个部门的产出和就业情况。
这一步需要借助计量经济学方法和软件工具进行分析和计算。
3. 效果评估:通过比较不同部门之间的相互依赖关系和资源流动情况,可以评估不同政策或决策对整体经济效果的影响。
这有助于政府和企业制定更合理的发展战略和政策。
4. 推广应用:投入产出模型可以应用于各个领域,包括宏观经济政策制定、区域发展规划、环境影响评估等。
通过将模型推广到不同领域中,可以更好地理解各个部门之间的相互作用,并为决策者提供科学依据。
三、投入产出模型的应用案例1. 宏观经济政策制定:投入产出模型可以帮助政府评估不同政策对经济的影响。
政府可以通过模型计算出增加某个部门的投入会对整体就业和产出造成怎样的影响,从而制定合理的产业政策。
投入产出-CGE模型及其应用

n 1
~ V j avibij
n i 1
n
j vj bij
i 1
n
*
j vj bij
i 1
就业乘数
Ej
*
a ei ~ zij
i 1
n 1
~ E j aei bij
n i 1
产出乘数
产出乘数=初始值+直接消耗系数+间接消耗系数+诱导系数 初始值=1( 一个单位的最终产品) 直接消耗:直接消耗系数按列相加的值。
前提
在进行经济影响分析时,需要确定以下方面: • • • • 经济影响分析的对象是什么(基础设施建设、旅游消费、体育赛事)? 经济影响分析的区域范围(市、省国家)? 经济影响分析的时间范围(哪一年)? 经济影响分析的结果表现(总产出、GDP、居民收入、就业)?
经济影响的三个方面
• 产出:某一部门增加一个单位最终产品对国民经济各个部门所产生 的生产需求量(产出乘数) • 居民收入:增加最终产品→扩大生产规模→增加居民收入(居民收 入乘数) • 就业:增加最终产品→扩大生产规模→增加劳动力需求(就业乘数)
投入产出、CGE模型及其应用
张伟 博士 环境保护部环境规划院 环境规划与政策模拟重点实验室
目录页
CONTENTS PAGE
1.投入产出模型 介绍
2.相关研究 介绍
3.CGE模型现有 工作基础
4.未来设想
投入产出模型介绍
Part
1
Part 1
Part 2
Part 3
Part 4
什么是投入产出法
投入产出法:在一定经济理论指导下,通过编制投入产出表,建立相应的投入产出数学模型, 综合系统地分析国民经济各部门、再生产各环节之间数量依存关系的一种经济数量分析方法。 是经济学、统计学、数学、计算机技术相结合的产物。属于宏观经济的范畴。 (一)投入:指一项经济活动中的各种消耗。 包括:物质和非物质产品消耗;有形和无形产品消耗 有形:原材料、辅助材料、燃料、动力、固定资产折旧、 无形:劳动力、金融、保险、技术专利、服务等。
投入产出模型

系统控制方法——投入产出分析模型及其应用投入产出分析是将研究对象视为黑箱,通过系统的输入与输出分析研究,来判断和了解系统的状态、行为和功能。
具体地讲,它是研究管理系统各个部分间表现为投入与产出相互关系的经济数量分析方法。
在微观管理系统, 所谓投入是指产品生产所需原材料、辅助材料、燃料动力、固定资产折旧和劳动等等;所谓产出是指产品生产的总量及其分配使用方面的数量,如生产消费、外销量及增加储备等等,其中生产消费称为中间产品,外销产品和增加储备称为最终产品。
投入产出分析法最初是由国民经济各个产业部门(工业,农业等)间的联系发展起来的,故称其为部门联系平衡法或产业关联法,但它的应用十分广泛,不仅可应用于国民经济、地区经济的综合平衡,也可以有效地应用于企业内部的综合平衡,尤其适用于产品种类繁多,产品间联系复杂的企业。
在企业中应用投入产出分析通常包括三个步骤:一是编制投入产出表,二是建立投入产出数学模型;三是应用模型进行经济分析或实施优化分析。
一、企业投入产出表企业投入产出表按其用途不同和计量单位分为实物型投入产出表和价值型投入产出表两类。
现分述于下(一)实物型投入产出表企业实物型投入产出表的基本格式如表1所示。
实物型表包括四个象限(部分)。
Ⅰ象限是本企业自产产品用于本企业生产消耗的数量(以产量表示,)是反映企业内部中间产品间的技术联系,现以X ij代表本企业第i种自产产品用作第j种产品生产的消耗数量,称之为流量,表的这一部分称之为自产产品流量矩阵,以符号[X ij]表示,是一个方阵,表内i,j=1,2,…,n;Ⅱ象限(部分)是本企业自产产品的最终产品数量,包括外销产品、增加库存的数量及其他用途的数量,以Y i表示;Ⅲ象限(部分)是本企业生产中外购产品用作中间产品消耗的数量,以符号U ij表示外购产品i用于本企业第j种产品的生产消耗数量,表的这一部分称为外购产品流量矩阵,以[U ij]表示,基中的i=1,2,…,m为外购产品的品种数。
投入产出分析论文 投入产出模型应用与分析
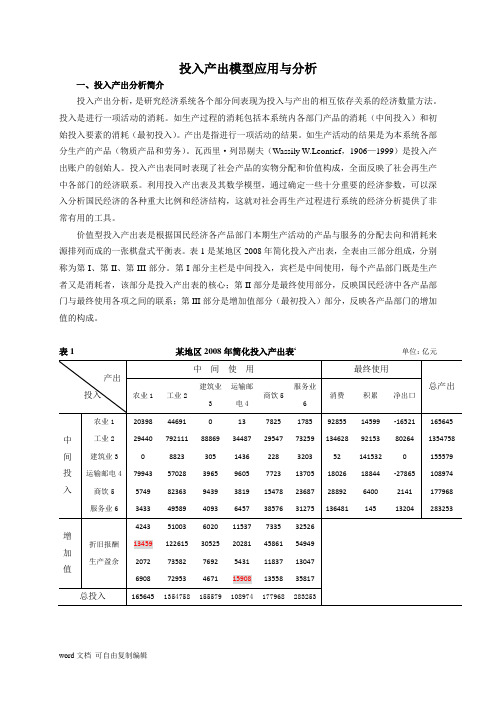
投入产出模型应用与分析一、投入产出分析简介投入产出分析,是研究经济系统各个部分间表现为投入与产出的相互依存关系的经济数量方法。
投入是进行一项活动的消耗。
如生产过程的消耗包括本系统内各部门产品的消耗(中间投入)和初始投入要素的消耗(最初投入)。
产出是指进行一项活动的结果。
如生产活动的结果是为本系统各部分生产的产品(物质产品和劳务)。
瓦西里·列昂剔夫(Wassily W.Leontief,1906—1999)是投入产出账户的创始人。
投入产出表同时表现了社会产品的实物分配和价值构成,全面反映了社会再生产中各部门的经济联系。
利用投入产出表及其数学模型,通过确定一些十分重要的经济参数,可以深入分析国民经济的各种重大比例和经济结构,这就对社会再生产过程进行系统的经济分析提供了非常有用的工具。
价值型投入产出表是根据国民经济各产品部门本期生产活动的产品与服务的分配去向和消耗来源排列而成的一张棋盘式平衡表。
表1是某地区2008年简化投入产出表,全表由三部分组成,分别称为第I、第II、第III部分。
第I部分主栏是中间投入,宾栏是中间使用,每个产品部门既是生产者又是消耗者,该部分是投入产出表的核心;第II部分是最终使用部分,反映国民经济中各产品部门与最终使用各项之间的联系;第III部分是增加值部分(最初投入)部分,反映各产品部门的增加值的构成。
表1 某地区2008年简化投入产出表i单位:亿元二、投入产出模型(一)建立模型 1.行模型(1)建立行模型:i i X y nj ij x =+∑=1 (i =1,2,...,n) 引入直接消耗系数 ij a ,即:ij a =ij x /j X可得:i i X y jX nj ij a =+∑=1即用矩阵表示为: AX+Y=X化简后可得价值型行数学模型: X=(I-A)-1Y 或 X=B Y (2)计算相关矩阵A ,B=(I-A)-1-I ,B =(I-A)-1 =B+I直接消耗系数矩阵:A=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.1104 0.21680.05930.0263 0.0366 0.0207 0.0836 0.0870 0.0350 0.0607 0.0608 0.0347 0.0484 0.0434 0.0881 0.0255 0.0421 0.4826 0.0113 0.00130.0132 0.0020 0.0065 0.0000 0.2586 0.1660 0.3165 0.5712 0.5847 0.1777 0.0063 0.04400.0001 0.0000 0.03301231.0完全消耗系数矩阵:B=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.22350.34120.16110.1660 0.1902 0.1696 0.1885 0.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 0.1908 0.1689 0.2174 0.7095 0.02270.0133 0.0250 0.0178 0.0240 0.0197 1.00730.87641.11911.7485 1.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12040.1976完全需要系数矩阵:B =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12041.1976(3)价值型行数学模型 X=(I-A)-1Y=B Y⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.17310.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.1204 1.1976⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321Y Y Y Y Y Y2列模型 (1)建立列模型j j j j j X s t v d ni ij x =++++∑=1 (j =1,2,...,n)引入直接消耗系数 ij a 可得:j j j j j X s t v d j X ni ij a =++++∑=1即用矩阵表示为:AcX+N=X化简后可得价值型列数学模型: X=(I-Ac)-1N (2)计算相关矩阵A C ,(I-Ac)-1物耗系数矩阵:Ac=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.5187000000 0.5584000000 0.5122000000 0.6856000000 0.76370000000.8389增加值系数矩阵:(I-Ac)-1=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 2.0775*******.26440000002.0500000003.181********.231590000006.2081(3)价值型列数学模型 X=(I-Ac)-1N⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ 2.0775*******.26440000002.05000000003.181********.231590000006.2081⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321N N N N N N ij x :第i 部门(行部门)生产的产品或服务分配给第j 部门(列部门)用于生产消耗的产品产值;第j 部门(列部门)生产过程中直接消耗第i 部门的产品或服务的产品产值;i y :第i 部门在本期产品中提供的最终使用额,包括消费和积累;j d 、j v 、j t 、j s :分别为第j 部门的折旧,劳动报酬,生产税净额,和营业盈余; j m :为第j 部门的社会纯收入,等于j t +j s ; j N :为第j 部门的增加值,等于j d +j v +j t +j s ;i X :第i 部门总产出 ;j X :第j 部门总投入;A :直接消耗系数矩阵(ij a )n n ⨯X=(X 1 X 2.......X N )T —总产出的列向量;Y=(y 1 y 2.......y N )T —最终使用的列向量;j i ,=1,2,3,4,5,6分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门;n =6。
投入产出模型应用.docx

投入产出模型应用一、投入产岀分析的主要内容•投入产出表是进行结构分析的一种有力工具。
利用投入产岀量化分析工具,分析产业关联中有关产业间比例、产业内的投入结构、分配或销售结构,以及产业间联系广度、深度等有关“结构分析”的主要问题和内容。
(一)各产业部门的产出结构和投入结构在投入产出表中,横行表示每个产业的总产岀或总产品是由中间产品和最终产品组成;也就是说每个行业的产品需求,都可以分为所有产业对该产业的需求(中间需求)以及由积累、消费以及净出口组成的最终需求。
所以,中间需求和最终需求的构成比例反映了经济结构的一个重要特征。
中间需求和中间投入分析・中间需求为其他产业(包括该产业本身)在经济活动中对某产业 产出的消耗之和。
(横向关系)・中间投入则是指由投入系数所决定的、某产业在经济活动中从 其他产业(包括该产业本身)得到的投入之和。
・中间需求率,指各产业的中间需求和该产业的总需求之比. •最终需求率=1-中间需求率•中间需求率越高的产业,其产出用做其他产业原材料的成分就 越大,就越具有基础产业的特点。
而最终需求率越高的产业, 就越具有最终产品产业的特点。
>1X,.1 = 1,2, - .n(1)价值型投入产出表1中间投入率•中间投入率是各产业的中间投入与总投入之比。
表示各产业在各自的生产活动中,为生产单位产值的产出而需要从其他产业购进的中间产品所占的比例。
(纵向关系)毛附加价值二总投入-中间投入毛附加价值率=1-中间投入率・中间投入率越高的产业,其毛附加价值率就越低。
/ = h 2八••“反映产业关联程度的重甲需求率、中间投入(2)指标,其在产业关联分析中的作用在于:(1)可准确地确定按不同的中间需求率和中间投入率划分的不同产业群在国民经济中的地彳立。
(羲妫里、渡边的产业戈»分i衣据)(2)可较清楚的显示各产业相互关系、相互依存的不同程度。
(3)可解释各产业部门协调发展的“有序性”。
有序性是指国民经济运行中,各产业有先后的发展顺序,这种顺序是由产业关联的依存度决定的。
投入产出分析原理及应用

投入产出分析原理及应用投入产出分析是一种衡量经济活动效率的方法,主要用于度量一个经济体的产出与投入之间的关系。
它可以帮助决策者了解经济活动的效率水平,以及优化资源配置。
本文将介绍投入产出分析的原理、计算方法和应用。
投入产出分析的核心原理是通过建立产出与投入的关系模型,来衡量经济体所需的投入资源与其产出之间的关系。
一般来说,投入产出模型包括产出矩阵和投入矩阵。
产出矩阵以列向量的形式表示一个经济体所产出的各种产品或服务。
而投入矩阵则以行向量的形式表示经济体所使用的各种资源或要素。
这些矩阵之间的乘积将得出一个产出向量,它表示了经济体所能产出的各种产品或服务。
投入产出分析的关键在于计算投入产出矩阵。
一般情况下,投入产出矩阵可以通过调查和统计数据获得。
在计算投入产出矩阵时,我们需要注意考虑到投入产出关系的复杂性,例如资源之间的相互依赖关系和技术进步的影响。
利用投入产出矩阵,我们可以计算出一系列有关经济体效率的指标。
其中最重要的指标是生产率。
生产率是指单位投入资源所产出的产出量。
在投入产出分析中,我们可以通过计算产出矩阵与投入矩阵的乘积,再与投入矩阵相除得到一个生产率矩阵,从而衡量各种经济活动的效率水平。
投入产出分析的应用非常广泛。
首先,它可以用于优化资源配置。
通过衡量各种经济活动的效率,我们可以发现资源配置中的问题,并调整产业结构,实现资源的最佳利用。
例如,当某一部门的生产率较低时,我们可以考虑增加该部门的资源投入,以提高其产出。
而当某一部门的生产率过高时,我们可以减少其资源投入,以优化整体资源利用效率。
其次,投入产出分析可以用于预测和规划经济活动。
通过对历史数据的分析和对未来的预测,我们可以建立模型来预测某一经济体在特定条件下的产出和投入状况。
这对经济决策者来说非常重要,因为他们可以根据这些预测结果来制定合理的经济政策和规划。
此外,投入产出分析还可以用于评估政策和项目的影响。
通过建立一个投入产出模型,我们可以评估某一政策或项目对经济体的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
开题报告
信息与计算科学
动态投入产出模型理论及其在经济学中的应用
一、综述本课题国内外研究动态, 说明选题的依据和意义
投入产出分析是由美国经济学家列昂惕夫(W.Leontief)于1936年提出的, 1931年列昂惕夫在美国开始研究投入产出表的编制工作, 1932年他成功地编制了美国1919年的投入产出表. 1931年开始, 列昂惕夫便投入巨大精力和时间开展投入产出分析的研究, 他不仅仅是投入产出分析的创始人, 而且之后还提出了一系列实际应用的投入产出模型. 1973年荣获诺贝尔经济学奖. 之后投入产生分析在国际上获得了巨大的发展.
经过50多年的发展, 全世界学者的研究和推广, 投入产出法的理论和方法变得越来越完善, 其中在经济活动中的应用也越来越广泛了, 成为了各国研究经济活动, 进行经济预测和政策分析, 国家产业规划, 经济发展规划强有力的工具. 因此, 投入产出法也得到了很好的发展和推广.
18世纪法国重农学派魁奈使用采用棋盘式平衡表来描述社会总产品的生产和流通.经济学中提出了将国民经济生产划分为生产资料和生活资料两大部分, 19世纪后期数量经济学家里昂·瓦尔拉斯提出了全部均衡论及其数学模型. 后来, 列昂惕夫将全部均衡论中比较复杂的数学方程体系加以简化, 就建立了投入产出模型. 列昂惕夫的投入产出模型将经济平衡表, 现代数学, 统计学结合起来, 从而创造了为后来的动态投入产出模型创造基础的投入产出分析. 不仅如此, 他还成功地用投入产出分析来研究美国的经济结构, 产业结构.
从20世纪40年代开始, 由于国际上各国对投入产出分析的重视以及投入产出所产生的巨大作用, 世界上许多国家纷纷开始投入大量人力物力进行研究和推广应用. 首先是从美国以及欧洲各国开始慢慢推广开来的, 后来日本, 东欧等国家也开始引入. 从此以后, 投入产出分析在国际上的影响也越来越大.
近些年来, 投入产出分析在环境保护、信息经济、人口、教育、收入分配、财务核算和国民经济核算等领域的应用均有所扩展. 戴维·哈京斯等人于1948年提出以微分方程形式表示动态投入产出模型. 列昂惕夫于1953年和1965年先后提出微分形式的连续型动态模型和差分方程形式的离散型动态模型, 1970年又提出著名的“动态求逆”, 为建立动态投入
产出模型奠定了基础.
近年来, 我国在动态投入产出模型的研究和应用上取得了可喜的成果. 夏绍伟和赵纯均等建立了考虑投资延滞的动态优化模型, 并探讨了目标规划在动态模型中的应用. 另外, 对于非线性投入产出模型也有一些研究成果. 但由于动态模型的复杂性, 其研究还不够成熟, 还有不少问题有待解决.
二、研究的基本内容, 拟解决的主要问题
研究的基本内容: 动态投入产出模型理论及其在经济学中的应用
解决的主要问题: 1. 综述投入产出分析的基本概念和理论.
2. 静态投入产出模型与动态投入产出模型的区别.
3. 对列昂惕夫的动态投入产出模型进行简要介绍以及公式的演算.
4. 动态投入产出模型在经济领域中的应用.
三、研究步骤、方法及措施
研究步骤:
1. 查阅相关资料, 做好笔记;
2. 仔细阅读研究文献资料, 学习投入产出模型的基本理论, 整理文献综述;
3. 翻译英文资料, 修改英文翻译, 撰写文献综述;
4. 在老师指导下, 确定整个论文的思路, 列出论文提纲, 撰写文献综述;
5. 撰写毕业论文;
6. 上交论文初稿;
7. 反复修改论文;
8. 论文定稿.
方法、措施: 通过到图书馆、上网等查阅收集资料, 上万方数据库查找文章, 参考相关内容. 在老师指导下, 与同组同学研究讨论, 用数据调查结合文献论证的方法来解决问题.
四、参考文献
[1] 张红霞, 唐焕文, 林建华. 多目标动态投入产出优化模型应用研究. 大连理工大学学报, 2001, 41(5): 478-490.
[2] 李仁贵. 24位诺贝尔奖大师解读经济学与人生. 北京: 经济日报出版社, 2003.
[3] 陈锡康. 投入产出技术的发展趋势与国际动态. 系统工程理论与实践, 1991, 11(2):
36-48.
[4] 许宪春, 刘起运. 2001年中国投入产出理论与实践. 北京: 中国统计出版社, 2002: 2-9
[5] 赵新良等. 动态投入产出. 沈阳: 辽宁人民出版社, 1988.
[6] 陈锡康. 投入占用产出分析一投入产出表的扩展. 当代中国投入产出理论与实践. 北京:
中国国际广播出版社,1988.
[7] 钟契夫. 投入产出分析, 第2版(修订本). 北京: 中国财政经济出版社, 1997.
[8] Chonghui Guo, Huanwen Tang. Stability Analysis of the Dynamic Input-Output System.
Appl. Math. J. Chinese Univ. Ser. B, 2002.
[9] Leontief W. Quantitative Input-Output relations in the Economic Systems of the United
States. Review of Economics and Statistics, l936, 18: 98-115.
[10] Harrigan F. , and I. Buchanan. A quadratic programming approach to input-output estimation and simulation. Journal of Regional Science, 1984, 24(3): 310-332.。
