随机线性网络编码共24页文档

合集下载

信道编码-线性分组码2

标准阵列的陪集首和伴随式是一一对应的，因而码的可纠错误图样和伴随式是一一对应的，应用此对应关系可以构成比标准阵列简单得多的译码表，从而得到 (n,k) 线性码的一般译码步骤。 (n,k) 线性码的一般译码步骤

计算接收矢量 R 的伴随式 ST=HRT ；根据伴随式和错误图样一一对应的关系，利用伴随式译码表，由伴随式译出 R 的错误图样 E；将接收字减错误图样，得发送码矢的估值 C’=R－E 。
增广：保持 n 不变，增加码字数目 k。删信：保持 n 不变减小 k。
(3) 延长/Lengthening和缩短/Sportening
延长：同时增加 k 和 n。缩短：同时减小 k 和 n。
2013/4/11
22/41
9. 由已知码构造新码的方法
举例： (7,4,3) 汉明码的各种修正关系如图6.2.31所示。
[证明]：

(n,k) 线性码的标准阵列有 2k 列（和码矢矢量相等），2n/2k= 2n－k 行，且任何两列和两行都没有相同的元素。陪集：标准阵列的每一行叫做码的一个陪集。陪集首：每个陪集的第一个元素叫做陪集首。

每一列包含 2n－k 个元素，最上面的是一个码矢，其它元素是陪集首和该码矢之和，例如第 j 列为接下页
8/41

2013/4/11
6. 线性分组码的译码

若发送码矢为 Cj，信道干扰的错误图样是陪集首，则接收矢量 R 必在 Dj 中；若错误图样不是陪集首，则接收矢量 R不在 Dj 中，则译成其它码字，造成错误译码；当且仅当错误图样为陪集首时，译码才是正确的。可纠正的错误图样：这 2n－k 个陪集首称为可纠正的错误图样。
2/41

线性分组编码

背景
在通信中，由于信息码元序列是一种随机序列，接收端无法预知码元的取值，也无法识别其中有无错码。所以在发送端需要在信息码元序列中增加一些差错控制码元，它们称为监督码元（校验元）。这些监督码元和信息码元之间有确定的关系。
在信息码元序列中加监督码元就称为差错控制编码，差错控制编码属于信道编码。
信息码元和监督码元之间有一种关系，关系不同，形成的码类型也不同。可分为两大类：分组码和卷积码。其中，分组码是把信息码元序列以每k个码元分组，编码器将每个信息组按照一定规律产生r个多余的码元（称为校验元），形成一个长为n=k+r的码字。
感谢观看

校验矩阵H
这也表示由G的行矢量所扩张成的k维子空间与H矩阵行矢量所扩张成的r维子空间是正交的。
G与H中只要有一个确定，另一个就是可以确定的。只要校验矩阵给订=定，校验码元和信息码元之间的关系就完全确定了。
举例
下面是一个（7,3）线性分组码，有信息组(m2m1m0),信息组在码字的前部，即：生成矩阵为信息组和对应的码字由表3.1给出。则其校验矩阵为
基本概念
当分组码的信息码元与监督码元之间的关系为线性关系时（用线性方程组），这种分组码就称为线性分组码。包括汉明码和循环码。
对于长度为n的二进制线性分组码，它有种可能的码字，从中可以选择M=个码字（k<n）组成一种编码，其中码字称为许用码字，其余码字称为禁用码字。这样，一个k比特信息可以映射到一个长度为n的码组中，该码字是从M个码字构成的码字集合中选出来的，剩下的码字即可以对这个分组码进行检错或纠错。
在线性分组码中，两个码字对应位上数字不同的位数称为码字距离，简称距离，又称汉明距离。编码中各个码字间距离的最小值称为最小码距d，最小码距是衡量码组检错和纠错能力的依据，其关系如下：（1）为了检测e个错码，则要求最小码距d>e+1; （2）为了纠正t个错码，则要求最小码距d>2t+1; （3）为了纠正t个错码，同时检测e个错码，则要求最小码距d>e+t+1,e>t。

基于随机网络编码的无线网络可靠性研究

ＢｅｉｊｉｎｇＩｎｓｔｉｔｕｔｅｏｆＴｒａｃｋｉｎｇａｎｄＴｅｌｅｃｏｍｍｕｎｉｃａｔｉｏｎｓＴｅｃｈｎｏｌｏｇｙ，Ｂｅｉｊｉｎｇ１０００９４，Ｐ．Ｒ．Ｃｈｉｎａ
ＲＮＣ— ＭＲａｄｏｐｔｓｒａｎｄｏｍｎｅｔｗｏｒｋｃｏｄｉｎｇｔｏｅｎｃｏｄｅｐａｃｋｅｔｓａｎｄｔｒａｎｓｍｉｔｓｄｉｆｆｅｒｅｎｔｃｏｄｉｎｇｐａｃｋｅｔｓｏｎｄｉｆｆｅｒｅｎｔｐａｔｈｓ．ＲＮＣ— ＭＲｃａｎｅｌｉｍｉｎａｔｅｄｕｐｌｉｃａｔｅｐａｃｋｅｔｓｏｎｍｕｌｔｉｐｌｅｐａｔｈｓ．Ｆｏｒａｗｉｒｅｌｅｓｓｔｗｏ・ｈｏｐｍｕｌｔｉｐａｔｈｎｅｔｗｏｒｋ，ｔｈｅｓｏｕｒｃｅａｎｄｒｅｌａｙｎｏｄｅｓｅｎｃｏｄｅｐａｃｋｅｔｓａｎｄｆｏｒｗａｒｄｔｈｅｍ，ａｎｄｔｈｅｄｅｓｔｉｎａｔｉｏｎｒｅｃｅｉｖｅｓｃｏｄｉｎｇｐａｃｋｅｔｓａｎｄｄｅｃｏｄｅｓｔｈｅｍ．ＮｕｍｅｒｉｃａｌａｎａｌｙｓｉｓａｎｄｓｉｍｕｌａｔｉｏｎａｒｅｄｏｎｅｔｏｅｖａｌｕａｔｅｔｈｅｔｒａｎｓｍｉｓｓｉｏｎｒｅｌｉａｂｉｌｉｔｙｏｆＲＮＣ— ＭＲ．Ｃｏｍｐａｒｉｎｇｗｉｔｈｔｒａ — ｄｉｔｉｏｎａｌｒｅｌｉａｂｉｌｉｔｙｔｒａｎｓｍｉｓｓｉｏｎｍｅｃｈａｎｉｓｍｓ，ｔｈｅｎｕｍｅｒｉｃａｌａｎｄｓｉｍｕｌａｔｉｏｎｒｅｓｕｌｔｓｓｈｏｗｔｈａｔＲＮＣ— ＭＲｃａｎｉｍｐｒｏｖｅｔｈｅｔｒａｎｓｍｉｓｓｉｏｎｒｅｌｉａｂｉｌｉｔｙａｎｄｒｏｂｕｓｔｎｅｓｓｏｆｗｉｒｅｌｅｓｓｎｅｔｗｏｒｋｓ．Ｋｅｙｗｏｒｄｓ：ｃｏｍｍｕｎｉｃａｔｉｏｎｓｙｓｔｅｍ；ｗｉｒｅｌｅｓｓｎｅｔｗｏｒｋ；ｒｅｌｉａｂｉｌｉｔｙｒａｎｄｏｍｎｅｔｗｏｒｋｃｏｄｉｎｇ；ｓｉｎｇｌｅｐａｔｈｒｏｕｔｉｎｇ；ｆｏｗａｒｒｄｅｒｒｏｒｃｏｒｅｃｔｉｏｎ；ｍｕｈｉｐａｔｈｒｏｕｔｉｎｇ

网络编码

网络编码初步陆巍220080551摘要：网络编码是通信网络中信息处理和信息传输理论研究上的重大突玻，其核心思想是允许网络节点对传输信息进行编码处理。

运用网络编码能够提升网络吞吐量、均衡网络负载和提高网络带宽利用率等。

本文简单介绍网络编码的基本原理以及主要优缺点，归纳网络编码的主要实现算法和机制，并重点分析网络编码的在P2P网络中应用。

关键词：网络编码随机网络编码信息流多播1引言传统的多播传输很难使多播传输达到“最大流最小割”定理确定的最大理论传输容量。

这主要是因为现有通信网络中使用的路由机制认为网络中传输的信息是不能叠加的，只能进行存储和转发。

然而，香港中文大学R. Alshwede等在2000年的IEEE信息论会刊上发表的一篇论文，彻底推翻了这一结论。

该文首次提出了网络编码的概念并从理论上证明：如果允许网络信息按照合适的方式进行编码处理，则基于该方式的网络多播总能够实现理论上的最大传输容量。

网络节点对传输信息进行操作和处理的过程，就称为网络编码。

2网络编码的基本概念和优缺点2.1基本概念R. Alshwede等[1]以著名的“蝴蝶网络”（Butterfly Network）模型为例，阐述了网络编码的基本原理。

如图1所示的“单信源二信宿”蝴蝶网络，设各链路容量为1，S是信源节点，Y和Z是信宿节点，其余为中间节点，根据“最大流最小割”定理，该多播的最大理论传输容量为2，即理论上信宿Y和Z能够同时收到信源S发出的2个单位的信息，也就是说能同时收到b1和b2。

图1（a）表示的是传统的路由传输方式，节点W执行存储和转发操作，假定W转发信息b1，则链路WX、XY和XZ上传输的信息均为b1，虽然信宿Z收到b1和b2，但信宿Y却只能收到b1(同时收到一个多余的b1)，因此信宿Y和Z无法同时收到b1和b2，该多播不能实现最大传输容量。

图1(b)表示的是网络编码方法，节点W对输入的信息进行模二加操作，然后将操作结果b1+b2发送至输出链路WX，然后又通过链路XY和XZ，最终达到信宿Y和Z。

第二十四讲第六节线性分组码讲课文档

现在二十七页，总共四十五页。
校验矩阵
H(AT Ink)
其中 I n k 为 n k 阶单位阵， A T 为生成矩阵 G 中的子矩阵 A 的转置 .
即
g1,k1 H(AT Ink)g1,k2
g1,n
g2,k1 g2,k2
g2,n
gk,k1 1 0
0
gk,k2 0 1
码长： n2m1, m 3
例：构造一个 m 3的 2 元汉明码
由于 n 2 3 1 7 ,k 2 3 3 1 4 故构造的汉明码为( 7 , 4 ) 线性分组码
信息位长：k2mm 1 校验位长： r n k m 最小码距：d 3
汉明码 H 矩阵的构造方式：
0 H 0
0 1
11xx0010xx1110xx2201xx3300xx44
0 0
1x0 1x10x2 0x31x4 0
• 用矩阵可表示成：
校验矩阵
x0 0
1 1 1 0 1 1
1 0 0
0 1 0
0
0
1
x1 x2 x3
0
0
0
x 4 0
与任一码字的乘积为0
现在十七页，总共四十五页。
解： n=6; M=2k k=3.
映射 f:k n 称为一个线性编码
现在十五页，总共四十五页。
• 例2、（5，2）线性二元码的全部码字
• 设码字 x5(x0,x1,x2,x3,x4)，可得
x2
x3
x0 x0
x1
x 4 x 0 x 1
现在十六页，总共四十五页。
• 改写为
n
n
n
称码为(n, k)码.

线性分组码的编码原理

《通信原理课件》
如果用两个二进制码元来表示一个消息，有4 种可能的码字，即“00”、 “01”、“10”和
“11”。比如规定“00”表示消息A， “11”表示消息B。码字“01”或“10”不允许使用，称为禁
用码字，对应地，用来表示消息的码字称为许用码字。如果在传输消息的过程中发生一位错码，则变成禁用码字“01”或“10”，译码器就可判决为有错。这表明在信息码元后面附加一位监督码元以后，当只发生一位错码时，码字具有检错能力。但由于不能判决是哪一位发生了错码，所以没有纠错能力。
间的最小距离，称为该编码的最小汉明距离，简称为最小码距，用 d min 表示。例如码长 n =3 的重复码，只有 2 个许用码字，即 000 和 111，显然 d min ＝3。
《通信原理课件》
《通信原理课件》
信道编码的效用
《通信原理课件》
[例9.2.1]
《通信原理课件》
《通信原理课件》
9.2.2 信道编码的译码方法
《通信原理课件》
《通信原理课件》
9.4.1 循环码的码多项式
循环码可用多种方式进行描述。在代数编码理论中，通常用多项式去描述循环码，它把码字中各码元当作是一个多项式的系数，即把一个
n 长的码字 C ＝ cn1,cn2 ,cn3,,c1,c0 用一个次数不超过（n-1）的多
项式表示为
C x cn1 x n1 cn2 x n2 c1 x c0
《通信原理课件》
9.2 信道编码的基本原理
香农的信道编码定理指出：对于一个给
定的有扰信道，如果信道容量为C，只要发送端以低于C的信息速率R发送信息，则一
定存在一种编码方法，使译码差错概率随着码长的增加，按指数规律下降到任意小的值。这就是说，通过信道编码可以使通信过程不发生差错，或者使差错控制在允许的数值之下。

第8章线性分组码PPT课件

×
1
=
0
T r×1
，
则有
H
r×
nG
T n
×
k=
0
T r
×
k
或
G
k
×
n
H
T n
×
r
=
0
k×
r
• 线性系统码的监督矩阵 H 和生成矩阵 G 之间可以直接互换。
GS Ik Qkr
HS Prk Ir
GSHTS Ik
Qkr Prk
Ir T Ik
QkrLeabharlann (PrIrk)T(Prk
)T
h22
h2
n
hr 2
hrn
Cn2 C0
Hrn
CT n1
0T r1
或
C1n
HT nr
01r
称H为(n, k)线性分组码的一致监督矩阵。
第9页/共72页
一致监督矩阵特性:
• 对H 各行实行初等变换，将后面 r 列化为单位子阵，于是得到下面矩阵(行变换所得方程组与原方程组同解)。
p11 p12 p1k 1 0 0
g1
C1n
mk1mk2 m0
g 2
m1k
G
kn
gk
m mk1mk2 m0 是待编码的信息组
G是一个k n阶矩阵。
第13页/共72页
g1 g11 g12 g1n
显然：G k n
g 2
g
21
g22
g
2n
g
k
g
k1
gk2
g
kn
• G中每一行 gi=(gi1,gi2,…, gin ) 都是一个码字；

【国家自然科学基金】_无线网络编码_基金支持热词逐年推荐_【万方软件创新助手】_20140802

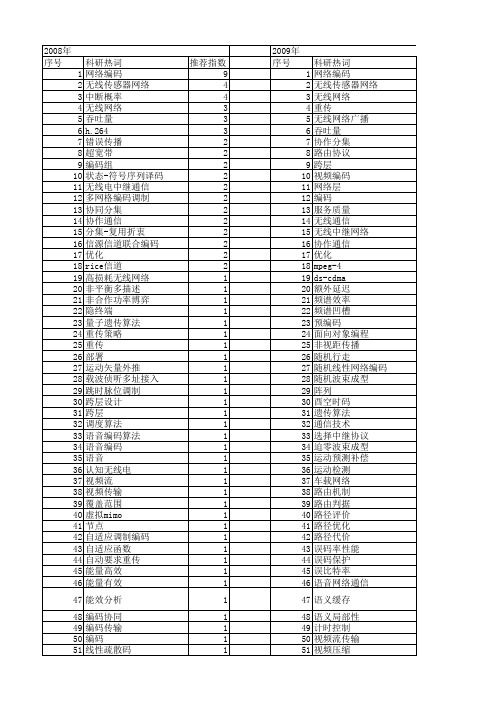
科研热词网络编码无线传感器网络无线网络重传无线网络广播吞吐量协作分集路由协议跨层视频编码网络层编码服务质量无线通信无线中继网络协作通信优化 mpeg-4 ds-cdma 额外延迟频谱效率频谱凹槽预编码面向对象编程非视距传播随机行走随机线性网络编码随机波测补偿运动检测车载网络路由机制路由判据路径评价路径优化路径代价误码率性能误码保护误比特率语音网络通信语义缓存语义局部性计时控制视频流传输视频压缩视频传输
推荐指数 9 4 4 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

编码模型
符号简介（2）
I (v)
定义 I (v) 为所有以节点V为结束点的边
的集合 I( v ) e E :h( e e ) a v d
定义 0 (v)为所有从节点V开始的边的集合
0 (v)
0 ( v ) e E :ta ( e ) iv l
接收机β处的终端链路的集合称为
A( dv d) yo X ur( v t, i1 t) leX in( v , h, 2 e) r e , , X ( v , u ( v ) 是) 在节点v收集到的
u(v)个离散随机过程
在边e上传输的随机过程称为Y(e)
编码模型
如图是一个非延迟网络，对于链路e上的随机处理过程满足
对于汇节点的输出Z是由属于 I (u) 的所有边上的随机过程Y(e)形成的
Add your title in here
这里的α，β，ε都是从伽罗华域中随机选择的
如果α，β，ε是独立的，则系统是时不变的，否则系统是时变的
另M表示一个网络的传输矩阵，这样z=x*M,对于固定的系数α，β， ε，我们不难看出，M矩阵里的数也是从伽罗华域中选取的。
编码模型
伽罗华域简介
GF(2 m)域
以m=4为例，它的本原多项式为 410,即4 1
在伽罗华域中，加法等于对应位异或
先给出推导过程
0 0000 3 1000 1 0001 4 0011
0010 5 0110
14 1001 15 0001
2 0100
…
Add y可our以ti看tle出in ，he当re m=4时，GF(4)是一个包含15个数的有限域，
且这15个数循环产生。
在伽罗华域中，每对应一个m，会有一个相应的本原多项
式，根据这个本原多项式，就可以推出域里面的值。
编码模型
编码模型
对有向网络来说，对网络节点进行排序，定义相应的邻接矩阵F，F矩阵的第i行第 j 列元素表示网络流图中第i条边与第 j 条边的连接关系，F可表示为
Fi,j
0,ei,ej
,hea (eid)ta(ielj) 其它
其中 he(aei)dta(eijl)表示有向边 e i的终点与有向边 e j的起点重合， ei ,e j 是有限域中的一非 0 元素，则M可表示为：
Add不yo考ur虑title in here 延迟
考虑延迟
编码模型
符号简介（1）
非循环图G=（V,E）表示的网络中，每条边可以根据网络拓扑进行顺序编号: 如 e1,e2,eE ，对于每条从属于E的边，它的源表示为 o( e i),它的目的节点表示为d( Ae id)d。y一ou个r t路itle径in就h是er一e 系列的链路集
合d(ei)o(ei1) ，对任意的
i ≠j,d (ei ) ≠ d (e j ) 。
O( e i )
边e i
边e i1
节点V 即d(e i ) 既称为head（e ）i
又称为tail( e i 1 )
进入一个节点的边数称为一个节点的入度，由一个节点发出的边数称为节点的出度，节点的入度和出度的和称为节点的度数
简要介绍
满足网络容量要求
网络容量问题
随机分布问题
最大流最小截定理
多源（包括相关源）多径问题
一般组播网络结构
简要介绍
对于除了信宿节点外的所有中间节点，只要在一个足够大的有限域上随机选择它们输入链路到输出链路的映射，且各节点映射关系的选取是相互独立的，从而保证各信宿能以较高概率成功译码
各链路上的系数向量和信源发送的信息进行同步传输，信息在通过编码节点时，系数向量根据随机选取的映射关系进行更新，最终信宿节点收到的输入信息将包含输入链路对应的全局编码向量和信源发送的信息流，然后采用高斯消元法（解线性方程组）正确译码获得信源原始传输的信息
编码模型
Add your title in here
x X ( v ,1 )X ( ,v ,2 ) ,X ( v ,u ( v )表)示在源节
点观察到的输入信号矢量
另v’点是一个网络的汇结点，我
们认为 z Z ( v ',1 )Z ( v ,',2 ) ,,Z ( v ',( v ')是)
这个节点的输出过程矢量
简要介绍
·怎样构建随机线性网络编码 ·怎样在分布网络中有效的将信息传输到接收节点
编码模型
·每条链路的容量是一比特每单元，如果某条边的容量大于一比特每单位时间，则看做是几条并行的边。如果边的容量不是整数，则将时间单元取得大一点，使得小数部分可以近似成整数。 ·假设每条链路的延迟是一样的。 ·对于线性相关源，我们认为每一个独立信源的熵率是一比特每单位时间，如果不是，则将它们变成一些并行的熵率是一比特每单位时间的源的集合。 ·对于任意相关源，我们要求信源的熵是整数，并且有着任意的联合概率分布 ·对于不同的节点，它们要处理的随机过程之间是相互独立的，这个假设符合通信网络一般的情况

编码模型
多信源的Slepian —Wolf定理：
有r个离散的无记忆信息源 X1,X2,,Xr,它们是随机二进制序列，对每个信源独立进行编码，再进行联合译码，其性能跟所有信源联合编码是一致的。只要满足在r个信源中任取k个信源的和速率，不能小于这k个信源以剩余的r-k个信源为条件的熵，而对于总的和速率不能小于这r个信源的联合熵。
Add your title in here
编码模型
考虑边容量为1的情况，每个节点在等到所有进入此节点的信息后才发往离开此节点的
出边
有着v个节点和信息传输速率是r的循环网络可以变成非循环网络，此网络有kv个节点，信息传输速率大于等于（k-v）r,信息在这种网络上的传输可以被模仿成原来循环网络k个时隙的步骤。这种情况我们假设每个链路的延迟是一样的。
Add your title in here
传输矩阵可以表示为
编码模型
传输矩阵可以表示为
Add your title in here
矩阵 A为源节点输入信息与边之间的关系矩阵，矩阵B为接收节点对接收到的数据进行线性组合。单源单汇的节点的信息传输时，只要相应的转移矩阵是满秩的，则源节点输出的信息在接收端就可以准确的恢复。单源多汇的节点的信息多播传输，利用网络编码时，只要能保证各个目的节点对应的网络转移矩阵是满秩的，则目的节点就可以准确的恢复出原始发送的信息。