北方工业大学2009《信号与系统》课程期末考试试卷
北方工业大学信号与系统期末试卷A
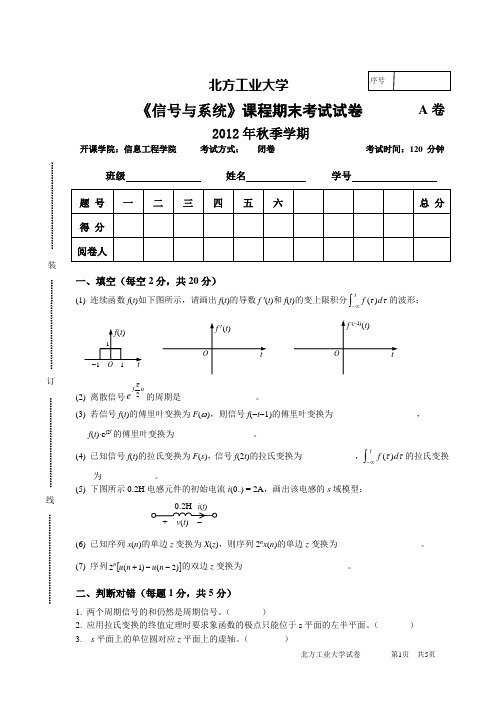
北方工业大学《信号与系统》课程期末考试试卷A 卷2012年秋季学期开课学院：信息工程学院考试方式： 闭卷考试时间：120 分钟班级 姓名 学号 一、填空（每空2分，共20分）(1) 连续函数f (t )如下图所示，请画出f (t )的导数f '(t )和f (t )的变上限积分⎰∞-t d f ττ)(的波形：(2)离散信号nj e 2π的周期是_________________。
(3) 若信号f (t )的傅里叶变换为F (ω)，则信号f (-t -1)的傅里叶变换为___________________， f (t )⋅e j2t 的傅里叶变换为__________________。
(4) 已知信号f (t )的拉氏变换为F (s )，信号f (2t )的拉氏变换为____________，⎰∞-t d f ττ)(的拉氏变换为____________。
(5) 下图所示0.2H 电感元件的初始电流i (0-) = 2A ，画出该电感的s 域模型：______________________(6) 已知序列x (n )的单边z 变换为X (z )，则序列2n x (n )的单边z 变换为___________________。
(7) 序列[])2()1(2--+n u n u n 的双边z 变换为________________________。
二、判断对错（每题1分，共5分）1. 两个周期信号的和仍然是周期信号。
（ ）2. 应用拉氏变换的终值定理时要求象函数的极点只能位于s 平面的左半平面。
（ ）3. s 平面上的单位圆对应z 平面上的虚轴。
（ ）0.2H + v (t )i (t ) 订线装4. 无失真传输系统的单位冲激响应为K δ (t - t 0)。
（ ）5. 因果离散系统的系统函数的收敛域必为某个圆外部分。
（ ）三、简答题（每题7分，共35分）(1) 已知离散信号x (n )的波形如下图所示，试画出x (n - 1)和x (-2n - 1)的波形。
《信号与系统》期末试卷与答案
《信号与系统》期末试卷与答案第 2 页 共 14 页《信号与系统》期末试卷A 卷班级： 学号：__________ 姓名：________ _ 成绩：_____________一． 选择题（共10题，20分） 1、n j n j een x )34()32(][ππ+=，该序列是 。
A.非周期序列B.周期3=NC.周期8/3=N D. 周期24=N2、一连续时间系统y(t)= x(sint)，该系统是 。
A.因果时不变B.因果时变C.非因果时不变D. 非因果时变3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u e t h t ，该系统是 。
A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定第 3 页 共 14 页4、若周期信号x[n]是实信号和奇信号，则其傅立叶级数系数a k 是 。
A.实且偶 B.实且为奇 C.纯虚且偶 D. 纯虚且奇5、一信号x(t)的傅立叶变换⎩⎨⎧><=2||02||1)(ωωω，，j X ，则x(t)为 。
A.tt 22sin B.tt π2sin C.tt 44sin D.ttπ4sin6、一周期信号∑∞-∞=-=n n t t x )5()(δ，其傅立叶变换)(ωj X 为 。
A.∑∞-∞=-k k )52(52πωδπB.∑∞-∞=-k k)52(25πωδπC. ∑∞-∞=-k k )10(10πωδπ D.∑∞-∞=-k k)10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ，则x[n]奇部的傅立叶变换为 。
第 4 页 共 14 页A. )}(Re{ωj e X jB.)}(Re{ωj e X C.)}(Im{ωj e X jD.)}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ，则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 。
A. 500B. 1000C. 0.05D. 0.0019、一信号x(t)的有理拉普拉斯共有两个极点s=－3和s=－5，若)()(4t x et g t=，其傅立叶变换)(ωj G 收敛，则x(t)是 。
信号与系统期末试卷-含答案全
一．填空题(本大题共10空，每空2分，共20分。
)1．()*(2)k k εδ-= . 2．sin()()2td πτδττ-∞+=⎰.3. 已知信号的拉普拉斯变换为1s a-，若实数a ，则信号的傅里叶变换不存在. 4. ()()()t h t f t y *=，则()=t y 2 . 5. 根据Parseval 能量守恒定律，计算⎰∞∞-=dt t t 2)sin (.6. 若)(t f 最高角频率为m ω，则对)2()4()(t f t f t y =取样，其频谱不混迭的最大间隔是 .7. 某因果线性非时变（LTI ）系统，输入)()(t t f ε=时，输出为：)1()()(t t e t y t--+=-εε；则)2()1()(---=t t t f εε时，输出)(t y f ＝ .8. 已知某因果连续LTI 系统)(s H 全部极点均位于s 左半平面，则∞→t t h )(的值为 .9. 若)()(ωj F t f ↔，已知)2cos()(ωω=j F ，试求信号)(t f 为 .10.已知某离散信号的单边z 变换为)3(,)3)(2(2)(2>+-+=z z z z z z F ，试求其反变换)(k f =.二．选择题(本大题共5小题，每题4分，共20分。
)1.下列信号的分类方法不正确的是 ：A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、因果信号与反因果信号2. )]2()()[2()]()2([2)(1--++-+=t t t t t t f εεεε，则)]1()21()[21()(--+-=t t t f t f εε的波形是。
3. 已知一连续时间LTI 系统的频响特性ωωωj j j H -+=11)(，该系统的幅频特性=)(ωj H ______，相频特性)(ωϕj =______，是否是无失真的传输系统______A 、2，2arctan()ω，不是B 、2，arctan()ω，是C 、1，2arctan()ω，不是D 、1，arctan()ω，是4. 设有一个离散反馈系统，其系统函数为：)1(2)(k z zz H --=，问若要使该系统稳定，常数应k 该满足的条件是A 、5.15.0<<kB 、5.0>kC 、5.1<kD 、+∞<<∞-k5. 函数2sgn(4)t -等价于下面哪个函数？A 、(2)(2)t t εε-+--B 、12(2)2(2)t t εε--+--C 、(2)(2)(2)t t t εεε-+---+D 、12(2)2(2)t t εε-++-三．计算题（本大题共4小题，每题9分，共36分）1. 已知某系统：)()(n nf n y =试判断其线性，时不变性，因果性，稳定性等特性，并说明理由（可在下页作答）。
09级信号期末考试参考答案
1． 。
2． 。
3． 。
4． 。
5． ， 。
6.离散性，谐波性，收敛性。
7. 。
8． ， 。
9.对信号截断或者对信号加窗。补零，不能。
10.14。
11.0.9-0.4j， =1。
12.125.8086s，0.7168s。
二、简单计算题（2个小题，共20分）。
1.（10分）已知 ，分别求：
解：
三、应用题（3个小题，共40分）。
1.（10分）设带限信号 的最高频率为3kHZ，带限信号 的最高频率为6kHZ，试求下列信号的最小采样频率：
（1） ；（2） 。
解：（1） 的最高频率为3kHZ，那么 的最高频率为6 kHZ，由抽样定理，最小采样频率为信号频率的2倍，所以 的最小采样频率为12 kHZ。（5分）
（2） ， 的最高频率为3kHZ， 的最高频率为6kHZ，那么它们频谱卷积后的最高频率为9 kHZ，由抽样定理， 的最小采样频率为18 kHZ。（5分）
2.（15分）设 ，求其DTFT序列傅里叶变换 ，4点DFT离散傅里叶变换 和8点DFT离散傅里叶变换 的表达式，并说明 ， 与 的关系。
解： 的DTFT：
0.1ms，试确定以下各参数：
（1）信号最小记录时间 ；
（2）所允许处理的信号最高频率 ；
（3）在一个记录中的最少采样点数N；
（4）在频带宽度不变的情况下，将频率分辨率提高一倍的方法。
解：时间采样间隔 为0.1ms，则采样频率
（1）信号最小记录时间 ；（4分）
（2）所允许处理的信号最高频率 ；（4分）
（4分）
的4点DFT：
（4分）
的8点DFT：
信号与系统期末考试题及答案（第一套）
信号与系统期末考试题及答案（第⼀套）信号与系统期末考试题及答案（第⼀套）符号说明：为符号函数，为单位冲击信号，为单位脉冲序列，为单位阶跃信号，为单位阶跃序列。
⼀、填空（共30分，每⼩题3分）1. 已知某系统的输⼊输出关系为（其中X(0)为系统初始状态，为外部激励），试判断该系统是（线性、⾮线性）（时变、⾮时变）系统。
线性时变2. 。
03.4. 计算=。
5. 若信号通过某线性时不变系统的零状态响应为则该系统的频率特性=，单位冲激响应。
系统的频率特性，单位冲激响应。
6. 若的最⾼⾓频率为，则对信号进⾏时域取样，其频谱不混迭的最⼤取样间隔。
为7. 已知信号的拉式变换为，求该信号的傅⽴叶变换=。
不存在8. 已知⼀离散时间系统的系统函数，判断该系统是否稳定。
不稳定9.。
310. 已知⼀信号频谱可写为是⼀实偶函数，试问有何种对称性)sgn(t )(t δ)(k δ)(t ε)(k ε)0(2)()()(2X dt t df t f t t y +=)(t f ________________?∞-=-+32_________)221()32(dt t t t δ?∞∞-=--_________)24()22(dt t t εε??∞∞-==--1)24()22(21dt dt t t εε},3,5,2{)()},3()({2)(021=↓=--=K k f k k k f kεε)()(21k f k f *________}12,26,21,9,2{)()(21↓=*k f k f )(t f ),(),()(00为常数t K t t Kf t y f -=)(ωj H ________=)(t h ________0)(t j Ke j H ωω-=)()(0t t K t h -=δ)(t f )(Hz f m )2()()(t f t f t y ==max T ________m ax T )(6121max max s f f T m==)1)(1(1)(2-+=s s s F )(ωj F ______2121)(---+=z z z H ______=+-+?∞∞-dt t t t )1()2(2δ______)(,)()(3ωωωωA e A j F j -=)(t f。
西北工业大学信号与系统2009_2010期末试题及答案
诚信保证本人知晓我校考场规则和违纪处分条例的有关规定，保证遵守考场规则，诚实做人。
规则，诚实做人。
本人签字：本人签字：本人签字： 编号：编号：西北工业大学考试试题（卷）2009 － 2010 学年第学年第 2 学期学期开课学院开课学院 计算机学院计算机学院 课程课程 信号与系统信号与系统 学时学时 48 考试日期考试日期 2010年6月9日 考试时间考试时间 2 小时小时 考试形式（闭开）（B A）卷）卷考生班级考生班级学 号姓 名★注：请将各题答案做在答题纸上，答在试题纸上无效。
一、单项选择题（每题有且仅有一个答案是正确的，共20分） 1、已知某系统方程为dt t de t r )()(=，则该系统是 ① 。
① A ．线性时不变系统 B ．非线性时变系统C ．线性时变系统D ．非线性时不变系统2、已知某连续线性时不变系统的初始状态为零，设当激励为e(t)时，全响应为r(t)，则当激励增大一倍为2e(t)时，其全响应为 ② 。
② A ．21r(t) B ．2r(t) C ． r(t) D ．发生变化，但以上答案均不正确3、复频率为-1,对应的时间函数模式为()t Ae te -，问复频率为21j ±-，对应的时间函数为 ③ 。
③ A ． )(θt cos Ae 2t+- B ． )()cos(2t t Aete q +-C ．)2cos(q +-t Ae tD ． )()(t εθ2t cos Ae t +-注：1. 命题纸上一般不留答题位置，试题请用小四、宋体打印且不出框。
2. 命题教师和审题教师姓名应在试卷存档时填写。
共 7 页 第 1 页成绩4、若)()(w j F t f «，则«-)26(t f ④ 。
④ A ．()w w 6j2-2j e F - B ．ww 32j 21j e F ÷øöçèæ C ．()ww 3j22jeF - D ．ww 32j -21j e F -÷øöçèæ5、已知信号)(t f 的波形如图1所示，其表达式=)(t f 2 ⑤ ，对应的拉普拉斯变换为 ⑥ 。
《信号与系统》考试试题及参考答案
《信号与系统》期末考试姓名 学号 班级 成绩一、选择及填空（20分 每题2分）：1. 以下系统，哪个可进行无失真传输＿B ＿ωωϕωωωδωωωωωωωω-6)( )1()(H )( )()(H )( 3)(H )( )1()1()(H )( 33=-===--=-且；；；D ej C e j B e j A j j j U答：(B)2. 下列哪一项是理想低通滤波器的系统函数＿C ＿⎩⎨⎧<>=⎩⎨⎧><==--=-20 020 )(H )( 20 020 )(H )( 3)(H )( )1()1()(H )(3 33ωωωωωωωωωωωωωωj j j j e j D e j C e j B e j A ；；；U答：（C ）3. 对于一个LTI ，如果激励f 1(t)对应响应是)(3t U e t -, 激励f 2(t)对应响应是t 3sin ，则激励f 1(t)+5f 2(t)对应响应是＿t t U e t 3sin 5)(3+-＿＿；则激励3f 1(t+1)+5f 2(t-3)对应响应是＿)3 (3sin 5)1(33-++--t t U e t ＿＿。
4. 已知},2,2,2,2{01)( --=n f ，}32,8,4,2,1{)(2↑=n f ，则=+)2()1(21f f ＿10＿，用)(n δ表示)3(32)2(8)1(4)(2)1()(2-+-+-+++=n n n n n n f δδδδδ＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
5. }2,8,4{}3,1,2,3{11----*＝＿{12,32,14,-8,-26,-6}-2＿＿，}2,1,0{}5,3,6{00*＝＿{0,6,15,11,10}0＿＿ 6. （课本P152 例4-17）已知)(t f 的象函数ss s s s F 5323)(23+++=，则)0(+f ＝＿＿0＿；)(∞f ＝＿2/5＿＿。
信号与系统》期末试卷与答案
信号与系统》期末试卷与答案信号与系统》期末试卷A卷班级：__________ 学号：_________ 姓名：_________ 成绩：_________一．选择题（共10题，20分）1、序列x[n] = e^(j(2πn/3)) + e^(j(4πn/3))，该序列的周期是：A。
非周期序列B。
周期 N = 3C。
周期 N = 3/8D。
周期 N = 242、连续时间系统 y(t) = x(sin(t))，该系统是：A。
因果时不变B。
因果时变C。
非因果时不变D。
非因果时变3、连续时间LTI 系统的单位冲激响应h(t) = e^(-4t)u(t-2)，该系统是：A。
因果稳定B。
因果不稳定C。
非因果稳定D。
非因果不稳定4、若周期信号 x[n] 是实信号和奇信号，则其傅立叶级数系数 a_k 是：A。
实且偶B。
实且为奇C。
纯虚且偶D。
纯虚且奇5、信号x(t) 的傅立叶变换X(jω) = {1，|ω|2}，则x(t) 为：A。
sin(2t)/2tB。
sin(2t)sin(4t)sin(4t)/πtC。
0D。
16、周期信号x(t) = ∑δ(t-5n)，其傅立叶变换X(jω) 为：A。
∑δ(ω-5)B。
∑δ(ω-10πk)C。
5D。
10πjω7、实信号 x[n] 的傅立叶变换为X(e^jω)，则 x[n] 奇部的傅立叶变换为：A。
jRe{X(e^jω)}B。
Re{X(e^jω)}C。
jIm{X(e^jω)}D。
Im{X(e^jω)}8、信号 x(t) 的最高频率为 500Hz，则利用冲激串采样得到的采样信号 x(nT) 能唯一表示出原信号的最大采样周期为：A。
500B。
1000C。
0.05D。
0.0019、信号 x(t) 的有理拉普拉斯共有两个极点 s = -3 和 s = -5，若 g(t) = e^(xt)，其傅立叶变换G(jω) 收敛，则 x(t) 是：A。
左边B。
右边C。
双边D。
不确定10、系统函数 H(s) = (s+1)/s，Re(s)。
(完整word版)信号与系统期末考试试题(有答案的)
信号与系统期末考试试题一、选择题（共10题，每题3分 ，共30分，每题给出四个答案，其中只有一个正确的）1、 卷积f 1(k+5)*f 2(k-3) 等于 。
（A ）f 1(k)*f 2(k) （B ）f 1(k)*f 2(k-8)（C ）f 1(k)*f 2(k+8)（D ）f 1(k+3)*f 2(k-3)2、 积分dt t t ⎰∞∞--+)21()2(δ等于 。
（A ）1.25（B ）2.5（C ）3（D ）5 3、 序列f(k)=-u(-k)的z 变换等于 。
（A ）1-z z （B ）-1-z z（C ）11-z （D ）11--z4、 若y(t)=f(t)*h(t),则f(2t)*h(2t)等于 。
（A ）)2(41t y （B ）)2(21t y （C ）)4(41t y （D ）)4(21t y 5、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —t u(t)时，系统的零状态响应y f (t)等于（A ）(-9e -t +12e -2t )u(t) （B ）(3-9e -t +12e -2t )u(t)（C ）)(t δ+(-6e -t +8e -2t )u(t) （D ）3)(t δ +(-9e -t +12e -2t )u(t)6、 连续周期信号的频谱具有（A ） 连续性、周期性 （B ）连续性、收敛性 （C ）离散性、周期性 （D ）离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于（A ） 1（B ）2（C ）3（D ）4 8、序列和()∑∞-∞=-k k 1δ等于（A ）1 (B) ∞ (C) ()1-k u (D) ()1-k ku9、单边拉普拉斯变换()se s s s F 2212-+=的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D 10、信号()()23-=-t u tet f t的单边拉氏变换()s F 等于()A ()()()232372+++-s e s s ()()223+-s e B s()()()2323++-s se C s ()()332++-s s e D s二、填空题（共9小题，每空3分，共30分）1、卷积和[（0.5）k+1u(k+1)]*)1(k -δ=________________________2、单边z 变换F(z)=12-z z的原序列f(k)=______________________ 3、已知函数f(t)的单边拉普拉斯变换F(s)=1+s s，则函数y(t)=3e -2t ·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、单边拉普拉斯变换ss s s s F +++=2213)(的原函数f(t)=__________________________ 6、已知某离散系统的差分方程为)1(2)()2()1()(2-+=----k f k f k y k y k y ，则系统的单位序列响应h(k)=_______________________7、已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=2)()(t dx x f t y 的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为()()()()()t f t f t y t y t y +=++''''52该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ，=k t 22三、（8分）四、（10分）如图所示信号()t f ，其傅里叶变换()()[]t f jw F F =，求（1） ()0F （2）()⎰∞∞-dw jw F六、（10分）某LTI 系统的系统函数()1222++=s s s s H ，已知初始状态()(),20,00=='=--y y 激励()(),t u t f =求该系统的完全响应。
信号与系统期末考试题库及答案
信号与系统期末考试题库及答案1.以下信号的分类方法不正确的选项是〔 A 〕： A 、数字信号和离散信号 B 、确定信号和随机信号 C 、周期信号和非周期信号 D 、因果信号与反因果信号2.以下说法正确的选项是〔 D 〕：A 、两个周期信号x (t )，y (t )的和x (t )+y(t )一定是周期信号。
B 、两个周期信号x (t )，y (t )的周期分别为2和2，那么其和信号x (t )+y(t ) 是周期信号。
C 、两个周期信号x (t )，y (t )的周期分别为2和π，其和信号x (t )+y(t )是周期信号。
D 、两个周期信号x (t )，y (t )的周期分别为2和3，其和信号x (t )+y(t )是周期信号。
3.以下说法不正确的选项是〔 D 〕。
A 、一般周期信号为功率信号。
B 、 时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。
C 、ε(t )是功率信号；D 、e t 为能量信号;f (t )变换为〔 A 〕称为对信号f (t )的平移或移位。
A 、f (t –t 0) B 、f (ｋ–k 0) C 、f (at ) D 、f (-t )f (t )变换为〔 A 〕称为对信号f (t )的尺度变换。
A 、f (at ) B 、f (t –k 0) C 、f (t –t 0) D 、f (-t )6.以下关于冲激函数性质的表达式不正确的选项是〔 B 〕。
A 、)()0()()(t f t t f δδ=B 、()t aat δδ1)(=C 、)(d )(t tεττδ=⎰∞- D 、)()-(t t δδ=7.以下关于冲激函数性质的表达式不正确的选项是〔 D 〕。
A 、⎰∞∞-='0d )(t t δ B 、)0(d )()(f t t t f =⎰+∞∞-δC 、)(d )(t tεττδ=⎰∞- D 、⎰∞∞-=')(d )(t t t δδ8.以下关于冲激函数性质的表达式不正确的选项是〔 B 〕。
《信号与系统》考试试题及参考答案
《信号与系统》期末考试姓名 学号 班级 成绩一、选择及填空（20分 每题2分）：1. 以下系统，哪个可进行无失真传输＿B ＿ωωϕωωωδωωωωωωωω-6)( )1()(H )( )()(H )( 3)(H )( )1()1()(H )( 33=-===--=-且；；；D ej C e j B e j A j j j U答：(B)2. 下列哪一项是理想低通滤波器的系统函数＿C ＿⎩⎨⎧<>=⎩⎨⎧><==--=-20 020 )(H )( 20 020 )(H )( 3)(H )( )1()1()(H )(3 33ωωωωωωωωωωωωωωj j j j e j D e j C e j B e j A ；；；U答：（C ）3. 对于一个LTI ，如果激励f 1(t)对应响应是)(3t U e t -, 激励f 2(t)对应响应是t 3sin ，则激励f 1(t)+5f 2(t)对应响应是＿tt U e t 3sin 5)(3+-＿＿；则激励3f 1(t+1)+5f 2(t-3)对应响应是＿)3 (3sin 5)1(33-++--t t U e t ＿＿。
4. 已知},2,2,2,2{01)( --=n f ，}32,8,4,2,1{)(2↑=n f ，则=+)2()1(21f f ＿10＿，用)(n δ表示)3(32)2(8)1(4)(2)1()(2-+-+-+++=n n n n n n f δδδδδ＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
5. }2,8,4{}3,1,2,3{11----*＝＿{12,32,14,-8,-26,-6}-2＿＿，}2,1,0{}5,3,6{00*＝＿{0,6,15,11,10}0＿＿ 6. （课本P152 例4-17）已知)(t f 的象函数ss s s s F 5323)(23+++=，则)0(+f ＝＿＿0＿；)(∞f ＝＿2/5＿＿。
《信号与系统》期末试题1(含答案)
4
6
2
低抽样频率为
（A）
A、 6Hz B、 8Hz
C、10Hz
D、 12Hz
（6） 单边拉普拉斯变换 F (s) se s 的原函数是 s2 4
（D ）
A、 cos(2t) (t 1)
B、 cos[2(t 1)] (t)
C、 cos(2t 1) (t 1)
D、 cos[2(t 1)] (t 1)
（7） 离散序列 f1(k) {1,0,2,1}（ k 0,1,2,3）、 f2 (k) {3,7,2}（ k 1,0,1, ）设离散卷
积和 y(k) f1(k) f2 (k) ，则 y(2)
（B ）
A、8
B、17
C、11
D、2
（8） 某离散信号的 z 变换为 F (z) z2 2z ，已知该序列为右边序列，则该序列的收 z2 2z 3
作出
f2 (t)
的导数
df2 (t) dt
的波形；
（3） 利用卷积积分的性质，作出 f1 (t) f2 (t) 的波形。
（D ）
1 f1(t)
1 0
1
t
f2 (t) 1
解
t
1 f1(t)dt
1 0 1
t
1 0 1 t
f
2
(t
)
1
1 0 1 t
2
f1(t) f2 (t) 1
0
2t
期末考试试题
第 1-3 页
s
2
3
进行 laplace 反变换可得：
yzs (t)
(3 2
e t
2e 2t
1 e3t ) (t) 2
3. 全响应：
全响应为
09级信号与系统期末B卷
姓名 学号 专业： 班级 任课教师： 密 封 线仰恩大学2010--2011学年第二学期期末考试试题信号与系统 试卷 (B) (闭卷)适用班级:09级电子信息,09通信工程（共2页，第1页）（只能用函数计算器，不许使用学习机、手机。
作弊开除）一、填空题（共15个空，每空2分，共30分)1. 非周期信号，在有限区间有值，为 信号。
2. 线性时不变系统可由 线性微分方程式或差分方程式描述。
3. 离散时间虚指数信号的振荡频率 随角频率Ω0的增加而增加。
4. 初始状态单独作用于系统而产生的输出称为 响应，记作 。
5. 周期为N 的离散周期信号x [k ]号可以表达为一系列 信号加权叠加。
6. 信号周期T 0越小，w 0 ，谱线则 。
7. 实离散周期序列的幅度频谱为 ，相位频谱为 。
8. 抽样间隔T 越小， 可能越小，但是 该离散信号传输和处理的效率。
9. 信号的最高频率为f m ，则 f s = 为最小取样频率，称为Nyquist Rate.10. 已知x (t )的Fourier 变换是 X (j ω)，则t j e t x 0ω)( 的Fourier 变换是 。
11. 若 H (s )具有位于左半s 平面的共轭单极点，则冲激响应 h (t) 为按衰减指数变化的 。
二、问答题（每小题4分，共16分）1. 什么是因果系统？2. 什么是不稳定系统？3. 什么是瞬态响应yt(t) ？4. 判断一个系统是否为线性系统，应从哪三个方面来判断？三、计算题 (每小题5分，共20分) （要有计算过程步骤）1. ?)()]()([=-*--312t u t u t u2. 已知()sin x t t = ，求⎰∞∞-=-?)()(dt t t x δπ4 3. ?)()(=*-t u et u t 2 4. 求 )()(t u et 24-- 的 Laplace 变换。
信号与系统 试卷 (B) (闭卷) 适用班级:09级电子信息,09通信工程 （共2页，第2页）四、（12分）试求下面连续时间LTI 系统的零输入响应？（要有计算过程）五、画图题 (本大题共2小题，共14分)1. (7分)已知信号()f t 如图所示，试画出()(2)f t f t +-的波形图（要求转换过程）。
信号与系统课程考试样题及答案
《信号与系统》课程考试样题一、 填空题 （每空2分，共30分）1．线性系统是指同时满足 （1） 性和 (2) 性的系统。
2．连续时间系统的分析方法有 （3） 、 （4） 和 （5） 。
3． ＝ （6） 。
4．已知信号f(t)的带宽为△ω，则信号f(5t+3)的频带宽度为 （7） 。
5．f(t)的傅立叶变换为F(w)，则f(t)cos(ω0t)是频谱搬移，其傅立叶变换为 （8） 。
6．连续时间系统因果的时域条件是 （9） ，稳定的充要条件是 （10） 。
7．已知某离散系统激励为单位阶跃信号之零状态响应（阶跃响应）是g(n)，则其冲激响应h(n)＝ (11） 。
8．该序列的周期为 （12） 。
9．离散时间系统的基本运算单元有 （13） ， （14） ，和 （15） 。
二、选择题 （每个2分，共16分）1．下列叙述正确的有（ ）（A ）各种离散信号都是数字信号； （B ）各种数字信号都是离散信号； （C ）数字信号的幅度只能取1或0； （D ）将模拟信号采样直接得数字信号； 2．已知f(t) F(ω)，则y(t)=f(t)*δ(t+3)的频谱函数Y （ω）＝（ ） （A ）F(ω)e j3ω （B ）F(ω)e -j3ω （C ）F(ω) （D ）f(3)e j3ω 3．若f(t)代表已录制声音的磁带上的信号，则下列表述正确的是（ ） （A ） 2f(t)表示将此磁带的音量减小一倍播放； （B ） f(2t)表示将此磁带以二倍速度加快播放； （C ） f(2t)表示将此磁带放音速度降低一半播放； （D ） f(-t)表示将此磁带上信号延时播放产生的信号。
4．系统的冲激响应与（ ）（A ）输入激励信号有关 （B ）系统的结构有关 （C ）冲激强度有关 （D ）产生冲激时刻有关 5．已知022cos()()st u t LTs ωω+则000cos ()()t t u t t LT ω--（ ）0022220000000222200cos()()()cos()sin()()()st st s t s A eB s s s t t s seCD s s ωωωωωωωω--+++-++6．系统函数为23()56H s s s =++的因果系统属于（ ）系统。
信号与系统期末试题与解答
,考试作弊将带来严重后果！《 信号与系统 》试卷 A1. 考前请将密封线内各项信息填写清楚； 所有答案请直接答在试卷上(或答题纸上)； ．考试形式：闭卷；3分/每题，共21 分,单选题） 、下列哪个系统不属于因果系统（ A ）]1[][][+-=n x n x n y B 累加器 ∑-∞==nk k x n y ][][一LTI 系统，其)()(2t u e t h t-= D LTI 系统的)(s H 为有理表达式，ROC ：1->σ 、信号45[]cos()2jn x n n eππ=+，其基波周期为（A ）A 20B 10C 30D 5 、设]3[]1[2][][---+=n n n n x δδδ和]1[2]1[2][-++=n n n h δδ，][*][][n h n x n y =，求=]0[y （ B ）A 0B 4C ][n δD ∞、已知一离散LTI 系统的脉冲响应h[n]= δ[n]+2δ[n-1]-3δ[n-2]，则该系S[n]等于（B ）A δ[n ]+δ[n-1]-5δ[n-2]+ 3δ[n-3]B δ[n]+3δ[n-1]C δ[n]D δ[n]+ δ[n-1]-2δ[n-2]、信号)}2()2({-+--t u t u dt d的傅立叶变换是（ C ）A ω2sin 2jB )(2ωπδC -2j ω2sinD 、己知)(t x 的频谱函数⎩⎨⎧>=<==2rad/s ||0,2rad/s,||1,)X(j ωωω 设t t x t f 2cos )()(=，对信号)(t f C ）A 4 rad/sB 2 rad/sC 8 rad/sD 3 rad/s 、下列说法不正确的是（D ）当系统的频率响应具有增益为1和线性相位时，系统所产生的输出就是输入ωωj e j 2-信号的时移；B 取样示波器和频闪效应是欠采样的应用；C 对离散时间信号最大可能的减采样就是使其频谱在一个周期内的非零部分扩 展到将π-到π的整个频带填满；D 听觉系统对声音信号的相位失真敏感。
(完整版)《信号与系统》期末测验试题及答案(13P)
《信号与系统》测验一、单项选择题 ................................................. 1 二、简答题 ..................................................... 4 三、计算题 .. (8)一、单项选择题1．设系统的初始状态为()0t x ，输入为()t f ，完全响应为()t y ，以下系统为线性系统的是 D 。
(A) ()()()[]t f t x t y lg 02•= (B) ()()()t f t x t y 20+=(C) ()()()ττd f t x t y tt ⎰+=00 (D) ()()()()ττd f dtt df t x e t y tt t ⎰++=-00 2．一个矩形脉冲信号，当脉冲幅度提高一倍，脉冲宽度扩大一倍，则其频带宽度较原来频带宽度 A 。
（A ）缩小一倍 （B ） 扩大一倍 （C ） 不变 （D ）不能确定 3. 某系统的系统函数为)2)(5.0()(--=z z zz H ，若该系统是因果系统，则其收敛区为B 。
（A ）|z|<0.5 （B ）|z|>2 （C ）0.5<|z|<2 （D ）以上答案都不对 4. 下面关于离散信号的描述正确的是 B 。
(A) 有限个点上有非零值，其他点为零值的信号。
(B) 仅在离散时刻上有定义的信号。
(C) 在时间t 为整数的点上有非零值的信号。
(D) 信号的取值为规定的若干离散值的信号。
5．下列信号中为周期信号的是 D 。
t t t f 5sin 3sin )(1+= t t t f πcos 2cos )(2+=k k k f 2sin 6sin )(3ππ+= )(21)(4k k f kε⎪⎭⎫⎝⎛=()A )(1t f 和)(2t f ())(),(21t f t f c 和)(3k f())(2t f B 和)(3k f ())(1t f D 和)(3k f6. 连续周期信号的频谱具有 D 。
信号与系统期末考试试卷(有详细答案)
《信号与系统》考试试卷（时间120 分钟）院/系专业姓名学号题号一二三四五六七总分得分一、填空题（每小题 2 分，共20 分）得分1．系统的激励是e(t ) ，响应为r( t ) ，若满足de( t )r(t ) ，则该系统为线性、时不变、因果。
dt（是否线性、时不变、因果？）2 的值为5 。
2．求积分( t 1) ( t 2 )dt3．当信号是脉冲信号f(t) 时，其低频分量主要影响脉冲的顶部，其高频分量主要影响脉冲的跳变沿。
4．若信号f(t) 的最高频率是2kHz，则f( 2t) 的乃奎斯特抽样频率为8kHz 。
5．信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为一常数相频特性为_一过原点的直线（群时延）。
6．系统阶跃响应的上升时间和系统的截止频率成反比。
7．若信号的F(s)= 3s(s+4)(s+2) ，求该信号的F( j )j3(j +4)(j +2)。
8．为使LTI 连续系统是稳定的，其系统函数H ( s)的极点必须在S平面的左半平面。
19．已知信号的频谱函数是0）( ）F( ( ，则其时间信号f(t) 为0j ) sin( t)j。
10．若信号f(t) 的s 1F(s)，则其初始值 f ( 0 ) 1 。
2( s 1)得分二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。
（每小题 2 分，共10 分）《信号与系统》试卷第 1 页共7 页1. 单位冲激函数总是满足( t) ( t) （√）2. 满足绝对可积条件f(t)dt的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。
（×）3. 非周期信号的脉冲宽度越小，其频带宽度越宽。
（√）4. 连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。
（√）5. 所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。
（×）得分三、计算分析题（1、3、4、5 题每题10 分，2 题5 分，6 题15 分，共60 分）t1. 信号f ( t ) 2e u( t )1 ，信号1 0 t 1，f ，试求f1( t )* f2( t ) 。
(完整版)《信号与系统》期末试卷与答案
信号与系统》期末试卷 A 卷6、一周期信号x(t)(t n5n) ，其傅立叶变换 X(j) 为 A 2( 2k 5(2kA.) B.) 5k52k 51kC. 10(10 k)D.()k10 k107、一实信号 x[n]的傅立叶变换为 X(e j )，A. jRe{X(e j )}B. Re{X(e j )}C. jIm{ X(e j )}D.班级： 学号：姓名：成绩：1、 选择题(共 2j(3)nx[n] e 310题， 20 分)4j(3 )ne 3 ，该序列是2、 3、 4、 5、 A.非周期序列一连续时间系统 A. 因果时不变连续时间 A. 因果稳定若周期信号 A.实且偶LTI B. 周期 N 3C.周期 N 3/8y(t)= x(sint) ，该系统是B.因果时变C.非因果时不变D. 周期 N 24D. 非因果时变系统的单位冲激响应 4th(t) e 4tu(t 2) ，该系统是 AB.因果不稳定C.非因果稳定D. 非因果不稳定x[n] 是实信号和奇信号，则其傅立叶级数系数 B.实且为奇C.纯虚且偶a k 是DD. 纯虚且奇一信号 x(t)的傅立叶变换 X( j1，| | 0，| |222，则 x(t)为 sin2tA.2tB.sin2tsin4t C.4tsin4t D.t则 x[n] 奇 部 的 傅 立 叶 变 换 为Im{ X(e j )}8、一信号x(t) 的最高频率为500Hz，则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 D 。
A. 500B. 1000C. 0.05D. 0.0019、一信号x(t) 的有理拉普拉斯共有两个极点s=－3 和s=－5，若g(t) e4t x(t) ，其傅立叶变换G( j ) 收敛，则x(t)是 C 。
A. 左边B. 右边C. 双边D. 不确定10、一系统函数H(s)se，Re{ s} 1 ，该系统是 C 。
s1A. 因果稳定B. 因果不稳定C. 非因果稳定D. 非因果不稳定二．简答题(共 6 题，40 分)1、 (10 分)下列系统是否是( 1)无记忆；(2)时不变；(3)线性；(4)因果；(5) 稳定，并说明理由。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
t 1
为防止在抽样过程中发生频谱混叠，先对x(t)进行低通滤波。试确定理想低通滤波器的最高截 止频率Cm ； (2) 若理想低通滤波器HL(j)采用最高截止频率Cm，画出x(t)，x1(t)，y(t)的频谱。
北方工业大学试卷 共5页
第5页
Байду номын сангаас
第3页
四、（12分）某LTI离散时间系统的系统函数为 H ( z )
z2 。 ( z 0.5) 2
(1) 写出系统的差分方程，求出系统的单位样值响应。
n (2) 若系统的零状态响应 y ( n) 2( n 1)0.5 u ( n) ，求系统的输入序列x(n)；
(3) 定性画出系统的幅频响应特性 H (e
=
利用单位阶跃信号u(t)写出如下函数f(t)的表达式：f(t) ________________________________；并画出f (t)的波形。 f(t)
2 O 1 O 1 3
订
f (t)
t
t
(3) (5 n) ( n) =_____________,
k
(5 k ) (k ) =_________________________。
二、简答题（每题8分，共32分）
(1) 已知连续信号f(32t)的波形如下图所示，试画出f(2t)和f(t)的波形。
f(32t) 1 (1)
O 1 2 3
t
(2)
判断连续系统 r (t ) e(1 2t ) 的线性和时不变性。
(3)
n 已知离散LTI系统的单位样值响应 h( n) 0.6 u ( n) ，输入信号 x( n) ( n 2) u ( n 1) ，要
n
线
(4) 利用傅立叶变换的对称性，频谱 F ( ) 2u ( ) 的原函数为________________________。 (5) 若信号f(t)的傅里叶变换为F()，则信号f(2t1)的傅里叶变换为___________________， f(2t1)ejt的傅里叶变换为_______________________。 (6) 已知某因果系统函数 H ( s ) h() = _____________。 (7)
j
)。
北方工业大学试卷 共5页
第4页
五、（12分）如下抽样系统，已知抽样脉冲 T (t ) 1ms。输入信号x(t)如图所示， = 2ms。
n
(t nT
S
) ，TS
=
x(t) x(t) 理想低通 HL(j) x1(t) y(t) 1
T(t)
(1)
/2
O
/2
。 (1) 求该系统的系统函数H(s)，判断该系统是否稳定，并说明原因； (2) 若系统的起始条件y(0) = 1，y(0) =
0， x(t ) (t ) e t u (t ) ，求系统的零输入响应、零状态响应和全响应；并指出全响应中 的强迫响应分量和自由响应分量。
北方工业大学试卷 共5页
北方工业大学
序号
《信号与系统》课程期末考试试卷
2009年秋季学期
开课学院：信息工程学院 考试方式： 闭卷
A卷
考试时间：120 分钟
班级 题号 得分 阅卷人
装
姓名 一 二 三 四
学号 五 总分
一、填空（每空2分，共30分）
(1) 离散信号 x(n) 2 cos (2)
5 n 的周期是_________________。 3 7
( s 1) 2 ，单位冲激响应为h(t)，则h(0+) = ___________， s 2 3s 3
北方工业大学试卷 共5页
第1页
已知连续线性时不变系统 H ( s )
1 s 3
，输入信号 x(t ) cos t
2 cos 3t ，则 4 3
求用时域分析方法求解系统的零状态响应y(n)。
北方工业大学试卷 共5页 第2页
(4) 已知离散系统的系统函数 H ( z ) 输出方程。
2z 1 ，画出系统框图，并写出矩阵形式的状态方程和 z 4z 3
2
d 2 y (t ) dy (t ) dx(t ) 三、（14分）已知某因果连续时间LTI系统的微分方程是 5 6 y (t ) 4 x(t ) 2 dt dt dt
输出的稳态响应为________________________。 (8) 序列u(n2)的单边z变换为___________________，序列u(n+2)的单边z变换为_______________ ____。
n (9) 序列 2 u ( n 1) 的z变换为________________________，收敛域为_____________________。