测量系统分析报告GRR
测量系统分析--GRR

测量系统分析--“量具R&R”第一节概述测量数据的使用比以前更频繁﹑更广泛.例如,是否调整制造过程,现在普遍依据测量数据来决定.把测量数据或由它们计算出的一些统计量,与这一过程统计控制限值相比较,如果比较结果表明这一过程在统计控制之外,那么要做某种调整,否则,这一过程就允许运行而勿须调整.测量数据的另外一个用途是确定两个或多个变量之间是否存在某种显著关系.例如,人们可以推测一模制塑料料件的关键尺寸与浇注材料温度有关系.这种可能的关系可通过采用所谓回归分析的统计方法进行研究.即比较关键尺寸的测量结果与浇注材料温度的测量结果.应用以数据为基础的方法的益处,很大程度上决定于所用测量数据的质量.如果测量数据质量低,则这种方法的益处很可能低,类似地,如果测量数据的质量高,这一方法的益处也很可能高.为了确保应用测量数据所得到的益处大于它们所花的费用,就必须把注意力集中在数据的质量上.测量数据的质量测量数据质量与稳定条件下运行的某一测量系统得到的多次测量结果的统计特性有关.例如,假定用在稳定条件下运行的某测量系统,得到某一特性的多次测量结果.如果数据的质量会很低,以致这些数据是无用的. ,那么可以说这些测量数据的质量“高”,类似地,如果一些或全部测量结果“远离”标准值,那么可以说这些数据的质量“低”.低质量数据最普通的原因之一是数据变差太大.例如,测量某容器内的流体的容积,使用的测量系统可能对它周围的环境温度敏感,在这种情况下,数据的变差可能由于其体积的变化或周围温度的变化,使得解释这些数据更困难.因些这一测量系统是不太合乎需要的.一组测量的变差大多是由于测量系统和它的环境之间的交互作用造成的. 如果这种交互作用产生太大的变差,那么数据的质量会很低,以致这些数据是无用的. 例如,一个具有大量变差的测量系统,用来分析一个制造过程,可能是不恰当的,因为这一测量系统的变差,可能会掩盖制造过程中的变差.绝大部分变差是不希望有的,但也有一些重要的例外.例如这一变差是由于被测量特性的小变化而引起的,一般情况下这一变差被认为是有用的.一个测量系统对这种变化越灵敏,这个系统越良好.因为这一系统是一个较敏感的测量系统.如果数据的质量是不可接受的,则必须改进,通常是通过改进测量系统来完成,而不是改进数据本身.测量过程术语“测量”定义为“赋值给具体事物以表示它们之间关于特殊特性的关系”. 赋值过程定义为测量过程,而赋予的值定义为测量值.从这些定义得出,应将一种测量过程看成一个制造过程,它产生数字(数据)作为输出.术语量具: 任何用来获得测量结果的装置;包括用来测量合格/不合格装置.测量系统: 用来对被测特性赋值的操作、程序、量具、设备、软件以及操作人员的集合;用来获得测量结果的整个过程.测量系统的分辨力(或分辩率): 测量系统捡出并如实指示被测特性中极小变化的能力.重复性: 指同一个人使用同一量具,多次测量同一零件上的同一参数所测结果的变差.再现性: 指不同人使用同一量具,测量同一零件上的同一参数所测结果的变差.C重复性量具精确度: 指测量观察平均值与真实值(基准值)的差异。
GRR测量系统分析报告范例

GRR测量系统分析报告范例一、引言GRR(Gage Repeatability and Reproducibility)是用来评估测量系统可重复性和一致性的方法。
该方法主要应用于检测设备的校准和评估,以确保测量结果的准确性和稳定性。
本报告旨在分析并评估测量系统的GRR。
二、实验目的本次实验的目的是评估测量设备所引入的测量误差和变异性,并确定该设备能否在溢出范围内提供一致准确的测量结果。
三、实验方法1.选择合适的测量设备:确保测量设备满足所需测量范围和准确性的要求。
2.根据测量需求,选择一组典型样本。
制定测量方案,包括测量次数和不同操作员的参与。
3.实施测量:根据测量方案要求,分别由不同操作员对样本进行多次测量。
4.数据收集:记录每次测量的数值,并整理成数据表格。
5.数据分析:使用GRR统计方法,对测量数据进行分析。
四、实验结果与讨论通过对测量数据进行分析,我们得到了以下结论:1. 测量设备的可重复性(Repeatability):根据GRR方法的定义,可重复性是指在同一操作员对样本进行多次测量时,测量结果的变异性。
可重复性通过测量系统内部误差来衡量。
经过分析,我们得到了测量设备的可重复性为X%。
根据测量标准的要求,此可重复性符合要求。
2. 测量设备的一致性(Reproducibility):一致性是指在不同操作员对同一样本进行测量时,测量结果之间的变异性。
一致性通过测量系统间误差来衡量。
经过分析,我们得到了测量设备的一致性为X%。
根据测量标准的要求,此一致性符合要求。
3.单次测量误差:通过计算测量系统的稳定性指标,我们得到了单次测量误差为X。
根据测量标准的要求,此误差在可接受范围内。
五、结论与建议根据我们对测量系统的分析,结合测量标准的要求,我们得出以下结论:1.所评估的测量系统的可重复性和一致性符合要求,能够满足预期的测量准确性和稳定性。
2.单次测量误差也在可接受的范围内。
3.根据实验结果,我们建议对测量系统进行定期的校准和维护,以确保其性能的稳定性和准确性。
测量系统分析MSAGRR

测量系统分析MSAGRRMSA(测量系统分析)GRR(重复性与再现性)是一种统计方法,用于评估测量系统的准确性和可靠性。
在质量控制和过程改进中,准确的测量是确保产品或过程符合规范要求的关键因素。
本文将详细介绍MSAGRR的概念、目的、步骤以及如何进行数据分析。
一、MSAGRR概念MSAGRR是通过测量系统进行多次测量,并评估测量数据重复性和再现性的一种方法。
重复性是指在相同条件下,同一测量人对同一测量对象进行多次测量得到的结果的一致性;再现性是指在相同条件下,不同的测量人对同一测量对象进行多次测量得到的结果的一致性。
MSAGRR利用统计分析的方法确定各个组成部分对测量结果的影响程度,进而评估测量系统的准确性和可靠性。
二、MSAGRR目的MSAGRR的目的是评估测量系统的准确性和可靠性,确定测量系统是否适用于特定的质量控制和过程改进需求。
通过进行MSAGRR分析,可以识别出测量系统中的问题,进而采取相应的措施进行改进,以提高测量数据的准确性和可靠性。
三、MSAGRR步骤1.确定测量目标:明确需要评估的测量系统和测量对象,明确需要测量的特定要素。
2.收集数据:选择代表性的样本,并由多个测量人在相同条件下对同一测量对象进行多次测量。
每个测量人至少进行10次测量。
3.分析数据:使用统计软件和工具对收集到的数据进行分析,包括计算测量系统的重复性、再现性和误差等指标。
4.判断测量系统的准确性和可靠性:根据分析结果,判断测量系统是否满足质量控制和过程改进的要求。
5.提出改进建议:如果分析结果显示测量系统存在问题,需要提出相应的改进建议,并采取相应的措施进行改进,以提高测量系统的准确性和可靠性。
四、数据分析MSAGRR的数据分析主要包括以下几个方面:1.重复性和再现性分析:分别计算测量系统的重复性和再现性指标。
重复性指标通常采用方差分析方法进行计算,包括组内变异和总变异;再现性指标通常采用方差分析方法进行计算,包括测量人变异和总变异。
5.测量系统分析研究D-GRR报告

Ð Ð Ó §· Ö ± æ Â Ê = 1.41(PV R & R)
= 1.41×( 0.001 /0.009 ) = 0.2002
TV = R & R 2 + PV 2 = 0.009 2 +0.001 2
= 0.0090
判定:
%R&R≥30%,测量系统不可以接受!
分析 评价 措施
制定: 审核:
量具重复性和再现性报告
量具名称: 内径千分尺 量具编号: ND15211 量具量程: 120~135mm 来自数据表: 零件名称: 传动端轴承座 测量参数: 125 参数规格: ±0.01 分析日期: 2016.10.10 评价人员: A周长林B胡军良 C黄彪 评价人数量: 3 试验次数 r = 3 零件数量 n= % 总 变 差(TV) 10
= 100×( 0.009 / 0.009 ) = 99.01%
=
0.009 +0.000
2
3 4 5
= 0.0089 零件变差(PV)
6 7 8 9 10
% PV = 100 ´ ( PV / TV )
= 100×( 0.001 / 0.009 ) = 14.06%
PV = RP ´ K 3
= 0.0040 ´ 0.315 = 0.0013 总变差(TV)
R=
#####
X DIFF = 0.0003
RP = 0.0040
测 量 系 统 分 析 重复性-设备变差(EV)
% EV = 100 ´ ( EV / TV )
= 100×( 0.009 / 0.009 ) 试验次数 2 3 K1 0.8862 0.5908 = 99.01%
ห้องสมุดไป่ตู้
MSA量测系统分析中关于NDC与GRR的理解

MSA量测系统分析中关于NDC与GRR的理解在MSA(测量系统分析)中,NDC(Numerical Discrepancy Calculation)和GRR(Gage R&R)是两个重要的概念。
NDC是用来衡量测量系统的稳定性和准确性的指标,而GRR则是评估测量系统的可重复性和再现性的方法。
首先,NDC是通过对测量结果与参考值之间的差异进行计算得出的。
它可以反映出测量系统的偏差和变异程度,并判断测量系统是否足够准确。
NDC采用统计学方法分析数据,通过计算平均数、标准差、方差等指标来评估测量系统的精度。
通常情况下,NDC应该尽可能接近于零,这意味着测量系统与参考值之间的差异较小,测量结果较为准确和可靠。
在实际应用中,NDC和GRR通常会结合使用来对测量系统进行全面评估。
首先进行NDC分析,确定测量系统的准确性和稳定性,即测量结果与参考值之间的差异是否在可以接受的范围内。
然后进行GRR分析,评估测量系统的可重复性和再现性,并确定不同因素对测量结果的影响程度。
通过综合NDC和GRR的结果,可以得出测量系统的整体可靠性和稳定性。
需要注意的是,NDC和GRR的结果只能作为指导性的参考,不能完全代表测量系统的准确性和可靠性。
在实际应用中,还需要考虑其他因素如仪器的精度、操作员的技术水平等对测量结果的影响。
因此,在进行MSA量测系统分析时,需要综合考虑多种因素,以确保测量结果的准确性和可靠性。
总而言之,NDC和GRR是MSA量测系统分析中两个重要的概念。
NDC用来评估测量系统的稳定性和准确性,GRR则用来评估测量系统的可重复性和再现性。
两者结合使用可以对测量系统进行全面评估,为测量结果的准确性和可靠性提供指导。
GRR测量系统分析报告范例

GRR测量系统分析报告范例
摘要
本报告旨在评估GRR(一致性比率)测量系统的性能。
报告分析了GRR测量系统的重要功能,包括强制校准,可重复性测量,跨设备可比性测量以及可靠性和可验证性。
本报告由对GRR测量系统的实际实施情况进行评估。
最后,报告建议将GRR作为给定产品系列的产品质量保证。
关键词:GRR测量系统;可重复性测量;可靠性;可验证性;质量保证
1. Introduction
GRR(一致性比率)测量系统是一种测量系统,用于评估和监控批量制造过程中产品的一致性。
它是用于评估机加工过程中产品变动的重要工具,它的主要功能是强制校准,可重复性测量,跨设备可比性测量,可靠性和可验证性。
本报告将评估GRR测量系统的性能,以帮助客户使用GRR 测量系统来控制产品质量。
2.GRR测量系统
GRR测量系统实际上是一种计量学方法,用于评估指定批次产品的多个尺寸特征(如深度、宽度或高度)的变化程度。
GRR测量系统由一组量规(或称为测量设备)和一套软件组成。
GRR测量系统量规一般用于计算变量特征的测量值,同时软件程序用于计算多个变量特征的一致性比率,以评估产品的一致性水平,并判断产品是否合格。
视觉测量系统grr分析报告

视觉测量系统grr分析报告视觉测量系统是一种先进的测量技术,可以实现高精度的尺寸测量和外形分析。
为了保证视觉测量系统的可靠性和准确性,需要进行GRR(重复性与再现性)分析。
本报告基于对某视觉测量系统的GRR分析结果进行详尽描述和解读。
起首,我们对视觉测量系统进行了10次重复测量,并记录了每次测量的结果。
通过统计分析,我们得出了各个测量结果的平均值、标准偏差和范围。
结果显示,视觉测量系统对于相同尺寸的测量结果具有较好的重复性,平均值和标准偏差的差异较小。
接着,我们进行了再现性分析。
我们邀请了3名不同操作者对同一尺寸进行测量,并记录了各自的测量结果。
通过统计分析,我们得出了不同操作者之间的差异。
结果显示,再现性较好,不同操作者之间的测量结果差异较小。
综合重复性和再现性分析结果,我们得出了视觉测量系统的GRR值。
GRR值是衡量测量系统可靠性和准确性的重要指标。
结果显示,该视觉测量系统的GRR值较小,表示系统的重复性和再现性较好,可以满足实际应用的需求。
除此之外,我们还对视觉测量系统的测量误差进行了分析。
通过对比测量结果与已知标准值的差异,我们得出了系统的测量误差范围。
结果显示,系统的测量误差在可接受的范围内,可以满足实际应用的要求。
最后,我们对GRR分析结果进行了评估和总结。
通过对比分析,我们发现该视觉测量系统具有较好的重复性和再现性,测量误差在可接受范围内。
因此,该视觉测量系统可以可靠地用于尺寸测量和外形分析,在生产过程中发挥重要作用。
总之,本报告详尽介绍了对视觉测量系统进行的GRR分析结果。
通过该分析,我们可以评估该系统的可靠性和准确性,并为实际应用提供参考。
视觉测量系统的GRR分析是保证测量结果可靠的重要步骤,对于提高产品质量和生产效率具有重要意义。
GRR测量系统分析报告范例
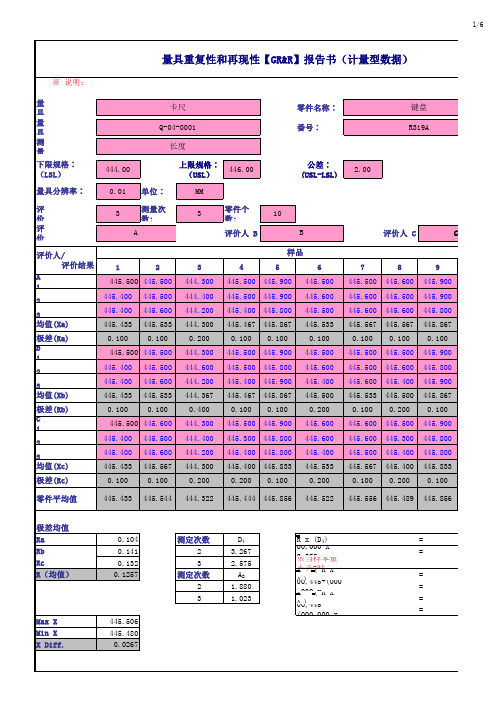
重复性和再现性 (R&R) R&R =
% R&R= 100(R&R/TV) % R&R= 14.55% 测量系统条件附可接受 % PV= 100(PV/TV) % PV= 98.94% 零件数 10 K3 0.3146 %TV=
EV2 +AV2 R&R = SQRT(D58^2+D64^2) R&R = 0.07434
445.433 0.100 2 445.400 3 445.400
1 445.500 445.500 445.500 445.600 445.533 0.100
445.500 445.900 445.500 445.800 445.400 445.900 445.467 445.867 0.100 0.100
26测量单元分析100evtv100evtolev14542228ev0125705908测定次数007426k10886205908av100avtv100avtolavav064098avsqrtabsd50ifd173i64h642d582f16h16评价人数000328k20707105231rr100rrtv100rrtolrrrr14552230rrsqrtd582d642测量系统条件附可接受rrpv100pvtv100pvtolpvpv989415164pvo3803146零件数pv0505461003146tv100tvtoltv15327tvsqrtd702d772tv0510894ndc141pvrrndcok均值图公差tol重复性设备变差ev再现性评价人变差av重复性和再现性rr零件变差pv总变差tv测量系统可靠的辨别的分级数ndc均值图中超出控制线的点应该至少在50以上
零件变差 (PV) PV = Rp x K3 PV = O38*0.3146 PV = 0.50546 总变差 (TV) TV = GRR2 +PV2 TV = SQRT((D70)^2+(D77)^2) TV = 0.510894
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
操作者之间
A&C
B&C
A&D
第三次 B&D
第一次
检验员C 检验员C()
第二次
第三次
C&D
操作者
Kappa
100.00%
80.00%
80.00%
60.00%
60.00%
40.00%
40.00%
20.00% 0.00%
0.00% A&B
0.00% A&C
0.00% B&C
0.00% A&D
标准
0
1
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
标准
0
1
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
两个人 三个人 四个人
总计
0 #DIV/0!
0 #DIV/0!
0 #DIV/0!
0.00% B&D
0.00% C&D
20.00% 0.00%
0.00% A
操作者
检验总数
匹配数
有效性
操作者与标准之 漏报率
A B C D
有效性
漏报率
100.00% 80.00% 60.00% 40.00% 20.00% 0.00%
0.00% A
0.00% B
0.00% C
0.00% D
100.00% 80.00% 60.00% 40.00% 20.00% 0.00%
误报率
0.00% A
0.00% B
0.00% C
0.00% D
格记录为1,不合格记录为0; 30,不得超过50;否则请重新设计算法; (≤5.00%)、误报率(≤10.00%);操作者之
操作之间的Kappa分析
C 总计
0 观测 期望
1 观测 期望
观测 期望
D与标准的交叉表
D 总计
0 观测 期望
1 观测 期望
观测 期望
标准
0
1
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
标准
0
1
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
属性要求
日期
检验员D
第一次
检验员D() 第二次 第三次
操作者与标准之间
A
B
C
标准值
1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 1 0
D
0.00%
0.00%
B 漏报率
0.00% C
0.00% D
误报率
100.00% 80.00% 60.00% 40.00% 20.00% 0.00%
A与B的交叉表
A
0
1
总计
观测 期望
A与C的交叉表
A
0
1
总计
观测 期望
B与C的交叉表
B
0
1
总计
观测 期望
A与D的交叉表
A
0
1
总计
观测 期望
项目
操作者之间
操作者与标准之间 有效性 漏报率 误报率
的Kappa分析
A与B的交叉表
观测 期望 观测 期望 观测 期望
A与C的交叉表
观测 期望 观测 期望 观测 期望
总计
0 #DIV/0!
0 #DIV/0!
0 #DIV/0!
总计
0 #DIV/0!
0 #DIV/0!
0 #DIV/0!
总计
0 #DIV/0!
0 #DIV/0!
0 #DIV/0!
A与标准的交叉表
A 总计
0 观测 期望
1 观测 期望
观测 期望
B与标准的交叉表
B 总计
0 观测 期望
1 观测 期望
观测 期望
C与标准的交叉表
车间
生产线
零件名称
量具名称
量具编号
测量特性
检验员A
样品 序号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
第一次
操作者对比 Kappa
100.00%
检验员A() 第二次
A&B
第三次
检验员B 检验员B()
总计
0 #DIV/0!
0 #DIV/0!
0 #DIV/0!
总计
0 #DIV/0!
0 #DIV/0!
0 #DIV/0!
总计
0 #DIV/0!
0 #DIV/0!
0 #DIV/0!
0.00% 0.00% 0.00% 0.00%
A
B
C
D
100.00% 80.00% 60.00% 40.00% 20.00% 0.00%
结论
备注
表单使用说明:
1、检测结果栏目中如果是合格记录为1,如果不合格记录为0,标准值中样件合格记录为1,不合格记录为 2、检验员至少需要2名,最多4名;每人至少检测2次,最多3次;样件数至少为30,不得超过50;否则请 3、测量结果可接受标准:评价人可接受标准为:有效性(≥80.00%)、漏报率(≤5.00%)、误报率(≤ 间Kappa值、操作者与标准之间Kappa值≥75.00% 5、备注栏使用:用于记录现场检查发现的相关问题及相关的建议.
C
0
1
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
D
0
1
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
操作者与标准之间的Kappa分析
总计
0 #DIV/0!
0 #DIV/0!
0 #DIV/0!
B与C的交叉表
观测 期望 观测 期望 观测 期望
A与D的交叉表
观测 期望 观测 期望 观测 期望
B
0
1
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
C
0
1
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
0
0
#DIV/0! #DIV/0!
