高数 函数的作图
高数课件3-4曲线的凹凸、拐点与函数的分析作图法-精选文档

C
yf (x )
P M N
yk x b
x
L
O
a
则曲线 y = f ( x) 有斜渐近线 y kx b
例
x3 求曲线 y 2 x 2x 3
的渐近线.
解
x3 令 f ( x) 2 x 2x 3
,因为
f ( x) x2 k lim lim 2 1, x x x x 2x 3
) (x)的符号决定,故曲线 y f (x 单调性可由 f 的凹凸 性与的 f (x)符号有关.
定理(曲线凹凸性的判定法)
设f(x)在[a, b]上连续, 在(a, b)内具有二阶导数 若在(a, b)内f (x)>0, 则f(x)在[a, b]上的图形是凹的 若在(a, b)内f (x)<0, 则f(x)在[a, b]上的图形是凸的
在区间 (,0] 和 [2/3,) 上曲线是凹的 在区间 [0,2/3] 上 曲线是凸的 点(0, 1)和(2/3, 11/27)是曲线的拐点
•讨论 曲线yx4是否有拐点? •提示 y4x 3, y12x 2 当x0时, y>0, 在区间(, )内曲线是凹的, 因此曲线无拐点
例
3 3 x x y 2 , x 2 x 3 ( x 3 )( x 1 )
二、曲线的渐近线
定义 若曲线 C 上动点 P 沿着曲线无限地远离原 点时,点 P 与某一固定直线 L 的距离趋于零, 则称直线 L 为曲线 C 的渐近线.
y
1.斜渐近线
定理 若 f ( x) 满足: f ( x) k; (1) lim x x (2) lim[ f ( x) kx] b ,
定义: 设函数 y f (x)在区间 ( a , b ) 内,曲线 弧位于其任意一点切线的上方,则称曲线在 ( a , b )
常见函数图像作图

(2)
(1)解 : f ( 3 ) 2 3 8 5, 22
f (1 ) 1 5,
f (1) 1 3 5 2,
f f (2) f (1) 2.
现在您正浏览在第17页,共44页。
学习案
2.作出下列函数的图象
(1)yx2(x Z,且 x2)
现在您正浏览在第18页,共44页。
5.函数的图象 对于函数的图象要会作图、识图、用图. 作函数图象有两种基本方法:一是描点法,二是图象变换法, 其中图象变换有平移变换、伸缩变换、对称变换.
重要结论:(1)若函数 y=f(x)满足 f(a+x)=f(a-x),即 f(x) =f(2a-x),则 f(x)的图象关于直线 x=a 对称. (2)若 f(x)满足 f(a+x)=f(b-x),则函数 f(x)的图象关于直线 x=a+2 b对称. (3)若函数 y=f(x)满足 f(x)=2b-f(2a-x),则该函数图象关 于点(a,b)成中心对称.
常见函数图像作图
现在您正浏览在第1页,共44页。
例2、旅行社为某旅游团包飞机去旅游,
其中旅行社的包机费为15000元,旅游
团中的每人的飞机票按以下方式与旅行社
结算:若旅游团的人数在30人或30人以 下,飞机票每张收费900元;若旅游 团的人数多于30人,则给与优惠,每
多1人,机票费每张减少10元,但旅游团
法一: 规律:在 x=1的右边看图象,图象越高
底数越小. 即图高底小 y
y loga1 x
01
y loag2 x
y loga3 x
x
y loag4 x
y loga5 x y loga6 x
法2:做直线y=1,观察与各图像交点横坐标即可知道底数大小。
高数数学必修一《5.4.3正切函数的性质与图像》教学课件

对称性
π
π
在每一个区间_________________上都是增函数
kπ
(
,0)(k∈Z)
对称中心________________
2
【即时练习】
π
1.函数y=tan (x+ )的定义域是(
4
π
A.{x|x≠- }
4
π
C.{x|x≠kπ- ,k∈Z}
4
π
B.{x|x≠ }
4
π
D.{x|x≠kπ+ ,k∈Z}
3π
|x|在(- ,
2
(2) 借 助 正 切 函 数 的 图 象 , 不 等 式 |tan x|≤ 3 的 解 集 是
π
π
{x|kπ- 3 ≤x≤kπ+ 3 ,k∈Z}
____________________.
解析:|tan x|≤ 3,则- 3≤tan x≤ 3,
π
π
则kπ- 3 ≤x≤kπ+ 3 ,k∈Z.
π
π
(3) 正 切 函 数 在 ( - + kπ , + kπ)(k∈Z) 上 递 增 , 不 能 写 成 闭 区
2
2
间.正切函数无单调减区间.
π
离为 3 .故选C.
2.函数f(x)=tan
π
π
( x+ )的单调区间是(
2
3
5
1
A.(- +2k, +2k)(k∈Z)
3
3
5
1
B.[- +2k, +2k](k∈Z)
3
3
5
1
C.(- +4k, +4k)(k∈Z)
3
3
5
1
D.[- +4k, +4k](k∈Z)
14高数(上) 3.4凹向、拐点、作图

1 1 , 20 是 拐 点 . 2 2
1 x 是拐点 2
补例4. 求y 3 x 4 4 x 3 1的拐点及凹凸的区间 .
解
2 y 36 x 24 x 36 x x 3 2 2 0 3 0 得 x1 0 , x2 令y · · 3 x 0时, y 0; 在区间(-∞,0]内曲线是凹的。 2 2 0 ; 在区间[0, ]上曲线是凸的。 0 x 时, y 3 3 2 x 时, y 0. 在区间[ 2 ,+∞)内曲线是凹的。 3 3 2 11 0 , 1、 , 是拐点. 3 27
一 曲线的凹向与拐点 1.凹凸性的定义 f x1 f x2
f x1
2
x x2 f 1 2 f
x2
f x1
f x1 f x2 2
f x2
x2 x1 设f x 在区间I上连续,
x2 x1 设f x 在区间I上连续,
如果我们接受某条信息时, 和我们头脑中已有的信息有密 切的联系,就好像往仓库中放 东西时作了许多的标记,寻找 时就比较容易。 可见,有效地提取信息, 是记忆的核心。而有效提取的关 键,是接收信息时“做好标记”。
§3.4
曲线的凹向与拐点 · 函数作图
x x2 f 1 2
另外
3 5 f , 2 8 3 5 辅助点 ( 1,0)、(0, )、( , ) 1 2 8 f 1 0 , f 0 1,
补例2. 画出y 解
1 2
x2 e 2 的图形.
1 定 义 域 ,,
y 1 2
x2 e 2
高数总结:基本初等函数图像及其性质
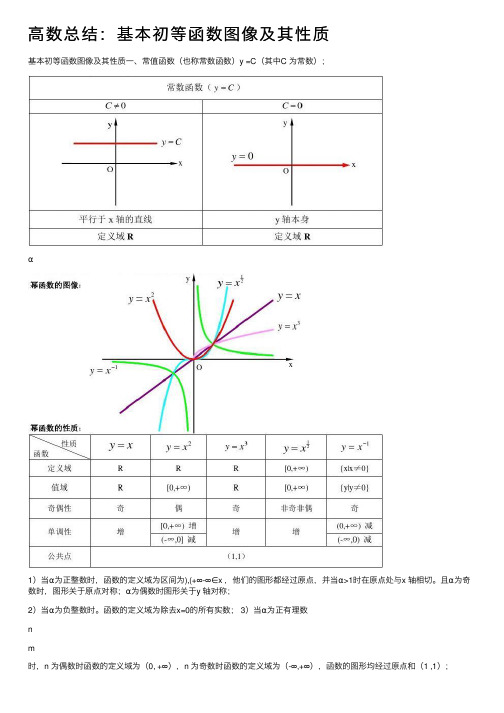
⾼数总结:基本初等函数图像及其性质基本初等函数图像及其性质⼀、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数n4)如果m>n 图形于x 轴相切,如果m5)当α为负有理数时,n 为偶数时,函数的定义域为⼤于零的⼀切实数;n 为奇数时,定义域为去除x=0以外的⼀切实数。
三、指数函数xa y =(x 是⾃变量,a 是常数且0>a ,1≠a ),定义域是R ;[⽆界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上⽅; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的⼤⼩⽐较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ?=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越⼤,xa y =的图像越靠近y 轴;b.2.当10<的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=?m n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m n m(2))1,,,0(11*>∈>==-n Z n m a a amnm nm yxf x xxx g ?=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [⽆界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式⼦N a log 叫做对数式。
人教版高数必修一第4讲:函数的表示方法(学生版)

函数的表示方法__________________________________________________________________________________ __________________________________________________________________________________1、 能根据不同需要选择恰当的方法(如图像法、列表法、解析法)表示函数;2、 了解简单的分段函数,并能简单应用;一、函数的常用表示方法简介: 1、解析法如果函数()()y f x x A =∈中,()f x 是用代数式(或解析式)来表达的,则这种表达函数的方法叫做解析法(公式法)。
例如,s =602t ,A =π2r ,2S rl π=,2(2)y x x =-≥等等都是用解析式表示函数关系的。
特别提醒:解析法的优点:(1)简明、全面地概括了变量间的关系;(2)可以通过解析式求出任意一个自变量的值所对应的函数值;(3)便于利用解析式研究函数的性质。
中学阶段研究的函数主要是用解析法表示的函数。
解析法的缺点:(1)并不是所有的函数都能用解析法表示;(2)不能直观地观察到函数的变化规律。
2、列表法:通过列出自变量与对应函数值的表格来表示函数关系的方法叫做列表法。
例如:初中学习过的平方表、平方根表、三角函数表。
我们生活中也经常遇到列表法,如银行里的利息表,列车时刻表,公共汽车上的票价表等等都是用列表法来表示函数关系的.特别提醒:列表法的优点:不需要计算就可以直接看出与自变量的值相对应的函数值。
这种表格常常应用到实际生产和生活中。
列表法的缺点:对于自变量的有些取值,从表格中得不到相应的函数值。
3、图象法:用函数图象表示两个变量之间的函数关系的方法,叫做图像法。
例如:气象台应用自动记录器描绘温度随时间变化的曲线,工厂的生产图象,股市走向图等都是用图象法表示函数关系的。
函数图像的画法

04 利用计算器或软件绘制函 数图像
使用计算器绘制函数图像
确定函数表达式
首先需要确定要绘制的函数表达式, 例如 y = x^2。
选择计算器功能
在计算器上找到绘制函数图像的功能, 通常在科学计算器上会有专门的图形 功能键。
输入函数表达式
将函数表达式输入到计算器的相应位 置。
开始绘图
按下绘图功能键,计算器会自动绘制 出该函数的图像。
函数图像的画法
contents
目录
• 函数图像的基本概念 • 常见函数的图像画法 • 函数图像的变换 • 利用计算器或软件绘制函数图像 • 函数图像的应用
01 函数图像的基本概念
函数图像的定义
函数图像
函数图像是将函数的每一个自变 量x值与对应的因变量y值,用点 表示出来,并将这些点用线连接 起来形成的图形。
二次函数的图像
总结词
抛物线形状
详细描述
二次函数图像是抛物线。根据抛物线的开口方向和顶点位置,二次函数可以分为开口向上、向下、向左和向右四 种类型。在直角坐标系中,二次函数的标准形式为 y = ax^2 + bx + c,其中 a、b、c 是常数,a 不等于 0。
三角函数的图像
总结词
周期性波形
详细描述
THANKS FOR WATCHING
感谢您的观看
缺点
需要一定的编程基础,对于初学者来说可能需要一定的学习 成本。另外,软件绘图可能需要较长时间才能掌握其各种功 能和操作技巧。
05 函数图像的应用
在数学中的应用
解析几何
函数图像可以用来表示解析几何中的曲线、曲面等,帮助理解几 何概念和性质。
微积分
函数图像在微积分中用于描述函数的单调性、极值、拐点等,有助 于理解函数的性质和变化规律。
高数A上册3-6

要点:
1. 曲线渐近线的求法 水平渐近线 ; 垂直渐近线. 2. 函数图形的描绘 按作图步骤进行.
令 y 0, 得 x 0,x 2 (驻点)
当 x 1, y不存在.
当 x 1,
( y的分界点)
y不存在.
( y的分界点)
x ( ,2) 2 (2,1) 1
f ( x )
(1,0)
0 (0, )
0
0
不存在 不存在 间断点
f ( x )
1 ) 2e
x2 2
0
极大值
1 2
(1,
0
拐点
1 ) 2e
1 lim ( x ) lim e x x 2
0, 得水平渐近线 y 0.
y
1
o
1
x
1 ( x ) e 2
x2 2
x2 1 例3 作函数 y 的图形. 或 y x 1 x 1 x 1
二、函数图形的描绘
变量之间的关系用函数来表达,作出函数的 图形就可以形象地看出变量之间的关系。 作图步骤:
1.确定函数的定义域 ,并考察其奇偶性及周期性 ; 2.讨论函数的单调性和极值 ;(用y判断)
4.确定曲线的渐近线; 5.描出某些特殊点,由此作出函数的图形 . 3.讨论曲线的凹凸性和拐点;(用y判断)
列表
例1 作函数 f ( x ) x 3 x 2 x 1 的图形.
解: 定义域 : (,), 无奇偶性及周期性.
f ( x) 3 x 2 2 x 1 (3 x 1)( x 1), 1 f ( x ) 6 x 2 6( x ). 3 1 令 f ( x ) 0, 得驻点 x , x 1. ( y的分界点) 3 1 令 f ( x ) 0, 得 x . ( y的分界点) 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x2 x
o
x1
x1 x2 2
x2 x
4
定理(凹凸判定法) 设函数
(1) 在 I 内
(2) 在 I 内 拐点:
在区间I 上有二阶导数
则
则
在 I 内图形是凹的 ;
在 I 内图形是凸的 .
定义2 连续曲线上有切线的凹凸分界点称为拐点 .
y
o
x
5
定理 (凹凸判定法) 设函数
(1) 在 I 内 则
22
6)绘图
x ( , 1) 1 (1,1)
y
铅直渐近线 斜渐近线 特殊点
1
无 定 义
(1, 3) 3
(3 , )
2
(极大)
0
(极小)
x 1 1 5 y x 4 4
( x 3) 2 y 4( x 1)
x
y
0 9 4
2 1 4
1
0 12 3
23
例4. 描绘函数
27
5、设函数
由参数方程
确定, 的凹凸区间及拐点。
求 解
的极值和曲线
令 由
时
时
时 ,列表
28
36 x( x 2 ) 3
(0,1) ( 2 , 11 ) 3 27
2) 求拐点可疑点坐标
11 , y 1 , y 对应 令 y 0 得 x1 0 , x2 2 1 2 27 3 2 3 3) 列表判别
x ( , 0) y y 凹
0 0 1
(0 , 2 ) 3
x 3 2 y 2 y 2 xy 0
x 3 2y y 2( x 1) 1 4 y 1 2 y 4 y 2 xy 0 y 2( x 1)
令 y 0 得 x 1, 3 ;
20
3) 判别曲线形态
x ( , 1) 1 (1,1) y 0 y y 2
f ( x) b k lim [ ] x x x f ( x) k lim x x) k x]
x (或 x )
16
例1. 求曲线
的渐近线 .
x3 解: y , lim y , ( x 3)(x 1) x3
21
y 1 1 又因 lim , 即 k x x 4 4 2 ( x 3 ) 1 1 x] b lim ( y x) lim [ x 4( x 1) 4 x 4 5x 9 5 lim 2 ( x 3 ) x 4( x 1) 4 y 4( x 1) 1 5 y x 为斜渐近线 ( x 3)( x 1) 4 4 y 4( x 1) 2 0 2 5) 求特殊点 x 2 1 y y 9 3 ( x 1 ) 4 4
10
x y x y 例5 求证 2 2
n
n
n
x 0, y 0, x y, n 1
证明: 因为不等式中同时含有 x, y 则用单调性证明
有困难,利用凹凸性证明
设 f (t ) t n t x, y 求证 f (t ) 在 (0, ) 是凹函数
f (t ) nt
n 1
f (t ) n(n 1)t
n2
0 t (0,)
f (t ) 是凹函数,必满足在 t (0,) 内取 x, y
n n x y x y 2 2
x y f ( x) f ( y ) f 2 n 2
解: 1) 定义域为 2) 求关键点 2 x 1 xe 2 , y 2
的图形. 图形对称于 y 轴.
1 y e 2
2 x 2
(1 x 2 )
令 y 0 得 x 0 ; 令 y 0 得 x 1
3) 判别曲线形态
x y y y
0 0
1 2
7
例2. 求曲线
的拐点。
2 3
x 解: y 1 3
x
,
y x
2 9
5
3
2 9 x
3 5
( , 0) 0 不存在 y y 凹 0
因此点 ( 0 , 0 ) 为曲线
(0 , )
凸
的拐点 .
8
例3. 求曲线 解: 1) 求 y
的凹凸区间及拐点。
y 12 x3 12 x 2 ,
例2. 描绘
2 y x 2 x x x 2 2) y 2 x 2 2 x 1 令 y 0 , 令 y 0 ,
解: 1) 定义域为
的图形. 无对称性及周期性.
1
1 2 3
3)
x ( , 0) y y y
0 0
(0 ,1)
在区间I 上有二阶导数
在 I 内图形是凹的 ;
(2) 在 I 内 证:
则 在 I 内图形是凸的 . 利用一阶泰勒公式可得
f (1 ) x1 x2 x1 x2 x1 x2 2 x1 x2 f ( x1 ) f ( ) f ( ) ) ( x1 ) 2 ! ( x1 2 2 2 2 x1 x2 x1 x2 f ( 2 ) x1 x2 x1 x2 2 f ( ) f ( x2 ) f ( ) ) ( x2 ) 2 ! ( x2 2 2 2 2 两式相加
y 2 为水平渐近线; 1 lim ( 2) , x 1为垂直渐近线. x1 x 1
15
2. 斜渐近线 定义5 若
(或 x )
( k x b)
斜渐近线 y k x b .
( k x b)
f ( x) b lim x[ k ]0 x x x f ( x) b lim [ k ]0 x x x
(或 x 1)
y x2
所以有铅直渐近线 x 3 及 x 1 f ( x) x2 又因 k lim lim 2 x x x x 2 x 3
3
1
2 x 2 3x b lim [ f ( x) x] lim 2 x x x 2 x 3
2
证明: 令 F ( x) sin x
x, 则 F (0) 0, F ( ) 0 2 2 F ( x) cos x
2
x.
F ( x)
F ( x) 是凸函数
0
F ( x) min F (0), F ( ) 0 (自证) 2 2 sin x x 即
y x 2 为曲线的斜渐近线 .
17
三、函数图形的描绘
步骤 : 1. 确定函数 期性 ; 的定义域 , 并考察其对称性及周 并求出 及 为 0 和不存在
2. 求
的点 ;
3. 列表判别增减及凹凸区间 , 求出极值和拐点 ; 4. 求渐近线 ; 5. 确定某些特殊点 , 描绘函数图形 .
18
从而三个拐点为
(1 , 1) , (2 3 , 1 3 ) , (2 3 , 1 3 ) 84 3 84 3 1 3 1 3 1 1 8 4 3 8 4 3 因为
2
2 3 1
3 1
所以三个拐点共线.
13
二、 曲线的渐近线
定义 3. 若曲线 C上的点M 沿着曲线无限地远离原点 时, 点 M 与某一直线 L 的距离趋于 0, 则称直线 L 为 曲线C 的渐近线 . 或为“纵坐标差” 例如, 双曲线
(2 , ) 3 0
2 3 11 27
凸
凹
2) 上 2 在 ( 0 , ( , 0 ) 上为凹 , 故该曲线在 及 ( 3 , ) 3 2 , 11 ) ( 点 ( 0 , 1 ) 及 均为拐点. 为凸 , 3 27
9
例4
证明: 当 0 x
2
时, 有 sin x
1
0
4 3
(1, 2)
2 ( 2 , ) 0
2 3
2
4)
(极大) 3 1 x y 2 2 3
(拐点)
(极小)
19
例3. 描绘方程
的图形.
( x 3) 2 , 定义域为 解: 1) y 4( x 1)
2) 求关键点 2( x 3) 4 y 4 y 4 x y 0
(极大)
(1, 3) 3 0 无 定
1
(3 , )
义
0
(极小)
4) 求渐近线
lim y , x 1 为铅直渐近线
x1
( x 3)( x 1) 2 ( x 3) 2 , y y , y 2 4( x 1) 4( x 1) ( x 1)3
(0 , 1)
1
0
1 2 e
(1, )
(极大)
(拐点)
24
y
1 2
e
x2 2
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
(拐点)
y
4) 求渐近线
lim y 0
x
1 2
y
1 2
e
x2 2
A
B
y 0 为水平渐近线
2( x 1)( x 2 3)( x 2 3) ( x 2 1)3
12
x 1 2( x 1)( x 2 3)( x 2 3) y 2 2 3 x 1 y ( x 1) 令 y 0 得 x1 1 , x2 2 3 , x3 2 3
