2013年中考数学压轴题全面突破之三:点的存在性(含答案)
点的存在性

配方得y ,顶点D(1,9). ---------3分
(2)假设满足条件的点 存在,依题意设 ,
由 求得直线 的解析式为 ,
它与 轴的夹角为 .
过点P作PN⊥y轴于点N.
依题意知,∠NPO=30°或∠NPO=60°.
∵PN=2,∴ON= 或2 .
∴存在满足条件的点 , 的坐标为(2, )和(2,2 ).-----------6分
(3)在对称轴右侧的抛物线上是否存在点P,使△PAC为直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
25.解:(1)∵抛物线 ∴顶点M的坐标为 .-------- 1分
(2)抛物线与 与x轴的两交点为A(-1,0),B(2,0).
设线段BM所在直线的解析式为 .
∴ 解得 ∴线段BM所在直线的解析式为 .--------- 2分
∴△AOD是等腰Rt△ ………………………………1分
∵∠AOE+∠BDC=∠BCD+∠BDC=90°
∴∠AOE=∠BCD
∴△AED≌△BDC
∴AE=DB=1
∴D(2,2),E(0,1),C(3,0) …………………………2分
则过D、E、C三点的抛物线解析式为: ……………3分
(2)DH⊥OC于点H,
∴2-x=2x-1,
∴x=1.
∴G(1,0) ……………………………………………5分
(3)由题意可知点P若存在,则必在AB上,假设存在点P使△PCG是等腰三角形
1)当点P为顶点,既CP=GP时,
易求得P1(2,2),既为点D时,
此时点Q、与点P1、点D重合,
∴点Q1(2,2) ……………………………………………6分
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
中考压轴题—存在性问题
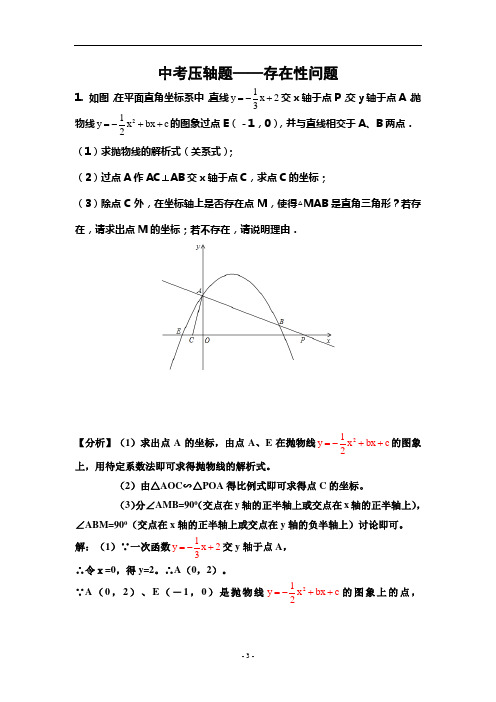
中考压轴题——存在性问题1. 如图,在平面直角坐标系中,直线1y x 23=-+交x 轴于点P ,交y 轴于点A .抛物线21y x bx c 2=-++的图象过点E (-1,0),并与直线相交于A 、B 两点. (1)求抛物线的解析式(关系式);(2)过点A 作AC ⊥AB 交x 轴于点C ,求点C 的坐标;(3)除点C 外,在坐标轴上是否存在点M ,使得△MAB 是直角三角形?若存在,请求出点M 的坐标;若不存在,请说明理由.【分析】(1)求出点A 的坐标,由点A 、E 在抛物线21y x bx c 2=-++的图象上,用待定系数法即可求得抛物线的解析式。
(2)由△AOC ∽△POA 得比例式即可求得点C 的坐标。
(3)分∠AMB=900(交点在y 轴的正半轴上或交点在x 轴的正半轴上),∠ABM=900(交点在x 轴的正半轴上或交点在y 轴的负半轴上)讨论即可。
解:(1)∵一次函数1y x 23=-+交y 轴于点A , ∴令x=0,得y=2。
∴A (0,2)。
∵A (0,2)、E (-1,0)是抛物线21y x bx c 2=-++的图象上的点,∴c 21b c 02=⎧⎪⎨--+=⎪⎩,解得3b 2c 2⎧=⎪⎨⎪=⎩ 。
∴抛物线的解析式是:213y x x 222=-++。
(2)∵一次函数交x轴于点P ,∴令y=0,得x=6。
∴P (6,0)。
∵AC ⊥AB ,OA ⊥OP ,∴△AOC ∽△POA 。
∴CO AO AO PO=。
∵AO=2,PO=6,∴CO 226=。
∴2CO 3=。
∴点C 的坐标为2,03⎛⎫- ⎪⎝⎭ 。
(3)存在。
设除点C 外,在坐标轴上还存在点M ,使得△MAB 是直角三角形,即∠AMB=900或∠ABM=900。
∵点B 是直线1y x 23=-+和抛物线213y x x 222=-++的交点, ∴21y x 2313y x x 222⎧=-+⎪⎪⎨⎪=-++⎪⎩,解得11x=37y 9⎧⎪⎪⎨⎪=⎪⎩。
2013中考数学压轴题(含答案)

1、如图12,已知直线12y x =与双曲线(0)k y k x =>交于A B ,两点,且点A 的横坐标为4. (1)求k 的值;(2)若双曲线(0)ky k x =>上一点C 的纵坐标为8,求A O C △的面积;(3)过原点O 的另一条直线l 交双曲线(0)ky k x =>于P Q ,两点(P 点在第一象限),若由点A B P Q ,,,为顶点组成的四边形面积为24,求点P 的坐标.解:(1)∵点A 横坐标为4 , ∴当 x = 4时,y = 2 .∴ 点A 的坐标为( 4,2 ).∵ 点A 是直线 与双曲线 (k>0)的交点 , ∴ k = 4 ×2 = 8 .(2) 解法一:如图12-1,∵ 点C 在双曲线上,y = 8时,x = 1∴ 点C 的坐标为 ( 1, 8 ) .过点A 、C 分别做x 轴、y 轴的垂线,垂足为M 、N ,得矩形DMON .S 矩形ONDM = 32 , S △ONC = 4 , S △CDA = 9, S △OAM = 4 .S △AOC = S 矩形ONDM - S △ONC - S △CDA - S △OAM = 32 - 4 - 9 - 4 = 15 .解法二:如图12-2,过点 C 、A 分别做x 轴的垂线,垂足为E 、F ,∵ 点C 在双曲线8y x =上,当y = 8时,x = 1 .∴ 点C 的坐标为 ( 1, 8 ).图12O x A y B x y 21x y 8=∵ 点C 、A 都在双曲线8y x =上 ,∴ S △COE = S △AOF = 4 。
∴ S △COE + S 梯形CEFA = S △COA + S △AOF .∴ S △COA = S 梯形CEFA .∵ S 梯形CEFA = 12×(2+8)×3 = 15 ,∴ S △COA = 15 .(3)∵ 反比例函数图象是关于原点O 的中心对称图形 ,∴ OP=OQ ,OA=OB .∴ 四边形APBQ 是平行四边形 .∴ S △POA = S 平行四边形APBQ = ×24 = 6 .设点P 的横坐标为m (m > 0且4m ≠),得P ( m , ) .过点P 、A 分别做x 轴的垂线,垂足为E 、F ,∵ 点P 、A 在双曲线上,∴S △POE = S △AOF = 4 .若0<m <4,如图12-3,∵ S △POE + S 梯形PEFA = S △POA + S △AOF ,∴ S 梯形PEFA = S △POA = 6 .∴ 18(2)(4)62m m +⋅-=.4141m8解得m = 2,m = - 8(舍去) .∴ P (2,4).若 m > 4,如图12-4,∵ S △AOF + S 梯形AFEP = S △AOP + S △POE ,∴ S 梯形PEFA = S △POA = 6 .∴18(2)(4)62m m +⋅-=,解得m = 8,m = - 2 (舍去) .∴ P (8,1).∴ 点P 的坐标是P (2,4)或P (8,1).2、如图,抛物线212y x mx n =++交x 轴于A 、B 两点,交y 轴于点C ,点P 是它的顶点,点A的横坐标是-3,点B 的横坐标是1.(1)求m 、n 的值;(2)求直线PC 的解析式;(3)请探究以点A 为圆心、直径为5的圆与直线 PC 的位置关系,并说明理由.(参考数:2 1.41≈,3 1.73≈,5 2.24≈) 解: (1)由已知条件可知: 抛物线212y x mx n =++经过A (-3,0)、B (1,0)两点. ∴ 903,210.2m n m n ⎧=-+⎪⎪⎨⎪=++⎪⎩ ……………………………………2分解得 31,2m n ==-. ………………………3分 (2) ∵21322yx x =+-, ∴ P (-1,-2),C 3(0,)2-. …………………4分设直线PC 的解析式是y kx b =+,则2,3.2k b b -=-+⎧⎪⎨=-⎪⎩ 解得13,22k b ==-. ∴ 直线PC 的解析式是1322yx =-. …………………………6分 说明:只要求对1322k b ==-,,不写最后一步,不扣分.(3) 如图,过点A 作AE ⊥PC ,垂足为E .设直线PC 与x 轴交于点D ,则点D 的坐标为(3,0). ………………………7分 在Rt△O CD 中,∵ O C =32,3O D =, ∴ 2233()3522C D =+=. …………8分∵ O A =3,3O D =,∴AD =6. (9)分 ∵ ∠C O D =∠AED =90o ,∠CD O 公用,∴ △C O D ∽△AED . ……………10分 ∴ OCC D AEAD =, 即335226AE =. ∴ 655AE =. …………………11分 ∵ 65 2.688 2.55> ,∴ 以点A 为圆心、直径为5的圆与直线PC 相离. …………12分。
中考数学压轴题“存在性”问题的解题策略(含解答)

数学“存在性”问题的解题策略存在性问题是指判断满足某种条件的事物是否存在的问题,这类问题的知识覆盖面较广,综合性较强,题意构思非常精巧,解题方法灵活,对学生分析问题和解决问题的能力要求较高,是近几年来各地中考的“热点”。
这类题目解法的一般思路是:假设存在→推理论证→得出结论。
若能导出合理的结果,就做出“存在”的判断,导出矛盾,就做出不存在的判断。
由于“存在性”问题的结论有两种可能,所以具有开放的特征,在假设存在性以后进行的推理或计算,对基础知识,基本技能提出了较高要求,并具备较强的探索性,正确、完整地解答这类问题,是对我们知识、能力的一次全面的考验。
【典型例题】 例1.223(1)9200x x m x m m -++-+=若关于的一元二次方程有两个实数根,390cos 5a b c ABC A B C C B ==又已知、、分别是△的∠、∠、∠的对边,∠°,且,3b a m Rt -=,是否存在整数,使上述一元二次方程两个实数根的平方和等于ABC c m △的斜边的平方?若存在,求出满足条件的的值,若不存在,请说明理由。
分析:这个题目题设较长,分析时要抓住关键,假设存在这样的m ,满足的条件有m 是整数,一元二次方程两个实数根的平方和等于Rt △ABC 斜边c 的平方,隐含条件判别式Δ≥0等,这时会发现先抓住Rt △ABC 的斜边为c 这个突破口,利用题设条件,运用勾股定理并不难解决。
解:在△中,∠°,∵Rt ABC C B ==9035cos ∴设a=3k ,c=5k ,则由勾股定理有b=4k , 33343==-=-k k k a b ∴,∴,∵ ∴,,a b c ===91215设一元二次方程的两个实数根为,x m x m m x x 2212319200-++-+=() 则有:,x x m x x m m 1212231920+=+=-+()∴x x x x x x m m m 122212212222312920+=+-=+--+()[()]()=+-736312m m 由,x x c c 1222215+==有,即73631225736256022m m m m +-=+-= ∴,m m 124647==-∵不是整数,应舍去,m =-647当时,m =>40∆∴存在整数m=4,使方程两个实数根的平方和等于Rt △ABC 的斜边c 的平方。
2013中考压轴题解析

2013中考压轴题解析解析:二次函数压轴题必有求解析式的一问,而且第二问大部分都是各种存在性的问题,如果出现了第三问,那么很可能就是拓展内容,当然也可能不是3个小题,但是只要没有拓展类的问题,就不能算是难题了。
(1)抛物线解析式中有两个参数b、c,但是只给了一个坐标点D,所以我们还需要一个点才能解出两个参数,刚好直线CD的解析式给出了,那么可得到点C的坐标(0,2),那么可直接获取c=2,将点D坐标代入抛物线解析式-9+3b+2=7/2b=7/2所以解析式y=-x²+7/2x+2(2)O、C、P、F围成平行四边形,那么已知OC//PF,那么只要令OC=PF即可,根据第一问可知OC=2,所以PF=2,而我们则需要表示出PF的长度,P的坐标可知(m,-m²+7/2m+2),而F的坐标则需要借助CD所在的直线,直线CD:y=1/2x+2则可知F(m,1/2m+2)那么PF的长度怎么表示呢?是P在F上面,还是F在P上面呢?(这一点必须考虑到)题中只说了P是y轴右侧的,所以势必会存在两种情况,因此我们用坐标表示的时候加个绝对值,即PF=|-m²+3m|=2这样得到两个方程m²-3m+2=0和m²-3m-2=0;第二个方程解出的m有一个负值,舍去;那么最终可得到3个m的值;(3)第三小题这种直线夹角问题,初中阶段势必要借助相似,而这一题又是让直接写出结果,所以过程不用说,一定不会少;直接借助题上的图形,假设P就在这个位置上(P在CD上方,当然还可能出现在CD下方);那么∠PCD=45°,有45°角,根据我们平时学的知识,唯有等腰直角三角形最适合,所以我们过P向CD做垂线,来构造等腰直角;如图,可知PG=CG,但是没啥用,因为条件太少,所以仍然不知道如何去解决P的位置,那么观察图形,我们做了PG⊥CD,同时构造了一个Rt△PFG,而这里还出现了个对顶角,∠PFG=∠CFE,如果过C向PE做垂线,垂线长度不仅=m,构造的三角形还能与△PFG相似,如图,利用对应角相等可得△CHF∽△PGF那么CH:PG=FH:FG其中CH=m,FH=m/2,FG=CG-CF=PG-CF而CF在Rt△CHF中,可知CF=m√5/2所以全部代入比例式中,可解出PG长度,而根据相似,或者勾股定理在△PGF中可得PF长度,那么PE=PF+FH+EH,即P的纵坐标可得,将P的横纵坐标代入抛物线解析式可解出m;第二种情况,P在CD下方的时候,如图,根据45°角可知绿色的CP线和第一种情况红色的CP关于CD对称,所以我们可以利用对称性找出绿色CP线的解析式,而不用非得再来一次相似,延长红色PG交绿色CP于K,如图,可知上方的P和绿色的K关于G对称,根据刚才的P的坐标,可以解出G的坐标(在△PGF中,过G向PF做垂线,得到G到x轴和y轴距离可得G坐标)利用中点坐标公式可求出K的坐标结合C和K的坐标获取直线CK的解析式联合抛物线解析式可得绿色P的坐标;(由于分号太多了,所以不提供计算过程)。
函数专题存在性问题(讲义)

中考压轴题之点的存在性技巧全攻略【例1】如图,在平面直角坐标系中,函数212y x =+的图象分别交x 轴、y 轴于A B 、两点.过点A 的直线交y 轴正半轴于点M ,且点M 为线段OB 的中点. (1)求直线AM 的函数解析式.(2)若点H 为坐标平面内任意一点,在坐标平面内是否存在这样的点H ,使以A B M 、、、H 为顶点的四边形是等腰梯形?若存在,请直接写出点H 的坐标;若不存在,请说明理由.【例 2】已知(1)A m -,与(233)B m +,是双曲线ky x=图象上的两个点. (1)求k 的值;(2)若点(10)C -,,则在反比例函数ky x=图象上是否存在点D ,使得以A B C D ,,,四点为顶点的四边形为梯形?若存在,求出点D 的坐标;若不存在,请说明理由.ABCxy111-1-O【例3】如图,已知抛物线)0(2≠++=acbxaxy的顶点坐标为Q()1,2-,且与y轴交于点C()3,0,与x轴交于A、B两点(点A在点B的右侧),点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.(1)求该抛物线的函数关系式;(2)当△ADP是直角三角形时,求点P的坐标;(3)在问题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.【中考真题1】已知二次函数2y ax bx c=++(0a≠)的图象经过点(10)A,,(20)B,,(02)C-,,直线x m=(2m>)与x轴交于点D.(1)求二次函数的解析式;(2)在直线x m=(2m>)上有一点E(点E在第四象限),使得E D B、、为顶点的三角形与以A O C、、为顶点的三角形相似,求E点坐标(用含m的代数式表示);(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出m的值及四边形ABEF的面积;若不存在,请说明理由.yxO【中考真题2】 在平面直角坐标系中,已知抛物线经过A )0,4(-,B )4,0(-,C )0,2(三点. (1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.(3)若点P 是抛物线上的动点,点Q 是直线x y -=上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.【测试 1】已知抛物线2y x bx c =++交x 轴于A (1,0)、B (3,0)两点,交y 轴于点C,其顶点为D .(1)求b 、c 的值并写出抛物线的对称轴;(2)连接BC ,过点O 作直线OE ⊥BC 交抛物线的对称轴于点E .求证:四边形ODBE 是等腰梯形;(3)抛物线上是否存在点Q ,使得△OBQ 的面积等于四边形ODBE 的面积的31?若存在,求点Q 的坐标;若不存在,请说明理由.。
2013年中考数学压轴题分类解析汇编三角形四边形存在性问题

三角形四边形存在性问题1. (2012海南省I13分)如图,顶点为P (4,-4)的二次函数图象经过原点(0,0),点A 在该图象上,OA 交其对称轴l 于点M ,点M 、N 关于点P 对称,连接AN 、ON(1)求该二次函数的关系式.(2)若点A 的坐标是(6,-3),求△ANO 的面积.(3)当点A 在对称轴l 右侧的二次函数图象上运动,请解答下列问题:①证明:∠ANM=∠ONM②△ANO 能否为直角三角形?如果能,请求出所有符合条件的点A 的坐标,如果不能,请说明理由.【答案】解:(1)∵二次函数图象的顶点为P (4,-4),∴设二次函数的关系式为()2y=a x 44--。
又∵二次函数图象经过原点(0,0),∴()20=a 044--,解得1a=4。
∴二次函数的关系式为()21y=x 444--,即21y=x 2x 4-。
(2)设直线OA 的解析式为y=kx ,将A (6,-3)代入得3=6k -,解得1k=2-。
∴直线OA 的解析式为1y=-x 2。
把x=4代入1y=x 2-得y=2-。
∴M(4,-2)。
又∵点M 、N 关于点P 对称,∴N(4,-6),MN=4。
∴ANO 1S 64122∆=⋅⋅=。
(3)①证明:过点A 作AH⊥l 于点H ,,l 与x 轴交于点D 。
则设A (20001x x 2x 4- ,), 则直线OA 的解析式为200001x 2x 14y=x=x 2x x 4-⎛⎫- ⎪⎝⎭。
则M (04 x 8-,),N (04 x -,),H (20014x 2x 4- ,)。
∴OD=4,ND=0x ,HA=0x 4-,NH=2001x x 4-。
∴()()()00022000000004x 44x 4x 4OD 4HA 4tan ONM=tan ANM===1ND x NH x x 4x x 4x +64x x 4---∠=∠==--- ,。
∴tan ONM=∠tan ANM ∠。
2013中考部分地市中考数学压轴题集(含答案)

2013中考压轴试题代数几何综合1、(2013年潍坊市压轴题)如图,抛物线c bx ax y ++=2关于直线1=x 对称,与坐标轴交于C B A 、、三点,且4=AB ,点⎪⎭⎫ ⎝⎛232,D 在抛物线上,直线是一次函数()02≠-=k kx y 的图象,点O 是坐标原点.()求抛物线的解析式;()若直线平分四边形OBDC 的面积,求k 的值.()把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线与直线交于N M 、两点,问在y 轴正半轴上是否存在一定点P ,使得不论k 取何值,直线PM 与PN 总是关于y 轴对称?若存在,求出P 点坐标;若不存在,请说明理由.答案:(1)因为抛物线关于直线x=1对称,AB=4,所以A(-1,0),B(3,0),由点D(2,1.5)在抛物线上,所以⎩⎨⎧=++=+-5.1240c b a c b a ,所以3a+3b=1.5,即a+b=0.5,又12=-a b ,即b=-2a,代入上式解得a =-0.5,b =1,从而c=1.5,所以23212++-=x x y . ()由(1)知23212++-=x x y ,令x=0,得c(0,1.5),所以CD//AB,令kx -2=1.5,得l 与CD 的交点F(23,27k ),令kx -2=0,得l 与x 轴的交点E(0,2k),根据S 四边形OEFC =S 四边形EBDF 得:OE+CF=DF+BE,即:,511),272()23(272=-+-=+k k k k k 解得 (3)由(1)知,2)1(21232122+--=++-=x x x y所以把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线的解析式为221x y -=假设在y 轴上存在一点P(0,t),t >0,使直线PM 与PN 关于y 轴对称,过点M 、N 分别向y 轴作垂线MM 1、NN 1,垂足分别为M 1、N 1,因为∠MPO=∠NPO,所以Rt △MPM 1∽Rt △NPN 1, 所以1111PN PM NN MM =,………………(1) 不妨设M(x M ,y M )在点N(x N ,y N )的左侧,因为P 点在y 轴正半轴上, 则(1)式变为NMN M y t y t x x --=-,又y M =k x M -2, y N =k x N -2,把2交(((D (点A(-1,0)、点B 是二次函数y=ax 2-2 的图象与x 轴的交点,a-2=0,a=2. 二次函数的解析式为y=2x 2-2;②点B 与点A(-1,0)关于直线x=0对称,点B 的坐标为(1,0); (2)∠BOC=∠PDB=90º,点P 在直线x=m 上,设点P 的坐标为(m,p ), OB=1, OC=2, DB= m-1 , DP=|p| ,①当△BOC ∽△PDB 时,OB OC = DP DB ,12= |p|m-1 ,p= m-12 或p = 1- m2,点P 的坐标为(m ,m-12 )或(m ,1- m2 );②当△BOC ∽△BDP 时,OB OC = DB DP ,12= m-1|p|,p=2m-2或p=2-2m, 点P 的坐标为(m ,2m-2)或(m ,2-2m );综上所述点P 的坐标为(m ,m-12 )、(m ,1- m2 )、(m ,2m-2)或(m ,2-2m );(3)不存在满足条件的点Q 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年中考数学压轴题全面突破之三:点的存在性(含答案)
中考数学压轴题全面突破之三•点的存在性
题型特点
存在性问题是指判断某种特殊条件或状态是否存在的问题,比如长度、角度、面积满足一定关系的点的存在性、特殊三角形的存在性
、特殊四边形的存在性等.
点的存在性问题常以函数为背景,探讨是否存在点,满足某种关系或构成某种特殊图形.比如线段倍分、平行垂直、角度定值、面积
成比例、全等三角形、相似三角形、特殊四边形等.
解题思路
解决点的存在性问题,遵循函数与几何综合中处理问题的原则.难点拆解
点的存在性问题关键是利用几何特征建等式.建等式的方式有:
①直接表达建等式.分析点存在所满足的特殊条件或关系,直接表
达线段长.
②转化表达建等式.如面积关系问题,转化面积关系为线段关系,
结合关键点所在图形的边角信息及几何特征,建等式.
③构造模型建等式.如角度间关系,需转化、构造将其放到三角形中
,再借助线段间关系建等式.
1.(2009湖北武汉)如图,抛物线经过A(﹣1,0),C(0,4)两点,
与x轴交于另一点B.
2. (2012江苏南通改编)如图,经过点A (0,﹣4)的抛物线
与x 轴
交于点B (﹣2,0)和点C ,O 为坐标原点. (1)求抛物线的解析式. (2)将抛物线
先向上平移个单位长度、再向左平移m
(m >0)个单位长度,得到新抛物线,若新抛物线的顶点P 在△ABC 内,求m 的取值范围.
(3)若点M 在y 轴上,且∠OMB +∠OAB =∠ACB ,求点M 的坐标.
A B C O x y
A
B C O x
y
3. (2011广东深圳)如图1,抛物线
(a ≠0)的顶点为C (1,4),
与x 轴交于A ,B 两点,与y 轴交于点D ,其中点B 的坐标为(3,0). (1)求抛物线的解析式.
(2)如图2,过点A 的直线与抛物线交于点E ,与y 轴交于点F ,其中点E 的横坐标为2,若直线PQ 为抛物线的对称轴,点G 为直线PQ 上一动点,则x 轴上是否存在一点H ,使以D ,G ,F ,H 四点为顶点的四边形周长最小?若存在,求出这个最小值及G ,H 两点的坐标;若不存在,请说明理由. (3)如图3,抛物线上是否存在一点T ,过点T 作x 轴的垂线,垂足为M ,过点M 作直线MN ∥BD ,交线段AD 于点N ,连接MD ,使△DNM ∽△BMD ?若存在,求出点T 的坐标;若不存在,请说明理由.
图2
Q
P F
E
O y
x
D C
B
A
图1A
B
C
D x
y
O 图3
A
B
D
x
y
O
4. (2012浙江温州)如图,过原点的抛物线
(m >0)与x 轴的另一
个交点为A .过点P (1,m )作直线PM ⊥x 轴于点M ,交抛物线于点B .记点B 关于抛物线对称轴的对称点为C (B ,C 不重合).连接CB ,CP . (1)当m =3时,求点A 的坐标及BC 的长. (2)当m >1时,连接CA ,问m 为何值时CA ⊥CP ?
(3)过点P 作PE ⊥PC 且PE =PC ,问是否存在m ,使得点E 落在坐标轴上?若存在,求出所有满足要求的m 的值,并求出相对应的点E 的坐标;若不存在,请说明理由.
A O y
x P
C
B
M x y O x
y
O
5. (2012辽宁沈阳)如图,已知在平面直角坐标系中,点A 的坐标为(﹣2,0),点
B 的坐标为(0,2),点E 为线段AB 上的一动点(点E 不与点A ,B 重合).以E 为顶点作∠OET =45°,射线ET 交线段OB 于点F ,
C 为y 轴正半轴上一点,且OC AB ,抛物线
的图象经过A ,C 两点.
(1)求此抛物线的函数表达式. (2)求证:∠BEF =∠AOE .
(3)当△EOF 为等腰三角形时,求点E 的坐标.
(4)在(3)的条件下,设直线EF 交x 轴于点D ,P 为(1)中抛物线上一动点,直线PE 交x 轴于点G ,在直线EF 上方的抛物线上是否存在一点P ,使得△EPF 的面积是△EDG 面积的()倍?若存在,请直接写出点P 的坐标;若不存在,请
说明理由.
y x
C
E
T
B F O
A
y x
C E T
B F
O
A
点的存在性
1.(1)抛物线的解析式为234
y x x
=-++.(2)点D关于直线BC对称的点的坐标为(0,1).
(3)点P的坐标为
266
525
⎛⎫
-
⎪⎝⎭
,.
2.(1)抛物线的解析式为y=1
2
x2-x-4.
(2)符合条件的m的取值范围为0<m<5
2
.(3)M(0,6)或M(0,-6).
3.(1)抛物线的解析式为y=-(x-1)2+4.
(2)存在,四边形DFHG的周长最小为225
+,点G坐
标为(1,1),点H坐标为(1
2
,0).
(3)存在,点T的坐标为(3
2,15
4
).
4.(1)A(6,0),BC=4.
(2)m=3
2
.
(3)当m>1时,
当点E在x轴上,m=2,点E的坐标是(2,0);
当点E在y轴上,m=2,点E的坐标是(0,4).
当0<m<1时,
当m=2
3时,点E的坐标是(4
3
,0).
5.(1)抛物线的表达式为y=-2x2-2x+22.
(2)证明略.
(3)E(-1,1)或E(-2,2-2).
(4)存在,P(0,22)或P(-1,22).。
