高铁梅老师的EVIEWS教学课件第十五章 定义和诊断检验
诊断试验-PPT

稳定
似然比
诊断试验
阳性 阴性 合计
金标准 实际有病 a(真阳性) c(假阴性) a+c
实际无病
合计
b(假阳性) a+b
d(真阴性) c+d
b+d
a+b+c+d
阳性似然比(positive likelihood ratio, +LR) 阴性似然比(negative likelihood ratio, -LR)
影像诊断 长期随访的结果 公认地综合临床诊断标准
选择研究对象
病例组 用金标准确诊‘有病’的病例,应包含典型的、
不典型病例,早、中、晚期病例,轻、中、重病例、 有和无并发症的患者 对照组
用金标准证实没有目标疾病的其他病例,特别 是与该病容易混淆的病例 正常人一般不宜纳入对照组
诊断试验的评价
先确定适宜的“金标准”,接着用它诊断适量的 目标疾病患者(病例组)和非患者(对照组),同时用待 评价诊断试验再对他们检测一次,最后将所获结果与 金标准诊断结果进行比较,并用一系列指标来评价诊 断试验对某病的诊断标准价值。
似然比
诊断试验
阳性 阴性 合计
金标准 实际有病 a(真阳性) c(假阴性) a+c
实际无病 b(假阳性) d(真阴性) b+d
合计
a+b c+d a+b+c+d
阳性似然比(+LR)=真阳性率/假阳性率 即病人中出现阳性结果的机会是非病人的多少倍 说明正确判断阳性的可能性是错判阳性可能性的倍数 表明试验结果呈阳性时患病与不患病机会的比例 +LR≥10,预示试验有较高的诊断价值
高铁梅老师的EVIEWS教学课件第二十二章状态空间模型和卡尔曼滤波

(22.19)
上面的两个方程称为预测方程(Prediction Equations)。
当得到新的观测值 yt,就能够修正 t 的估计a t t1,更新方程(Updating
Equations)是:
a t a t t1 Pt t1ZtFt1 ( yt Zt a t t1 ct ) Pt Pt t1 Pt t1ZtFt1Zt Pt t1 Ft Zt Pt t1Zt Ht
t
t
式中 Zt Zt B 1 。
(22.7) (22.8)
[例2] 对二阶自回归模型AR(2)
yt 1 yt1 2 yt2 t ,
t 1,,T
(22.9)
考虑两个可能的状态空间形式( k 1 , m 2)是
yt (1, 0)t
t
yt 2 yt
1
பைடு நூலகம்
12
1 0
t
1
10 t
换一种形式
a tn t Et (tn )
Ptn t Et [(tn a tn t )(tn a tn t )]
n 步向前预测:
~ytn t Et ( ytn ) ct Zt atn t
(22.29) (22.30)
(22.31)
相应的n 步向前预测的最小均方误差矩阵为:
Ftn t MSE(~ytn t ) Ztn Ptn t Ztn Ht
则对第 t +1期我们计算一步向前预测,对第t +2期计算2步向前预测,持续下去,
直到对第 t + n*期计算n*步向前预测。这表明对n步向前预测,我们只需初始化
时刻t +1的卡尔曼滤波,并且运用期内信息对期外进行滤波。然而对于动态预
测,要求计算所有的预测值,因为从预测期开始信息系统没有被更新。
eviews基本操作介绍

•
此外,还可以利用EViews的强大的命令功能和它的大量的程序处理语
言,进入命令窗口修改命令,并可以将计算工作的一系列操作建立成相应
的计算程序,并存储,从而可以通过直接运行程序来完成复杂的计算工作。
7
Eviews 统计分析 从入门到精通
二、Eviews的主窗口
软件安装后,启动Eviews程序,进入主窗口。
基本对象操作
1.建立对象
在建立对象之前必须打开工作文件集合而且工作文件窗口必须是激活的。然后选择主菜 单或工作文件菜单上的“Objects/ New Object”,EViews将会出现下面的窗口:
33
Eviews 统计分析 从入门到精通
对象名称 Equation Factor Graph Group LogL Matrix-Vector-Coef Model Pool Sample Series Series Link Series Alpha SSpace System Table Text ValMap VAR
可以用工作文件窗口菜单上的“Procs”或对象窗口工具栏上的“Procs”来选择过 程。
31
4. 对象类型
除了序列对象和方程对象外还有许多其他类型的对象,每种对象在对象集合 中都有一个特定的图标表示。对象集合虽然也是对象但对象集合没有图标,因 此工作文件和数据库不能放在其他的工作文件或数据库中。
32
中文含义 方程 因子 图形 序列组 对数似然函数 矢量系数矩阵 模型 面板数据 样本 序列 序列连接 α序列 状态空间模型 系统 表格 文本 数值映射 向量自回归
2. 对象窗口 在“Type of Object”中选择新建对象的类型,如选择Series,在“Name for Object” 中输入对象名。单击“OK” 会出现下面的窗口:
Eviews操作教程_完整版

Eviews操作教程_完整版1.EVIEWS基础 (3)1.1. E VIEWS简介 (3)1.2. E VIEWS的启动、主界⾯和退出 (3)1.3. E VIEWS的操作⽅式 (6)1.4. E VIEWS应⽤⼊门 (6)1.5. E VIEWS常⽤的数据操作 (15)2.⼀元线性回归模型 (24)2.1. ⽤普通最⼩⼆乘估计法建⽴⼀元线性回归模型 (24) 2.2. 模型的预测 (30)2.3. 结构稳定性的C HOW检验 (34)3. 多元线性回归 (39)3.1. ⽤OLS建⽴多元线性回归模型 (39)3.2. 函数形式误设的RESET检验 (45)4. ⾮线性回归 (48)4.1. ⽤直接代换法对含有幂函数的⾮线性模型的估计 (48) 4.2. ⽤间接代换法对含有对数函数的⾮线性模型的估计 (50) 4.3. ⽤间接代换法对CD函数的⾮线性模型的估计 (53)4.4. NLS对可线性化的⾮线性模型的估计 (55)4.5. NLS对不可线性化的⾮线性模型的估计 (58)4.6. ⼆元选择模型 (62)5. 异⽅差 (68)5.1. 异⽅差的⼽得菲尔德——匡特检验 (68)5.2. 异⽅差的WHITE检验 (72)5.3. 异⽅差的处理 (75)6. ⾃相关 (79)6.1. ⾃相关的判别 (79)6.2. ⾃相关的修正 (83)7. 多重共线性 (87)7.1. 多重共线性的检验 (87)7.2. 多重共线性的处理 (92)8. 虚拟变量 (94)8.1. 虚拟⾃变量的应⽤ (94)8.2. 虚拟变量的交互作⽤ (99)8.3. ⼆值因变量:线性概率模型 (101)9. 滞后变量模型 (106)9.1. ⾃回归分布滞后模型的估计 (106)9.2. 多项式分布滞后模型的参数估计 (111)10. 联⽴⽅程模型 (116)10.1. 联⽴⽅程模型的单⽅程估计⽅法 (116)10.2. 联⽴⽅程模型的系统估计⽅法 (120)2..1.Eviews基础1.1.Eviews简介Eviews:Econometric Views(经济计量视图),是美国QMS公司(Quantitative Micro Software Co.,⽹址为/doc/8e38170bbed126fff705cc1755270722192e59b1.html )开发的运⾏于Windows环境下的经济计量分析软件。
计量经济学经典eviews定义和诊断检验

计量经济学经典eviews 定义和诊断检验本章描述的每一检验过程包括假设检验的原假设定义。
检验指令输出包括一个或多个检验统计量样本值和它们的联合概率值(p 值)。
p 值说明在原假设为真的情况下,样本统计量绝对值的检验统计量大于或等于临界值的概率。
这样,低的p 值就拒绝原假设。
对每一检验都有不同假设和分布结果。
方程对象菜单的View 中给出三种检验类型选择来检验方程定义。
包括系数检验、残差检验和稳定性检验。
其他检验,如单位根检验(13章)、Granger 因果检验(8章)和Johansen 协整检验(19章)。
§15.1 系数检验一、Wald 检验——系数约束条件检验Wald 检验没有把原假设定义的系数限制加入回归,通过估计这一无限制回归来计算检验统计量。
Wald 统计量计算无约束估计量如何满足原假设下的约束。
如果约束为真,无约束估计量应接近于满足约束条件。
考虑一个线性回归模型:εβ+=X y 和一个线性约束:0:0=-r R H β,R 是一个已知的k q ⨯阶矩阵,r 是q 维向量。
Wald 统计量在0H 下服从渐近分布)(2q χ,可简写为: )())(()(112r Rb R X X R s r Rb W -'''-=--进一步假设误差ε独立同时服从正态分布,我们就有一确定的、有限的样本F-统计量q W k T u u q u u u u F /)/(/)~~(=-''-'= u~是约束回归的残差向量。
F 统计量比较有约束和没有约束计算出的残差平方和。
如果约束有效,这两个残差平方和差异很小,F 统计量值也应很小。
EViews 显示2χ和F 统计量以及相应的p 值。
假设Cobb-Douglas 生产函数估计形式如下:εβα+++=K L A Q log log log (1)Q 为产出增加量,K 为资本投入,L 为劳动力投入。
系数假设检验时,加入约束1=+βα。
eviews单位根检验解读

中有一种模型旳检验成果拒绝了零假设,就可以为时间序列是平稳旳。
13
分析数据旳平稳性软 件 操 作
在Pool对象,View/Unit Root Test,输入相应旳Pool序列名
填写序列 名
选择检验 措施
填写秩序
右边 全部 栏目 软件
自动 填写 无需 更改
填写模式,先做 序列图再选择
14
例10.4中I?旳水平变量旳全部措施旳单位根检验成果:
序图做出模式选择)。
秩序:水平(level)、一阶差分、二阶甚至高阶差分直至序列平稳为止。
备注:ADF检验是经过三个模型来完毕,首先从具有截距和趋势项旳模型开始,
再检验只含截距项旳模型,最终检验两者都不含旳模型。而且以为,只有三个模
型旳检验成果都不能拒绝原假设时,我们才以为时间序列是非平稳旳,而只要其
单位根检验
第一节 单序列单位根检验 第二节 面板数据单位根检验
1
第一节 单序列单位根检验
一 序列单位根检验在时间序列分析中旳地位 二 序列单位根检验软件有关操作
三 不同检验成果后续分析思绪
四 协整检验
2
一 序列单位根检验在时间序列分析中旳地位
时间序列总体分析思绪
时间序列
平稳性检验 原:不平稳
若是平稳序列
非平稳序列
单序列 多序列
考虑差分平稳
ARMA 多元回归分析 差分平稳I(d) 不平稳
单序列 多序列(同阶) 无规律分析终止
ARIMA
协整检验 原:不协整
协整 不协整
长久关系模型 分析终止
进一步考虑ECM(误差修正模型) 3
二 序列单位根检验软件有关操作
阐明 操作 成果
4
Eviews操作手册.
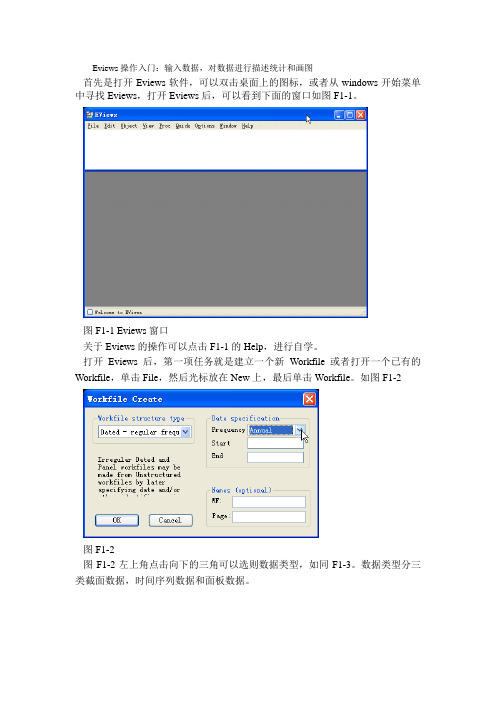
Eviews操作入门:输入数据,对数据进行描述统计和画图首先是打开Eviews软件,可以双击桌面上的图标,或者从windows开始菜单中寻找Eviews,打开Eviews后,可以看到下面的窗口如图F1-1。
图F1-1 Eviews窗口关于Eviews的操作可以点击F1-1的Help,进行自学。
打开Eviews后,第一项任务就是建立一个新Workfile或者打开一个已有的Workfile,单击File,然后光标放在New上,最后单击Workfile。
如图F1-2图F1-2图F1-2左上角点击向下的三角可以选则数据类型,如同F1-3。
数据类型分三类截面数据,时间序列数据和面板数据。
图F1-3图F1-2右上角可以选中时间序列数据的频率,见图F1-4。
图F1-4对话框中选择数据的频率:年、半年、季度、月度、周、天(5天一周或7天1周)或日内数据(用integer data)来表示。
对时间序列数据选择一个频率,填写开始日期和结束日期,日期格式:年:1997季度:1997:1月度:1997:01周和日:8:10:1997表示1997年8月10号,美式表达日期法。
8:10:1997表示1997年10月8号,欧式表达日期法。
如何选择欧式和美式日期格式呢?从Eviews窗口点击Options再点击dates and Frequency conversion,得到窗口F1-5。
F1-5的右上角可以选择日期格式。
图F1-5假设建立一个月度数据的workfile,填写完后点OK,一个新Workfile就建好了。
见图F1-6。
保存该workfile,单击Eviews窗口的save命令,选择保存位置即可。
图F1-6新建立的workfile之后,第二件事就是输入数据。
数据输入有多种方法。
1)直接输入数据,见F1-7在Eviews窗口下,单击Quick,再单击Empty group(edit series),直接输数值即可。
注意在该窗口中命令行有一个Edit+/-,可以点一下Edit+/-就可以变成如图所示的空白格,输完数据后,为了避免不小心改变数据,可以再点一下Edit+/-,这时数据就不能被修改了。
2024版艾梅乙教育课件

传播途径
艾滋病的传播途径主要包括性接触传播、 血液传播和母婴传播。其中,性接触传 播是最主要的传播途径,包括同性或异 性之间的无保护性行为。
2024/1/27
7
临床表现与诊断方法
临床表现
艾滋病病毒感染后,患者可能出现发热、头痛、乏力、淋巴结肿大等非特异性 症状。随着病情发展,患者可能出现机会性感染和恶性肿瘤等严重并发症。
艾梅乙教育课件
2024/1/27
1
contents
目录
2024/1/27
• 引言 • 艾滋病基本知识 • 梅毒基本知识 • 乙肝基本知识 • 艾梅乙在青少年中的影响 • 艾梅乙教育课件制作技巧 • 总结与展望
2
01
引言
2024/1/27
3
目的和背景
提高人们对艾梅乙的 认识和理解,增强防 范意识。
提供心理支持
针对感染艾梅乙的青少年提供心 理支持和辅导,帮助他们积极面 对疾病和治疗。
加强家庭和社会参与
鼓励家庭和社会积极参与青少年 艾梅乙感染的防治工作,共同为 青少年创造一个健康、安全的环
境。 19
06
艾梅乙教育课件制作技巧
2024/1/27
20
课件内容选择与组织
选择与艾梅乙相关的核心内容, 包括定义、症状、传播途径、 预防措施等。
25
未来发展趋势预测
教育内容综合化
未来的艾梅乙教育将更加注重知识、技能和情感态度价值观 的综合培养,以满足学生全面发展的需要。
教育资源均衡化
政府和社会各界将加大对艾梅乙教育的投入,推动优质教育 资源的均衡分布,让更多人享受到优质的教育服务。
2024/1/27
教育方式多样化
随着互联网和人工智能等技术的发展,艾梅乙教育方式将更 加多样化,如在线教育、虚拟现实等,以提高教育的趣味性 和实效性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LR = 2(Lr Lu )
2 下,LR统计量服从渐近 χ 分布,自由度等于约束条件数,即加入变量数。
Lr 和 Lu是约束和无约束约束回归(Gaussion)对数似然函数的最大值。在H 0
注意: 1. 遗漏变量检验要求在原始方程中和检验方程中观测值数相等。如果要 加入变量的任一序列与原方程样本相比,含有缺失观测值(当加入滞后变量 时这种情况常见),检验统计量将无法建立。 2. 遗漏变量检验可应用于线性LS,TSLS,ARCH,Binary, Ordered, Censored, Truncated, Count模型估计方程。只有通过列表法列出回归因子定 义方程而不能通过公式,检验才可以进行。 2、如何进行遗漏变量检验 选择View/Coefficient Tests/Omitted Variables—Likelihood Ration,在打开 的对话框中,列出检验统计量名,用至少一个空格相互隔开。
2
归因子数。 本例中,检验结果不能拒绝原假设,即添加变量不显著。
三、冗余(Redundant Variables)变量 冗余(Redundant Variables)变量
1、冗余变量检验原理 冗余变量检验可以检验方程中一部分变量的统计显著性。更正式,可以 确定方程中一部分变量系数是否为0,从而可以从方程中剔出去。原假设: 被检验变量系数为0。冗余变量检验可以应用于线性LS,TSLS,ARCH(仅 均值方程),Binary, Ordered, Censored, Truncated, Count模型估计方程。只有 以列表法列出回归因子形式,而不是公式定义方程,检验才可以进行。 2、如何进行冗余变量检验 选择View/Coefficient Tests/Redundant Variable—likelihood Ratio,在对话 框中,输入每一检验的变量名,相互间至少用一空格隔开。
§15.1
情况的检验。
系数检验
系数检验对估计系数的约束进行评价,包括对遗漏变量和冗余变量特殊
一、Wald检验——系数约束条件检验 Wald检验 检验——系数约束条件检验
1、Wald检验原理 Wald检验原理 Wald检验没有把原假设定义的系数限制加入回归,通过估计这一无限制 回归来计算检验统计量。Wald统计量计算无约束估计量如何满足原假设下的 约束。如果约束为真,无约束估计量应接近于满足约束条件。下面给出计算 Wald 检验统计量的一般公式。
log Q = A+α log L + β log K + ε
果如下:
(1)
利用美国主要金属工业企业的数据(27个企业的数据),C-D生产函数估计结
从结果看LogL和logK的系数和小于1,但为确定这种差异是统计相关的, 我们常进行有约束的Wald系数检验。选择View/Coefficient Tests/Wald-Coefficient Restrictions,在编辑对话框中输入约束条件。约束条件应表示为含有估计参数 和常数(不可以含有序列名)的方程,系数应表示为c(1),c(2)等等,除非在估 计中已使用过一个不同的系数向量。为检验 在对话框中输入下列约束: c(2) + c(3) = 1 单击ok,EViews显示Wald检验如下结果(原假设:约束条件有效 原假设:约束条件有效): 的规模报酬不变的假设, α + β =1
第十五章 定义和诊断检验
经验研究经常是一种相互影响的过程。这一过程从估计关系的定义开 始。选择定义常含有几个选择:变量,连接这些变量的函数,以及当数据 是时间序列时表示变量间关系的动态结构。 不可避免地,在初始定义的恰当性方面存在不确定性。一旦估计了方 程,EViews提供了评价方程定义质量的工具。随着改进,检验结果将影响 所选择的定义,这一过程将重复下去,直到方程定义恰当为止。 本章描述了在方程对象的View和Procs中关于定义检验统计量的多个菜 单。我们试图提供足够的统计方法来进行这些检验,但是实际考虑的许多 描述是不完全的,建议查阅标准统计和经济计量学参考资料。
log 2 L log 2 K log Q = β1 + β2 log L + β3 log K + β4 + β5 + β6 log Llog K + ε 2 2 β 检验约束条件: 4 = β5 = β6 = 0 。这个非线性模型的估计结果如下:
检验多个约束条件,应用逗号隔开约束条件。在方程对话框中选择 View/Coefficient tests/Wald Coefficient Restrictions。在Wald检验对话框中输入如 下约束条件:c(4)=0, c(5) = 0,c(6)=0,结果如下:
考虑一个一般非线性回归模型
y = f (β ) + ε
其中y和 是T 维向量, β是待估计参数的k维向量。对参数的任何约束可以 写为:
H0 : g(β) = 0
g是一个光滑函数 式计算:
g : Rk → Rq ,(对β 加入q个约束条件)。Wald统计量由下
1
g(b) g(b) W = Tg(b)′ V (b) g(b) b′ b T 为观测值个数,b是非限制参数估计向量。下式给出b的估计方差V:
下面描述的每一检验过程包括假设检验的原假设定义。检验指令输出包 括一个或多个检验统计量样本值和它们的联合概率值(p值)。p值说明在原 假设为真的情况下,样本统计量绝对值的检验统计量大于或等于临界值的概 率。这样,低的p值就拒绝原假设。例如,如果p值在0.05和0.1之间,原假设 在5%被拒绝而不是在1%水平。切记:对每一检验都有不同假设和分布结果。 例如,有些检验统计量有确切的有限的样本分布(常为t或F分布)。其它是 服从近似分布的大样本检验统计量。每一检验的内容都不同,将分别描述。 方程对象菜单的View中给出三种检 验类型选择来检验方程定义。包括系数 检验、残差检验和稳定性检验: 其它检验在其它章节讨论。它们包括单位根检验(13章)、Granger因果 检验(8章)和Johansen协整检验(19章)。
出了C-D生产函数的改进型,即取消了 α + β = 1的假定,允许要素的产出弹性 之和大于1或小于1,即承认研究对象可以是规模报酬递增的,也可以是规模报 酬递减的,取决于参数的估计结果。 即当资本与劳动的数量同时增长λ 倍时,产出量也增长 λ倍。1937年,提
Cobb-Douglas生产函数估计形式如下:
α + β =1
EViews显示F统计量和 χ 统计量及相应的P值。χ 2统计量等于F 统计量乘以
2
检验约束条件数。本例中,仅有一个约束条件,所以这两个检验统计量等价。 它们的p值表明我们可以确定地接受规模报酬不变的原假设。
下面考虑检验多个约束条件的情况。例如,改变前面的C-D生产函数为非 线性形式,我们估计一个如下形式的生产函数
2
§15.4 残差检验
EViews提供了对估计方程残差的序列相关,正态性,异方差性和自回归 条件异方差性检验。这些检验不是对所有定义都适用。
§15.4.1 相关图和Q—统计量 相关图和Q
显示直到定义滞后阶数的残差自相关性和偏自相关性。如果残差不存在序 如果残差不存在序 列相关,在各阶滞后的自相关和偏自相关值都接近于零。所有的Q 列相关,在各阶滞后的自相关和偏自相关值都接近于零。所有的Q-统计量不显 著 , 并且有大的P 值 。 在计算Q-统计量的概率时,要调整自由度来解释估计 并且有大的 P ARMA项。在方程菜单中,选择View/Residual Tests/Correlogram-Q-Statistics,显 示相关图和Q-统计量。在滞后定义对话框中,定义计算相关图时所使用的滞后 数。
2 g(b) g(b) V = Ts b b′ 1
,
u′u s = T k
2
u是无约束残差向量,s2是无约束残差方差。进一步,在原假设下,Wald
统计量服从渐近 χ 2 分布。q是 H0 下的约束数。
Wald检验可以应用到LS,TSLS,非线性LS等模型和系统估计的方程。 Wald检验是本章描述的唯一可应用到系统方法估计的方程的检验方法。 对于一个线性回归模型 一个线性约束:
例如:原始回归为 ls log(q) c log(L) log(k) 。输入:K L EViews将显示含有这两个附加解释变量的无约束回归结果,而且显示原 原 假设:新添变量系数为0 假设:新添变量系数为0 的检验统计量。输出的结果如下:
如果误差独立且服从正态分布,在 H0下,F统计量将有确定样本F分布, 分子自由度为添加回归因子数。分母自由度为小于总回归因子的观测值数。对 数似数比统计量就是LR检验统计量且渐进服从于χ 分布,自由度等于添加回
Q = AKα Lβ
Q为产出增加量,K为资本投入,L为劳动力投入。很容易推出参数α, β 分别是资本和劳动的产出弹性。那么由产出弹性的经济意义,应该有
0 ≤ α ≤1 , 0 ≤ β ≤1
在最初提出的C-D生产函数中,假定参数满足 α + β = 1 ,也就是假定研 究对象满足规模报酬不变。
A(λK)α (λL)β = λα+β AKα Lβ = λAKα Lβ
§15.4.2
平方残差相关图
显示直到所定义的滞后阶数的平方残差的自相关性和偏自相关性,计算出 相应滞后阶数的Ljung-Box统计量。平方残差相关图可以用来检查残差自回归条 件异方差性(ARCH)。如果残差中不存在ARCH,在各阶滞后自相关和偏自相 如果残差中不存在ARCH, 关应为0 关应为0,且Q统计量应不显著。可适用于使用LS,TSLS,非线性LS估计方程。 统计量应不显著。 显示平方残差相关图和Q-统计量,选择View/Residual Tests/Correlogram Squared Residual,在打开的滞后定义对话框,定义计算相关图的滞后数。
§15.4.3 直方图和正态检验
