13-3理想气体的等体过程和等压过程
合集下载
理想气体的热力学过程
6
dV d p 0 V p
式中
Cp CV
, 在温度变化不很大时,可以看作常量。
将上式积分,得
ln V + ln p = 恒量
pV γ 恒量 或 这个关系称为泊松 (S.D.Poisson)公式。
根据泊松公式和理想气体物态方程, 可以分别得到
TV γ 1 恒量
T γ pγ 1 恒量
Qp = H 气 H水
= (2676.3103 419.06103 ) Jkg1
= 2257.2103 Jkg1
16
17
经绝热过程压缩气体做的功:
CV 20.44J mol K
1
1
m 4 A CV T2 T1 4.70 10 J M
在等压过程中,系统从外界获得的热量,一部分用 以增大内能,一部分用以对外作功。 三、等温过程 (isothermal process) 等温过程 特征: 过程方程: 系统的温度保持恒定的过程。 T=0
p1V1 p2V2
p p1
T=恒量
恒温热源
1(p1,V1,T)
过程曲线:
内能增量:
等温线为等轴双曲线。
=1.40,可得:
p2 T2 T1 p 1
1 /
1 300 50
0.286
98.0K
19
例6 一定质量的理想气体先后经历 P 两个绝热过程即1态到2态,3态到4
态(如图所示)且T1=T3、T2=T4,在 1态与3态,2态与4态之间可分别连 接 两 条 等 温 线 。 求 证 :
考虑到 T1=T3,T2=T4,
T2 V1 1 2 T1 V2
理想气体等容过程定容摩尔热容理想气体等压过程定

V2 V
E1
W
E2
绝热压缩
p
p2
2( p2,V2,T2)
p1
o V2
( p1,V1,T1)
W1 V1 V
E2
E1
W
三 绝热线和等温线
p
T 常量
Q0
pA papT A C
B
o VA V VB V
绝热线的斜率大于 等温线的斜率.
绝热过程曲线的斜率
pV 常量
pV 1dV V dp 0
( dp dV
与外界无热量交换的过程
特征 dQ O
p
p1
1( p1,V1,T1)
热一律 dW dE 0
dW dE
p2
( p2,V2,T2 )
2
dE
m M
CV ,mdT
W
V2 V1
pdV
T2 T1
m M
CV
,m
dT
mo V1 dV V2 V
绝热的汽缸壁和活塞
由热力学第一定律有
W E
CV ,mdT
分离变量得 dV CV ,m dT
V
RT
dV V
1 dT 1 T
p
p1
1( p1,V1,T1)
Q0
p2
o V1
( p2,V2,T2 ) 2
V2 V
绝 V 1T 常量
热 方
pV
常量
程 p 1T 常量
绝热膨胀
p
p1
1( p1,V1,T1)
p2
( p2,V2,T2 )
W2
o V1
W
m M
CV ,m (T1
T2 )
若已知 p1,V1, p2 ,V2 及
物理课件4.4理想气体的等体过程和等压过程

特点上的比较
比较:等体过程气体体积不变,等 压过程气体压力不变
添加标题
添加标题
添加标题
添加标题
等压过程:气体压力不变,体积可 以变化
结论:等体过程和等压过程在特点 上有明显区别
理想气体等体过程和等 压过程的实例分析
等体过程的实例分析
等体过程的概念和特点 等体过程的实例:水银柱的升降实验 等体过程中气体状态的变化 等体过程在日常生活中的应用
07 理想气体等体过程和 等压过程的应用前景
添加章节标题
理想气体等体过程的定 义和特点
Байду номын сангаас
等体过程的定义
等体过程是指气体 体积不变的过程
温度是理想气体内 能变化的量度
等体过程中,气体 吸收的热量全部转 化为内能
等体过程中,气体 的状态参量如压强 和温度随时间发生 变化
体积不变:等体过程中气体的体积 始终保持不变。
实验验证的结果分析和讨论
实验数据整理:对实验数据进行整理,包括实验数据表格和图表 结果分析:对实验结果进行分析,包括数据变化趋势、误差分析等
讨论:对实验结果进行讨论,包括理想气体等体过程和等压过程的原理、影响因素等
结论:总结实验验证的结果,得出结论
理想气体等体过程和等 压过程的应用前景
在物理学中的应用前景
在航天工程中,理想气体等体过程和等压过程可以用来 研究航天器内部的热环境,对于航天器的设计和运行具 有重要意义。
在能源工程中,理想气体等体过程和等压过程可以用来 研究热能转换和传输过程中的效率和优化,对于提高能 源利用效率和减少能源浪费具有重要意义。
在工程和技术领域的应用前景
能源领域:利用理想气体等体和等压过程的理论,可以优化能源转换和储存效率,提高能源利用效 率。
理想气体的等体过程和等压过程

CV ,m
dQV dT
dQV CV ,mdT
单位 J mol1 K1
3
mol 理想气体
CV ,m
dQV dT
dQV dE CV ,mdT
由热力学第一定律
QV CV ,m (T2 T1) E2 E1
4
p
等 p2
体
升 压
p1
o
2 ( p2,V ,T2 )
1 ( p1,V ,T1)
V
V
摩尔热容比
Cp,m CV ,m
8
三个量:
W p(V2 V1) R(T2 T1) Qp C p,m (T2 T1)
E2 E1 CV ,m (T2 T1)
9
p
等 p ( p,V1,T1) ( p,V2,T2)
压
1
2
膨
W
胀 o V1
V2 V
Qp
E2
E1
W
p
等 p ( p,V2,T2) ( p,V1,T1)
压2
1
压
W
缩 o V2
V1 V
Qp E1
W
E2
10
四 比热容
热容
C dQ dT
比热容
c dQ C mdT m
11
p
等 p1
体
降 压
p2
o
1( p1,V ,T1)
2( p2,V ,T2 )
V
V
QV
E1
E2
E1
QV
E2
5
二 等压过程 摩尔定压热容
特性 p 常量
过程方程 VT 1 常量 p
功 W p(V2 V1)
p ( p,V1,T1) ( p,V2,T2)
工程热力学第四章理想气体热力过程

详细描述
03
CHAPTER
等容过程
等容过程是指气体在变化的整个过程中,其容积保持不变的过程。
定义
特点
适用场景
气体在等容过程中,气体温度和压力会发生变化,但容积保持不变。
等容过程常用于高压、高温或低温等极端条件下的气体处理。
03
02
01
等容过程定义
在等容过程中,气体吸收的热量等于气体所做的功和气体温度升高所吸收的热量之和。
多变过程的具体形式取决于气体所经历的压力和温度的变化规律。
多变过程定义热力学第一定律 Nhomakorabea热力学第二定律
理想气体状态方程
热效率
多变过程的热力学计算
01
02
03
04
能量守恒定律,用于计算多变过程中气体吸收或释放的热量。
熵增原理,用于分析多变过程中气体熵的变化。
描述气体压力、体积和温度之间的关系,可用于多变过程的计算。
衡量多变过程能量转换效率的指标,通过比较输入和输出的热量来计算。
提高热效率的方法
优化多变过程参数,如压力和温度的变化规律,以减少不可逆损失和提高能量转换效率。
热效率与熵增的关系
根据熵增原理,不可逆过程会导致熵的增加,从而降低热效率。因此,减少不可逆损失是提高多变过程热效率的关键。
热效率计算公式
$eta = frac{Q_{out}}{Q_{in}}$,其中$Q_{out}$为输出热量,$Q_{in}$为输入热量。
计算公式
通过优化气体的初态和终态,以及选择合适的加热和冷却方式,可以提高等容过程的热效率。同时,也可以通过改进设备结构和操作方式来提高热效率。
提高热效率的方法
等容过程的热效率
04
CHAPTER
03
CHAPTER
等容过程
等容过程是指气体在变化的整个过程中,其容积保持不变的过程。
定义
特点
适用场景
气体在等容过程中,气体温度和压力会发生变化,但容积保持不变。
等容过程常用于高压、高温或低温等极端条件下的气体处理。
03
02
01
等容过程定义
在等容过程中,气体吸收的热量等于气体所做的功和气体温度升高所吸收的热量之和。
多变过程的具体形式取决于气体所经历的压力和温度的变化规律。
多变过程定义热力学第一定律 Nhomakorabea热力学第二定律
理想气体状态方程
热效率
多变过程的热力学计算
01
02
03
04
能量守恒定律,用于计算多变过程中气体吸收或释放的热量。
熵增原理,用于分析多变过程中气体熵的变化。
描述气体压力、体积和温度之间的关系,可用于多变过程的计算。
衡量多变过程能量转换效率的指标,通过比较输入和输出的热量来计算。
提高热效率的方法
优化多变过程参数,如压力和温度的变化规律,以减少不可逆损失和提高能量转换效率。
热效率与熵增的关系
根据熵增原理,不可逆过程会导致熵的增加,从而降低热效率。因此,减少不可逆损失是提高多变过程热效率的关键。
热效率计算公式
$eta = frac{Q_{out}}{Q_{in}}$,其中$Q_{out}$为输出热量,$Q_{in}$为输入热量。
计算公式
通过优化气体的初态和终态,以及选择合适的加热和冷却方式,可以提高等容过程的热效率。同时,也可以通过改进设备结构和操作方式来提高热效率。
提高热效率的方法
等容过程的热效率
04
CHAPTER
大学物理-热力学基础-课件
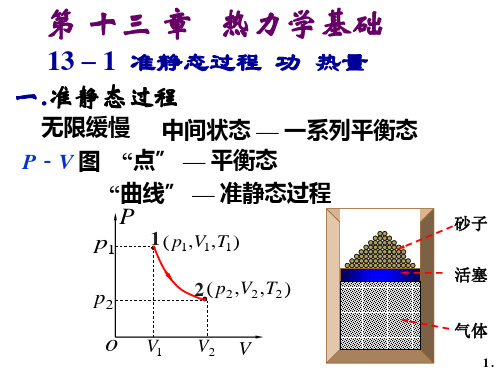
Wa
CV m (T2
T1)
p1V1 p2V2
1
本题用 Wa E 计算较方便
关键用绝热方程
T2
T1
( V1 V2
)
1
先求出 T2
p
p2
2 T2
T2' T1
Q0
p2'
2'
p1
TC
T1
1
o V2 V2' V1 10 V1 V
18.
*四. 多方过程 — 实际过程( 满足 PV n C)
绝热 n = ( CPm / CVm )
等温 n = 1 等压 n = 0
W p1V1 p2V2 n 1
满足 E CV (T2 T1)
Q Cn (T2 T1)
等体 n = ∞
p
可以证明
n= n=∞
n=1
Cn
(
n
n 1
)CV
n=0
o
V
19.
13 – 5 循环过程 卡诺循环
一. 循环过程
1. 特点 E 0 W = Q ( 热功转换 )
1
2
W
(2)热一定律 dQP dE PdV
o V1
V2 V
QP
E
V2 PdV
V1
v
i 2
R(T2
T1 )
P(V2
V1 )
7.
2.摩尔定压热容 CPm
1mol
:
CPm
dQp dT
理论值:
CPm
dE pdV dT
CVm
R
i2R 2
(近似)
实验值:查表 (精确)
QP
dQP
10 13-3 理想气体的等体过程和等压过程 摩尔热容
实际上,气体所进行的过程,常常既 不是等温又不是绝热的,而是介于两 者之间,可表示为 PVn =常量 (n为多方指数) 凡满足上式的过程称为多方过程。 n =1 —— 等温过程 n = —— 绝热过程 n= 0 —— 等压过程 n = —— 等容过程 一般情况1 n ,多方过程可近似 代表气体内进行的实际过程。
PV RT PV RT
C p,m CV ,m R
理想气体的定压摩尔热容比定体摩尔热容大一个恒量R •在等体过程中,气体吸收的热量全部用来增加系统的内能 •等压过程中,气体吸收的热量,一部分用来增加系统的内能, 还有一部分用于气体膨胀时对外界作功 气体升高相同的温度,在等压过程吸收的热量要比在等温过 程中吸收的热量多。
3
水蒸气
m
蒸气 0.598kg m
3
水
100 C 热源
W pdV pV pm(
1
蒸气
1
1
水
1
)
E Q W m L pm(
蒸气
水
)
E 1 1 L p( ) 2.09106 J kg1 m 蒸气 水
四、多方过程
2、比热容:
单位质量的热容称为比热容。
C 1 dQ c m m dT
13-4 理想气体的等温过程和绝热过程
一、等温过程
•特点:
理想气体的温度保持不变, T=const
•过程曲线:
在PV图上是一条双曲线, 叫等温线。
恒 温 热 源 T
•过程方程:
p1V1 p2V2
p p1
p2
1 ( p1 ,V1 , T )
p
T 常量
Q0
papT
PV RT PV RT
C p,m CV ,m R
理想气体的定压摩尔热容比定体摩尔热容大一个恒量R •在等体过程中,气体吸收的热量全部用来增加系统的内能 •等压过程中,气体吸收的热量,一部分用来增加系统的内能, 还有一部分用于气体膨胀时对外界作功 气体升高相同的温度,在等压过程吸收的热量要比在等温过 程中吸收的热量多。
3
水蒸气
m
蒸气 0.598kg m
3
水
100 C 热源
W pdV pV pm(
1
蒸气
1
1
水
1
)
E Q W m L pm(
蒸气
水
)
E 1 1 L p( ) 2.09106 J kg1 m 蒸气 水
四、多方过程
2、比热容:
单位质量的热容称为比热容。
C 1 dQ c m m dT
13-4 理想气体的等温过程和绝热过程
一、等温过程
•特点:
理想气体的温度保持不变, T=const
•过程曲线:
在PV图上是一条双曲线, 叫等温线。
恒 温 热 源 T
•过程方程:
p1V1 p2V2
p p1
p2
1 ( p1 ,V1 , T )
p
T 常量
Q0
papT
13-3理想气体的等体、等压和等温过程
第十三章 热力学基础
19
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容 摩尔热容比
γ = Cp,m CV,m
等压过程的三个量
W = p (V2 − V1 ) = ν R (T2 − T1 )
Q p = νC p,m (T2 − T1 )
E2 − E1 =νCV ,m (T2 − T1 )
由热力学第一定律
p2
2
V1
o
dQT = dWT = pdV
dV
V2 V
QT = W T =
∫
V2
V1
pdV
10
第十三章 热力学基础
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容
QT = WT = ∫ pdV
V1
V2
RT p =ν V
V2
p1V1 = p 2V2
RT V2 QT = W = ∫ ν dV = ν RT ln V1 V V1
p1 = νRT ln p2
第十三章 热力学基础
11
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容 等温过程热量与功的转换情况 等温膨胀 等温膨胀 等温压缩 等温压缩
p p1
1 ( p1 , V1 , T )
14
第十三章 热力学基础
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容
(一)摩尔定体热容
d 理想气体,等体过程, 1mol 理想气体,等体过程, QV ,dT 。
CV ,m
∵
19
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容 摩尔热容比
γ = Cp,m CV,m
等压过程的三个量
W = p (V2 − V1 ) = ν R (T2 − T1 )
Q p = νC p,m (T2 − T1 )
E2 − E1 =νCV ,m (T2 − T1 )
由热力学第一定律
p2
2
V1
o
dQT = dWT = pdV
dV
V2 V
QT = W T =
∫
V2
V1
pdV
10
第十三章 热力学基础
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容
QT = WT = ∫ pdV
V1
V2
RT p =ν V
V2
p1V1 = p 2V2
RT V2 QT = W = ∫ ν dV = ν RT ln V1 V V1
p1 = νRT ln p2
第十三章 热力学基础
11
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容 等温过程热量与功的转换情况 等温膨胀 等温膨胀 等温压缩 等温压缩
p p1
1 ( p1 , V1 , T )
14
第十三章 热力学基础
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容
(一)摩尔定体热容
d 理想气体,等体过程, 1mol 理想气体,等体过程, QV ,dT 。
CV ,m
∵
13-4理想气体的等温过程和绝热过程
第十三章 热力学基础
13
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
后为P 例1,一定量的理想气体 1,V1,T1,后为 2,V2, ,一定量的理想气体P T2, 已知 V2>V1, T2=T1 以下说法哪种正确? 以下说法哪种正确? (A)不论经历什么过程,气体对外净作功一定为正值 )不论经历什么过程, (B)不论经历什么过程,气体对外界净吸热一定为正值 )不论经历什么过程, (C)若是等温过程,气体吸的热量最少 )若是等温过程, (D)若不知什么过程,则A,Q的正负无法判断 )若不知什么过程, , 的正负无法判断 [D]
第十三章 热力学基础
14
物理学
第五版
1313-4 理想气体的等温过程和绝热过程 态到b态 例2,一定量的理想气体从 态到 态,这个过程 ,一定量的理想气体从a态到 是什么过程? 是什么过程?
P
b
a
T
(A)绝热压缩(B)等容吸热 )绝热压缩( ) (C)吸热压缩(D)吸热膨胀 )吸热压缩( )
第十三章 热力学基础
γ
E
0
p1V1 p 2V2 γ 1
νcV T
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
P
T
D
A
B
C
T
图中曲线为等 温线.问A, B,C,D状态 时系统的温度 关系.
V
T
PV = νRT
等压过程中,体积越大温度越高;等体过程 中,压强越大温度越大. 在PV图中,等温线上方温度较高,等温线 下方温度较低.
第十三章 热力学基础
8
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
13
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
后为P 例1,一定量的理想气体 1,V1,T1,后为 2,V2, ,一定量的理想气体P T2, 已知 V2>V1, T2=T1 以下说法哪种正确? 以下说法哪种正确? (A)不论经历什么过程,气体对外净作功一定为正值 )不论经历什么过程, (B)不论经历什么过程,气体对外界净吸热一定为正值 )不论经历什么过程, (C)若是等温过程,气体吸的热量最少 )若是等温过程, (D)若不知什么过程,则A,Q的正负无法判断 )若不知什么过程, , 的正负无法判断 [D]
第十三章 热力学基础
14
物理学
第五版
1313-4 理想气体的等温过程和绝热过程 态到b态 例2,一定量的理想气体从 态到 态,这个过程 ,一定量的理想气体从a态到 是什么过程? 是什么过程?
P
b
a
T
(A)绝热压缩(B)等容吸热 )绝热压缩( ) (C)吸热压缩(D)吸热膨胀 )吸热压缩( )
第十三章 热力学基础
γ
E
0
p1V1 p 2V2 γ 1
νcV T
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
P
T
D
A
B
C
T
图中曲线为等 温线.问A, B,C,D状态 时系统的温度 关系.
V
T
PV = νRT
等压过程中,体积越大温度越高;等体过程 中,压强越大温度越大. 在PV图中,等温线上方温度较高,等温线 下方温度较低.
第十三章 热力学基础
8
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
1-理想气体的等体过程和等压过程摩尔热容
2019年10月25日星期五
理学院 物理系
大学物理
§13-3 理想气体的等体过程和等压过程 摩尔热容
4.摩尔热容量C 和热量 Q 的关系 dQ=νCdT
5.摩尔定容热容CV (molar heat capacity at constant volume) (1)CV 和热量的关系 (dQ)V=vCVdT (2)CV 和内能的关系 vCVdT=(dE)V (3)内能 E 和状态 (T, V, P) 的关系
PV RT
P dV RdT
d Q CV dT P dV
d Q CV dT R dT
CV RdT
d Q CP dT
CP CV R
2019年10月25日星期五
理学院 物理系
§13-3 理想气体的等体过程和等压过程 摩尔热容
7.迈耶公式及其物理意义
(1)迈耶公式
CP
CV
R
i 2
R
R
Байду номын сангаас
i 2
1
R
(2)迈耶公式的物理意义
(3)摩尔气体常数R
(4)热容比
CP
i 2
1
R
i2
CV
iR
i
2
2019年10月25日星期五
理学院 物理系
8.7
28.8 20.4
8.4
28.6 20.4
8.2
29.3 21.2
8.1
28.9 21.0
7.9
36.2 27.8
8.4
35.5 27.2
8.4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三个量:
W p(V2 V1 ) R(T2 T1 )
Qp C p,m (T2 T1 )
E2 E1 CV ,m (T2 T1 )
第十三章 热力学基础
12
13-3 理想气体的等体和等压过程 摩尔热容
等 p 压 膨 胀
p
( p,V1, T1 ) ( p,V2 , T2 )
1
2
W
o
V1
V2
V
等 p 压 压 缩
p
( p,V2 , T2 ) ( p,V1, T1 )
2
1
W
o
V2
V1
V
Qp
E2
E1
W
Qp
E1
W
E2
13
第十三章 热力学基础
13-3 理想气体的等体和等压过程 摩尔热容 3、关于摩尔热容的讨论
•Mayer公式
推导
C P ,m-CV ,m=R
C p,m CV ,m R
由热力学第一定律
QV CV ,m (T2 T1 ) E2 E1
第十三章 热力学基础
5
13-3 理想气体的等体和等压过程 摩尔热容
p
等 体 升 p1 压
p2
2 ( p ,V , T ) 2 2 1
( p1 ,V , T1 )
p
o
等 体 降 p2 压
p1
1 ( p1,V , T1 )
m dQ p C p ,m dT dE pdV M m m dE CV ,m T2 T1 pdV RdT M M
可得摩尔定压热容和摩尔定体热容的关系
M
C p ,m
摩尔热容比
i2 CV ,m R R 2
C p,m CV ,m
第十三章 热力学基础
11
13-3 理想气体的等体和等压过程 摩尔热容
15
气体
CV,m
γ 1.67
He 12.47 Ne H2 20.78 N2 O2 H2O 24.93 CH4 CHCl3
20.09
1.40
33.24
1.33
第十三章 热力学基础
13-3 理想气体的等体和等压过程 摩尔热容
三、比热容
1、热容:
使物质温度升高1K所需要的热量称为该物质的热容。
2、比热容:
o
V
2
第十三章 热力学基础
13-3 理想气体的等体和等压过程 摩尔热容 •内能、功和热量的变化
dV 0, W pdV 0
p
p2
由热力学第一定律
( p2 ,V , T2 )
( p1 ,V , T1 )
V
dQV dE
QV E E2 E1
p1
o
V
•特征: 系统对外界不作功,系统吸收的热量全 部用来增加系统的内能。
理论值 CP,m 20.78
C P ,m CV ,m
CV,m 12.61 12.53 20.47 20.56 21.16 27.8 27.2 63.7 实验值 CP,m 20.95 20.90 28.83 28.88 29.61 36.2 35.2 7ห้องสมุดไป่ตู้.0 γ 1.66 1.67 1.41 1.40 1.40 1.31 1.30 1.13
系统吸收热量 系统放出热量
4
T2 T1 0 T2 T1 0
QV 0 QV 0
第十三章 热力学基础
13-3 理想气体的等体和等压过程 摩尔热容 •气体内能的增量
m E E 2 E1 CV ,m T2 T1 M
mol 理想气体
dQV dE CV ,mdT
第十三章 热力学基础
3
13-3 理想气体的等体和等压过程 摩尔热容
2、定体摩尔热容
•定义
1mol理想气体在等体过程中,温度升高1K时所吸 收的热量,称为该物质的定体摩尔热容。
CV ,m
dQV dE i R dT dT 2
单位 J mol K
1
1
•等体过程的热量公式
m QV CV ,m (T2 T1 ) M
m Qp C p ,m (T2 T1 ) M
系统吸收热量
系统放出热量
9
•等压过程的热量公式
T2 T1 0 T2 T1 0
Qp 0 Qp 0
第十三章 热力学基础
13-3 理想气体的等体和等压过程 摩尔热容 •气体内能的增量
m E E 2 E1 CV ,m T2 T1 M
( p2 ,V , T2 )
V
2
V
V
V
o
QV
E1
E2
QV
E1
E2
第十三章 热力学基础
6
13-3 理想气体的等体和等压过程 摩尔热容
二、等压过程 定压摩尔热容
1、等压过程 •特点:
理想气体的压强保持不变,p=const
•过程曲线:
p ( p,V1, T1 ) p
1 W
V1
( p,V2 ,T2 )
在PV 图上是一条平行于V 轴的直线, 叫等压线。
第十三章 热力学基础
1
13-3 理想气体的等体和等压过程 摩尔热容
一、等体过程 定体摩尔热容
1、等体过程 •特点:
理想气体的体积保持不变, V=const
p
p2
•过程曲线:
在PV图上是一条平行于
( p2 ,V , T2 )
( p1 ,V , T1 )
V
p轴的直线,叫等体线。 •过程方程:
p1
p1 p2 T1 T2
mol 理想气体
CV , m dQV dT
dQV dE CV ,mdT
由热力学第一定律
QV CV ,m (T2 T1 ) E2 E1
第十三章 热力学基础
10
13-3 理想气体的等体和等压过程 摩尔热容
•气体内能的增量 E E E m C T T 2 1 V ,m 2 1
dQ C dT
单位质量的热容称为比热容。
C 1 dQ c m m dT
第十三章 热力学基础
16
13-3 理想气体的等体和等压过程 摩尔热容
计算各等值过程的热量、功和内能的 理论基础.
(1) (2)
pV RT (理想气体的共性)
dQ dE pdV
V2 V1
解决过程中能
Q E pdV 量转换的问题
(3) E E (T )(理想气体的状态函数) (4) 各等值过程的特性 .
V2
V
•特征: 系统吸收的热量一部分用来增加系统的内能, 另一部分使系统对外界作功。
第十三章 热力学基础
8
13-3 理想气体的等体和等压过程 摩尔热容 2、定压摩尔热容 •定义
1mol理想气体在等压过程中,温度升高1K时所吸收 的热量,称为该物质的定压摩尔热容。
C p ,m
dQp dT
J mol1 K 1 单位
理想气体的定压摩尔热容比定体摩尔热容大一个恒量R •在等体过程中,气体吸收的热量全部用来增加系统的 内能 •等压过程中,气体吸收的热量,一部分用来增加系统 的内能,还有一部分用于气体膨胀时对外界作功 气体升高相同的温度,在等压过程吸收的热量要比 在等温过程中吸收的热量多。
第十三章 热力学基础
14
13-3 理想气体的等体和等压过程 摩尔热容 •摩尔热容比
2
•过程方程:
V1 V2 T1 T2
第十三章 热力学基础
o
V2
V
7
13-3 理想气体的等体和等压过程 摩尔热容
•内能、功和热量的变化
W
V2
pdV p(V2 V 1)
V1
p ( p,V1, T1 ) p
1
( p,V2 ,T2 )
由热力学第一定律
2
W
o
V1
dQ p dE dW
Qp E2 E1 p(V2 V1 )
