二元一次方程组试题及答案(模拟试题)
二元一次方程练习题及答案百度文库

二元一次方程练习题及答案百度文库8.1二元一次方程组一、填空题1、二元一次方程4x-3y=12,当x=0,1,2,3时,y=____2、在x+3y=3中,若用x表示y,则y表示x,则x=3、已知方程x2+x+y=k+2,当k=______时,方程为一元一次方程;当k=______时,方程为二元一次方程。
4、对二元一次方程2-3=10,当x=0时,则y=____;当y=0时,则x=____。
5、方程2x+y=5的正整数解是______。
6、若2+|2y+1|=0,则?x?2?x?y?a7、方程组?的一个解为?,那么这个方程组的另一个解是。
y?3xy?b??8、若x?1时,关于x、y的二元一次方程组2?ax?2y?1的解互为倒数,则??x?by?2a?2b?二、选择题1、方程2x-3y=5,xy=3,x?二元一次方程的有个。
A、1B、2C、3D、42、方程2x+y=9在正整数范围内的解有A、1个B、2个C、3个D、4个3、与已知二元一次方程5x-y=2组成的方程组有无数多个解的方程是A、10x+2y=B、4x-y=C、20x-4y=D、15x-3y=64、若是5x2ym与4xn?m?1y2n?2同类项,则m2?n的值为A、1B、-1C、-D、以上答案都不对5、在方程x2+x+y+3k=0中,若此方程为二元一次方程,则k值为?3,3x-y+2z=0,x2?y?6中是yA、2B、-C、2或-D、以上答案都不对.6、若??x?2是二元一次方程组的解,则这个方程组是 ?y??1?x?3y?5?y?x?3?2x?y?5?x?2yA、? B、? C、?D、?x?y?5y?2x?5x?y?1x?3y?17、在方程2?3?3中,用含x的代数式表示y,则A、y?5x?B、y??x?C、y?5x?D、y??5x?38、已知x=3-k,y=k+2,则y与x的关系是A、x+y=5B、x+y=1C、x-y=1D、y=x-19、下列说法正确的是A、二元一次方程只有一个解B、二元一次方程组有无数个解C、二元一次方程组的解必是它所含的二元一次方程的解D、三元一次方程组一定由三个三元一次方程组成?3x?5y?610、若方程组? 的解也是方程3x+ky=10的解,则k的值是x?15y?16?A、k=6= B、k=10C、k=9D、k=三、解答题1、解关于x的方程x?a?22、已知方程组?1 10?x?y?7,试确定a、c的值,使方程组:?ax?2y?c有一个解;有无数解;没有解3、关于x、y的方程3kx?2y?6k?3,对于任何k的值都有相同的解,试求它的解。
二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选(含答案)一.解答题(共16小题)1.求适合的x,y的值.2.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?3.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.4.二元一次方程组解法练习题精选(含答案)参考答案与试题解析1.求适合的x,y的值.考解二元一次方程组.点:分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.点评:2.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?解二元一次方程组.考点:专计算题.题:分析:(1)将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.3.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点此题难度较大,需同学们仔细阅读,弄清题意再解答.评:4.考解二元一次方程组.点:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.分析:解:由原方程组,得解答:,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=,∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.。
二元一次方程组练习题(含问题详解)
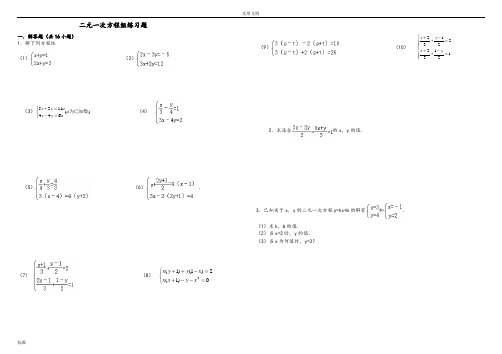
实用文档标准二元一次方程组练习题一.解答题(共16小题) 1.解下列方程组 (1)(2)(3))(6441125为已知数a a y x ay x ⎩⎨⎧=-=+ (4)(5)(6).(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x(9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2.求适合的x ,y 的值.3.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值. (3)当x 为何值时,y=3?1.解下列方程组(1)(2);(3);(4)(5).(6)(7)(8)(9)(10);2.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.word版本二元一次方程组解法练习题精选参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x ﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考点:解二元一次方程组.word版本专题:计算题.分析:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:;二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点:解二元一次方程组.专题:计算题.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.分析:(1)将两组x ,y 的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k、b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.word 版本(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.word版本10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y )+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.word版本专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a ,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;word版本2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.点评:解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.word版本。
第八章二元一次方程组测试题(二)

第八章二元一次方程组测试题(二)一、选择题(本大题共10小题,每小题3分,共30分)1.【导学号68490301】下列方程组中,不是二元一次方程组的是()A.21,346x yx z=+⎧⎨-=⎩B.1,4x yx y-=⎧⎨+=⎩C.5,5x yx+=⎧⎨=⎩D.2,2223x yyy x⎧+=⎪⎪⎨⎪=⎪⎩2.【导学号68490943】关于二元一次方程5a-11b=23的解,下列说法正确的是()A.有且只有一组解B.有无数组解C.无解D.有且只有两组解3.【导学号68490300】解方程组2344,1569x yx y+=⎧⎨-=⎩①②时,你认为最简单的方法是()A.用代入法先消去x或y B.用①×15-②×23,先消去xC.用①×6-②×4,先消去y D.用①×3+②×2,先消去y4.【导学号68490722】下列各组中,不是二元一次方程x+2y=5的解的是()A.1,2xy=⎧⎨=⎩B.2,1.5xy=⎧⎨=⎩C.6,1xy=⎧⎨=-⎩D.9,2xy=⎧⎨=-⎩5.【导学号68490317】已知a,b满足方程组512,34,a ba b+=⎧⎨-=⎩则a+b的值为()A.-4 B.4 C.-2 D.26.【导学号68490487】为了丰富学生课外小组活动,培养学生动手操作能力,王老师让学生把5 m长的彩绳截成2 m或1 m的彩绳,用来做手工编织,在不造成浪费的前提下,你有几种不同的截法()A.4 B.3 C.2 D.17.【导学号68490298】我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问:有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,则可列方程组为()A.100,33100x yx y+=⎧⎨+=⎩B.100,3100x yx y+=⎧⎨+=⎩C.100,131003x yx y+=⎧⎪⎨+=⎪⎩D.100,3100x yx y+=⎧⎨+=⎩8.【导学号68490296】已知(x-y+3)2,则x+y的值为()A.0 B.-1 C.1 D.59. 【导学号68490308】若方程组431,(1)3x yax a y+=⎧⎨--=⎩的解x与y互为相反数,则a的值等于()A.1 B.2 C.3 D.410.【导学号68490292】为了鼓励市民节约用电,某市对居民用电实行阶梯收费(总电费=第一阶梯电费+第二阶梯电费).规定:用电量不超过200度按第一阶梯电价收费,超过200度的部分按第二阶梯电价收费.图1是张磊家2016年9月和10月所交电费的收据,则该市规定的第一阶梯电价和第二阶梯电价分别为每度()A.0.5元,0.6元B.0.4元,0.5元C.0.3元,0.4元D.0.6元,0.7元图1二、填空题(本大题共8小题,每小题4分,共32分)11.【导学号68490315】已知方程3x-ay=8,若3,1xy=⎧⎨=⎩是它的一组解,则a的值为__________.12. 【导学号68490726】已知方程x-2y=6,用含x的式子表示y,y=__________;用含y的式子表示x,x=__________.13.【导学号92700702】已知x m-1+2y m+n+1=0是关于x,y的二元一次方程,那么m-n= .14.【导学号92700688】以方程组22,1y xy x=+⎧⎨=-+⎩的解为坐标的点P(x,y)在第象限.15.【导学号68490312】若方程组7,353,x yx y+=⎧⎨-=-⎩则3(x+y)-(3x-5y)的值是__________.16.【导学号68490639】已知2,1xy=⎧⎨=⎩是二元一次方程组7,1ax byax by+=⎧⎨-=⎩的解,则a-b=__________.17.【导学号68490314】如图2,在长为14 m,宽为10 m的长方形展厅中划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为__________m.18. 【导学号68490293】定义新运算“※”,规定x※y=ax2+by,其中a,b 图2 为常数,若1※2=5,2※1=6,则2※3= __________.三、解答题(本大题共5小题,共58分)19. 【导学号68490295】(每小题6分,共12分)解方程组:(1)237,x3y8.x y+=⎧⎨-=⎩①②(2)3(1)5, 5(y-1)3(5).x yx-=+⎧⎨=+⎩20. 【导学号68490303】(10分)已知关于x,y的二元一次方程x-y=3a和x+3y=4-a.(1)如果5,1xy=⎧⎨=-⎩是方程x-y=3a的一个解,求a的值;(2)当a=1时,求两方程的公共解.21. 【导学号68490316】(10分)如图3-①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分剪拼成一个长方形,如图3-②.这个拼成的长方形的长为30,宽为20,求图②中Ⅱ部分的面积.①②图322.【导学号92700693】(12分)观察下列方程组,解答问题:(1)解下列方程组(直接写出方程组的解):①2,21x yx y-=⎧⎨+=⎩的解为;②26,322x yx y-=⎧⎨+=⎩的解为;③312,433x yx y-=⎧⎨+=⎩的解为.(2)在以上三个方程组的解中,你发现x与y有什么数量关系.(不必说理)(3)请你构造第④个方程组,使其满足上述方程组的结构特征,并验证(2)中的结论.23.【导学号68490699】(14分)小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B 同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如下表:购买商品A的数量(个)购买商品B的数量(个)购买总费用(元)第一次购物 6 5 1140第二次购物 3 7 1110第三次购物9 8 1062 (1)小林以折扣价购买商品A、B是第次购物;(2)求出商品A、B的标价;(3)若商品A、B的折扣相同,则商店是打几折出售这两种商品的?附加题(15分,不计入总分)【导学号68490484】阅读理解:解方程组327,2114x yx y⎧+=⎪⎪⎨⎪-=⎪⎩时,如果设1x=m,1y=n,则原方程组可变形为关于m,n的方程组327,214,m nm n+=⎧⎨-=⎩解这个方程组得5,4.mn=⎧⎨=-⎩由15x=,14y=-,求得原方程组的解为1,51.4xy⎧=⎪⎪⎨⎪=-⎪⎩利用上述方法解方程组:5211,3213.x yx y⎧+=⎪⎪⎨⎪-=⎪⎩(辽宁陈琴)第八章二元一次方程组测试题(二)参考答案一、1.A 2.B 3.D 4. C 5. B 6. B 7. C 8.C 9. B10. A 提示:设第一阶梯电价每度x元,第二阶梯电价每度y元.根据题意,得20020112, 20065139,x yx y+=⎧⎨+=⎩解得0.5,0.6.xy=⎧⎨=⎩二、11.1 12.12x-3 6+2y 13. 4 14. 二15. 24 16. -117. 16 提示:设小长方形的长为x m,宽为y m. 由图可得214,210.x yx y+=⎧⎨+=⎩将两个方程相加,化简得x+y=8,所以每个小长方形的周长为8×2=16(m).18. 10 提示:根据题意,得25,4 6.a ba b+=⎧⎨+=⎩解得1,2.ab=⎧⎨=⎩所以2※3=1×22+2×3=4+6=10.三、19. 解:(1)①+②,得3x=15,解得x=5. 把x=5代入①,得10+3y=7,解得y=-1.所以原方程组的解为5,1. xy=⎧⎨=-⎩(2)原方程组化简,得38,5y-3x20. x y-=⎧⎨=⎩①②①+②,得4y=28,解得y=7.把y=7代入①,得3x-7=8,解得x=5.所以原方程组的解为5,7. xy=⎧⎨=⎩20. 解:(1)将5,1xy=⎧⎨=-⎩代入方程x-y=3a中,得5+1=3a,解得a=2.(2)当a=1时,将两方程联立得:3,3 3. x yx y-=⎧⎨+=⎩①②由①得x=3+y,代入②得3+y+3y=3,解得y=0. 将y=0代入①中,得x=3.所以两方程的公共解为3,0. xy=⎧⎨=⎩21. 解:根据题意,得30,20.a ba b+=⎧⎨-=⎩解得25,5.ab=⎧⎨=⎩故图②中Ⅱ部分的面积是:b·(a-b)=5×20=100.22. 解:(1)①1,1xy=⎧⎨=-⎩②2,2xy=⎧⎨=-⎩③3,3xy=⎧⎨=-⎩(2)在以上三个方程组的解中,x与y的数量关系为:x+y=0.(3)第④个方程组为420, 54 4.x yx y-=⎧⎨+=⎩①②①+②,得6x=24,解得x=4.把x=4代入①,解得y=-4.所以x+y=4-4=0.23. 解:(1)三(2)设商品A的标价为x元,商品B的标价为y元.根据题意,得651140,371110.x yx y+=⎧⎨+=⎩解得90,120.xy=⎧⎨=⎩答:商品A的标价为90元,商品B的标价为120元.(3)设商店是打a 折出售这两种商品. 由题意,得(9×90+8×120)×10a=1062.解得a=6. 答:商店是打6折出售这两种商品的. 附加题 解:设11,m n x y ==,原方程组可化为5211,3213.m n m n +=⎧⎨-=⎩解得3,2.m n =⎧⎨=-⎩所以原方程组的解为1,31.2x y ⎧=⎪⎪⎨⎪=-⎪⎩。
二元一次方程组试题及答案-(1)

班级: 姓名:一、填空题:(本大题共10小题,每小题3分,共30分)1. 在方程25x y +=中,用x 的代数式表示y ,得_______y =.2. 若一个二元一次方程的一个解为21x y =⎧⎨=-⎩,则这个方程可以是: (只要求写出一个)3. 下列方程: ①213y x -=; ②332x y +=; ③224x y -=; ④5()7()x y x y +=+;⑤223x =;⑥14x y+=.其中是二元一次方程的是 . 4. 若方程456m n m n x y -+-=是二元一次方程,则____m =,____n =.5. 方程4320x y +=的所有非负整数解为:6. 若23x y -=-,则52____x y -+=.7. 若2(5212)3260x y x y +-++-=,则24____x y +=.8. 有人问某男孩,有几个兄弟,几个姐妹,他回答说:“有几个兄弟就有几个姐妹.”再问他妹妹有几个兄弟,几个姐妹,她回答说:“我的兄弟是姐妹的2倍.”若设兄弟x 人,姐妹y 人,则可列出方程组: .9. 某次足球比赛的记分规则如下:胜一场得3分,平一场得1分,负一场是0分.某队踢了14场,其中负5场,共得19分。
若设胜了x 场,平了y 场,则可列出方程组: .10. 分析下列方程组解的情况.①方程组12x y x y +=⎧⎨+=⎩的解 ;②方程组1222x y x y +=⎧⎨+=⎩的解 .二、选择题:(本大题共6小题,每小题3分,共18分)11. 用代入法解方程组124y x x y =-⎧⎨-=⎩时,代入正确的是( ) A.24x x --=B .224x x --= C.224x x -+=D.24x x -+= 12. 已知10x y =-⎧⎨=⎩和23x y =⎧⎨=⎩都是方程y ax b =+的解,则a 和b 的值是 ( ) A.11a b =-⎧⎨=-⎩ B.11a b =⎧⎨=⎩ C.11a b =-⎧⎨=⎩ D. 11a b =⎧⎨=-⎩13. 若方程组4314(1)6x y kx k y +=⎧⎨+-=⎩的解中x 、y 的值相等,k 为( ) A.4 B.3 C.2 D.114. 已知方程组5354x y ax y +=⎧⎨+=⎩和2551x y x by -=⎧⎨+=⎩有相同的解,则a ,b 的值为 ( )A.12a b =⎧⎨=⎩ B.46a b =-⎧⎨=-⎩ C.62a b =-⎧⎨=⎩ D.142a b =⎧⎨=⎩15. 已知二元一次方程30x y +=的一个解是x a y b =⎧⎨=⎩,其中0a ≠,那么( )A.0b a > B.0b a = C.0b a< D.以上都不对 16. 如图1,宽为50 cm 的矩形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )A. 400 cm 2B. 500 cm 2C. 600 cm 2D. 4000 cm 2三、解答题:(本大题共8小题,共52分)17.(6分)解方程组356415x z x z -=⎧⎨+=-⎩ ①②18. (6分)解方程组22314m n m n -=⎧⎨+=⎩ ① ②19. (6分)解方程组4(1)3(1)2223x y y x y --=--⎧⎪⎨+=⎪⎩20. (8分)已知方程组45321x y x y +=⎧⎨-=⎩和31ax by ax by +=⎧⎨-=⎩有相同的解,求222a ab b -+的值. 图121. (8分)上杭县某中学七年级学生外出进行社会实践活动,如果每辆车坐45人,那么有15个学生没车坐;如果每辆车坐60人,那么可以空出一辆车。
(完整版)二元一次方程组练习题含答案

二元一次方程组专题训练1.⎩⎨⎧=-=+33651643y x y x 2. ⎩⎨⎧=+=-6251023x y x y ⎩⎨⎧=-=+19542023b a b a 1、 2、 3、 ⎩⎨⎧=-=+1572532y x y x4、⎩⎨⎧=+-=18435276t s t s 5、 ⎩⎨⎧=-=+574973p q q p 6、⎩⎨⎧=-=+42634y x y x7、⎩⎨⎧-=-=+22223n m n m 8、⎩⎨⎧=--=-495336y x y x 9、10、⎩⎨⎧=-=-yx y x 23532 11、⎩⎨⎧=-=+124532n m n m12、⎩⎨⎧=+=+10232556y x y x13、⎩⎨⎧=+=+2.54.22.35.12y x y x 14、⎪⎩⎪⎨⎧=-+-=+6)(3)1(26132y x x y x15、⎪⎩⎪⎨⎧=+--=-+-04235130423512y x y x 16、⎪⎩⎪⎨⎧=--=+-4323122y x y x yx17、⎪⎩⎪⎨⎧-=-++=-+52251230223x y x y x二元一次方程组练习题一、选择题:1.下列方程中,是二元一次方程的是( ) A .3x -2y=4z B .6xy+9=0 C .1x+4y=6 D .4x=2.下列方程组中,是二元一次方程组的是( )A .228423119...23754624x y x y a b xBCD x y b c y x x y +=+=-=⎧⎧=⎧⎧⎨⎨⎨⎨+=-==-=⎩⎩⎩⎩3.二元一次方程5a -11b=21 ( )A .有且只有一解B .有无数解C .无解D .有且只有两解4.方程y=1-x 与3x+2y=5的公共解是( )A .3333...2422x x x x B C D y y y y ==-==-⎧⎧⎧⎧⎨⎨⎨⎨===-=-⎩⎩⎩⎩5.若│x -2│+(3y+2)2=0,则的值是( )A .-1B .-2C .-3D .326.方程组43235x y kx y -=⎧⎨+=⎩的解与x 与y 的值相等,则k 等于( )7.下列各式,属于二元一次方程的个数有( )①xy+2x -y=7; ②4x+1=x -y ; ③1x+y=5; ④x=y ; ⑤x 2-y 2=2⑥6x -2y ⑦x+y+z=1 ⑧y (y -1)=2y 2-y 2+x A .1 B .2 C .3 D .48.某年级学生共有246人,其中男生人数y 比女生人数x 的2倍少2人,•则下面所列的方程组中符合题意的有( ) A .246246216246 (22222222)x y x y x y x y B C D y x x y y x y x +=+=+=+=⎧⎧⎧⎧⎨⎨⎨⎨=-=+=+=+⎩⎩⎩⎩ 二、填空题9.已知方程2x+3y -4=0,用含x 的代数式表示y 为:y=_______;用含y 的代数式表示x 为:x=________. 10.在二元一次方程-12x+3y=2中,当x=4时,y=_______;当y=-1时,x=______.11.若x 3m -3-2y n -1=5是二元一次方程,则m=_____,n=______.12.已知2,3x y =-⎧⎨=⎩是方程x -ky=1的解,那么k=_______.13.已知│x -1│+(2y+1)2=0,且2x -ky=4,则k=_____.14.二元一次方程x+y=5的正整数解有______________. 15.以57x y =⎧⎨=⎩为解的一个二元一次方程是_________. 16.已知2316x mx y y x ny =-=⎧⎧⎨⎨=--=⎩⎩是方程组的解,则m=_______,n=______.三、解答题17.当y=-3时,二元一次方程3x+5y=-3和3y -2ax=a+2(关于x ,y 的方程)•有相同的解,求a 的值.18.如果(a -2)x+(b+1)y=13是关于x ,y 的二元一次方程,则a ,b 满足什么条件?19.二元一次方程组437(1)3x y kx k y +=⎧⎨+-=⎩的解x ,y 的值相等,求k .20.已知x,y是有理数,且(│x│-1)2+(2y+1)2=0,则x-y的值是多少?21.已知方程12x+3y=5,请你写出一个二元一次方程,使它与已知方程所组成的方程组的解为41xy=⎧⎨=⎩.22.根据题意列出方程组:(1)明明到邮局买0.8元与2元的邮票共13枚,共花去20元钱,•问明明两种邮票各买了多少枚?(2)将若干只鸡放入若干笼中,若每个笼中放4只,则有一鸡无笼可放;•若每个笼里放5只,则有一笼无鸡可放,问有多少只鸡,多少个笼?23.方程组2528x yx y+=⎧⎨-=⎩的解是否满足2x-y=8?满足2x-y=8的一对x,y的值是否是方程组2528x yx y+=⎧⎨-=⎩的解?24.(开放题)是否存在整数m ,使关于x 的方程2x+9=2-(m -2)x 在整数范围内有解,你能找到几个m 的值?你能求出相应的x 的解吗?《二元一次方程组》单元测试题一、选择题(每题3分,共30分) 1.下列方程组中,是二元一次方程组的是( ). (A ) 2311089x y x y ⎧+=⎨-=-⎩ (B )426xy x y =⎧⎨+=⎩ (C )21734x y y x-=⎧⎪⎨-=-⎪⎩(D )24795x y x y +=⎧⎨-=⎩ 2.二元一次方程组⎩⎨⎧==+xy y x 2,102的解是( ) (A )⎩⎨⎧==;3,4y x (B )⎩⎨⎧==;6,3y x (C )⎩⎨⎧==;4,2y x (D )⎩⎨⎧==.2,4y x 3.根据图1所示的计算程序计算y 的值,若输入2=x , 则输出的y 值是( )(A )0 (B )2- (C )2 (D )44.如果2315a b 与114x x y a b ++-是同类项,则x ,y 的值是( )(A )⎩⎨⎧==31y x (B )⎩⎨⎧==22y x (C )⎩⎨⎧==21y x (D )⎩⎨⎧==32y x 5.已知12x y =⎧⎨=⎩ 是方程组错误!未找到引用源。
二元一次方程组解法练习题精选(含答案)(1)
二元一次方程组解法练习题精选(含答案)一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).解方程组:4.解方程组:5.解方程组:3.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).解方程组:9.解方程组:8.10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2).13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1);(2).解下列方程组:(1)(2)16.第二十六章《二次函数》检测试题1,(2008年芜湖市)函数2yax b y axbx c 和在同一直角坐标系内的图象大致是()2,在一定条件下,若物体运动的路程s (米)与时间t (秒)的关系式为s =5t 2+2t ,则当t =4时,该物体所经过的路程为()3,已知二次函数y =ax 2+bx+c(a ≠0)的图象如图2所示,给出以下结论:① a+b+c <0;② a -b+c <0;③ b+2a <0;④ abc >0 .其中所有正确结论的序号是()A. ③④B. ②③C. ①④D. ①②③4,二次函数y =ax 2+bx+c 的图象如图3所示,若M =4a+2b+c ,N =a -b+c ,P =4a+2b ,则()A.M >0,N >0,P >0B. M >0,N <0,P >0C. M <0,N >0,P >0D. M <0,N >0,P <05,如果反比例函数y =kx的图象如图4所示,那么二次函数y =kx 2-k 2x -1的图象大致为()6,用列表法画二次函数y =x 2+bx+c 的图象时先列一个表,当表中对自变量x 的值以相等间隔的值增加时,函数y所对应的函数值依次为:20,56,110,182,274,380,506,650.其中有一个值不正确,这个不正确的值是() A. 506B.380C.274D.187,二次函数y =x 2的图象向上平移2个单位,得到新的图象的二次函数表达式是()A. y =x 2-2B. y =(x -2)2C. y =x 2+2D. y =(x+2)2图3y xO 图4y xO A .y xOB .yxO C .yxO D .图4x-11yO图2图18如图6,小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数h =3.5t -4.9t 2(t 的单位:s ,h 的单位:m )可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是()A.0.71sB.0.70sC.0.63sD.0.36s9,如果将二次函数y =2x 2的图象沿y 轴向上平移1个单位,那么所得图象的函数解析式是.10,平移抛物线y =x 2+2x -8,使它经过原点,写出平移后抛物线的一个解析式______ .11,若二次函数y =x 2-4x +c 的图象与x 轴没有交点,其中c 为整数,则c =12,二次函数y =ax 2+bx+c 的图像如图7所示,则点A(a ,b)在第___象限.13,已知抛物线y =x 2-6x+5的部分图象如图8,则抛物线的对称轴为直线x =,满足y <0的x 的取值范围是.14,已知一抛物线与x 轴的交点是)0,2(A 、B (1,0),且经过点C (2,8)。
二元一次方程组解法练习题精选(含答案)
二元一次方程组解法练习题精选(含答案)一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).3.解方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).8.解方程组:9.解方程组:10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2).13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1);(2).16.解下列方程组:(1)(2)第二十六章《二次函数》检测试题1,(2008年芜湖市)函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是 ( )2,在一定条件下,若物体运动的路程s (米)与时间t (秒)的关系式为s =5t 2+2t ,则当t =4时,该物体所经过的路程为( )3,已知二次函数y =ax 2+bx +c (a ≠0)的图象如图2所示,给出以下结论:① a +b +c <0;② a -b +c <0;③ b +2a <0;④ abc >0 .其中所有正确结论的序号是( )A. ③④B. ②③C. ①④D. ①②③4,二次函数y =ax 2+bx +c 的图象如图3所示,若M =4a +2b +c ,N =a -b +c ,P =4a +2b ,则( )A.M >0,N >0,P >0B. M >0,N <0,P >0C. M <0,N >0,P >0D. M <0,N >0,P <05,如果反比例函数y =k x的图象如图4所示,那么二次函数y =kx 2-k 2x -1的图象大致为( )6y 所对应的函数值依次为:20,56,110,182,274,380,506,650.其中有一个值不正确,这个不正确的值是()A. 506B.380C.274D.18图3图4 A . B . 图5 图1A. y =x 2-2B. y =(x -2)2C. y =x 2+2D. y =(x +2)28如图6,小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数h =3.5t -4.9t 2(t 的单位:s ,h 的单位:m )可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )A.0.71sB.0.70sC.0.63sD.0.36s9,如果将二次函数y =2x 2的图象沿y 轴向上平移1个单位,那么所得图象的函数解析式是 .10,平移抛物线y =x 2+2x -8,使它经过原点,写出平移后抛物线的一个解析式______ .11,若二次函数y =x 2-4x +c 的图象与x 轴没有交点,其中c 为整数,则c =12,二次函数y =ax 2+bx +c 的图像如图7所示,则点A (a ,b )在第___象限.13,已知抛物线y =x 2-6x +5的部分图象如图8,则抛物线的对称轴为直线x = ,满足y <0的x 的取值范围是 .14,已知一抛物线与x 轴的交点是)0,2( A 、B (1,0),且经过点C (2,8)。
二元一次方程组解法练习题精选(含答案)
二元一次方程组解法练习题精选(含答案)一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).3.解方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).8.解方程组:9.解方程组:10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2).13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1);(2).16.解下列方程组:(1)(2)第二十六章《二次函数》检测试题1,(2008年芜湖市)函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是 ( )2,在一定条件下,若物体运动的路程s (米)与时间t (秒)的关系式为s =5t 2+2t ,则当t =4时,该物体所经过的路程为( )3,已知二次函数y =ax 2+bx +c (a ≠0)的图象如图2所示,给出以下结论:① a +b +c <0;② a -b +c <0;③ b +2a <0;④ abc >0 .其中所有正确结论的序号是( )A. ③④B. ②③C. ①④D. ①②③4,二次函数y =ax 2+bx +c 的图象如图3所示,若M =4a +2b +c ,N =a -b +c ,P =4a +2b ,则( )A.M >0,N >0,P >0B. M >0,N <0,P >0C. M <0,N >0,P >0D. M <0,N >0,P <05,如果反比例函数y =k x的图象如图4所示,那么二次函数y =kx 2-k 2x -1的图象大致为( )6y 所对应的函数值依次为:20,56,110,182,274,380,506,650.其中有一个值不正确,这个不正确的值是()A. 506B.380C.274D.18图3图4 A . B . 图5 图1A. y =x 2-2B. y =(x -2)2C. y =x 2+2D. y =(x +2)28如图6,小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数h =3.5t -4.9t 2(t 的单位:s ,h 的单位:m )可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )A.0.71sB.0.70sC.0.63sD.0.36s9,如果将二次函数y =2x 2的图象沿y 轴向上平移1个单位,那么所得图象的函数解析式是 .10,平移抛物线y =x 2+2x -8,使它经过原点,写出平移后抛物线的一个解析式______ .11,若二次函数y =x 2-4x +c 的图象与x 轴没有交点,其中c 为整数,则c =12,二次函数y =ax 2+bx +c 的图像如图7所示,则点A (a ,b )在第___象限.13,已知抛物线y =x 2-6x +5的部分图象如图8,则抛物线的对称轴为直线x = ,满足y <0的x 的取值范围是 .14,已知一抛物线与x 轴的交点是)0,2( A 、B (1,0),且经过点C (2,8)。
二元一次方程组同步测试(答案)
二元一次方程组同步测试学校:___________姓名:___________班级:___________考号:___________一、选择题1.(本题3分)已知方程组321(1)3x y ax a y ⎧+=⎨--=⎩的解x 和y 互为相反数,则a 的值为( ).A .﹣1B .﹣2C .1D .2【答案】D .【解析】试题分析:因为x 和y 的值互为相反数,所以有x=﹣y ,把它代入方程1中,将直接求出x 和y ,然后把所求结果代入方程2中,求出a 的值即可.∵x 和y 的值互为相反数,∴x=﹣y ,代入方程3x+2y=1中得:y=﹣1,∴x=1.把x=1,y=﹣1代入第二个方程得:a+a ﹣1=3,解得:a=2;故选:D .考点:二元一次方程组的解.2.(本题3分)已知x 、y 满足方程组3125x y x y +=⎧⎨-=⎩,则x+y 的值为( ) A .1 B .﹣3 C .﹣2 D .﹣1【答案】D【解析】 试题分析:利用加减消元法解出方程组,计算3125x y x y +=⎧⎨-=⎩ ①② , ①×2+②得,7x=7,解得,x=1,把x=1代入①得,y=﹣2,则x+y=﹣1,故选:D .考点:二元一次方程组的解3.(本题3分)为了开展阳光体育活动,丰富同学们的课余生活,体育委员欧阳锋到体育用品商店购羽毛球拍和乒乓球拍,若购1副羽毛球拍和1副乒乓球拍共需50元,欧阳锋一共用320元购买了6副同样的羽毛球拍和10副同样的乒乓球拍,若设每副羽毛球拍为x 元,每副乒乓球拍为y 元,列二元一次方程组得( ) A. ⎩⎨⎧=+=+320y 10x 650y x B. ⎩⎨⎧=+=+320)y x (650y x C. ⎩⎨⎧=+=+320y x 650y x D. ⎩⎨⎧=+=+320y 6x 1050y x 【答案】A【解析】试题分析:根据题意可知:两个等量关系,若购1副羽毛球拍和1副乒乓球拍共需50元,欧阳锋一共用320元购买了6副同样的羽毛球拍和10副同样的乒乓球拍,然后可列方程组为:⎩⎨⎧=+=+320y 10x 650y x .故选:A考点:二元一次方程组4.(本题3分)足球比赛规定:胜一场得3分,平一场得1分,负一场得0分.某足球队共进行了6场比赛,得了12分,该队获胜的场数可能是( )A .1或2B .2或3C .3或4D .4或5【答案】C .【解析】试题分析:设该队胜x 场,平y 场,则负(6﹣x ﹣y )场,根据题意,得:3x+y=12,即:x 、y 均为非负整数,且x+y ≤6,所以当y=0时,x=4;当y=3时,x=3;即该队获胜的场数可能是3场或4场,故选C .考点:二元一次方程的应用.5.(本题3分)已知⎩⎨⎧==12y x 是二元一次方程组⎩⎨⎧=-=+128my x ny mx 的解,则(2m -n )2=( )A .4B .2C .16D .2或-2【答案】C【解析】分析:把x=2,y=1代入方程组得到一个关于m n 的方程组,求出方程组的解,代入代数式求出即可.解答:解:把x=2,y=1代入方程组得:2m n 84m 1+=⎧⎨-=⎩①②, 由①得:m=3,m=3代入①得:6+n=8,∴n=2,把m=3,n=2代入得:(2m-n )2=(2×3-2)2=16.故选C .6.(本题3分)若x a - b -2y a + b - 2=11是二元一次方程,那么的a 、b 值分别是( )A 、1,0B 、0,-1C 、2,1D 、2-3【答案】C 【解析】由二元一次方程的定义可得121a b a b -=⎧⎨+-=⎩, 解之得21a b =⎧⎨=⎩,故选C 7.(本题3分)若方程组⎩⎨⎧=++=+3313y x k y x 的解为x ,y ,且x +y >0,则k 的范围是 A .k >-4B .k >4C .k <4D .k <-4【答案】A【解析】 试题分析:根据方程组的特征可把两个方程直接相加可得444+=+k y x ,即得x +y >0即可得到关于k 的不等式,再解出即可. 由题意得444+=+k y x ,即∵0>+y x ,解得4->k 故选A.考点:解方程组,解一元一次不等式点评:计算题是中考必考题,一般难度不大,要特别慎重,尽量不在计算上失分.8.(本题3分)如图,10块相同的长方形墙砖拼成一个矩形,设长方形墙砖的长和宽分别为x 厘米和y 厘米,则依题意列方程组正确的是A .x 2y 75y 3x +==⎧⎨⎩B .x 2y 75x 3y +==⎧⎨⎩C .2x y 75y 3x -==⎧⎨⎩D .2x y 75x 3y +==⎧⎨⎩【答案】B【解析】试题分析:根据图示可得:长方形的长可以表示为x+2y ,长又是75厘米,故x+2y=75,长方形的宽可以表示为2x ,或x+3y ,故2x=3y+x ,整理得x=3y ,联立两个方程得x 2y 75x 3y +=⎧⎨=⎩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题
(时间:90分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.方程2x -1y =0,3x+y=0,2x+xy=1,3x+y -2x=0,x 2-x+1=0中,二元一次方程的个数是( ) A .1个 B .2个 C .3个 D .4个
2.二元一次方程组32325x y x y -=⎧⎨
+=⎩的解是( ) A .3217 (2301)
22x x x x B C D y y y y =⎧⎧===⎧⎧⎪⎪⎨⎨⎨⎨==-=⎩⎩⎪⎪=⎩⎩ 3.关于x ,y 的二元一次方程组59x y k x y k +=⎧⎨
-=⎩
的解也是二元一次方程2x+3y=6的解,则k 的值是(• ) A .k=-34 B .k=34 C .k=43 D .k=-43
4.如果方程组1x y ax by c +=⎧⎨+=⎩有唯一的一组解,那么a ,b ,c 的值应当满足( ) A .a=1,c=1 B .a ≠b C .a=b=1,c ≠1 D .a=1,c ≠1
5.方程3x+y=7的正整数解的个数是( )
A .1个
B .2个
C .3个
D .4个
6.已知x ,y 满足方程组45x m y m +=⎧⎨-=⎩
,则无论m 取何值,x ,y 恒有关系式是( ) A .x+y=1 B .x+y=-1 C .x+y=9 D .x+y=9
7.如果│x+y -1│和2(2x+y -3)2互为相反数,那么x ,y 的值为( )
A .1
122 (2211)
x x x x B C D y y y y ==-==-⎧⎧⎧⎧⎨⎨⎨⎨==-=-=-⎩⎩⎩⎩
8、 如图1,宽为50 cm 的矩形图案,由10个全等的小长方形
拼成,其中一个小长方形的面积为( )
A. 400 cm2
B. 500 cm2
C. 600 cm2
D. 800 cm2
二、填空题(每小题3分,共18分)
9.==--y y x y x 得表示用,,06911_______,=x x y 得表示,_______。
10.如果⎩⎨⎧=-=+.
232,12y x y x 那么=-+-+3962242y x y x _______。
11.如果1032162312=--+--b a b a y x 是一个二元一次方程,那么数a =___, b =_____
12.面值为20分、30分的邮票共27枚,用款6.6元,购20分邮票_____枚,30分邮票_____枚。
13.已知⎩⎨⎧==⎩⎨⎧=-=3
10y 2x y x 和是方程022=--bx ay x 的两个解,那么a = ,b =
14.如果b a a b y x y x 4222542-+-与是同类项,那么 a = ,b = 。
三、解答题
15.解方程组(每小题4分,共8分)
(1)257320
x y x y -=⎧⎨-=⎩ 33(2)255(2)4x y x y +⎧=⎪⎨⎪-=-⎩
16.已知y=3xy+x ,求代数式
2322x xy y x xy y +---的值.(本小题6分)
17.方程组256351648
x y x y ax by bx ay +=--=⎧⎧⎨⎨-=-+=-⎩⎩与方程组的解相同.求(2a+b )2004的值.(本小题6分)
18.已知x=1是关于x 的一元一次方程ax -1=2(x -b )的解,y=1是关于y 的一元一次方程
b (y -3)=2(1-a )的解.在y=ax2+bx -3中,求当x=-3时y 值.(本小题6分)
19.某商场按定价销时,每台可获利48元,按定价的九折销售该电器6台与将定价降低30元销售该电器9台所获得的利润相等.求该电器每台的进价、•定价各是多少元?(本小题6分)
20.一张方桌由1个桌面,4条桌腿组成,如果1m 3木料可以做方桌的桌面50•个或做桌腿300条,现有10m 3木料,那么用多少立方米的木料做桌面,•多少立方米的木料做桌腿,做出的桌面与桌腿,恰好能配成方桌?能配成多少张方桌.(本小题6分)
21.甲、乙二人在上午8时,自A 、B 两地同时,已知甲每小时比乙多走2km ,求A ,B 两地的距离.(•本小题10分)
22.某中学组织学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45•座客车每日每辆租金为220元,60座客车每日每辆租金为300元.试问:
(1)春游学生共多计划租45座客车多少辆?
(2)若租用同一种车,要使每位同学都有座位,怎样租车更合算?(本小题10分)
题(答案)
1.B 2.C 3.B 4.B 5.B 6.C 7.C 8.A 9、1169,9611+-y x 10、2 11、7
18 12、15 13、2,31- 14、5
3,115-
15.解:(1)257320
x y x y -=⎧⎨-=⎩ ①×3得,6x -3y=15 ③, ②-③,得x=5.将x=5代入①,得y=5,所以原方程组的解为55x y =⎧⎨=⎩. (2)原方程组变为51565104x y x y +=⎧⎨-=-⎩y=25.将y=25代入①,得5x+15×25=6,x=0, 所以原方程组的解为025x y =⎧⎪⎨=⎪⎩
. 16.解:因为y=3xy+x ,所以x -y=-3xy .
当x -y=-3xy 时,2322()32(3)332()2325
x xy y x y xy xy xy x xy y x y xy xy xy +--+-+===------. 解析:首先根据已知条件得到x -y=-3xy ,再把要求的代数式化简成含有x -y 的式子,然后整体代入,使代数式中只含有xy ,约分后得解.
17.解:因为两个方程组的解相同,所以解方程组25623562
x y x x y y +=-=⎧⎧⎨⎨-==-⎩⎩解得
代入另两个方程得2143
a b a a b b +=-=⎧⎧⎨⎨-+=-=-⎩⎩解得,∴原式=(2×1-3)2004=1. 18.解:将x=1,y=1分别代入方程得512(1)3(13)2(1)23a a b b a b ⎧=⎪-=-⎧
⎪⎨⎨-=-⎩⎪=⎪⎩解方程组得 所以原式=53x 2+23x -3.当x=-3时,原式=53×(-3)2+23
×(-3)-3=15-2-3=10.
19.解:设该电器每台的进价为x 元,定价为y 元.
由题意得48,162,6(0.9)9(30)210.
y x x y x y x y -==⎧⎧⎨⎨-=--=⎩⎩解得. 答:该电器每台的进价是162元,定价是210元.(解析:打九折是按定价的90%销售,利润=售价-进价)
20.解:设用xm 3木料做桌面,ym 3木料做桌腿.由题意,得
106,450300 4.
x y x x y y +==⎧⎧⎨⎨⨯==⎩⎩解得(2)6×50=300(张).答:用6m 3木料做桌面,4m 3木料做桌腿恰好能配成方桌,能配成300张方桌.解析:问题有两个条件:①做桌面用的木料+做桌腿用的木料=10;②4×桌面个数=桌腿个数.
21.解:设A 、B 两地相距xkm ,乙每小时走ykm ,则甲每小时走(y+2)km .
根据题意,•得2(2)361084(2)3617
y y x x y y x y ++=-=⎧⎧⎨⎨++=+=⎩⎩解这个方程组得.答:略. 22.解:(1)设参加春游的学生共x 人,原计划租用45座客车y 辆.
根据题意,得451524060(1)5
y x x y x y +==⎧⎧⎨⎨-==⎩⎩解这个方程组,得 . 答:春游学生共240人,原计划租45座客车5辆.
(2)租45座客车:240÷45≈5.3,所以需租6辆,租金为220×6=1320(元);租60•座客车:240÷60=4,所以需租4辆,租金为300×4=1200(元).
所以租用4辆60座客车更合算. (解析:租车不管几个人都要用一辆,所以在计算车的辆数时用“收0尾法”,而不是“四舍五入”)。
