数据转换与欧拉角
ebsd平均kam计算公式

ebsd平均kam计算公式全文共四篇示例,供读者参考第一篇示例:在电子背散射衍射(EBSD)技术中,KAM(Kernel Average Misorientation)是一个重要的参数,用于描述材料微结构中晶粒内部的晶界密度和晶粒的错向程度。
KAM的计算可以帮助研究者了解材料的变形和再结晶过程,从而指导工程应用和材料设计。
在EBSD实验中,KAM的计算是非常常见的操作,而其中的平均KAM计算公式是研究者们在分析数据时经常需要用到的。
平均KAM的计算公式可以通过以下步骤来实现:1. 从EBSD实验中获取到完整的晶粒取向数据,通常以欧拉角(φ1、Φ、φ2)的形式存储。
2. 然后,通过晶粒取向数据计算出晶界的错向角度。
晶界的错向角度是指在两个相邻晶粒之间的晶界上,晶粒取向之间的角度差值。
通过计算每个晶粒和其相邻晶粒之间的角度差值,可以得到每个晶粒的KAM值。
3. 接下来,将每个晶粒的KAM值进行平均处理,即将所有晶粒的KAM值相加并除以晶粒数目,即可得到材料的平均KAM值。
4. 根据平均KAM的数值大小,可以判断材料内部的晶界密度和晶粒的错向程度。
一般来说,平均KAM值越大,表示材料的晶界密度越高,晶粒之间的错向程度也越大。
需要注意的是,平均KAM的计算公式是一个相对简单的数学运算,但是在实际应用中需要考虑到一些因素,比如数据的质量、算法的准确性等。
对于不同材料体系和实验条件,可能需要采用不同的计算方法或参数来得出更准确的结果。
在进行平均KAM计算时,研究者们需要结合具体的实验情况和研究目的来选择合适的计算方法和参数,从而得到准确的研究结果。
平均KAM的计算公式是EBSD实验中一个重要的计算方法,可以帮助研究者了解材料内部晶粒的错向程度和晶界密度。
通过对平均KAM的计算和分析,可以为材料科学和工程技术领域的研究和应用提供重要的参考信息。
希望本文对平均KAM的计算公式有所帮助。
第二篇示例:EBSD平均KAM计算公式是用于确定电子背散射衍射技术(EBSD)中晶体取向与晶界取向之间的关系的一种方法。
imu数据处理公式

IMU(惯性测量单元)数据处理通常包括数据预处理、姿态解算和融合算法等步骤。
以下是一些常用的数据处理公式和方法:
1. 数据预处理:
零偏校正:将加速度计和陀螺仪的偏移量进行修正,常用的方法包括零偏校正和尺度因子校正。
2. 姿态解算:
四元数法:将IMU的测量值进行积分,得到姿态四元数,通过四元数来计算姿态角。
欧拉角法:将IMU的测量值进行积分,得到欧拉角,通过欧拉角来计算姿态角。
卡尔曼滤波法:将IMU的测量值和加速度计数据融合,通过卡尔曼滤波算法来估计姿态角。
3. 融合算法:
互补滤波器:将加速度计和陀螺仪数据按照一定的权重进行融合,得到姿态角。
常用的权重方法包括一阶互补滤波和二阶互补滤波等。
卡尔曼滤波器:将加速度计和陀螺仪数据融合,通过卡尔曼滤波算法来估计姿态角。
卡尔曼滤波器可以处理噪声和误差,提高数据精度。
4. 速度和位置计算:
基于IMU的数据,可以通过积分和滤波算法计算速度和位置信息。
常用的方法包括基于加速度计的积分、基于陀螺仪的积分、融合算法等。
以上是一些常见的IMU数据处理公式和方法,具体的实现方式可能因应用场景、传感器型号和数据处理需求而有所不同。
matlab欧拉角到旋转矩阵

MATLAB是一种用于数学计算和工程模型设计的高级编程语言和交互环境。
在MATLAB中,欧拉角到旋转矩阵的转换是非常常见且重要的数学运算之一。
欧拉角是描述刚体在空间中姿态的一种常用方式,而旋转矩阵则是描述刚体变换的重要数学工具。
本文将详细介绍如何利用MATLAB实现欧拉角到旋转矩阵的转换。
1. 欧拉角的表示欧拉角通常用三个角度来描述刚体在空间中的姿态,常见的表示方式有欧拉角的旋转顺序不同。
在MATLAB中,通常采用Z-Y-X的旋转顺序,即先绕Z轴旋转、再绕Y轴旋转、最后绕X轴旋转。
这样的表示方式比较符合常规的坐标系变换规则,也便于与旋转矩阵相互转换。
2. 旋转矩阵的定义旋转矩阵是描述刚体在空间中旋转变换的一个重要工具,通常用一个3x3的矩阵来表示。
在欧拉角到旋转矩阵的转换中,需要根据欧拉角的具体取值来确定旋转矩阵的元素值。
3. MATLAB实现步骤在MATLAB中,实现欧拉角到旋转矩阵的转换通常分为以下几个步骤:- 定义欧拉角变量:在MATLAB中可以使用符号变量来表示欧拉角,也可以直接使用数值变量来代表具体的角度数值。
- 计算旋转矩阵:根据欧拉角的具体取值,利用MATLAB中提供的旋转矩阵计算函数,如`eul2rotm`,来计算对应的旋转矩阵。
- 输出结果:将计算得到的旋转矩阵进行输出,可以通过命令窗口输出,也可以在MATLAB图形界面中可视化显示。
4. 示例代码以下是利用MATLAB实现欧拉角到旋转矩阵转换的示例代码:```matlab定义欧拉角变量phi = 30; 绕X轴旋转角度theta = 45; 绕Y轴旋转角度psi = 60; 绕Z轴旋转角度计算旋转矩阵R = eul2rotm([psi, theta, phi], 'ZYX');输出结果disp('欧拉角到旋转矩阵的转换结果:');disp(R);```在这段示例代码中,首先定义了绕X轴、Y轴、Z轴的欧拉角值,然后利用`eul2rotm`函数计算了对应的旋转矩阵,并通过命令窗口输出了结果。
数据转换与欧拉角 22页PPT文档
ex1 ez2
e
y1
e
z
2
z1
ez1 ex 2 ez1 e y 2 ez1 ez 2 z2
r
y2
A12 e1 e2T r1 A12r2
坐标转换矩阵
O y1
x1
x2
特例
cos sin 0
AXx sin cos 0
0
0 1
z1
但其分量与坐标系有关
x1
r1
y
1
z 1
x2
r2
y2
z 2
z2
r
y2
O y1
x1
x2
rx1ex1y1ey1z1ez1 x2ex2y2ey2z2ez2
x1
x2
e1Tr1 ex1
ey1
d 2r dt2
r r3
而轨道根数表示法是 在卫星轨道平面内的 极坐标中列写的
a (1 e 2 ) r
1 e cos f
Z
y'
z' i
x'
fp
O
ω
Y
Ω
λ
N
X
在卫星轨道平面内的轨道坐标系Ox’y’z’中
Z
x ' r
y
'
0
很容易得到
z ' 0
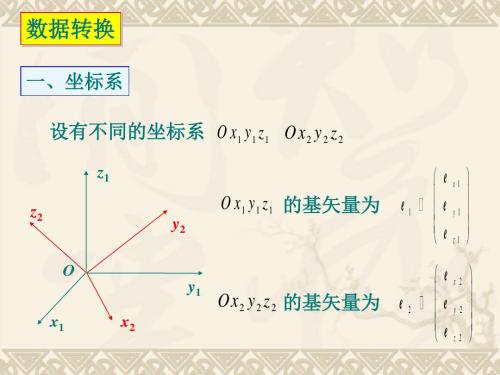
数据转换
一、坐标系
设有不同的坐标系 O x1 y1 z1 O x2 y2 z2
z1 z2
e x1
gyro acc计算欧拉角 单位

Gyro Acc计算欧拉角单位1. 概述在飞行器、无人机、航天器等领域,欧拉角是描述飞行器姿态的重要参数之一。
欧拉角包括俯仰角、横滚角和偏航角,用于描述飞行器在空间中的姿态变化。
而在实际应用中,常常需要利用陀螺仪和加速度计等传感器来计算欧拉角。
本文将重点介绍如何利用陀螺仪(Gyro)和加速度计(Acc)计算欧拉角,并探讨计算过程中的单位问题。
2. 陀螺仪和加速度计的原理陀螺仪是一种测量角速度的传感器,常用于确定飞行器的姿态变化。
加速度计则用于测量物体的加速度,可用于确定物体的姿态。
在飞行器中,通常会配备三轴陀螺仪和三轴加速度计,用于测量飞行器在空间中的姿态变化。
3. 欧拉角的计算在利用陀螺仪和加速度计计算欧拉角时,常使用“互补滤波”等算法,通过融合两种传感器的数据来获得更加稳定和准确的姿态角度。
具体的计算过程涉及到角速度的积分、加速度的测量等多个步骤,需要综合考虑各种误差对计算结果的影响。
4. 单位的转换在欧拉角的计算过程中,常涉及到不同传感器的输出单位。
陀螺仪通常输出的是角速度(rad/s),而加速度计输出的是加速度(m/s^2),在计算过程中需要将其转换为统一的单位,以确保计算的准确性。
4.1 角速度单位的转换陀螺仪通常输出的是角速度,常见的单位有弧度每秒(rad/s)和度每秒(°/s)。
在进行欧拉角计算时,需要将角速度统一转换为弧度每秒的单位,以便与加速度计的输出单位保持一致。
4.2 加速度单位的转换加速度计输出的是加速度,通常的单位是米每平方秒(m/s^2)。
在进行欧拉角计算时,需要确保加速度的单位与角速度统一,通常会直接使用加速度的单位进行计算。
5. 结论利用陀螺仪和加速度计计算欧拉角是飞行器姿态确定的重要方法之一。
在计算过程中,需要注意传感器输出的单位,并进行必要的转换,以确保计算结果的准确性。
在实际应用中,还需要考虑到传感器的误差、测量精度等因素,以获得更加稳定和可靠的姿态角度。
三轴加速度计算欧拉角

三轴加速度计算欧拉角
三轴加速度计通常采用电容式感应方式来测量加速度。
它包含一个或多个微电子机械系统(MEMS)加速度传感器,传感器内部有一个质量可以在受力时移动的结构。
当物体受到外力作用时,传感器内部的质量结构会发生位移,由位移量可以计算得到物体的加速度。
为了得到物体的欧拉角,首先需要根据三轴加速度计的数据计算出物体的加速度值,然后再根据加速度值计算出物体的姿态角度。
具体的计算过程如下:
1.将三轴加速度计的数据转化为加速度的物理量。
三轴加速度计通常输出的是模拟电压值或数字数值,需要经过转换才能得到物体的加速度。
转换过程通常涉及到校准、放大或数字信号处理等步骤。
2. 根据加速度数据计算物体的倾斜角度。
三轴加速度计的数据包含了物体在X、Y、Z轴方向上的加速度值,可以通过计算向量和力的夹角来得到物体的倾斜角度。
根据三角函数的关系,有sinθ = Ax / g,cosθ = Ay / g,其中Ax和Ay是物体在X和Y轴方向上的加速度值,g是重力加速度。
通过计算反余弦函数可以得到物体的倾斜角度。
3. 根据倾斜角度计算物体的偏航角。
倾斜角度只能得到物体的俯仰(pitch)和横滚(roll)角度,要得到物体的偏航(yaw)角度还需要考虑物体的自旋(rotation)。
可以通过结合磁力计等其他传感器的数据来计算物体的偏航角度。
综上所述,三轴加速度计可以通过测量物体在三个方向上的加速度来计算物体的姿态角度。
计算欧拉角的过程主要包括将加速度数据转化为加速度的物理量、计算物体的倾斜角度和偏航角度。
MPU6050教程
第错误!未定义书签。
页共10页MPU6050教程1.1MPU6050简介如果你想玩四轴,想搞什么空中鼠标,平衡车等待,那么MPU6050真的是太强大了,能做很多东西。
玩MPU6050的步骤:1.学习I2C ,I2C 就是MPU6050传送数据到单片机的一种协议,类似于USB ,当然USB 还是比较有难度的。
2.了解MPU6050相关寄存器,有中文版本的,一边学一边看例程就可以获取数据了。
3.把获取的数据进行各种处理。
1.2IIC 简介IIC 可以去看下我们野火相关的教程,在这里只是简单地介绍下,先看下我们的书或者教程,从EEPROM 里面写入和读取数据,因为EEPROM 写入和读取数据也是根据I2C 协议来的。
I2C 有分软件和硬件,软件就你通过对I2C 的时钟线和数据线,可能你不知道时钟线和数据线,那还是先去学I2C 的基础教程。
软件模拟I2C 就是根据下面的图然后再适当的时候给时钟线和数据线高低,具体可以看I2C 的协议见图1-1。
图1-1IIC 起始字节时序图这部分学习的诀窍就是:先写下I2C通讯的一个环节就好了,比如起始字节,其他的也是大同小异,直接上网找例程就好了,想要用软件模拟出全部的时序当然也可以。
还有一个方式可以用I2C读写数据,就是硬件I2C,硬件I2C就是单片机内部的电路,可以将I2C的时序用硬件电路搞出来,这样子你读写数据就方便很多了。
STM32硬件I2C可以去看我们野火的教程。
1.3读取MPU6050原始数据我们先来认识下MPU6050的硬件,这是MPU6050模块的图片,注意是模块,中间那个才是MPU6050,只有MPU6050是不够的,还要有一些外围电路才行,这就跟51芯片跟最小系统的区别一样。
图1-2MPU6050模块正面图1-3MPU6050模块背面管脚名称说明VCC 3.3-5V(内部有稳压芯片)GND地线SCL MPU6050作为从机时IIC时钟线SDA MPU6050作为从机时IIC数据线XCL MPU6050作为主机时IIC时钟线XDA MPU6050作为主机时IIC数据线AD0地址管脚,该管脚决定了IIC地址的最低一位INT中断引脚这里重点讲解AD0的作用,I2C通讯中从机是要有地址的,以区别多个从机。
pcl 法向量转欧拉角
pcl 法向量转欧拉角点云(Point Cloud)是一个由大量点构成的三维数据结构,常用于表示三维空间中的物体或环境。
而PCL(Point Cloud Library)是一个开源的库,专门用于处理点云数据。
在点云处理中,常常需要利用法向量来描述点云的表面特征。
本文将详细介绍如何将法向量转换为欧拉角,以及这一过程的意义和应用。
首先,我们需要了解什么是法向量。
在数学和几何学中,法向量是指与曲线、曲面或其他几何对象正交的向量。
对于点云而言,法向量可以看作是垂直于表面的向量,它可以帮助我们理解点云的形状和拓扑结构。
在PCL中,可以通过计算点云的法向量来获取每个点的法向量信息。
而将法向量转换为欧拉角的过程实际上是将法向量的方向信息转换为欧拉角的表示形式,从而更好地理解点云的几何特征。
具体而言,欧拉角是指将旋转描述为绕不同轴旋转的角度。
在三维空间中,常用的欧拉角表示形式有三种:滚动角(roll)、俯仰角(pitch)和偏航角(yaw)。
滚动角表示绕X轴旋转的角度,俯仰角表示绕Y轴旋转的角度,偏航角表示绕Z轴旋转的角度。
通过将法向量转换为欧拉角,我们可以更加直观地理解点云中的旋转信息。
然而,法向量转换为欧拉角并非一件简单的事情。
由于欧拉角存在奇异性和不唯一性,一般采用四元数(quaternion)来进行中间转换。
事实上,四元数是一种复数扩展,由一个实部和三个虚部组成。
通过将法向量转换为四元数,再通过四元数转换为欧拉角,可以避免奇异性和不唯一性的问题。
在通过PCL进行点云处理时,法向量的转换为欧拉角具有一定的指导意义。
首先,通过欧拉角的表示形式,我们可以更好地理解点云的旋转特征,比如表面的倾斜角度、物体的朝向等。
其次,欧拉角可以作为点云特征的一部分,用于点云分类、配准和识别等任务中,从而提高点云处理的准确性和效率。
总结起来,本文介绍了如何将法向量转换为欧拉角,并阐述了这一过程的意义和应用。
通过将法向量转换为欧拉角,我们可以更加全面地理解点云的几何特征,行使更加精确的点云处理任务。
骨科手术仿真模拟训练系统的构建研究
现代电子技术Modern Electronics TechniqueJun.2023Vol.46No.122023年6月15日第46卷第12期0引言虚拟现实技术通常是通过计算机的模拟,将现实世界的真实场景模拟到虚拟环境中,并且可以提供给用户多种交互方式,这样就会给使用者一种等同于真实环境的沉浸式体验[1]。
现阶段虚拟现实技术已在自动驾驶、VR 影视、虚拟游戏、医疗等领域取得了广泛的应用[2⁃3]。
而虚拟手术则是将虚拟现实中的物体碰撞检测、姿态传感、3D 物体旋转、虚拟场景构建等相关理论技术引入到医学领域[4⁃5]。
现有的医学临床实践培训相对比较依赖尸体、模型、动物等,而且成本高、风险系数大。
而虚拟现实技术的出现给这一医学问题提供了解决方法,在减少手术成本、提高培训效率、降低可行性风险方面,虚拟交互手术比传统临床培训更具优势[4⁃5]。
国内外目前针对虚拟现实系统的开发在医学各个领域也取得了很多成效[6⁃7]。
在智能仿真医学方面,研究人员将计算机技术与医学进一步融合拓展,市面上已经有很多成熟的产品投入使用[8]。
肖文君等人设计了医学图像观察系统,为医师在医学中的诊断提供了支持[9]。
为了能够增强使用者的沉浸感和体验感,虚拟过程复现医生在使用手术器械对人体器官进行触碰、感知、操作等情景,虚拟手术仿真系统具有提供实时力反馈的能力[10]。
王穗源等人探讨研究了数字化虚拟技术在胫骨DOI :10.16652/j.issn.1004⁃373x.2023.12.024引用格式:弭博岩,王鹏龙,王萌,等.骨科手术仿真模拟训练系统的构建研究[J].现代电子技术,2023,46(12):141⁃145.骨科手术仿真模拟训练系统的构建研究弭博岩,王鹏龙,王萌,郑奋(海军军医大学计算机与仿真技术教研室,上海200000)摘要:针对现阶段骨科手术培训实践性弱、手术风险系数大、耗材成本高的缺点,文中提出一种将虚拟现实技术与骨科手术相结合的骨科手术训练系统。
旋转向量转欧拉角 python
旋转向量转欧拉角python欧拉角是一种在三维空间中表示旋转的常用角度,它包括三个角度:ψ、θ、φ。
在许多计算机图形学和机器人学的应用中,欧拉角具有重要的地位。
为了方便表示和计算,我们可以通过旋转向量来转换欧拉角。
在Python中,我们可以利用常用的线性代数库numpy来实现旋转向量转欧拉角的功能。
旋转向量与欧拉角的关系可以通过以下公式表示:ω= [ωx, ωy, ωz] = [cos(ψ) * sin(θ), sin(ψ) * sin(θ), cos(ψ) * cos(θ)]接下来,我们来看一下如何利用Python实现旋转向量转欧拉角的方法。
首先,我们需要导入numpy库:```pythonimport numpy as np```然后,我们可以编写一个函数来实现旋转向量转欧拉角:```pythondef rotation_vector_to_euler_angle(rotation_vector):"""将旋转向量转换为欧拉角:param rotation_vector: 旋转向量,长度为3的numpy 数组:return: 欧拉角,长度为3的numpy 数组"""# 计算欧拉角euler_angle = np.array([np.arctan2(rotation_vector[1], rotation_vector[0]),np.arctan2(rotation_vector[2], rotation_vector[0]),np.atan2(rotation_vector[2], rotation_vector[1])])return euler_angle```接下来,我们通过一个示例代码来解析这个函数:```python# 生成一个随机的旋转向量rotation_vector = np.random.rand(3)# 将旋转向量转换为欧拉角euler_angle = rotation_vector_to_euler_angle(rotation_vector)print("旋转向量:", rotation_vector)print("欧拉角:", euler_angle)```这个示例代码会随机生成一个旋转向量,然后将其转换为欧拉角并打印结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
e x1 位矢量在第1个坐标系 T e1 e2 e y1 e x 2 e y 2 e z 2 中的投影(列阵) e z1 e x1 e x 2 e x1 e y 2 e x1 e z 2 z1 e e y1 x 2 e y1 e y 2 e y1 e z 2 e z 1 e x 2 e z 1 e y 2 e z 1 e z 2 z2 r y2
T 1 1
T r1 e1 e2 r2
r
O
T 2 2
y2
y1 x1 x2
e x1 e1 e1T e y1 e x1 e z1
e y1
e z1
1 0 0 0 1 0 0 0 1
T r1 e1 e2 r2
y
Y
R = Ro + r
cos sin A 0 sin cos 0 0 0 1
r R o Ro
x θ
X’
O
T
X
R Ro Ar
r A ( R Ro )
四、轨道的转换关系
卫星的运动微分方程 是在惯性坐标系 OXYZ中列写的
Z
dr r 3 2 dt r
y1 y4 y y 2 5 y3 y6 2 y4 y1 2 y5 y 2 y 2 y 5 2 4 y6 g
可以用matlab的程序求解
A在惯性坐标系中,其动力学方程为
m F r
其分量形式为
正是刚体转动中的欧拉角:
z' i O Ω λ y'
Z
x'
f
ω N
p Y
, ,
0,2 进动角 0, 章动角 0,2 自转角
X
五、欧拉角定义
z2
OXYZ:固定坐标系,定系 Oxi yi zi:与刚体固连的结体 系,动系,下标表示第几次 转动。初始时结体系与参考 系重合
Ω
X
ω
N
e
i ( f )
轨道坐标系
AXx ' A() A(i) A( f )
六、两种轨道计算的转换关系
(1)已知轨道根数,求出轨道后
r, f , , i, 均已知,对每一个计算点,
y’ y x’ x
X x ' Y AXx ' y ' Z z '
T A12 e1 e2
第2个坐标系的z轴单
坐标转换矩阵
O y1 x1 x2
r1 A12 r2
特例
cos AXx sin 0
1 rx 0 0
sin cos 0
0 0 1
Y y
r
θ O
x
X
cos rX AXx rx sin 0
sin cos 0
0 0 1
X
x1x2 x3
下面把欧拉角与轨道根数联系起来 i 表示轨道顷角;ON 表示节线,是轨道平面与地 球赤道平面的交线。 Ω 表示升交点赤径,节线 ON与X轴的夹角。 ω 表示近地点幅角,节线ON 与 e 的夹角。
Z
r
S
h
i
O
i
Y
极坐标系
e1T r1 e x1
e y1
x1 T e z1 y1 e2 r2 e x 2 z 1
ey2
x2 e z 2 y2 z 2
二、坐标转换矩阵
T r e1T r1 e2 r2
z1 z2
e1 e r e1 e r
Z A O Y X o x y z B
B在非惯性坐标系中,其动力学方程为
m F mω×(ω×r) 2 mω×r r
其分量形式为
z
2 x 2 y x 2 y 2 x y g z x 0 初始条件为 y r z 0
B
o x
y
x vx y vy z vz
根据相对运动微分方程求解:
2 x 2 y x 2 y 2 x y g z
设
y1 x, y2 y, y3 z y4 x, y5 y, y6 z
y' z' i
x'
r
O
Ω
f
p Y
根据前面的分析,有
X x ' Y AXx ' y ' Z z '
λ
ω N
AXx ' ?
X
如果让 Ox ' y ' z ' 开始时 与 OXYZ 重合,则图中 定义的三个角度
, i, ( f )
z x y
(1)点头同意――主要是章动角在变化,另两个角为零; (2)摇头不同意――主要是自转角在变化,另两个角为零; (3)摇头晃脑――主要是进动角在变化,自转角为零,章动角不为零。
欧拉角的方向余弦矩阵
A AXx3 AXx1 Ax1 x2 Ax2 x3 A( ) A( ) A( )
T r2 A121r1 A12 r1 A21r1
(3)传递性
r1 A12 r2
r2 A23r3
r1 A12 r2 A12 A23r3
A13 A12 A23
r1 A13r3
例题 两位观察者,A 在地面(惯性坐标系)上, B 在匀速转动的转盘(非惯性系)上。B随手 抛出一物体,求两位观察者认为物体应遵守的 动力学方程,看到的运动轨迹,以及相应的转 换关系。
这样就把轨道平面内卫 星轨道坐标系中的曲线 转化到惯性坐标系中了
Z
AXx ' A() A(i) A( f )
X Y
x' r y ' 0 z ' 0
(2)已知初始位置、速度,求出轨道后 根据初始的位置和速度,可以求出全部的轨道根数 (ppt中给出过计算公式) ,特别是 , i, 均已知,对每一个计算点, Z Y
mx 0 my 0 mz mg x a y b r z c
Z A O Y X
初始条件为
x vx r y vy z vz
坐标转换关系 设OXYZ为惯性系 oxyz为非惯性系 Y’
z3
Z z1
y3 y2 y1
欧拉角的转动次序:
1.绕Z轴转动 2.绕x1轴转动 3.绕z2轴转动
O
Y
X
x1 x2
x3
欧拉角与方位是一一对应的: 给定欧拉角 , , 坐标系可唯一确定。 给定坐标系, 欧拉角也是唯一确定的。 O Z
z
y
角容易确定
如何确定、?
X
Y
x
N(节线)
找xy平面与XY平面 的交线,称为节线
关于欧拉角的具体例子 人的头部相对身体可以认为是作定点运动。如果 初始状态头部的固连坐标系定义为:前后是x方向, 左右是y方向,上下是z方向,如图所示。 请说出下列常见的头部动作主要是什么欧拉角在 变化? (1)点头同意; (2)摇头不同意; (3)摇头晃脑吟诗。
sin cos 0
0 1 cos 0 0 sin 1 0 0
三、坐标转换矩阵的性质 (1) A11 A22 I (2)单位正交矩阵 AT A1
r1 A12 r2
X y
x X T y AXx Y z Z
这样就把惯性坐标系中 的曲线转化到了轨道平 面内的极坐标中
AXx A() A(i) A()
x
设 r 是矢量,其与坐标系无关。
z1 z2 O
但其分量与坐标系有关
x1 r1 y1 z 1 x2 r2 y2 z 2
r
y2
y1
x1 x2
r x1ex1 y1e y1 z1ez1 x2ex 2 y2e y 2 z2ez 2
2
y' z' i
x'
f
OΩpຫໍສະໝຸດ Y而轨道根数表示法是 在卫星轨道平面内的 极坐标中列写的
ω N
λ
a (1 e ) r 1 e cos f
2
X
在卫星轨道平面内的轨道坐标系Ox’y’z’中
Z
x' r y ' 0 很容易得到 z ' 0
数据转换
一、坐标系 设有不同的坐标系 Ox1 y1 z1 Ox2 y2 z2
z1 z2 O
Ox1 y1 z1 的基矢量为
y2
e x1 e1 e y1 e z1 ex 2 e2 e y 2 e z2
y1
x1 x2
Ox2 y2 z2 的基矢量为
cos A( ) sin 0 sin cos 0 0 0 1
z2
Z
z3
z1
y3
y2
y1
O
0 1 A( ) 0 cos 0 sin
sin cos 0
Y
cos A( ) sin 0
