人教版八年级上册第十一章三角形复习课教学设计
人教版八年级上册第十一章三角形复习课教学设计

人教版八年级上册第十一章三角形复习课教学设计教学目标】1、进一步理解并掌握三角形及三角形的重要线段的概念,会利用三角形的内角和定理及外角公式、多边形的内角和公式及外角和计算角度。
2、复本章内容,整理本章知识,形成知识体系,体会研究几何问题的思路和方法。
3、进一步发展推理能力,能够有条理地思考、解决问题。
教学重点】复本章内容并运用它们进行有关的计算和证明,构建本章知识结构【教学难点】灵活运用、解决问题教材分析】本章主要内容有三角形的有关线段、角,多边形及内角和、镶嵌等。
这些知识加深了学生对三角形的认识,既是研究特殊三角形的基础,也是研究其他图形的基础。
【学情分析】学生在学完本章知识后,对三角形的有关知识已有所了解,本节课将进一步对知识加以理解、运用。
课型】复课教学时间分配】1课时教学准备】PPT教学方法】讲授法、谈话法、演示法、练法教学过程】一、情景导入、直击主题根据网上一句流行的话“世界那么大,我想去看看”带领大家出去看看。
由三哥和娇妹先带大家去往埃及金字塔,引出本节课的复知识——三角形。
出示金字塔照片,让学生说出熟悉的图形——三角形,给出概念填空:由的线段相接所组成的图形叫做三角形。
出示一张路标,让学生说出特殊三角形——等边三角形,将它放入框中。
2、复旧知、梳理脉络让学生自由选择目的地——法国、英国、美国,开始复三角形的知识。
法国(卢浮宫)——三角形的有关线段情景题:在参观XXX前,三哥和娇妹决定将肚子填饱,但是由于三哥的XXX,两人只带了一个三明治,要想两人吃得同样多的三明治,应该怎么分?答:任意一边的中线。
任何一边的中线可以将三角形分成两个面积相等的三角形。
由中线引出三角形有关的线段如图:1)若AD⊥BC,垂足为D,则:90°;在三角形中,有高线。
计算面积有关2)若∠BAE =∠CAE,AE与BC相交于点E,则:线段AE是△ABC的_________;3)若AF =CF,BF与AC相交于点F。
人教版八年级上册数学教案:第11章三角形复习

3、下列各图中,正确画出 AC 边上的高的是(
B
B
B
E
D. − +
)
B
2 题图
AE
A
C
AB
CE
C
C EA
4、点到直线的距离是指这点到这条直线的(
).
A、垂线段 B、垂线 C、垂线的长度 D、垂线段的长度
5、某零件如图,要求∠A=90°,∠B=32°,∠C=21°,当检验员量
得∠BDC=145°,就断定这个零件不合格,你能说出其中的道理吗?
2.在△ABC 中,两条角平分线 BD、CE 相交于点 O,∠BOC=116°,那么∠A 的度数是______.
3.在△ABC 中,∠B-∠A=15°,∠C-∠B=60°,则△ABC 的形状为
_________.
4.将两块直角三角尺的直角顶点重合为如图的位 A
C
置,若∠AOD=100 0 ,则∠BOC=
=180°.
证明:过点 A 作直线 MN,使 MN∥BC
C
B
▲三角形的一边与另一边的 ●结论:三角形的一个外角等于与它
推论:三角形的一个外角大于与它
求下列图中∠1 和∠2
组成的角叫做三角形的外角. 两个内角的和. 任何一个内角.
1 40° 2
A
70°
B 40°
C
1
2
D AB∥ CD
l 2 1
30°
∠1= ,∠2= ;
A.锐角三角形
B.直角三角形
成,让
C.钝角三角形
D.锐角三角形或钝角三角形
学生及
练 2.如果三条线段的比是:
时巩固
习 (1)5:20:30
(2)5:10:15
第十一章三角形综合复习教案人教版数学八年级上册

三角形综合1三边关系定理三角形三边关系定理:三角形任意两边之和大于第三边.(推论:两边之差<第三边<两边之和)求三角形第三边的范围2中线的性质三角形中的几条重要线段:(1)三角形的中线(三条中线的交点叫重心)(2)三角形的角平分线(三条角平分线的交点叫做内心)(3)三角形的高(三条高线的交点叫垂心)3三角形内角和与外角三角形内角和定理:三角形的内角和等于180°.定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.三角形外角定理:三角形的一个外角等于与它不相邻的两个内角的和.多边形的内角和:(n2)×1800.正n边形的单个内角为.多边形的外角和:360°.正n边形的单个外角为.多边形的对角线条4飞镖模型与“8”字模型飞镖模型:如图:∠BDC=∠A+∠B+∠C.8字模型:如图:∠A+∠D=∠B+∠C.例1.(1)下列各组线段,不能组成三角形的是()A.1,2,3B.2,3,4C.3,4,5D.5,12,13(2)若三角形的三边分别为4,x,9,则x的取值范围是______________,三角形周长的取值范围是______________.1.一个等腰三角形的两边长分别是3和7 ,则它的周长为().A.17 B.15 C.13 D.13或172.有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为().A.1B.2 C.3D.43.(1)等腰三角形的腰长为6,它底边长a的范围是;(2)等腰三角形的底边长为4,则它腰长b的范围是.4.已知a ,b ,c 是△ABC 的三条边长,化简c a b c b a ----+的结果为( )A .2a+2bB .2a+2b ﹣2cC .2b ﹣2cD .2a例2.如图所示,在△ABC 中,AD 为BC 边上的中线,若AB =5cm ,AC =3cm ,则△ABD 的周长比△ACD 周长多( )A .5cmB .3cmC .8cmD .2cm例3.如图,△ABC 中,D 、E 分别为BC 、AD 的中点,S △ABC =20,则阴影部分的面积是( )A .18B .10C .5D .11.如图AD 是△ABC 的中线,DE 是△ADC 的中线,EF 是△DEC 的中线,FG 是△EFC 的中线,若S △GFC =1cm 2,则S △ABC =______________.2.如图,已知点D 、E 、F 分别是BC 、AD 、BE 的中点,S △ABC =4,则S △EFC =______________.3.如图,AD 是△ABC 的中线,DE=2AE ,若△ABC 的面积是18平方厘米,则△ABE 的面积=______________.4.如图,在△ABC 中,E 为AC 的中点,AD 平分∠BAC ,BD :CD =2:3,AD 与BE 相交于点O ,若△OAE 的面积比△BOD 的面积大1,则△ABC 的面积是( )A .8B .9C .10D .115.如图,在△ABC 中E 是AC 上的一点,EC =2AE ,点D 是BC 的中点,连接AD 、BE 交于点F ,若△ABC 的面积为36,则四边形CDFE 的面积为 .6.如图,在△ABC 中,∠BAC =90°,AB =6,AC =8,BC =10,AD 是高,BE 是中线,CF 是角平分线,CF 交AD 于点G ,交BE 于点H ,下面说法正确的是( ) ①△ABE 的面积=△BCE 的面积;②∠AFG =∠AGF ;③∠F AG =2∠ACF ;④AD =2.4.A .①②③④B .①②③C .①②④D .③④例4.在△ABC 中,∠A :∠B :∠C=2:3:4,则∠B= .1.已知在△ABC 中,∠A=60°,∠B ﹣∠C=40°,则∠B= .2.锐角三角形ABC 中,∠C =2∠B ,则∠B 的范围是( )A. 10°<∠B<20°B. 20°<∠B<30°C. 30°<∠B<45°D. 45°<∠B<60°例5.已知一个凸多边形的每个内角都是150°,则它的边数为. 1.一个多边形的内角和比它的外角和的3倍还多180度,求这个多边形的边数.2.已知正多边形的一个外角为40°,则这个正多边形的边数是.3.正多边形的一个外角是40°,则这个正多边形从一个顶点出发有条对角线.例6.把一副三角板按如图所示的方式摆放,则两条斜边所成的钝角x为度.1.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:(1)图1中的∠ABC的度数为.(2)图2中已知AE∥BC,则∠AFD的度数为.例7.(1)如图1,有一个五角星ABCDE,你能说明∠A+∠B+∠C+∠D+∠E=180°吗?(2)如图2、图3,如果点B向右移到AC上,或AC的另一侧时,上述结论仍然成立吗?1.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F=_ __.2.如图,∠O=140°,∠P=100°,BP、CP分别平分∠ABO、∠ACO,则∠A=_______.3.如图(1),求出∠A+∠B+∠C+∠D+∠E+∠F的度数;如图(2),求出∠A+∠B+∠C+∠D+∠E+∠F的度数.1.已知:如图1,线段AB、CD相交于点O,连接AD、CB,如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:__________;(2)在图2中,若∠D=40°,∠B=30°,试求∠P的度数;(写出解答过程)(3)如果图2中∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间的数量关系.(直接写出结论即可)例8.如图,已知∠1=48°,∠2=56°,∠3=66°,则∠4的度数为.1.如图,已知∠1=48°,∠2=56°,则∠3+∠4的度数为.例9.如图,在折纸活动中,小明制作了一张△ABC的纸片,点D、E分别是边AB、AC上的点,将△ABC沿着DE折叠压平,A与A’重合,若∠A=70°,则∠1+∠2= .1.现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.研究(1):如果折成图①的形状,使点A落在CE上,则∠1与∠A的数量关系是;研究(2):如果折成图②的形状,猜想∠1+∠2与∠A的数量关系是;研究(3):如果折成图③的形状,猜想∠1、∠2和∠A的数量关系,并说明理由.例10.如图,CD⊥AB,BE⊥AC,垂足分别为D、E,求证:∠C=∠B,∠CFE=∠A.1.如图,AB⊥BD,AC⊥CE,ED⊥BD,已知∠A=35°,则∠E= .2.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,∠A=65°,则∠BCD= .3.小明在学习过程中,对教材中的一个有趣问题做如下探究:【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;【探究廷伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.。
人教版八年级数学上册集体备课(教案设计)第十一章《三角形》(复习)

你能用三角形的内角和说明n边形的内角和吗?
5、三角形的外角和是多少?n边形的外角和是多少?
你能说明为什么多边形的外ቤተ መጻሕፍቲ ባይዱ和与边数无关吗?
6、怎样才算是平面镶嵌?平面镶嵌的条件是什么?能单独进行平面镶嵌的多边形有哪些?
你能举一个几个多边形进行平面镶嵌的例子吗?
三、难点释疑拓展延伸
例题导引
例1如图,在△ABC中,∠A︰∠B︰∠C=3︰4︰5,BD、CE分别是边AC、AB上的高,BD、CE相交于点H,求∠BHC的度数。
例2如图,把△ABC沿DE折叠,当点A落在四边形BCDE内部时,
探索∠A与∠1+∠2有什么数量关系?并说明理由。
例3.⊿ABC中,⑴如图⑷,∠DBC和∠ECB的角平分线相交于点O;⑵如图⑸,∠ABC的角平分线BD和∠ACE的角平分线相交于点O;如图⑹,∠CBD的角平分线BO和∠BCE的角平分线CO相交于点0,试猜想∠A与∠D的关系,并选择其中一个进行证明.
四、反思小结当堂测评
(一)反思小结:
回顾知识结构图
(二)当堂测评:
长江作业单元测试题
课前准备及预习:
一、激趣导入,呈现目标
(一)复习导入:
(二)呈现目标
二、自学探究,交流展示
回顾与思考
1、什么是三角形?什么是多边形?什么是正多边形?
三角形是不是多边形?
2、什么是三角形的高、中线、角平分线?什么是对角线?
三角形有对角线吗?n边形的的对角线有多少条?
3、三角形的三条高,三条中线,三条角平分线各有什么特点?
初备人:谢彬审核人:八年级数学组编写时间:2018-9-1
总课题
第十一章三角形
新人教版八年级数学上册第十一章三角形总复习教案

4、解决问题。
(2)一个等腰三角形的底是23厘米,腰是32厘米。则它的周长是多少厘米?
五、全课总结,质疑评价提升。
总结:今天的复习中你还有什么疑问吗?有新的收获吗?学得高兴吗?
小组汇报,教师小结。
形成知识结构网络
三角形特征、各部分名称及字母表示
通过同学们刚才的整理,所有的知识形成了一个整体,这就是复习与整理的作用了。这样做有什么好处呢?
三、巩固训练,拓展提升。
(一)复习三角形的特性,出示判断题,错的请说明原因
1.任何三角形都有三条高和三条底边。()
2.由三条直线围成的图形叫做三角形。()
3.三角形不容易变形。()
4.我能画一个边长分别是4厘米、3厘米、5厘米的三角形。()
A
B
C
D
四、知识应用,能力拓展
3、猜一猜。
(1)下面的三角形都被一张纸遮住了一部分。你能确定它们各是什么三角形吗?
(2)有一个三角形,其中一个角是20。,它可能是什么三角形?如果还知道第二个角是65。,那么你知道它是什么三角形了吗?
5.智慧角
⑴已知三角形中的两条边分别是4cm、6cm,那么第三条边必须大于()cm,必须小于()cm;如果这是一个等腰三角形,那么第三条边可以是()cm。
师:你会联想到哪个图形正好和他有相反的特性吗?
⑤三角形按角分:锐角三角形、直角三角形、钝角三角形。
师:什么样的三角形是锐角三角形呢?……你的三角形属于哪一类?为什么?判断的简单方法:以最大角判断)
⑥三角形的内角和是180度。
师:已经知道两个角的度数,如何求第三个角的度数呢?
⑦三角形按边分:等腰三角形、等边三角形。
新人教版八年级上册数学第11章《三角形》复习课教学设计
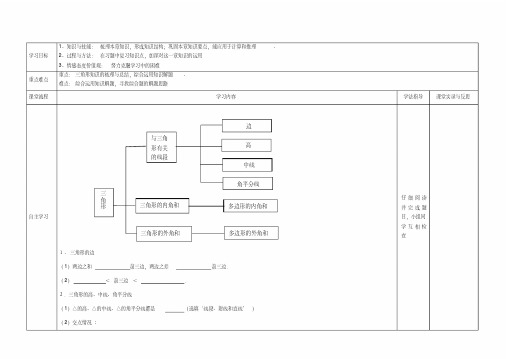
课堂流程
学习内容
与三角 形有关 的线段
边 高 中线
自主学习
三
角
形
三角形的内角和
三角形的外角和
角平分线 多边形的内角和 多边形的外角和
1 . 三角形的边
( 1)两边之和
第三边,两边之差
( 2)
< 第三边 <
2.三角形的高、中线、角平分线
( 1)△的高、△的中线、△的角平分线都是
( 2)交点情况 :
第三边. .
A2009 =
.
A
A
A
B
C
D
2):如图,△ ABC中, ABC的角平分线与 ACB的外角 ACD的平分线交于 A1 ,若 E 为 BA延长线上一动点,连 EC, AEC与 ACE的角
平分线交于 Q,当 E 滑动时有下面两个结论:
E
① Q+ A1 的值为定值;② Q- A1 的值为定值,其中有且只有一个是正确的,请写出正确的结论,并求出其值
合作探究
c. 三角形的三条角平分线交于一点,交点位于三角形的
.
3 . 三角形内角和定理: 任何三角形的内角和都等于
度.
推论:直角三角形两锐角
.
.
4 . 三角形的一个外角等于
.
5.
的多边形叫做正多边形 .
6 . 多边形的内角和公式: n 边形内角和 =_________________. 多边形的外角和等于 ________.
7. 过多边形的一个顶点可以引 9 条对角线,那么这个 .1980° D . 2160°
8.若一个正多边形的每一个外角为 20°,则这个多边形的边数为(
)
A .9 B .10 C .11 D .18
初中数学人教八年级上册(2023年新编)第十一章 三角形三角形小结复习教案(2)

《三角形复习》第1课时教案一:教学目的对三角形这一章的内容进行梳理总结,建立知识体系,综合运用本章知识解决问题。
在复习课中让学生在原有的基础上进行知识的建构,建立起不同知识之间的内在联系,从而建立起本章的知识结构。
通过三角形的高,中线,角平分线的复习让学生掌握分类讨论数学思想以及方程思想等,让学生体会研究几何问题的一般思路和方法。
二:教学目标知识与技能:1、复习三角形的概念及 基本要素。
2 掌握三角形边角关系、高,中线以及角平分线的相关知识的并能运用。
过程与方法:经历探索三角形有关知识的过程,发展表达能力、推理能力 情感态度与价值观:体会掌握分类讨论数学思想以及方程思想,感受数学的美,体会三角形在现实生活中的应用价值。
三:教学重难点重点; 三角形的概念、边角关系,内角和定理,三角形的“三线”。
难点:三角形的三边关系,以及三角形的高,中线,角平分线的实际运用。
四:教学过程(一)、提问导入活动1:请学生回答下列问题(1)三角形的三边之间有怎样的关系?(2)三角形的三个内角之间有怎样的关系?如何证明这个结论呢?(3)三角形的一个外角与它不相邻的两个内角之间有怎样的关系?(注:画图说明) (4)直角三角形的两个锐角之间有怎样的关系?活动2回忆复习本章知识结构教师组织学生学习本章知识结构图,让学生在草稿纸上画任意画一个三角形的高,中线,角平分线。
)(二)、课堂练习复习与三角形有关的线段:A 组1.若三角形的两边分别为3 和5 ,则第三边长m 的取值 范围是__________. ( 注:抽同学起来回答自己是怎么做的,叙述运用那个知识点) 2.如图:(1)若AD ⊥BC ,垂足为D ,则:∠_____=∠_____ =______(注:在学生回答完之后再延伸提问有哪些直角三角形)(2)若∠BAE =∠CAE ,AE 与BC 相交于点 E ,则:线段AE 是△ABC 的_________; (注:延伸提问∠AEC ,∠AEB 是那个三角形的外角)FD CEAB(3)若AF =CF ,BF 与AC 相交于点F ,则:△ABC 的中 线是_______ (注:延伸提问中线把三角形分成面积相等的两个部分) .B 组 巩固与三角形有关的角:如图,在△ABC 中,∠BAC =80°,∠ABC =60°.(1)∠C =_____ ;(2)若AE 是△ABC 的角平分线,则: ∠AEC = ; (3)若BF 是△ABC 的 高,与角平分线 AE 相交于点O ,则∠EOF = ______ .典型例题例1 已知等腰三角形的两边长分别为10 和6 ,则三角形的周长是 .(注:分类讨论,要求学生画图观察,教师请两位同学上台展示)变式1 若等腰三角形的周长为20,一边长为4,则其他两边长为 .(注意提醒最后看三角形的三条边是否满足三边关系。
初中八年级数学教案-八年级上册数学人教版教案《第十一章 三角形》章节复习【全国一等奖】

《第十一章三角形》复习课教学设计【知识与技能】1.了解与三角形有关的线段(边、高、中线、角平分线).理解三角形两边的和大于第三边,会根据三条线段的长度判断它们能否构成三角形.会画任意三角形的高、中线、角平分线.了解三角形的稳定性.2.了解与三角形有关的角(内角、外角),会用平行线的性质与平角的定义证明三角形内角和等于180°,探索并了解三角形的一个外角等于与它不相邻的两个内角的和.3.了解多边形的有关概念(边、内角、对角线、正多边形),探索并了解多边形的内角和与外角和公式.4.通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌平面,并能运用这几种图形进行简单的镶嵌设计.【过程与方法】结合图形回顾本章知识点,复习几种基本的画图,复习简单的证明技巧,在此基础上,进行典型题、热点题的较大量的训练,旨在提高同学们对三角形有关知识、多边形内角和、外角和知识综合运用能力.【情感态度】通过初步的几何证明的学习培养学生的推理能力,通过由特殊到一般的探究过程的训练培养学生的探索能力,创新能力,以达到培养学生良好学习习惯的目的.【教学重点】三角形的三条重要线段、三角形的内角和、外角和、多边形的内角和、外角和等知识的灵活运用.【教学难点】简单的几何证明及几何知识的简单应用.一、知识框图,整体把握二、回顾思考,梳理知识1.本章的主要内容是:三角形的概念,三角形的三边关系定理,三角形的三条重要线段(高线、中线和角平分线).三角形内角和定理.三角形的外角,多边形的内、外角和定理,简单的平面镶嵌.三角形的稳定性和四边形的不稳定性.2.经历三角形内角和等于180°的验证与证明过程,初步体验对一个规律的发现到确认的艰辛历程.体会证明的重要性,初步接触辅助线在几何研究中不可或缺的作用.3.三角形是我们认识许多其他图形的基础,如研究多边形的内角和时,就是过多边形的某顶点作出它的全部对角线,将多边形的内角和问题转化为三角形的内角和问题.三、典例精析,复习新知例1如图,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为.分析:由三角形内角和定理得∠C=180°-∠A-∠B=180°-65°-75°=40°.折叠以后,变成了四边形,因四边形的内角和为360°,故∠AED∠BDE=360°-∠A-∠B=220°.在△CDE中,∠CDE∠CED=180°-∠C=180°-40°=140°.所以∠2=220°-140°-∠1=60°.例2 在绿茵场上,足球队带球进攻,总是向球门AB冲近,说明这是为什么解:如图,设球员接球时位于点C,他尽力向球门冲近到D,此时不仅距离球门近,射门更有力,而且对球门AB 的张角也扩大,球就更容易射中,理由说明如下:延长CD 到E ,则∠ADE >∠ACE ,∠BDE >∠BCE ,所以∠ADE ∠BDE >∠ACE ∠BCE ,即∠ADB >∠ACB . 【教学说明】1.本题作了一条辅助线,构造了两个三角形的外角,在说理中发挥了至关重要的作用;2.辅助线要画成虚线.例3 已知一个等腰三角形的三边长分别为,2-1,5-3,求其周长.解:本题分类讨论,求出后再求出三边,一定要检验是否符合三角形三边关系定理,若不符合,必须舍去. (1)若=2-1,则=1,此时三边为1,1,2,因为11=2,不符合三角形三边关系,舍去;(2)若=5-3,=43.此时三边为43,21,43,符合三角形三边关系,周长为432143=2. (3)若2-1=5-3,=32.此时三边为32,31,31,因为3131=32,所以不符合三角形三边关系,舍去.综上,此等腰三角形周长为2.例4 如图,D 、E 为△ABC 内的两点,试说明ABAC >BDECDE 的理由.解:本题显然要运用三角形三边关系定理证明.由于BD 、DE 、CE 不是三角形的边,于2121212121212121,所以延长BD 、CE 交于F ,再延长BF 交AC ∠D=m ,∠F=3m .由(1)得m2m=2×3m , ∴=4.例7 阅读下面的问题及解答:如图(1),△ABC 中∠ABC 、∠ACB 的角平分线交于O 点,则∠BOC=90°21∠A=21×180°21∠A ,如图(2),△ABC 中∠ABC 、∠ACB 的三等分线交于O1、O2,则∠BO 1C=32×180°31∠A ,∠BO2C=31×180°32∠A .根据以上信息:(1)你能猜想出它的规律n 等分时[内部有(n-1)个点],∠BO1C=,∠BO n-1C=(用含n 的代数式表示). (2)根据你的猜想,当n=4时说明∠BO 3C 的度数成立. 解:(1)当n=2时,∠BOC=21×180°21∠A ,当n=3时,∠BO 1C=32×180°31∠A ,∠BO2C=31×180°32∠A .由此可见,系数分母即是n ,∠BO 1C 的系数的第一个分子是n-1,第二个分子是1.由此可猜想∠BO 1C=n n 1-×180°n 1∠A .同理:∠BO n-1C=n 1×180°nn 1-∠A . (2)当n=4时,代入所猜想的公式得∠BO 3C=41×180°43∠A .另外,在△BO 3C 中,由三角形内角和定理得∠BO 3C=180°-(∠O 3BC ∠O 3CB )=180°-43(∠ABC ∠ACB )=180°-43(180°-∠A )=41×180°43∠A .结果与猜想一致.【教学说明】本题是阅读猜想题,是热点题型,能大大激发学生的求知欲,深受师生欢迎. 例8 求证:两条平行线被第三条直线所截得的一组同旁内角的平分线互相垂直.(仿照教材证明三角形内角和等于180°的过程进行证明,先画出图形,按图形写出已知和求证,再进行证明.)解:已知:如图,AB ∥CD ,EF 交AB 、CD 于E 、F ,EM 平分∠BEF ,FN 平分∠DFE ,EM 与FN 交于G . 求证:EM ⊥FN 证明:∵AB ∥CD , ∴∠BEF ∠DFE=180°.∵EM 平分∠BEF ,FN 平分∠DFE ,∴∠1=21∠BEF ,∠2=21∠DFE . ∴∠1∠2=21(∠BEF ∠DFE )=21×180°=90°.∴∠EGF=180°-(∠1∠2)=90°.∴EM ⊥FN .【教学说明】证明过程由“∵、∴”构成,要求每一步都有依据.例9 一个多边形从某一个顶点出发截取一个角后,所形成的多边形的内角和是2520°,求原多边形的边数. 解:设原多边形是n 边形,分两种情况讨论:(1)若截线不经过多边形的另一个顶点,则新多边形仍是n 边形(如图(1)).由题设得(n-2)·180°=2520°.解得n=16;(2)若截线经过多边形的顶点,则新多边形(n-1)边形(如图(2)),由题设得(n-1-2)·180°=2520°.解得n=17.综上n=16或17.1.布置练习:从教材“复习题11”中选取.2.完成练习册中本课时的练习.利用知识回顾与典型剖析,使学生进一步巩固和深化对所学知识的理解,建立起清晰的知识框架,形成严谨的思维习惯.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版数学八年级上册三角形复习课教学设计
当阳市慈化初级中学史君姣
【教学目标】
1、进一步理解并掌握三角形及三角形的重要线段的概念,会利用三角形的内角和定
理及外角公式、多边形的内角和公式及外角和计算角度。
2、复习本章内容,整理本章知识,形成知识体系,体会研究几何问题的思路和方法。
3、进一步发展推理能力,能够有条理地思考、解决问题。
【教学重点】
复习本章内容并运用它们进行有关的计算和证明,构建本章知识结构
【教学难点】
灵活运用、解决问题
【教材分析】
本章主要内容有三角形的有关线段、角,多边形及内角和、镶嵌等。
这些知识加深了学生对三角形的认识,既是学习特殊三角形的基础,也是研究其他图形的基础。
【学情分析】
学生在学完本章知识后,对三角形的有关知识已有所了解,本节课将进一步对知识加以理解、运用。
【课型】复习课
【教学时间分配】1课时
【教学准备】PPT
【教学方法】讲授法、谈话法、演示法、练习法
【教学过程】
一、情景导入、直击主题
根据网上一句流行的话“世界那么大,我想去看看”带领大家出去看看。
由三哥和娇妹先带大家去往埃及金字塔,引出本节课的复习知识——三角形。
出示金字塔照片,让学生说出熟悉的图形——三角形,给出概念填空:
由的线段相接所组成的图形叫做三角形。
出示一张路标,让学生说出特殊三角形——等边三角形,将它放入框中。
二、复习旧知、梳理脉络
让学生自由选择目的地——法国、英国、美国,开始复习三角形的知识。
情景题:在参观卢浮宫博物馆前,三哥和娇妹决定将肚子填饱,但是由于三哥的马虎,两人只带了一个三明治,要想两人吃得同样多的三明治,应该怎么分?
答:任意一边的中线。
任何一边的中线可以将三角形分成两个面积相等的三角形。
由中线引出三角形有关的线段
如图:
(1)若AD ⊥BC,垂足为D,则:
∠ =∠ = 90°;
在三角形中,有高线。
计算面积有关
(2)若∠BAE =∠CAE,AE 与BC 相交于点E,则:
线段AE 是△ABC 的_________;
(3)若AF =CF,BF 与AC 相交于点F,
则:△ABC 的中线是________.
三角形的三条中线相交于一点,交点在三角形的内部,叫三角形的重心。
1、下列条件中能组成三角形的是()
A、1cm 2cm 3cm
B、4cm 6cm 5cm
C、5cm 3cm 1cm
D、2cm 8cm 4cm
应用:判断三条线段能否组成三角形
方法:只要看较短的两条线段之和是否大于较长的线段.
2、三角形的三条高所在的直线相交于一点,此点在()
A. 三角形的内部
B.三角形的外部
C.三角形的一条边上
D.不能确定
英国(大英博物馆)——三角形的有关角
出示大英博物馆的图片,提问:为什么房顶是三角形结构?
答:因为三角形具有稳定性。
为了是房屋建造美观,设计师会通过计算角度确定,那三角形的三个角之间又有什么关系呢?那外角呢?
答:三角形的三个内角的和是180o
三角形的外角等于与它不相邻的两个内角的和。
问题:直角三角形的两个锐角相等,则每一个锐角等于度。
问题:如图所示,图中的∠CAB=___________º.
美国(五角大楼)——多边形
出示五角大楼图片,复习多边形内角和公式和外角和。
多边形内角和公式:________________外角和:_________
100°40°
D
B
A
三、典例分析、明确思想 深入五角大楼
例1 一个正多边形的每一个内角都等于120o ,求它的边数。
细品卢浮宫
例2 如图△ABC 中,CD 平分∠ACB,DE ∥BC,∠A =70°,
∠ADE =50°, 求∠BDC 的度数。
探险埃及
例3 如图, △ABC 的∠ABC 、∠ACB 的角平分线交于点O 。
(1)如果∠A=70O ,求∠BOC 的度数。
(2)如果∠A=n o ,求∠BOC 的度数。
(3)如果∠A=100o ,求∠BOC 的度数。
四、当堂检测、巩固升华
小马虎三哥和娇妹不小心弄丢了大家的护照,看看大家能不能通过自己的努力顺利回国呢?大家加油哦!
1、下面四个图形中,线段BE 是⊿ABC 的高的图是( )
A .
B .
C .
D .
2、已知等腰三角形的两边长分别为3和6,则它的周长为( )
A.9
B.12
C.15
D.12或15
B A
C E B A C E B A C E
B A C
E
3、设四边形的内角和等于a,五边形的外角和等于b,则a与b的关系是().
A.a>b B.a=b
C.a<b D.b=a+180o
4、()能铺满地面。
A.正五角形
B.正六边形
C.正七边形
D.正八边形
5、如图所示,在△ABC中,AD⊥BC于D,AE平分∠BAC,且∠B=36°,
∠C=76°,求∠EAD的度数。
思考题
6、如图,∠ACD为△ABC的一个外角,∠ABC、∠ACD的角平分线交于点P 。
(1)若∠ACD=110°,∠ABC=50°,则∠A=_______,∠P=_______
(2)若∠ACD –∠ABC =74°,则∠A=_______,∠P=_______
(3)若∠A=62°, 则∠P=_______
(4)试猜想∠P与∠A之间的数量
关系是: __________________
五、课堂小结、积累沉淀
通过这段旅程,你一定有不少收获吧,和我们一起分享一下吧!
六、布置作业、课后反思
课本P28复习题11 第6、7、8、11题
【板书设计】
P
D
C
B
A。
