材料力学习题答案2
材料力学习题册答案-第2章-拉压

一、 选择题
1.图 1 所示拉杆的外表面上有一斜线,当拉杆变形时,斜线将(
A.平动
B.转动
C.不动
D.平动加转动
D)
2.轴向拉伸细长杆件如图 2 所示,则正确的说法是 ( C )
A.1-1、2-2 面上应力皆均匀分布 B.1-1、2-2 面上应力皆非均匀分布 C. 1-1 面上应力非均匀分布,2-2 面上应力均匀分布 D.1-1 面上应力均匀分布,2-2 面上应力非均匀分布
30KN 1
300mm
l1 解:(1) 轴力图如下
2
400mm
l2
10KN
-
40KN
50KN 3
400mm
l3
10KN
+
10KN
(2)
(3)右端面的位移
=
= 即右端面向左移动 0.204mm。
8.一杆系结构如图所示,试作图表示节点 C 的垂直位移,设 EA 为常数。
A
30
C
30 ΔL2 60 ΔL1
CD 段:σ3= =
Pa=25MPa
2.图为变截面圆钢杆 ABCD,已知 =20KN, = =35KN, = =300mm, =400mm,
D
3
C
P3
2
,绘出轴力图并求杆的最大最小应力。
B
1 P2
A
P1
l3 解:
-
50KN
l2 15KN
l1
20KN
+
AB 段:σ1=
=
=176.9MPa
BC 段:σ2=
反力均匀分布,圆柱承受轴向压力 P,则基座剪切面的剪力
。ห้องสมุดไป่ตู้
材料力学习题册_参考答案(1-9章)

第一章 绪 论一、选择题1.根据均匀性假设,可认为构件的( C )在各处相同。
A.应力B. 应变C.材料的弹性系数D. 位移2.构件的强度是指( C ),刚度是指( A ),稳定性是指( B )。
A.在外力作用下构件抵抗变形的能力B.在外力作用下构件保持原有平衡 状态的能力C.在外力作用下构件抵抗强度破坏的能力3.单元体变形后的形状如下图虚线所示,则 A 点剪应变依次为图(a) ( A ),图(b)( C ),图(c) ( B )。
A. 0B. 2rC. rD.1.5 r4.下列结论中( C )是正确的。
A.内力是应力的代数和; B.应力是内力的平均值; C.应力是内力的集度; D.内力必大于应力; 5. 两根截面面积相等但截面形状和材料不同的拉杆受同样大小的轴向拉力,它们的应 力是否相等( B )。
A.不相等; B.相等; C.不能确定; 6.为把变形固体抽象为力学模型,材料力学课程对变形固体作出一些假设,其中均匀性假设是指( C )。
A. 认为组成固体的物质不留空隙地充满了固体的体积; B. 认为沿任何方向固体的力学性能都是相同的; C. 认为在固体内到处都有相同的力学性能; D. 认为固体内到处的应力都是相同的。
二、填空题1.材料力学对变形固体的基本假设是 连续性假设 , 均匀性假设 , 各向同性假设 。
2.材料力学的任务是满足 强度 , 刚度 , 稳定性 的要求下,为设计经济安全的构-1-件提供必要的理论基础和计算方法。
3.外力按其作用的方式可以分为 表面力 和 体积力 ,按载荷随时间的变化情况可以分为 静载荷 和 动载荷 。
4.度量一点处变形程度的两个基本量是 (正)应变ε 和 切应变γ。
三、判断题1.因为构件是变形固体,在研究构件平衡时,应按变形后的尺寸进行计算。
( × )2.外力就是构件所承受的载荷。
(×)3.用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
材料力学习题及答案
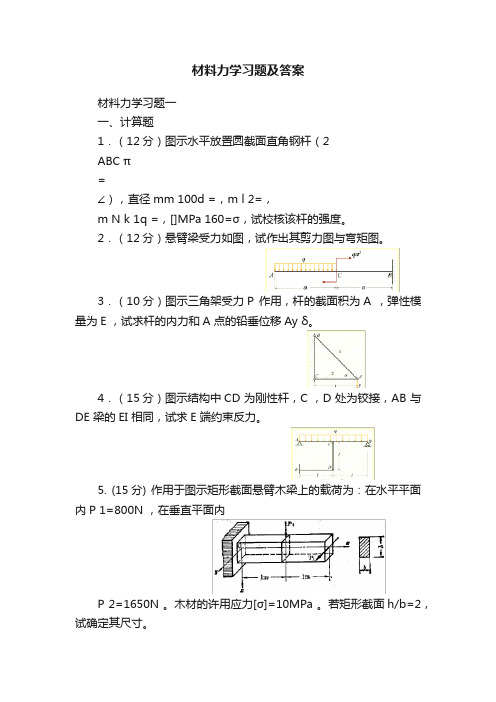
材料力学习题及答案材料力学习题一一、计算题1.(12分)图示水平放置圆截面直角钢杆(2ABC π=∠),直径mm 100d =,m l 2=,m N k 1q =,[]MPa 160=σ,试校核该杆的强度。
2.(12分)悬臂梁受力如图,试作出其剪力图与弯矩图。
3.(10分)图示三角架受力P 作用,杆的截面积为A ,弹性模量为E ,试求杆的内力和A 点的铅垂位移Ay δ。
4.(15分)图示结构中CD 为刚性杆,C ,D 处为铰接,AB 与DE 梁的EI 相同,试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为:在水平平面内P 1=800N ,在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2,试确定其尺寸。
三.填空题(23分)1.(4分)设单元体的主应力为321σσσ、、,则单元体只有体积改变而无形状改变的条件是__________;单元体只有形状改变而无体积改变的条件是__________________________。
2.(6分)杆件的基本变形一般有______、________、_________、________四种;而应变只有________、________两种。
3.(6分)影响实际构件持久极限的因素通常有_________、_________、_________,它们分别用__________、_____________、______________来加以修正。
4.(5分)平面弯曲的定义为______________________________________。
5.(2分)低碳钢圆截面试件受扭时,沿____________截面破坏;铸铁圆截面试件受扭时,沿____________面破坏。
四、选择题(共2题,9分)2.(5分)图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:()材料力学习题二二、选择题:(每小题3分,共24分)1、危险截面是______所在的截面。
材料力学习题答案
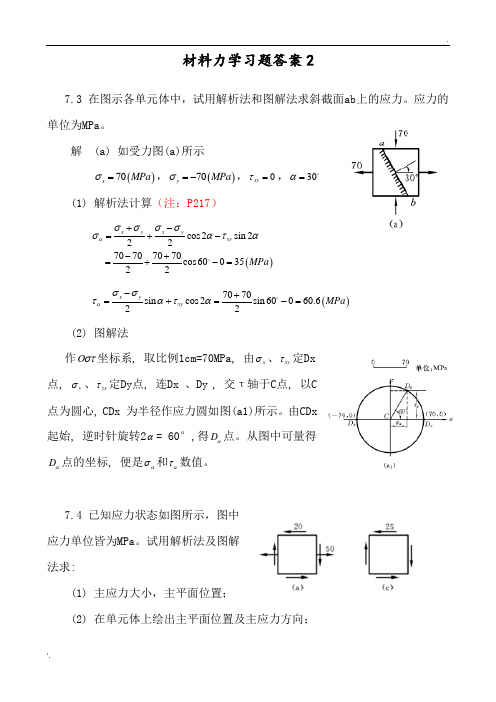
.材料力学习题答案27.3在图示各单元体中,试用解析法和图解法求斜截面ab上的应力。
应力的单位为MPa。
解(a) 如受力图(a)所示()70xMPaσ=,()70yMPaσ=-,0xyτ=,30α=(1) 解析法计算(注:P217)()cos2sin22270707070cos6003522x y x yxyMPaασσσσσατα+-=+--+=+-=()7070sin cos2sin60060.622x yxyMPaασστατα-+=+=-=(2) 图解法作Oστ坐标系, 取比例1cm=70MPa, 由xσ、xyτ定Dx点,yσ、yxτ定Dy点, 连Dx 、Dy , 交τ轴于C点, 以C点为圆心, CDx 为半径作应力圆如图(a1)所示。
由CDx起始, 逆时针旋转2α= 60°,得Dα点。
从图中可量得Dα点的坐标, 便是ασ和ατ数值。
7.4 已知应力状态如图所示,图中应力单位皆为MPa。
试用解析法及图解法求:(1) 主应力大小,主平面位置;(2) 在单元体上绘出主平面位置及主应力方向;.(3) 最大切应力。
解 (a) 受力如图(a)所示()50x MPa σ=,0y σ=,()20xy MPa τ=(1) 解析法 (数P218)2max 2min 22x y x y xy σσσσστσ+-⎛⎫⎫=±+⎬ ⎪⎭⎝⎭()()225750050020722MPa MPa ⎧+-⎪⎛⎫=±+=⎨ ⎪-⎝⎭⎪⎩ 按照主应力的记号规定()157MPa σ=,20σ=,()37MPa σ=-02220tan 20.8500xyx yτασσ⨯=-=-=---,019.3α=-()13max 5773222MPa σστ-+=== (2) 图解法作应力圆如图(a1)所示。
应力圆与σ轴的两个交点对应着两个主应力1σ、3σ 的数值。
由x CD 顺时针旋转02α,可确定主平面的方位。
材料力学第2版 课后习题答案 第2章 轴向拉压与伸缩

习题2-1一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量MPa .如不计柱自重,试求:51010.0×=E (1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形.解:(1)轴力图(2)AC 段应力a a ΜΡΡσ5.2105.22.010100623−=×−=×−=CB 段应力aa ΜΡΡσ5.6105.62.010260623−=×−=×−=(3)AC 段线应变45105.2101.05.2−×−=×−==ΕσεN-图CB 段线应变45105.6101.05.6−×−=×−==Εσε(4)总变形m 3441035.15.1105.65.1105.2−−−×=××−××−=ΑΒ∆2-2图(a)所示铆接件,板件的受力情况如图(b)所示.已知:P =7kN ,t =0.15cm ,b 1=0.4cm ,b 2=0.5cm ,b 3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(2)aΜΡσ4.194101024.015.0767311=×××××=−a ΜΡσ1.311101025.015.0767322=×××××=−a ΜΡσ9.388101026.015.07673=××××=−最大拉应力aΜΡσσ9.3883max ==2-3直径为1cm 的圆杆,在拉力P =10kN 的作用下,试求杆内最大剪应力,以及与横截面夹角为=30o 的斜截面上的正应力与剪应力。
α解:(1)最大剪应力a d ΜΡππΡστ66.6310101102212672241max =××××===−(2)界面上的应力°=30α()a ΜΡασσα49.952366.632cos 12=×=+=a ΜΡαστα13.5530sin 66.632sin 2=×=×=°2-4图示结构中ABC 与CD 均为刚性梁,C 与D 均为铰接,铅垂力P =20kN 作用在C 铰,若(1)杆的直径d 1=1cm ,(2)杆的直径d 2=2cm ,两杆的材料相同,E =200Gpa ,其他尺寸如图示,试求(1)两杆的应力;(2)C 点的位移。
材料力学练习册答案

第二章 轴向拉伸和压缩2.1 求图示杆11-、22-、及33-截面上的轴力。
解:11-截面,取右段如)(a 由0=∑x F ,得 01=N F22-截面,取右段如)(b由0=∑x F ,得 P F N -=233-截面,取右段如)(c由0=∑x F ,得 03=N F2.2 图示杆件截面为正方形,边长cm a 20=,杆长m l 4=,kN P 10=,比重3/2m kN =γ。
在考虑杆本身自重时,11-和22-截面上的轴力。
解:11-截面,取右段如)(a 由0=∑xF,得kN la F N 08.04/21==γ22-截面,取右段如)(b由0=∑xF,得kN P la F N 24.104/322=+=γ2.3 横截面为210cm 的钢杆如图所示,已知kN P 20=,kN Q 20=。
试作轴力图并求杆的总伸长及杆下端横截面上的正应力。
GPa E 200=钢。
解:轴力图如图。
杆的总伸长:m EA l F l N59102001.0102001.02000022-⨯-=⨯⨯⨯-⨯==∆ 杆下端横截面上的正应力:MPa A F N 20100020000-=-==σ 2.4 两种材料组成的圆杆如图所示,已知直径mm d 40=,杆的总伸长cm l 21026.1-⨯=∆。
试求荷载P 及在P 作用下杆内的最大正应力。
(GPa E 80=铜,GPa E 200=钢)。
解:由∑=∆EAl F l N ,得)104010806.0410********.04(1026.16296294---⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯=⨯ππP4/4/4/4/)(a )(b )(c 2N1N )(a kNkN 图NF cm cmcm解得: kN P 7.16= 杆内的最大正应力:MPa A F N 3.13401670042=⨯⨯==πσ 2.5 在作轴向压缩试验时,在试件的某处分别安装两个杆件变形仪,其放大倍数各为1200=A k ,1000=B k ,标距长为cm s 20=,受压后变形仪的读数增量为mm n A 36-=∆,mm n B 10=∆,试求此材料的横向变形系数ν(即泊松比)。
材料力学全部习题解答

弹性模量
b
E 2 2 0 M P a 2 2 0 1 0 9P a 2 2 0 G P a 0 .1 0 0 0
s
屈服极限 s 240MPa
强度极限 b 445MPa
伸长率 ll010000m ax2800
由于 280;故0该50 材0料属于塑性材料;
13
解:1由图得
弹性模量 E0 3.550110063700GPa
A x l10.938m m
节点A铅直位移
A ytan 4 l150co sl4 2503.589m m
23
解:1 建立平衡方程 由平衡方程
MB 0 FN1aFN22aF2a
FN 2 FN1
得: FN12F1N22F
l1
l2
2.建立补充方程
3 强度计算 联立方程1和方
程(2);得
从变形图中可以看出;变形几何关
l
l0
断面收缩率
AAA110000d22d22d2121000065.1900
由于 2故.4 属6 % 于 塑5 性% 材料;
15
解:杆件上的正应力为
F A
4F D2 -d2
材料的许用应力为
要求
s
ns
由此得
D 4Fns d2 19.87mm
s
取杆的外径为
D19.87m m
16
FN1 FN 2
Iz= I( za) I( zR ) =1 a2 4
2R4 a4 R 4 =
64 12 4
27
Z
解 a沿截面顶端建立坐标轴z;,y轴不变; 图示截面对z,轴的形心及惯性矩为
0 .1
0 .5
y d A 0 .3 5 y d y2 0 .0 5 y d y
材料力学II习题解答 最终版

显然,B’C’段内的切应力分布和BC段的切应力分布相对于z 轴对称,方向相同,因此切应力的合力必大小相等,方向 相同,(题12.8图(c))
材料力学(II )Mechanics of Materials 上海电力学院
材料力学(II )Mechanics of Materials 上海电力学院
cc截面与B截面之间的面积(题12.8图(b))对z轴 的面矩为
b1 0
τ1δ1dξ
=
ξ F b1 Sy b1 −ξ
0
2Iz
δ1dξ
= FSyb13δ1
12Iz
根据合力矩定理,合力对一点之矩,等于其分力对同一点之
矩的代数和,可以证明
为 和 F S y
F S1
F S2
的合力。如
对B点取矩,水平方向剪应力的合力和剪力对B点之矩为零,
故有
FS y e = FS1 h
从上上式求得弯曲中心位置
⎤ ⎥ ⎦
=
24 bh2
Fl
=
24 × 6 × 103 × 1.25 75 × 10 −3 × 150 2 × 10 −6
Pa
= 107 M P a (拉 )
材料力学(II )Mechanics of Materials 上海电力学院
B点的坐标为
yOB
=
h 3
zOB
=
−
b 3
带入广义弯曲应力公式,得
的壁厚 δ为常量,且壁厚及开口切缝都很小。
解: 如图(b)所示。开口处B面与bb截面间的面积 对在z轴的面距为
S
* z
=
(ξ δ
)ξ
2
=
δξ 2
2
⎛ ⎜⎝
0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学习题答案27.3 在图示各单元体中,试用解析法和图解法求斜截面ab 上的应力。
应力的单位为MPa 。
解 (a) 如受力图(a)所示()70x MPa σ=,()70y MPa σ=-,0xy τ=,30α=(1) 解析法计算(注:P217)()cos 2sin 22270707070 cos 6003522x yx y xy MPa ασσσσσατα+-=+--+=+-= ()7070sin cos 2sin 60060.622x yxy MPa ασστατα-+=+=-= (2) 图解法作O στ坐标系, 取比例1cm=70MPa, 由x σ、xy τ定Dx点, y σ、yx τ定Dy 点, 连Dx 、Dy , 交τ轴于C 点, 以C点为圆心, CDx 为半径作应力圆如图(a1)所示。
由CDx起始, 逆时针旋转2α= 60°,得D α点。
从图中可量得D α点的坐标, 便是ασ和ατ数值。
7.4 已知应力状态如图所示,图中应力单位皆为MPa 。
试用解析法及图解法求:(1) 主应力大小,主平面位置;(2) 在单元体上绘出主平面位置及主应力方向;(3) 最大切应力。
解 (a) 受力如图(a)所示()50x MPa σ=,0y σ=,()20xy MPa τ=(1) 解析法 (数P218)2max 2min 22x y x y xy σσσσστσ+-⎛⎫⎫=±+⎬ ⎪⎭⎝⎭()()225750050020722MPa MPa ⎧+-⎪⎛⎫=±+=⎨ ⎪-⎝⎭⎪⎩按照主应力的记号规定()157MPa σ=,20σ=,()37MPa σ=-02220tan 20.8500xyx yτασσ⨯=-=-=---,019.3α=-()13max 5773222MPa σστ-+===(2) 图解法作应力圆如图(a1)所示。
应力圆与σ轴的两个交点对应着两个主应力1σ、3σ 的数值。
由x CD 顺时针旋转02α,可确定主平面的方位。
应力圆的半径即为最大切应力的数值。
主应力单元体如图(a2)所示。
(c) 受力如图(c)所示0x σ=,0y σ=,()25xy MPa τ=(1) 解析法max min 2x y σσσσ+⎫=±⎬⎭()()2500252MPa MPa ⎧+⎪==⎨-⎪⎩ 按照主应力的记号规定()125MPa σ=,20σ=,()325MPa σ=-02225tan 200xyx yτασσ⨯=-=-=-∞--,045α=- ()13max 25252522MPa σστ-+=== (2) 图解法作应力圆如图(c1)所示。
应力圆与σ轴的两个交点对应着两个主应力1σ、3σ 的数值。
由x CD 顺时针旋转02α, 可确定主平面的方位。
x CD 的长度即为最大切应力的数值。
主应力单元体如题图(c2)所示。
7.33 对题7.4中的各应力状态,写出四个常用强度理论及莫尔强度理论的相当应力。
设0.25μ=,14t c σσ=。
解(a) ()157MPa σ=,20σ=,()37MPa σ=-()1157r MPa σσ== (书:247)()()()2123570.250758.8r MPa σσμσσ=-+=-⨯-=()31357764r MPa σσσ=-=+=4r σ=()60.8MPa == ()13157758.84t rM c MPa σσσσσ=-=+⨯= (书:P250,讲课没有讲)(c) ()125MPa σ=,20σ=,()325MPa σ=-()1125r MPa σσ==()()()2123250.2502531.3r MPa σσμσσ=-+=-⨯-=()313252550r MPa σσσ=-=+=4r σ=()43.4MPa == ()131252531.34t rM c MPa σσσσσ=-=+⨯=7.35 车轮与钢轨接触点处的主应力为-800MPa 、-900MPa 、-1100MPa 。
若[σ] = 300MPa ,试对接触点作强度校核。
解 ()1800MPa σ=-,()2900MPa σ=-,()31100MPa σ=-()[]()3138001100300300r MPa MPa σσσσ=-=-+===4r σ=()264MPa == []()300MPa σ≤=用第三和第四强度理论校核, 相当应力等于或小于许用应力,所以安全。
8.3 图(a)示起重架的最大起吊重量( 包括行走小车等)为W=40kN ,横梁AC 由两根No.18槽钢组成, 材料为Q235钢,许用应力[σ]=120MPa 。
试校核横梁的强度。
解 梁AC 受压弯组合作用。
当载荷W 移至AC 中点处时梁弯矩最大,所以AC 中点处横截面为危险截面。
危险点在梁横截面的顶边上。
查附录三型钢表(P406),No.18槽钢的A=29.30cm 2,Iy=1370cm 4 W=152cm 3。
根据静力学平衡条件, AC 梁的约束反力为:()0C i M F =∑, 3.5sin 30 1.750RA F W -= ①0ix F =∑, cos300x RA RC F F -=由式①和②可得:RA F W =, cos30cos30x RC RA F F W ==危险截面上的力分量为:() cos3040cos3034.6x N RC F F W kN ===⨯=()3.5sin 30 1.75sin 30 1.75400.5352RA M F W kN m =⨯==⨯⨯= 危险点的最大应力()33max 4634.6103510121229.310215210N y F M MPaA W σ--⨯⨯=+=+=⨯⨯⨯⨯ (压) 最大应力恰好等于许用应力, 故可安全工作。
8.8 图(a)示钻床的立柱由铸铁制成,F=15kN ,许用拉应力[]t σ=35 MPa 。
试确定立柱所需直径d 。
解 立柱横截面上的力分量如图(b)所示,F N =F=15kN ,M=0.4F=6kN ·m ,这是一个拉弯组合变形问题,横截面上的最大应力33max 23234324151032610N N y F F M M A W d d d d σππππ⨯⨯⨯⨯=+=+=+ 根据强度条件[]max σσ≤,有3362341510326103510d dππ⨯⨯⨯⨯+≤⨯ 由上式可求得立柱的直径为:()()0.122122d m mm ≥=。
8.12 手摇绞车如图(a)所示,轴的直径d=30mm ,材料为Q235钢,[]σ=80MPa 。
试按第三强度理论,求绞车的最大起吊重量P 。
解 圆轴受力图、扭矩图、弯矩图如图(b)所示。
这是一个弯扭组合变形问题, 由力图可以判定,C 处为危险截面。
其上的弯矩和扭矩分别为()0.40.2C RA M F P N m ==()0.18C T P N m =按第三强度理论:[]Wσ≤ (书P273)将CM、C T值代入上式得()360.03801032788P Nπ⎛⎫⨯⨯ ⎪≤=绞车最大起吊重量为P=788N。
8.13 电动机的功率为9kW,转速为715r/min,带轮直径D=250mm,主轴外伸部分长度120l mm=,主轴直径d=40mm。
若[σ]=60MPa,试用第三强度理论校核轴的强度。
解这是一个弯扭组合变形问题。
显然危险截面在主轴根部。
该处的力分量分别为:扭矩:()995499549120715PT N mn==⨯=根据平衡条件,222D DF F T⨯-⨯=,得()221209600.25TF ND⨯===弯矩:()339600.12346M Fl N m==⨯⨯=应用第三强度理论()()()[]()max33325830000058.3604010Pa MPa MPa Wσσπ-====≤=⨯⨯最大工作应力小于许用应力,满足强度要求,故安全。
8.14 图(a)为操纵装置水平杆,截面为空心圆形,径d=24mm,外径D=30mm 。
材料为Q235钢,[σ]=100MPa 。
控制片受力F 1=600 N 。
试用第三强度理论校核杆的强度。
解 这是一个弯扭组合变形问题。
空心水平圆杆的受力图如图(b)所示。
利用平衡条件可以求出杆上的反力,并作力图(b)。
从力图可以判定危险截面在B 处,其上的扭矩和弯矩为:()10.20.2600120T F N m ==⨯=()71.3M N m ===应用第三强度理论()()[]()max 43328920000089.2100240.03130Pa MPa MPa W σσπ====≤=⎡⎤⎛⎫⨯⨯-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦最大工作应力小于许用应力,满足强度要求,可以安全工作。
9.3 图示蒸汽机的活塞杆AB ,所受的压力F=120kN ,l =180cm ,横截面为圆形,直径d=7.5cm 。
材料为Q255钢,E=210GPa ,240p MPa σ=。
规定st n = 8,试校核活塞的稳定性。
解 活塞杆的回转半径4d i === 对于两端铰支杆,μ=1,所以杆的柔度1 1.8960.075/4li μλ⨯===192.9λ=== 因 1λλ>,故可用欧拉公式计算活塞杆的临界载荷,即()()()()294222210100.075649940009941 1.8cr EI F N kN l πππμ⨯⨯⨯⨯====⨯ 工作安全因数:st 9948.288120cr F n n F ===>= 工作安全因数大于规定的安全因数,故安全。
9.7 无缝钢管厂的穿孔顶杆如图所示。
杆端承受压力。
杆长 4.5l m =,横截面直径d=15cm 。
材料为低合金钢,200p MPa σ=,E =210GPa 。
两端可简化为铰支座,规定的稳定安全因数为 3.3st n =。
试求顶杆的许可载荷。
解1102λ=== (书P301) 顶杆的柔度为:1 4.5120/40.15/4lli d μμλ⨯==== 因 1λλ>,属于大柔度杆,故可用欧拉公式计算临界载荷,即()()()()294222210100.1564254000025401 4.5cr EI F N kN l πππμ⨯⨯⨯⨯====⨯顶杆的许可载荷:()25407703.3cr st F F kN n ===9.8 某轧钢车间使用的螺旋推钢机的示意图如图所示。
推杆由丝杆通过螺母来带动。
已知推杆横截面的直径d=13cm,材料为Q255钢,E=210GPa ,240p MPa σ=。
当推杆全部推出时,前端可能有微小的侧移,故简化为一端固定、一端自由的压杆。
这时推杆的伸出长度为最大值,max 3l m =。
