九年级数学竞赛专题讲座 二次函数的最值问题(含答案)
北师大版数学九年级下册第二章二次函数综合探究——最值问题及存在性问题课时对应练习(Word版含答案)
第13课时二次函数综合探究——最值问题及存在性问题1．已知抛物线y1＝﹣x2+mx+n,直线y2＝kx+b,y1的对称轴与y2交于点A（﹣1,5）,点A与y1的顶点B的距离是4．（1）求y1的解析式；（2）若y2随着x的增大而增大,且y1与y2都经过x轴上的同一点,求y2的解析式．2．如图,已知抛物线y＝ax2+bx+c（a≠0）经过点A（1,0）、B（3,0）、C（0,3）．（1）试求出抛物线的解析式；（2）问：在抛物线的对称轴上是否存在一个点Q,使得△QAC的周长最小,试求出△QAC 的周长的最小值,并求出点Q的坐标；（3）现有一个动点P从抛物线的顶点T出发,在对称轴上以1个单位长度每秒的速度向y 轴的正方向运动,试问,经过几秒后,△P AC是等腰三角形？3．如图,抛物线y＝x2﹣2x﹣3与直线y＝﹣x+b交于A,C两点,与x轴交于点A,B．点P为直线AC下方抛物线上的一个动点（不包括点A和点C）,过点P作PN⊥AB交AC与点M,垂足为N,连接AP,CP．设点P的横坐标为m．（1）求b的值；（2）用含m的代数式表示线段PM的长并写出m的取值范围；（3）求△P AC的面积S关于m的函数解析式,并求使得△APC面积最大时,点P的坐标；（4）直接写出当△CMP为等腰三角形时点P的坐标．4．已知抛物线y＝﹣mx2+4x+2m与x轴交于点A（α,0）,B（β,0）,且1α+1β=−2,（1）求抛物线的解析式．（2）抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E,是否存在x轴上的点M,y轴上的点N,使四边形DNME的周长最小？若存在,请画出图形（保留作图痕迹）,并求出周长的最小值；若不存在,请说明理由．（3）若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标．5．如图,抛物线y＝ax2+bx+4与x轴交于A（﹣2,0）,D两点,与y轴交于点C,对称轴x＝3交x轴交于点B．（1）求抛物线的解析式．（2）点M是x轴上方抛物线上一动点,过点M作MN⊥x轴于点N,交直线BC于点E．设点M的横坐标为m,用含m的代数式表示线段ME的长,并求出线段ME长的最大值．（3）若点P在y轴的正半轴上,连接P A,过点P作P A垂线,交抛物线的对称轴于点Q．是否存在点P,使以点P、A、Q为顶点的三角形与△BAQ全等？若存在,直接写出点P的坐标；若不存在,请说明理由．6．（2019•广州）已知抛物线G ：y ＝mx 2﹣2mx ﹣3有最低点．（1）求二次函数y ＝mx 2﹣2mx ﹣3的最小值（用含m 的式子表示）；（2）将抛物线G 向右平移m 个单位得到抛物线G 1．经过探究发现,随着m 的变化,抛物线G 1顶点的纵坐标y 与横坐标x 之间存在一个函数关系,求这个函数关系式,并写出自变量x 的取值范围；（3）记（2）所求的函数为H ,抛物线G 与函数H 的图象交于点P ,结合图象,求点P 的纵坐标的取值范围．7．已知抛物线y ＝mx 2+（1﹣2m ）x +1﹣3m 与x 轴相交于不同的两点A 、B（1）求m 的取值范围；（2）证明该抛物线一定经过非坐标轴上的一点P ,并求出点P 的坐标；（3）当14＜m ≤8时,由（2）求出的点P 和点A ,B 构成的△ABP 的面积是否有最值？若有,求出该最值及相对应的m 值．8．已知O 为坐标原点,抛物线y 1＝ax 2+bx +c （a ≠0）与x 轴相交于点A （x 1,0）,B （x 2,0）,与y 轴交于点C ,且O ,C 两点间的距离为3,x 1•x 2＜0,|x 1|+|x 2|＝4,点A ,C 在直线y 2＝﹣3x +t 上．（1）求点C 的坐标；（2）当y 1随着x 的增大而增大时,求自变量x 的取值范围；（3）将抛物线y 1向左平移n （n ＞0）个单位,记平移后y 随着x 的增大而增大的部分为P ,直线y 2向下平移n 个单位,当平移后的直线与P 有公共点时,求2n 2﹣5n 的最小值．【参考答案】1．（1）∵抛物线y 1＝﹣x 2+mx +n ,直线y 2＝kx +b ,y 1的对称轴与y 2交于点A （﹣1,5）,点A 与y 1的顶点B 的距离是4．∴B （﹣1,1）或（﹣1,9）,∴−m 2×(−1)=−1,4×(−1)n−m 24×(−1)=1或9, 解得m ＝﹣2,n ＝0或8,∴y 1的解析式为y 1＝﹣x 2﹣2x 或y 1＝﹣x 2﹣2x +8；（2）①当y 1的解析式为y 1＝﹣x 2﹣2x 时,抛物线与x 轴交点是（0,0）和（﹣2,0）, ∵y 1的对称轴与y 2交于点A （﹣1,5）,∴y 1与y 2都经过x 轴上的同一点（﹣2,0）,把（﹣1,5）,（﹣2,0）代入得{−k +b =5−2k +b =0, 解得{k =5b =10, ∴y 2＝5x +10．②当y 1＝﹣x 2﹣2x +8时,解﹣x 2﹣2x +8＝0得x ＝﹣4或2,∵y 2随着x 的增大而增大,且过点A （﹣1,5）,∴y 1与y 2都经过x 轴上的同一点（﹣4,0）,把（﹣1,5）,（﹣4,0）代入得{−k +b =5−4k +b =0, 解得{k =53b =203； ∴y 2=53x +203．2．（1）∵抛物线y ＝ax 2+bx +c （a ≠0）经过点A （1,0）、B （3,0）、C （0,3）,∴把此三点代入得{a +b +c =09a +3b +c =0c =3,解得{a =1b =−4c =3,故抛物线的解析式为,y ＝x 2﹣4x +3；（2）点A 关于对称轴的对称点即为点B ,连接B 、C ,交x ＝2于点Q ,可得直线BC：y＝﹣x+3,与对称轴交点Q（2,1）,BC=3√2,可得△QAC周长为√10+3√2．（3）设t秒后△P AC是等腰三角形,因为P在对称轴上,所以P点坐标为（2,t﹣1）于是①当P A＝CA时；根据勾股定理得：（2﹣1）2+（t﹣1）2＝12+32；解得t＝4秒或t＝﹣2秒（负值舍去）．②PC＝P A时；根据勾股定理得：22+（t﹣4）2＝（2﹣1）2+（t﹣1）2；解得t＝3秒；③CP＝CA时；根据勾股定理得：22+（t﹣4）2＝12+32；解得t＝（4+√6）秒或t＝（4−√6）秒所以经过4秒,或3秒,或4+√6秒,或4−√6秒时,△P AC是等腰三角形．3．（1）令x2﹣2x﹣3＝0,解得：x1＝﹣1,x2＝3,即A＝（﹣1,0）,B（3,0）,把A（﹣1,0）代入y＝﹣x+b,得b＝﹣1,则一次函数解析式为y＝﹣x﹣1；（2）把x＝m代入抛物线解析式得：y＝m2﹣2m﹣3,把x＝m代入直线解析式得：y＝﹣m﹣1,∴NP＝﹣（m2﹣2m﹣3）,MN＝﹣（﹣m﹣1）,∴MP＝NP﹣NM＝﹣（m2﹣2m﹣3）+（﹣m﹣1）＝﹣m2+m+2,m 的取值范围是﹣1＜m ＜2；（3）过点作CE ⊥AB 于点E ,则S △APC ＝S △AMP +S △CMP =12MP •AN +12MP •NE =12MP •AE =−32m 2+32m +3, ∵﹣1＜0,开口向下,∴当m =−b 2a =12时,S △APC 面积最大,此时P （12,−154）；（4）分三种情况：①当P 为抛物线顶点时,此时MC ＝PC ,△CMP 为等腰三角形,P 点坐标为P 1（1,﹣4）；②当P 为C 关于抛物线对称轴对称的点时,此时MP ＝MC 时,△CMP 为等腰三角形,∵点C （2,﹣3）,对称轴为：x ＝1,∴点P 坐标为P 2（0,﹣3）；③当P 为MC 的垂直平分线上点时,此时PM ＝PC ,△CMP 为等腰三角形,P 3（√2−1,2﹣4√2）．4．（1）由题意可得：α,β是方程﹣mx 2+4x +2m ＝0的两根,由根与系数的关系可得, α+β=4m ,αβ＝﹣2,∵1α+1β=−2,∴α+βαβ=−2,即4m −2=−2,解得：m＝1,故抛物线解析式为：y＝﹣x2+4x+2；（2）存在x轴上的点M,y轴上的点N,使得四边形DNME的周长最小,∵y＝﹣x2+4x+2＝﹣（x﹣2）2+6,∴抛物线的对称轴l为x＝2,顶点D的坐标为：（2,6）,又∵抛物线与y轴交点C的坐标为：（0,2）,点E与点C关于l对称,∴E点坐标为：（4,2）,作点D关于y轴的对称点D′,点E关于x轴的对称点E′,则D′的坐标为；（﹣2,6）,E′坐标为：（4,﹣2）,连接D′E′,交x轴于M,交y轴于N,此时,四边形DNME的周长最小为：D′E′+DE,如图1所示：延长E′E,′D交于一点F,在Rt△D′E′F中,D′F＝6,E′F＝8,则D′E′=√D′F2+E′F2=√62+82=10,设对称轴l与CE交于点G,在Rt△DGE中,DG＝4,EG＝2,∴DE=√DG2+EG2=√42+22=2√5,∴四边形DNME的周长最小值为：10+2√5；（3）如图2,P为抛物线上的点,过点P作PH⊥x轴,垂足为H,若以点D、E、P、Q为顶点的四边形为平行四边形,则△PHQ≌△DGE,∴PH＝DG＝4,∴|y|＝4,∴当y＝4时,﹣x2+4x+2＝4,解得：x1＝2+√2,x2＝2−√2,当y＝﹣4时,﹣x2+4x+2＝﹣4,解得：x3＝2+√10,x4＝2−√10,无法得出以DE为对角线的平行四边形,故P点的坐标为；（2−√2,4）,（2+√2,4）,（2−√10,﹣4）,（2+√10,﹣4）．5．（1）由题意得,点D 的坐标为（8,0）,把点A 、D 的坐标代入y ＝ax 2+bx +4{4a −2b +4=064a +8b +4=0, 解{a =−14b =32． 故抛物线解析式为y =−14x 2+32x +4．（2）由题意,点C ,点B 坐标分别为（0,4）,（3,0）,则直线CB 解析式y =−43x +4,点M 坐标为（m ,−14m 2+32m +4）,点E 坐标为（m ,−43m +4）,①当﹣2＜m ≤0时,ME =−43m +4﹣（−14m 2+32m +4）=14m 2−176m , m ＝﹣2时,ME =203,由二次函数性质可知,ME ＜203；②当0＜m ＜8时,ME =−14m 2+32m +4﹣（−43m +4）=14m 2−176m =−14（m −173）2+28936 当m =173时,ME 取得最大值,最大值为28936． 综上所述,当﹣2＜m ≤0时,ME =14m 2−176m ,当0＜m ＜8时,ME =−14m 2+176m ．当m =173时,ME 取得最大值,最大值为28936． （3）存在,∵P A ⊥PQ ,BQ ⊥x 轴∴∠APQ ＝∠ABQ ＝90°,∴△APQ 和△ABQ 中．点P 和点B 是对应点,∵以点P 、A 、Q 为顶点的三角形与△BAQ 全等,只有两种情况：设点P （0,c ）,Q （3,n ）（c ＞0）,∴AB ＝5,BQ ＝n ,P A =√4+c 2,PQ =√9+(c −n)2,①△P AQ ≌△BAQ ,∴P A ＝BA ,PQ ＝BQ ,∴√4+c 2=5,√9+(c −n)2=n ,∴c =√21或c =−√21（舍）,∴P （0,√21）,②△PQA ≌△BAQ ,∴P A ＝BQ ,PQ ＝AB ,∴√4+c 2=n ,√9+(c −n)2=5,∴c 1=32,n 1=−52或c 2=−32,n 2=52（舍）故点P 坐标为P 1（0,√21）,P 2（0,32）． 6．（1）∵y ＝mx 2﹣2mx ﹣3＝m （x ﹣1）2﹣m ﹣3,抛物线有最低点 ∴二次函数y ＝mx 2﹣2mx ﹣3的最小值为﹣m ﹣3（2）∵抛物线G ：y ＝m （x ﹣1）2﹣m ﹣3∴平移后的抛物线G 1：y ＝m （x ﹣1﹣m ）2﹣m ﹣3∴抛物线G 1顶点坐标为（m +1,﹣m ﹣3）∴x ＝m +1,y ＝﹣m ﹣3∴x +y ＝m +1﹣m ﹣3＝﹣2即x +y ＝﹣2,变形得y ＝﹣x ﹣2∵m ＞0,m ＝x ﹣1∴x ﹣1＞0∴x ＞1∴y 与x 的函数关系式为y ＝﹣x ﹣2（x ＞1）（3）法一：如图,函数H ：y ＝﹣x ﹣2（x ＞1）图象为射线x ＝1时,y ＝﹣1﹣2＝﹣3；x ＝2时,y ＝﹣2﹣2＝﹣4∴函数H 的图象恒过点B （2,﹣4）∵抛物线G ：y ＝m （x ﹣1）2﹣m ﹣3x ＝1时,y ＝﹣m ﹣3；x ＝2时,y ＝m ﹣m ﹣3＝﹣3∴抛物线G 恒过点A （2,﹣3）由图象可知,若抛物线与函数H 的图象有交点P ,则y B ＜y P ＜y A ∴点P 纵坐标的取值范围为﹣4＜y P ＜﹣3法二：{y =−x −2y =mx 2−2mx −3整理的：m （x 2﹣2x ）＝1﹣x∵x ＞1,且x ＝2时,方程为0＝﹣1不成立∴x ≠2,即x 2﹣2x ＝x （x ﹣2）≠0∴m =1−x x(x−2)＞0∵x ＞1∴1﹣x＜0∴x（x﹣2）＜0∴x﹣2＜0∴x＜2即1＜x＜2∵y P＝﹣x﹣2∴﹣4＜y P＜﹣37．（1）解：当m＝0时,函数为一次函数,不符合题意,舍去；当m≠0时,∵抛物线y＝mx2+（1﹣2m）x+1﹣3m与x轴相交于不同的两点A、B,∴△＝（1﹣2m）2﹣4×m×（1﹣3m）＝（1﹣4m）2＞0,∴1﹣4m≠0,∴m≠1 4,∴m的取值范围为m≠0且m≠1 4；（2）证明：∵抛物线y＝mx2+（1﹣2m）x+1﹣3m,∴y＝m（x2﹣2x﹣3）+x+1,抛物线过定点说明在这一点y与m无关,显然当x2﹣2x﹣3＝0时,y与m无关,解得：x＝3或x＝﹣1,当x＝3时,y＝4,定点坐标为（3,4）；当x＝﹣1时,y＝0,定点坐标为（﹣1,0）,∵P不在坐标轴上,∴P（3,4）；（3）解：|AB|＝|x A﹣x B|=√b2−4ac|a|=√(1−2m)2−4m(1−3m)|m|=√1−4m+4m2−4m+12m2m2=√(1−4m)2m2=|1−4mm|＝|1m−4|,∵14＜m ≤8, ∴18≤1m ＜4, ∴−318≤1m−4＜0, ∴0＜|1m−4|≤318, ∴|AB |最大时,|1m−4|=318, 解得：m ＝8,或m =863（舍去）,∴当m ＝8时,|AB |有最大值318,此时△ABP 的面积最大,没有最小值,则面积最大为：12|AB |y P =12×318×4=314． 8．（1）令x ＝0,则y ＝c ,故C （0,c ）,∵OC 的距离为3,∴|c |＝3,即c ＝±3,∴C （0,3）或（0,﹣3）；（2）∵x 1x 2＜0,∴x 1,x 2异号,①若C （0,3）,即c ＝3,把C （0,3）代入y 2＝﹣3x +t ,则0+t ＝3,即t ＝3, ∴y 2＝﹣3x +3,把A （x 1,0）代入y 2＝﹣3x +3,则﹣3x 1+3＝0, 即x 1＝1,∴A （1,0）,∵x 1,x 2异号,x 1＝1＞0,∴x 2＜0,∵|x 1|+|x 2|＝4,∴1﹣x 2＝4,解得：x 2＝﹣3,则B （﹣3,0）,代入y 1＝ax 2+bx +3得,{a +b +3=09a −3b +3=0, 解得：{a =−1b =−2,∴y 1＝﹣x 2﹣2x +3＝﹣（x +1）2+4,则当x ≤﹣1时,y 随x 增大而增大．②若C （0,﹣3）,即c ＝﹣3,把C （0,﹣3）代入y 2＝﹣3x +t ,则0+t ＝﹣3,即t ＝﹣3, ∴y 2＝﹣3x ﹣3,把A （x 1,0）,代入y 2＝﹣3x ﹣3,则﹣3x 1﹣3＝0,即x 1＝﹣1,∴A （﹣1,0）,∵x 1,x 2异号,x 1＝﹣1＜0,∴x 2＞0∵|x 1|+|x 2|＝4,∴1+x 2＝4,解得：x 2＝3,则B （3,0）,代入y 1＝ax 2+bx ﹣3得,{a −b −3=09a +3b −3=0, 解得：{a =1b =−2, ∴y 1＝x 2﹣2x ﹣3＝（x ﹣1）2﹣4,则当x ≥1时,y 随x 增大而增大,综上所述,若c ＝3,当y 随x 增大而增大时,x ≤﹣1； 若c ＝﹣3,当y 随x 增大而增大时,x ≥1；（3）①若c ＝3,则y 1＝﹣x 2﹣2x +3＝﹣（x +1）2+4,y 2＝﹣3x +3, y 1向左平移n 个单位后,则解析式为：y 3＝﹣（x +1+n ）2+4, 则当x ≤﹣1﹣n 时,y 随x 增大而增大,y 2向下平移n 个单位后,则解析式为：y 4＝﹣3x +3﹣n , 要使平移后直线与P 有公共点,则当x ＝﹣1﹣n ,y 3≥y 4, 即﹣（﹣1﹣n +1+n ）2+4≥﹣3（﹣1﹣n ）+3﹣n , 解得：n ≤﹣1,∵n ＞0,∴n ≤﹣1不符合条件,应舍去；②若c ＝﹣3,则y 1＝x 2﹣2x ﹣3＝（x ﹣1）2﹣4,y 2＝﹣3x ﹣3, y 1向左平移n 个单位后,则解析式为：y 3＝（x ﹣1+n ）2﹣4, 则当x ≥1﹣n 时,y 随x 增大而增大,y 2向下平移n 个单位后,则解析式为：y 4＝﹣3x ﹣3﹣n , 要使平移后直线与P 有公共点,则当x ＝1﹣n ,y 3≤y 4,即（1﹣n﹣1+n）2﹣4≤﹣3（1﹣n）﹣3﹣n,解得：n≥1,综上所述：n≥1,2n2﹣5n＝2（n−54）2−258,∴当n=54时,2n2﹣5n的最小值为：−258．。
初中数学竞赛：最值问题求法应用举例[附答案]
![初中数学竞赛：最值问题求法应用举例[附答案]](https://img.taocdn.com/s3/m/9093e0372af90242a895e5b2.png)
最值问题求法例题（1）、若实数a ，b ，c 满足a2 + b2+ c2= 9，则代数式（a － b）2 + （b —c）2 +（c － a）2的最大值是（）A．27 B、 18 C、15 D、 12例题（2）、如果对于不小于8的自然数N ，当3N+1是一个完全平方数时，N + 1都能表示成K个完全平方数的和，那么K的最小值是（）A、 1B、 2C、 3D、 4例题（3）、设a、b为实数，那么a2＋ab＋b2－a－2b的最小值是——————————。
例题（4）、已知实数a、b满足a2＋ab＋b2=1 ，则a2－ab＋b2的最小值和最大值的和是————————。
例题5、若a、b满足3a＋5∣b∣= 7 ，则S= 2a－3∣b∣的最大值为-------------------，最小值为--------------------。
（二）、直接运用a 2＋b 2≥ 2ab ( a ＋b ≥ 2ab )性质求最值。
例题（6）、若X > 0，则函数Y =3X ＋31X＋21++XX 的最小值。
例题（7）、已知 a 、b 、c 、d 均为实数，且a ＋b ＋c ＋d = 4 ，a 2＋b 2＋c 2＋d 2 =316，求a 的最小值与最大值。
（三）、用一元二次方程根的判别式Δ=b 2－4ac （结合韦达定理）求最值。
例题（8）、已知实数a 、b 、c 满足a ＋b ＋c = 2 ，abc = 4 ，○1求a 、b 、c 中最大者的最小值 ；○2求∣a ∣＋∣b ∣＋∣c ∣的最小值。
例题（9）、求函数Y = 12156322++++X X X X 的最小值。
（四）、用绝对值的几何意义和取零点、分段讨论法求最值。
例题（10）、a b c d e是一个五位自然数，其中a ，b ，c ，d ，e 为阿拉伯数字，且a<b<c<d ,则│a-b │＋│b-c │＋│c －d │＋│d －e │的最大值是 ———。
部编数学九年级下册专项10二次函数和线段和差最值问题(解析版)含答案
专项10 二次函数和线段和差最值问题“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现。
“两点定点一定长”模型一：当两定点 A、B 在直线l异侧时，在直线l上找一点 P，使 PA+PB 最小。
作法：连接AB交直线l 于点 P，点P即为所求作的点。
结论：PA+PB值最小模型二：作法：作点B关于直线l的对称点B’，连接AB’与直线l相交的点P即为所求结论：AP+PB’值最小模型三：PA-最大。
当两定点 A、B 在直线l同侧时，在直线l上找一点 P，使PB作法：接 AB并延长交直线l于点 P，点P即为所求作的点。
PA-的最大值为 AB。
结论：PBPA-最大。
当 l 两B定点 A、B 在直线l 异侧时，在直线l 上找一点 P，使PB作法：作点B关于直线l的对称点B′，连接AB′并延长交直线于点 P，点P即为所求作的点。
PA-的最大值为AB′结论：PB模型四：当 l 两定点 A、B 在直线l同侧时，在直线l上找一点 P，使PBPA-最小。
作法：连接 AB，作AB的垂直平分线交直线l于点 P，点 P 即为所求作的点。
PA-的最小值为 0结论：PB【考点1 线段最值问题】【典例1】（盘锦）如图，在平面直角坐标系中，抛物线y＝ax2+bx+4交y轴于点C，交x 轴于A、B两点，A（﹣2，0），a+b＝，点M是抛物线上的动点，点M在顶点和B点之间运动（不包括顶点和B点），ME∥y轴，交直线BC于点E．（1）求抛物线的解析式；（2）求线段ME的最大值；【解答】解：（1）将点A的坐标代入抛物线表达式得：0＝4a﹣2b+4，则，解得：，故抛物线的表达式为：y＝﹣x2+x+4；（2）y＝﹣x2+x+4，令x＝0，则y＝4，令y＝0，则x＝4或﹣2，故点A、B、C的坐标分别为：（﹣2，0）、（4，0）、（0，4），设直线BC的表达式为：y＝kx+b，则，解得：，故直线BC的表达式为：y＝﹣x+4，设点M（x，﹣x2+x+4），则点E（x，﹣x+4），则ME＝（﹣x2+x+4）﹣（x﹣4）＝﹣x2+2x，∵，故ME有最大值，当x＝2时，ME的最大值为2；【变式1-1】（2021•柳南区校级模拟）如图，已知二次函数图象的顶点坐标为C（1，0），直线y＝x+m与该二次函数的图象交于A、B两点，其中A点的坐标为（3，4），B点在轴y上．（1）求m的值及这个二次函数的关系式；（2）P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于点E点，设线段PE的长为h，点P的横坐标为x．①求h与x之间的函数关系式，并写出自变量x的取值范围；②线段PE的长h是否存在最大值？若存在，求出它的最大值及此时的x值；若不存在，请说明理由？【解答】解：（1）∵点A（3，4）在直线y＝x+m上，∴4＝3+m．∴m＝1．设所求二次函数的关系式为y＝a（x﹣1）2．∵点A（3，4）在二次函数y＝a（x﹣1）2的图象上，∴4＝a（3﹣1）2，∴a＝1．∴所求二次函数的关系式为y＝（x﹣1）2．即y＝x2﹣2x+1．（2）①设P、E两点的纵坐标分别为y P和y E．∴PE＝h＝y P﹣y E＝（x+1）﹣（x2﹣2x+1）＝﹣x2+3x．即h＝﹣x2+3x（0＜x＜3）．②存在．∵h＝﹣（x﹣）2+，又∵a＝﹣1＜0，∴x＝时，h的值最大，最大值为．【变式1-2】（2022春•丰城市校级期末）如图，已知二次函数y＝ax2+bx+c的图象与x轴相交于A（﹣1，0），B（3，0）两点，与y轴相交于点C（0，﹣3）．（1）求这个二次函数的表达式；（2）若P是第四象限内这个二次函数的图象上任意一点，PH⊥x轴于点H，与BC交于点M，连接PC．求线段PM的最大值；【解答】解：（1）将A，B，C代入函数解析式得，，解得，∴这个二次函数的表达式y＝x2﹣2x﹣3；（2）设BC的解析式为y＝kx+b，将B，C的坐标代入函数解析式得，，解得，∴BC的解析式为y＝x﹣3，设M（n，n﹣3），P（n，n2﹣2n﹣3），PM＝（n﹣3）﹣（n2﹣2n﹣3）＝﹣n2+3n＝﹣（n﹣）2+，＝，当n＝时，PM最大∴线段PM的最大值；【典例2】（2020秋•椒江区校级月考）如图，已知抛物线y＝ax2+bx+3（a≠0）经过点A （1，0）和点B（3，0），与y轴交于点C．（1）求此抛物线的解析式；（2）若点T为对称轴直线x＝2上一点，则TC﹣TB的最大值为多少？【解答】解：（1）设抛物线的表达式为y＝a（x﹣x1）（x﹣x2）＝a（x﹣1）（x﹣3）＝a（x2﹣4x+3）＝ax2+bx+3，解得a＝1，故抛物线的表达式为y＝x2﹣4x+3①；（2）点B关于函数对称轴的对称点为点A，连接CA交函数对称轴于点T，则点T为所求点，则TC﹣TB＝TC﹣TA＝AC为最大，故TC﹣TB的最大值为AC＝＝，故答案为；【变式2】（2020•连云港）在平面直角坐标系xOy中，把与x轴交点相同的二次函数图象称为“共根抛物线”．如图，抛物线L1：y＝x2﹣x﹣2的顶点为D，交x轴于点A、B（点A在点B左侧），交y轴于点C．抛物线L2与L1是“共根抛物线”，其顶点为P．（1）若抛物线L2经过点（2，﹣12），求L2对应的函数表达式；（2）当BP﹣CP的值最大时，求点P的坐标；【解答】解：（1）当y＝0时，x2﹣x﹣2＝0，解得x＝﹣1或4，∴A（﹣1，0），B（4，0），C（0，﹣2），由题意设抛物线L2的解析式为y＝a（x+1）（x﹣4），把（2，﹣12）代入y＝a（x+1）（x﹣4），﹣12＝﹣6a，解得a＝2，∴抛物线的解析式为y＝2（x+1）（x﹣4）＝2x2﹣6x﹣8．（2）∵抛物线L2与L1是“共根抛物线”，A（﹣1，0），B（4，0），∴抛物线L1，L2的对称轴是直线x＝，∴点P在直线x＝上，∴BP＝AP，如图1中，当A，C，P共线时，BP﹣PC的值最大，此时点P为直线AC与直线x＝的交点，∵直线AC的解析式为y＝﹣2x﹣2，∴P（，﹣5）【典例3】（2022•澄海区模拟）如图，抛物线y＝ax2+bx+c交x轴于A、B两点，交y轴于点C，点A的坐标为（﹣1，0），点C坐标为（0，3），对称轴为x＝1．点M为线段OB上的一个动点（不与两端点重合），过点M作PM⊥x轴，交抛物线于点P，交BC 于点Q．（1）求抛物线及直线BC的表达式；（2）过点P作PN⊥BC，垂足为点N．求线段PN的最大值；【解答】解：（1）∵抛物线对称轴为x＝1，点B与A（﹣1，0）关于直线x＝1对称，∴B（3，0），设y＝a（x﹣3）（x+1），把C（0，3）代入得：﹣3a＝3，解得：a＝﹣1，∴y＝﹣（x﹣3）（x+1）＝﹣x2+2x+3，设直线BC的解析式为y＝kx+d，则，解得：，∴直线BC的解析式为y＝﹣x+3，故抛物线解析式为y＝﹣x2+2x+3，直线BC的解析式为y＝﹣x+3；（2）设P（t，﹣t2+2t+3），则Q（t，﹣t+3），∴PQ＝﹣t2+2t+3﹣（﹣t+3）＝﹣t2+3t，∵OB＝OC＝3，∠BOC＝90°，∴∠BCO＝45°，∵PQ⊥x轴，∴PQ∥y轴，∴∠PQN＝∠BCO＝45°，∵PN⊥BC，∴PN＝PQ•sin∠PQN＝（﹣t2+3t）•sin45°＝﹣（t﹣）2+，∵＜0，∴当t＝时，PN的最大值为；【变式3】（2022•广元）在平面直角坐标系中，直线y＝﹣x﹣2与x轴交于点A，与y轴交于点B，抛物线y＝ax2+bx+c（a＞0）经过A，B两点，并与x轴的正半轴交于点C．（1）求a，b满足的关系式及c的值；（2）当a＝1时，若点Q是直线AB下方抛物线上的一个动点，过点Q作QD⊥AB于点D，当QD的值最大时，求此时点Q的坐标及QD的最大值．【解答】解：（1）直线y＝﹣x﹣2中，当x＝0时，y＝﹣2，∴B（0，﹣2），当y＝0时，﹣x﹣2＝0，∴x＝﹣2，∴A（﹣2，0），将A（﹣2，0），B（0，﹣2）代入抛物线y＝ax2+bx+c（a＞0）中，得，，∴2a﹣b＝1，c＝﹣2；（2）当a＝1时，2×1﹣b＝1，∴b＝1，∴y＝x2+x﹣2，∴A（﹣2，0），B（0，﹣2），C（1，0），∴OA＝OB，∴△AOB是等腰直角三角形，∴∠OAB＝45°，如图2，过点Q作QF⊥x轴于F，交AB于E，则△EQD是等腰直角三角形，设Q（m，m2+m﹣2），则E（m，﹣m﹣2），∴QE＝（﹣m﹣2）﹣（m2+m﹣2）＝﹣m2﹣2m＝﹣（m+1）2+1，∴QD＝QE＝﹣（m+1）2+，当m＝﹣1时，QD有最大值是，当m＝﹣1时，y＝1﹣1﹣2＝﹣2，综上，点Q的坐标为（﹣1，﹣2）时，QD有最大值是．【考点2 线段和最小】【典例4】（2019秋•东莞市校级期末）已知，抛物线y＝ax2+bx+c，过A（﹣1，0）、B （3，0）、C（0，﹣3），M为顶点．（1）求抛物线的解析式；（2）在该抛物线的对称轴上找一点P，使得PA+PC的值最小，并求出P的坐标；【解答】解：（1）设抛物线解析式为y＝a（x+1）（x﹣3），把C（0，﹣3）代入得a×（0+1）×（0﹣3）＝﹣3，解得a＝1，∴抛物线解析式为y＝（x+1）（x﹣3），即y＝x2﹣2x﹣3；（2）抛物线的对称轴为直线x＝1，点A与点B关于直线x＝1对称，连接BC交直线x＝1于P点，则PA＝PB，∵PA+PC＝PB+PC＝BC，∴此时PA+PC的值最小，设直线BC的解析式为y＝mx+n，把B（3，0），C（0，﹣3）代入得，解得，∴直线BC的解析式为y＝x﹣3，当x＝1时，y＝x﹣3＝﹣2，则满足条件的P点坐标为（1，﹣2）；【变式4-1】（2019•赤峰）如图，直线y＝﹣x+3与x轴、y轴分别交于B、C两点，抛物线y＝﹣x2+bx+c经过点B、C，与x轴另一交点为A，顶点为D．（1）求抛物线的解析式；（2）在x轴上找一点E，使EC+ED的值最小，求EC+ED的最小值；【解答】解：（1）直线y＝﹣x+3与x轴、y轴分别交于B、C两点，则点B、C的坐标分别为（3，0）、（0，3），将点B、C的坐标代入二次函数表达式得：，解得：，故函数的表达式为：y＝﹣x2+2x+3，令y＝0，则x＝﹣1或3，故点A（﹣1，0）；（2）如图1中，作点C关于x轴的对称点C′，连接CD′交x轴于点E，则此时EC+ED 为最小，函数顶点D坐标为（1，4），点C′（0，﹣3），将C′、D的坐标代入一次函数表达式并解得：直线C′D的表达式为：y＝7x﹣3，当y＝0时，x＝，故点E（，0），则EC+ED的最小值为DC′＝；【变式4-2】（2016•黑龙江二模）如图，抛物线y＝x2+bx﹣2与x轴交于A、B两点，与y轴交于C点，且A（﹣1，0）．（1）求抛物线的解析式及顶点D的坐标；（2）点M（m，0）是x轴上的一个动点，当CM+DM的值最小时，求m的值．【解答】解：（1）∵点A（﹣1，0）在抛物线y＝x2+bx﹣2上，∴×（﹣1）2+b×（﹣1）﹣2＝0，解得：b＝﹣，∴抛物线的解析式为：y＝x2﹣x﹣2．∵y＝x2﹣x﹣2＝（x2﹣3x﹣4 ）＝，∴顶点D的坐标为（，﹣）．（2）设点C关于x轴的对称点为C′，直线C′D的解析式为y＝kx+n，则，解得：．∴y＝﹣x+2．∴当y＝0时，﹣x+2＝0，解得：x＝．∴m＝．【典例5】（2022•恩施州模拟）如图1，已知抛物线．点A（﹣1，2）在抛物线的对称轴上，是抛物线与y轴的交点，D为抛物线上一动点，过点D 作x轴的垂线，垂足为点C．（1）直接写出h，k的值；（2）如图1，若点D的坐标为（3，m），点Q为y轴上一动点，直线QK与抛物线对称轴垂直，垂足为点K．探求DK+KQ+QC的值是否存在最小值，若存在，求出这个最小值及点Q的坐标；若不存在，请说明理由；【解答】解：（1）∵点A（﹣1，2）在抛物线的对称轴上，∴抛物线的对称轴为直线x＝﹣1，∴h＝1，∴y＝（x+1）2+k，∵是抛物线与y轴的交点，∴+k＝，∴k＝1；（2）存在最小值，理由如下：由（1）可知y＝（x+1）2+1，作C点关于直线x＝﹣的对称点C'，连接C'D交抛物线对称轴于点K，连接CQ，由对称性可知C'K＝CQ，∴CQ+KQ+KD＝C'K+KD+KQ≥C'D+KQ，当C'、K、D三点共线时，CQ+KQ+KD的值最小，∵抛物线的对称轴为直线x＝﹣1，∴KQ＝1，∵D（3，5），CD⊥x轴，∵C（3，0），∴C'（﹣4，0），∴C'D＝，∴CQ+KQ+KD的最小值为+1，设直线C'D的解析式为y＝kx+b，∴，解得，∴y＝x+，∴K（﹣1，），∴Q（0，）；【变式5】（2022•桂林）如图，抛物线y＝﹣x2+3x+4与x轴交于A，B两点（点A位于点B 的左侧），与y轴交于C点，抛物线的对称轴l与x轴交于点N，长为1的线段PQ（点P位于点Q的上方）在x轴上方的抛物线对称轴上运动．（1）直接写出A，B，C三点的坐标；（2）求CP+PQ+QB的最小值；【解答】解：（1）在y＝﹣x2+3x+4中，令x＝0得y＝4，令y＝0得x＝﹣1或x＝4，∴A（﹣1，0），B（4，0），C（0，4）；（2）将C（0，4）向下平移至C'，使CC'＝PQ，连接BC'交抛物线的对称轴l于Q，如图：∵CC'＝PQ，CC'∥PQ，∴四边形CC'QP是平行四边形，∴CP＝C'Q，∴CP+PQ+BQ＝C'Q+PQ+BQ＝BC'+PQ，∵B，Q，C'共线，∴此时CP+PQ+BQ最小，最小值为BC'+PQ的值，∵C（0，4），CC'＝PQ＝1，∴C'（0，3），∵B（4，0），∴BC'＝＝5，∴BC'+PQ＝5+1＝6，∴CP+PQ+BQ最小值为6；【考点3 周长最值问题】【典例6】（2020春•五华区校级期末）如图，抛物线y＝x2+bx﹣3与x轴交于A，B两点，与y轴交于C点，且A（﹣1，0）．（1）求抛物线的解析式及顶点D的坐标；（2）点M是对称轴上的一个动点，当△ACM的周长最小时，求点M的坐标．【解答】解：（1）∵点A（﹣1，0）在抛物线y＝x2+bx﹣3上，∴b＝﹣2，∴抛物线解析式y＝x2﹣2x﹣3，∵抛物线y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴顶点D的坐标（1，﹣4）；（2）对于y＝x2﹣2x﹣3，当x＝0时，y＝﹣3，∴C（0，﹣3），当y＝0时，0＝x2﹣2x﹣3，解得：x＝3或﹣1，∴B（3，0），由抛物线的性质可知：点A和B是对称点，∴连接BC交函数的对称轴于点M，此时AM+CM＝BC为最小值，而BC的长度是常数，故此时△ACM的周长最小，设直线BC的表达式为y＝mx+n，则，解得，故直线BC的表达式为y＝x﹣3，当x＝1时，y＝﹣2，故点M（1，﹣2）．【变式6-1】（2021•富拉尔基区模拟）如图，已知抛物线y＝ax2+bx+3（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C．（1）求抛物线解析式；（2）若M是抛物线对称轴上的一点，则△ACM周长的最小值为多少？【解答】解：（1）∵抛物线y＝ax2+bx+3（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），∴，解得，∴抛物线解析式为y＝﹣x2﹣2x+3；（2）∵△ACM周长的值最小，∴MC+AM的值最小，即点M即为直线BC与抛物线对称轴的交点，∴△ACM周长的最小值为BC+AC，∵点B（﹣3，0），C（0，3），∴BC＝＝3，AC＝＝，∴△ACM周长的最小值为，故答案为：；【变式6-2】（2022•齐河县模拟）如图1，抛物线y＝ax2+bx+3过A（1，0）、B（3，0）两点，交y轴于点C．（1）求抛物线的函数解析式；（2）在抛物线的对称轴上是否存在点M，使△ACM的周长最小？若存在，求出△ACM 周长的最小值；若不存在，请说明理由．（3）如图2，连接BC，抛物线上是否存在一点P，使得∠BCP＝∠ACB？若存在，求出点P的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+bx+3过A（1，0）、B（3，0）两点，∴方程ax2+bx+3＝0的两根为x＝1或x＝3，∴1+3＝﹣，1×3＝，∴a＝1，b＝﹣4，∴二次函数解析式是y＝x2﹣4x+3；（2）∵二次函数解析式是y＝x2﹣4x+3，∴抛物线的对称轴为直线x＝2，C（0，3）．∵点A、B关于对称轴对称，∴点M为BC与对称轴的交点时，MA+MC＝BC的值最小．设直线BC的解析式为y＝kx+t（k≠0），则，解得：．∴直线BC的解析式为y＝﹣x+3．∵抛物线的对称轴为直线x＝2．∴当x＝2时，y＝1．∴抛物线对称轴上存在点M（2，1）符合题意，∵A（1，0）、B（3，0），C（0，3）．∴AC＝＝，BC＝＝3，∴AC+BC＝+3，∴在抛物线的对称轴上存在点M，使△ACM的周长最小，△ACM周长的最小值为+3；【典例7】（2022春•衡阳期中）如图，直线y＝﹣x+3与x轴交于点A，与y轴交于点B，抛物线y＝ax2+x+c经过A、B两点．（1）求二次函数解析式；（2）如图1，点E在线段AB上方的抛物线上运动（不与A、B重合），过点E作ED⊥AB，交AB于点D，作EF⊥AC，交AC于点F，交AB于点M，求△DEM的周长的最大值；【解答】解：（1）∵直线y＝﹣x+3与x轴交于点A，与y轴交于点B，∴A（4，0），B（0，3）．∵抛物线y＝ax2+x+c经过A、B两点，∴，解得．∴二次函数的解析式为：y＝﹣x2+x+3．（2）∵A（4，0），B（0，3）．∴OA＝4，OB＝3，∴AB＝5．∵ED⊥AB，∴∠EDM＝∠AOB＝90°，∵∠DEM+∠EMD＝∠FMA+∠BAO＝90°，∠FMA＝∠EMD，∴∠DEM＝∠BAO，∴△AOB∽△EDM，∴AO：OB：AB＝ED：DM：EM＝4：3：5，设E的横坐标为t，则E（t，﹣t2+t+3），∴M（t，﹣t+3），∴EM＝﹣t2+t+3﹣（﹣t+3）＝﹣t2+t．∴△DEM的周长为：ED+DM+EM＝EM＝﹣（t﹣2）2+，∴当t＝2时，△DEM的周长的最大值为．【变式7】（2022春•北碚区校级期中）如图，在平面直角坐标系中，抛物线C1：y＝ax2+bx+2交x轴于A、B两点（点A在点B的左侧），交y轴于点C，一次函数y＝﹣x﹣1交抛物线于A，D两点，其中点D（3，﹣4）．（1）求抛物线C1的解析式；（2）点G为抛物线上一点，且在线段BC上方，过点G作GH∥y轴交BC于H，交x 轴于点N，作GM⊥BC于点M，求△GHM周长的最大值；【解答】解：（1）∵一次函数y＝﹣x﹣1交抛物线于A点，且点A在x轴上，∴A（﹣1，0）；将A（﹣1，0）和D（3，﹣4）代入抛物线C1：y＝ax2+bx+2，∴，解得，∴抛物线C1：y＝﹣x2+x+2．（2）由（1）知抛物线C1：y＝﹣x2+x+2．令y＝0，解得x＝﹣1或x＝2，∴B（2，0）；令x＝0，则y＝2，∴C（0，2）．∴OB＝OC＝2，直线BC的解析式为：y＝﹣x+2；∴△OBC是等腰直角三角形，且∠OBC＝∠OCB＝45°；∵GH∥y轴，∴∠GNB＝90°，∴∠BHN＝45°，∵GM⊥BC，∴∠GMH＝90°，∵∠MGH＝∠GHM＝45°，∴GM＝MH＝GH；设点G的横坐标为t，则G（t，﹣t2+t+2），H（t，﹣t+2），∴GH＝﹣t2+2t＝﹣（t﹣1）2+1．∵﹣1＜0，∴当t＝1时，GH有最大值1；∵△GHM的周长为：GM+MH+GH＝（+1）GH，∴△GHM周长的最大值为+1．1．（2022春•丰城市校级期末）如图，已知二次函数y＝ax2+bx+c的图象与x轴相交于A （﹣1，0），B（3，0）两点，与y轴相交于点C（0，﹣3）．（1）求这个二次函数的表达式；（2）若P是第四象限内这个二次函数的图象上任意一点，PH⊥x轴于点H，与BC交于点M，连接PC．求线段PM的最大值；【解答】解：（1）将A，B，C代入函数解析式得，，解得，∴这个二次函数的表达式y＝x2﹣2x﹣3；（2）①设BC的解析式为y＝kx+b，将B，C的坐标代入函数解析式得，，解得，∴BC的解析式为y＝x﹣3，设M（n，n﹣3），P（n，n2﹣2n﹣3），PM＝（n﹣3）﹣（n2﹣2n﹣3）＝﹣n2+3n＝﹣（n﹣）2+，＝，当n＝时，PM最大∴线段PM的最大值；2．（2022•宁远县模拟）如图，抛物线y＝x2+bx+c与x轴交于A，B两点，其中点A的坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．（1）求抛物线的解析式；（2）抛物线的对称轴上有一动点P，求出PA+PD的最小值；【解答】解：（1）∴二次函数y＝x2+bx+c的图象经过A（﹣3，0），D（﹣2，﹣3），∴，解得：．∴二次函数解析式为y＝x2+2x﹣3；（2）∵抛物线y＝x2+2x﹣3的对称轴x＝﹣＝﹣1，D（﹣2，﹣3），C（0，﹣3），∴C、D关于抛物线的对称轴x＝﹣1对称，连接AC与对称轴的交点就是点P，此时PA+PD＝PA+PC＝AC＝＝＝3．∴PA+PD的最小值为3；3．（2022•昭平县二模）如图1，对称轴为直线x＝1的抛物线经过B（3，0）、C（0，4）两点，抛物线与x轴的另一交点为A．（1）求抛物线的解析式；（2）若点P为抛物线对称轴上的一点，使PA+PC取得最小值，求点P的坐标；【解答】解：（1）由对称性得：A（﹣1，0），设抛物线的解析式为：y＝a（x+1）（x﹣3），把C（0，4）代入：4＝﹣3a，a＝﹣，∴y＝﹣（x+1）（x﹣3），∴抛物线的解析式为：y＝﹣x2+x+4；（2）如图，点A与点B关于对称轴直线x＝1对称，连接BC，交抛物线对称轴于点P，连接PA，即点P为所求点，此时PA+PC＝PB+PC＝BC的值最小，∵B（3，0）、C（0，4），设直线BC的函数解析式为y＝kx+b，∴，解得，∴直线BC的函数解析式为y＝﹣x+4，当x＝1时，y＝，∴P点的坐标为（1，）；4．（2022春•石鼓区校级月考）已知：二次函数y＝x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．（1）求抛物线的解析式；（2）抛物线的对称轴上有一动点P，求△PAD周长的最小值．【解答】解：（1）将（﹣3，0），（﹣2，﹣3）代入y＝x2+bx+c得，解得，∴抛物线解析式为y＝x2+2x﹣3．（2）∵y＝x2+2x﹣3，∴抛物线对称轴为直线x＝﹣1，连接BD，交对称轴于点P，∵点A坐标为（﹣3，0），抛物线对称轴为直线x＝﹣1，∴点B坐标为（1，0），∴BD＝＝3，又∵AD＝＝，∴△PAD周长的最小值为3+．5．（2022•江阴市校级一模）如图1，在平面直角坐标系xOy中，抛物线y＝ax2+bx+c与x 轴分别相交于A（﹣1，0）、B（3，0）两点，与y轴相交于点C（0，3）．（1）求出这条抛物线的解析式及顶点M的坐标；（2）PQ是抛物线对称轴上长为1的一条动线段（点P在点Q上方），求AQ+QP+PC 的最小值；【解答】解：（1）∵抛物线过点A（﹣1，0），B（3，0），C（0，3），∴设抛物线解析式为y＝a（x+1）（x﹣3），将C（0，3）代入，得：3＝a（0+1）（0﹣3），解得：a＝﹣1，∴y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴该抛物线解析式为y＝﹣x2+2x+3，顶点坐标为M（1，4）．（2）如图1，将点C沿y轴向下平移1个单位得C′（0，2），连接BC′交抛物线对称轴x＝1于点Q′，过点C作CP′∥BC′，交对称轴于点P′，连接AQ′，∵A、B关于直线x＝1对称，∴AQ′＝BQ′，∵CP′∥BC′，P′Q′∥CC′，∴四边形CC′Q′P′是平行四边形，∴CP′＝C′Q′，Q′P′＝CC′＝1，在Rt△BOC′中，BC′＝，＝＝．∴AQ′+Q′P′+P′C＝BQ′+C′Q′+Q′P′＝BC′+Q′P′＝+1，此时，C′、Q′、B三点共线，BQ′+C′Q′的值最小，∴AQ+QP+PC的最小值为+1．6．（2022•常德）如图，已知抛物线过点O（0，0），A（5，5），且它的对称轴为x＝2，点B是抛物线对称轴上的一点，且点B在第一象限．（1）求此抛物线的解析式；（2）当△OAB的面积为15时，求B的坐标；（3）在（2）的条件下，P是抛物线上的动点，当PA﹣PB的值最大时，求P的坐标以及PA﹣PB的最大值．【解答】解：（1）∵抛物线过点O（0，0），A（5，5），且它的对称轴为x＝2，∴抛物线与x轴的另一个交点坐标为（4，0），设抛物线解析式为y＝ax（x﹣4），把A（5，5）代入，得5a＝5，解得：a＝1，∴y＝x（x﹣4）＝x2﹣4x，故此抛物线的解析式为y＝x2﹣4x；（2）∵点B是抛物线对称轴上的一点，且点B在第一象限，∴设B（2，m）（m＞0），设直线OA的解析式为y＝kx，则5k＝5，解得：k＝1，∴直线OA的解析式为y＝x，设直线OA与抛物线对称轴交于点H，则H（2，2），∴BH＝m﹣2，＝15，∵S△OAB∴×（m﹣2）×5＝15，解得：t＝8，∴点B的坐标为（2，8）；（3）设直线AB的解析式为y＝cx+d，把A（5，5），B（2，8）代入得：，解得：，∴直线AB的解析式为y＝﹣x+10，当PA﹣PB的值最大时，A、B、P在同一条直线上，∵P是抛物线上的动点，∴，解得：，（舍去），∴P（﹣2，12），此时，PA﹣PB＝AB＝＝3．7．（2022•玉州区一模）如图，抛物线y＝﹣x2x+4交x轴于A，B两点（点B在A的右边），与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，点P 的横坐标为m，过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．（1）求A、B两点坐标；（2）过点P作PN上BC，垂足为点N，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？【解答】解：（1）当y＝0，﹣x2+x+4＝0，解得x1＝﹣3，x2＝4，∴A（﹣3，0），B（4，0），（2）设点P（m，﹣m2+m+4），则点Q（m，﹣m+4），∵OB＝OC，∴∠ABC＝∠OCB＝45°＝∠PQN，P～N＝PQ•sin∠PQN＝（﹣m2+m+4+m﹣4）＝﹣（m﹣2）2+，∵﹣＜0，∴PN有最大值，当m＝2时，PN的最大值为．8．（2022•怀化）如图一所示，在平面直角坐标中，抛物线y＝ax2+2x+c经过点A（﹣1，0）、B（3，0），与y轴交于点C，顶点为点D．在线段CB上方的抛物线上有一动点P，过点P作PE⊥BC于点E，作PF∥AB交BC于点F．（1）求抛物线和直线BC的函数表达式．（2）当△PEF的周长为最大值时，求点P的坐标和△PEF的周长．【解答】解：（1）∵抛物线y＝ax2+2x+c经过点A（﹣1，0）、B（3，0），∴，解得，∴抛物线的解析式为y＝﹣x2+2x+3，令x＝0，可得y＝3，∴C（0，3），设直线BC的解析式为y＝kx+b，则，∴，∴直线BC的解析式为y＝﹣x+3；（2）如图一中，连接PC，OP，PB．设P（m，﹣m2+2m+3），∵B （3，0），C （0，3），∴OB ＝OC ＝3，∴∠OBC ＝45°，∵PF ∥AB ，∴∠PFE ＝∠OBC ＝45°，∵PE ⊥BC ，∴△PEF 是等腰直角三角形，∴PE 的值最大时，△PEF 的周长最大，∵S △PBC ＝S △POB +S △POC ﹣S △OBC＝×3×（﹣m 2+2m +3）+×3×m ﹣×3×3＝﹣m 2+m＝﹣（m ﹣）2+，∵﹣＜0，∴m ＝时，△PBC 的面积最大，面积的最大值为，此时PE 的值最大，∵×3×PE ＝，∴PE ＝，∴△PEF 的周长的最大值＝++＝+，此时P （，）；。
2023年中考高频数学专题突破--二次函数的最值问题(含解析)
2023年中考高频数学专题突破--二次函数的最值问题1．永嘉某商店试销一种新型节能灯，每盏节能灯进价为18元，试销过程中发现，每周销量y（盏）与销售单价x（元）之间关系可以近似地看作一次函数y=﹣2x+100．（利润=售价﹣进价）（1）写出每周的利润w（元）与销售单价x（元）之间函数解析式；（2）当销售单价定为多少元时，这种节能灯每周能够获得最大利润？最大利润是多少元？（3）物价部门规定，这种节能灯的销售单价不得高于30元．若商店想要这种节能灯每周获得350元的利润，则销售单价应定为多少元？2．经市场调查，某种商品在第x天的售价与销量的相关信息如下表；已知该商品的进价为每件30元，设销售该商品每天的利润为y元．（1）求出y与x的函数关系式（2）问销售该商品第几天时，当天销售利润最大？最大利润是多少？．3．为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym2．（1）求y与x之间的函数关系式，并注明自变量x的取值范围；（2）x为何值时，y有最大值？最大值是多少？4．小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现：每月的销售量y(件)与销售单价x(元/件)之间的关系可近似地看作一次函数y＝－10x＋500，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%.（1）设小明每月获得利润为w(元)，求每月获得利润w(元)与销售单价x(元/件)之间的函数表达式，并确定自变量x的取值范围；（2）当销售单价定为多少元/件时，每月可获得最大利润？每月的最大利润是多少？5．自2020年3月开始，我国生猪、猪肉价格持续上涨，某大型菜场在销售过程中发现，从2020年10月1日起到11月9日的40天内，猪肉的每千克售价与上市时间的关系用图1的一条折线表示：猪肉的进价与上市时间的关系用图2的一段抛物线()2=-+表示.y a x30100（1）a=；（2）求图1表示的售价P与时间x的函数关系式；（3）问从10月1日起到11月9日的40天内第几天每千克猪肉利润最低，最低利润为多少？6．2022年冬奥会即将在北京召开，某网络经销商购进了一批以冬奥会为主题的文化衫进行销售，文化衫的进价每件40元，每月销售量y（件）与销售单价x（元）之间的函数关系如图所示，设每月获得的利润为W（元）．（1）求出每月的销售量y（件）与销售单价x（元）之间的函数关系式；（2）这种文化衫销售单价定为多少元时，每月的销售利润最大？最大利润是多少元？（3）为了扩大冬奥会的影响，物价部门规定这种文化衫的销售单价不高于60元，该商店销售这种文化衫每月要获得最大利润，销售单价应定为多少元？每月的最大利润为多少元？7．我市绿色和特色农产品在国际市场上颇具竞争力，其中香菇远销日本和韩国等地.上市时，外贸商李经理按市场价格10元/千克在我市收购了2000千克香菇存放入冷库中.请根据李经理提供的预测信息（如下图）帮李经理解决以下问题：（1）若存放x天后，将这批香菇一次性出售，设这批香菇的销售总金额．．．．．为y 元，试写出y与x之间的函数表达式；（销售总金额=销售单价×销售量）（2）将这批香菇仔放多少天后出售可获得最大利润．．?最大利润是多少?8．“绿水青山就是金山银山”的理念已融入人们的日常生活中，因此，越来越多的人喜欢骑自行车出行，某自行车店在销售某型号自行车时，标价1500元已知拔标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同。
最新二次函数的最值问题举例(附练习、答案)
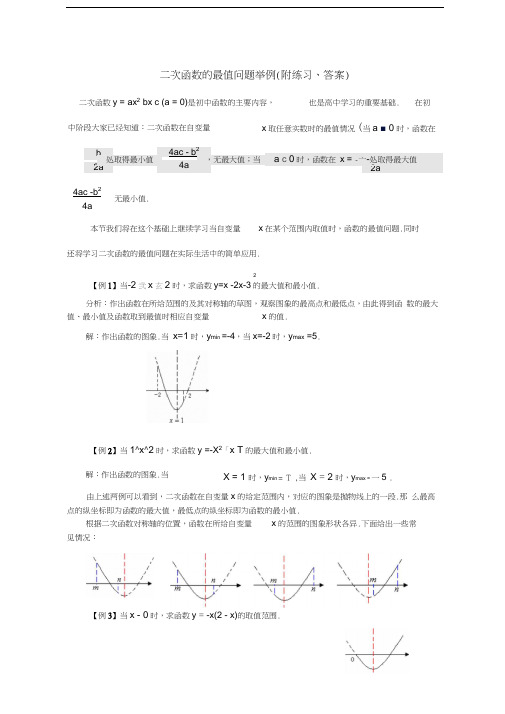
二次函数的最值问题举例(附练习、答案)二次函数y = ax2bx c (a = 0)是初中函数的主要内容，也是高中学习的重要基础. 在初x取任意实数时的最值情况(当a ■ 0时，函数在本节我们将在这个基础上继续学习当自变量x在某个范围内取值时，函数的最值问题.同时还将学习二次函数的最值问题在实际生活中的简单应用.2【例1】当-2弐x玄2时，求函数y=x -2x-3的最大值和最小值.分析：作出函数在所给范围的及其对称轴的草图，观察图象的最高点和最低点，由此得到函数的最大值、最小值及函数取到最值时相应自变量x的值.解：作出函数的图象.当x=1时，y mi n =-4，当x=-2时，y max=5.【例2】当1^x^2时，求函数y =-X2「x T的最大值和最小值.X = 1 时，y min = T ,当X = 2 时，y max = 一5 .由上述两例可以看到，二次函数在自变量x的给定范围内，对应的图象是抛物线上的一段.那么最高点的纵坐标即为函数的最大值，最低点的纵坐标即为函数的最小值.根据二次函数对称轴的位置，函数在所给自变量x的范围的图象形状各异.下面给出一些常见情况：【例3】当x - 0时，求函数y = -x(2 - x)的取值范围.中阶段大家已经知道：二次函数在自变量b2a处取得最小值4ac - b24a，无最大值；当 a c 0时，函数在x = -亠-处取得最大值2a4ac -b24a无最小值.解：作出函数的图象.当解：作出函数y =-x(2 - x) n x? — 2x在x_0内的图象.可以看出：当x = 1时，ymin - -1，无最大值.所以，当X _ 0时，函数的取值范围是y _ -1 .1 25【例4】当t <x <t 1时，求函数y x「x 的最小值(其中t为常数).2 2分析：由于x所给的范围随着t的变化而变化，所以需要比较对称轴与其范围的相对位置.1 25解：函数y x2-X 的对称轴为x=1 .画出其草图.2 21 25(1)当对称轴在所给范围左侧•即t 1时：当X = t时，『min t -t-2 2⑵当对称轴在所给范围之间•即t乞1乞t • 1 = 0乞t乞1时：1 25当X=1 时，『min -1—? = 一3 ；⑶当对称轴在所给范围右侧.即t • 1 ：：： 1= t ：：： 0时：1 2 5 1 2当X=t 1 时，y min —(t 1) -(t 1)—?=?t -3 .1 2—t —3,t < 02综上所述：y二-3,0乞t乞1-1 -5,t A1.2 2在实际生活中，我们也会遇到一些与二次函数有关的问题：【例5】某商场以每件30元的价格购进一种商品，试销中发现这种商品每天的销售量与每件的销售价x(元)满足一次函数m =162 -3x,30 _ x _ 54 .(1)写出商场卖这种商品每天的销售利润y与每件销售价x之间的函数关系式；(2)若商场要想每天获得最大销售利润，每件商品的售价定为多少最合适？最大销售利润为多少？解：(1)由已知得每件商品的销售利润为(x-30)元，m (件)那么m件的销售利润为y = m(x - 30)，又m = 162 - 3x .2y = (x - 30)(162 - 3x)二-3x 252x - 4860,30 - x - 54(2)由⑴知对称轴为x=42，位于x的范围内，另抛物线开口向下.当x=42 时，y max - -3 421 2252 42 -4860 =432•当每件商品的售价定为42元时每天有最大销售利润，最大销售利润为432元.A 组21.抛物线y =x —(m —4)x +2m -3，当m = _________ 时，图象的顶点在y轴上；当m = _______ 时, 图象的顶点在x轴上；当m = _____ 时，图象过原点.2•用一长度为I米的铁丝围成一个长方形或正方形，则其所围成的最大面积为 _______ .3.求下列二次函数的最值：2(1) y = 2x -4x 5 ；(2) y = (1 - x)(x 2).24.求二次函数y = 2x -3x - 5在-2 _ x _ 2上的最大值和最小值，并求对应的x的值.25•对于函数y =2x • 4x -3，当x _0时，求y的取值范围.6.求函数y = 3 —€5x —3x —2的最大值和最小值.7 .已知关于x的函数y = x2• (2t T)x • t2-1，当t取何值时，y的最小值为0 ?B 组21 当a - -1时，求函数的最大值和最小值；2 当a为实数时，求函数的最大值.2.函数y =x2• 2x 3在m^x乞0上的最大值为3，最小值为2,求m的取值范围.23 .设a • 0,当-1乞x乞1时，函数y x - ax b 1的最小值是-4，最大值是0,求a,b的值.4.已知函数y = x2 2ax 1在-1空x乞2上的最大值为4,求a的值.25.求关于x的二次函数y=x -2tx 1在-1辽x^1上的最大值(t为常数).1 .已知关于x的函数y =x2• 2ax • 2在-5辽x乞5上.第五讲二次函数的最值问题答案ymin- 0 •(1)当 X =1 时，Y min =1 ；当 X 「-5 时, ⑵当 a - 0 时，Y max =2710a ；当 a 0 时，Y max =27 —10a •一2空m 乞一1 • a =2,b 一2 •1a 或 a - -1.4123 4567123 44 14或 2,I 2 2 —m 16(1)有最小值 3, 无最大值；(2)有最大值9-，无最小值•4 --5时,Y min3 ；当x 「2时, 8Y max =19 •ymin2i 或 1 时，Ymaxymax- 37 •5.当t <0时，y max =2 —2t，此时X = 1 ；当t 0 时，y max =2 • 2t，此时X = -1 .。
奥数基础讲座 二次函数(含解答)-
二次函数讲座问题选讲1．二次函数y=ax 2，y=a （x-h ）2，y=a （x-h ）2+k ，y=ax 2+b x+c （各式中，a ≠0）•的图象形状相同，只是位置不同，它们的顶点坐标及对称轴如下表：2．抛物线y=ax 2+bx+c （a ≠0）的图象；当a>0时，开口向上，当a<0时开口向下，•对称轴是直线x=-2b a ，顶点坐标是（-2b a ，244ac b a-）． 3．抛物线y=a x 2+bx+c （a ≠0），若a>0，当x ≤-2b a 时，y 随x 的增大而减小；当x ≥-2b a时，y•随x 的增大而增大．若a<0，当x ≤-2b a 时，y 随x 的增大而增大；当x ≥-2b a 时，y 随x 的增大而减小． 4．抛物线y=a x 2+bx+c 的图象与坐标轴的交点：（1）图象与y 轴一定相交，交点坐标为（0，c ）；（2）当△=b 2-4ac>0，图象与x 轴交于两点A （x 1，0）和B （x 2，0），其中的x 1，x 2是一元二次方程ax 2+bx+c=0（a ≠0）的两根．这两点间的距离AB=│x 1-x 2│． 当△=0，图象与x 轴只有一个交点；当△<0，图象与x 轴没有交点．当a>0时，图象落在x 轴的上方，x 为任何实数，•都有y>0；当a<0时，图象落在x 轴的下方，x 为任何实数时，都有y<0．5．用待定系数法求二次函数的解析式（1）当题给条件为已知图象经过三个已知点或已知x 、y 的三对对应值时，可设解析式为一般形式：y=a x 2+bx +c （a ≠0）．（2）当题给条件为已知图象的顶点坐标或对称轴时，可设解析式为顶点式：y=•a （x-h ）2+k （a ≠0）．（3）当题给条件为已知图象与x 轴的两个交点坐标时，可设解析式为两根式：y=a （x-x 1）（x-x 2）（a ≠0）．6．二次函数知识很容易与其他知识综合应用，而形成较为复杂的综合题目．因此，以二次函数知识为主的综合性题目是热点考题，往往以大题形式出现．例题剖析例1 （2006年全国初中数学竞赛（浙江赛区）初赛试题）作抛物线A关于x•轴对称的抛物线B，再将抛物线B向左平移2个单位，向上平移1个单位，得到的抛物线C的函数解析式是y=2（x+1）2-1，则抛物线A所对应的函数表达式是（）（A）y=-2（x+3）2-2; （B）y=-2（x+3）2+2;（C）y=-2（x-1）2-2; （D）y=-2（x-1）2+2例2 （2006年全国初中数学竞赛（海南赛区））根据下列表格的对应值，判断方程a x2+bx+c=0（a≠0，a，b，c为常数）一个解x的范围是（）（A）3<x<3.23 （B）3.23<x<3.24（C）3.24<x<3.25 （D）3.25<x<3.26例3 （2006年芜湖市鸠江区初中数学竞赛试题）函数y=ax2+bx+c图象的大致位置如右图所示，则ab，bc，2a+b，（a+c）2-b2，（a+b）2-c2，b2-a2等代数式的值中，正数有（）（A）2个（B）3个（C）4个（D）5个例4 （2004年河北省初中数学创新与知识应用竞赛决赛试题）一条抛物线y=ax2+bx+c的顶点为（4，-11），且与x轴的两个交点的横坐标为一正一负，则a、b、c中为正数的（）（A）只有a （B）只有b （C）只有c （D）只有a和b例5 （2006年“信利杯”全国初中数学竞赛（广西赛区）初赛试题）设b>0，二次函数y=ax2+bx+a2-1的图象为下列图象之一，则a的值是（）（A）1 （B）-1 （C(D例6 （2006年芜湖市鸠江区初中数学竞赛试题）若二次函数y=ax2+bx+c（a≠0）的图象的顶点在第一象限，且过点（0，1）和（-1，0）•，•则S=•a+•b+•c•的值的变化范围是__________．例7 （2005年全国初中数学竞赛试题）Rt △ABC 的三个顶点A ，B ，C•均在抛物线y=x 2上，并且斜边AB 平行于x 轴．若斜边上的高为h ，则（ ）（A ）h<1 （B ）h=1 （C ）1<h<2 （D ）h>2例8 （1993年江苏初中数学竞赛试题）已知mn 是两位数，二次函数y=x 2+mx+n•的图象与x 轴交于不同的两点，这两点间距离不超过2．（1）求证：0<m 2-4n ≤4；（2）求出所有这样的两位数mn ．例9 （1997年天津市初中数学竞赛试题）已知函数y=x 2-│x │-12的图象与x 轴交于相异两点A ，B ，另一抛物线y=ax 2+bx+c 过点A ，B ，顶点为P ，且△APB 是等腰直角三角形，求a ，b ，c ．例10 （2006年全国初中数学竞赛（浙江赛区）初赛试题）已知二次函数y=x 2+2（m+1）x-m+1．（1）随着m 的变化，该二次函数图象的顶点P 是否都在某条抛物线上？如果是，请求出该抛物线的函数表达式；如果不是，请说明理由．（2）如果直线y=x+1经过二次函数y=x 2+2（m+1）x-m+1图象的顶点P ，求此时m 的值．例11 （2004年河北省初中数学创新与知识应用竞赛决赛试题）通过实验研究，•专家们发现：初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的，讲课开始时，学生的兴趣激增，中间有一段时间，学生的兴趣保持平衡的状态，随后开始分散．学生注意力指标数y 随时间x （分钟）变化的函数图象如图所示（y•越大表示学生注意力越集中）．当0≤x ≤10时，图象是抛物线的一部分，当10≤x ≤20和20≤x≤40时，图象是线段．（1）当0≤x ≤10时，求注意力指标数y 与时间x 的函数关系式；（2）一道数学竞赛题需要讲解24分钟．问老师能否经过适当安排，•使学生在听这道题时，注意力的指标数都不低于36．例12 （2006年全国初中数学竞赛（海南赛区））已知A 1、A 2、A 3是抛物线y=12x 2上的三点，A 1B 1、A 2B 2、A 3B 3分别垂直于x 轴，垂足为B 1、B 2、B 3，直线A 2B 2交线段A 1A 3于点C ．（1）如图（a ），若A 1、A 2、A 3三点的横坐标依次为1、2、3，求线段CA 2的长；（2）如图（b ），若将抛物线y=12x 2改为抛物线y=12x 2-x+1，A 1、A 2、A 3•三点的横坐标为连续整数，其他条件不变，求线段CA 2的长；（3）若将抛物线y=12x 2改为抛物线y=ax 2+bx+c ，A 1、A 2、A 3三点的横坐标为连续整数，其他条件不变，请猜想线段CA 2的长（用a 、b 、c 表示，并直接写出答案）．例13 设抛物线C 的解析式为y=x 2-2kx+）k ，k 为实数．（1）求抛物线的顶点坐标和对称轴方程（用k 表示）；（2）任意给定k 的三个不同实数值，请写出三个对应的顶点坐标，试说明当k•变化时，抛物线C 的顶点在一条定直线L 上，求出直线L 的解析式并画出图象；（3）在第一象限有任意两圆O 1、O 2相外切，且都与x 轴和（2）中的直线L 相切，设两圆在x 轴上的切点分别为A 、B （OA<OB ），试问：OA OB是否为一定值？若是，请求出该定值；若不是，请说明理由； （4）已知一直线L 1与抛物线C 中任意一条都相截，且截得的线段长都为6，求这条直线的解析式．巩固练习一、选择题1．直线y=52x-2与抛物线y=x 2-12x 的交点个数是（ ） （A ）0个 （B ）1个 （C ）2个 （D ）互相重合的两个 2．关于抛物线y=a x 2+bx+c （a ≠0），下面几点结论中，正确的有（ ）①当a>0时，对称轴左边y 随x 的增大而减小，对称轴右边y 随x 的增大而增大，•当a<0时，情况相反．②抛物线的最高点或最低点都是指抛物线的顶点．③只要解析式的二次项系数的绝对值相同，两条抛物线的形状就相同．④一元二次方程a x 2+bx+c=0（a ≠0）的根，就是抛物线y=ax 2+bx+c 与x 轴交点的横坐标．（A ）①②③④ （B ）①②③ （C ）①② （D ）①③④3．若函数y=a x的图象经过点（1，-2），那么抛物线y=ax 2+（a-1）x+a+3的性质说得全对的是（ ） （A ）开口向下，对称轴在y 轴右侧，图象与正半y 轴相交（B ）开口向下，对称轴在y 轴左侧，图象与正半y 轴相交（C）开口向上，对称轴在y轴左侧，图象与负半y轴相交（D）开口向下，对称轴在y轴右侧，图象与负半y轴相交4．函数y=a x2与y=ax（a<0）在同一直角坐标系中的大致图象是（）5．如图，抛物线y=x2+bx+c与y轴交于A点，与x轴正半轴交于B，C两点，且BC=3，S△ABC=6，则b的值是（）（A）b=5 （B）b=-5 （C）b=±5 （C）b=4（第5题）（第5题）6．不论x为何值，函数y=ax+bx+c（a≠0）的永远小于0的条件是（）（A）a>0，△>0 （B）a>0，△<0 （C）a<0，△>0 （D）a<0，△<07．已知抛物线y=a x2+bx+c如图所示，则关于x的方程a x2+bx+c-3=0的根的情况是（• ）（A）有两个不相等的正实数根（B）有两个异号实数根（C）有两个相等的实数根（D）没有实数根8．为了备战世界杯，中国足球队在某次训练中，一队员在距离球门12米处挑射，•正好射中了2.4米高的球门横梁．若足球运行的路线是抛物线y=a x2+bx+c（如图），则下列结论：①a<-160；②-160<a<0；③a-b+c>0；④0<b<-12a，其中正确的结论是（）（A）①③（B）①④（C）②③（D）②④(第8题) (第12题) (第15题)9．已知：二次函数y=x2+b x+c与x轴相交于A（x1，0），B（x2，0）两点，其顶点坐标为P（-24,24b c b），AB=│x1-x2│，若S△APB=1，则b与c的关系式是（）（A）b2-4c+1=0 （B）b2-4c-1=0 （C）b2-4c+4=0 （D）b2-4c-4=010．若函数y=12（x2-100x+196+│x2-100x+196│），则当自变量x取1、2、3、…、•10这100个自然数时，函数值的和是（）A.540;B.390;C.194;D.9711．已知二次函数y=ax2+bx的图象经过点A（-1，1），则ab有（）（A）最小值0 （B）最大值1 （C）最大值2 （D）有最小值1 412．抛物线y=ax2+bx+c的图象如图，OA=OC，则（）（A）ac+1=b （B）ab+1=c （C）bc+1=a （D）以上都不是13．若二次函数y=a x2+bx+c的顶点在第一象限，且经过点（0，1），（-1，0），则S=a+b+c的变化范围是（）（A）0<S<2 （B）S>1 （C）1<S<2 （D）-1<S<114．如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3，那么c的值等于（）（A）8 （B）14 （C）8或14 （D）-8或-1415．（2005年全国初中数学联赛初赛试题）如图，直线x=1是二次函数y=a x2+bx+c的图象的对称轴，则有（）（A）a+b+c=0 （B）b>a+c （C）c>2b （D）abc<0二、填空题1．二次函数y=a x2+c（c不为零），当x取x1，x2（x1≠x2）时，函数值相等，则x1与x2的关系是________．2．已知直线y=2x-1与抛物线y=5x2+k交点的横坐标为2，则k=________，•交点坐标为________．3．已知二次函数y1=ax2+b x+c（a≠0）与一次函数y2=kx+m（k≠0）的图象相交于点A（-2，4）和B（8，2）（如图所示），则能使y1>y2成立的x的取值范围是________．(第3题) (第6题) (第9题)4．有一个二次函数的图象，三位学生分别说出了它的一些特点：甲：对称轴是直线x=4；乙：与x轴两个交点的横坐标都是整数；丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为3．请你写出满足上述全部特点的一个二次函数解析式：_______．5．对于反比例函数y=-2x与二次函数y=-x2+3，•请说出它们的两个相同点①______②________；再说出它们的两个不同点①______，②_______．6．如图，已知点M（p，q）在抛物线y=x2-1上，以M为圆心的圆与x轴交于A、B两点，且A、B两点的横坐标是关于x的方程x2-2px+q=0的两根，则弦AB的长等于_______．7．设x、y、z满足关系式x-1=1223y z+-=，则x2+y2+z2的最小值为_______．8．已知二次函数y=ax2（a≥1）的图象上两点A、B的横坐标分别是-1、2，点O•是坐标原点，如果△AOB 是直角三角形，则△OAB的周长为________．9．如图，A、B、C是二次函数y=a x2+bx+c（a≠0）的图像上三点，根据图中给出的三点的位置，可得a_____0，c_____0，△_____0．10．炮弹从炮口射出后，飞行的h（m）高度与飞行的时间t（s）之间的函数关系是h=vtsina-5t2，其中v是炮弹发射的初速度，a是炮弹的发射角，当v0=300（m/s），sina=12时，炮弹飞行的最大高度是_______．11．抛物线y=-（x-L）（x-3-k）+L与抛物线y=（x-•3）2•+•4•关于原点对称，•则L+•k=________．12．（2000年全国初中数学联合竞赛试题）a，b是正数，并且抛物线y=x2+ax+2b和y=x2+2bx+a都与x 轴有公共点，则a2+b2的最小值是________．13．已知直线y=-2x+3与抛物线y=x2相交于A、B两点，O为坐标原点，那么△OAB•的面积等于________．14．（2003年“TRULY@信利杯”全国初中数学竞赛试题）已知二次函数y=ax 2+bx+c （其中a 是正整数）的图象经过点A （-1，4）与点B （2，1），并且与x 轴有两个不同的交点，则b+c 的最大值为________．15．（2005年全国初中数学竞赛浙江赛区试题）在直角坐标系中，抛物线y=x 2+mx-34m 2（m>0）与x 轴交于A ，B 两点，若A ，B 两点到原点的距离分别为OA ，OB ，且满足11OB OA =23，则m•的值等于_______． 三、解答题1．已知抛物线y=23x 2与直线y=x+k 有交点，求k 的取值范围． 2．如图，P 是抛物线y =x 2上第一象限内的一个点，A 点的坐标是（3，0）．（1）令P 点坐标为（x ，y ），求△OPA 的面积S ；（2）S 是y 的什么函数？（3）S 是x 的什么函数？（4）当S=6时，求点P 的坐标；（5）在抛物线y=x 2上求一点P ′，使△OP ′A 的两边P ′O=P ′A ．3．抛物线y=ax 2+bx+c 的顶点位于直线y=x-1和y=-2x-4的交点上，且与直线y=•4x-4有唯一交点，试求函数表达式．4．已知实数p<q ，抛物线y 1=x 2-px+2q 与y 2=x 2-qx+2p 在x 轴上有相同的交点A ．（1）求A 点坐标；（2）求p+q 的值．5．已知抛物线y =x 2+kx+k-1．（1）求证：无论k 是什么实数，抛物线经过x 轴上一个定点；（2）设抛物线与y 轴交于C 点，与x 轴交于A （x 1，0），B （x 2，0）两点，且满足：x 1<x 2，│x 1│<│x 2│，S △ABC =6，问：过A 、B 、C 三点的圆与抛物线是否有第四个交点，试说明理由，•如果有，求出其坐标．6．如图，已知直线y=-2x+2在x 轴、y 轴分别交于点A 、B ，以线段AB•为直角边在第一象限内作等腰直角△ABC ，∠BAC=90°，过C 作CD ⊥x 轴，垂足为D ．（1）求点A 、B 的坐标和AD 的长．（2）求过B 、A 、D 三点的抛物线的解析式．7．如图有一座抛物线形拱桥，桥下面在正常水位是AB 宽20m ，水位上升3m•就达到警戒线CD ，这是水面宽度为10m ．（1）在如图的坐标系中求抛物线的解析式．（2）若洪水到来时，水位以每小时0.2m 的速度上升，从警戒线开始，再持续多少小时才能到拱桥顶？8．先阅读下面一段材料，再完成后面的问题：材料：过抛物线y=a x 2（a>0）的对称轴上一点（0，-14a ）作对称轴的垂线L ，•则抛物线上任一点P 到点F （0，14a）的距离与P 到L 的距离一定相等．我们将点F 与直线L•分别称作这抛物线的焦点和准线，如y=x 的焦点为（0，14）．问题：若直线y=kx+b 交抛物线y=14x 2于A 、B ，•AC 、BD 垂直于抛物线的准线L ，垂足分别为C 、D （如图）．（1）求抛物线y=14x 2的焦点F 的坐标；（2）求证：直线AB 过焦点F 时，CF ⊥DF ； （3）当直线AB 过点（-1，0），且以线段AB 为直径的圆与准线L 相切时，求这直线对应的函数解析式．9．已知某绿色蔬菜生产基地收获的蒜苔，从四月一日起开始上市的30天内，蒜苔每10千克的批发价y （元）是上市时间x （元）的二次函数，•由近几年的行情可知如下信息：（1）求y 关于x 的函数解析式；（2）蒜台每10千克的批发价为10.8元时，问是在上市的多少天？10．已知：抛物线y=ax 2+4ax+t 与x 轴的一个交点为A （-1，0）．（1）求抛物线与x 轴的另一个交点B 的坐标；（2）D 是抛物线与y 轴的交点，C 是抛物线上的一点，且以AB 为一底的梯形ABCD 的面积为9，求此抛物线的解析式；（3）E 是第二象限内到x 轴、y 轴的距离的比为5：2的点，如果点E 在（2）中的抛物线上，且它与点A 在此抛物线对称轴的同侧，问：在抛物线的对称轴上是否存在点P ，使△APE 的周长最小？若存在，求出点P 的坐标；若不存在，请说明理由．11．已知二次函数y=x 2+b x+c 的图像与x 轴的两个交点的横坐标分别为x 1、x 2，•一元二次方程x 2+b 2x+20=0的两实数为x 3、x 4，且x 2-x 3=x 1-x 4=3，求二次函数的解析式，•并写出顶点坐标．12．改革开放以来，某镇通过多种途径发展地方经济，1995•年该镇国民生产总值为2亿元，根据测算，该镇国民生产总产值为5亿元时，可达到小康水平．（1）若从1996年开始，该镇国民生产总值每年比上一年增加0.6亿元，该镇通过几年可达到小康水平？（2）设以2001年为第一年，该镇第x 年的国民生产总值为y 亿元，y 与x•之间的关系是y=19x 2+23x+5（x ≥0）该镇那一年的国民生产总值可在1995•年的基础上翻两番（•即达到1995年的年国民生产总值的4倍）？13．已知：二次函数y=-x 2+3b x+c 与x 轴交于点M （x ，0），N （x ，0）两点，与y 轴交于点H ．（1）若∠HMO=45°，∠MHN=105°时，求：函数解析式；（2）若│x 1│2+│x 2│2=1，当点Q （b ，c ）在直线y=19x+13上时，求二次函数y=-x+3b x+c 的解析式．14．如图，一次函数y=kx+n 的图象与x 轴和y 轴分别交于点A （6，0）和B （0，• 线段AB 的垂直平分线交x 轴于点C ，交AB 于点D ．（1）试确定这个一次函数关系式；（2）求过A 、B 、C 三点的抛物线的函数关系式．15．如图，在直角坐标系中，O 是原点，A 、B 、C 三点的坐标分别为A （18，0），B （•18，6），C （8，6），四边形OABC 是梯形，点P 、Q 同时从原点出发，分别坐匀速运动，•其中点P 沿OA 向终点A 运动，速度为每秒1个单位，点Q 沿OC 、CB 向终点B 运动，•当这两点有一点到达自己的终点时，另一点也停止运动．（1）求出直线OC 的解析式及经过O 、A 、C 三点的抛物线的解析式．（2）试在（1）中的抛物线上找一点D ，使得以O 、A 、D 为顶点的三角形与△AOC 全等，请直接写出点D 的坐标．（3）设从出发起，运动了t 秒，如果点Q 的速度为每秒2个单位，试写出点Q 的坐标，•并写出此时t 的取值范围．（4）设从出发起，运动了t 秒，当P 、Q 两点运动的路程之和恰好等于梯形OABC 的周长的一半，这时，直线PQ 能否把梯形的面积也分成相等的两部分，如有可能，•请求出t 的值；如不可能，请说明理由．16．抛物线y=ax 2+bx+c 交x 轴于A ，B 两点，交y 轴于点C ，已知抛物线的对称轴为x=1，B （3，0），C （0，-3）．（1）求二次函数y=ax 2+bx+c 的解析式；（2）在抛物线对称轴上是否存在一点P ，使点P 到B 、C 两点距离之差最大？若存在，求出P 点坐标；若不存在，请说明理由；（3）平行于x 轴的一条直线交抛物线于M 、N 两点，若以MN 为直径的圆恰好与x 轴相切，求此圆的半径．答案：一、1～9．CDBDD DCBD10．B ．提示：∵x 2-100x+196=（x-2）（x-98），∴当2≤x ≤98时，│x 2-100x+196│=-（x 2-100x+196）． ∴当自变量x 取2、3、…、98时，函数值都为0． 而当x 取1、99、100时，│x 2-100x+196│=x 2-100x+196，故所求的和为：（1-2）（1-98）+（99-2）（99-98）+（100-•2）（100-98）=97+97+196=390． 11～15．DAACC二、1．互为相反数 2．-17，（2，3）． 3．x<-2或x>8 4．y=15x 2-85x+3等 5．图象都是曲线，都过点（-1，2）；图象形状不同，x 取值范围不同6．13.2 7．59148．．<、<、> 10．1125m 11．-9 12．2013．如图，直线y=-2x+3与抛物线y =x 2的交点坐标为A （1，1），B （-3，9），作AA 1，BB 1分别垂直于x 轴，垂足为A 1，B 1， ∴S △OAB =S梯形AA1BB1-S △AA1O -S △BB1O =12³（1+9）³（1+3）-12³1³1-12³9³3=6．14．由于二次函数的图象过点A （-1，4），点B （2，1），所以4,1,421,32.a b c b a a b c c a -+==--⎧⎧⎨⎨++==-⎩⎩解得 • 因为二次函数图象与x 轴有两个不的交点，所以△=b 2-4ac>0，（-a-1）2-4a （3-2a ）>0，即（9a-1）（a-1）>0，• 由于a 是正整数，故a>1，所以a ≥2．又因为b+c=-3a+2≤-4，且当a=2，b=-3，c=-1时，•满足题意， 故b+c 的最大值为-4． 15．2．提示：设方程x 2+mx-34m 2=0的两根分别x 1，x 2，且x 1<x 2， 则有x 1+x 2=-m<0，x 1x 2=-34m 2<0，•所以x 1<0，x 2>0，由11OB OA -=23，可知OA>OB ，又m>0， 所以抛物线的对称轴y 轴的左侧，于是OA=│x 1│=-x 1，OB=x 2． 所以2111x x +=23，1212x x x x +=23，故234mm --=23，解得m=2．三、1．由题意知，方程组22,3.y k y x k ⎧=⎪⎨⎪=+⎩有实数解，即方程23x 2=x+k 有实数解， 整理，得2x 2-3x-3k=0，∴△=9-4³2³（-3k ）≥0，∴k ≥-38． 2．（1）S=32y ，又y =x 2，∴S=32x 2；（2）正比例函数；（3）二次函数；（4）P （2，4）；（5）P ′（32，94）．3．y=23x2+43x-43．4．（1）A（-2，0）；（2）p+q=-2．5．（1）（-1，0）；（2）过A，B，C三点的圆与抛物线有第四个交点D．∵│x1│<│x2│，•C点在y轴上，∴点C不是抛物线的顶点，由于抛物线都是轴对称图形，过A、B、C三点的圆与抛物线组成一个轴对称图形，所以过A、B、C•三点的圆与抛物线第四个交点与C是对称点．∵x1=-1<0，x1<x2，│x1│<│x2│，∴x2>1，即x2>-1，-k>1，∴k<0，∵S△ABC=6，∴12│1-•k│）²（1+│1-k│）=6，∴（1-k）2+（1-k）-12=0，解得1-k=-4或1-k=3，∴k=-2或k=5（舍去），∴y=x2-2x-3．其对称轴为x=1，据对称性，D点坐标为（2，-3）．6．（1）A（1，0），B（0，2），AD=2；（2）y=23x2-83x+2．7．y=-125x2；5小时8．（1）F（0，1）；（2）∵AC=AF，∴∠ACF=∠AFC．又∵AC∥OF，∴∠ACF=∠CFO，∴CF平分∠AFO．同理DF平分∠BFO．而∠AFO+∠BFO=180°，∴∠CFO+∠DFO=12（∠AFO+∠BFO）=90°，∴CF⊥DF．（3）设圆心为M切L于N，连结MN，∴MN=12 AB．在直角梯形ACDB中，M•是AB中点，∴MN=12（AC+BC）．而AC=AF，BD=BF，∴MN=12（AF+BF），∴AF+BF=AB．∴AB过焦点F（0，1），又AB过点（-1，0），∴1bk b=⎧⎨-+=⎩∴AB对应的函数解析式为y=x+1．9．（1）设这个二次函数解析式为y=ax2+bx+c．根据题意，得15255 1022515 1562525a b ca b ca b c=++⎧⎪=++⎨⎪=++⎩• 解这个三元一次方程组，得12032854a y c ⎧=⎪⎪⎪=-⎨⎪⎪=⎪⎩∴这个函数解析式为：y=120x 2-32x+854．（或y=120（x-15）2+10） （2）把y=10.8代入上式，得10.8=120（x-15）2+10，（或10.8=120x 2-32x+854）．整理，得x 2-30x+209=0，（x-11）（x-19）=0，∴x 1=11，x 2=19， 经检验x=11，x=19都符合题意．即蒜苔每10千克批发价为10.8元时，是上市11天、9天．10．（1）依题意，抛物线的对称轴为y=x-2．∵抛物线与x 轴的一个交点为A （-1，0），∴由抛物线的对称性，可得抛物线与x 轴的另一个交点B 的坐标为（-3，0）． （2）∵抛物线y=a x 2+4ax+t 与x 轴的一个交点为A （-1，0），∴a （-1）2+4a （-1）+t=0，•∴t=3a ．∴y=ax 2+4ax+3a ．∴D （0，3a ）． ∵梯形ABCD 中，AB ∥CD ，且点C 在抛物线y=a x 2+4ax+3a 上， ∴C （-4，3a ），∴AB=2，CD=4， ∵梯形ABCD 的面积为9，∴12（AB+CD ）²OD=9． ∴12（2+4）│3a │=9，∴a=±1． ∴所求抛物线的解析式为y=x 2+4x+3或y=-x 2-4x-3．（3）设点E 坐标为（x 0，y 0），依题意x 0<0，y 0>0，且00||y x =52．∴y=-52．①设点E 在抛物线y=x 2+4x+3上，∴y 0=x 02+4x 0+3．解方程组000200005621540y x x y x x x ⎧=-=-⎧⎪⎨⎨=⎩⎪=++⎩得∴001`25`4x y ⎧=-⎪⎪⎨⎪=⎪⎩∵点E 与点A•在对称轴x=-2的同侧，∴点E 坐标为（-12，54）， 设在抛物线的对称轴x=-2上存在一点P ，使△APE 的周长最小． ∵AE 长为定值，∴要使△APE 的周长最小，只须PA+PE 最小． ∵点A•关于对称轴x=-2的对称点是B （-3，0）， ∴几何知识可知，P 是直线BE 与对称轴x=-2的交点．•设过点E 、B 的直线的解析式为y=mx+n ，∴1152243302m m n m n n ⎧=⎧⎪-+=⎪⎪⎨⎨⎪⎪-+==⎩⎪⎩解得 ∴直线BE 的解析式为y=12x+32，把x=-2•代入上式，得y=12， ∴点P 坐标为（-2，-12）． ②设点E 在抛物线y=-x 2-4x-3上，∴y 0=-x 02-4x 0-3．解方程0020005243y x x x x ⎧=-⎪⎨⎪=---⎩ 消去y 0，得x 02+32x 0+3=0， ∴△<•0，∴此方程无实数根．综上．在抛物线的对称轴上存在点P （-2，12），使△APE 的周长最小． 11．y=x 2+3x+2；（-32，-14）． 12．（1）5；（2）2003． 13．（1）y=-x 2+（2）y=-x 2+13x+94，y=-x 2-x ．14．（1）2）先求出点C （2，0），故（x-2）（x-6）． 15．（1）∵O ，C 两点的坐标分别为O （0，0），C （8，6），设OC 的解析式为y=kx+b ，将两点坐标代入得：k=34，b=0，∴y=34x ． ∵抛物线过O ，A ，C 三点，这三点的坐标为O （0，0），A （18，0），C （8，6）． ∵A ，O 是x 轴上两点，故可设抛物线的解析式为y=a （x-0）（x-18）． 再将C （8，6）代入得：a=-340．∴y=-340x 2+2720x ．（2）D （10，6）．（3）当Q 在OC 上运动时，可设Q （m ，34m ）， 依题意有：m 2+（34m ）2=（2t ）2，∴m=85t ，∴Q （85t ，65t ）•，•（0≤t ≤5）．当Q 在CB 上时，Q 点所走过的路程为2t ． ∵OC=10，∴CQ=2t-10，∴Q 点的横坐标为2t-10+8=2t-2．∴Q （2t-2，6），（5<t ≤10）．（4）∵梯形OABC 的周长为44，当Q 点在OC 上时，P 运动的路程为t ， 则Q 运动的路程为（22-t ）．△OPQ 中，OP 边上的高为：（22-t ）³35．∴S △OPQ =12t （22-t ）³35，S 梯形OABC =12（18+10）³6=84．• 依题意有：12t （22-t ）³35=84³12．整理得：t 2-22t+140=0．∵△=222-4³140<0，∴这样的t 不存在．当Q 在BC 上时，Q 走过的路程为22-t ，∴CQ 的长为：22-t-10=12-t ， ∴S梯形OCQP=12³6（22-t-10+t ）=36≠84³12． ∴这样的t 值也不存在．综上所述，不存在这样的t 值，使得P 、Q 两点同时平分梯形的周长和面积． 16．（1）将C （0，-3）代入y=ax 2+bx+c ，得c=-3，将c=-3，B （3，0）代入y=a x 2+bx+c ，得9a+3b+c=0． ∵x=1是对称轴，∴-2ba=-1．（2）． 将（2）代入（1）得a=1，b=-2．•所以二次函数得解析式是y=x 2-2x-3．（2）AC 与对称轴的交点P 即为到B 、C 的距离之差最大的点．∵C 点的坐标为（0，-3），A 点的坐标为（-1，0）．∴直线AC 的解析式是y=-3x-3，又对称轴为x=1，∴点P 的坐标（1，-6）．（3）设M （x 1，y ），N （x 2，y ），所求圆的半径为r ，则x 2-x 1=2r ，（1）∵对称轴为x=1，∴x 2+x 1=2．（2） 由（1）、（2）得：x 2=r+1． （3）将N （r+1，y ）将代入解析式y=x 2-2x-3，得y=（r+1）2-2（r+1）-3，（4） 整理得：y=r 2-4．由于r=±y ，当y>0时，r 2-r-4=0，解得r 1，r 2（舍去），•当y<0时，r 2+r-4=0，解得r 1，r 2（舍去），所以圆的半径是12+或12．。
二次函数最值问题(含标准答案)
二次函数最值问题(含答案)————————————————————————————————作者：————————————————————————————————日期：二次函数最值问题一．选择题（共8小题）1．如果多项式P=a2+4a+2014，则P的最小值是（）A．2010 B．2011 C．2012 D．20132．已知二次函数y=x2﹣6x+m的最小值是﹣3，那么m的值等于（）A．10 B．4 C．5 D．63．若二次函数y=ax2+bx+c的图象开口向下、顶点坐标为（2，﹣3），则此函数有（）A．最小值2 B．最小值﹣3 C．最大值2 D．最大值﹣34．设x≥0，y≥0，2x+y=6，则u=4x2+3xy+y2﹣6x﹣3y的最大值是（）A．B．18 C．20 D．不存在5．二次函数的图象如图所示，当﹣1≤x≤0时，该函数的最大值是（）A．3.125 B．4 C．2 D．06．已知二次函数y=（x﹣h）2+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为（）A．1或﹣5 B．﹣1或5 C．1或﹣3 D．1或37．二次函数y=﹣（x﹣1）2+5，当m≤x≤n且mn＜0时，y的最小值为2m，最大值为2n，则m+n的值为（）A．B．2 C．D．8．如图，抛物线经过A（1，0），B（4，0），C（0，﹣4）三点，点D是直线BC 上方的抛物线上的一个动点，连结DC，DB，则△BCD的面积的最大值是（）A．7 B．7.5 C．8 D．9二．填空题（共2小题）9．已知二次函数y=2（x+1）2+1，﹣2≤x≤1，则函数y的最小值是，最大值是．10．如图，在直角坐标系中，点A（0，a2﹣a）和点B（0，﹣3a﹣5）在y轴上，=6．当线段OM最长时，点M的坐标为．点M在x轴负半轴上，S△ABM三．解答题（共3小题）11．在平面直角坐标系中，O为原点，直线l：x=1，点A（2，0），点E，点F，点M都在直线l上，且点E和点F关于点M对称，直线EA与直线OF交于点P．（Ⅰ）若点M的坐标为（1，﹣1），①当点F的坐标为（1，1）时，如图，求点P的坐标；②当点F为直线l上的动点时，记点P（x，y），求y关于x的函数解析式．（Ⅱ）若点M（1，m），点F（1，t），其中t≠0，过点P作PQ⊥l于点Q，当OQ=PQ时，试用含t的式子表示m．12．已知关于x的函数y=kx2+（2k﹣1）x﹣2（k为常数）．（1）试说明：不论k取什么值，此函数图象一定经过（﹣2，0）；（2）在x＞0时，若要使y随x的增大而减小，求k的取值范围；（3）试问该函数是否存在最小值﹣3？若存在，请求出此时k的值；若不存在，请说明理由．13．函数y=（m+2）是关于x的二次函数，求：（1）满足条件的m值；（2）m为何值时，抛物线有最低点？求出这个最低点．这时，当x为何值时，y 随x的增大而增大？（3）m为何值时，函数有最大值？最大值是多少？这时，当x为何值时，y随x 的增大而减小．二次函数最值问题（含答案）一．选择题（共8小题）1．A；2．D；3．D；4．B；5．C；6．B；7．D；8．C；9．1；9；10．（﹣3，0）；三．解答题（共3小题）11．【解答】解：（Ⅰ）①∵点O（0，0），F（1，1），∴直线OF的解析式为y=x．设直线EA的解析式为：y=kx+b（k≠0）、∵点E和点F关于点M（1，﹣1）对称，∴E（1，﹣3）．又∵A（2，0），点E在直线EA上，∴，解得，∴直线EA的解析式为：y=3x﹣6．∵点P是直线OF与直线EA的交点，则，解得，∴点P的坐标是（3，3）．②由已知可设点F的坐标是（1，t）．∴直线OF的解析式为y=tx．设直线EA的解析式为y=cx+d（c、d是常数，且c≠0）．由点E和点F关于点M（1，﹣1）对称，得点E（1，﹣2﹣t）．又点A、E在直线EA上，∴，解得，∴直线EA的解析式为：y=（2+t）x﹣2（2+t）．∵点P为直线OF与直线EA的交点，∴tx=（2+t）x﹣2（2+t），即t=x﹣2．则有y=tx=（x﹣2）x=x2﹣2x；（Ⅱ）由（Ⅰ）可得，直线OF的解析式为y=tx．直线EA的解析式为y=（t﹣2m）x﹣2（t﹣2m）．∵点P为直线OF与直线EA的交点，∴tx=（t﹣2m）x﹣2（t﹣2m），化简，得x=2﹣．有y=tx=2t﹣．∴点P的坐标为（2﹣，2t﹣）．∵PQ⊥l于点Q，得点Q（1，2t﹣），∴OQ2=1+t2（2﹣）2，PQ2=（1﹣）2，∵OQ=PQ，∴1+t2（2﹣）2=（1﹣）2，化简，得t（t﹣2m）（t2﹣2mt﹣1）=0．又∵t≠0，∴t﹣2m=0或t2﹣2mt﹣1=0，解得m=或m=．则m=或m=即为所求．12.解：（1）将x=﹣2代入，得y=k（﹣2）2+（2k﹣1）•（﹣2）﹣2=0，故不论k取何值，此函数图象一定经过点（﹣2，0）．（2）①若k=0，此函数为一次函数y=﹣x﹣2，当x＞0时，y随x的增大而减小，∴k=0符合题意．②若k≠0，此函数为二次函数，而图象一定经过（﹣2，0）、（0，﹣2）∴要使当x＞0时，y随x的增大而减小，开口向下，须满足k＜0即可．综上，k的取值范围是k≤0．（3）若k=0，此函数为一次函数y=﹣x﹣2，∵x的取值为全体实数，∴y无最小值，若k≠0，此函数为二次函数，若存在最小值为﹣3，则=﹣3，且k＞0，解得：k=符合题意，∴当k=时，函数存在最小值﹣3．13．解：（1）根据题意得m+2≠0且m2+m﹣4=2，解得m1=2，m2=﹣3，所以满足条件的m值为2或﹣3；（2）当m+2＞0时，抛物线有最低点，所以m=2，抛物线解析式为y=4x2，所以抛物线的最低点为（0，0），当x≥0时，y随x的增大而增大；（3）当m=﹣3时，抛物线开口向下，函数有最大值；抛物线解析式为y=﹣x2，所以二次函数的最大值是0，这时，当x≥0时，y随x的增大而减小．。
专题07 二次函数的最值问题-九年级数学上册(解析版)
专题07二次函数的最值问题考点1：定轴动区间；考点2：动轴定区间。
1．在二次函数y ＝x 2﹣2x ﹣3中，当0≤x ≤3时，y 的最大值和最小值分别是（）A ．0，﹣4B ．0，﹣3C ．﹣3，﹣4D ．0，0解：抛物线的对称轴是直线x ＝1，则当x ＝1时，y ＝1﹣2﹣3＝﹣4，是最小值；当x ＝3时，y ＝9﹣6﹣3＝0是最大值．答案：A ．2．（易错题）已知二次函数y ＝a （x ﹣1）2﹣a （a ≠0），当﹣1≤x ≤4时，y 的最小值为﹣4，则a 的值为（）A ．12或4B ．43或−12C ．−43或4D ．−12或4解：y ＝a （x ﹣1）2﹣a 的对称轴为直线x ＝1，顶点坐标为（1，﹣a ），当a ＞0时，在﹣1≤x ≤4，函数有最小值﹣a ，∵y 的最小值为﹣4，∴﹣a ＝﹣4，∴a ＝4；当a ＜0时，在﹣1≤x ≤4，当x ＝4时，函数有最小值，∴9a ﹣a ＝﹣4，解得a =−12；综上所述：a 的值为4或−12，答案：D．3．（易错题）当a ≤x ≤a +1时，函数y ＝x 2﹣2x +1的最小值为1，则a 的值为（）A ．﹣1B ．2C ．0或2D ．﹣1或2解：当y ＝1时，有x 2﹣2x +1＝1，解得：x 1＝0，x 2＝2．题型01定轴动区间∵当a≤x≤a+1时，函数有最小值1，∴a＝2或a+1＝0，∴a＝2或a＝﹣1，答案：D．4．已知函数y＝﹣3（x﹣2）2+4，当x＝2时，函数取得最大值为4．解：∵y＝﹣3（x﹣2）2+4，∴抛物线的顶点坐标为（2，4），又∵a＝﹣3＜0，∴抛物线的开口向下，顶点是它的最高点，∴x＝2时，函数有最大值为4．答案：2，4．5．若函数y＝x2﹣6x+5，当2≤x≤6时的最大值是M，最小值是m，则M﹣m＝9．解：原式可化为y＝（x﹣3）2﹣4，可知函数顶点坐标为（3，﹣4），当y＝0时，x2﹣6x+5＝0，即（x﹣1）（x﹣5）＝0，解得x1＝1，x2＝5．如图：m＝﹣4，当x＝6时，y＝36﹣36+5＝5，即M＝5．则M﹣m＝5﹣（﹣4）＝9．故答案为9．6．已知二次函数y＝ax2﹣4ax+3a（1）若a＝1，则函数y的最小值为﹣1．（2）若当1≤x≤4时，y的最大值是4，则a的值为43或﹣4．解：（1）当a＝1时，y＝x2﹣4x+3＝（x﹣2）2﹣1∵a＝1＞0∴抛物线的开口向上，当x＝2时，函数y的最小值为﹣1．（2）∵二次函数y＝ax2﹣4ax+3a＝a（x﹣2）2﹣a∴抛物线的对称轴是直线x＝2，∵1≤x≤4，∴当a＞0时，抛物线开口向上，在对称轴直线x＝2右侧y随x的增大而增大，当x＝4时y有最大值，a×（4﹣2）2﹣a＝4，解得a=43，当a＜0时，抛物线开口向下，x＝2时y有最大值，a×（2﹣2）2﹣a＝4，解得a＝﹣4．答案：（1）﹣1；（2）43或−4．7．（易错题）设a，b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于任何一个二次函数，它在给定的闭区间上都有最小值．（1）函数y＝﹣x2+4x﹣2在区间[0，5]上的最小值是﹣7（2）求函数=(+12)2+34在区间[0，32]上的最小值．（3）求函数y＝x2﹣4x﹣4在区间[t﹣2，t﹣1]（t为任意实数）上的最小值y min的解析式．解：（1）y＝﹣x2+4x﹣2其对称轴为直线为x＝2，顶点坐标为（2，2），函数图象开口向下．如图1所示：当x＝5时，函数有最小值，最小值为﹣7．答案：﹣7．（2）=(+12)2+34，其对称轴为直线=−12，顶点坐标(−12，34)，且图象开口向上．其顶点横坐标不在区间[0，32]内，如图2所示：当x＝0时，函数y有最小值m=1．（3）将二次函数配方得：y＝x2﹣4x﹣4＝（x﹣2）2﹣8其对称轴为直线：x＝2，顶点坐标为（2，﹣8），图象开口向上若顶点横坐标在区间[t﹣2，t﹣1]左侧，则2＜t﹣2，即t＞4．当x＝t﹣2时，函数取得最小值：m=(−4)2−8=2−8+8若顶点横坐标在区间[t﹣2，t﹣1]上，则t﹣2≤2≤t﹣1，即3≤t≤4．当x＝2时，函数取得最小值：y min＝﹣8若顶点横坐标在区间[t﹣2，t﹣1]右侧，则t﹣1＜2，即t＜3．当x＝t﹣1时，函数取得最小值：m=(−3)2−8=2−6+1综上讨论，得m=2−8+8(＞4)−8(3≤≤4)2−6+1(＜3)．8．（易错题）已知二次函数y ＝﹣x 2+6x ﹣5．（1）求二次函数图象的顶点坐标；（2）当1≤x ≤4时，函数的最大值和最小值分别为多少？（3）当t ≤x ≤t +3时，函数的最大值为m ，最小值为n ，若m ﹣n ＝3，求t 的值．解：（1）∵y ＝﹣x 2+6x ﹣5＝﹣（x ﹣3）2+4，∴顶点坐标为（3，4）；（2）∵a ＝﹣1＜0，∴抛物线开口向下，∵顶点坐标为（3，4），∴当x ＝3时，y 最大值＝4，∵当1≤x ≤3时，y 随着x 的增大而增大，∴当x ＝1时，y 最小值＝0，∵当3＜x ≤4时，y 随着x 的增大而减小，∴当x ＝4时，y 最小值＝3．∴当1≤x ≤4时，函数的最大值为4，最小值为0；（3）当t ≤x ≤t +3时，对t 进行分类讨论，①当t +3＜3时，即t ＜0，y 随着x 的增大而增大，当x ＝t +3时，m ＝﹣（t +3）2+6（t +3）﹣5＝﹣t 2+4，当x ＝t 时，n ＝﹣t 2+6t ﹣5，∴m ﹣n ＝﹣t 2+4﹣（﹣t 2+6t ﹣5）＝﹣6t +9，∴﹣6t +9＝3，解得t ＝1（不合题意，舍去），②当0≤t ＜3时，顶点的横坐标在取值范围内，∴m ＝4，i ）当0≤t ≤32时，在x ＝t 时，n ＝﹣t 2+6t ﹣5，∴m ﹣n ＝4﹣（﹣t 2+6t ﹣5）＝t 2﹣6t +9，∴t2﹣6t+9＝3，解得t1＝3−3，t2＝3+3（不合题意，舍去）；ii）当32＜t＜3时，在x＝t+3时，n＝﹣t2+4，∴m﹣n＝4﹣（﹣t2+4）＝t2，∴t2＝3，解得t1=3，t2=−3（不合题意，舍去），③当t≥3时，y随着x的增大而减小，当x＝t时，m＝﹣t2+6t﹣5，当x＝t+3时，n＝﹣（t+3）2+6（t+3）﹣5＝﹣t2+4，.m﹣n＝﹣t2+6t﹣5﹣（﹣t2+4）＝6t﹣9，∴6t﹣9＝3，解得t＝2（不合题意，舍去），综上所述，t＝3−3或3．9．已知二次函数y＝ax2+4x+a﹣1的最小值为2，则a的值为（）A．3B．﹣1C．4D．4或﹣1解：∵二次函数y＝ax2+4x+a﹣1有最小值2，∴a＞0，y最小值=4a−24=4oK1)−424=2，整理，得a2﹣3a﹣4＝0，解得a＝﹣1或4，∵a＞0，∴a＝4．答案：C．10．设二次函数y＝a（x﹣m）（x﹣m﹣k）（a＞0，m，k是实数），则（）A．当k＝2时，函数y的最小值为﹣aB．当k＝2时，函数y的最小值为﹣2aC．当k＝4时，函数y的最小值为﹣aD．当k＝4时，函数y的最小值为﹣2a题型02动轴定区间解：令y＝0，则（x﹣m）（x﹣m﹣k）＝0，∴x1＝m，x2＝m+k，∴二次函数y＝a（x﹣m）（x﹣m﹣k）与x轴的交点坐标是（m，0），（m+k，0），∴二次函数的对称轴是：=1+22=rr2=2r2，∵a＞0，∴y有最小值，当=2r2时y最小，即=o2r2−p(2r2−−p=−24，当k＝2时，函数y的最小值为=−224=−；当k＝4时，函数y的最小值为=−424=−4，答案：A．11．在平面直角坐标系中，二次函数y＝x2+mx+m2﹣m（m为常数）的图象经过点（0，6），其对称轴在y轴左侧，则该二次函数有（）A．最大值5B．最大值154C．最小值5D．最小值154解：由题意可得：6＝m2﹣m，解得：m1＝3，m2＝﹣2，∵二次函数y＝x2+mx+m2﹣m，对称轴在y轴左侧，∴m＞0，∴m＝3，∴y＝x2+3x+6，∴二次函数有最小值为：4a−24=4×1×6−324×1=154．答案：D．12．已知二次函数y＝x2﹣2mx（m为常数），当﹣1≤x≤2时，函数值y的最小值为﹣2，则m的值是（）A．32B．2C．32或2D．−32或2解：y＝x2﹣2mx＝（x﹣m）2﹣m2，①若m＜﹣1，当x＝﹣1时，y＝1+2m＝﹣2，解得：m=−32；②若m＞2，当x＝2时，y＝4﹣4m＝﹣2，解得：m=32＜2（舍）；③若﹣1≤m≤2，当x＝m时，y＝﹣m2＝﹣2，解得：m=2或m=−2＜−1（舍），∴m的值为−32或2，答案：D．13．（易错题）当﹣1≤x≤2时，二次函数y＝x2+2kx+1的最小值是﹣1，则k的值可能是32或−解：对称轴：x=−22=−k，分三种情况讨论：①当﹣k＜﹣1时，即k＞1时，此时﹣1≤x≤2在对称轴的右侧，y随x的增大而增大，＝（﹣1）2+2k×（﹣1）+1＝﹣1，∴当x＝﹣1时，y有最小值，y小k=32，②当﹣1≤﹣k≤2时，即﹣2≤k≤1，对称轴在﹣1≤x≤2内，此时函数在﹣1≤x≤﹣k，y随x的增大而减小，在﹣k≤x≤2时，y随x的增大而增大，＝（﹣k）2+2k•（﹣k）+1＝﹣1，∴当x＝﹣k时，y有最小值，y小k2﹣2k2+2＝0，k2﹣2＝0，k=±2，∵﹣2≤k≤1，∴k=−2，③当﹣k＞2时，即k＜﹣2，此时﹣1≤x≤2在对称轴的左侧，y随x的增大而减小，∴当x＝2时，y有最小值，y＝22+2k×2+1＝﹣1，小k=−32（舍），综上所述，k的值可能是32或−2，答案：32或−2．14．已知y＝﹣x（x+3﹣a）是关于x的二次函数，当x的取值范围在1≤x≤5时，若y在x＝1时取得最大值，则实数a的取值范围是a≤5．解：第一种情况：当二次函数的对称轴不在1≤x≤5内时，此时，对称轴一定在1≤x≤5的左边，函数方能在这个区域取得最大值，x=K32＜1，即a＜5，第二种情况：当对称轴在1≤x≤5内时，对称轴一定是在顶点处取得最大值，即对称轴为x＝1，∴K32=1，即a＝5综合上所述a≤5．答案：a≤5．15．（易错题）已知二次函数y＝x2﹣2hx+h，当自变量x的取值在﹣1≤x≤1的范围中时，函数有最小值n，则n的最大值是14．解：二次函数y＝x2﹣2hx+h图象的对称轴为直线x＝h．当h≤﹣1时，x＝﹣1时y取最小值，此时n＝1+2h+h＝1+3h≤﹣2；当﹣1＜h＜1时，x＝h时y取最小值，此时n＝h2﹣2h2+h＝﹣h2+h＝﹣（h−12）2+14≤14；当h≥1时，x＝1时y取最小值，此时n＝1﹣2h+h＝1﹣h≤0．综上所述：n的最大值为14．答案：14．16．（易错题）已知二次函数y＝x2﹣2x+2在t≤x≤t+1时的最小值是t，则t的值为1或2．解：y＝x2﹣2x+2＝（x﹣1）2+1，分类讨论：（1）若顶点横坐标在范围t≤x≤t+1右侧时，有t+1＜1，即t＜0，此时y随x的增大而减小，＝t＝（t+1）2﹣2（t+1）+2，∴当x＝t+1时，函数取得最小值，y最小值方程无解．（2）若顶点横坐标在范围t≤x≤t+1内时，即有t≤1≤t+1，＝1，解这个不等式，即0≤t≤1．此时当x＝1时，函数取得最小值，y最小值∴t＝1．（3）若顶点横坐标在范围t≤x≤t+1左侧时，即t＞1时，y随x的增大而增大，＝t＝t2﹣2t+2，解得t＝2或1（舍弃），∵当x＝t时，函数取得最小值，y最小值∴t＝1或2．答案：1或2．17．已知函数y＝﹣x2+bx+c（b，c为常数）的图象经过点（0，﹣3），（﹣6，﹣3）．（1）求b，c的值．（2）当﹣4≤x≤0时，求y的最大值．（3）当m≤x≤0时，若y的最大值与最小值之和为2，求m的值．解：（1）把（0，﹣3），（﹣6，﹣3）代入y＝﹣x2+bx+c，得b＝﹣6，c＝﹣3．（2）∵y＝﹣x2﹣6x﹣3＝﹣（x+3）2+6，又∵﹣4≤x≤0，∴当x＝﹣3时，y有最大值为6．（3）①当﹣3＜m≤0时，当x＝0时，y有最小值为﹣3，当x＝m时，y有最大值为﹣m2﹣6m﹣3，∴﹣m2﹣6m﹣3+（﹣3）＝2，∴m＝﹣2或m＝﹣4（舍去）．②当m≤﹣3时，当x＝﹣3时y有最大值为6，∵y的最大值与最小值之和为2，∴y最小值为﹣4，∴﹣（m+3）2+6＝﹣4，∴m=−3−10或m=−3+10（舍去）．综上所述，m＝﹣2或−3−10．18．（易错题）已知二次函数y＝x2+bx+c（b，c为常数）．（Ⅰ）当b＝2，c＝﹣3时，求二次函数的最小值；（Ⅱ）当c＝5时，若在函数值y＝1的情况下，只有一个自变量x的值与其对应，求此时二次函数的解析式；（Ⅲ）当c＝b2时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式．解：（Ⅰ）当b＝2，c＝﹣3时，二次函数的解析式为y＝x2+2x﹣3＝（x+1）2﹣4，∴当x＝﹣1时，二次函数取得最小值﹣4；（Ⅱ）当c＝5时，二次函数的解析式为y＝x2+bx+5，由题意得，x2+bx+5＝1有两个相等是实数根，∴△＝b2﹣16＝0，解得，b1＝4，b2＝﹣4，∴二次函数的解析式y＝x2+4x+5，y＝x2﹣4x+5；（Ⅲ）当c＝b2时，二次函数解析式为y＝x2+bx+b2，图象开口向上，对称轴为直线x=−2，①当−2＜b，即b＞0时，在自变量x的值满足b≤x≤b+3的情况下，y随x的增大而增大，∴当x＝b时，y＝b2+b•b+b2＝3b2为最小值，∴3b2＝21，解得，b1=−7（舍去），b2=7；②当b≤−2≤b+3时，即﹣2≤b≤0，∴x=−2，y=34b2为最小值，∴34b2＝21，解得，b1＝﹣27（舍去），b2＝27（舍去）；③当−2＞b+3，即b＜﹣2，在自变量x的值满足b≤x≤b+3的情况下，y随x的增大而减小，故当x＝b+3时，y＝（b+3）2+b（b+3）+b2＝3b2+9b+9为最小值，∴3b2+9b+9＝21．解得，b1＝1（舍去），b2＝﹣4；∴b=7时，解析式为：y＝x2+7x+7b＝﹣4时，解析式为：y＝x2﹣4x+16．综上可得，此时二次函数的解析式为y＝x2+7x+7或y＝x2﹣4x+16．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
九年级数学竞赛专题讲座 ---二次函数的最值问题一、内容概述对二次函数2(0)y ax bx c a =++≠，若自变量为任意实数，则取最值情况为：（1）当0,2ba x a>=-时，244ac b y a -=最小值（2）当0,2ba x a<=-时，244ac b y a -=最大值若自变量x 的取值范围为()x αβαβ≤≤≠，则取最值分0a >和0a <两种情况，由α、β与2b a-的大小关系确定。
1．对于0a >：（1）当2baαβ<≤-，因为对称轴左侧y 随x 的增大而减小，所以y 的最大值为()y α，最小值为()y β。
这里()y α、()y β分别是y 在x α=与x β=时的函数值。
（2）当2baαβ-≤≤，因为对称轴右侧y 随x 的增大而增大，所以y 的最大值为()y β，最小值为()y α。
（3）当2b a αβ≤-≤，y 的最大值为()y α、 ()y β中较大者，y 的最小值为()2by a-.2．对于0a <（1）当2baαβ<≤-，y 的最大值为()y β，最小值为()y α。
（2）当2baαβ-≤≤，y 的最大值为()y α，最小值为()y β。
（3）当2b a αβ≤-≤，y 的最小值为()y α、 ()y β中较大者，y 的最大值为()2by a-.综上所述，求函数的最大、最小值，需比较三个函数值：()y α、()y β、()2by a-二、例题解析例1 已知12,x x 是方程22(2)(35)0x k x k k --+++=的两个实数根，求2212x x +的最大值和最小值。
解：由于题给出的二次方程有实根，所以0∆≥，解得443k -≤≤-∴y ＝2212x x +＝21212()2x x x x +-＝2106k k ---∵函数y 在443k -≤≤-随着k 的增大而减小 ∴当4k =-时，8y =最大值；当43k =-时，509y =最小值例2 （1）求函数243y x x =--在区间25x -≤≤中的最大值和最小值。
（2）已知：1y ≤，且21x y +=，求222163x x y ++的最小值。
解 （1）若240,2,x x -≥≥即则234y x x =-- ∴2325()24y x =--若240,2,x x -≤≤即则234y x x =--+ ∴2325()24y x =-++由此在25x -≤≤画出草图∴2325()24y x =--（25x ≤≤），当5x =时，6y =最大值；当2x =时，6y =最小值－ 对2325()24y x =-++（22x -≤≤），当32x =－时，254y =最大值；2x =时，6y =最小值－综上所述，2x =时，6y =最小值－；当32x =－时，254y =最大值.（2）由21x y +=得12yx -=，12y x =-由1y ≤ 得11x -≤≤ 故01x ≤≤∴22221192163144314()77z x x y x x x =++=++=++z 为开口向上，对称轴为17x =－的抛物线，虽然有最小值197，但17x =－不在01x ≤≤的范围内，因此不是所求的最值。
又0x =时，3z =；1x =时，21z = ∴所求的最小值为3例3 有两条抛物线223,9y x x y x =-=-+，通过点(,0)P t 且平行于y 轴的直线，分别交这两条抛物线于点A 和B ，当t 在0到3的范围内变化时，求线段AB 的最大值。
解：∵A 和B 的纵坐标分别为223,9t t t --+，∴AB =2222381(9)(3)2392()48t t t t t t -+--=-++=--+ ∴当34t =时，线段AB 取得最大值818例4 已知二次函数22962y x ax a a =---+11()33x -≤≤有最大值－3，求实数a 的值。
分析：本题是关于二次函数最值的“逆向问题”，由题设知，二次函数22962y x ax a a =---+的对称轴是3a x =-，而x 的取值范围是1133x -≤≤，所以要对3a -是否在x 的取值范围内讨论求解。
解：（1）若11333a -≤-≤，即11a -≤≤，抛物线开口向下，当3ax =-时，2y a =最大值∵二次函数最大值3-，即32a =-与11a -≤≤矛盾，舍去。
（2）若1,133a a -<->即当1133x -≤≤时，y 随x 增大而减小，当13x =-时，241y a a =-+-最大值，由2413,2a a a -+-=-=解得又1a >，∴2a =（3）若1,133a a -><-即 当1133x -≤≤时，y 随x 增大而增大，当13x =时，21y a =--最大值，由213,2a a --=-=±解得又1a <-，∴2a =-综上所述，26a =+或2a =-例5 在坐标平面上，纵坐标与横坐标都是整数的点称为整点，试在二次函数2910105x x y =-+的图像上找出满足y x ≤的所有整点(),x y ，并说明理由。
解：∵y x ≤，即21810x x x -+≤ ∴21810x x x -+≤ ①当0x ≥时，①式即为21810x x x -+≤，解得29x ≤≤ 此时，满足条件的点有()()()()2,2,4,3,7,6,9,9 当0x <时，21810x x x -+≤-，解得63x -≤≤- 此时满足条件的点有()()6,6,3,3-- 综上所述，满足条件的整点，共有6个。
例6求分式22365112x x x x +++＋的最小值解：令2223652612212x x y x x x x +==-++++＋，问题转化为考虑函数222z x x =++的最小值。
∵2222(1)1z x x x =++=++ ∴当1x =-时，min 1z =，min 4y =例7已知边长为4的正方形截去一个角后成为五边形ABCDE （如图），其中AF=2，BF=1.试在AB 上求一点P ，使矩形PNDM 有最大面积。
解：设矩形PNDM 的边DN=x ,NP=y ，于是矩形PNDM 的面积S xy =，24x ≤≤易知CN ＝4x -, EM ＝4y -，且有NP BC BF CN AF -=,即3142y x -=-所以152y x =-+，2152S xy x x ==-+,24x ≤≤ 所有根据二次函数的性质可得当4x =时max 12S =例7二次函数的最值问题训练题班级 姓名 学号1．填空（1）已知函数211(03)22y x x x =-++≤≤，当x =________时，y 取最大值是______；当x =________时，y 取最小值是______.（2）已知抛物线2(0)y ax bx c a =++≠的开口向上，对称轴是直线2x =，当1230,3x x x ==，对应的值y 分别是1y 、2y 、3y ，则1y 、2y 、3y 的大小关系是_________.（3）函数24)y x =≤≤的最大值与最小值分别是___________.（4）已知二次函数22y x x a =++（01x ≤≤）的最大值是3，那么a 的值为__________. 2．设x 为正整数，则函数21y x x x=-+的最小值是多少？3．已知：01x ≤≤，函数22ay x ax =-+的最小值为m ，试求m 的最大值。
4．对于任意实数x ，不等式210kx kx --<恒成立，求k 的取值范围。
5．如图，半径为1的半圆内接等腰梯形，其下底是半圆的直径，试求：（1）它的周长y 与腰长x 之间的函数关系式，并求出自变量x 的取值范围。
（26．已知实数a 、b 满足等式()2223a b -+=，求：ba的最大值和最小值。
7．已知：方程222(1)212170x k x k k --+-+=，两根为1x 、2x ，求2212x x +的最大值与最小值，并求此时方程的根。
8．根据某服装店统计，服装价格每提高3％，出售服装的件数就要降低2％，设某种服装提价x%，结果每天的经营收入（价格×出售价数）为原来的y 倍，（1）写出y 与x 的函数关系；（2）要使经营收入不降低，x 应控制在什么范围内？ （3）当x 是什么值时，能使经营收入最多？9．求函数222121x ax y x bx ++=++的最值。
参考答案1．(1)x=1,y=1,x=3,y=-1;(2) 231y y y <<;（3）最大值与最小值分别为：2，0；（4）a=0； 2．1；3．a ＝0时，m 有最大值0；a ＝1时，m 有最大值0.25；a ＝2时，m 有最大值0 4．－4<k ≤0;(2)x=1时，周长最大为56．当1,22a b =-=-时，b a 取得最小值1,22a b ==时，b a7．k=8时，最大值为98，方程为214490x x -+=，两根为7；k ＝2时，最小值为2，方程为2210x x -+=，两根为1。
8．（1）(1)(1)100150x xy =+- （2）0≤x ≤50 （3）当x=25时，最多。
9．解：把222121x ax y x bx ++=++化为关于x 的二次方程()212()(1)0y x a by x y -+-+-=，要使这个方程有实数根，则根据222(1)2(1)10b y ab y a ∆=---+-≥① 210b ->，即1b >，∴1,22(1)1ab a b y b -±-=-，∴2(1)1ab a b y b ---≤-或2(1)1ab a b y b -+-≥- ∴2(1)1ab a b y b ---=-极大值，2(1)1ab a by b -+-=-极小值②210b -<，即1b <，则有 22(1)(1)11ab a b ab a b y b b -+----≤≤-- ∴2(1)1ab a b y b ---=-极大值，2(1)1ab a by b -+-=-极小值 ③210b -=，即1b =，得()2112a ab y --≤2112(1)a ab y ab ->≤-时，，∴212(1)a y ab -=-极大值2112(1)a ab y ab -<≥-时，，∴212(1)a y ab -=-极小值。