高中数学必修第一册 5.3诱导公式第1课时公开课优秀课件(好用、与人教版教材同步)
合集下载
数学人教A版必修第一册5.3诱导公式课件
归 思 想
tan(180 ° -α) = -tanα
诱导公式（一）
sin(2k ) +sin sin( ) sin
公 式
cos(2k
) cos
cos( ) cos
公 式
一 tan(2k ) + tan tan( ) tan 二
公 sin( ) sin 式 cos( ) cos 三 tan( ) tan
)
2
sin tan . cos
变式
3. 已 知
f(α)
＝
cos π2＋α sin 32π－α cos－π－αtanπ－α
，
则
f
－25π 3
的值为
____解_．析：因为f(α)＝cocsos－π2π＋－ααsitnan32ππ－－αα
＝ －sin －cos
αα－－ccsoiosnsααα＝cos
例3.化简:
cos(
)sin(3
2
)sin(
2
)sin( 9
)
.
2
解：
( sin )( cos )( sin )cos[5 ( )]
原式
( cos )sin(
)[ sin(
2
)]sin[4 (
)]
2
sin2 cos[ cos( )]
2
( cos )sin[( sin )]sin(
3
sin(2 + 2 ) sin 2
3
3
sin（ ） sin
3
3
3 2
(3)
sin(
16 3
)
sin
16 3
sin(5
3
)
sin(
高一上学期数学人教A版必修第一册5.3诱导公式(第1课时)课件-
现
在
是
数
学
时
间
导语
在前面的学习中，我们知道终边相同的角的同一三角函数值相等，即
公式一，并且利用公式一可以把求绝对值较大的三角函数值转化为求
0°～360°角的三角函数值，对于90°～360°角的三角函数值，我们能否
进一步把它们转化到锐角范围内来求解，这是我们今天要解决的内容.
问题1
提示
请同学们写出公式一.
sin(α＋2kπ)＝sin α，cos(α＋2kπ)＝cos α，tan(α＋2kπ)＝tan α，其
中k∈Z.
问题2
提示
视察下图，思考我们是如何定义三角函数的？
三角函数的定义核心是角的终边与单位圆的交点的坐标，终边相
同的角的三角函数值相等.由图象可知，点P1与P2关于原点对称，点P1
与P2 两点的横坐标、纵坐标分别互为相反数，以OP2 为终边的角β可以
y
＋α)＝x.显然，我们可以根据相同的方法找出点 P1 关于 x 轴和 y 轴的
对称点，大家试一试吧.
知识点 诱导公式二、三、四
1.诱导公式二
(1)P2是点P1关于
原点 的对称点(如图所示).
(2)诱导公式二:sin(π+α)= -sin α ,cos(π+α)= -cos α ,tan(π+α)= tan α .
(2)
.
cos(-180°-)sin(--180°)
cos(-)tan(7π+)
解(1)
sin(π-)
=
costan(π+)
sin
(2)由题可知 sin α≠0,cos
sincos
=-1.
(-cos)sin
在
是
数
学
时
间
导语
在前面的学习中，我们知道终边相同的角的同一三角函数值相等，即
公式一，并且利用公式一可以把求绝对值较大的三角函数值转化为求
0°～360°角的三角函数值，对于90°～360°角的三角函数值，我们能否
进一步把它们转化到锐角范围内来求解，这是我们今天要解决的内容.
问题1
提示
请同学们写出公式一.
sin(α＋2kπ)＝sin α，cos(α＋2kπ)＝cos α，tan(α＋2kπ)＝tan α，其
中k∈Z.
问题2
提示
视察下图，思考我们是如何定义三角函数的？
三角函数的定义核心是角的终边与单位圆的交点的坐标，终边相
同的角的三角函数值相等.由图象可知，点P1与P2关于原点对称，点P1
与P2 两点的横坐标、纵坐标分别互为相反数，以OP2 为终边的角β可以
y
＋α)＝x.显然，我们可以根据相同的方法找出点 P1 关于 x 轴和 y 轴的
对称点，大家试一试吧.
知识点 诱导公式二、三、四
1.诱导公式二
(1)P2是点P1关于
原点 的对称点(如图所示).
(2)诱导公式二:sin(π+α)= -sin α ,cos(π+α)= -cos α ,tan(π+α)= tan α .
(2)
.
cos(-180°-)sin(--180°)
cos(-)tan(7π+)
解(1)
sin(π-)
=
costan(π+)
sin
(2)由题可知 sin α≠0,cos
sincos
=-1.
(-cos)sin
高中数学必修第一册人教A版5.3《诱导公式---第一课时》名师课件
2
；
47
cos
；
6
(3)tan945° .
解析
(1)sin −1200° = sin −4 × 360° + 240° = sin240° = sin 180° + 60° = −sin60° = −
(2)cos
47
6
= cos
11
6
+ 6 = cos
11
6
= cos 2 −
6
6
= cos =
y
y
tan( )
x
x
公式四
sin( ) sin
cos( ) cos
tan( ) tan
y
tan
x
探究新知
sin( k 2 ) sin
cos( k 2 ) cos
公式一 tan( k 2 ) tan
= −1.
=
1−2sin70° cos70°
−sin70° +cos70°
=
|cos70° −sin70° |
cos70° −sin70°
=
方法归纳
化简是一种不指明答案的恒等变形，将三角函数式化为
最简形式的标准是相对的，一般是指函数种类最少，项数最
少，函数次数最低，能求出数值的求出数值，分母上不含三
sin(−)+5cos(2+)
3cos(−)−sin(−)
解析
由已知得−sin = 2cos，所以tan = −2.
左边=
sin+5cos
−3cos+sin
高一数学新人教版(A版)必修第1册《5.3.1 诱导公式》第1课时 精品课件
如图 5.3-3，作 P1 关于 x 轴的对称点 P3 ，以 OP3 为终边的角 b 都是与角 -a 终边相同的角，即 b = 2kπ +(-a)(k Î Z)．
如图 5.3-4，作 P1 关于 y 轴的对称点 P4 ，以 OP4 为终边的角 b 都是与角 π - a 终边相同的角，即 b = 2kπ +(π - a)(k Î Z)．
3
3
sin 2
3
sin( )
3
sin 3
32
例 1 利用公式求下列三角函数值：
（3）sin(- 8π)； 3
解：sin(16 ) sin 16
3
3
sin(5 ) 3
sin( )
3
（4） tan(-2040o)．
tan(2040 ) tan 2040
tan(120 360 6) tan(120 ) tan120 tan(180 60 )
公式 一
公式 三
公式 二
公式 四
公式一~公式四：分别表示α+2kπ，-α，(π±α)的三角函数值 与α的同名函数值的关系。
记忆方法：“函数名不变，符号看象限.”（看成锐角）
例 1 利用公式求下列三角函数值：Βιβλιοθήκη （1） cos 225 °；
cos 45 2 2
（2）sin 8π ； 3
sin 8 sin(2 2 )
例 2 化简： cos(180o + a)sin(a + 360o ) ． tan(-a -180o)cos(-180o + a)
解：tan( 180 ) tan[( 180 )] - tan（ 180 ) - tan
cos(180 ) cos[(180 )] cos(180 ) cos
5.3.1诱导公式(第一课时)课件(人教版)
(
2
+ ) = 6 ,
(
2
=
+
+ ) = 6
= 1 , = 1 ，
公式六
( + ) = ，
2
( + ) = − .
2
sin( ) sin[ ( )] sin( ) cos
cos( ) cos
cos( ) cos
tan( ) tan 负化正
tan( ) tan
与的终边关于x轴对称
与的终边关于y轴对称
大化小
(锐角)
典例精析
例1.利用公式求下列三角函数值：
8
16
(1) 225°；(2) ；(3) (−
3
从而得： ( − ) = ，
公式四 ( − ) = − ，
( − ) = − .
−
( , )
归纳总结
y
α的终边
P1 ( x, y )
r=1
α
O
x
A(1,0)
归纳总结
α
sin
cos α
3
2
2
2
1
根据三角函数的定义，得：
1
= 1 , = 1 ， = ；
1
2
( + ) = 2 , ( + ) = 2 ，( + ) = .
2
从而得：( + ) = −1 , ( + ) = 1 ，( + ) =
人教版高中数学必修第一册5.3诱导公式 第1课时 诱导公式(1)【课件】
怎样判断任意角所在的象限呢?
【问题8】从诱导公式二、三、四的结构特征来看,它们的主要作用
是什么?
【问题9】我们可以怎样运用诱导公式二、三、四来计算任意角的三
角函数值? 请举例说明.
【问题10】你能归纳出运用诱导公式一、二、三、四求任意角的三
角函数值的一般步骤吗?
典例精析
【例1】 [教材改编题]求下列三角函数值：
化简条件和结论后再求值.
【变式训练3】已知k∈
(−) [(−)−]
，求证则
[(+)+](+)
= −
【解】
(−)(−)(+)
（备选例题）已知α是第三象限角,且f(α)=
(−−)(−−)
(1)
【问题5】在之前的讨论中我们知道角的终边除了关于原点对
称的情况外，还有关于x轴、y轴对称的情况．请你试着探究当角
的终边关于x轴、y轴对称时，三角函数值之间的关系．
【问题6】你能发现公式一、二、三、四的共同特征吗？
【活动3】归纳总结求任意角三角函数值的一般流程
【问题7】诱导公式二、三、四中等式右端的符号由角的象限确定,
第五章
三角函数
5.3
诱导公式
第 课时
诱导公式
教学目标
1. 借助单位圆和任意角的三角函数的定义,探究和推导三
角函数诱导公式二、三、四.
2. 在推导诱导公式二、三、四的过程中,理解和掌握诱导
公式二、三、四的结构特征.
3. 能熟练运用诱导公式二、三、四进行简单三角函数式
的求值、化简与恒等式的证明.
学习目标
若sin(α-3π)= ,求f(α)的值;
(2) 若α=-1920°,求f(α)的值.
【问题8】从诱导公式二、三、四的结构特征来看,它们的主要作用
是什么?
【问题9】我们可以怎样运用诱导公式二、三、四来计算任意角的三
角函数值? 请举例说明.
【问题10】你能归纳出运用诱导公式一、二、三、四求任意角的三
角函数值的一般步骤吗?
典例精析
【例1】 [教材改编题]求下列三角函数值：
化简条件和结论后再求值.
【变式训练3】已知k∈
(−) [(−)−]
，求证则
[(+)+](+)
= −
【解】
(−)(−)(+)
（备选例题）已知α是第三象限角,且f(α)=
(−−)(−−)
(1)
【问题5】在之前的讨论中我们知道角的终边除了关于原点对
称的情况外，还有关于x轴、y轴对称的情况．请你试着探究当角
的终边关于x轴、y轴对称时，三角函数值之间的关系．
【问题6】你能发现公式一、二、三、四的共同特征吗？
【活动3】归纳总结求任意角三角函数值的一般流程
【问题7】诱导公式二、三、四中等式右端的符号由角的象限确定,
第五章
三角函数
5.3
诱导公式
第 课时
诱导公式
教学目标
1. 借助单位圆和任意角的三角函数的定义,探究和推导三
角函数诱导公式二、三、四.
2. 在推导诱导公式二、三、四的过程中,理解和掌握诱导
公式二、三、四的结构特征.
3. 能熟练运用诱导公式二、三、四进行简单三角函数式
的求值、化简与恒等式的证明.
学习目标
若sin(α-3π)= ,求f(α)的值;
(2) 若α=-1920°,求f(α)的值.
5.3诱导公式(第一课时)课件-高一上学期数学人教A版必修第一册
5.3 诱导公式
• 1.利用单位圆的对称性推导诱导公式； • 2.掌握三角函数的诱导公式； • 3.能运用诱导公式化简简单的三角函数； • 重点：诱导公式的探究 • 难点：圆的几何性质与三角函数性质的联系；
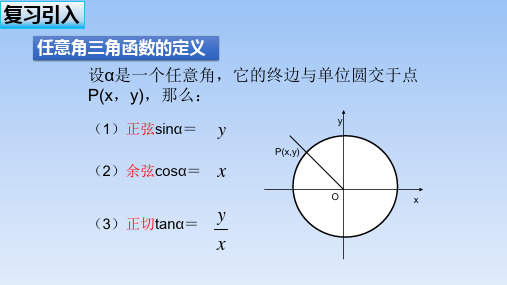
复习引入
问题1：三角函数的定义？
三角函数第一定义：y sin ; x cos; y tan x 0.
的对称点P4，那么又可以得到什么结论？
以OP4为终边的角β=2kπ+(π-α)(k∈Z)
P1(x,y)与P4(-x,y)关于y轴对称
sinα=y
sin(π-α)=y
cosα=x
tan y
x
cos(π-α)= -x
tan - - y
x
公式四 sin(π-α)=sinα
cos(π-α)=-cosα
公式三 sin(-α)=-sinα cos(-α)= cosα tan(-α)= -tanα
公式四 sin(π-α)=sinα cos(π-α)=- cosα tan(π-α)= -tanα
典例分析
【例1】利用公式求下列三角函数值：
(1) cos 225 (2) sin 8π (3) sin(16π )
P4
π-α
P1
α
1
tan(π-α)=-tanα
创设问题情境
诱导公式 (公式一~ 公式四)
简记： 函数名不变， 符号看象限.
公式一 sin(α+2kπ)=sinα cos(α+2kπ)=cosα tan(α+2kπ)=tanα
公式二 sin(π+α)=-sinα cos(π+α)= -cosα tan(π+α)= tanα
求值（4） cos420 ；（5） sin( 7 ) ；（6） tan 1140 ； 6
• 1.利用单位圆的对称性推导诱导公式； • 2.掌握三角函数的诱导公式； • 3.能运用诱导公式化简简单的三角函数； • 重点：诱导公式的探究 • 难点：圆的几何性质与三角函数性质的联系；
复习引入
问题1：三角函数的定义？
三角函数第一定义：y sin ; x cos; y tan x 0.
的对称点P4，那么又可以得到什么结论？
以OP4为终边的角β=2kπ+(π-α)(k∈Z)
P1(x,y)与P4(-x,y)关于y轴对称
sinα=y
sin(π-α)=y
cosα=x
tan y
x
cos(π-α)= -x
tan - - y
x
公式四 sin(π-α)=sinα
cos(π-α)=-cosα
公式三 sin(-α)=-sinα cos(-α)= cosα tan(-α)= -tanα
公式四 sin(π-α)=sinα cos(π-α)=- cosα tan(π-α)= -tanα
典例分析
【例1】利用公式求下列三角函数值：
(1) cos 225 (2) sin 8π (3) sin(16π )
P4
π-α
P1
α
1
tan(π-α)=-tanα
创设问题情境
诱导公式 (公式一~ 公式四)
简记： 函数名不变， 符号看象限.
公式一 sin(α+2kπ)=sinα cos(α+2kπ)=cosα tan(α+2kπ)=tanα
公式二 sin(π+α)=-sinα cos(π+α)= -cosα tan(π+α)= tanα
求值（4） cos420 ；（5） sin( 7 ) ；（6） tan 1140 ； 6
高中数学必修1人教版必修一5.3诱导公式(一)课件(60张)
故cos 15°=-a(a<0),得sin 15°= 1－a2，
tan 195°=tan(180°+15°)=tan 15°=
1－a 2 －a
.
【内化·悟】 怎样找两个角之间的关系? 提示:解题时,我们一般把含有参变量的两个角相加或 相减,寻找两个角之间的关系.对于不含参变量的角,我 们一般直接观察两个角之间的关系,或者寻找给出角与 特殊角之间的关系.
【解析】1.选C.
原式= sin 4 cos(2＋7 ) tan(4＋5 )＝sin 4 cos 7 tan 5
3
6
4
3
6
4
＝sin(＋ ) cos(＋ ) tan(＋ )
3
6
4
＝(－sin ) (－cos ) tan
3
64
＝( 3 ) ( 3 ) 1 3 .
2
2
4
2.(1)原式=cos 120°(-sin 150°)+tan (135°+
.
【解析】原式= 1＋2sin (360－70)cos (360＋70)
sin (180＋70)＋cos (720＋70)
＝ 1－2sin 70cos 70 ＝| cos 70－sin 70 | sin 70＋cos 70 cos 70－sin 70
＝sin cos
70－cos 70－sin
70 70
6
6
6
＝－sin( 5 － )＝－m.
6
方法二:
sin( 5 － ) sin[－( )] sin( ) m.
6
6
6
所以 sin( 7 ) sin[ ( )] sin( ) m.
6
5.3诱导公式(第一课时)高一数学课件(人教A版必修第一册)
锐求值
得到锐角的三角函数后求值
跟 踪 训 练 1
利用诱导公式，求三角函数值
(1)cos 210°；
11
(2)sin
4
(3)sin
43
−
6
；
；
(4)cos(－1920°).
典 型 例 题 2
例2 化简
化简求值问题
(180°+)(+360°)
(−−180°)(−180°+)
所以π+α可以看成第三象限角，-α可以看成第
四象限角，π-α可以看成第二象限角
自我检测
判断正误(正确的打“√”，错误的打“×”)
(1)诱导公式中角α是任意角．(
)
(2)点P(x，y)关于x轴的对称点是P′(－x，y).(
)
(3)诱导公式中的符号是由角α的象限决定的．(
(4)诱导公式一、二、三、四函数的名称都不变．(
已知 tan
，则 tan
6
3
6
课堂小结
诱导公式一
诱导公式二
sin (π＋α)＝-sinα
cos (π＋α)＝-cosα
tan (π＋α)＝tanα
诱导公式三
诱导公式四
sin (-α)＝sinα
sin (π - α)＝sinα
cos (-α)＝-cosα
tan (-α)＝-tanα
值之间有什么关系？
β
3
角-α与角α的终边关于 x轴 对称
诱导公式三
(x,y)
sin (-α)＝
3
(x,-y)
，
cos (-α)＝
，
tan (-α)＝________
5.3诱导公式(一)课件-高一上学期数学人教A版 (1)
3
4、已知 cos( ) 3 ，且 2 ，则 sin( 3 ) cos( )
1 5
。
5
课堂总结
一、诱导公式
公式 角 正弦 余弦 正切
一
二
2k
sin
cos
sin
cos
tan tan
三
sin
cos
tan
四
sin
cos
tan
注意：
（1）函数名称不变；（2）运用公式时把 “看成”锐角；
y2
P2
O
P1(x, y)
x
角α的终边与单位圆的交点P1坐标 为(x,y).
y=x
由三角函数的定义得：
2 诱导公式(二)
y 的终边
2
P2(y，x)
P1(x，y) O
x
诱导公式五
sin(
)
cos
2
cos( ) sin
2
2 诱导公式
P3
y2
P2
O
P1(x, y)
x
角α的终边与单位圆的交点P1坐标 为(x,y).
2
诱导公式六
sin( ) cos
2
cos( ) sin
2
2 诱导公式(二)
公式概括：
函数名称变，符号看象限 作用：实现正弦函数与余弦函数的互相转化.
【例1】证明：
【例2】
（1）若 sin( ) 1 ，则 cos
1 3.
2
（2）若 cos(
3
) 1 ，则 cos(
)
1 2
sin 250o cos 790o
（3） sin(2 )sin(2 ) cos(6 ) .
诱导公式一【新教材】人教A版高中数学必修第一册优质课件1
第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT) 第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT)
第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT) 第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT)
第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT) 第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT)
第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT) 第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT)
第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT) 第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT)
第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT) 第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT)
第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT) 第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT) 第五章 5.3 诱导公式（一）-【新教材】人教A版 （2019 ）高中 数学必 修第一 册课件( 共67张 PPT)
5.3 诱导公式(第1课时)-(新教材人教版必修第一册)(32张PPT)
解：(1)cos
210°＝cos(180°＋30°)＝－cos
30°＝－
3 2.
(2)sin114π＝sin2π＋34π＝sin34π＝sinπ－π4＝sinπ4＝
2 2.
(3)sin－463π＝－sin6π＋76π＝－sin76π＝－sinπ＋π6＝sinπ6＝12.
(4)cos(－1 920°)＝cos 1 920°＝cos(5×360°＋120°)＝cos 120°＝
(3)公式三：sin(－α)＝_－__s_in__α__，cos(－α)＝_co_s__α__，tan(－α)＝ _－__ta_n__α__.
(4)公式四：sin(π－α)＝_s_i_n_α__，cos(π－α)＝_－__co_s__α__，tan(π－α) ＝_－__t_a_n_α__.
2．诱导公式的整合与记忆 2kπ＋α(k∈Z)，π＋α，π－α，－α 的三角函数值，等于 α 的 _同__名__函__数__值__，前面加上一个把 α 看成锐角时__原__函__数__值__的__符__号___．简 记为“_函__数__名__不__变__，__符__号__看__象__限__”．
求 sin2nπ＋23π·cosnπ＋43π(n∈Z)的值． 解：分类讨论：
①当 n 为奇数时，原式＝sin23π·－cos43π＝sinπ－π3·－cosπ＋π3
＝sinπ3·cos
π3＝
23×21＝
3 4.
②当
n
为偶数时，原式＝sin
2π 3 ·cos
43π＝sinπ－π3·cosπ＋π3＝
sinπ3·－cosπ3＝－
探究题 2 已知 cos(α－75°)＝－13，且 α 为第四象限角，求 sin(105°＋α)的值．
5.3诱导公式(第一课时)课件(人教版)
cosπ－αsinπ－α
(3)sin2kπ＋23πcoskπ＋43π(k∈Z)．
－sinα－sinα
＝ －cosαsinα
＝－csoinsαα
＝－tanα.
例 3 化简下列各式：
(2) 1s＋in225s0in°2＋90co°cso7s9403°0°；
1＋2sin360°－70°cos360°＋70°
4－tanα
＝－sin(α－55°)＝2
2 3.
－2＋3×3
＝
＝7.
4－3
例 3 化简下列各式：
题型三 三角函数式的化简
(1)tan2π－coαssαin－－π2siπn－5απ－coαs6π－α；
sin2π－α
(2) 1s＋ in225s0in°2＋90co°cso7s9403°0°；
·sin－αcos－α cos2π－α [解] (1)原式＝
解 (1)原式＝sin(120°－4×360°)cos(30°＋3×360°)＋cos(60°－3×360°)sin(30° ＋2×360°)＋tan(135°＋360°)
＝sin120°cos30°＋cos60°sin30°＋tan135°
＝ 23× 23＋12×12－1＝0.
答案
[跟踪训练1] 求下列各式的值： (1)sin(－1320°)cos1110°＋cos(－1020°)sin750°＋tan495°； (2)sin83πcos316π＋tan－243π.
终边与单位圆的交点坐标如何？
α的终 y 边
o
x π+α的终边
α的终边
P(x ， y)
y
o x Q(-x，-y) π+α的终边
形如 的三角函数值与 的三角函数值之间的关系
(3)sin2kπ＋23πcoskπ＋43π(k∈Z)．
－sinα－sinα
＝ －cosαsinα
＝－csoinsαα
＝－tanα.
例 3 化简下列各式：
(2) 1s＋in225s0in°2＋90co°cso7s9403°0°；
1＋2sin360°－70°cos360°＋70°
4－tanα
＝－sin(α－55°)＝2
2 3.
－2＋3×3
＝
＝7.
4－3
例 3 化简下列各式：
题型三 三角函数式的化简
(1)tan2π－coαssαin－－π2siπn－5απ－coαs6π－α；
sin2π－α
(2) 1s＋ in225s0in°2＋90co°cso7s9403°0°；
·sin－αcos－α cos2π－α [解] (1)原式＝
解 (1)原式＝sin(120°－4×360°)cos(30°＋3×360°)＋cos(60°－3×360°)sin(30° ＋2×360°)＋tan(135°＋360°)
＝sin120°cos30°＋cos60°sin30°＋tan135°
＝ 23× 23＋12×12－1＝0.
答案
[跟踪训练1] 求下列各式的值： (1)sin(－1320°)cos1110°＋cos(－1020°)sin750°＋tan495°； (2)sin83πcos316π＋tan－243π.
终边与单位圆的交点坐标如何？
α的终 y 边
o
x π+α的终边
α的终边
P(x ， y)
y
o x Q(-x，-y) π+α的终边
形如 的三角函数值与 的三角函数值之间的关系
《诱导公式(第一课时)》示范公开课教学课件【高中数学人教】
cos（－180°＋α）＝cos［－（180°－α）］ ＝cos（180°－α）＝－cos α，
所以，原式＝ cosα sinα ＝－cos α． tan α (cos α)
梳理小结
问题4 诱导公式与三角函数和圆之间有怎样的关系？你学 到了哪些基本知识，获得了怎样的研究问题的经验？
（1）诱导公式是圆的对称性的代数化，是三角函数的性质． （2）学到了三组诱导公式．研究方法是数形结合，注重联系．
新知探究
追问3 角π＋α还可以看作是角α的终边经过怎样的变换得到的？
按逆时针方向旋转角π得到的．
新知探究
问题2 借助于平面直角坐标系，类比问题1，你能说出单位圆 上点P1的哪些特殊对称点？并按照如上问题1总结得到的求解 步骤，尝试求出相应的关系式．
单位圆上点P1的特殊对称点： 第一类，点P1关于x轴、y轴的对称点； 第二类，点P1关于特殊直线的对称点，如y＝x，y＝－x； 第三类，点P1关于x轴的对称点，再关于特殊直线的对称点． 或者是点P1关于特殊直线的对称点，再关于坐标轴的对称点．等等．
tan（π＋α）＝tan α．
新知探究
追问1 应用公式二时，对角α有什么要求？
只要在定义域内的角α都成立．
新知探究
追问2 探究公式二的过程，可以概括为哪些步骤？每一步蕴含的数 学思想是什么？
第一步，根据圆的对称性，建立角之间的联系．从形的角度研究． 第二步，建立坐标之间的关系．将形的关系代数化，并从不同的角度 进行表示，体现了数形结合的思想方法． 第三步，根据等量代换，得到三角函数之间的关系，即公式二．体现 了联系性．
任意负角的三 用公式三或一 任意正角的
角函数
三角函数
用公式一
0～2π的角的 三角函数
所以，原式＝ cosα sinα ＝－cos α． tan α (cos α)
梳理小结
问题4 诱导公式与三角函数和圆之间有怎样的关系？你学 到了哪些基本知识，获得了怎样的研究问题的经验？
（1）诱导公式是圆的对称性的代数化，是三角函数的性质． （2）学到了三组诱导公式．研究方法是数形结合，注重联系．
新知探究
追问3 角π＋α还可以看作是角α的终边经过怎样的变换得到的？
按逆时针方向旋转角π得到的．
新知探究
问题2 借助于平面直角坐标系，类比问题1，你能说出单位圆 上点P1的哪些特殊对称点？并按照如上问题1总结得到的求解 步骤，尝试求出相应的关系式．
单位圆上点P1的特殊对称点： 第一类，点P1关于x轴、y轴的对称点； 第二类，点P1关于特殊直线的对称点，如y＝x，y＝－x； 第三类，点P1关于x轴的对称点，再关于特殊直线的对称点． 或者是点P1关于特殊直线的对称点，再关于坐标轴的对称点．等等．
tan（π＋α）＝tan α．
新知探究
追问1 应用公式二时，对角α有什么要求？
只要在定义域内的角α都成立．
新知探究
追问2 探究公式二的过程，可以概括为哪些步骤？每一步蕴含的数 学思想是什么？
第一步，根据圆的对称性，建立角之间的联系．从形的角度研究． 第二步，建立坐标之间的关系．将形的关系代数化，并从不同的角度 进行表示，体现了数形结合的思想方法． 第三步，根据等量代换，得到三角函数之间的关系，即公式二．体现 了联系性．
任意负角的三 用公式三或一 任意正角的
角函数
三角函数
用公式一
0～2π的角的 三角函数
人教版(新教材)高中数学第一册(必修1)精品课件3：5.3 诱导公式(一)
2.四组诱导公式的作用 公式一的作用：把不在 0～2π 范围内的角化为 0～2π 范围内的角； 公式二的作用：把第三象限角的三角函数化为第一象限角的三角函数； 公式三的作用：把负角的三角函数化为正角的三角函数； 公式四的作用：把第二象限角的三角函数化为第一象限角的三角函数.
4．α＋k·2π(k∈Z)，－α，π±α 的三角函数值，等于 α 的 同名 函数值，前面加上一个把 α 看成 锐角 时 原函数值 的符号．
【思考诊断】
1．设 α 为锐角，则 180°－α，180°＋α，360°－α 分别是第几象限角？ [答案] 分别为第二、三、四象限角
2．判断正误(正确的打“√”，错误的打“×”) (1)诱导公式中角 α 是任意角. ( ) (2)公式 sin(－α)＝－sinα，α 是锐角才成立．( ) (3)公式 tan(π＋α)＝tanα 中，α＝2π不成立．( ) (4)在△ABC 中，sinA＝sin(B＋C)．( ) [答案] (1)× (2)× (3)√ (4)√
[解析] (1)因为 cos(2π－α)＝cosα＝ 35，α∈－2π，0，
所以 sinα＝－ 1－cos2α＝－23，
则
tan(π－α)＝－tanα＝－csoinsαα＝－－523＝
2 ＝2 5
5
5 .
3
(2)sin54π－α＝sinπ－α－π4＝sinα－π4＝
3 2.
[答案]
25 (1) 5
)
4 A.3
3 B.4
C．－43
D．－34
[解析] 因为 sinα＝35且 α 为第二象限角，
所以 cosα＝－ 1－sin2α＝－45，
所以 tanα＝csoinsαα＝－34.所以 tan(π＋α)＝tanα＝－34.故选 D.
人教A版高中数学必修第一册5.3 第1课时诱导公式二、三、四【课件】
5.3 诱导公式
第1课时 诱导公式二、三、四
课标定位
素养阐释
1.借助单位圆的对称性,利用定义推导出诱导公
式二、三、四.
2.能应用有关诱导公式解决一些三角函数的求
值、化简和证明问题.
3.体会逻辑推理的过程,提升数学运算素养.
自主预习·新知导学
合作探究·释疑解惑
易 错 辨 析
随 堂 练 习
自主预习·新知导学
0°~360°的角.(3)“角化锐”:用公式二或公式四将大于90°的角
转化为锐角. (4)“锐求值”:得到锐角的三角函数后求值.
【变式训练1】 求sin(-1 200°)·cos 1 290°+cos(-1 020°)
·sin(-1 050°)+tan 945°的值.
解:原式=-sin(3×360°+120°)·cos(3×360°+210°)
式向已知式转化.
【变式训练 2】 已知 sin
A.
C.
B.-
D.-
解析:sin
=-sin
答案:B
- =- .
=
,则
sin
- =sin +
-
-α
的值为(
)
探究三 利用诱导公式化简
【例 3】 化简下列各式:
(-)(--)(-)
=
.
=cos
=cos + =cos
答案:
=
第1课时 诱导公式二、三、四
课标定位
素养阐释
1.借助单位圆的对称性,利用定义推导出诱导公
式二、三、四.
2.能应用有关诱导公式解决一些三角函数的求
值、化简和证明问题.
3.体会逻辑推理的过程,提升数学运算素养.
自主预习·新知导学
合作探究·释疑解惑
易 错 辨 析
随 堂 练 习
自主预习·新知导学
0°~360°的角.(3)“角化锐”:用公式二或公式四将大于90°的角
转化为锐角. (4)“锐求值”:得到锐角的三角函数后求值.
【变式训练1】 求sin(-1 200°)·cos 1 290°+cos(-1 020°)
·sin(-1 050°)+tan 945°的值.
解:原式=-sin(3×360°+120°)·cos(3×360°+210°)
式向已知式转化.
【变式训练 2】 已知 sin
A.
C.
B.-
D.-
解析:sin
=-sin
答案:B
- =- .
=
,则
sin
- =sin +
-
-α
的值为(
)
探究三 利用诱导公式化简
【例 3】 化简下列各式:
(-)(--)(-)
=
.
=cos
=cos + =cos
答案:
=
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3 2
1
cos
3
2
1
0
2
2
2
tan
3 3
1
3
例2 化简
cos180
tan
0
sin cos
360
180
。
解：tan（ 180 ） tan (180 )
tan（180 ） tan
cos（180 ） cos[(180 )]
cos（180 ） cos
所以，原式
-
- cossin
，
y
并且有公式四
sin sin cos cos tan tan
P4 x, y O
P1x, y
x
知识梳理
归纳： 诱导公式一～四可用口诀“函数名称不变，符号看象限”记忆， 其中“函数名不变”是指等式两边的三角函数同名， “符号”是指等号右边是正号还是负号，
“看象限”是指把α看成锐角时等式左边三角函数值的符号．
函数，其一般步骤：①化负角的三角函数为正角的 三角函数；②化为[0°，360°)内的三角函数；③ 化为锐角的三角函数． 可概括为：“负化正，大化小，化到锐角为终了”
因此，只要探究角 与 的三角函数值之间
的关系即可．
P2
y
P1
O
x
知识梳理
设 P1 x1, y1 , P2 x2 , y2 。因为 P2 是点 P1 关于原点的对称点，
y 所以 x2 x1, y2 y1
根据三角函数的定义，得
sin y1,
cos x1,
tan
y1 , x1
sin y2, cos x2,
O
P2
P1
x
tan y2 ,
x2
从而得公式二
sin sin
cos cos
tan tan
如图，作P1 关于 x 轴的对称点 P3 ，则以 OP3为终边的角为 ，
并且有公式三
sin sin cos cos tan tan
y
P1x, y
O x
P3x, y
如图，作P1 关于 y轴的对称点 P4 ，则以 OP4为终边的为
sintan 603 3
32
思考：
由例１，你对公式一～公式四的作用有什么进一步的认识？你能 自己归纳一下把任意角的三角函数转化为锐角三角函数的步骤吗 ？
利用公式一～公式四，可以把任意角的三角函数转化为锐角三角函 数，一般可按下面步骤进行：
任意负角的 用公式 任意正角的
0 ~ 2 的角 用公式 锐角的三角
解：原式＝－tan－αs·in－αc2o·s－αc3·os－αtanα
＝ －sin2αcosα －tan2α·cos3α
sin2 cos
s in cos
2
cos3
1
课堂小结
11 牢记0°，30°，45°，60°，90°角的正弦、余弦
和正切值对给角求值问题很重要
2 用诱导公式可将任意角的三角函数化为锐角的三角
三角函数
三或一 三角函数 用公式一 的三角函数 二或四 函数
数学史上，求三角函数值曾经是一个重要而困难的题。数学家制作 了锐角三角函数表，并通过公式一～公式四，按上述步骤解决了问 题。现在，我们可以利用计算工具方便地求任意角的三角函数值， 所以这些公式的 “求值”作用已经不重要了，但它们所体现的三角 函数的对称性，在解决三角函数的各种问题中却依然有重要的作用 ．
人教版高中数学新教材必修第一册
5.3 诱导公式第一课时
前面利用圆的几何性质，得到了同角三角函数 之间的基本关系。
我们知道，圆的最重要的性质是对称性，而对 称性（如奇偶性）也是函数的重要性质。由此想到 ，可以利用圆的对称性，研究三角函数的对称性。
探究：
如图，在直角坐标系内，设任意角 的终边与单位圆交于点 P1。
3
解（：3）（s1in）cos126325
cossin181063
45
sin
5cos45
3
2;sin 2
3
3; 2
（4（）t2a）nsi-n28040 sin 2tan20240 3 tan 63360 120
sin 2 sin
ta3n120 tan 1380 60
知识梳理
利用诱导公式求任意角三角函数的步骤： (1)“负化正”——用公式一或三来转化；
(2)“大化小”——用公式一将角化为 0°到 360°间的角；
(3)“小化锐”——用公式二或四将大于 90°的角转化为锐角；
(4)“锐求值”——得到锐角的三角函数后求值．
锐角三角函数表：
6
4
3
2
sin
1 2
2 2
sin sin cos cos tan tan
sin sin sin sin cos cos cos cos
tan tan tan tan
例1
利用公式求下列三角函数值：
（1）cos 225 ；
（2）sin
8
3
；
（3）sin 16 ； （4）tan - 2040 。
tan - cos
- cossin cos
-
sin cos
-
cos
知识梳理
三角函数式的化简方法 (1)利用诱导公式将任意角的三角函数转化为锐角三角函数； (2)常用“切化弦”法，即通常将表达式中的切函数化为弦函数； (3)注意“1”的变形应用．
巩固练习
练习
化简
sin2α＋πcosπ＋α
tanπ－αcos3－α－πtan－α－2π
（1）作 P1 关于原点的对称点 P2 ，以 OP2为终边的角 与角 有
什么关系？角 , 的三角函数值之间有什么关系？
(2)如果作 P1 关于 x 轴(或 y 轴)的对称点P3(或 P4 )，那么又可
以得到什么结论？
下面，借助单位圆的对称性进行探究．
如图，以OP2为终边的角 都是与角
终边相同的角，即 2k k Z 。