大学物理基础教程答案1-4力-4ppt课件
合集下载
大学物理4PPT课件

大学物理4ppt课件
• 大学物理4课程简介 • 力学基础 • 电场与磁场 • 电磁感应与麦克斯韦方程组 • 相对论基础 • 实验与习题
01
大学物理4课程简介
课程目标
01
掌握大学物理的基本概念、原理和方法。
02
培养学生对物理现象的观察、分析和解决问题的能力。
培养学生的科学素养和创新能力,为后续专业课程和科研工作
详细描述
电磁波是由电场和磁场相互激发并传播的波。它们的传播速度与介质有关,在真空中等于光速。电磁波的应用广 泛,如无线电通信、雷达和微波炉等。
05
相对论基础
狭义相对论
狭义相对论的基本
假设
所有惯性参照系中光速都是一样 的,即光速的不变性。同时,物 理定律在所有惯性参照系中都是 一样的,即参照系的相对性。
课程考核方式包括平时作业、实验报告和期末考 试等。
02
力学基础
牛顿运动定律
01
02
03
牛顿第一定律
物体若不受外力作用,将 保持静止或匀速直线运动 状态不变。
牛顿第二定律
物体加速度的大小与作用 力成正比,与物体的质量 成反比。
牛顿第三定律
作用力和反作用力大小相 等,方向相反,作用在同 一条直线上。
等效原理
在任何局部区域内,不能通过任何实验区分均匀引力场和加速参照 系。
广义协变原理
物理定律在任何参照系中都应具有相同的数学形式。
黑洞与宇宙学
黑洞的形成
黑洞是由于大质量恒星坍缩形成 的,其强大的引力使得周围的物
质和光线都不能逃脱。
霍金辐射
根据量子力学的不确定性原理,黑 洞会向外辐射能量,即霍金辐射。
磁场概念
磁体或电流周围存在的一种特 殊物质,对放入其中的磁体或
• 大学物理4课程简介 • 力学基础 • 电场与磁场 • 电磁感应与麦克斯韦方程组 • 相对论基础 • 实验与习题
01
大学物理4课程简介
课程目标
01
掌握大学物理的基本概念、原理和方法。
02
培养学生对物理现象的观察、分析和解决问题的能力。
培养学生的科学素养和创新能力,为后续专业课程和科研工作
详细描述
电磁波是由电场和磁场相互激发并传播的波。它们的传播速度与介质有关,在真空中等于光速。电磁波的应用广 泛,如无线电通信、雷达和微波炉等。
05
相对论基础
狭义相对论
狭义相对论的基本
假设
所有惯性参照系中光速都是一样 的,即光速的不变性。同时,物 理定律在所有惯性参照系中都是 一样的,即参照系的相对性。
课程考核方式包括平时作业、实验报告和期末考 试等。
02
力学基础
牛顿运动定律
01
02
03
牛顿第一定律
物体若不受外力作用,将 保持静止或匀速直线运动 状态不变。
牛顿第二定律
物体加速度的大小与作用 力成正比,与物体的质量 成反比。
牛顿第三定律
作用力和反作用力大小相 等,方向相反,作用在同 一条直线上。
等效原理
在任何局部区域内,不能通过任何实验区分均匀引力场和加速参照 系。
广义协变原理
物理定律在任何参照系中都应具有相同的数学形式。
黑洞与宇宙学
黑洞的形成
黑洞是由于大质量恒星坍缩形成 的,其强大的引力使得周围的物
质和光线都不能逃脱。
霍金辐射
根据量子力学的不确定性原理,黑 洞会向外辐射能量,即霍金辐射。
磁场概念
磁体或电流周围存在的一种特 殊物质,对放入其中的磁体或
大学物理教程ppt课件

2024/1/26
牛顿第二定律
动量定理的推导、质点系的动量定理、 变力作用下的动量定理
万有引力定律
万有引力定律的表述、引力常量的测定 、万有引力定律的应用
9
动量定理和动量守恒定律
2024/1/26
动量定理
01
冲量的定义、动量定理的表述、动量定理的推导
动量守恒定律
02
系统不受外力或所受外力之和为零的条件下的动量守恒、两体
2024/1/26
16
2024/1/26
04
电磁学
17
静电场
库仑定律
描述点电荷之间的相互作用力,是静电场的 基本定律。
电场强度
反映电场对电荷的作用力大小,是矢量场。
电势和电势差
描述电场中某点的电势能和电势差,是标量 场。
2024/1/26
静电场中的导体和电介质
探讨导体和电介质在静电场中的性质和行为 。
黑体辐射和光电效应
黑体辐射定律,光电效应实验和爱因斯坦光电效应方程。
康普顿效应
康普顿散射实验和康普顿效应的意义。
波粒二象性
德布罗意波,电子衍射实验,波粒二象性的统一。
量子力学基础
测不准原理,薛定谔方程,原子结构和光谱。
2024/1/26
26
06
近代物理学基础
2024/1/26
27
狭义相对论基础
洛伦兹变换
推导及物理意义
相对论动力学基础
动量、能量及力的变换
2024/1/26
狭义相对论的时空观
时间膨胀与长度收缩
质能关系
爱因斯坦质能方程及其意义
28
量子力学基础
德布罗意波
物质波的提出及实验验证
牛顿第二定律
动量定理的推导、质点系的动量定理、 变力作用下的动量定理
万有引力定律
万有引力定律的表述、引力常量的测定 、万有引力定律的应用
9
动量定理和动量守恒定律
2024/1/26
动量定理
01
冲量的定义、动量定理的表述、动量定理的推导
动量守恒定律
02
系统不受外力或所受外力之和为零的条件下的动量守恒、两体
2024/1/26
16
2024/1/26
04
电磁学
17
静电场
库仑定律
描述点电荷之间的相互作用力,是静电场的 基本定律。
电场强度
反映电场对电荷的作用力大小,是矢量场。
电势和电势差
描述电场中某点的电势能和电势差,是标量 场。
2024/1/26
静电场中的导体和电介质
探讨导体和电介质在静电场中的性质和行为 。
黑体辐射和光电效应
黑体辐射定律,光电效应实验和爱因斯坦光电效应方程。
康普顿效应
康普顿散射实验和康普顿效应的意义。
波粒二象性
德布罗意波,电子衍射实验,波粒二象性的统一。
量子力学基础
测不准原理,薛定谔方程,原子结构和光谱。
2024/1/26
26
06
近代物理学基础
2024/1/26
27
狭义相对论基础
洛伦兹变换
推导及物理意义
相对论动力学基础
动量、能量及力的变换
2024/1/26
狭义相对论的时空观
时间膨胀与长度收缩
质能关系
爱因斯坦质能方程及其意义
28
量子力学基础
德布罗意波
物质波的提出及实验验证
大学物理-力学课件(全)

详细描述
牛顿第二定律
总结词
描述力对物体转动效应的定律。
详细描述
力的矩与转动定律指出,力矩是力和力臂的乘积,其方向垂直于力和力臂所在的平面。公式表示为M=FL,其中M表示力矩,F表示作用力,L表示力臂。转动定律则说明,对于定轴转动系统,系统的角加速度与作用于转轴上的合力矩成正比,与转动惯量成反比。
力的矩与转动定律
万有引力定律
04
CHAPTER
弹性力学
能够恢复其原始形状和大小的物体。
弹性体定义
线弹性体、非线弹性体、超弹性体等。
弹性体的分类
杨氏模量、泊松比等。
弹性体的物理属性
拉伸、压缩、弯曲、剪切等。
弹性体的变形
弹性体的基本性质
物体内部相邻部分之间的相互作用力。
弹性体的应力与应变
应力定义
正应力和剪应力。
应力的分类
动量的计算方法
动量与动量守恒定律
在没有外力作用的情况下,一个系统内各个物体的动量总和保持不变。这一定律是经典力学中重要的基本定律之一,适用于宏观低速的物体系统。
动量守恒定律
通过分析系统的受力情况和动量变化情况,根据动量守恒定律可以求出系统内各个物体的动量和速度变化情况。在解决实际问题时,通常需要先对系统进行受力分析和动量分析,然后根据动量守恒定律列方程求解。
应用方法
动量与动量守恒定律
02
CHAPTER
运动学
描述物体位置变化的物理量,表示为矢量,由起点指向终点的有向线段。
位移
描述物体运动快慢的物理量,等于位移对时间的导数,表示为矢量。
速度
位移与速度
加速度
描述物体速度变化快慢的物理量,等于速度对时间的导数,表示为矢量。
牛顿第二定律
总结词
描述力对物体转动效应的定律。
详细描述
力的矩与转动定律指出,力矩是力和力臂的乘积,其方向垂直于力和力臂所在的平面。公式表示为M=FL,其中M表示力矩,F表示作用力,L表示力臂。转动定律则说明,对于定轴转动系统,系统的角加速度与作用于转轴上的合力矩成正比,与转动惯量成反比。
力的矩与转动定律
万有引力定律
04
CHAPTER
弹性力学
能够恢复其原始形状和大小的物体。
弹性体定义
线弹性体、非线弹性体、超弹性体等。
弹性体的分类
杨氏模量、泊松比等。
弹性体的物理属性
拉伸、压缩、弯曲、剪切等。
弹性体的变形
弹性体的基本性质
物体内部相邻部分之间的相互作用力。
弹性体的应力与应变
应力定义
正应力和剪应力。
应力的分类
动量的计算方法
动量与动量守恒定律
在没有外力作用的情况下,一个系统内各个物体的动量总和保持不变。这一定律是经典力学中重要的基本定律之一,适用于宏观低速的物体系统。
动量守恒定律
通过分析系统的受力情况和动量变化情况,根据动量守恒定律可以求出系统内各个物体的动量和速度变化情况。在解决实际问题时,通常需要先对系统进行受力分析和动量分析,然后根据动量守恒定律列方程求解。
应用方法
动量与动量守恒定律
02
CHAPTER
运动学
描述物体位置变化的物理量,表示为矢量,由起点指向终点的有向线段。
位移
描述物体运动快慢的物理量,等于位移对时间的导数,表示为矢量。
速度
位移与速度
加速度
描述物体速度变化快慢的物理量,等于速度对时间的导数,表示为矢量。
大学物理第四章习题解答PPT演示课件

注意:最高点处摆锤(刚体)的速度恰好为零 时, 完成一个圆周运动。(区别:3-30)
16
解: 冲击:子弹和摆锤角动量守恒
mlvm2 vl(J1J2)0
J1
1 3
ml 2
J2 ml2
v 0
摆动:摆锤和地球机械能守恒
Ek Ep
1 2(J1J2)0 2mg2lmgl
4m vmin m
2gl
17
解:子弹+杆系统: M外 0
m 22 lv(1 JJ2) J2)(1JJ2)
J1
1 12
m1l
2
J2
m1(
l )2 2
v v r l/2
J2 6m 2v 2.1 9r3a/sd
J1J2 m 1l3m 2l
11
426:一质量 m/、 为半径 R的 为转台,以a角 转速 动度 ,转轴的
不计, 1)( 有一质 m的 量蜘 为蛛垂直地边 落缘 在上 转, 台此时角 ,
解: JJ盘2J柱
J盘 12m盘R盘 2
R盘
3
01 2
02
m
J柱 12m柱R柱 2
10102 R柱 2 m
m盘 V盘
m柱 V柱
J0.13k6gm2
7
413:如图所示m1, 1质 6kg的 量实心圆 A,柱 其体 半r径 15c为 m ,可 绕其固定水平 阻轴 力转 忽动 略, 不计 的。 柔一 绳条 绕轻 在圆 其柱 一
(A) 角速度从小到大,角加速度不变 O
A
(B) 角速度从小到大,角加速度从小 到大
(C) 角速度从小到大,角加速度从 大到小
(D) 角速度不变,角加速度为零
2
绕过O点的轴做定轴转动。求:运动过程中角速度和角 加速度的变化情况
16
解: 冲击:子弹和摆锤角动量守恒
mlvm2 vl(J1J2)0
J1
1 3
ml 2
J2 ml2
v 0
摆动:摆锤和地球机械能守恒
Ek Ep
1 2(J1J2)0 2mg2lmgl
4m vmin m
2gl
17
解:子弹+杆系统: M外 0
m 22 lv(1 JJ2) J2)(1JJ2)
J1
1 12
m1l
2
J2
m1(
l )2 2
v v r l/2
J2 6m 2v 2.1 9r3a/sd
J1J2 m 1l3m 2l
11
426:一质量 m/、 为半径 R的 为转台,以a角 转速 动度 ,转轴的
不计, 1)( 有一质 m的 量蜘 为蛛垂直地边 落缘 在上 转, 台此时角 ,
解: JJ盘2J柱
J盘 12m盘R盘 2
R盘
3
01 2
02
m
J柱 12m柱R柱 2
10102 R柱 2 m
m盘 V盘
m柱 V柱
J0.13k6gm2
7
413:如图所示m1, 1质 6kg的 量实心圆 A,柱 其体 半r径 15c为 m ,可 绕其固定水平 阻轴 力转 忽动 略, 不计 的。 柔一 绳条 绕轻 在圆 其柱 一
(A) 角速度从小到大,角加速度不变 O
A
(B) 角速度从小到大,角加速度从小 到大
(C) 角速度从小到大,角加速度从 大到小
(D) 角速度不变,角加速度为零
2
绕过O点的轴做定轴转动。求:运动过程中角速度和角 加速度的变化情况
大学物理力学(全) ppt课件

ppt课件
14
例. 已知质点的运动方程为
x(t) R cost
y(t) R sin t
R和 为常量。(1)求其轨道
形和和态自加和然速特 坐 度征 标a。 系( 中写2)出在质直点角速坐度标v系
ppt课件
15
(1) x2 y2 R2
vx
dx dt
R sin t
lim lim
t0 t
t t 0
ppt课件
dt
3
a dv d (v) dv v d
dt dt
dt dt
如果轨道在点A 的内切圆的曲率半径为 ,
an
v
d
dt
n
v
d
dt
n
v2
n
at
dv
dt
一般情况下, 质点的加速度矢量应表示为
dv dt
R
d
dt
R
v
R
矢量
ppt课件
10
(t) (t) (t)
t 0 (0) 0 (0) 0
(t )
(t)
0 0
t
(t)dt
0 t
(t )dt
0
ppt课件
11
例 质点作匀加速圆周运动, 0 const,
ppt课件
21
牛顿第二定律: F ma
Fx
直角坐标系分量形式Fy
Fz
max may maz
m m m
dvx
大学物理第4章PPT课件

设有两个质点m1和m2相互作用,把它们看成一个系统,若 m1受到m2的作用力是f1,发生的位移为dr1;m2受到m1的作用 力是f2,发生的位移为dr2,则这一对相互作用的内力的功为
dW=dW1+dW2
第一节 功 和 功 率
因为
所以
f1=-f2
dW=f1·dr1+f2·dr2=f1·dr1-f1·dr2=f1·(dr1-dr2)=f2·dr12 4- 5) 在式(4- 5)中, dr12是m1相对于m2的位移,此相对位移与参考系的 选择无关.由式(4- 5)分析可知,系统内的质点没有相对位移时,一对相互
第二节 动能 动能定理
动量是矢量,不但有大小,而且有方向,这是机械运动 的性质;动能是标量,而且永远为正,它是能量的一种形式, 能量并不限于机械运动.除了动能外,还有其他各种形式的能 量,如电能、热能、光能、原子能等.动能与这些能量是可以 相互转化的.
另外,与动量变化相联系的是力的冲量,冲量是力的时 间累积作用,其效果是使物体的动量发生变化.而与动能变化 相联系的是力所做的功,功是力的空间累积作用,其效果是使 物体的动能发生变化.这两个物理量各自遵从一定的规律,它 们是从不同侧面来描写物体机械运动的物理量.
力做的功等于力的大小与位移沿力的方向的分量的乘积.由
此看出,功是力的空间累积作用.功也可以用力F与位移Δr的标
积表示,即
W=F·Δr
(4- 2)
功是一个标量,但有正负之分,功的正负由F与Δr之间的
夹角θ决定.在国际单位制中,功的单位是牛顿·米(N·m).
第一节 功 和 功 率
2. 变力的功
式(4- 2)为恒力做功的定义式,但在一般情况下作用 在物体上的力不一定都是恒力,质点也不一定做直线运动.这 时,不能直接用式(4- 2)来讨论变力的功,那么如何计算 变力的功呢?设有一个质点,在大小和方向都随时间变化的 力F作用下,沿任意曲线从a点运动到b点,如图4-2所示.
dW=dW1+dW2
第一节 功 和 功 率
因为
所以
f1=-f2
dW=f1·dr1+f2·dr2=f1·dr1-f1·dr2=f1·(dr1-dr2)=f2·dr12 4- 5) 在式(4- 5)中, dr12是m1相对于m2的位移,此相对位移与参考系的 选择无关.由式(4- 5)分析可知,系统内的质点没有相对位移时,一对相互
第二节 动能 动能定理
动量是矢量,不但有大小,而且有方向,这是机械运动 的性质;动能是标量,而且永远为正,它是能量的一种形式, 能量并不限于机械运动.除了动能外,还有其他各种形式的能 量,如电能、热能、光能、原子能等.动能与这些能量是可以 相互转化的.
另外,与动量变化相联系的是力的冲量,冲量是力的时 间累积作用,其效果是使物体的动量发生变化.而与动能变化 相联系的是力所做的功,功是力的空间累积作用,其效果是使 物体的动能发生变化.这两个物理量各自遵从一定的规律,它 们是从不同侧面来描写物体机械运动的物理量.
力做的功等于力的大小与位移沿力的方向的分量的乘积.由
此看出,功是力的空间累积作用.功也可以用力F与位移Δr的标
积表示,即
W=F·Δr
(4- 2)
功是一个标量,但有正负之分,功的正负由F与Δr之间的
夹角θ决定.在国际单位制中,功的单位是牛顿·米(N·m).
第一节 功 和 功 率
2. 变力的功
式(4- 2)为恒力做功的定义式,但在一般情况下作用 在物体上的力不一定都是恒力,质点也不一定做直线运动.这 时,不能直接用式(4- 2)来讨论变力的功,那么如何计算 变力的功呢?设有一个质点,在大小和方向都随时间变化的 力F作用下,沿任意曲线从a点运动到b点,如图4-2所示.
大学物理基础教程答案1-6力ppt课件
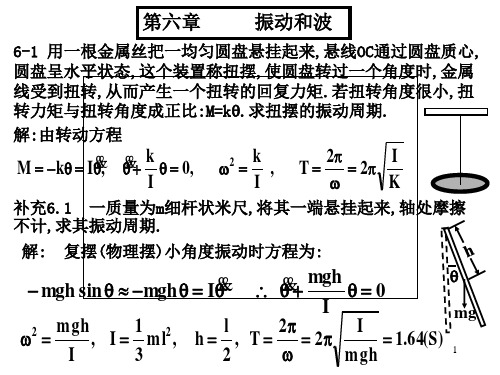
解:(1)振动频率 1 g 1.6(Hz) 2 2 l
k
(2)振幅
A
x
2 0
( v0 )2
0.02(m)
m
(3)初相位
cos1 x0 cos1 0.9 0.46(rad)
A
(v0>0取正号, v0 <0取负号)
(4)振动表达式. X=0.02cos(10t-0.46) (m)
4
最大响度的音(即拍声),问拍频是多少?音叉的频率可能是多
少?为了进一步唯一确定其值,可以在待测测音叉上滴上一点
石蜡,重做上述实验,若此时拍频变低,则说明待测音叉的频率
是多少?
解:以知T=0.5s,得拍频
f 1 2 0.5
f2 f1 2 f2 2 f1 440(Hz)
或
f2 f1 2 438(Hz)
求(1)振动的圆频率、周期、振幅和初始相位;(2)振动的速度
和加速度(函数式);(3)振动的总能量E(4)振动的平均动能和平
均势能;(5) t =1.0秒、10秒等时刻的相位。
11
解:
(1)
x
0.5cos(8t
)
与振动表达式
x Acos(t )
3
比较便直接可得:
2 1
A 0.5(cm) , 8 T (s)
t3ln2
A A0 ,A A0 ,
16
3213
6-9 火车在铁轨上行驶,每经过铁轨接轨处即受一次震动, 使装在弹簧上面的车厢上下振动。设每段铁轨长12.5米,弹簧 平均负重5.5吨,而弹簧每受1.0吨力将压缩16毫米。试问,火 车速度多大时,振动特别强?
解: 固有振动周期等于强迫力周期时发生共振
分深度为a.若用力稍稍压下,使其浸入水中深度为b,如图所示,然 后放手,任其作自由振动,求其振动的周期和振幅.
大学物理教学课件1-第4章 56页PPT文档

x
dmdx0xdx
L
M dm0LL 0xdx1 20L
xc
xdm
Lx2
0
L 0dx2L
M
M
3
例题补充 如图所示,浮吊的质量M = 20 t,从岸上吊起m = 2 t的重物后,再将吊杆与竖直方向的夹角θ由600转到300 ,设杆 长l = 8 m,水的阻力与杆重略而不计,求浮吊在水平方向上移 动的距离。
n
p pi mivi
i
i1
二、质点的动量定理
由牛顿第二定律
F
d p
dt
F dtdp
1、 冲量
1)微分形式: dIF dt
Fdt 表示力的时间累积,叫时间d t 内合外力 F的冲量。
2)积分形式:
I
t2
Fdt
若为恒力: IFt
v02 2gh
t F
2s v0 h Mg
s
设人从 2m 处跳下,重心下移 1cm,则:
FMgh20M 0 g 可能发生骨折。 s
设人的体重为70 kg,此时平均冲力:F7 0 9.820 1 0 .3 7 150 (N
例题4-2 一辆装煤车以v = 3m/s 的速率从煤斗下面通过,每
I
t2
Fdt
t2
Ixtt12Fxdtp2xp1x Iytt12Fydtp2yp1y
Iz tt12Fzdtp2zp1z
系统所受合外力的冲量在某一方向上的分量等于系统动 量在该方向上分量的增量。
例题4-1 人在跳跃时都本能地弯曲关节,以减轻与地面的 撞击力。 若有人双腿绷直地从高处跳向地面,将会发生什么情况?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆盘边缘绕有绳子,上端固定在天花板上,大圆盘也绕有绳子,下
端挂以质量为m的物体,如图所示.求(1)要使圆盘向上加速、向下
加速,静止或匀速运动的条件?(2)在静止条件下两段绳中的张力.
轴处摩擦和绳的质量忽略.绳与滑轮之间没有相对滑动发生. 9
解:圆盘的运动属于纯滚动.小圆盘与绳的切
点O’为 瞬时轴,则有:
mg l 1 ( 1 ml 2 )2 2 23
( 1 ml 2 ) ( 1 ml 2 )'m' vl
3
3
om l
碰时角动量守恒
1 (1 ml 2 )2 1 (1 ml 2 )'2 1 m' v2
m
23
23
2
碰时能量守恒: m m'
v 1 3gl
2
13
4-15一个质量为m,半径为R的匀质圆柱体,在一块以加速度A运
F
相同
在质心参照系中: aF dLC dt
LC IC
15
IC为通过质心垂直于棒轴的转动惯量,已知: IC mk 2
(0) 0
mk2 (t) (0) aF
t
(t )
aF mk 2
t
在L系中若要
vQ 0
vQ vC b
F m
t
aF mk 2
t
b
0
k2 b
a
交换a、b可证明p、Q互为共轭点
gh 3
E kC
1 2
I(
vC R
)2
1 3
mgh
4-9 长为2a的匀质细杆AB,以铰链固结于A点,起初使杆在水平
位置,当放开B端,棒绕A点无摩擦地转至竖直位置时,铰链自
动脱落,棒变为抛体,在以后的运动中,棒的质心轨迹为一抛
物线,而棒本身则绕质心C转动,试求当它的质心从C’位置下
降h距离时(如图所示),棒共转了多少转?
z
y r x
y dm
x
4-2 计算由三根质量均为m长为l的均匀细杆组成的正三角形
绕通过一顶点并垂直于三角形平面的轴的转动惯量.
1
解: OA相对于O点的转动惯量:
I1
1 3
ml 2
OB相对于O点的转动惯量: AB相对于O点的转动惯量:
I2
1 3
ml
2
l
I3
1 12
ml
2
m(
3 l)2 2
5 ml 2 4
aC R 4 vC 3
解法2:
gh
d
vC R
dt
aC
末 初 Fi外
1 EkC 2
driC
I( vC )2 1 mgh
末R T
初
3
dr边C
2g 3
(Eik内末
Rm T
mg
Eik内初 )
i
(
1 2
IC2 末
1 2
i
IC2 初
)
(1 )
末 末
末
初 migdriC
(m1g m2g时)
T2 m2g m2a
(T1
T2
)R
I
a R
a (m1 m2 )g
(
I R2
m1
m2
)
T2
(m1
m2
I R2
)m2
g
I (R2 m1 m2)
T1
m1g(
I R2
m1
m2
)
I
(R2
m1
m2) 4
4-6 从刚体定轴转动定律推导出刚体绕定轴转动的动能定理.
解: 刚体饶定轴转动角速度为,角加速度为,转动惯量
T(RA RB ) (mA mB )gRB
(1) 圆盘静止或匀速运动,则m也匀速运动或 静止 ,则有T = mg
T’
O’
O RA RB
mg (RA RB ) (mA mB )gRB
圆盘向上加速运动
T (mA+mB)g
当mg(RA RB ) (mA mB )gRB
圆盘向下加速运动 当mg(RA RB ) (mA mB )gRB T
解:以知 1=2n接合过程中,摩擦属内力,又
无其他外力矩,角动量守恒I1 = (I1+I2)
所以
n
2
I1
I1 I2
n1
200
(转/分)
AB
E
1 2
I112
1 2 (I1
I2 )2
2I12n12
I2 I1 I2
1.32104(J)
4-11 质量为mA和mB,半径为RA和RB的两个圆盘同心地粘在一起,小
1
a k2
b
0
a k2 b
16
2
4-4 以垂直于盘面的力F 将一粗糙平面紧压在一飞轮的盘面上,
使其制动,如图所示.飞轮可以看作是质量为m、半径为R的匀质圆
盘,盘面与粗糙平面间的摩擦系数为µ,轴的粗细可略,飞轮的初始
角速度为.(1)求摩擦力矩.(2)经过多长时间飞轮才停止转动?
解:
F dN R2 2rdr
dM rdN
0 R
R
A
总的转动惯量为:II1I2I33 2
ml
2
O
3 2
l
l
lB
4-3 一半圆形均匀细杆,其半径为R,质量为m,如图所示,试
求细杆对过圆形圆心和端点的轴AA’的转动惯量.
解: dI r2dm (R sin)Rd
dl Rd
I dI R3 sin2d R3 1 mR 2
0
22
A'
d
R
rA
d R a' dt
mA 1 ma' ma' 2
a' 2 A 3
2
1
圆柱体相对于地面的加速度a为
a
AA 3
A 3
14
新教材4-16:一根长为 l质量为 m的棒,置于无摩擦的水平面
上,在一很短的时间间隔 t内,这棒受一力F打击而产生一个冲 量,这力作用在 p点上, p至质心的距离为a,试求: 质心的速
4-5解: (1)如图所示分为三个隔离体求解。 m2 T2
I
m1g T1 m1a T2 m2a
(T1
T2
)R
I
a R
(2)
a m1 g
I ( R2 m1 m2 )
T1
T2 m1m2 g
(
I R2
m1
m2 )
m1
T1
I m1g( R2
m2
)
(
I R2
m1
m2)
m1g T1 m1a
(2) 在静止条件下将圆盘和物体m视为一整体,则: T’=(m+mA+mB)g 物体m静止则有: T=mg
m mg10
4-12 一质量m=10千克,半径为R=0.20米的圆柱体,用绳子系住
它的旋转中心轴,此绳子跨过一质量m1 =2千克,半径r =0.1米 的定滑轮,在绳的下端悬一质量m2=5.0千克的重物。设绳长不变
31
(m2 2 m 2 m1)
T1'
r
m1
T2'
T2
m2
m2g
3 T1 2 ma 35(N)
T2 m2(g a) 37.3(N)
11
4-13 一根长为 l 、质量为m的均匀细杆可绕其一端的水平轴O 自由摆动。当被一发质量为m’的子弹在离O点的a处水平方向击 中后,子弹埋入杆内,杆的最大偏转角为 ,求子弹的初速度 。已知 l =1.0米,m =2千克,m’ =20千克,a=0.7米, =60o
第四章 刚体的运动规律
4-1 证明适用于薄的平面刚体的垂直轴定理:一个平面刚体薄板, 对于垂直板面的某轴的转动惯量,等于绕平面内与该垂直轴相交 的任意两个相互垂直的轴的转动惯量之和,即
Iz=Ix+Iy
证明: 依题意作右图所示,由定义求得:
Iz r2dm (x2 y2 )dm x2dm y2dm Ix Iy
2
M
0
dM
FR 3
又 M I ( 1 mR 2 )
2
0 t
r dr
t
1 2
mR 2
0
M 3mR 0 4F
4-5 如图,两物体的质量分别为m1 和m2,滑轮的转动惯量为I, 半径为R。(1)如果m2与桌面之间为光滑接触,求系统的加速度a 及绳中张力T1和T2 .(2)如果m2与桌面之间的摩擦系数为 ,求系 统的加速度和及绳中张力T1和T2 .绳子与滑轮间没有相对滑动3 。
为Iz ,外力对定轴z的力矩为Mz,转动定律数学表达式:
d
z
而力矩的功:
Mz Iz Iz dt
d
w
Mzd
Iz
dt dt
0 Iz d
1 2
Iz2
1 2
I
z
02
力矩的功等于末初转动动能之差称转动动能定理.
4-7 如图所示,有一个半径为R=0.2米,质量m1=2.5千克的匀质
圆盘状定滑轮,轴处摩擦可略,当在圆盘边缘上绕一轻绳,绳
v02
2
3
m'2 a2
v0 186(m s1 )
12
4-14 质量为m长为l的匀质细杆,可绕端点O的固定水平轴转动,
把杆抬平后无初速地释放,当杆摆至竖直位置时刚好和光滑水平 桌面上的小球相碰。小球的转动不计,它的质量和杆相同,并且
碰撞是完全弹性的,轴上摩擦也忽略不计,求碰后小球的速度v。
解:下摆(定轴转动)能量守恒,
g d(
初
miriC ) 初 g md rCC 0
i
