三视图小结与复习PPT教学课件
合集下载
《三视图》课件(共55张PPT)

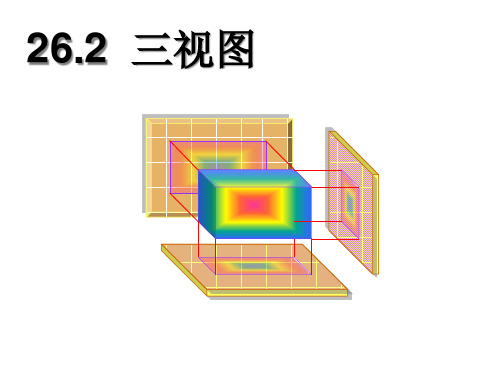
如果物体向三个互相垂直 的投影面分别投影,所得到 的三个图形摊平在一个平面 上,则就是三视图。
练习: 根据三视图想 像物体的形状。
圆柱
圆台
手电筒
从左向右看
圆柱
正六棱柱
螺丝杆
从左向右看
柱
四棱柱
螺丝杆
从左向右看
圆柱
半圆球
螺丝钉
从左向右看
圆柱
圆台
圆柱
热水瓶
从上向下看
N
S
前后看 从上向下看
左右看
马蹄形磁铁
从下向上看
环的形成
有关概念
物体向投影面投影所得 到的图形称为视图。
接下一张幻灯片
在主视图、俯视 图中都体现形体的长 度,且长度在竖直方 向上是对正的,我们 称之为长对正。
返回
在主视图、左视 图上都体现形体的高 度,且高度在水平方 向上是平齐的,我们 称之为高平齐。
返回
在左视图、俯视 图上都体现形体的宽 度,且是同一形体的 宽度,是相等的,我 们称之为宽相等。
错误的三视图 —长未对正1
错误的三视图 —长未对正2
错误的三视图 —高不平齐1
错误的三视图 —高不平齐2
错误的三视图 —宽不相等1
错误的三视图 —宽不相等1
错误的三视图
错误的三视图
体验三视 图的作法
三视图的作图步骤
俯视图方向 1.确定视图方向 2.先画出能反映物体 真实形状的一个视图 左视图方向
三视图欣赏
观察左图:说 说下列三副 图是从哪个 角度看的?
甲、乙、丙、丁四人分别面向 桌坐在一张四方形桌子旁边。 桌上一张纸上写着数字“9”, 甲看到“6”,乙看到“ ” ,丙看到“ ”,丁看到 “9”,问四人是怎样的座次 丁正对着数字“9”;甲坐在丁的对面 ? ,
练习: 根据三视图想 像物体的形状。
圆柱
圆台
手电筒
从左向右看
圆柱
正六棱柱
螺丝杆
从左向右看
柱
四棱柱
螺丝杆
从左向右看
圆柱
半圆球
螺丝钉
从左向右看
圆柱
圆台
圆柱
热水瓶
从上向下看
N
S
前后看 从上向下看
左右看
马蹄形磁铁
从下向上看
环的形成
有关概念
物体向投影面投影所得 到的图形称为视图。
接下一张幻灯片
在主视图、俯视 图中都体现形体的长 度,且长度在竖直方 向上是对正的,我们 称之为长对正。
返回
在主视图、左视 图上都体现形体的高 度,且高度在水平方 向上是平齐的,我们 称之为高平齐。
返回
在左视图、俯视 图上都体现形体的宽 度,且是同一形体的 宽度,是相等的,我 们称之为宽相等。
错误的三视图 —长未对正1
错误的三视图 —长未对正2
错误的三视图 —高不平齐1
错误的三视图 —高不平齐2
错误的三视图 —宽不相等1
错误的三视图 —宽不相等1
错误的三视图
错误的三视图
体验三视 图的作法
三视图的作图步骤
俯视图方向 1.确定视图方向 2.先画出能反映物体 真实形状的一个视图 左视图方向
三视图欣赏
观察左图:说 说下列三副 图是从哪个 角度看的?
甲、乙、丙、丁四人分别面向 桌坐在一张四方形桌子旁边。 桌上一张纸上写着数字“9”, 甲看到“6”,乙看到“ ” ,丙看到“ ”,丁看到 “9”,问四人是怎样的座次 丁正对着数字“9”;甲坐在丁的对面 ? ,
05900_三视图培训ppt课件

投影线
投影线分为实线和虚线两种,实 线表示可见轮廓线,虚线表示不 可见轮廓线。
5
视图方位及对应关系
视图方位
主视图位于图纸的主要位置,俯视图 在主视图的下方,左视图在主视图的 右侧。
对应关系
主视图与俯视图长对正,主视图与左 视图高平齐,俯视图与左视图宽相等 。同时,各视图之间要保持一定的比 例关系。
三视图培训ppt课件
2024/1/24
1
目
CONTENCT
录
2024/1/24
• 三视图基本概念与原理 • 绘制三视图方法与步骤 • 常见几何体三视图绘制技巧 • 复杂零件三视图识别与绘制技巧 • 实际案例分析与讨论 • 课程总结与回顾
2
01
三视图基本概念与原理
2024/1/24
3
三视图定义及作用
粗糙度、公差与配合等技术要求。注意各组成部分之间的尺寸协调和技
术要求的统一。
22
06
课程总结与回顾
2024/1/24
23
重点知识点总结
三视图基本概念
三视图投影规律
三视图绘制步骤
三视图识读方法
正视图、俯视图、侧视 图
长对正、高平齐、宽相 等
选主视、定比例、布图 位、绘底稿、描深图
分线框、对投影、识形 体
得的图形称为剖视图。
2024/1/24
应用场景
当机件的内部结构形状较复杂,用 视图不易表达清楚时,常采用剖视 图来表达机件的内部结构形状。
绘制技巧
选择合适的剖切位置,使得剖切后 能够清晰地表达机件的内部结构; 标注剖切符号和剖切线,标明剖视 图的名称和投影方向。
16
断面图概念及应用场景
01
02
投影线分为实线和虚线两种,实 线表示可见轮廓线,虚线表示不 可见轮廓线。
5
视图方位及对应关系
视图方位
主视图位于图纸的主要位置,俯视图 在主视图的下方,左视图在主视图的 右侧。
对应关系
主视图与俯视图长对正,主视图与左 视图高平齐,俯视图与左视图宽相等 。同时,各视图之间要保持一定的比 例关系。
三视图培训ppt课件
2024/1/24
1
目
CONTENCT
录
2024/1/24
• 三视图基本概念与原理 • 绘制三视图方法与步骤 • 常见几何体三视图绘制技巧 • 复杂零件三视图识别与绘制技巧 • 实际案例分析与讨论 • 课程总结与回顾
2
01
三视图基本概念与原理
2024/1/24
3
三视图定义及作用
粗糙度、公差与配合等技术要求。注意各组成部分之间的尺寸协调和技
术要求的统一。
22
06
课程总结与回顾
2024/1/24
23
重点知识点总结
三视图基本概念
三视图投影规律
三视图绘制步骤
三视图识读方法
正视图、俯视图、侧视 图
长对正、高平齐、宽相 等
选主视、定比例、布图 位、绘底稿、描深图
分线框、对投影、识形 体
得的图形称为剖视图。
2024/1/24
应用场景
当机件的内部结构形状较复杂,用 视图不易表达清楚时,常采用剖视 图来表达机件的内部结构形状。
绘制技巧
选择合适的剖切位置,使得剖切后 能够清晰地表达机件的内部结构; 标注剖切符号和剖切线,标明剖视 图的名称和投影方向。
16
断面图概念及应用场景
01
02
三视图汇总版精品PPT课件
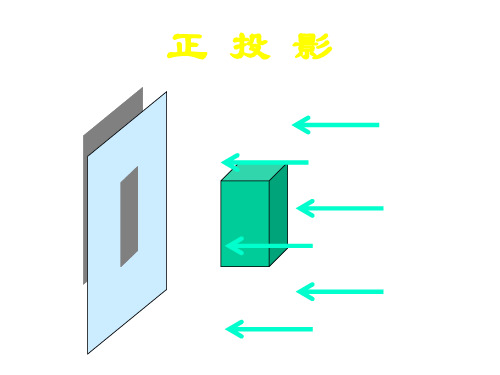
(4)看得见部分的轮廓线画成实线,而 看不见部分的轮廓线画成虚线.
例1:
画出下面一些基本几何体的三视图:
圆柱 (1)
正三菱柱 (2)
球 (3)
你会画圆柱的三视图吗?试一试吧!
演示
圆柱的三视图:
主视图
左视图
俯视图
三菱柱的三视图:
可见轮廓线用 粗实线绘制
球的三视图:
主视图
左视图
俯视图
例2:画出下图支架的三视图(支架的两 个台阶的高度和宽度都是同一长度.)
主视图
俯视图
左视图
主视图
俯视图
左视图
探究 根据三视图摆出它的立体图形
主视图 左视图
俯视图
做一做:由几个相同的小立方块搭成的几何体的 俯视图如图所示。方格中的数字表示该位置的小 方块的个数.请画出这个几何体的三视图。
13 2
用小正方体搭一个几何体,它的主视图
和俯视图如图所示,最多要多少个小正方体? 最少呢?
主视图
11 1111
23
俯视图
∴最小为11
由物知图——利用正方体组合提升空间想象力
如图都是由7个小立方体搭成的几何体,从不 同方向看几何体,分别画出它们的主视图、左视 图与俯视图,并在小正方形内填上表示该位置的 小正方体的个数.
(1)
(2)
(3)
(4)
由图想物——利用正方体组合提升空间想象力
用小正方体搭一个几何体,它的主视图 和俯视图如图所示,最多要多少个小正方体 最少呢?
11
122 1
下列是一个物体的三视图,请描述出它的形状
主视图 左视图
俯视图
我思我进步
(2).右图是由一些相同的小正方体构成的几何
例1:
画出下面一些基本几何体的三视图:
圆柱 (1)
正三菱柱 (2)
球 (3)
你会画圆柱的三视图吗?试一试吧!
演示
圆柱的三视图:
主视图
左视图
俯视图
三菱柱的三视图:
可见轮廓线用 粗实线绘制
球的三视图:
主视图
左视图
俯视图
例2:画出下图支架的三视图(支架的两 个台阶的高度和宽度都是同一长度.)
主视图
俯视图
左视图
主视图
俯视图
左视图
探究 根据三视图摆出它的立体图形
主视图 左视图
俯视图
做一做:由几个相同的小立方块搭成的几何体的 俯视图如图所示。方格中的数字表示该位置的小 方块的个数.请画出这个几何体的三视图。
13 2
用小正方体搭一个几何体,它的主视图
和俯视图如图所示,最多要多少个小正方体? 最少呢?
主视图
11 1111
23
俯视图
∴最小为11
由物知图——利用正方体组合提升空间想象力
如图都是由7个小立方体搭成的几何体,从不 同方向看几何体,分别画出它们的主视图、左视 图与俯视图,并在小正方形内填上表示该位置的 小正方体的个数.
(1)
(2)
(3)
(4)
由图想物——利用正方体组合提升空间想象力
用小正方体搭一个几何体,它的主视图 和俯视图如图所示,最多要多少个小正方体 最少呢?
11
122 1
下列是一个物体的三视图,请描述出它的形状
主视图 左视图
俯视图
我思我进步
(2).右图是由一些相同的小正方体构成的几何
小学数学立体图形三视图复习ppt课件

51
从正面看 从上面看
从左面看
52
从正面看 从上面看
从左面看
53
从正面看 从上面看
从左面看
54
从正面看 从上面看
从左面看
55
从正面看 从上面看
从左面看
56
57
10
11
12
13
14
15
16
17
由立体图形到视图
工人在建造房子之前,首先要看房子的图纸.但在平面上画 空间的物体不是一件简单的事,因为必须把它画得从各个方面 看都很清楚.为了解决这个问题,创造了三视图法.
什么是三视图法呢?
就是从三个不同的方向看一个 物体,一般是从正面、上面和 侧面,然后描绘三张所看到的 图,即视图.
1
F-22,是美国空军委托洛克希德、 波音以及通用动力公司合作研制的新一代 战斗机,也是专家们所指的目前唯一面世 的“第四代战斗机”,它将成为本世纪初 叶的主战机种。主要用途是压取战区制空 权,因而也是F-15的后继型号。
F—22可以在本个世纪进行 “超视距作战”,美国空军对此充满信心 并已接近成功。它甚至认为如果F—22早问 世十年,那么海湾战争可能打不起来。
(A)从上面、正面、左面看 (B面看
2
49
这个图是由9个正方体组成的立体图形,分别 从正面、左面、上面观察这个图形,各能得到 什么平面图形?
H
BM
O
Q
S
U
W
A1
C1
N
P
R
T
V
X
B1
D1
演示
50
试画出从正面、侧面、上面看下列各几何体得到的几何图形
2
3
4
5
从正面看 从上面看
从左面看
52
从正面看 从上面看
从左面看
53
从正面看 从上面看
从左面看
54
从正面看 从上面看
从左面看
55
从正面看 从上面看
从左面看
56
57
10
11
12
13
14
15
16
17
由立体图形到视图
工人在建造房子之前,首先要看房子的图纸.但在平面上画 空间的物体不是一件简单的事,因为必须把它画得从各个方面 看都很清楚.为了解决这个问题,创造了三视图法.
什么是三视图法呢?
就是从三个不同的方向看一个 物体,一般是从正面、上面和 侧面,然后描绘三张所看到的 图,即视图.
1
F-22,是美国空军委托洛克希德、 波音以及通用动力公司合作研制的新一代 战斗机,也是专家们所指的目前唯一面世 的“第四代战斗机”,它将成为本世纪初 叶的主战机种。主要用途是压取战区制空 权,因而也是F-15的后继型号。
F—22可以在本个世纪进行 “超视距作战”,美国空军对此充满信心 并已接近成功。它甚至认为如果F—22早问 世十年,那么海湾战争可能打不起来。
(A)从上面、正面、左面看 (B面看
2
49
这个图是由9个正方体组成的立体图形,分别 从正面、左面、上面观察这个图形,各能得到 什么平面图形?
H
BM
O
Q
S
U
W
A1
C1
N
P
R
T
V
X
B1
D1
演示
50
试画出从正面、侧面、上面看下列各几何体得到的几何图形
2
3
4
5
三视图 -完整版课件

学习目标
1 课堂讲解 由几何体确定三视图
画几何体的三视图
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
课时导入
这首诗教会 了我们怎样观察 物体(横看、侧看、 近看、身处其中 看),这类似于本 节课所研究的内 容——三视图.
感悟新知
知识点 1 由几何体确定三视图
知1-导
当我们从某一方向观察一个物体时,所看到的平面 图形叫做物体的一个视图(view). 视图可以看作物体在某 一方向光线下的正投影.对于同一个物体, 如果从不同 方向观察,所得 到的视图可能不 同.如图是同一本 书的三个不同的 视图.
(2)主视图正确,左视图 、
俯视图如图②所示.
知2-练
4 画出如图所示立体图形的三 视图.(相当于在桌面的中间 靠后放着一个盒子) 解:三视图如图所示.
知2-练
课堂小结
1 知识小结
1. 三视图是指主视图、左视图与俯视图. 2. 画物体三视图的具体步骤为:
(1)确定主视图的位置,画出主视图; (2)在主视图的正下方画出俯视空心圆柱体,它的左视图 是( B )
知1-练
4 【中考·贵阳】如图是一个水平放置的圆柱形物体, 中间有一个细棒,则此几何体的俯视图是( C )
知1-练
5 【中考·菏泽】下列几何体是由4个相同的小正方体 搭成的,其中左视图与俯视图相同的是( C )
知1-练
6 (中考·攀枝花)如图所示的几何体为圆台,其俯视图正 确的是( C )
对正”; (3)在主视图的正右方画出左视图,注意与主视图“高
平齐”与俯视图“宽相等”.
2 易错小结
如图是一个由3个相同的正方体组成的立体图形,它的三 视图是( A )
易错点:画图时忽视被遮挡部分的轮廓线.
1 课堂讲解 由几何体确定三视图
画几何体的三视图
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
课时导入
这首诗教会 了我们怎样观察 物体(横看、侧看、 近看、身处其中 看),这类似于本 节课所研究的内 容——三视图.
感悟新知
知识点 1 由几何体确定三视图
知1-导
当我们从某一方向观察一个物体时,所看到的平面 图形叫做物体的一个视图(view). 视图可以看作物体在某 一方向光线下的正投影.对于同一个物体, 如果从不同 方向观察,所得 到的视图可能不 同.如图是同一本 书的三个不同的 视图.
(2)主视图正确,左视图 、
俯视图如图②所示.
知2-练
4 画出如图所示立体图形的三 视图.(相当于在桌面的中间 靠后放着一个盒子) 解:三视图如图所示.
知2-练
课堂小结
1 知识小结
1. 三视图是指主视图、左视图与俯视图. 2. 画物体三视图的具体步骤为:
(1)确定主视图的位置,画出主视图; (2)在主视图的正下方画出俯视空心圆柱体,它的左视图 是( B )
知1-练
4 【中考·贵阳】如图是一个水平放置的圆柱形物体, 中间有一个细棒,则此几何体的俯视图是( C )
知1-练
5 【中考·菏泽】下列几何体是由4个相同的小正方体 搭成的,其中左视图与俯视图相同的是( C )
知1-练
6 (中考·攀枝花)如图所示的几何体为圆台,其俯视图正 确的是( C )
对正”; (3)在主视图的正右方画出左视图,注意与主视图“高
平齐”与俯视图“宽相等”.
2 易错小结
如图是一个由3个相同的正方体组成的立体图形,它的三 视图是( A )
易错点:画图时忽视被遮挡部分的轮廓线.
课件《三视图》PPT全文课件_人教版1

2.正视图与俯视图的长度一样
3.侧视图与俯视图宽度一样
正视图
侧视图
高平齐
长
宽
相
长对正
等
宽
俯视图
举例画出三视图
圆锥
正视图
侧视图
俯视图
举例画出三视图
光线从几何体的前面向后面正投影所得的投影图称为“正视图” “视图”是将物体按正投影法向投影面投射时所得到的投影图. 侧视图与俯视图宽度一样 正视图与俯视图的长度一样 光线从几何体的上面向下面正投影所得的投影图称为“俯视图”. 侧视图与俯视图宽度一样 光线从几何体的左面向右面正投影所得的投影图称为“侧视图” 光线从几何体的前面向后面正投影所得的投影图称为“正视图” “视图”是将物体按正投影法向投影面投射时所得到的投影图. 根据三视图想象其表示的几何体 侧视图与俯视图宽度一样 正视图与俯视图的长度一样 根据三视图想象它们表示的几何体的结构特征 根据三视图想象其表示的几何体 光线从几何体的上面向下面正投影所得的投影图称为“俯视图”. 光线从几何体的左面向右面正投影所得的投影图称为“侧视图”
“视图”是将物体按正投影法向投影面投射时所得到的投影图. 光线从几何体的左面向右面正投影所得的投影图称为“侧视图”
侧视图
正视图 光线从几何体的上面向下面正投影所得的投影图称为“俯视图”.
侧视图与俯视图宽度一样
光线从几何体的左面向右面正投影所得的投影图称为“侧视图”
正视图、侧视图、俯视图在平面图中的一般位置
正视图、侧视图、俯视图统称为三视图
侧视图与俯视图宽度一样
光线从几何体的上面向下面正投影所得的投影图称为“俯视图”.
根据三视图想象其表示的几何体
“视图”是将物体按正投影法向投影面投射时所得到的投影图.
3.侧视图与俯视图宽度一样
正视图
侧视图
高平齐
长
宽
相
长对正
等
宽
俯视图
举例画出三视图
圆锥
正视图
侧视图
俯视图
举例画出三视图
光线从几何体的前面向后面正投影所得的投影图称为“正视图” “视图”是将物体按正投影法向投影面投射时所得到的投影图. 侧视图与俯视图宽度一样 正视图与俯视图的长度一样 光线从几何体的上面向下面正投影所得的投影图称为“俯视图”. 侧视图与俯视图宽度一样 光线从几何体的左面向右面正投影所得的投影图称为“侧视图” 光线从几何体的前面向后面正投影所得的投影图称为“正视图” “视图”是将物体按正投影法向投影面投射时所得到的投影图. 根据三视图想象其表示的几何体 侧视图与俯视图宽度一样 正视图与俯视图的长度一样 根据三视图想象它们表示的几何体的结构特征 根据三视图想象其表示的几何体 光线从几何体的上面向下面正投影所得的投影图称为“俯视图”. 光线从几何体的左面向右面正投影所得的投影图称为“侧视图”
“视图”是将物体按正投影法向投影面投射时所得到的投影图. 光线从几何体的左面向右面正投影所得的投影图称为“侧视图”
侧视图
正视图 光线从几何体的上面向下面正投影所得的投影图称为“俯视图”.
侧视图与俯视图宽度一样
光线从几何体的左面向右面正投影所得的投影图称为“侧视图”
正视图、侧视图、俯视图在平面图中的一般位置
正视图、侧视图、俯视图统称为三视图
侧视图与俯视图宽度一样
光线从几何体的上面向下面正投影所得的投影图称为“俯视图”.
根据三视图想象其表示的几何体
“视图”是将物体按正投影法向投影面投射时所得到的投影图.
《三视图》ppt全文课件

《三视图》上课实用课件(PPT优秀课 件)
《三视图》上课实用课件(PPT优秀课 件) 《三视图》上课实用课件(PPT优秀课 件)
主视图 左视图
宽
《三视图》上课实用课件(PPT优秀课 件) 《三视图》上课实用课件(PPT优秀课 件)
《三视图》上课实用课件(PPT优秀课 件)
例2 画出如图所示的支架的三视图,其中支架 的两个台阶的高度和宽度相等。
《三视图》上课实用课件(PPT优秀课 件)
解:图是支架的三视图.
主
左
视
视
图
图
俯 视 图
《三视图》上课实用课件(PPT优秀课 件)
《三视图》上课实用课件(PPT优秀课 件)
理一理:
1、从正面看到的图形叫做主视图,从上 面看到的图形叫做俯视图,从左面看到的 图形叫做左视图。
2、画三视图必须遵循的法则: “长对正,高平齐,宽相等”
《三视图》上课实用课件(PPT优秀课 件)
主视图
左视图 高
长
宽
宽 俯视图
从正面看
主视图
三视图
正面
主视图
左视图 高
长
宽
宽 俯视图
主视图
三视图
正面
主视图
左视图
高
长
宽
宽
俯视图
主视图
从上面看
正面
主视
左视图
图高
长
宽
宽
俯视 图
三视图位置 有规定,主视 图要在左上边, 它的下方应是 俯视图,左视 图坐落在右边
主视图 长
俯视图
左视图 高
宽
宽
从上面看
《三视图》上课实用课件(PPT优秀课 件)
4.反思与小结
《三视图》上课实用课件(PPT优秀课 件) 《三视图》上课实用课件(PPT优秀课 件)
主视图 左视图
宽
《三视图》上课实用课件(PPT优秀课 件) 《三视图》上课实用课件(PPT优秀课 件)
《三视图》上课实用课件(PPT优秀课 件)
例2 画出如图所示的支架的三视图,其中支架 的两个台阶的高度和宽度相等。
《三视图》上课实用课件(PPT优秀课 件)
解:图是支架的三视图.
主
左
视
视
图
图
俯 视 图
《三视图》上课实用课件(PPT优秀课 件)
《三视图》上课实用课件(PPT优秀课 件)
理一理:
1、从正面看到的图形叫做主视图,从上 面看到的图形叫做俯视图,从左面看到的 图形叫做左视图。
2、画三视图必须遵循的法则: “长对正,高平齐,宽相等”
《三视图》上课实用课件(PPT优秀课 件)
主视图
左视图 高
长
宽
宽 俯视图
从正面看
主视图
三视图
正面
主视图
左视图 高
长
宽
宽 俯视图
主视图
三视图
正面
主视图
左视图
高
长
宽
宽
俯视图
主视图
从上面看
正面
主视
左视图
图高
长
宽
宽
俯视 图
三视图位置 有规定,主视 图要在左上边, 它的下方应是 俯视图,左视 图坐落在右边
主视图 长
俯视图
左视图 高
宽
宽
从上面看
《三视图》上课实用课件(PPT优秀课 件)
4.反思与小结
三视图教学PPT课件
,侧棱长为
2的正四棱锥叠放而成.故该几何体的体积为
V 12 1 ( 2 )2 3
3
2 2 3.
3
[答案] C
│要点探究 要点探究
探究点3 三视图的画法 例3 画出如图36-1所示几何体的三视图.
│要点探究
【思路】 图36-1(1)为正六棱柱,可按棱柱画法画出; 图36-1(2)为一个圆锥和一个圆台的组合体,按圆锥、圆台 的三视图画法画出它们的组合形状.
左视图
能看见的轮廓线 和棱用实线表示,不 能看见的轮廓线和棱 用虚线表示。
圆锥的三视图
主视图
左视图
俯视图
圆台
俯
左
圆台
正视图
侧左视视图图
俯视图
棱锥的三视图
俯
左
正四棱锥
四棱锥的三视图
主
左
视
视
图
图
主视
俯 视
图
总结:三视图的概念
1.视图:将物体按正投影向投影 面投射所得到的图形.
正视图
c
侧 视
ba
答案:D
三基能力强化
3.关于如图所示几何体的正确说 法为( )
①这是一个六面体 ②这是一个 四棱台
③这是一个四棱柱 ④这是一个 四棱柱和三棱柱的组合体 ⑤这是一 个被截去一个三棱柱的四棱柱
三基能力强化
A.①②③④⑤ ④⑤
C.①④⑤ D.①③④
答案:A
B.①③
三视图是新课标新增的内容,是一个知识交汇的载 体,因而是高考的重点内容之一.但新课标对这部分内 容的要求较低,一般不会直接考查画图的问题,而经常 会与立体几何中有关的计算问题融合在一起考查.2009年 广东高考将三视图与几何体的体积计算、空间位置关系 融为一体,考查了学生的空间想象能力,是一个新的考 查方向.)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正投影 (视图)
黄鹤楼
黄鹤楼送孟浩然之广陵
李白
故人西辞黄鹤楼, 烟花三月下扬州. 孤帆远影碧空尽, 惟见长江天际流.
• 黄鹤楼
•
(唐)崔颢
•昔人已乘黄鹤去,
•此地空余黄鹤楼。
•黄鹤一去不复返,
•白云千载空悠悠。
•晴川历历汉阳树,
•芳草萋萋鹦鹉洲。
•日暮乡关何处是?
•烟波江上使人愁。
岳 阳 楼
上倚河汉,下临江流;
事列《神仙》之传 迹存《述异》之志
耸重檐构翼巍馆峨,高标 巃 嵸,
课文以哪个字贯穿全 文?并说说理由。
有感情地 朗读课文
黄鹤楼 阎伯理
州城西南隅,有黄鹤楼者。
鄂州城西南角上,有一座黄鹤嵝。
《图经》云:“费祎登仙,尝驾黄鹤返憩 于此,遂 以 名楼。”
《图经》上说:“三国时代蜀汉大将费祎成了仙 人,曾经骑着黄鹤返回到这里休息,于是就用 ‘黄鹤’命名这座楼。”
事列《神仙》之传,迹存《述异》之志。
有关这件事记载在《神仙传》上,有关事迹还保存在 《述异志》上。
主视图 俯视图
巩固 6、用小方块搭一个几何体,使得它的主 视图和俯视图如图所示,这样的几何体 只有一种吗?它至少要多少个小方块? 最多要多少个小方块?分别画出它们的 几何体与左视图,并在左视图中表出小 方块的个数。
主视图 俯视图
范例 例5、如图是一个立体图形的三视图,请 写出这个立体图形的名称,并计算这个 立体图形的体积。
小结与复习
知识构架
物体 光照 (立体图形)
投影
点光源 中心投影 平行光线 平行投影
画想 图象
由前向后看 主视图
于光 投线 影垂 面直
三视图
俯视图 由上向下看 左视图 由左向右看
正投影 (视图)
范例
例1、下列现象属于平行投影的是( ) A. 皮影 B. 灯光下的手影 C. 太阳光下房屋的影子 D. 台灯下铅笔的影子
位于湖南岳阳,以范仲淹的名篇《岳阳 楼记》而名闻天下。文中名句“先天下之忧 而忧,后天下之乐而乐。”
滕 王 阁
位于江西南昌,因王勃的《滕王阁序》而著名。 文中名句有“物华天宝,人杰地灵。”“落霞与孤 鹜齐飞,秋水共长天一色。”“老当益壮,宁移白 首之心?穷且益坚,不坠青云之志。”等。
黄 鹤 楼
位于湖北武汉,历代名士崔颢、李 白、白居易、贾岛、陆游、杨慎、张居 正等都先后到这里游乐,吟诗作赋。
学习目标:
1、参考书下注释和教师适当点拨, 正确朗读课文并用现代汉语翻译 全文。 2、体会本文结构严谨,语言优美 的特点。 3、领略中国古代建筑艺术的魅力, 体会作者热爱山川胜迹和仰慕仙 人的思想感情。
龙隅憩山山从(((yqúìló))ngzōn费g遂祎)((巍s峨yuī)ì) wēi’é 倚坐荆( 窥 吴( (yǐjk)īnugī))井邑闼((yìtà))
QB
巩固
3、在一次数学活动课上,李老师带领学
生去测教学楼的高度,在阳光下,测得
身高1.65m的黄丽同学BC的影子长BA为
1.1m,与此同时,测得教学楼DE E
的影子长DF为12.1m。
(1)请你在图中画出此
时教学楼DE在阳光下
的投影DF;
C
AB
D
巩固
3、在一次数学活动课上,李老师带领学
生去测教学楼的高度,在阳光下,测得
身高1.65m的黄丽同学BC的影子长BA为
1.1m,与此同时,测得教学楼DE E
的影子长DF为12.1m。
(2)请你根据已测得的数据,
求出教学楼DE的高度
(精确到0.1m)。
C
AB
D
范例
例3、将如图所示的Rt△ABC绕直角边 AC所在的直线旋转一周,所得到的几 何体的主视图是( )
A
A.
B.
CB
三视图
10 10
10
巩固 7、根据展开图画出物体的三视图,并 求出物体的体积和表面积。
10
20
31.4
巩固 8、根据下列的三视图,求出几何体的 体积。
10
8 6
小结
物体 光照 (立体图形)
投影
点光源 中心投影 平行光线 平行投影
画想 图象
由前向后看 主视图
三视图
俯视图 由上向下看 左视图 由左向右看
“平行投影”与“中心投影”的区别
巩固
1、在同一时刻,小明的影子比小强的 影子长,那么在同一路灯下( ) A. 小明的影子比小强的影子长 B. 小明的影子比小强的影子短 C. 小明和小强的影子一样长 D. 无法判断谁的影子长
巩固
2、小华拿一个矩形木框在阳光下玩, 矩形木框在地面上形成的投影不可能 是( )
C.
D.
巩固 4、下列图形中左视图是
的是( )
A.
B.
C.
D.
巩固 5、画出下列几何体的三视图:
线的“实”与“虚”
范例 例4、如图是由一些大小相同的小正方体 组成的简单几何体是主视图和俯视图。 (1)请你画出这个几何体的一种左视图; (2)若组成这个几何体的小正方体的块数 为n,请写出n的所有可能值。
QB
范例
例2、如图,晚上王华由路灯AC走向路
灯BD。当他走到点P时,身后影子的顶
部恰好接触到路灯AC的底部;当他继
续向前步行12m到达点Q时,身前影子
的顶部刚好接触到路灯BD的底部。已
知王华身高1.6m, C
D
两路灯的高度都是
9.6m。(2)求王华走到
路灯BD处时,他在路
M
N
灯AC下的影子长。 A P
探究学习 分析课文
• 1.文章写出了黄鹤楼的什么特征? • 2.从原文中哪些语句可以看出? • 3.哪一句话写出了黄鹤楼的价值?
高大:耸构巍峨
高标巃嵸
雄伟:上倚河汉
坐窥 井邑
俯拍 云烟 四闼霞敞 重檐翼馆
“亦荆吴形胜之最也”
思考:作者对黄鹤楼景物描
写的顺序及其所采用的修辞手法。
有上有下,有远有 近,有内有外,其 角度还有实有虚
观其耸构巍峨,高标龙山从,上倚河汉,下临江流; 山
观看这矗立着的楼宇,高高耸立,十分雄伟,它 顶端靠着银河,底部临近大江;
重檐翼馆,四闼霞敞;坐窥井邑,俯拍云烟:
两层飞檐像鸟翼高翘在房舍之上,四面的 大门高大宽敞;坐在楼上,可以远眺城乡 景色,低下头可以拍击云气和烟雾:
亦荆吴形胜之最也。
这里也是楚地和吴地山川胜迹中的最美的地方。A.Leabharlann B.C.D.
正投影的概念
范例
例2、如图,晚上王华由路灯AC走向路
灯BD。当他走到点P时,身后影子的顶
部恰好接触到路灯AC的底部;当他继
续向前步行12m到达点Q时,身前影子
的顶部刚好接触到路灯BD的底部。已
知王华身高1.6m, C
D
两路灯的高度都是
9.6m。(1)求两个路 灯之间的距离;
M
N
AP
