2010年湖南省衡阳市中考数学试卷(word版)

合集下载

衡阳中考试题数学及答案

衡阳中考试题数学及答案一、选择题1. 已知x + 3 = 7，则x的值是多少？A. 3B. 4C. 6D. 7答案：C2. 若a = 2，b = -3，则a - b的值为多少？A. -1B. 1C. 5D. -5答案：D3. 如果m + n = 10，且m - n = 4，则m和n的值分别为多少？A. m = 7, n = 3B. m = 3, n = 7C. m = 8, n = 2D. m = 6, n = 4答案：A4. 已知直角三角形的两直角边分别为3cm和4cm，求斜边的长度是多少？A. 5cmB. 6cmC. 7cmD. 8cm答案：A二、填空题1. 已知一个边长为5cm的正方形的面积是__________平方厘米。

答案：252. 一个长方体的长、宽、高分别为3cm、4cm和5cm，它的体积是__________立方厘米。

答案：603. 设x = 3，y = 4，则x² + y² = ________。

答案：254. 一个数加上5等于12，这个数是__________。

答案：7三、解答题1. 某商店以原价200元出售一件衣服，现在正在打折活动，折扣为20%，请问该衣服现在的售价是多少？解答：折扣为20%表示该衣服现在的价格是原价的80%。

所以，200元 * 80% = 160元。

该衣服现在的售价是160元。

2. 某图书馆有中文书籍3000本，英文书籍2000本，若要将这些书籍按照比例存放在两个书架上，并且两个书架上的书籍总数要一样多，那么每个书架应该分别放置多少中文书籍和英文书籍？解答：两个书架上的书籍总数为3000 + 2000 = 5000本。

根据比例，中文书籍占总数的3/5，即3000/5000 * 3/5 = 1800本。

同理，英文书籍占总数的2/5，即2000/5000 * 2/5 = 800本。

所以，每个书架应该分别放置1800本中文书籍和800本英文书籍。

中考湖南衡阳数学试卷真题

中考湖南衡阳数学试卷真题一、选择题（共20题，每题2分，共40分）1. 设函数"y=2sin(x-π/6)"的一个周期为T，下列表示中正确的是（）A. T=2πB. T=π/2C. T=πD.T=4π2. 一根长36cm的线段，两端分别固定在两个顶点A和B，线段可以在A，B两个顶点之间来回摆动，A，B两个顶点之间的距离是（）A. 36cmB. 18cmC. 72cmD. 9cm3. 已知直线L1：y=-2x+1与直线L2：kx-y-3=0相交于点P，且点P到x轴的距离是4，那么k的值是（）A. 1B. 2C. 3D. 44. 已知在一个算式中，每个数字都用它的平方代替，让原算式的值减少137，这个算式的值原来是（）A. 169B. 156C. 144D. 1005. 在平面直角坐标系中，点A(0，2)和点B(a，1)都在直线y=3x-1上，那么点B的坐标是（）A. (1，2)B. (2，5)C. (1，2)D. (3，8)6. 二次函数y=ax²+bx+c(a>0)的图像与x轴相交于P，Q两点，如果PQ的中点坐标是(2，0)，则a的值是（）A. 2B. 4C. 1D. 0.57. 在直立的正方体ABCD-A'B'C'D'中，垂直于ABCD区域的平面与矩形ABCD的交线与⊙O交于点P，连接OP，如图所示，∠BOP的弧度值是（）A. π/4B. π/3C. π/2D. 2π/38. 几何平面中，已知△ABC中，m∠BAC=30°，△ABD平动到△ACE，使得点D运动到点E，∠BAE的度数是（）A. 30°B. 45°C. 60°D. 90°9. AB为直径的⊙O，P为⊙O上一点，PA，PB分别与⊙O交于点A'，B'，且PA'=PB'，则A'B'平行于AB的充分必要条件是（）A. P在直径的一侧B. P在⊙O的内部C. P在⊙O的外部D. P 是⊙O的圆心10. 设两条直线L1:x-y+2=0和L2:2x+y-2=0的交点为P,交点到x轴距离的平方与交点到y轴距离的平方之和是（）A. 1B. 2C. 4D. 811. 下列运算关系中，错的是：（）A. 7-11=7-7+4B. 7÷(11-7)=7C. 7-(11-7)=0D. 7-11=-(11-7)12. 水桶已装了640升水，如果再加满40%的容积，水桶就溢满。

2010年湖南衡阳中考数学模拟试卷

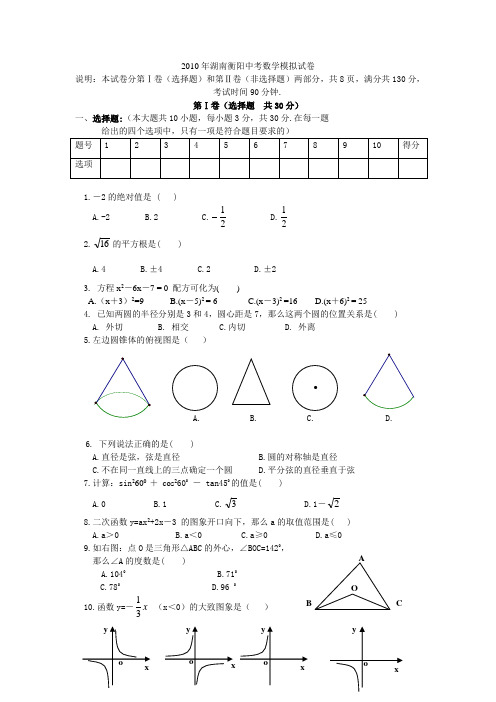
2010年湖南衡阳中考数学模拟试卷说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共8页，满分共130分，考试时间90分钟.第Ⅰ卷（选择题共30分）一、选择题:（本大题共10小题，每小题3分，共30分.在每一题给出的四个选项中，只有一项是符合题目要求的）1.－2的绝对值是 ( )A.-2B.2C.21D.212.16的平方根是( )A.4B.±4C.2D.±23. 方程x 2－6x －7 = 0 配方可化为( )A.（x ＋3）2=9B.(x －5)2 = 6C.(x －3)2 =16D.(x ＋6)2 = 254. 已知两圆的半径分别是3和4，圆心距是7，那么这两个圆的位置关系是( )A. 外切B. 相交C.内切D. 外离 5.左边圆锥体的俯视图是（）6. 下列说法正确的是( )A.直径是弦，弦是直径B.圆的对称轴是直径C.不在同一直线上的三点确定一个圆D.平分弦的直径垂直于弦7.计算：sin 2600 ＋ cos 2600 － tan450的值是( )A.0B.1C.3D.1－2 8.二次函数y=ax 2+2x －3 的图象开口向下，那么a 的取值范围是( ) A.a ＞0 B.a ＜0 C.a ≥0 D.a ≤09.如右图：点O 是三角形△ABC 的外心，∠BOC=1420，那么∠A 的度数是( )A.1040B.710C.780D.96 010.函数y=－x 31（x ＜0）的大致图象是（） A BO CA. B. C. D.第Ⅱ卷（非选择题共100分）二.填空题:（本大题共5小题，每小题3分，共15分。

把答案填在题中横线上）. 11. 找一个与3是同类二次根式是 .12. 方程 x 2= x 的解是 .13.在菱形ABCD 中，其中对角线的长分别为6和8.则它的面积是 . 14. 三角形的三边为3、4、5. 那么它的外接圆的直径是 . 15. 圆锥体的母线长为3 ，底面圆的半径为4，那么圆锥体的全．面积是 . 三. 解答题:（要有必要的解题步骤，每小题6分，共30分）16. 关于x 的方程x 2＋mx ＋9=0的一个根是－1.求m 的值和方程的另一个根.17. 在压力不变的情况下，某物体承受的压强p （pa ）是它的受力面积s （m 2）的反比例函数，其图象如图所示：（1）求p 与s 之间的函数关系式；（2）求当s=0.5m 2时物体承受的压强；2)18.在平行四边形ABCD中，BF=DE.写出图中一对你认为全等的三角形，并说明理由.19、已知⊙o上有一点A，过点A作出⊙o的切线。

衡阳中考数学试题及答案

衡阳中考数学试题及答案一、选择题1. 设函数 f（x）= |x - 4| + 2，当x ≥ 4 时，f（x）的值等于（）A. x - 2B. x + 2C. 2D. 4 - x2. 在抛物线 y = 2x^2 - 3x - 2 的图象上，点 P（a, -10）为切点，则实数 a 的值为（）A. 3B. -3C. 1D. -13. 在平面直角坐标系中，点 A（1, 3）和点 B（-2, 4）关于原点 O 的对称点记为 C，点 A 和 C 的中点记为 D，则线段 BD 的斜率为（）A. -2B. 1C. 2D. -14. 已知 x = 2^(-2t) + 2^(-t)，则当 t = 0 时，x 的值等于（）A. 0B. 0.5C. -1D. 15. 若正整数 a 和 b 满足 a^2 - b^2 = 35，则 a 的最小值为（）A. 2B. 3C. 4D. 5二、填空题6. 某公司在去年全年的销售额为 600 万元，今年增长了 25%，则今年全年的销售额为 __________万元。

7. 在平面直角坐标系中，点 P(a, -2) 与点 Q(-2, b) 是关于原点 O 对称的点，则 a + b 的值为 __________。

8. 有一篮子里有红、黄、蓝三种颜色的球，红球占总数的 20%，黄球占总数的 30%，蓝球占总数的 50%。

已知篮子中一球为红色的概率是 1/3，则篮子中蓝球的数目为 __________个。

9. 一辆汽车原来是满油状态，已知全程共耗油 35 升，第一部分耗油与第二部分耗油的比值为 1:2，那么第一部分行程的长度是全程长度的 __________。

10. 若 y = kx 是函数 y = x^2 的图象上的一条弦，且弦与 x 轴的交点横坐标分别为 1 和 2，则实数 k 的值为 __________。

三、解答题11. 【解答】已知函数 f（x）= mx + 2，当 x = 3 时，f（x） = 4。

湖南省衡阳市中考数学试卷

湖南省衡阳市中考数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分）若a，b互为相反数，那么（）A . ab<0B .C .D . |a|=|b|2. （2分）(2018·扬州模拟) 下列各式计算正确的是（）．A .B .C .D .3. （2分） (2018九上·成都期中) 已知函数y= ，则自变量x的取值范围是（）A . ﹣1＜x＜1B . x≥﹣1且x≠1C . x≥﹣1D . x≠14. （2分）某班第一小组7名同学的毕业升学体育测试成绩（满分30分）依次为：25，23，25，23，27，30，25，这组数据的中位数和众数分别是（）A . 25，23B . 23，23C . 23，25D . 25，255. （2分）三峡大坝坝顶从2005年7月到9月共92天对游客开放，每天限接待1000人，在整个开放期间最多能接待游客的总人数用科学记数法表示为（）A . 92×103人B . 9.2×104人C . 9.2×103人D . 9.2×105人6. （2分） (2020九上·醴陵期末) 已知二次函数y=ax2+bx+c（）的图像如图所示，则下列结论：（1）ac>0;（2）方程ax2+bx+c=0的两根之积小于0；（3）a+b+c<0；（4）ac+b+1 <0,其中符合题意的个数（）A . 1个B . 2个C . 3个D . 4个7. （2分）(2018·济宁) 如图，点B，C，D在⊙O上，若∠BCD=130°，则∠BOD的度数是（）A . 50°B . 60°C . 80°D . 100°8. （2分）(2017·江津模拟) 已知函数图象如图，以下结论，其中正确有（）个：①m＜0；②在每个分支上y随x的增大而增大；③若A（﹣1，a），点B（2，b）在图象上，则a＜b④若P（x，y）在图象上，则点P1（﹣x，﹣y）也在图象上．A . 4个B . 3个C . 2个D . 1个9. （2分）化简÷（1+ ）的结果是（）A .B .C .D .10. （2分）如果点B与点C的横坐标相同，纵坐标不同，则直线BC与x轴的关系为（）A . 平行B . 垂直C . 相交D . 以上均不对二、填空题： (共8题；共8分)11. （1分） (2017七下·南京期末) 若，，则的值为________．12. （1分）分解因式：x2﹣16=________ ．13. （1分） (2017八下·安岳期中) 要使与的值相等，则x=________．14. （1分）一个不透明的袋子中装有3个黑球和2个红球，这些球除了颜色外都相同，搅匀后从袋子中随机摸出一个球，则摸到黑球的概率是________.15. （1分）若已知x+y=3，xy=﹣4，则（1+3x）﹣（4xy﹣3y）的值为________16. （1分） (2016九上·重庆期中) 一个扇形的圆心角为60°，它所对的弧长为2πcm，则这个扇形的半径为________．17. （1分） (2019八下·北京期中) 如图，在平面直角坐标系xOy中，四边形ABOC是矩形，点A在y轴上,若点C的坐标为(1,2)，则点B的坐标为________.18. （1分）(2014·宜宾) 如图，在Rt△ABC中，∠B=90°，AB=3，BC=4，将△ABC折叠，使点B恰好落在边AC上，与点B′重合，AE为折痕，则EB′=________．三、解答题 (共11题；共90分)19. （5分）(2017·岳阳模拟) 计算：（）﹣1﹣2cos30°+ +（2017﹣π）0 ．20. （5分）(2011·宿迁) 解不等式组．21. （5分）先化简，再求值：÷（x2﹣2xy），其中x=1，y=﹣2．22. （5分）我市某中学初一、初二两个年段学生去劳动基地参加劳动，两个年级共安装零件3000个，其中初二年段安装的数量比初一年段安装数量的2倍少3个，两个年段各安装多少个零件？23. （15分）(2017·丹东模拟) 为了了解青少年形体情况，现随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况．我们对测评数据作了适当处理（如果一个学生有一种以上不良姿势，以他最突出的一种作记载），并将统计结果绘制了如下两幅不完整的统计图，请你根据图中所给信息解答下列问题：（1）请问这次被抽查形体测评的学生一共是多少人？（2）请将两幅统计图补充完整．（3）如果全市有5万名初中生，那么全市初中生中，坐姿和站姿不良的学生有多少人？24. （10分）(2016·丹阳模拟) 依据闯关游戏规则，请你探究“闯关游戏”的奥秘：（1）用列表的方法表示有可能的闯关情况；（2）求出闯关成功的概率．25. （10分） (2019九上·港南期中) 如图，某市郊外景区内一条笔直的公路经过、两个景点，景区管委会又开发了风景优美的景点 .经测量，位于的北偏东的方向上，的北偏东的方向上，且 .（1）求景点与的距离.（2）求景点与的距离.(结果保留根号)26. （10分） (2018九上·镇海期末) 已知：如图，在中，，，点分别在，上，且 .（1）求证：；（2）若，，求的长.27. （7分）如图，AB是⊙O的直径，DO⊥AB于点O，连接DA交⊙O于点C，过点C作⊙O的切线交DO于点E，连接BC交DO于点F．（1）求证：CE=EF；（2）连接AF并延长，交⊙O于点G．填空：①当∠D的度数为________时，四边形ECFG为菱形；②当∠D的度数为________时，四边形ECOG为正方形．28. （8分） (2019八下·义乌期末) 八年级数学兴趣小组组织了以“等积变形”为主题的课题研究．第一学习小组发现：如图(1)，点A、点B在直线l1上，点C、点D在直线l2上，若l1∥l2 ，则S△ABC=S△ABD；反之亦成立．第二学习小组发现：如图(2)，点P是反比例函数y= 上任意一点，过点P作x轴、y轴的垂线，垂足为M，N，则矩形OMPN的面积为定值|k|．请利用上述结论解决下列问题：（1）如图(3)，四边形ABCD与四边形CEFG都是正方形，点E在CD上，正方形ABCD边长为2，则S△BDF=________．（2）如图(4)，点P、Q在反比例函数y= 图象上，PQ过点O，过P作y轴的平行线交x轴于点H，过Q作x轴的平行线交PH于点G，若S△PQG=8，则S△POH=________，k=________．（3）如图(5)点P、Q是第一象限的点，且在反比例函数y= 图象上，过点P作x轴垂线，过点P作y轴垂线，垂足分别是M、N，试判断直线PQ与直线MN的位置关系，并说明理由．29. （10分）(2017·江北模拟) 我市“尚品”房地产开发公司预计今年10月份将竣工一商品房小区，其中包括高层住宅区和别墅区一共60万平方米，且高层住宅区的面积不少于别墅区面积的3倍．（1）别墅区最多多少万平方米？（2）今年一月初，“尚品”公司开始出售该小区，其中高层住宅区的销售单价为8000元/平方米，别墅区的销售单价为12000元/平方米，并售出高层住宅区6万平方米，别墅区4万平方米，二月时，受最新政策“去库存，满足刚需”以及银行房贷利率打折的影响，该小区高层住宅区的销售单价比一月增加了a%，销售面积比一月增加了2a%；别墅区的销售单价比一月份减少了10%，销售面积比一月增加了a%，于是二月份该小区高层住宅区的销售总额比别墅区的销售总额多10080万元，求a的值．参考答案一、选择题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题： (共8题；共8分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、三、解答题 (共11题；共90分)19-1、20-1、21-1、22-1、23-1、23-2、23-3、24-1、24-2、25-1、25-2、26-1、26-2、27-1、27-2、28-1、28-2、28-3、29-1、29-2、。

中考衡阳数学试卷真题

中考衡阳数学试卷真题（篇幅较长，仅摘录部分内容）【篇一】字数：1522一、选择题1. 集合 A = {1, 2, 3, 4}，B = {x | x是A的元素的平方}，则 B = ______。

A. {1, 4, 9, 16}B. {1, 2, 3, 4}C. {1, 2, 3}D. {2, 3, 4}2. 化简：(3a - 2b)² - (b - a)²。

A. 8a² - 4ab + 4b²B. 8a² - 4ab - 4b²C. 8a² + 4ab - 4b²D. 8a² + 4ab + 4b²二、填空题1. 若两个数x和y满足|x - y| = 8，且x + y = 19，则x和y的值分别是______和______。

三、解答题1. 计算：3/4 ÷ 5/6。

解：将除法变成乘法，有3/4 ÷ 5/6 = 3/4 × 6/5 = 18/20 = 9/10。

2. 一个数字，该数的百、十位数的和为5，它的个位数比百位数小2，且百位数是个位数的3倍，求该数。

解：设该数的百位数为a，十位数为b，个位数为c。

根据题意，得到以下等式：a +b = 5c = a - 2a = 3c解方程组可得：a = 6，b = -1，c = 2。

因此，该数为621。

四、解答题1. 现有一地板，其长和宽分别为x米和y米，若要用正方形砖铺满整个地板，且每块砖边长为z米，若知z能整除x和y，且x、y、z之间没有其他的公因数，求砖的边长z与x、y的关系。

解：由题意可知，地板的长和宽分别为x和y，而砖的边长为z。

在地板上铺满正方形砖时，可以知道地板的长和宽都可以被砖的边长整除，即：x = nzy = mz其中，n和m是正整数。

五、计算题有一架飞机从A地沿直线飞往B地，全程400公里，飞行时间为1小时40分。

2009年湖南省衡阳市中考数学试卷及答案(word整理版)

2010年湖南省衡阳市中考数学试卷一、选择题（本大题共10小题，每小题3分，满分30分） 1、函数2-=x y 中自变量的取值范围是（）A ．0≥xB ．2≤xC ．2≥xD ．2<x2、已知空气的单位体积质量为31024.1－⨯克/厘米3，31024.1－⨯用小数表示为（） A ．0.000124 B ．0.0124C ．－0.00124D ．0.001243、下面计算正确的是（）A ． 3333=+B ．3327=÷ C ． 532=⋅ D ．24±=4、一个直角三角形的两直角边长分别为y x ，，其面积为2，则y 与x 之间的关系用图象表示大致为（）5、如图1所示几何体的左视图是（）6、如图2所示，A 、B 、C 分别表示三个村庄，AB=1000米，BC=600米， AC=800米，在社会主义新农村建设中，为了丰富群众生活，拟建一个文化活动中心，要求这三个村庄到活动中心的距离相等，则活动中心P 的位置应在（）A ．AB 中点 B ．BC 中点 C ．AC 中点D ．∠C 的平分线与AB 的交点7、已知33-=-y x ，则y x 35+-的值是（）A ．0B ．2C ．5D ．88、两圆的圆心距为3，两圆的半径分别是方程0342=+-x x 的两个根，则两圆的位置关系是（）A ．相交B ．外离C ．内含D ．外切9、如图3，菱形ABCD 的周长为20cm ，DE ⊥AB ，垂足为E ，54A cos =，则下列结论中正确的个数为（）①DE=3cm ；②EB=1cm ；③2A BCD 15S cm =菱形．A ．3个B ．2个C ．1个D ．0个10、如图4，矩形纸片ABCD 中，AB=4，AD=3，折叠纸片使AD 边与对角线BD 重合，折痕为DG ，则AG 的长为（）A ．1B ．34C ．23D ．2二、填空题（本大题共6个小题，每小题3分，满分18分．） 11、分解因式：x x 44x -23+= ．12、某人沿着有一定坡度的坡面前进了10米，此时他与水平地面的垂直距离为52米，则这个破面的坡度为．13、某果农2006年的年收入为5万元，由于党的惠农政策的落实，2008年年收入增加到7.2万元，则平均每年的增长率是．14、点A 的坐标为（2，0），把点A 绕着坐标原点顺时针旋转135º到点B ，那么点B 的坐标是． 15、如图5，四边形OABC 是边长为1的正方形，反比例函数xky =的图象过点B ，则k 的值为．16、如图6，直线AB 切⊙O 于C 点，D 是⊙O 上一点，∠EDC=30º，弦EF ∥AB ，连结OC 交EF 于H 点，连结CF ，且CF=2，则HE 的长为．三、解答题（本大题共10个小题，满分72分） 17、（6分）解下列不等式组，并把解集在数轴上表示出来．⎩⎨⎧≥+-<-　x x x )2(33)1(2)1(02图5OCABDEFH 图6A B C DA B C D图2C 图3 A 图418、（6分）先化简，再求值：212)14(-÷-+-a a a a a ，其中31=a ．19、（6分）甲、乙两人在相同的条件下各射靶5次，每次射靶的成绩情况如图7所示．（1（220、（6分）已知二次函数的图象过坐标原点，它的顶点坐标是（1，－2），求这个二次函数的关系式． 21、（7分）一个不透明口袋中装有红球6个，黄球9个，绿球3个，这些球除颜色处没有任何其他区别现．从中任意摸出一个球．（1）计算摸到的是绿球的概率．（2）如果要使摸到绿球的概率为41，需要在这个口袋中再放入多少个绿球？ 22、（7分）如图8，圆心角都是90º的扇形OAB 与扇形OCD 叠放在一起，连结AC ，BD ．（1）求证：AC=BD ；（2）若图中阴影部分的面积是2 43cm π，OA=2cm ，求OC 的长．（次）甲乙图823、（8分）如图9，△ABC中，AB=AC，AD、AE分别是∠BAC和∠BAC和外角的平分线，BE⊥AE．（1）求证：DA⊥AE；（2）试判断AB与DE是否相等？并证明你的结论．24、（8分）在一次远足活动中，某班学生分成两组，第一组由甲地匀速步行到乙地后原路返回，第二组由甲地匀速步行经乙地继续前行到丙地后原路返回，两组同时出发，设步行的时间为t（h），两组离乙地的距离分别为S1（km）和S2(km)，图10中的折线分别表示S1、S2与t之间的函数关系．（1）甲、乙两地之间的距离为km，乙、丙两地之间的距离为km；（2）求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少？（3）求图中线段AB所表示的S2与t间的函数关系式，并写出自变量t的取值范围．图9 ABC D EF25、（9分）如图11，AB 是⊙O 的直径，弦BC=2cm ，∠ABC=60º．（1）求⊙O 的直径；（2）若D 是AB 延长线上一点，连结CD ，当BD 长为多少时，CD 与⊙O 相切；（3）若动点E 以2cm/s 的速度从A 点出发沿着AB 方向运动，同时动点F 以1cm/s 的速度从B 点出发沿BC 方向运动，设运动时间为)20)((<<t s t ，连结EF ，当t 为何值时，△BEF 为直角三角形．26、（9分）如图12，直线4+-=x y 与两坐标轴分别相交于A 、B 点，点M 是线段AB 上任意一点（A 、B 两点除外），过M 分别作MC ⊥OA 于点C ，MD ⊥OB 于D ．（1）当点M 在AB 上运动时，你认为四边形OCMD 的周长是否发生变化？并说明理由；（2）当点M 运动到什么位置时，四边形OCMD 的面积有最大值？最大值是多少？（3）当四边形OCMD 为正方形时，将四边形OCMD 沿着x 轴的正方向移动，设平移的距离为)40<<a a （，正方形OCMD 与△AOB 重叠部分的面积为S ．试求S 与a 的函数关系式并画出该函数的图象．图12（1）图12（2）图12（3）图10（3）ABA图10（1）AB图10（2）2010年湖南省衡阳市中考数学试卷答案1、（ C ）2、（ D ）3、（ B ）4、（ C ）5、（ D ）6、（ A ）7、（ D ）8、（ A ）9、（ A ）10、（ C ） 11、 x(x-2)2 ．12、1：2 ．13、20% ．14、（1，－1）．15、－1 ．16、． 17、解：由（1）得：2<x由（2）得：11 3322≤-≥-≥+-　x x xx 把它们的解集在数轴上表示如下：∴原不等式组的解集是21<≤x ．18、解：原式12214-⋅-+-=a a a a a a --=14 13-=a 把31=a 代入得：原式0111313=-=-⨯=19、解：甲、乙两人射靶成绩的平均数都是6，但甲比乙的方差要小，说明甲的成绩较为稳定，所以甲的成绩比乙的成绩要好些．20、解：设这个二次函数的关系式为2)1(2--=x a y 得： 2)10(02--=a解得：2=a∴这个二次函数的关系式是2)1(22--=x y ，即x x y 422-= 21、解：（1）P （摸到绿球）61183==．(2) 设需要在这个口袋中再放入x 个绿球，得：41183=++x x解得：2=x∴需要在这个口袋中再放入2个绿球． 22、解：（1）证明：BDAC BOD AOC DO CO BO AB BOD AOC AODBOD AOD AOC COD AOB =⇒∆≅∆⇒⎪⎭⎪⎬⎫==∠=∠⇒∠+∠=∠+∠⇒∠∠ 900＝＝（2）根据题意得：360)(9036090360902222OC OA OC OA S -=-=πππ阴影；∴360)2(904322OC -=ππ解得：OC ＝1cm ．23、解：（1）证明：AEDA DAE BAF BAC ⊥⇒︒=∠⇒︒=︒⨯=∠+∠∠+∠⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫︒=∠+∠∠∠⇒∠∠∠⇒∠909018021)(21BAE BAD 180BAF BAC BAF 21BAE BAF AE BAC 21BAD BAC AD ＝＝平分＝平分（2）AB ＝DE ，理由是：DE AB D AE DAE AEB AE BE ADB BC AD BAC AD ACAB =⇒⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫︒=∠︒=∠⇒⊥︒=∠⇒⊥⇒⎭⎬⎫∠=是矩形四边形平分B 90 90 90 24、解：（2）第二组由甲地出发首次到达乙地所用的时间为：[]0.81082)28(28=÷=÷+⨯÷（小时）第二组由乙地到达丙地所用的时间为：[]0.21022)28(22=÷=÷+⨯÷（小时）（3）根据题意得A 、B 的坐标分别为（0.8，0）和（1，2），设线段AB 的函数关系式为：b kt S +=2，根据题意得： ⎩⎨⎧+=+= 28.00b k bk解得：⎩⎨⎧==-810b k ∴图中线段AB 所表示的S 2与t 间的函数关系式为：8102－t S =，自变量t 的取值范围是：10.8≤≤t ．25、解：（1）∵AB 是⊙O 的直径（已知）∴∠ACB ＝90º（直径所对的圆周角是直角） ∵∠ABC ＝60º（已知） ∴∠BAC ＝180º－∠ACB －∠ABC ＝ 30º（三角形的内角和等于180º） ∴AB ＝2BC ＝4cm （直角三角形中，30º锐角所对的直角边等于斜边的一半）即⊙O 的直径为4cm ．（2）如图10（1）CD 切⊙O 于点C ，连结OC ，则OC ＝OB ＝1/2·AB ＝2cm ．∴CD ⊥CO （圆的切线垂直于经过切点的半径） ∴∠OCD ＝90º（垂直的定义）－１０１２３图8图9AB CD EF∵∠BAC ＝ 30º（已求） ∴∠COD ＝2∠BAC ＝ 60º（在同圆或等圆中一条弧所对的圆周角等于它所对的圆心角的一半） ∴∠D ＝180º－∠COD －∠OCD ＝ 30º（三角形的内角和等于180º） ∴OD ＝2OC ＝4cm （直角三角形中，30º锐角所对的直角边等于斜边的一半） ∴BD ＝OD －OB ＝4－2＝2（cm ） ∴当BD 长为2cm ，CD 与⊙O 相切．（3）根据题意得：BE ＝（4－2t ）cm ，BF ＝tcm ；如图10（2）当EF ⊥BC 时，△BEF 为直角三角形，此时△BEF ∽△BAC ∴BE ：BA ＝BF ：BC 即：（4－2t ）：4＝t ：2 解得：t ＝1如图10（3）当EF ⊥BA 时，△BEF 为直角三角形，此时△BEF ∽△BCA ∴BE ：BC ＝BF ：BA 即：（4－2t ）：2＝t ：4 解得：t ＝1.6∴当t ＝1s 或t ＝1.6s 时，△BEF 为直角三角形．26、解：（1）设点M 的横坐标为x ，则点M 的纵坐标为－x+4（0<x<4，x>0，－x+4>0）；则：MC ＝∣－x+4∣＝－x+4，MD ＝∣x ∣＝x ； ∴C 四边形OCMD ＝2（MC+MD ）＝2（－x+4+x ）＝8∴当点M 在AB 上运动时，四边形OCMD 的周长不发生变化，总是等于8；（2）根据题意得：S 四边形OCMD ＝MC ·MD ＝（－x+4）· x ＝－x 2+4x ＝－(x-2)2+4∴四边形OCMD 的面积是关于点M 的横坐标x （0<x<4）的二次函数，并且当x ＝2，即当点M 运动到线段AB 的中点时，四边形OCMD 的面积最大且最大面积为4；（3）如图10（2），当20≤<a 时，42121422+-=-=a a S ；如图10（3），当42<≤a 时，22)4(21)4(21-=-=a a S ；∴S 与a 的函数的图象如下图所示：))4<≤a。

2010年湖南省衡阳市中考真题数学试卷(word版含答案)

2010年湖南省衡阳市初中学业水平暨高级中等学校招生考试试卷数学注意事项：1．本试卷共8页，三大题，满分100分，考试时间100分钟。

请用钢笔或圆珠笔直接答在试卷上。

参考公式：y=a x 2+bx+c(a ≠0)图像的一选择题（每小题3分，共18分）下列各小题均有四个答案，其中只有一个正确答案，请把正确答案写在题后的括号内。

1．21-的绝对值是A. 2-B. 2C. 21-D. 212.从n 个苹果和3个雪梨中，任选1个，若选中苹果的概率是12，则n 的值是（） A ． 6 B ． 3 C ． 2 D ． 13．如图，将三角尺的直角顶点放在直尺的一边上，130250∠=∠=°，°，则3∠的度数等于（） A ．50° B ．30° C ．20° D ．15°4．如图，已知⊙O 的两条弦AC ，BD 相交于点E ，∠A=70o ，∠c=50o ，那么sin ∠AEB 的值为( ) A. 21 B.33 C.22 D. 23第3题第4题1235．某农机厂四月份生产零件50万个，第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x ，那么x 满足的方程是（） A 、182)1(502=+x B ．182)1(50)1(50502=++++x x C 、50(1+2x)＝182D ．182)21(50)1(5050=++++x x6．如图6，在ABCD 中，AB=6，AD=9，∠BAD 的平分线交BC 于点E ，交DC 的延长线于点F ，BG ⊥AE ，垂足为G ，BG=24，则ΔCEF 的周长为（） A.8 B.9.5 C.10 D.11.5二填空题（每空3分，共27分）7．3的绝对值是8．1若523m x y +与3n x y 的和是单项式，则m n = ．。

9．据统计，去年我国粮食产量达10570亿斤，这个数用科学记数法可表示为亿斤．10．某校九年级（2）班（1）组女生的体重（单位：kg ）为：38，40，35，36，65，42，42，则这组数据的中位数是．11．如图所示，AB ∥CD ，∠ABE ＝66°，∠D ＝54°，则∠E 的度数为_______________．12．如图，已知双曲线)0k (xk y ＞=经过直角三角形OAB 斜边OB 的中点D ，与直角边AB 相交于点C ．若△OBC 的面积为3，则k ＝____________．第11题第12题13．如图，已知零件的外径为25mm ，现用一个交叉卡钳（两条尺长AC 和BD 相等，OC=OD ）量零件的内孔直径AB ．若OC ∶OA=1∶2，量得CD ＝10mm ，则零件的厚度_____x mm =．第13题第14题14．如图7，在Rt ABC △中，9042C AC BC ===∠°，，，分别以AC .BC 为直径画半圆，则图中阴影部分的面积为．（结果保留π）15．如下图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第n (n 是正整数)个图案中由个基础图形组成．-三解答题（本大题8个小题，共75分）16．(8分) 先化简再求值：244()33x x x x x ---÷--，其中5x =．17．（9分）已知：如图，在等边三角形ABC 的AC 边上取中点D ，BC的延长线上取一点E ，使 CE ＝ CD ．求证：BD ＝ DE ．(1) (2) (3) …… CAB18．（9分）在“首届中国西部（银川）房·车生活文化节”期间，某汽车经销商推出A B C D 、、、四种型号的小轿车共1000辆进行展销．C 型号轿车销售的成交率为50%，其它型号轿车的销售情况绘制在图1和图2两幅尚不完整的统计图中．（1）参加展销的D 型号轿车有多少辆？（2）请你将图2的统计图补充完整；（3）通过计算说明，哪一种型号的轿车销售情况最好？（4）若对已售出轿车进行抽奖，现将已售出A B C D 、、、四种型号轿车的发票（一车一票）放到一起，从中随机抽取一张，求抽到A 型号轿车发票的概率．19．（9分）为申办2010年冬奥会，须改变哈尔滨市的交通状况。

2010年湖南省衡阳市中考数学试卷及答案(word整理版)

2010年湖南省衡阳市中考数学试卷一选择题（每小题3分，共18分）1．21-的绝对值是（）A. 2-B. 2C. 21- D. 212.从个苹果和个雪梨中，任选个，若选中苹果的概率是，则的值是（）A ．B ．C ．D ．3．如图，将三角尺的直角顶点放在直尺的一边上，130250∠=∠=°，°，则3∠的度数等于（） A ．50° B ．30° C ．20° D ．15°4．如图，已知⊙O 的两条弦AC ，BD 相交于点E ，∠A=70o ，∠c=50o ，那么sin ∠AEB 的值为( )A. 21 B. 33 C.22 D. 23第3题图第4题图第6题图5．某农机厂四月份生产零件50万个，第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x ，那么x 满足的方程是（） A 、182)1(502=+x B ．182)1(50)1(50502=++++x x C 、50(1+2x)＝182D ．182)21(50)1(5050=++++x x6．如图，在ABCD 中，AB=6，AD=9，∠BAD 的平分线交BC 于点E ，交DC 的延长线于点F ，BG ⊥AE ，垂足为G ，BG=24，则ΔCEF的周长为（） A.8 B.9.5 C.10 D.11.5 二填空题（每空3分，共27分） 7．3的绝对值是8．1若523m x y +与3n x y 的和是单项式，则m n = ．。

9．据统计，去年我国粮食产量达10570亿斤，这个数用科学记数法可表示为亿斤．10．某校九年级（2）班（1）组女生的体重（单位：kg ）为：38，40，35，36，65，42，42，则这组数据的中位数是．11．如图所示，AB ∥CD ，∠ABE ＝66°，∠D ＝54°，则∠E 的度数为_______________．12．如图，已知双曲线)0k (xk y ＞=经过直角三角形OAB 斜边OB 的中点D ，与直角边AB 相交于点C ．若△OBC 的面积为3，则k ＝____________．13．如图，已知零件的外径为25mm ，现用一个交叉卡钳（两条尺长AC 和BD 相等，OC=OD ）量零件的内孔直径AB ．若OC ∶OA=1∶2，量得CD ＝10mm ，则零件的厚度_____x mm =．第11题图第12题图第13题图第14题图 14．如图7，在中，分别以.为直径画半圆，则图中阴影部分的面积为．（结果保留）15．如下图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第n (n 是正整数)个图案中由个基础图形组成．-三解答题（本大题8小题，共75分）16．(8分) 先化简再求值：244()33x x x x x ---÷--，其中5x =．17．（9分）已知：如图，在等边三角形ABC 的AC 边上取中点D ，BC 的延长线上取一点E ，使 CE ＝ CD ．求证：BD ＝ DE ．n 3112n 6321Rt ABC △9042C AC BC ===∠°，，，AC BC π (1) (2) (3) ……18．（9分）在“首届中国西部（银川）房·车生活文化节”期间，某汽车经销商推出A B C D 、、、四种型号的小轿车共1000辆进行展销．C 型号轿车销售的成交率为50%，其它型号轿车的销售情况绘制在图1和图2两幅尚不完整的统计图中．（1）参加展销的D 型号轿车有多少辆？（2）请你将图2的统计图补充完整；（3）通过计算说明，哪一种型号的轿车销售情况最好？（4）若对已售出轿车进行抽奖，现将已售出A B C D 、、、四种型号轿车的发票（一车一票）放到一起，从中随机抽取一张，求抽到A 型号轿车发票的概率．19．（9分）为申办2010年冬奥会，须改变哈尔滨市的交通状况。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2010年湖南省衡阳市初中学业水平暨高级中等学校招生考试试卷
数学
注意事项：
1．本试卷共8页，三大题，满分100分，考试时间100分钟。

请用钢
笔或圆珠笔直接答在试卷上。

参
考公式：y=a x 2+b
x+c(a ≠0)图像的
一选择题（每小题3分，共18分）
下列各小题均有四个答案，其中只有一个正确答案，请把正确答案写在题后的括号内。

1．2
1-的绝对值是
A. 2-
B. 2
C. 2
1-
D.
2
1
2.从n 个苹果和3个雪梨中，任选1个，若选中苹果的概率是12
，则n 的值是（）
A ． 6
B ． 3
C ． 2
D ． 1
3．如图，将三角尺的直角顶点放在直尺的一边上，130250∠=∠=°，°，则3∠的度数等于（） A ．50° B ．30° C ．20° D ．15° 4．如图，已知⊙O 的两条弦AC ，BD 相交于点E ，∠A=70o ，∠c=50o ，那么sin ∠AEB 的值为( ) A. 2
1 B.
3
3 C.
2
2 D.
2
3
第3题第4题
1
2
3
5．某农机厂四月份生产零件50万个，第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x ，那么x 满足的方程是（） A 、182)1(502=+x B ．182)1(50)1(50502=++++x x C 、50(1+2x)＝182
D ．182)21(50)1(5050=++++x x
6．如图6，在
ABCD 中，AB=6，AD=9，∠BAD 的平分线交BC 于点E ，交
DC 的延长线于点F ，BG ⊥AE ，垂足为G ，BG=24，则ΔCEF 的周长为（） A.8 B.9.5 C.10 D.11.5
二填空题（每空3分，共27分）
7．3的绝对值是
8．1若523m x y +与3n x y 的和是单项式，则m n = ．。

9．据统计，去年我国粮食产量达10570亿斤，这个数用科学记数法可表示为亿斤．
10．某校九年级（2）班（1）组女生的体重（单位：kg ）为：38，40，35，36，65，42，42，则这组数据的中位数是．
11．如图所示，AB ∥CD ，∠ABE ＝66°，∠D ＝54°，则∠E 的度数为_______________． 12．如图，已知双曲线)0k (x
k y ＞=
经过直角三角形
OAB 斜边OB 的中点D ，与直角
边AB 相交于点C ．若△OBC 的面积为3，则k ＝____________．
第11题第12题
13．如图，已知零件的外径为25mm ，现用一个交叉卡钳（两条尺长AC 和BD 相等，OC=OD ）量零件的内孔直径AB ．若OC ∶OA=1∶2，量得CD ＝10mm ，
则零件的厚度_____x m m =．
第13题第14题
14．如图7，在R t ABC △中，9042C A C B C ===∠°，，，分别以A C .B C 为直径画半圆，则图中阴影部分的面积为．（结果保留π）
15．如下图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第n (n 是正整数)个图案中由个基础图形组成．
-
三解答题（本大题8个小题，共
75分）
16．(8分) 先化简再求值：2
44()3
3
x x x x x ---
÷
--，其中
5x =．
17．（9分）已知：如图，在等边三角形ABC 的AC 边上取中点
D ，
BC 的延长线上取一点E ，使 CE ＝ CD ．求证：BD ＝ DE ．
(1) (2) (3) …… C
A
B
18．（9分）在“首届中国西部（银川）房·车生活文化节”期
间，某汽车经销商推出A B C D 、、、四种型号的小轿车共1000
辆进行展销．C 型号轿车销售的成交率为50%，其它型号轿车的
销售情况绘制在图1和图2两幅尚不完整的统计图中．（1
）参加展销的D 型号轿车有多少辆？（2）请你将图2的统计图补充完整；
（3）通过计算说明，哪一种型号的轿车销售情况最好？
（4）若对已售出轿车进行抽奖，现将已售出A B C D 、
、、四种型号轿车的发票（一车一票）放到一起，从中随机抽取一张，求抽到A 型号轿车发票的概率．
19．（9分）为申办2010年冬奥会，须改变哈尔滨市的交通状况。

在大直街拓宽工程中，要伐掉一棵树AB ，在地面上事先划定以B
为圆心，半径与AB 等长的圆形危险区，现在某工人站在离B 点3
米远的D 处，从C 点测得树的顶端A 点的仰角为60°，树的底部B 点
的俯角为30°.
问：距离B 点8米远的保护物是否在危险区内？9分
A
20．（9分）如图，R t ABC
△中，90
A B C
∠=°，以A B为直径的O
⊙交A C于点D，过点D的切线交B C于E．
（1）求证：
1
2
D E B C
=；
（2
）若tan2
2
C D E
==，求A D的长．
21．（10分）．如图，在正方形ABCD中，点E、F分别在BC、
CD上移动，但A到EF的距离AH始终保持与AB长相等，问在E、
F移动过程中：
（1）∠EAF的大小是否有变化？请说明理由．
（2）△ECF的周长是否有变化？请说明理由．
22．（10分）某汽车制造厂开发了一款新式电动汽车，计划一年
生产安装240辆。

由于抽调不出足够的熟练工来完成新式电动汽车的安装，工厂决定招聘一些新工人；他们经过培训后上岗，也能独立进行电动汽车的安装。

生产开始后，调研部门发现：1名熟
练工和2名新工人每月可安装8辆电动汽车；2名熟练工和3名新工人每月可安装14辆电动汽车。

（1）每名熟练工和新工人每月分别可以安装多少辆电动汽车？
（2）如果工厂招聘n （0<n <10）名新工人，使得招聘的新工人和抽调的熟练工刚好．．能完成一年的安装任务，那么工厂有哪几种．．．
新工人的招聘方案？（3）在（2）的条件下，工厂给安装电动汽车的每名熟练工每月发2000元的工资，给每名新工人每月发1200元的工资，那么工厂应招聘多少名新工人，使新工人的数量多于熟练工，同时工厂每月支出的工资总额W （元）尽可能的少？
23．（11分）已知：等边三角形ABC 的边长为4厘米，长为1
厘米的线段M N 在A B C △的边A B 上沿A B 方向以1厘米/秒的速度向B 点运动（运动开始时，点M 与点A 重合，点N 到达点B 时运动终止），过点M N 、分别作A B 边的垂线，与A B C △的其
它边交于P Q
、两点，线段M N运动的时间为t秒．
（1）线段M N在运动的过程中，t为何值时，四边形M NQP恰为矩形？并求出该矩形的面积；
（2）线段M N在运动的过程中，四边形M NQP的面积为S，运动的时间为t．求四边形M NQP的面积S随运动时间t变化的函数关系式，并写出自变量t的取值范围．
C
Q
P
A M N
C
P
Q
A M N
C
Q
P
B
A M N。