高数教案第十章重积分
同济大学(高等数学)-第十章-重积分

同济大学(高等数学)-第十章-重积分第十章重积分一元函数积分学中,我们曾经用和式的极限来上的定积分,并已经建定义一元函数()f x在区间,a b⎡⎤⎣⎦立了定积分理论,本章将把这一方法推广到多元函数的情形,便得到重积分的概念. 本章主要讲述多重积分的概念、性质、计算方法以及应用.第1节二重积分的概念与性质1.1 二重积分的概念下面我们通过计算曲顶柱体的体积和平面薄片的质量,引出二重积分的定义.1.1.1. 曲顶柱体的体积曲顶柱体是指这样的立体,它的底是x Oy平面上的一个有界闭区域D,其侧面是以D的边界为准线的母线平行于z轴的柱面,其顶部是在区域D上的连续函数(),=,且(),0z f x yf x y≥所表示的曲面(图10—1).234分为n 个小曲顶柱体.(2)在每个小闭区域上任取一点()()()1122,, ,, , ,n n ξηξηξη对第i 个小曲顶柱体的体积,用高为,()i i f ξη而底为iΔσ的平顶柱体的体积来近似代替.(3)这n 个平顶柱体的体积之和1(,)ni i ii f ξησ=∆∑ 就是曲顶柱体体积的近似值.(4)用λ表示n 个小闭区域i Δσ的直径的最大值,即()max 1i i n λd Δσ≤≤=.当0λ→ (可理解为i Δσ收缩为一点)时,上述和式的极限,就是曲顶柱体的体积:01lim (,).ni i ii V f λξησ→==∆∑ 1.1.2 平面薄片的质量设薄片在x Oy 平面占有平面闭区域D ,它在点,()x y 处的面密度是,()ρρx y =.设()0x y ρ>,且在D 上连续,求薄片的质量(见图10-3).图10-3先分割闭区域D 为n 个小闭区域n σσσ∆∆∆12,,, 在每个小闭区域上任取一点5()()()1122,, ,, , ,n n ξηξηξη 近似地,以点,()i i ξη处的面密度,()i i ρξη代替小闭区域i Δσ上各点处的面密度,则得到第i 块小薄片的质量的近似值为,()i i iρξηΔσ,于是整个薄片质量的近似值是1(,)ni i ii ρξησ=∆∑ 用()max 1i i n λd Δσ≤≤=表示n 个小闭区域i Δσ的直径的最大值,当D 无限细分,即当0λ→时,上述和式的极限就是薄片的质量M ,即01lim (,)ni i iλi M ρξηΔσ→==∑. 以上两个具体问题的实际意义虽然不同,但所求量都归结为同一形式的和的极限.抽象出来就得到下述二重积分的定义.定义1 设D 是x Oy 平面上的有界闭区域,二元函数,()z f x y =在D 上有界.将D 分为n 个小区域n σσσ∆∆∆12,,,同时用i Δσ表示该小区域的面积,记i Δσ的直径为()i d Δσ,并令()max 1i i n λd Δσ≤≤=.在i Δσ上任取一点,, 1,2,,()()i i ξηi n =,作乘积()Δ,i i i f ξησ并作和式Δ1(,)ni i ii n S f ξησ==∑. 若0λ→时,n S 的极限存在(它不依赖于D 的分法及点(,)i iεη的取法),则称这个极限值为函数,()z f x y =在D6上的二重积分,记作(,)d Df x y σ⎰⎰,即01(,)d lim (,)Δn i ii i D f x y f λσξησ→==∑⎰⎰,(10-1-1)其中D 叫做积分区域,,()f x y 叫做被积函数,d σ叫做面积元素,,d ()f x y σ叫做被积表达式,x 与y 叫做积分变量,Δ1(,)ni i ii f ξησ=∑叫做积分和. 在直角坐标系中,我们常用平行于x 轴和y 轴的直线(y =常数和x =常数)把区域D 分割成小矩形,它的边长是x ∆和Δy ,从而ΔΔΔσx y =⋅,因此在直角坐标系中的面积元素可写成d dx dy σ=⋅,二重积分也可记作01(,)d d lim (,)ni i ii D f x y x y f λξησ→==∆∑⎰⎰. 有了二重积分的定义,前面的体积和质量都可以用二重积分来表示.曲顶柱体的体积V 是函数,()z f x y =在区域D 上的二重积分(,)d DV f x y σ=⎰⎰;薄片的质量M 是面密度,()ρρx y =在区域D 上的二重积分(,)d DM x y ρσ=⎰⎰.因为总可以把被积函数,()z f x y =看作空间的一曲面,所以当,()f x y 为正时,二重积分的几何意义就是曲顶柱体的体积;当,()f x y 为负时,柱体就在x Oy 平面下方,二重积分就是曲顶柱体体积的负值. 如果,()f x y 在某部分区域上是正的,而在其余的部分区域7上是负的,那么,()f x y 在D 上的二重积分就等于这些部分区域上柱体体积的代数和.如果,()f x y 在区域D 上的二重积分存在(即和式的极限(10-1-1)存在),则称,()f x y 在D 上可积.什么样的函数是可积的呢?与一元函数定积分的情形一样,我们只叙述有关结论,而不作证明.如果,()f x y 是闭区域D 上连续,或分块连续的函数,则,()f x y 在D 上可积.我们总假定,()z f x y =在闭区域D 上连续,所以,()f x y 在D 上的二重积分都是存在的,以后就不再一一加以说明.1.1.3 二重积分的性质设二元函数,,,()()f x y g x y 在闭区域D 上连续,于是这些函数的二重积分存在.利用二重积分的定义,可以证明它的若干基本性质.下面列举这些性质.性质1 常数因子可提到积分号外面.设k 是常数,则(,)d (,)d D Dkf x y k f x y σσ=⎰⎰⎰⎰.性质 2 函数的代数和的积分等于各函数的积分的代数和,即[]()()d ()d ()d D D Df x yg x y f x y g x y σσσ±=±⎰⎰⎰⎰⎰⎰,,,,.8性质3 设闭区域D 被有限条曲线分为有限个部分闭区域,则D 上的二重积分等于各部分闭区域上的二重积分的和.例如D 分为区域1D 和2D (见图10-4),则12(,)d (,)d (,)d D D D f x y f x y f x y σσσ=+⎰⎰⎰⎰⎰⎰. (10-1-2)图10-4性质3表示二重积分对积分区域具有可加性. 性质4 设在闭区域D 上,1()f x y =,σ为D 的面积,则1d d D D σσσ==⎰⎰⎰⎰.从几何意义上来看这是很明显的.因为高为1的平顶柱体的体积在数值上就等于柱体的底面积.性质5 设在闭区域D 上有,,()()f x y g x y ≤,则(,)d (,)d D Df x yg x y σσ≤⎰⎰⎰⎰.由于 (,)(,)(,)f x y f x y f x y -≤≤又有(,)d (,)d D D f x y f x y σσ≤⎰⎰⎰⎰.9这就是说,函数二重积分的绝对值必小于或等于该函数绝对值的二重积分.性质 6 设、M m 分别为()f x y ,在闭区域D 上的最大值和最小值,σ为D 的面积,则有(,)d Dm f x y M σσσ≤≤⎰⎰.上述不等式是二重积分估值的不等式.因为()m f x y M ≤≤,,所以由性质5有d (,)d d D D Dm f x y M σσσ≤≤⎰⎰⎰⎰⎰⎰,即 d (,)d d D D D m m f x y M M σσσσσ=≤≤=⎰⎰⎰⎰⎰⎰.性质7 设函数,()f x y 在闭区域D 上连续,σ是D 的面积,则在D 上至少存在一点,()ξη使得(,)d ()Df x y f σξησ=⋅⎰⎰,.这一性质称为二重积分的中值定理.证 显然0σ≠.因,()f x y 在有界闭区域D 上连续,根据有界闭区域上连续函数取到最大值、最小值定理,在D 上必存在一点()11x y ,使()11f x y ,等于最大值M ,又存在一点22()x y ,使22()f x y ,等于最小值m ,则对于D 上所有点,()x y ,有()()()2211.m f x y f x y f x y M =≤≤=,,,由性质1和性质5,可得d (,)d d D D Dm f x y M σσσ≤≤⎰⎰⎰⎰⎰⎰.10 再由性质4得(,)d D m f x y M σσσ≤≤⎰⎰,或 1(,)d Dm f x y M σσ≤≤⎰⎰.根据闭区域上连续函数的介值定理知,D 上必存在一点,()ξη,使得1(,)d ()Df x y f σξησ=⎰⎰,, 即(,)d ()D f x y f σξησ=⎰⎰,,,()ξηD ∈.证毕.二重积分中值定理的几何意义可叙述如下: 当:,()S z f x y =为空间一连续曲面时,对以S 为顶的曲顶柱体,必定存在一个以D 为底,以D 内某点,()ξη的函数值,()f ξη为高的平顶柱体,它的体积,()f ξησ⋅就等于这个曲顶柱体的体积.习题10—11.根据二重积分性质,比较ln()d D x y σ+⎰⎰与[]2ln()d Dx y σ+⎰⎰的大小,其中(1)D 表示以10,()、1,0()、1,1()为顶点的三角形;(2)D 表示矩形区域(){}|35,2,0x y x y ≤≤≤≤.2.根据二重积分的几何意义,确定下列积分的值:(1)(22d Da x y σ+⎰⎰,()222{|}D x y x y a =+≤,;(2)Dσ,()222{|}D x y xy a =+≤,.3.设(),f x y 为连续函数,求21lim (,)d πr Df x y rσ→⎰⎰,()()()22200{,}D x y x x y y r =-+-≤|.4.根据二重积分性质,估计下列积分的值:(1)DI σ=,()22{|00}D x y x y =≤≤≤≤,,;(2)22sinsin d DI x y σ=⎰⎰,()ππ{,|00}D x y x y =≤≤≤≤,; (3)()2249d DI xy σ=++⎰⎰,()224{,|}D x y x y =+≤.5.设[][]0,10,1D =⨯,证明函数()()()()1,,,,,为内有理点即均为有理数,,为内非有理点0x y D x y f x y x y D ⎧⎪=⎨⎪⎩在D 上不可积.第2节 二重积分的计算只有少数二重积分(被积函数和积分区域特别简单)可用定义计算外,一般情况下要用定义计算二重积分相当困难.下面我们从二重积分的几何意义出发,来介绍计算二重积分的方法,该方法将二重积分的计算问题化为两次定积分的计算问题.2.1 直角坐标系下的计算在几何上,当被积函数(),0f x y ≥时,二重积分(,)d Df x y σ⎰⎰的值等于以D 为底,以曲面,()z f x y =为顶的曲顶柱体的体积.下面我们用“切片法”来求曲顶柱体的体积V .设积分区域D 由两条平行直线,x a x b ==及两条连续曲线()()y x y x ϕϕ==12,(见图10—5)所围成,其中()()a b x x ϕϕ<<12,,则D 可表示为()()(){}12,,|D x y a x b φx y φx =≤≤≤≤.图10—5用平行于y Oz 坐标面的平面()0x x a x b =≤≤去截曲顶柱体,得一截面,它是一个以区间()()12x x φφ⎡⎤⎣⎦,为底,以,0()z f x y =为曲边的曲边梯形(见图10—6),所以这截面的面积为()d 2010()()(,)φx φx f x y y A x =⎰.图10—6由此,我们可以看到这个截面面积是0x 的函数.一般地,过区间[,]a b 上任一点且平行于y Oz 坐标面的平面,与曲顶柱体相交所得截面的面积为()d 21()()(,)φx φx f x y A y x =⎰,其中y 是积分变量,x 在积分时保持不变.因此在区间[,]a b 上,()A x 是x 的函数,应用计算平行截面面积为已知的立体体积的方法,得曲顶柱体的体积为d d d 21()()()(,)bbφx aaφx A x x f x y V y x ⎡⎤=⎢⎥⎣=⎦⎰⎰⎰, 即得21()()(,)d (,)d d b x a x Df x y f x y y xϕϕσ⎡⎤=⎢⎥⎣⎦⎰⎰⎰⎰, 或记作21()()(,)d d (,)d bx a x Df x y x f x y yϕϕσ=⎰⎰⎰⎰.上式右端是一个先对y ,后对x 积分的二次积分或累次积分.这里应当注意的是:做第一次积分时,因为是在求x 处的截面积()A x ,所以x 是,a b 之间任何一个固定的值,y 是积分变量;做第二次积分时,是沿着x 轴累加这些薄片的体积()A x dx ⋅,所以x 是积分变量.在上面的讨论中,开始假定了,()0f x y ≥,而事实上,没有这个条件,上面的公式仍然正确.这里把此结论叙述如下:若,()z f x y =在闭区域D 上连续,()():D a x b x y x ϕϕ≤≤≤≤12,,则21()()(,)d d d (,)d bx ax Df x y x y x f x y y ϕϕ=⎰⎰⎰⎰. (10-2-1)类似地,若,()z f x y =在闭区域D 上连续,积分区域D 由两条平行直线y a y b ==,及两条连续曲线()()x y x y ϕϕ==12,(见图10—7)所围成,其中()()c d x x ϕϕ<<12,,则D 可表示为()()(){},|D x y c y d y x y ϕϕ=≤≤≤≤12,.则有21()()(,)d d d (,)d dx cx Df x y x y y f x y x ϕϕ=⎰⎰⎰⎰. (10-2-2)图10—7以后我们称图10-5所示的积分区域为X 型区域,X 型区域D 的特点是:穿过D 内部且平行于y 轴的直线与D 的边界的交点不多于两个.称图10—7所示的积分区域为Y 型区域,Y 型区域D 的特点是:穿过D 内部且平行于x 轴的直线与D 的边界的交点不多于两个.从上述计算公式可以看出将二重积分化为两次定积分,关键是确定积分限,而确定积分限又依赖于区域D 的几何形状.因此,首先必须正确地画出D 的图形,将D 表示为X 型区域或Y 型区域.如果D 不能直接表示成X 型区域或Y 型区域,则应将D 划分成若干个无公共内点的小区域,并使每个小区域能表示成X 型区域或Y 型区域,再利用二重积分对区域具有可加性相加,区域D 上的二重积分就是这些小区域上的二重积分之和(图10—8).图10-8例1 计算二重积分d Dxy σ⎰⎰,其中D 为直线y x =与抛物线2y x =所包围的闭区域.解 画出区域D 的图形,求出y x =与2y x =两条曲线的交点,它们是()0,0及()1,1.区域D (图10—9)可表示为:20.x x y x ≤≤≤≤1,图10—9因此由公式(10-2-1)得()221120d d d 2x x xxDx xy x x ydy y xσ==⎰⎰⎰⎰⎰d 135011()224x x x -==⎰.本题也可以化为先对x ,后对y 的积分,这时区域D 可表为:1,0y y y x ≤≤≤≤.由公式(10-2-2)得1d d d yyDxy y y x x σ=⎰⎰⎰⎰.积分后与上面结果相同.例2 计算二重积分221d Dyx y σ+-⎰⎰,其中D 是由直线,1y x x ==-和1y =所围成的闭区域.解 画出积分区域D ,易知D :11,1x x y -≤≤≤≤ (图10-10),若利用公式(10-2-1),得图10-1011222211d (1d )d xDy x y y x y y xσ-+-=+-⎰⎰⎰⎰()d 1312221113xx y x -⎡=⎤-+-⎢⎥⎣⎦⎰()d 113310121(33x x -=--=--⎰⎰x 12=.若利用公式(10-2-2),就有()1222211d 1d d Dx y y x y x yσ--+-=+-⎰⎰⎰⎰,也可得同样的结果.例3 计算二重积分22d Dxyσ⎰⎰,其中D 是直线2,y y x==和双曲线1x y =所围之闭区域.解 求得三线的三个交点分别是1,(1,1)2,2⎛⎫ ⎪⎝⎭及2,2().如果先对y 积分,那么当121x ≤≤时,y 的下限是双曲线1y x =,而当12x ≤≤时,y 的下限是直线y x =,因此需要用直线x =1把区域D 分为1D 和2D 两部分(图10—11).1211, 21:D x y x≤≤≤≤; 22, 2:1D x x y ≤≤≤≤.图10—11于是12222221222112222212d d d d d d d x x DD D x x x x x x y x yy y y y y σσσ=+=+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰d d 2222121112x x x x x xy y ⎡⎤⎡⎤=-+-⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰ d d 2212311222x x x x x x⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭⎰⎰ 1243231124626x x x x ⎡⎤⎡⎤=-+-⎢⎥⎢⎥⎣⎦⎣⎦812719264==.如果先对x 积分,那么:12, 1 D y x y y≤≤≤≤,于是 223221222111d d d d 3yy y Dy x x x y x y y y y σ⎡⎤==⎢⎥⎣⎦⎰⎰⎰⎰⎰ d 22254111136312y y y y y ⎡⎤⎡⎤=-=+⎢⎥⎢⎥⎣⎦⎣⎦⎰2764=.由此可见,对于这种区域D ,如果先对y 积分,就需要把区域D 分成几个区域来计算.这比先对x 积分繁琐多了.所以,把重积分化为累次积分时,需要根据区域D 和被积函数的特点,选择适当的次序进行积分.例4 设,()f x y 连续,求证d d d d (,)(,)bxbbaaayx f x y y y f x y x =⎰⎰⎰⎰.证 上式左端可表为d d d (,)(,)b xaaDx f x y y f x y σ=⎰⎰⎰⎰,其中,:D a x b a y x ≤≤≤≤ (图10—12)区域D 也可表为:,a y b y x b ≤≤≤≤,图10—12于是改变积分次序,可得(,)d d (,)d bbayDf x y y f x y xσ=⎰⎰⎰⎰由此可得所要证明的等式.例5 计算二重积分d sin Dxσx⎰⎰,其中D 是直线y x =与抛物线2y x =所围成的区域. 解 把区域D 表示为x型区域,即(){}2D =x ,y |0x 1,x y x ≤≤≤≤.于是d d d d 221100sin sin sin xx x x Dxx x σx y y x x x x ⎛⎫== ⎪⎝⎭⎰⎰⎰⎰⎰()sin d 11x x x=-⎰()10cos cos sin x x x x =-+-1sin 10.1585=-≈ 注:如果化为y 型区域即先对x 积分,则有d d d 1sin sin yyDx xσy x x x =⎰⎰⎰⎰.由于sin x x的原函数不能由初等函数表示,往下计算就困难了,这也说明计算二重积分时,除了要注意积分区域D 的特点(区分是x 型区域,还是y 型区域)外,还应注意被积函数的特点,并适当选择积分次序.2.2 二重积分的换元法与定积分一样,二重积分也可用换元法求其值,但比定积分复杂得多.我们知道,对定积分()d b af x x ⎰作变量替换()x φt =时,要把()f x 变成()()f φt ,d x 变成d ()φt t ',积分限,a b 也要变成对应t 的值.同样,对二重积分(),d Df x y σ⎰⎰作变量替换()(),,,,x x u v y y u v ⎧=⎪⎨=⎪⎩时,既要把(),f x y 变成()()(),,,f x u v y u v ,还要把x Oy 面上的积分区域D 变成uOv 面上的区域uvD ,并把D 中的面积元素d σ变成uvD 中的面积元素d *σ.其中最常用的是极坐标系的情形.2.2.1 极坐标系的情形下面我们讨论利用极坐标变换,得出在极坐标系下二重积分的计算方法.把极点放在直角坐标系的原点,极轴与x 轴重合,那么点P 的极坐标(),P r θ与该点的直角坐标(),P x y 有如下互换公式:πcos ,sin ;0,02x r θy r θr θ==≤<+∞≤≤;22,arctan ;,yr x y θx y x=+=-∞<<+∞. 我们知道,有些曲线方程在极坐标系下比较简单,因此,有些二重积分(),d Df x y σ⎰⎰用极坐标代换后,计算起来比较方便,这里假设(),z f x y =在区域D 上连续.在直角坐标系中,我们是以平行于x 轴和y 轴的两族直线分割区域D 为一系列小矩形,从而得到面积元素d d d σx y =.在极坐标系中,与此类似,我们用“常数r =”的一族同心圆,以及“常数θ=”的一族过极点的射线,将区域D 分成n 个小区域(),1,2,,ijσi j n ∆=,如图10—13所示.图10—13小区域面积()2212ij i i j i j σr r θr θ⎡⎤∆=+∆∆-∆⎣⎦212i i j i jr r θr θ=∆∆+∆∆.记 ()()()22,,1,2,,iji j ρr θi j n ∆=∆+∆=,则有 ()ij i i j ijσr r θορ∆=∆∆+∆,故有d d d σr r θ=.则()()DD⎰⎰⎰⎰这就是直角坐标二重积分变换到极坐标二重积分的公式.在作极坐标变换时,只要将被积函数中的,x y 分别换成cos ,sin r θr θ,并把直角坐标的面积元素d d d σx y =换成极坐标的面积元素d d r r θ即可.但必须指出的是:区域D 必须用极坐标系表示.在极坐标系下的二重积分,同样也可以化为二次积分计算.下面分三种情况讨论:(1) 极点O 在区域D 外部,如图10—14所示.图10—14设区域D 在两条射线,θαθβ==之间,两射线和区域边界的交点分别为,A B ,将区域D 的边界分为两部分,其方程分别为()()12,r r θr r θ==且均为[],αβ上的连续函数.此时()()(){}12,|,D r θr θr r θαθβ=≤≤≤≤.于是()()()()d d d d 21cos ,sin cos ,sin βr θαr θDf r θr θr r θθf r θr θr r =⎰⎰⎰⎰(2) 极点O 在区域D 内部,如图10—15所示.若区域D 的边界曲线方程为()r r θ=,这时积分区域D 为()(){}且()r θ在π0,2⎡⎤⎣⎦上连续.图10—15于是()()()πd d d d 200cos ,sin cos ,sin r θDf r θr θr r θθf r θr θr r=⎰⎰⎰⎰.(3) 极点O 在区域D 的边界上,此时,积分区域D 如图10—16所示.图10—16()(){},|,0D r θαθβr r θ=≤≤≤≤, 且()r θ在π0,2⎡⎤⎣⎦上连续,则有()()()d d d d 0cos ,sin cos ,sin βr θαDf r θr θr r θθf r θr θr r=⎰⎰⎰⎰.在计算二重积分时,是否采用极坐标变换,应根据积分区域D 与被积函数的形式来决定.一般来说,当积分区域为圆域或部分圆域,及被积函数可表示为()22f x y +或y f x ⎛⎫ ⎪⎝⎭等形式时,常采用极坐标变换,简化二重积分的计算.例6 计算二重积分22221d d 1Dx y I x yx y --=++⎰⎰,其中()(){}222,|01D x y x y a a =+≤<<.解 在极坐标系中积分区域D 为(){}π,|0,02D r θr a θ=≤≤≤≤,则有2222π22211d d d d 11aDx y r I x y r r x y rθ---==+++⎰⎰⎰⎰ 222200211πd πd 11aa t r t r r r t r t--=+-=⎰⎰令()()22220πarcsin 1πarcsin 11a t ta a =+-=+--.例7 计算二重积分2d Dxy σ⎰⎰,其中D 是单位圆在第I 象限的部分.解 采用极坐标系. D可表示为π, 1002θr ≤≤≤≤(图10-17),图10-17于是有π12222d d cos sin d Dxy r r r r σθθθ=⋅⋅⎰⎰⎰⎰ πd d 12421cos sin 15θθθr r ==⎰⎰.例8 计算二重积分Dx σ⎰⎰2d ,其中D 是二圆221xy +=和224x y +=之间的环形闭区域.解 区域D :2,120θπr ≤≤≤≤,如图10—18所示.图10—18于是2π22π22230111cos 215d cos d d d π24Dx r r r r r θσθθθ+=⋅==⎰⎰⎰⎰⎰⎰2d .2.2.2. 直角坐标系的情形我们先来考虑面积元素的变化情况.设函数组,,,()()x x u v y y u v ==为单值函数,在uvD 上具有一阶连续偏导数,且其雅可比行列式(,)0(,)J x y u v ∂≠∂=, 则由反函数存在定理,一定存在着D 上的单值连续反函数,,,()()u u x y v v x y ==.这时uvD 与D 之间建立了一一对应关系,uOv 面上平行于坐标轴的直线在映射之下成为x Oy 面上的曲线,,,0()()u x y u v x y v ==.我们用uOv 面上平行于坐标轴的直线,1,,,1,,,(2;2)i j u u v v i n j m ====将区域uvD 分割成若干个小矩形,则映射将uOv 面上的直线网变成x Oy 面上的曲线网(图10—19).图10—19在uv D 中任取一个典型的小区域ΔuvD (面积记为*Δσ)及其在D 中对应的小区域ΔD (面积记为Δσ),如图10—20所示.图10—20设ΔD 的四条边界线的交点为1211322,,,,,0()()()P x y P x x y y P x x y y +∆+∆+∆+∆和ΔΔ433,0()P x x y y ++.当ΔΔ,u v 很小时,()ΔΔ123,,,iix y i =也很小,ΔD 的面积可用12P P 与14P P 构成的平行四边形面积近似.即Δ1214P P P P σ⨯≈.而 ()()ΔΔ1112x y P P =+i j()()()ΔΔ[][]00000000,,,(,x u u v x u v y u u v y u v =+-++-i j()()ΔΔ[][]0000,,u u x u v u y u v u ≈'+'i j.同理()()ΔΔ[][]001400,,v v P P x u v v y u v v ≈'+'i j.从而得ΔΔΔΔΔ1214y xu u u u P P P σP y x v v vv∂∂∂∂⨯=∂∂∂=∂的绝对值*(,)(,)(,)(,)x y x y Δu Δv u v u v Δσ∂∂==∂∂.因此,二重积分作变量替换,,,()()x x u v y y u v ==后,面积元素d σ与d *σ的关系为*(,),(,)x y d d u v σσ∂=∂ 或(,)(,)x y dxdy dudv u v ∂=∂.由此得如下结论:定理 1 若,()f x y 在x Oy 平面上的闭区域D 上连续,变换:,,,()()T x x u v y y u v ==,将uOv 平面上的闭区域uvD 变成x Oy 平面上的D ,且满足:(1),,,()()x u v y u v 在uvD 上具有一阶连续偏导数, (2)在uvD 上雅可比式(0(,),)x y J u v ∂∂=≠;(3)变换:uvT DD→是一对一的,则有[](,)d d (,),(,)d d .uvDD f x y x y f x u v y u v J u v =⎰⎰⎰⎰例9 计算二重积分e d d y x y x Dx y -+⎰⎰,其中D 是由x 轴,y 轴和直线2x y +=所围成的闭区域.解 令,u y x v y x =-=+,则,22x y v u v u -==+. 在此变换下,x Oy 面上闭区域D 变为uOv 面上的对应区域D '(图10—21).图10—21雅可比式为11(,)122(,)21122x y u v J -∂==-∂=, 则得1ed de d d 2y x u y xvDD x y u v -+'=-⎰⎰⎰⎰-1d e d (e e )22001122uv v v v u -==-⎰⎰⎰e e 1=--.例10 设D 为x Oy 平面内由以下四条抛物线所围成的区域:222,,x ay x by y px ===,2y qx =,其中<<, <<00a b p q ,求D 的面积.解 由D 的构造特点,引入两族抛物线22,y ux x vy ==,则由u 从p 变到q ,v 从a 变到b 时,这两族抛物线交织成区域D '(图10—22).图10—22雅可比行列式为(,)1(,)(,)(,)J x y u v u v x y ∂=∂∂∂= 222211322y y x x x x yy==---,则所求面积()()11d d d d 33D D S x y u v b a q p '===--⎰⎰⎰⎰.习题10—21.画出积分区域,把(,)d Df x y σ⎰⎰化为二次积分:(1)()1,1,{,0}D x y x y y x y =+≤-≤≥|;(2)()22{,}D x y y x x y =≥-≥|,.2.改变二次积分的积分次序: (1)2d d 22(,)yy y f x y x⎰⎰;(2)e1d d ln 0(,)xx f x y y ⎰⎰;(3)()220,xxdx f x y dy⎰⎰; (4)1-1d (,)d x f x y y ⎰.3.设(,)f x y 连续,且(,)(,)d Df x y xy f x y σ=+⎰⎰,其中D 是由直线0,1y x ==及曲线2y x =所围成的区域,求(,).f x y4.计算下列二重积分:(1)()22Dx y d σ+⎰⎰,(){},|1,1D x y x y =≤≤;(2)d sin Dxσx⎰⎰,其中D 是直线y x =与抛物线y x π=所围成的区域;(3)Dσ,(){}22,|D x y xy x =+≤;(4)22-y ed d ⎰⎰Dx x y,D 是顶点分别为()0,0O ,(),11A ,()0,1B 的三角形闭区域.5.求由坐标平面及2,3,4x y x y z ==++=所围的角柱体的体积.6.计算由四个平面0,0,1,1x y x y ====所围的柱体被平面0z =及236x y z ++=截得的立体的体积.7.在极坐标系下计算二重积分: (1)d Dx y ⎰⎰, ()ππ22224{,|}D x y x y =≤+≤;(2)()d d D x y x y +⎰⎰,(){},|22D x y x y x y =+≤+; (3)d d Dxy x y ⎰⎰,其中D 为圆域222x y a +≤;(4)22ln(1)d d Dxy x y++⎰⎰,其中D 是由圆周221xy +=及坐标轴所围成的在第一象限内的闭区域.8. 将下列积分化为极坐标形式:(1) 2d d 22)x x y y +⎰a;(2) d 0xx y ⎰⎰a.9.求球体2222x y z R ++≤被圆柱面222x y Rx +=所割下部分的体积.10.作适当坐标变换,计算下列二重积分:(1)22d d Dx x y y⎰⎰,由12,,xy x y x ===所围成的平面闭区域; (2)d d y x yDex y+⎰⎰,(){,|0,0}1,D x y x y x y =+≤≥≥;(3)d Dx y , 其中D 是椭圆22221y x a b +=所围成的平面闭区域;(4)()()sin d d Dx y x y x y +-⎰⎰,(){,|0,0}D x y x y x y ππ=≤+≤≤-≤.11.设闭区域D 由直线100,,x y x y +===所围成,求证:1cos d d sin1.2Dx y x y x y +⎛⎫= ⎪-⎝⎭⎰⎰ 12.求由下列曲线所围成的闭区域的面积:(1) 曲线334,8,5,15xy xy xy xy ====所围成的第一象限的平面闭区域;(2) 曲线,,,x y a x y b y x y x αβ+=+===所围的闭区域0,0()a b αβ<<<<.第3节 三重积分3.1 三重积分的概念三重积分是二重积分的推广,它在物理和力学中同样有着重要的应用.在引入二重积分概念时,我们曾考虑过平面薄片的质量,类似地,现在我们考虑求解空间物体的质量问题.设一物体占有空间区域Ω,在Ω中每一点,,()x y z 处的体密度为,,()ρx y z ,其中,,()ρx y z 是Ω上的正值连续函数.试求该物体的质量.先将空间区域Ω任意分割成n 个小区域12, , , nΔv Δv Δv(同时也用iΔv 表示第i 个小区域的体积).在每个小区域i Δv 上任取一点,,()i i iξηζ,由于,,()ρx y z 是连续函数,当区域iΔv 充分小时,密度可以近似看成不变的,且等于在点,,()i i i ξηζ处的密度,因此每一小块iΔv 的质量近似等于,,()i i i iρξηζΔv ,物体的质量就近似等于1(,,)ni i ii ρξηζΔv =∑i .令小区域的个数n 无限增加,而且每个小区域iΔv 无限地收缩为一点,即小区域的最大直径()max 10ii nλd Δv ≤≤=→时,取极限即得该物体的质量1lim (,,)ni i iλi ρξηζΔv M →==∑i .由二重积分的定义可类似给出三重积分的定义:定义1 设Ω是空间的有界闭区域,,,()f x y z 是Ω上的有界函数,任意将Ω分成n 个小区域12,,,nΔv Δv Δv ,同时用i Δv 表示该小区域的体积,记iΔv 的直径为()id Δv ,并令()max 1i i nλd Δv ≤≤=,在i Δv 上任取一点,,()i i iξηζ,1,2,,()i n =,作乘积,,()i i i if ξηζΔv ,把这些乘积加起来得和式1(,,)n i i ii f ξηζΔv =∑i ,若极限01lim (,,)ni i iλi f ξηζΔv →=∑i 存在(它不依赖于区域Ω的分法及点(,,)iiiξηζ的取法),则称这个极限值为函数,,()f x y z 在空间区域Ω上的三重积分,记作(),,f x y z dv Ω⎰⎰⎰,即 ()01,,lim (,,)ni i i ii f x y z dv f v λξηζ→=Ω=∆∑⎰⎰⎰,其中,,()f x y z 叫做被积函数,Ω叫做积分区域,d v 叫做体积元素.在直角坐标系中,若对区域Ω用平行于三个坐标面的平面来分割,于是把区域分成一些小长方体.和二重积分完全类似,此时三重积分可用符号(),,d d d f x y z x y z Ω⎰⎰⎰来表示,即在直角坐标系中体积元素d v可记为d d d x y z .有了三重积分的定义,物体的质量就可用密度函数,,()ρx y z 在区域Ω上的三重积分表示,即(),,M x y z dv Ωρ=⎰⎰⎰,如果在区域Ω上,,1()f x y z =,并且Ω的体积记作V ,那么由三重积分定义可知1d v dv V ΩΩ==⎰⎰⎰⎰⎰⎰.这就是说,三重积分dv Ω⎰⎰⎰在数值上等于区域Ω的体积.三重积分的存在性和基本性质,与二重积分相类似,此处不再重述.3.2 三重积分的计算 为简单起见,在直角坐标系下,我们采用微元分析法来给出计算三重积分的公式.三重积分(,,)d f x y z v Ω⎰⎰⎰表示占空间区域Ω的物体的质量.设Ω是柱形区域,其上、下分别由连续曲面()()z z x y z z x y ==12,,,所围成,它们在x Oy 平面上的投影是有界闭区域D ;Ω的侧面由柱面所围成,其母线平行于z 轴,准线是D 的边界线.这时,区域Ω可表示为(){}12,,, ,,,|()()()Ωx y z z x y z z x y x y D =≤≤∈ 先在区域D 内点,()x y 处取一面积微元d d d σx y =,对应地有Ω中的一个小条,再用与x Oy 面平行的平面去截此小条,得到小薄片(图10—23).图10—23于是以d σ为底,以dz 为高的小薄片的质量为,,d d d ()f x y z x y z .把这些小薄片沿z 轴方向积分,得小条的质量为d d d 21(,)(,)(,,)z x y z x y f x y z z x y ⎡⎤⎢⎥⎣⎦⎰. 然后,再在区域D 上积分,就得到物体的质量21(,)(,)(,,)d d d z x y z x y Df x y z z x y ⎡⎤⎢⎥⎣⎦⎰⎰⎰. 也就是说,得到了三重积分的计算公式(),,f x y z dv Ω⎰⎰⎰=21(,)(,)(,,)d d d z x y z x y Df x y z z x y ⎡⎤⎢⎥⎣⎦⎰⎰⎰21(,)(,)d d (,,)d z x y z x y Dx y f x y z z=⎰⎰⎰.(10-3-1)例1 计算三重积分d d d x x y z Ω⎰⎰⎰,其中Ω是三个坐标面与平面1x y z ++=所围成的区域(图10—24).图10—24解 积分区域Ω在x Oy 平面的投影区域D 是由坐标轴与直线1x y +=围成的区域:10x ≤≤,10y x ≤≤-,所以11110d d d d d d d d d x yxx yDx x y z x y x z x y x z -----Ω==⎰⎰⎰⎰⎰⎰⎰⎰⎰ d d 110(1)xx x x y y --=-⎰⎰d 21(1)1224x x x -==⎰.例2 计算三重积分d z vΩ⎰⎰⎰,其中2222:,,, 000Ωx y z x y z R ≥≥≥++≤(见图10—25).图10—25解 区域Ω在x Oy 平面上的投影区域222:,,00D x y x y R ≥≥+≤.对于D 中任意一点,()x y ,相应地竖坐标从0z =变到222R x z y --=.因此,由公式(10-3-1),得()2222221d d d d d d 2R x y DDz v x y z R x y x y --Ω==--⎰⎰⎰⎰⎰⎰⎰ π01d d 2222()R θR ρρρ-=⎰⎰221π240224RρρR ⎛⎫⋅⋅- ⎪ ⎪⎭=⎝π416R =.三重积分化为累次积分时,除上面所说的方法外,还可以用先求二重积分再求定积分的方法计算.若积分区域Ω如图10-26所示,它在z 轴的投影区间为[,]A B ,对于区间内的任意一点z ,过z 作平行于x Oy 面的平面,该平面与区域Ω相交为一平面区域,记作D (z ).这时三重积分可以化为先对区域()D z 求二重积分,再对z 在[]A B ,上求定积分,得()(,,)d d (,,)d d BAD z f x y z v z f x y z x y Ω=⎰⎰⎰⎰⎰⎰.(10-3-2)图10—26我们可利用公式(10-3-2)重新计算例2中的积分.区域Ω在z 轴上的投影区间为[,]0R ,对于该区间中任意一点z ,相应地有一平面区域():,00D z x y ≥≥与2222R x y z +≤-与之对应.由公式(10-3-2),得()zd d d d RD z v z z x y Ω=⎰⎰⎰⎰⎰⎰.求内层积分时,z 可以看作常数:并且()2222:R D z x y z +≤-是14个圆,其面积为()π224R z =-,所以 ()01πzd π416Rv =z R z z R Ω⋅-=⎰⎰⎰⎰224d . 例3 计算三重积分2d z v Ω⎰⎰⎰,其中:1222222y x z a b Ωc+≤+.解 我们利用公式(10-3-2)将三重积分化为累次积分.区域Ω在z 轴上的投影区间为[,]c c -,对于区间内任意一点z ,相应地有一平面区域()D z :122222222(1)(1)y xz za b c c --≤+ 与之相应,该区域是一椭圆(图10—27),其面积为π221z c ab ⎛⎫- ⎪⎝⎭.所以22222()d d d d π1d ccc c D z z z v =z z x y abz z c --Ω⎛⎫=- ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰π3415abc =π3415abc =.图10—27 3.3 三重积分的换元法对于三重积分(,,)f x y z dv Ω⎰⎰⎰作变量替换:(,,)(,,)(,,)x x r s t y y r s t z z r s t =⎧⎪=⎨⎪=⎩它给出了Orst 空间到Ox yz 空间的一个映射,若()()(),,,,,,,,x r s t y r s t z r s t 有连续的一阶偏导数,且(,,)(,,)0x y z r s t ∂≠∂,则建立了Orst 空间中区域*Ω和Ox yz 空间中相应区域Ω的一一对应,与二重积分换元法类似,我们有d d d d (,,)(,,)x y z r s t v r s t ∂∂=. 于是,有换元公式[]*(,,)(,,)(,,),(,,),(,,)d d d (,,)x y z f x y z dv f x r s t y r s t z r s t r s tr s t ΩΩ∂=⋅∂⎰⎰⎰⎰⎰⎰.作为变量替换的实例,我们给出应用最为广泛的两种变换:柱面坐标变换及球面坐标变换.3.3.1 柱面坐标变换三重积分在柱面坐标系中的计算法如下: 变换cos ,sin ,x r θy r θz z =⎧⎪=⎨⎪=⎩称为柱面坐标变换,空间点(),,M x y z 与,,()r θz 建立了一一对应关系,把,,()r θz 称为点(),,M x y z 的柱面坐标.不难看出,柱面坐标实际是极坐标的推广.这里,r θ为点M在x Oy 面上的投影P 的极坐标.π<,2,<<00r θz ≤+∞≤≤-∞+∞(图10—28).图10—28柱面坐标系的三组坐标面为 (1)常数r =,以z 为轴的圆柱面; (2)常数θ=,过z 轴的半平面; (3)常数z =,平行于x Oy 面的平面. 由于cos sin 0(,,)sin cos 0(,,)001θr θx y z θr r rθθz -∂==∂,则在柱面坐标变换下,体积元素之间的关系式为:d d d d d d x y z r r θz=.于是,柱面坐标变换下三重积分换元公式为:(,,)d d d (cos ,sin ,)d d d f x y z x y z =f r r z r r z θθθ'ΩΩ⎰⎰⎰⎰⎰⎰.(10-3-3)至于变换为柱面坐标后的三重积分计算,则可化为三次积分来进行.通常把积分区域Ω向x Oy 面投影得投影区域D ,以确定,r θ的取值范围,z 的范围确定同直角坐标系情形.例4 计算三重积分22d d d z x y x y z Ω+⎰⎰⎰,其中Ω是由锥面22z x y =+与平面1z =所围成的区域.解 在柱面坐标系下,积分区域Ω表示为π1,1,200r z r θ≤≤≤≤≤≤ (图10—29).图10—29所以有2π11222d d d d d d rz x y x y z r z r z θΩ+=⋅⎰⎰⎰⎰⎰⎰d π1221220(1)r r r =-⎰.例5 计算三重积分()22d d d xy x y zΩ+⎰⎰⎰,其中Ω是由曲线22,0yz x ==绕z 轴旋转一周而成的曲面与两平面2,8z z ==所围之区域.解 曲线2=2,0y z x =绕z 旋转,所得旋转面方程为222x y z +=.设由旋转曲面与平面2z =所围成的区域为1Ω,该区域在x Oy 平面上的投影为1D ,(){}4221|D x ,y x +y =≤.由旋转曲面与8z =所围成的区域为2Ω,2Ω在x Oy 平面上的投影为2D ,()21622{|}D x ,y x +y =≤.则有21ΩΩΩ=,如图10—30所示.图10—30()21288223322d d d d d d d d d r D D xy x y z r r z r r zθθΩ+=+⎰⎰⎰⎰⎰⎰⎰⎰⎰2d d d 8d 222243326ππθr r θr r ⎛⎫=+- ⎪⎝⎭⎰⎰⎰⎰r π336=.3.3.2 球面坐标变换三重积分在球面坐标系中的计算法如下: 变换sin cos ,sin sin ,cos x r φθy r φθz r φ=⎧⎪=⎨⎪=⎩称为球面坐标变换,空间点(),,M x y z 与,,()r φθ建立了一一对应关系,把,,()r φθ称为点(),,M x y z 的球面坐标(图10-31),其中ππ<,,2000r φθ≤+∞≤≤≤≤.图10-31球面坐标系的三组坐标面为: (1)常数r =,以原点为中心的球面;(2)常数φ=,以原点为顶点,z 轴为轴,半顶角为φ的圆锥面;(3)常数θ=,过z 轴的半平面.由于球面坐标变换的雅可比行列式为sin cos cos cos sin sin (,,)sin sin cos sin sin cos (,,)cos sin 0φθr φθr φθx y z φθr φθr φθr φθφr φ-∂=∂-2sin r φ=,则在球面坐标变换下,体积元素之间的关系式为:2d d d sin d d d x y z r φr θφ=.于是,球面坐标变换下三重积分的换元公式为 2(,,)d d d (sin cos ,sin sin ,cos )sin d d d f x y z x y z =f r r r r r ϕθϕθϕϕϕθ'ΩΩ⋅⎰⎰⎰⎰⎰⎰. (10-3-4)例6 计算三重积分222()d d d xy z x y zΩ++⎰⎰⎰,其中Ω表示圆锥面222x y z +=与球面2222x y z R z ++=所围的较大部分立体.解 在球面坐标变换下,球面方程变形为2cos r R φ=,锥面为π4φ=(图10—32).这时积分区域Ω表示为π2, , 2cos 4000θπφr R φ≤≤≤≤≤≤,图10—32所以22222()d d d sin d d d x y z x y z =r r r ϕϕθ'ΩΩ++⋅⎰⎰⎰⎰⎰⎰ππd d d 22cos 44sin R φθφr φr =⎰⎰⎰ππd π52cos 0540228sin ()515R φφr φR ==⎰.例7 计算三重积分22(2)d d d y x z x y zΩ++⎰⎰⎰,其中Ω是由曲面2222x y z a ++=,22224x y z a ++=,22x y z +=所围成的区域.解 积分区域用球面坐标系表示显然容易,但球面坐标变换应为sin cos sin sin cos ,,x r φθz r φθy r φ===,这时2d sin d d d v r φr φθ=,积分区域Ω表示为ππ224,00,a r a φθ≤≤≤≤≤≤ (图10—33).图10—33所以π2π2222400(2)d d d d d (2cos sin )sin d a a y x z x y z =r r r r θϕϕϕϕΩ+++⎰⎰⎰⎰⎰⎰ππ41515816a ⎛⎫ ⎪⎝⎭=+.值得注意的是,三重积分的计算是选择直角坐标,还是柱面坐标或球面坐标转化成三次积分,通常要综合考虑积分域和被积函数的特点.一般说来,积分域Ω的边界面中有柱面或圆锥面时,常采用柱面坐标系;有球面或圆锥面时,常采用球面坐标系.另外,与二重积分类似,三重积分也可利用在对称区域上被积函数关于变量成奇偶函数以简化计算.习题10-31.化三重积分(,,)d d d I f x y z x y z Ω=⎰⎰⎰为三次积分,其中积分区域Ω分别是.(1) 由双曲抛物面x y z =及平面100x y z +-==,所围成的闭区域;(2) 由曲面22z x y =+及平面1z =所围成的闭区域. 2.在直角坐标系下计算三重积分: (1)()d d d 2+xy z x y z Ω⎰⎰⎰,其中[][][]-2,5-3,30,1Ω=⨯⨯;。
高数 重积分 (1)
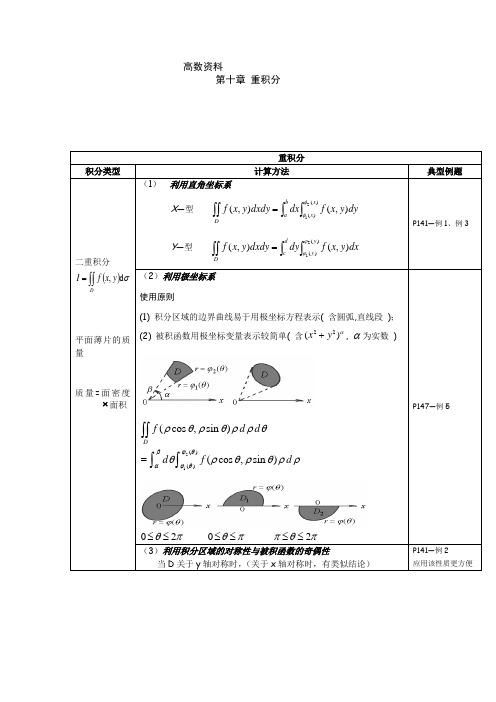
高数资料第十章重积分重积分积分类型计算方法典型例题二重积分()σd,⎰⎰=DyxfI平面薄片的质量质量=面密度⨯面积(1)利用直角坐标系X—型⎰⎰⎰⎰=Dbaxxdyyxfdxdxdyyxf)()(21),(),(φφY—型⎰⎰⎰⎰=d c y yDdxyxfdydxdyyxf)()(21),(),(ϕϕP141—例1、例3(2)利用极坐标系使用原则(1) 积分区域的边界曲线易于用极坐标方程表示( 含圆弧,直线段);(2) 被积函数用极坐标变量表示较简单( 含22()x yα+, α为实数)21()()(cos,sin)(cos,sin)Df d dd f dβϕθαϕθρθρθρρθθρθρθρρ=⎰⎰⎰⎰02θπ≤≤0θπ≤≤2πθπ≤≤P147—例5(3)利用积分区域的对称性与被积函数的奇偶性当D关于y轴对称时,(关于x轴对称时,有类似结论)P141—例2应用该性质更方便110(,)(,)(,)2(,)(,)(,)(,)D f x y x f x y f x y I f x y dxdyf x y x f x y f x y D D ⎧⎪⎪-=-⎪⎪=⎨⎪⎪-=⎪⎪⎩⎰⎰对于是奇函数,即对于是偶函数,即是的右半部分计算步骤及注意事项1. 画出积分区域2. 选择坐标系 标准:域边界应尽量多为坐标轴,被积函数关于坐标变量易分离3. 确定积分次序 原则:积分区域分块少,累次积分好算为妙 4. 确定积分限 方法:图示法 先积一条线,后扫积分域 5. 计算要简便 注意:充分利用对称性,奇偶性三重积分⎰⎰⎰Ω=dvz y x f I ),,(空间立体物的质量(1) 利用直角坐标⎩⎨⎧截面法投影法投影⎰⎰⎰⎰⎰⎰=Ωbay x z y x z x y x y z z y x f y x V z y x f ),(),()()(2121d ),,(d d d ),,(P159—例1P160—例2(2) 利用柱面坐标 cos sin x r y r z z θθ=⎧⎪=⎨⎪=⎩相当于在投影法的基础上直角坐标转换成极坐标 适用范围:○1积分区域表面用柱面坐标表示时方程简单;如 旋转体 ○2被积函数用柱面坐标表示时变量易分离.如2222()()f x y f x z ++ 21()()(,,)d d d (cos ,sin ,)d b r ar f x y z V z f z βθαθθρθρθρρΩ=⎰⎰⎰⎰⎰⎰P161—例3(3)利用球面坐标 cos sin cos sin sin sin cos x r y r z r ρθϕθρθϕθϕ==⎧⎪==⎨⎪=⎩dv r drd d =2sin ϕϕθ适用范围:○1积分域表面用球面坐标表示时方程简单;如,球体,锥体. P165—10-(1)质量=密度⨯面积○2被积函数用球面坐标表示时变量易分离. 如,222()f x y z++ 222111(,)2(,)d d(sin cos,sin sin,cos)sin d I fαβρθϕαβρθϕϕθρϕθρϕθρϕρϕρ=⎰⎰⎰(4)利用积分区域的对称性与被积函数的奇偶性。
重积分教案讲义

重积分教案讲义重积分教案讲义第一节二重积分的概念与性质与定积分类似,二重积分的概念也是从实践中抽象出来的,它是定积分的推广,其中的数学思想与定积分一样,也是一种“和式的极限”.所不同的是:定积分的被积函数是一元函数,积分范围是一个区间;而二重积分的被积函数是二元函数,积分范围是平面上的一个区域.它们之间存在着密切的联系,二重积分可以通过定积分来计算.分布图示★曲顶柱体的体积★非均匀平面薄片的质量★二重积分的概念★二重积分的性质★二重积分的中值定理★例1★例2★例3★例4★例5★内容小结★课堂练习★习题9-1★返回内容要点一、二重积分的概念引例1 1 求曲顶柱体的体积;引例2 2 求非均匀平面薄片的质量二重积分的定义二、二重积分的性质性质1—性质6 二重积分与定积分有类似的性质. 性质1 1性质2 2 如果闭区域D 可被曲线分为两个没有公共内点的闭子区域和,则这个性质表明二重积分对积分区域具有可加性. 性质3 3 如果在闭区域 D 上, 为 D 的面积,则这个性质的几何意义是:以D 为底、高为1 的平顶柱体的体积在数值上等于柱体的底面积. 性质 4 4 如果在闭区域 D 上,有则特别地,有性质5 5设分别是在闭区域D 上的最大值和最小值,为D 的面积,则这个不等式称为二重积分的估值不等式. . ) , ( ) , ( )] , ( ) , ( [D D Dd y x g d y x f d y x g y x f 1D2D. ) , ( ) , ( ) , (2 1 D D Dd y x f d y x f d y x f , 1 ) , ( y x f. 1 D Dd d), , ( ) , ( y x g y x f . ) , ( ) , ( D Dd y x g d y x f . | ) , ( | ) , ( D Dd y x f d y x f m M, ) , ( y x f . ) , ( M d y x f mD例题选讲二重积分的性质例例1 1 不作计算,估计的值,其中是椭圆闭区域:. 解区域D 的面积在上由性质6 知例例2 2 (E01 )估计二重积分的值,其中积分区域为矩形闭区域 . 解积分区域面积在上的最大值最小值故例例3 3 判断的符号. 解当时,d e IDy x) (2 2D__byax) 0 ( a b , abD , 02 2 2a y x , 12 2 20 a y xe e e ,2 2 2) ( aDy xe d e .2 2 2) ( aDy xe ab d e abD xy y xdI16 22 2 D } 2 0 , 1 0 | ) , {( y x y x,16 ) (1) , (2y xy x f , 2 D ) , ( y x f ), 0 (41 y x M ), 2 , 1 (514 312 2 y x m4252 I . 5 . 0 4 . 0 I12 2) ln(y x rdxdy y x ) 1 ( r1 | | | | y x r , 1 |) | | (| 02 2 2y x y x故又当时,于是例例4 4 积分有怎样的符号,其中解例例5(E02)比较积分与的大小,其中区域D 是三角形闭区域,三顶点各为(1,0),(1,1),(2,0). 解三角形斜边方程在内有故于是因此课堂练习1.将二重积分定义与定积分定义进行比较,找出它们的相同之处与不同之处.2.试用二重积分表示极限; 0 ) ln(2 2 y x1 | | | | y x , 0 ) ln(2 2 y x. 0 ) ln(1 | | | |22 y x rdxdy y xdxdy y xD32 21 . 4 :2 2 y xD Ddxdy y x32 21 3 132 2132 22 2 2 21 1y x y xdxdy y x dxdy y x 4 332 22 21y xdxdy y x 3 __ 2 2 21 1 0 1y x y xdxdy dxdy) 2 1 ( ) 3 4 )( 2 (3 3Dd y x )ln(Dd y x 2)] [ln(, 2 y x D , 2 1 e y x , 1 ) ln( 0 y x, )] [ln( ) ln(2y x y x . )] [ln( ) ln(2 D Dd y x d y x .1lim1 1222 2ninjnj inen。
高等数学-重积分PPT课件

重积分的性质
线性性质
若α、β为常数,则∫[αf+βg]=α∫f+β∫g。
积分区域的可加性
若D1、D2是两个不相交的区域,则∫[D1∪D2]f=∫[D1]f+∫[D2]f。
保序性
若在D上,f(x,y)≤g(x,y),则∫[D]f≤∫[D]g。
绝对可积性
若f在D上可积,则|f|在D上也可积,且|∫[D]f|≤∫[D]|f|。
课件内容与结构
课件内容
本课件主要介绍重积分的基本概念、性质、计算方法和应用实例,包括二重积分和三重积分的定义、性质、计算 方法和应用等。
课件结构
课件按照“概念引入-性质探讨-计算方法-应用实例”的逻辑顺序进行编排,层次分明,条理清晰,便于学生理解 和掌握。
02
重积分的定义与性质
重积分的定义
二重积分的定义
计算消费者剩余和生产者剩余
02 重积分可用于计算消费者剩余和生产者剩余,通过对
需求函数和供给函数进行积分得到。
计算社会福利
03
重积分可用于计算社会福利,通过对消费者剩余和生
产者剩余进行加总得到。
06
重积分的数值计算方法
矩形法则与梯形法则
矩形法则
将积分区间划分为若干个小矩形,每个小矩形的面积近似等于其底边长度与高的乘积,将所有小矩形 的面积相加得到积分的近似值。
计算转动惯量
重积分可用于计算物体绕某轴的 转动惯量,通过对物体质量分布 和到轴距离的平方进行积分得到。
计算引力
重积分可用于计算两个物体之间 的引力,通过对两物体间的质量 分布和距离进行积分得到。
在工程学中的应用
计算面积和体积
重积分可用于计算平面图形或立体图形的面积和体积,通过对图形 的边界函数进行积分得到。
重积分高等数学.pptx

连续必可积
六、极坐标系下面积元素
y
( )
取r :[r, r dr] 取 :[ , d ]
x r cos
y
r
sin
r x2 y2
arctan
y
x
d
o
d
r r dr x
则d rdrd -------极坐标系下面积元素
f (x, y)d f (r cos, r sin k , 做乘积f (M k )k ;
共
n
3 求和 f (M k )k ;
性
4
记
k 1
max
1k nn
k
,当 0
如果 lim 0
k 1
f
(M k )k存在,则称此极限为
f (M )在上的积分,记作 f (M )d. ()
注 : (1)区域 k的直径k : (2) maxk , k 1, 2, n
f (i ,i ) i.
9
第10页/共23页
2) 物体为薄板。
y
1.分( ) : k (k 1, 2, , n)
2.取M k (k ,k ) k , f (k ,k )
则mk f (k ,k ) k
o
n
3.
m
lim 0
k 1
f
(k ,k ) k
z
3) 物体为空间物质块。
1.分(V ) : Vk (k 1, 2, , n)
f (M )g(M )d f (C) g(M )d
()
()
证明 在上f (M )连续,则: m f (M ) M
mg(M ) f (M )g(M ) Mg(M )
(C )
m g(M )d f (M )g(M )d M g(M )d
高等数学(II)(第十章、重积分)

27
Z
A ( x )
(x)
z f ( x, y)
2
1
(x)
f ( x , y ) dy
y
1( x )
所以:
2(x)
2 (x)
D
f(x,y)dxdy
b
A(x)dx
a
[
a
b
f(x .y ) dy ]dx
1 (x)
3-12
28
注意: 1)上式说明: 二重积分可化为二次定 积分计算;
2)积分次序: X-型域 3)积分限确定法: 先Y后X;
域中一线穿—定内限, 域边两线夹—定外限
为方便,上式也常记为:
b
dx
a
2 (x)
f(x .y ) dy
1 (x)
29
3、Y-型域下二重积分的计算:
同理:
d
x 1( y)
D
x 2( y)
c
D
f ( x, y )d
6
得 (3) 求和. 将这 n 个小平顶柱体的体积相加,
到原曲顶柱体体积的近似值,即
V
i1
n
V i f ( i , i ) i .
i1
n
(4) 取极限. 将区域 D 无限细分且每一个子域趋 向于缩成一点, 这个近似值就趋向于曲顶柱体的体
积, 即
V lim
0
将区域 D 任意分成 n 个小区域
任取一点 若存在一个常数 I , 使 记作
则称 f ( x , y )
可积 , 称 I 为 f ( x , y ) 在D上的二重积分.
第十章____重积分(高等数学教案)
重积分【教学目标与要求】1.理解二重积分、三重积分的概念,了解重积分的性质,知道二重积分的中值定理。
2.掌握二重积分的(直角坐标、极坐标)计算方法。
3.掌握计算三重积分的(直角坐标、柱面坐标、球面坐标)计算方法。
4.会用重积分求一些几何量与物理量(平面图形的面积、体积、重心、转动惯量、引力等)。
【教学重点】1.二重积分的计算(直角坐标、极坐标);2.三重积分的(直角坐标、柱面坐标、球面坐标)计算。
3.二、三重积分的几何应用及物理应用。
【教学难点】1.利用极坐标计算二重积分;2.利用球坐标计算三重积分;3.物理应用中的引力问题。
【教学课时分配】 (10学时)第1 次课§1第2 次课§2 第3 次课§3第4 次课§4 第5次课习题课【参考书】[1]同济大学数学系.《高等数学(下)》,第五版.高等教育出版社.[2] 同济大学数学系.《高等数学学习辅导与习题选解》,第六版.高等教育出版社.[3] 同济大学数学系.《高等数学习题全解指南(下)》,第六版.高等教育出版社§10. 1 二重积分的概念与性质【回顾】定积分设函数y =f (x )在区间[a , b ]上非负、连续. 求直线x =a 、x =b 、y =0 及曲线y =f (x )所围成的曲边梯形的面积.(1)分割:用分点a =x 0<x 1<x 2< ⋅ ⋅ ⋅<x n -1<x n =b 把区间[a , b ]分成n个小区间 [x 0, x 1], [x 1, x 2], [x 2, x 3], ⋅ ⋅ ⋅ , [x n -1, x n ], 记∆x i =x i -x i -1 (i =1, 2, ⋅ ⋅ ⋅ , n ). (2)代替:任取ξ i[x i -1, x i ] 以[x i -1, x i ]为底的小曲边梯形的面积可近似为i i x f ∆)(ξ (i =1, 2, ⋅ ⋅ ⋅ , n )(3)作和:曲边梯形面积A 的近似值为 ∑=∆≈ni iix f A 1)(ξ.(4)取极限:记λ=max{∆x 1, ∆x 2,⋅ ⋅ ⋅, ∆x n }, 所以曲边梯形面积的精确值为 ∑=→∆=ni iix f A 1)(lim ξλ.则§10. 1 二重积分的概念与性质一、引例1曲顶柱体的体积V设有一立体, 它的底面是xOy 面上的闭区域D , 其侧面为母线平行于z 轴的柱面, 其顶是曲面z =f (x , y )非负连续. 称为曲顶柱体.若立体的顶是平行于xoy 面的平面。
高数-重积分
第十章 重积分§10. 1 二重积分的概念与性质教学目的:理解二重积分,了解重积分的性质,知道二重积分的中值定理。
教学重点:二重积分的定义。
教学难点:二重积分的定义的理解。
教学内容:一、二重积分的概念 1. 曲顶柱体的体积设有一立体, 它的底是xoy 面上的闭区域D 它的侧面是以D 的边界曲线为准线而母线平行于z 轴的柱面, 它的顶是曲面(,)z f x y =, 这里(,)0f x y ≥且在D 上连续. 这种立体叫做曲顶柱体. 现在我们来讨论如何计算曲顶柱体的体积.首先, 用一组曲线网把D 分成n 个小区域 12,,,.n δδδ∆∆∆分别以这些小闭区域的边界曲线为准线, 作母线平行于z 轴的柱面, 这些柱面把原来的曲顶柱体分为n 个细曲顶柱体. 在每个i δ∆中任取一点(,)i i ξη, 以(,)i i f ξη为高而底为i δ∆的平顶柱体的体积为 (,)i i i f ξηδ∆ (1,2,,)i n =.这个平顶柱体体积之和 1(,)ni i i i V f ξησ=≈∆∑可以认为是整个曲顶柱体体积的近似值. 为求得曲顶柱体体积的精确值, 将分割加密, 只需取极限, 即 01lim (,)ni i i i V f λξησ→==∆∑.其中λ是个小区域的直径中的最大值. 2. 平面薄片的质量.设有一平面薄片占有xoy 面上的闭区域D , 它在点(,)x y 处的面密度为(,)x y ρ, 这里(,)0x y ρ>且在D 上连续. 现在要计算该薄片的质量M .用一组曲线网把D 分成n 个小区域 12,,,.n δδδ∆∆∆把各小块的质量近似地看作均匀薄片的质量: (,)i i i ρξηδ∆各小块质量的和作为平面薄片的质量的近似值: 1(,)ni i i i M ρξησ=≈∆∑将分割加细, 取极限, 得到平面薄片的质量01lim (,)n i i i i M λρξησ→==∆∑,其中λ是个小区域的直径中的最大值.3.二重积分定义定义:设(,)f x y 是平面有界闭区域D 上有界函数,将闭域D 任意分成n 个小闭区域 12,,,n σσσ∆∆∆其中i σ∆表示第i 个小闭区域,也表示它的面积.在每一个i σ∆上任取一点(,)i i ξη,作乘积(,)(1,2,,)i i i f i n ξησ⋅∆=,并作和1(,)ni i i i f ξησ=⋅∆∑,如果当各小区域的直径中的最大值λ趋于零时,这和的极限总存在(与i σ∆分法及(,)i i ξη的取法均无关),则称此极限值为函数(,)f x y 在闭区域D 上的二重积分,记作(,)Df x y d σ⎰⎰,即01(,)lim (,)niiii Df x y d f λσξησ→==∆∑⎰⎰其中(,)f x y 叫被积函数, (,)f x y d δ叫被积表达式, d δ叫面积元素 ,D 积分区域。
第十章-重积分的应用
第九章(二) 重积分的应用重积分的应用十分广泛。
尤其是在几何和物理两方面。
几何方面的应用有利用二重积分求平面图形的面积;求曲面面积;利用三重积分求立体体积。
物理方面的应用有求质量;求重心;求转动惯量;求引力等。
在研究生入学考试中,该内容是《高等数学一》和《高等数学二》的考试内容。
通过这一章节的学习,我们认为应到达如下要求:1、掌握重积分的几何和物理意义,并能应用于实际计算。
2、对于重积分的应用领域和常见应用问题有全面的了解,并能利用重积分解决应用问题。
3、具备空间想象能力,娴熟的重积分计算技巧和将理论转化为应用的能力。
一、知识网络图⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧求引力求转动慣量求重心求质量物理应用求曲面面积求立体体积求平面图形面积几何应用重积分的应用 二、典型错误分析例1. 求如下平面区域D 的面积,其中D 由直线x y x ==,2及曲线1=xy 所围成。
如图: y[错解]89)2(2212221=-===⎰⎰⎰⎰⎰dy y dx dy d S y Dσ[分析]平面图形的面积可以利用二重积分来计算,这一点并没有错。
问题在于区域D ,假设先按x 积分,再按y 积分,则应注意到区域D 因此划分为两个部分,在这两个部分,x 、y 的积分限并不相同,因此此题假设先积x, 后积y ,则应分两部分分别积分,再相加。
[正确解] 2ln 2322112121-=+==⎰⎰⎰⎰⎰⎰yyDdx dy dx dy d S σ 例 2..设平面薄片所占的闭区域D 是由螺线θγ2=上一段弧)20(πθ≤≤与直线2πθ=所围成,它的面密度为22),(y x y x +=ρ,求该薄片的质量。
[错解] 24023420320220πθθθσρπθπ====⎰⎰⎰⎰⎰d r dr r d d MD[分析] 平面物体的质量是以面密度函数为被积函数的二重积分,因此解法的第一步是正确的。
注意到积分区域的边界有圆弧,而被积函数为22),(y x y x +=ρ,因此积分的计算采用极坐标系算,这一点也是正确的。
重积分高等数学课件.ppt
于是 ln(x2 y2 ) d x d y 0
x y 1
机动 目录 上页 下页 返回 结束
第三节 三重积分
一、三重积分的概念 二、三重积分的计算
第九章
机动 目录 上页 下页 返回 结束
一、三重积分的概念
引例: 设在空间有限闭区域 内分布着某种不均匀的
物质, 密度函数为(x, y, z) C,求分布在 内的物质的
的正负号.
y
D3 D2 o 1 32 x
D1
舍去此项
猜想结果为负
D1 d x d y
但不好估计 .
3 2 (4 3) (1 3 2) 0
机动 目录 上页 下页 返回 结束
例3. 估计下列积分之值
I
D
dxd y 100 cos2 x cos2
y
D : x y 10
y
解: D 的面积为 (10 2)2 200
体积, 则存在 ( ,, ) , 使得
f (x, y, z) d v f ( ,, )V
机动 目录 上页 下页 返回 结束
二、三重积分的计算
1. 利用直角坐标计算三重积分 先假设连续函数 f (x, y, z) 0, 并将它看作某物体
的密度函数 , 通过计算该物体的质量引出下列各计算 方法:
n
M
lim
0 k 1
(k , k
) k
(k ,k )
x
k
机动 目录 上页 下页 返回 结束
两个问题的共性:
(1) 解决问题的步骤相同 “大化小, 常代变, 近似和,取极限”
(2) 所求量的结构式相同
曲顶柱体体积:
n
V
lim
0 k 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高数教案第十章重积分 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN高等数学教案第十章 重积分§10-1 二重积分的概念与性质一、二重积分的概念 (一)引例 1. 曲顶柱体的体积设有一空间立体Ω,它的底是xoy 面上的有界区域D ,它的侧面是以D 的边界曲线为准线,而母线平行于z 轴的柱面,它的顶是曲面(.)z f x y =。
当(,)x y D ∈时,(,)f x y 在D 上连续且(,)0f x y ≥,以后称这种立体为曲顶柱体。
曲顶柱体的体积V 可以这样来计算:(1) 用任意一组曲线网将区域D 分成n 个小区域1σ∆,2σ∆,,n σ∆,以这些小区域的边界曲线为准线,作母线平行于z 轴的柱面,这些柱面将原来的曲顶柱体Ω分划成n 个小曲顶柱体1∆Ω,2∆Ω,,n ∆Ω。
(假设i σ∆所对应的小曲顶柱体为i ∆Ω,这里i σ∆既代表第i 个小区域,又表示它的面积值, i ∆Ω既代表第i 个小曲顶柱体,又代表它的体积值。
)图10-1-1从而 1ni i V ==∆Ω∑ (将Ω化整为零)(2) 由于(,)f x y 连续,对于同一个小区域来说,函数值的变化不大。
因此,可以将小曲顶柱体近似地看作小平顶柱体,于是∆Ω∆∆i i i ii i i f ≈∀∈()()()ξησξησ(以不变之高代替变高, 求i ∆Ω的近似值)(3) 整个曲顶柱体的体积近似值为V f i i ii n≈=∑()ξησ∆1(4) 为得到V 的精确值,只需让这n 个小区域越来越小,即让每个小区域向某点收缩。
为此,我们引入区域直径的概念:一个闭区域的直径是指区域上任意两点距离的最大者。
所谓让区域向一点收缩性地变小,意指让区域的直径趋向于零。
设n 个小区域直径中的最大者为λ, 则V f ni i ii =→=∑lim (),λξησ01∆2.平面薄片的质量设有一平面薄片占有xoy 面上的区域D , 它在(),x y 处的面密度为(),x y ρ,这里(),0x y ρ≥,而且(),x y ρ在D 上连续,现计算该平面薄片的质量M 。
图10-1-2将D 分成n 个小区域 1σ∆,2σ∆,,n σ∆,用i λ记i σ∆的直径, i σ∆既代表第i 个小区域又代表它的面积。
当{}1max i i nλλ≤≤=很小时, 由于(),x y ρ连续, 每小片区域的质量可近似地看作是均匀的, 那么第i 小块区域的近似质量可取为ρξησξησ(,)(,)i i ii i i ∆∆∀∈于是 ∑=∆≈ni i i i M 1),(σηξρM i i ii n=→=∑lim (,)λρξησ01∆两种实际意义完全不同的问题, 最终都归结同一形式的极限问题。
因此,有必要撇开这类极限问题的实际背景, 给出一个更广泛、更抽象的数学概念,即二重积分。
(二) 二重积分的定义1.定义:设(),f x y 是闭区域D 上的有界函数, 将区域D 分成个小区域∆∆∆σσσ12,,, n ,其中,i σ∆既表示第i 个小区域, 也表示它的面积, i λ表示它的直径。
λλ=≤≤max{}1i n i∀∈(,)ξησi i i ∆ 作乘积 (,)(1,2,)i i if i n ξησ∆=作和式 1(,)ni i i i f ξησ=∆∑若极限 ()01lim ,ni i i i f λξησ→=∆∑ 存在,则称此极限值为函数(),f x y 在区域D 上的二重积分,记作 (),Df x y d σ⎰⎰。
即 (),Df x y d σ=⎰⎰()01lim ,ni i i i f λξησ→=∆∑其中: (),f x y 称之为被积函数,(),f x y d σ称之为被积表达式,d σ称之为面积元素,,x y 称之为积分变量,D 称之为积分区域,()1,ni i i i f ξησ=∆∑称之为积分和式。
2. 几个事实(1) 二重积分的存在定理若(),f x y 在闭区域D 上连续, 则(),f x y 在D 上的二重积分存在。
声明: 在以后的讨论中,我们总假定在闭区域上的二重积分存在。
(2)(),Df x y d σ⎰⎰中的面积元素d σ象征着积分和式中的i σ∆。
图10-1-3由于二重积分的定义中对区域D 的划分是任意的,若用一组平行于坐标轴的直线来划分区域D ,那么除了靠近边界曲线的一些小区域之外,绝大多数的小区域都是矩形,因此,可以将d σ记作dxdy (并称dxdy 为直角坐标系下的面积元素),二重积分也可表示成为 (),Df x y dxdy ⎰⎰。
(3) 若(),0f x y ≥,二重积分表示以(),f x y 为曲顶,以D 为底的曲顶柱体的体积。
二、二重积分的性质二重积分与定积分有相类似的性质 1. 线性性[(,)(,)](,)(,)]αβσασβσ⋅+⋅=⋅+⋅⎰⎰⎰⎰⎰⎰f x y g x y d f x y d g x y d DDD其中: ,αβ是常数。
2. 对区域的可加性若区域D 分为两个部分区域12,D D ,则f x y d f x y d f x y d DD D (,)(,)(,)σσσ=+⎰⎰⎰⎰⎰⎰213. 若在D 上,(),1f x y ≡, σ为区域D 的面积,则σσσ==⎰⎰⎰⎰1d d DD几何意义: 高为1的平顶柱体的体积在数值上等于柱体的底面积。
4. 若在D 上,()(),,f x y x y ϕ≤,则有不等式⎰⎰⎰⎰≤DDd y x d y x f σϕσ),(),(特别地,由于()()(),,,f x y f x y f x y -≤≤,有σσd y x f d y x f DD⎰⎰⎰⎰≤),(),(5. 估值不等式设M 与m 分别是(),f x y 在闭区域D 上最大值和最小值,σ是M 的面积,则⎰⎰⋅≤≤⋅DM d y x f m σσσ),(6. 二重积分的中值定理设函数(),f x y 在闭区域D 上连续, σ是D 的面积,则在D 上至少存在一点(),ξη,使得⎰⎰⋅=Df d y x f σηξσ),(),(7 、对称性(偶倍奇零)设函数(),f x y 在闭区域D 上连续, D 关于x 轴对称, D 位于 x 轴上方的部分为1D ,在D 上(1)(,)(,),f x y f x y -=则(,)d Df x y σ⎰⎰12(,)d D f x y σ=⎰⎰(2)(,)(,),f x y f x y -=-则(,)d 0Df x y σ=⎰⎰当区域关于 y 轴对称, 函数关于变量 x 有奇偶性时, 仍有类似结果. 例1比较下列各对二重积分的大小(1)2()Dx y d σ+⎰⎰与3()Dx y d σ+⎰⎰,其中22:(2)(1)2D x y -+-≤。
(2)ln()Dx y d σ+⎰⎰与2[ln()]Dx y d σ+⎰⎰,其中D 是三角形区域,三顶点分别为(1,0),(1,1),(2,0)。
例2判断积分224d x y x y +≤⎰⎰的正负号.[负]例3 估计下列积分之值22d d I :10100cos cos Dx yD x y x y=+≤++⎰⎰[1.96 ≤ I ≤ 2]三、二重积分的几何意义1.若(,)0f x y >,(,)Df x y d σ⎰⎰ 表示曲顶柱体的体积2.若(,)0f x y <,(,)Df x y d σ⎰⎰ 表示曲顶柱体的体积的负值3.(,)Df x y d σ⎰⎰ 表示曲顶柱体的体积的代数和例4. 求两个底圆半径为R 的直角圆柱面所围的体积.[3163R ]小结: 二重积分的定义(和式的极限);二重积分的几何意义(曲顶柱体的体积);二重积分的性质。
作业:习题 10-1(P136)基础题:4(1) ;5(1)高等数学教案§10-2 二重积分的计算法利用二重积分的定义来计算二重积分显然是不实际的,二重积分的计算是通过两个定积分的计算(即二次积分)来实现的。
一、 利用直角坐标计算二重积分 1、x -型区域,y -型区域我们用几何观点来讨论二重积分(),Df x y d σ⎰⎰的计算问题。
讨论中,我们假定(),0f x y ≥; 假定积分区域D 可用不等式 a x b x y x ≤≤≤≤ϕϕ12()()表示,其中()()12,x x ϕϕ在[],a b 上连续。
图10-2-1 图10-2-2据二重积分的几何意义可知, (),Df x y d σ⎰⎰的值等于以D 为底,以曲面(),z f x y =为顶的曲顶柱体的体积。
图10-2-3在区间[],a b 上任意取定一个点0x ,作平行于yoz 面的平面0x x =,这平面截曲顶柱体所得截面是一个以区间()()1020,x x ϕϕ⎡⎤⎣⎦为底,曲线()0,z f x y =为曲边的曲边梯形,其面积为()()()()201000,x x A x f x y dy ϕϕ=⎰一般地,过区间[],a b 上任一点x 且平行于yoz 面的平面截曲顶柱体所得截面的面积为()()()()21,x x A x f x y dy ϕϕ=⎰利用计算平行截面面积为已知的立体之体积的方法,该曲顶柱体的体积为V A x a dx f x y dy dxbx x a b ==⎡⎣⎢⎢⎤⎦⎥⎥⎰⎰⎰()(,)()()ϕϕ12从而有dxdy y x f d y x f ba x x D⎰⎰⎰⎰⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=)(2)(1),(),(ϕϕσ (1)上述积分叫做先对Y ,后对X 的二次积分,即先把x 看作常数,),(y x f 只看作y 的函数,对),(y x f 计算从)(1x ϕ到)(2x ϕ的定积分,然后把所得的结果( 它是x 的函数 )再对x 从a 到b 计算定积分。
这个先对y , 后对x 的二次积分也常记作f x y d dx f x y dyDabx x (,)(,)()()σϕϕ⎰⎰⎰⎰=12在上述讨论中,假定了(),0f x y ≥,利用二重积分的几何意义,导出了二重积分的计算公式(1)。
但实际上,公式(1)并不受此条件限制,对一般的),(y x f (在D 上连续),公式(1)总是成立的。
类似地,如果积分区域D 可以用下述不等式c yd y x y ≤≤≤≤,()()φφ12表示,且函数φ1()y ,φ2()y 在[,]c d 上连续, (),f x y 在D 上连续,则f x y d f x y dx dy dy f x y dxD y y c dc d y y (,)(,)(,)()()()()σφφφφ⎰⎰⎰⎰⎰⎰=⎡⎣⎢⎢⎤⎦⎥⎥=1212(2)图10-2-4 图10-2-5显然,(2)式是先对x ,后对y 的二次积分。
