信息论与编码基础_教学课件
合集下载
信息论与编码课件910PPT
当以10为底时，单位为笛特Det（工程计算常用）
表
对数及常用公式
y=log10x y=logbx Example: log327 x=10y x=by log(xy)=log x+log y log(x/y)=log x-log y log(xp)=plog x log(1)=0 log(1/x)=-log x
（对于齐次马氏链） （对于齐次遍历马氏链）
常用的概率论的基本概念和性质1
无条件概率、条件概率、联合概率满足的一些性质和关系：
（1） 0 p( xi )、p( y j )、p( y j / xi )、p( xi / y j )、p( xi y j ) 1
（2）
p( x ) 1， p( y ) 1, p( x / y ) 1, p( y
离散(数字)消息，一组未知量，可用随机序列来描述： X=(X1…Xi…Xn) 连续(模拟)消息，未知量，它可用随机过程来描述： X(t)
信息：它是更高层次哲学上的抽象，是信号与消 息的更高表达层次。
信息、消息和信号
信息、消息和信号是既有区别又有联系的三 个不同的概念。 消息中包含信息，是信息的载体。 信号携带着消息，它是消息的运载工具。
i 1 j 1
n
m
条件熵
定义：条件自信息量的概率加权平均值（数学期望） 定义为条件熵。定义式为：
H (V | U ) E[ I ( Pji )] E[ log Pji ] rij log Pji
i 1 j 1
n m
n
m
H (U | V ) E[ I (Qi j )] E[ logQi j ] rij logQi j
信息论与编码全部课件-PPT精选文档398页
• 通常取对数的底为2，单位为比特（bit）。
37
2.1.1 自信息量
• 三个单位间的转换关系为：
• 1奈特=log2e 1.433比特 • 1哈特莱=log210 3.332比特
• 自信息量非负且单调递减。
f(x)
log2x
f(x)
34
2.1.1 自信息量
• 应用概率空间的概念分析上例，设取红球
的状态为x1，白球为x2，黑球为x3，黄球为 x4，则概率空间为：
• （1）
• （2）
PX(x)0x1.99 PX(x)0x1.5
x2 0.01
x2 0.5
• （3） P X (x) 0 x1 .250.x 2 2 5x30.25x0 4.25
• （7）按生成领域分：宇宙信息、自然信息、社会信息、 思维信息等。
• （8）按应用部门分：工业信息、农业信息、军事信息、 政治信息、科技信息、文化信息等。
（9）按信息源的性质分：语声信息、图像信息、文 字信息、数据信息、计算信息等。 （10）按载体性质分：电子信息、光学信息、生物信 息等。 （11）按携带信息的信号形式分：连续信息、离散信 息、半连续信息等。
19
1.2.2 数字信息传输系统
• 优点：
• （1）抗干扰能力强，特别在中继传输中尤为明 显。
• （2）可以进行差错控制，提高了信息传输的灵 活性。
（3）便于使用现代计算机技术对信号进行处 理、存储和变换。 （4）便于加密，实现保密信息传输。
20
1.2.2 数字信息传输系统
• （5）易于与其他系统配合使用，构成综合 业务信息传输网。
35
2.1.1 自信息量
• 结论： • （1）不确定度与信源概率空间的状态数及
37
2.1.1 自信息量
• 三个单位间的转换关系为：
• 1奈特=log2e 1.433比特 • 1哈特莱=log210 3.332比特
• 自信息量非负且单调递减。
f(x)
log2x
f(x)
34
2.1.1 自信息量
• 应用概率空间的概念分析上例，设取红球
的状态为x1，白球为x2，黑球为x3，黄球为 x4，则概率空间为：
• （1）
• （2）
PX(x)0x1.99 PX(x)0x1.5
x2 0.01
x2 0.5
• （3） P X (x) 0 x1 .250.x 2 2 5x30.25x0 4.25
• （7）按生成领域分：宇宙信息、自然信息、社会信息、 思维信息等。
• （8）按应用部门分：工业信息、农业信息、军事信息、 政治信息、科技信息、文化信息等。
（9）按信息源的性质分：语声信息、图像信息、文 字信息、数据信息、计算信息等。 （10）按载体性质分：电子信息、光学信息、生物信 息等。 （11）按携带信息的信号形式分：连续信息、离散信 息、半连续信息等。
19
1.2.2 数字信息传输系统
• 优点：
• （1）抗干扰能力强，特别在中继传输中尤为明 显。
• （2）可以进行差错控制，提高了信息传输的灵 活性。
（3）便于使用现代计算机技术对信号进行处 理、存储和变换。 （4）便于加密，实现保密信息传输。
20
1.2.2 数字信息传输系统
• （5）易于与其他系统配合使用，构成综合 业务信息传输网。
35
2.1.1 自信息量
• 结论： • （1）不确定度与信源概率空间的状态数及
《信息论与编码》课件第1章 绪论
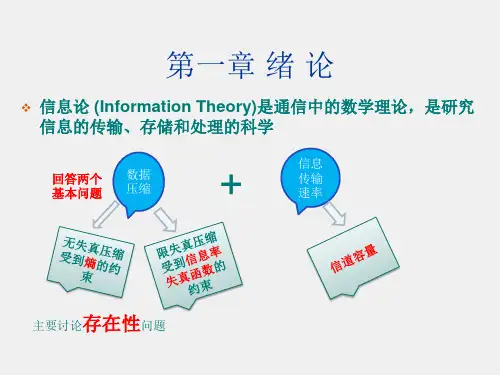
1.2 通信系统的模型
信源符号
信 源 编码 信 源
（序列）
编码器 信 道 译码器
x y yˆ
重建符号 （序列）
x
❖ 无失真编码： x xˆ
重建符号与信源发送符号一致， 即编码器输出码字序列与信源 发送序列一一映射；
限失真编码： x xˆ
总是成立的
y yˆ
分别是编码输出码字和接收到的码字
重建符号与信源发送符号不 完全一致；编码器输出码字 序列与信源输出符号序列之 间不是一一映射关系，出现 符号合并，使得重建符号的 熵减少了。
限失真、无失真是由于编译 码器形成的
信道编码
增加冗余
提高
对信道干 扰的抵抗 力
信息传输 的可靠性
❖ 由于信道中存在干扰， 数据传递过程中会出现 错误，信道编码可以检 测或者纠正数据传输的 错误，从而提高数据传 输的可靠性。
1.2 通信系统的模型
调制器
作用：
➢ 将信道编码的输出变换为适合信道传输的 要求的信号 ；
消息
信息的表现形 式；
文字，图像， 声音等；
信号
信号的变化描 述消息；
信息的基本特点
1.不确定性
受信者在接收到信息之前，不知道信源发送 的内容是什么，是未知的、不确定性事件；
2.受信者接收到信息后，可以减少或者消除不确定性；
3. 可以产生、消失、存储，还可以进行加工、处理；
4. 可以度量
1.2 通信系统的模型
冗 信源符号 余 变 相关性强 化 统计冗余强
信源编码器
码序列 相关性减弱 统计冗余弱
相关冗余 统计冗余 生理冗余
模型简化
信源输出前后符号之间存在一定相关性
信源输出符号不服从等概率分布
信息论与编码PPT课件
符号离散信源。信源的输出符号集就是四种不同的颜色A：{红
黄、蓝、白}，试构建这个信源的信源空间。
红(100) 黄(50) 蓝(25) 白(25)
P X(x)1a12
a2 1
4
a3 1
8
a4 18
样本 概率
信息论与编码基础
离散信源
定义2.2 若信源输出的是单个符号的消息，但是其可 能出现的消息数是不可数的无限值，即输出消息的取 值是连续的，这样的信源称为简单的连续信源。
五、信源的剩余度
信息论与编码基础
离散信源
信源的分类
D.S
离散信源：电报、文字、代码 连续信源信：源模输拟出语的音消、息模拟由由视随随频机机矢变量量描描述述
由随机过程描述 C.S
信息论与编码基础
离散信源
❖概念
样本空间
事物所有可能选择的消息的集合。
概率空间 一个样本空间和它的概率测度。
X
P
(
x
)
X p(x)
(a,b)
p(x)
或
R
p
(
x
)
b p(x)dx1
或
p(x)dx1
a
R
例如：语音信号；遥控系统中测得的电压、温度、压力等
➢复杂信源
例1：中文自然语言文字信源
牛气冲 天 例2：离散化的平面灰度图像信源
信息论与编码基础
离散信源
2) 信源输出的消息由随机矢量描述
信息论与编码基础
学而不思则罔， 思而不学则殆。
－孔子
信息论与编码基础
离散信源
一、信源的数学模型及分类 二、离散信源的信息熵及其性质 三、离散无记忆的扩展信源
四、离散平稳信源
信息论与编码基础_教学课件_4
信源压缩 编码基础
s1 s2 S 3 1 P(s) 4 4 随着N的增加，平均码长减小，有效性逐步提高；
当N趋于无穷时，平均码长可以无限制地减小吗？ N=3 N=4 H (S ) R3 0.985 (bit/code) R4 0.991 (bit/code) L3 / 3 H (S ) 3 0.985 4 0.991 L3 / 3 log 2
S N (S1,..., SN )
信源压缩 编码基础
Wi {xi1 , xi2 ..., xili }
编码器
Si {a1 ,..., aq } i 1, 2,..., N
X : x {x1,..., xr } i 1,2,..., q N
N次扩展信源无失真编码器
信息论与编码基础
1）请给出此信源的最佳码，并计算平均码长Lm. 2）哪些m值可使平均码长Lm等于熵？
3）定义变长码的冗余度为ρ= Lm – H。请问对怎样 的m值，编码冗余度可达到最大，其中2k≤m ≤ 2k+1? 当m→∞时，最坏情形下冗余度的极限值是什么？
信息论与编码基础
本课小结
信源编码器模型
性能指标
信源压缩 编码基础
01 00 111 110 101 10 1001 100 0.11 1000
0.35 0.26 11
0.39 0
平均码长 2.72 code/sig 信息熵 2.6 bit/sig 编码效率 95.6%
1000
信息论与编码基础
Huffman码
说明： 1、码字不唯一
信源压缩 编码基础
2、最佳性
所谓最佳性，就是指对于某个给定信源，在所有可能 3、输入、输出速率匹配问题 的唯一可译码中，此码的平均码长最短。
《信息论与编码》课件
优点
可以快速计算出哈希值，常用于数据完整性验证和密码存储。
缺点
对于某些输入，哈希函数可能产生冲突，即不同的输入可能会产生相同的哈希值。
信息论的应用
05
数据压缩
数据压缩是信息论的一个重要应用，通过编码技术减少数据冗余，提高存储和传输效率。
压缩算法
常见的压缩算法包括哈夫曼编码、算术编码、LZ77和LZ78等，这些算法利用数据的统计特性进行压缩。
定义
RSA（Rivest-Shamir-Adleman）、ECC（椭圆曲线加密）等。
常见的非对称加密算法
密钥管理相对简单，安全性较高。
优点
加密速度较慢，通常比对称加密算法慢几个数量级。
缺点
定义
哈希函数是一种将任意长度的数据映射为固定长度哈希值的函数。
常见的哈希函数
MD5（Message Digest Algorithm 5）、SHA（Secure Hash Algorithm）等。
互信息定义
条件互信息表示一个随机变量在给定另一个随机变量的条件下与第三个随机变量之间的相关性。
条件互信息定义
信源编码
02
无损压缩编码是一种完全保留原始数据，没有任何信息损失的编码方式。
有损压缩编码是一种允许一定信息损失的编码方式，通常用于图像、音频和视频等连续媒体数据的压缩。有损压缩编码通过去除数据中的冗余信息和细节来减少存储空间或传输时间。解压缩时，虽然不能完全恢复原始数据，但人眼或耳朵通常无法察觉到损失的信息。因此，它常用于需要快速传输或低成本存储的场景，如数字电视广播、互联网流媒体等。有损压缩编码的优点是压缩率高，适合处理大量数据；缺点是原始数据的完整性和真实性可能受到损失。常见的有损压缩算法包括JPEG、MPEG、MP3等。这些算法通过离散余弦变换、小波变换等技术来减少数据量，同时采用量化等技术来控制信息损失的程度。
《信息论与编码全部》课件
添加副标题
信息论与编码全部PPT课件
汇报人：PPT
目录
CONTENTS
01 添加目录标题 03 信息度量与熵
02 信息论与编码的基 本概念
04 信源编码
05 信道编码
06 加密与解密技术
07 信息安全与认证技 术
添加章节标题
信息论与编码的基本概 念
信息论的发展历程
1948年，香农提出信 息论，奠定了信息论
提高安全性
优点：安全性 高，速度快，
易于实现
应用：广泛应 用于电子商务、 网络通信等领
域
发展趋势：随 着技术的发展， 混合加密技术 将更加成熟和
完善
信息安全与认证技术
数字签名技术
数字签名：一种用于验证信息来源和完整性的技术 数字签名算法：RSA、DSA、ECDSA等 数字证书：用于存储数字签名和公钥的文件 数字签名的应用：电子邮件、电子商务、网络银行等
汇报人：PPT
熵越小，表示信息量越小，不确 定性越小
熵是概率分布的函数，与概率分 布有关
信源编码
定义：无损信源编码是指在编码过 程中不丢失任何信息，保持原始信 息的完整性。
无损信源编码
应用：无损信源编码广泛应用于音 频、视频、图像等媒体数据的压缩 和传输。
添加标题
添加标题
添加标题
添加标题
特点：无损信源编码可以保证解码 后的信息与原始信息完全一致，但 编码和解码过程通常比较复杂。
古典密码学：公元前400年，古希腊人使用替换密码 近代密码学：19世纪，维吉尼亚密码和Playfair密码出现 现代密码学：20世纪，公钥密码体制和数字签名技术出现 当代密码学：21世纪，量子密码学和后量子密码学成为研究热点
信息论与编码全部PPT课件
汇报人：PPT
目录
CONTENTS
01 添加目录标题 03 信息度量与熵
02 信息论与编码的基 本概念
04 信源编码
05 信道编码
06 加密与解密技术
07 信息安全与认证技 术
添加章节标题
信息论与编码的基本概 念
信息论的发展历程
1948年，香农提出信 息论，奠定了信息论
提高安全性
优点：安全性 高，速度快，
易于实现
应用：广泛应 用于电子商务、 网络通信等领
域
发展趋势：随 着技术的发展， 混合加密技术 将更加成熟和
完善
信息安全与认证技术
数字签名技术
数字签名：一种用于验证信息来源和完整性的技术 数字签名算法：RSA、DSA、ECDSA等 数字证书：用于存储数字签名和公钥的文件 数字签名的应用：电子邮件、电子商务、网络银行等
汇报人：PPT
熵越小，表示信息量越小，不确 定性越小
熵是概率分布的函数，与概率分 布有关
信源编码
定义：无损信源编码是指在编码过 程中不丢失任何信息，保持原始信 息的完整性。
无损信源编码
应用：无损信源编码广泛应用于音 频、视频、图像等媒体数据的压缩 和传输。
添加标题
添加标题
添加标题
添加标题
特点：无损信源编码可以保证解码 后的信息与原始信息完全一致，但 编码和解码过程通常比较复杂。
古典密码学：公元前400年，古希腊人使用替换密码 近代密码学：19世纪，维吉尼亚密码和Playfair密码出现 现代密码学：20世纪，公钥密码体制和数字签名技术出现 当代密码学：21世纪，量子密码学和后量子密码学成为研究热点
第6章信息论与编码课件
增大E(R)的途径
25
6.2.1 纠错编码的基本思路
增大信道容量C
扩展带宽 加大功率 降低噪声
减小码率R
Q、N不变而减小K Q、K不变而增大N N、K不变而减小Q
增大码长N
26
6.2.2 最优译码与最大似然译码
译码器的任务是从受损的信息序列中尽 可能正确地恢复出原信息。 译码算法的已知条件是：
实际接收到的码字序列{r}, r=(r1,r2,…,rN) 发端所采用的编码算法和该算法产生的码 集XN, 满足 c i = ( c i1 , c i 2 , L , c iN ) ∈ X N 信道模型及信道参数。
则称集合V是数域F上的n维矢量空间，或称n维线性空间， n维矢量又称n重(n-tuples)。
9
矢量空间中矢量的关系
对于域F上的若干矢量 V 1 , V 2 , L , V i 及 V k 线性组合：
V k = a1V1 + a 2V 2 + L a iVi , ( a i ∈ F )
线性相关：
a1V1 + a 2V 2 + L a iVi = 0, ( a i ∈ F且不全为零)
从功能角度：检错码 、纠错码 对信息序列的处理方法：分组码、卷积码 码元与原始信息位的关系：线性码、非线 性码 差错类型：纠随机差错码、纠突发差错 码、介于中间的纠随机/突发差错码。 构码理论：代数码、几何码、算术码、组 合码等
7
差错控制系统分类
前向纠错（FEC）：发端信息经纠错编码 后传送，收端通过纠错译码自动纠正传递 过程中的差错 反馈重发（ARQ）：收端通过检测接收码 是否符合编码规律来判断，如判定码组有 错，则通过反向信道通知发端重发该码 混合纠错（HEC）：前向纠错和反馈重发 的结合，发端发送的码兼有检错和纠错两 种能力
信息论与编码教学课件(全)
信息论与编码教学课件(全)
目录
• 课程介绍与背景 • 信息论基础 • 编码理论基础 • 信道编码技术 • 数据压缩技术 • 多媒体信息编码技术 • 课程总结与展望
01
课程介绍与背景
Chapter
信息论与编码概述
信息论的基本概念
01
信息、信息量、信息熵等
编码的基本概念
02
信源编码、信道编码、加密编码等
02
极化码（Polar Codes）
一种新型信道编码方式，通过信道极化现象实现高效可靠的信息传输。
03
深度学习在信道编码中的应用
利用深度学习技术优化传统信道编码算法，提高编码性能和效率。
05
数据压缩技术
Chapter
数据压缩概述与分类
数据压缩定义
通过去除冗余信息或使用更高效的编码方式，减小数据表示所需存储空间的过 程。
线性分组码原理：线性分组码是一 种将信息序列划分为等长的组，然 后对每组信息进行线性变换得到相 应监督位的编码方式。
具有严谨的代数结构，易于分析和 设计；
具有一定的检错和纠错能力，适用 于各种通信和存储系统。
循环码原理及特点
循环码原理：循环码是一种特殊的线 性分组码，其任意两个码字循环移位
后仍为该码的码字。
03
编码理论基础
Chapter
编码的基本概念与分类
编码的基本概念
编码是将信息从一种形式或格式转换为另一种形式的过程，以 满足传输、存储或处理的需要。
编码的分类
根据编码的目的和原理，可分为信源编码、信道编码、加密编 码等。
线性分组码原理及特点
线性分组码特点
监督位与信息位之间呈线性关系， 编码和解码电路简单；
目录
• 课程介绍与背景 • 信息论基础 • 编码理论基础 • 信道编码技术 • 数据压缩技术 • 多媒体信息编码技术 • 课程总结与展望
01
课程介绍与背景
Chapter
信息论与编码概述
信息论的基本概念
01
信息、信息量、信息熵等
编码的基本概念
02
信源编码、信道编码、加密编码等
02
极化码（Polar Codes）
一种新型信道编码方式，通过信道极化现象实现高效可靠的信息传输。
03
深度学习在信道编码中的应用
利用深度学习技术优化传统信道编码算法，提高编码性能和效率。
05
数据压缩技术
Chapter
数据压缩概述与分类
数据压缩定义
通过去除冗余信息或使用更高效的编码方式，减小数据表示所需存储空间的过 程。
线性分组码原理：线性分组码是一 种将信息序列划分为等长的组，然 后对每组信息进行线性变换得到相 应监督位的编码方式。
具有严谨的代数结构，易于分析和 设计；
具有一定的检错和纠错能力，适用 于各种通信和存储系统。
循环码原理及特点
循环码原理：循环码是一种特殊的线 性分组码，其任意两个码字循环移位
后仍为该码的码字。
03
编码理论基础
Chapter
编码的基本概念与分类
编码的基本概念
编码是将信息从一种形式或格式转换为另一种形式的过程，以 满足传输、存储或处理的需要。
编码的分类
根据编码的目的和原理，可分为信源编码、信道编码、加密编 码等。
线性分组码原理及特点
线性分组码特点
监督位与信息位之间呈线性关系， 编码和解码电路简单；
《信息论与编码》课件
发展趋势与未来挑战
探讨信息论和编码学领域面临的未 来挑战。
介绍多媒体数字信号压缩和编码技术的发展和应用。
可靠的存储与传输控制技术
解释可靠存储和传输控制技术在信息论中的重要性。
生物信息学中的应用
探讨信息论在生物信息学领域的应用和突破。
总结与展望
信息论与编码的发展历程
回顾信息论和编码学的发展历程和 里程碑。
信息技术的应用前景
展望信息技术在未来的应用前景和 可能性。
介绍误码率和信噪比的定义和关系。
2
码率与修正码率的概念
解释码率和修正码率在信道编码中的重要性。
3
线性码的原理与性质
探讨线性码的原理、特点和应用。
4
编码与译码算法的实现
详细介绍信道编码和译码算法的实现方法。
第四章 信息论应用
无线通信中的信道编码应用
探索无线通信领域中信道编码的应用和进展。
多媒体数字信号的压缩与编码技术
《信息论与编码》T课 件
# 信息论与编码 PPT课件
第一章 信息的度量与表示
信息的概念与来源
介绍信息的定义，以及信息在各个领域中的来源和 应用。
香农信息熵的定义与性质
介绍香农信息熵的概念和其在信息论中的重要性。
信息量的度量方法
详细解释如何度量信息的数量和质量。
信息压缩的基本思路
探讨信息压缩的原理和常用方法。
第二章 信源编码
等长编码与不等长编码
讨论等长编码和不等长编码的特点 和应用领域。
霍夫曼编码的构造方法与 性质
详细介绍霍夫曼编码的构造和优越 性。
香农第一定理与香农第二 定理
解释香农第一定理和香农第二定理 在信源编码中的应用。
信息论与编码课件(全部课程内容)
P(b1 | a1 ) P(b2 | a1 ) P(b | a ) P(b | a ) 2 2 [ PY | X ] 1 2 P(b1 | ar ) P(b2 | ar )
一.1.”输入符号 a,输出符号 b”的联合概率 i j
P{X a i ,Y=b j } p a i ,b j p a i p b j /a i
1。当p (ai / b j ) 1时， 1 I (ai ; b j ) log I (ai )(i 1, 2, , r; b 1, 2, , s) p (ai )
信号 a i ．
收信者收到输出符号 bj 后，推测信源以概率１发
2。当p (ai〈p (ai / b j〈1时， ) ) I (ai ; b j ) log p (ai / b j ) p (ai ) 〉 i 1, 2, , r ; b 1, 2, , s ) 0(
此式称为符号 a i 和 bj 之间的互信函数． 我们把信宿收到 bj 后，从 bj 中获取关于 a i 的信 息量 I (ai ; bj ) 称为输入符号 a i 和输出符号 bj 之间 的交互信息量，简称互信息．它表示信道在把 输入符号 a i 传递为输出符号 bj 的过程中，信道 所传递的信息量．
收信者收到 b j后，推测信源发信号 a i的后验概率，反而小于 收到 b j 前推测信源发信号 a i的先验概率.
例2.3 表2.1中列出某信源发出的八种不同消息ai(i=1,2,…,8),相应的
先验概率p(ai)(i=1,2,…,8),与消息ai(i=1,2,…,8)一一对应的码字wi
(i=1,2,…,8).同时给出输出第一个码符号“0”后，再输出消息a1,a2,a3,
信息论与编码PPT教学课件
4. 干扰源 • 是整个通信系统中各个干扰的集中反映，用以 表示消息在信道中传输时遭受干扰的情况。 • 对于任何通信系统而言，干扰的性质、大小是 影响系统性能的重要因素。
第二节 通信系统的模型
5. 密钥源 • 是产生密钥k的源 • 信源编码器输出信号x经过k的加密运算后，就 把明文x变换为密文y
三、通信系统的性能指标及相应的编码问题
第二节 通信系统的模型
问题：能否将三种码（信源编码、信道编码和密码） 合成一种码进行编译？
• 提高有效性必须去掉信源符号中的冗余部分， 此时信道误码会使接收端不能恢复原来的信息 ，也就是必须相应提高传送的可靠性，不然会 使通信质量下降；
• 反之，为了可靠而采用信道编码，往往需扩大 码率，也就降低了有效性。安全性也有类似情 况
▪ 到70年代，有关信息论的研究，从点与点间的单用 户通信推广到多用户系统的研究。1972年盖弗（Caer ）发表了有关广播信道的研究，以后陆续有关于多接 入信道和广播信道模型的研究，但由于这些问题比较 难，到目前为止，多用户信息论研究得不多，还有许 多尚待解决的课题。
第一节 信息论的形成和发展
➢ 几个概念
3．三处最有可能发展成为城 市的是哪一处？为什么？除此 而外，你知道哪些地方还分布 有较大的城市？ 4. 综上所述，影响聚落形成 和发展的因素有哪些？
• 通信系统的性能指标主要是有效性、可靠性、安全 性和经济性。通信系统优化就是使这些指标达到最 佳。
• 根据信息论的各种编码定理和上述通信系统的指标 ，编码问题可分解为三类：信源编码、信道编码和 密码。
第二节 通信系统的模型
1. 信源编译码器 信源编码器的作用 • 是把信源发出的消息变换成由二进制码元（或 多进制码元）组成的代码组，这种代码组就是 基带信号； • 同时通过信源编码可以压缩信源的冗余度（即 多余度），以提高通信系统传输消息的效率。
第二节 通信系统的模型
5. 密钥源 • 是产生密钥k的源 • 信源编码器输出信号x经过k的加密运算后，就 把明文x变换为密文y
三、通信系统的性能指标及相应的编码问题
第二节 通信系统的模型
问题：能否将三种码（信源编码、信道编码和密码） 合成一种码进行编译？
• 提高有效性必须去掉信源符号中的冗余部分， 此时信道误码会使接收端不能恢复原来的信息 ，也就是必须相应提高传送的可靠性，不然会 使通信质量下降；
• 反之，为了可靠而采用信道编码，往往需扩大 码率，也就降低了有效性。安全性也有类似情 况
▪ 到70年代，有关信息论的研究，从点与点间的单用 户通信推广到多用户系统的研究。1972年盖弗（Caer ）发表了有关广播信道的研究，以后陆续有关于多接 入信道和广播信道模型的研究，但由于这些问题比较 难，到目前为止，多用户信息论研究得不多，还有许 多尚待解决的课题。
第一节 信息论的形成和发展
➢ 几个概念
3．三处最有可能发展成为城 市的是哪一处？为什么？除此 而外，你知道哪些地方还分布 有较大的城市？ 4. 综上所述，影响聚落形成 和发展的因素有哪些？
• 通信系统的性能指标主要是有效性、可靠性、安全 性和经济性。通信系统优化就是使这些指标达到最 佳。
• 根据信息论的各种编码定理和上述通信系统的指标 ，编码问题可分解为三类：信源编码、信道编码和 密码。
第二节 通信系统的模型
1. 信源编译码器 信源编码器的作用 • 是把信源发出的消息变换成由二进制码元（或 多进制码元）组成的代码组，这种代码组就是 基带信号； • 同时通过信源编码可以压缩信源的冗余度（即 多余度），以提高通信系统传输消息的效率。
最新信息论与编码理论基础(第一章)课件教学讲义ppt
消息
是信息的载体，相对具体的概念，如语言，文字，数 字，图像
信号
表示消息的物理量，电信号的幅度，频率，相位等等
2021/5/21
21
音信消息
南唐 李中《暮春怀故人》诗： “梦断美人沉信息，目穿长路倚楼台。”
பைடு நூலகம்
宋 陈亮《梅花》诗： “欲传春信息，不怕雪埋藏。”
《水浒传》第四四回： 宋江大喜，说道：“只有贤弟去得快，旬日便知信息。”
香浓(Shannon)信息论： 1948年发表《通信的 数学理论》，创建了信息论，建立了通信系统 的模型，用概率和统计观点描述信息，包括信 源、信道、干扰等，给出了不确定的信息量度， 指出了客观有效、可靠的信息通信之路，宣告 了一门学科信息论的诞生，成为通信领域技术 革命的思想或者理论基础。
2021/5/21
信息论与编码理论基础(第 一章)课件
教材
王育民、李晖， 信息论与编码理论 （第2版）， 高等教育出版社， 2013.
2021/5/21
2
参考书
Thomas M. Cover, Joy A. Thomas, Elements of Information Theory，2nd ed, WILEY Press, 2006. 阮吉寿 张华 译 信息论基础，机械工业出版社，2007.
2021/5/21
29
类比
对于Shannon信息论，可将通信问题与普通的 运输问题做类比。
前者是传送信息，后者是传送货物。 传送货物有货源和运输通道，而货源和运输通
道又有货源的体积（或吨位）和运输通道的容 量。当运输通道的容量大于货源的体积（吨位） 时，就能实现货物的正常运输。 信源和信道编码理论则是解决信息的传输问题。 可以通过信息的度量来确定信息量（可形象地 称为信号体积）和信道容量。当信道容量大于 信息体积时，就能实现信息的正确传输。
是信息的载体，相对具体的概念，如语言，文字，数 字，图像
信号
表示消息的物理量，电信号的幅度，频率，相位等等
2021/5/21
21
音信消息
南唐 李中《暮春怀故人》诗： “梦断美人沉信息，目穿长路倚楼台。”
பைடு நூலகம்
宋 陈亮《梅花》诗： “欲传春信息，不怕雪埋藏。”
《水浒传》第四四回： 宋江大喜，说道：“只有贤弟去得快，旬日便知信息。”
香浓(Shannon)信息论： 1948年发表《通信的 数学理论》，创建了信息论，建立了通信系统 的模型，用概率和统计观点描述信息，包括信 源、信道、干扰等，给出了不确定的信息量度， 指出了客观有效、可靠的信息通信之路，宣告 了一门学科信息论的诞生，成为通信领域技术 革命的思想或者理论基础。
2021/5/21
信息论与编码理论基础(第 一章)课件
教材
王育民、李晖， 信息论与编码理论 （第2版）， 高等教育出版社， 2013.
2021/5/21
2
参考书
Thomas M. Cover, Joy A. Thomas, Elements of Information Theory，2nd ed, WILEY Press, 2006. 阮吉寿 张华 译 信息论基础，机械工业出版社，2007.
2021/5/21
29
类比
对于Shannon信息论，可将通信问题与普通的 运输问题做类比。
前者是传送信息，后者是传送货物。 传送货物有货源和运输通道，而货源和运输通
道又有货源的体积（或吨位）和运输通道的容 量。当运输通道的容量大于货源的体积（吨位） 时，就能实现货物的正常运输。 信源和信道编码理论则是解决信息的传输问题。 可以通过信息的度量来确定信息量（可形象地 称为信号体积）和信道容量。当信道容量大于 信息体积时，就能实现信息的正确传输。
12953_精品课课件信息论与编码(全套讲义)
2024/1/28
10
03
信道编码
2024/1/28
11
信道编码概述
01
信道编码的基本概念
为了提高信息传输的可靠性，在信源编码的基础上增加一些监督码元，
这些多余的码元与信息码元之间以某种确定的规则相互关联（约束）。
02
信道编码的目的
对传输的信息码元进行检错和纠错，提高信息传输的可靠性。
2024/1/28
编码的基本原则
有效性、可靠性、安全性、经 济性。
8
编码的分类与原理
2024/1/28
分类
根据编码对象的不同，可分为信源编码、信道编码和加密 编码等。
原理
不同的编码方式采用不同的编码原理和算法，如信源编码 中的哈夫曼编码、信道编码中的卷积码和LDPC码等。
编码与调制的关系
编码是数字通信中的关键技术之一，与调制技术密切相关 。编码后的信号需要通过调制技术转换为适合在信道中传 输的信号。
2024/1/28
信宿
接收并处理信息的实体或系统， 如人、计算机等。
译码器
将信道中传输的信号还原成原始 信息。
6
02
编码理论
2024/1/28
7
编码的基本概念
编码定义
将信息从一种形式或格式转换 为另一种形式的过程。
2024/1/28
编码的目的
提高信息传输效率，增强信息 抗干扰能力，实现信息的可靠 传输。
共同应对挑战
在信息传输和存储领域，信息论 和编码技术将共同应对诸如信道 噪声、数据压缩等挑战。
创新应用领域
通过信息论与编码的交叉融合， 将产生更多创新性的应用，如无 损压缩、加密通信等。
2024/1/28
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
信息论与编码基础
离散信道
一、信道疑义度与平均互信息
二、信道容量
•信道模型 •信道疑义度 •平均互信息及其性质
三、有噪信道编码定理
信息论与编码基础
ห้องสมุดไป่ตู้
离散信道
➢互信息
自信息 l o g 1
log1
P (a lo
P(ai)
条件自信息 lo g
i) 1
P(
g P(ai
|bj)
I (ai ;b
1）对称性
j
1
1
P (xy)lo g P (xy)lo g
X Y
P (x) X Y
P (x|y)
P(xy)logP(x| y) 互信息
XY
P(x)
信息论与编码基础
离散信道
➢平均互信息
I(X ;Y ) H (X ) H (X |Y )
平均互信息是 互信息的统计 平均值。
P(xy)logP(x| y)
H (X|bj) P (ai|bj)loP g (ai|bj) 后验熵
信道疑义度
i 1
s
H (X|Y )E [H (X|bj) ] P (bj)H (X|bj)
损失熵
js1P(bj)i r1P(a j i1 |bj)loP g (a1 i|bj)
r s
1
i1
j1P(aibj)loP g(ai |bj)
一、信道疑义度与平均互信息
二、信道容量
•信道模型 •信道疑义度 •平均互信息及其性质
三、有噪信道编码定理
信息论与编码基础
离散信道
➢互信息
由于条件引入获得的信息量
I (ai ;bj )
log 1 log 1 logP(ai|bj)
P(ai) P(ai|bj)
P(ai)
1）对称性 I(ai;bj) = I(bj;ai) 2）事件统计独立时
I(ai;bj) = 0 3）可正、可负
4）I(ai;bj) ≤ I(ai)
信息论与编码基础
离散信道
➢平均互信息
不获确得定信信性息息消量传除的输的大率多小少
定义 令 I(X ;Y ) H (X ) H (X |Y ) bit/sig
为信道输入X与输出Y之间的平均互信息
接I( 收X 到;Y 每) 个 X 输P 出(x 符)lo 号g 后P ( 1 获x )得 X 的YP 关(于x y ) Xl的o g 平P ( 均x 1 |信y ) 息量
高斯噪声信道
变参信道 短波信道 非高斯噪声信道
信息论与编码基础
➢离散信道的数学模型
离散信道
X
X (X1,X2,...,XN) Xi :(a1,a2,...,ar)
信道
P(y| x)
Y
Y (Y1,Y2,...,YN ) Yi :(b1,b2,...,bs)
{X,P(y|x),Y}
无扰（无噪）信道
P(y| x)10,,yyff((xx))
抽烟，y＝0表示抽烟，y＝1表示不抽烟。
（1）若（x，y）的联合概率分布如表1－1所示，求
“已知抽取人为男性”，对“该人抽烟”提供的
信息量。 表1－1（x，y）的联合概率分布 x＝0 x＝1
表1－2（x，y）的联合概率分布
x＝0 x＝1
y＝0 0.06 0.04 y＝1 0.54 0.36
y＝0 0.6 0.04 y＝1 0 0.36
X a00
. . . .
Y
1-p p
b00
Pr
1
Pr 2
...
Prs
s
Pij 1(i 1,2,..r.)
P(bj|ai) p
1
1
ar
1-p
bs
j0
信息论与编码基础
➢单符号离散信道
例2 二进制删除信道
一定比例的bit被删 除，并且接收者知 道是那些bit已经被 删除。
P
p 0
1 p 1q
0 q
离散信道
无记忆信道
有扰信道
N
P (y|x)P (y1...yN|x1...xN ) P (yi|xi)
有记忆信道
i 1
信息论与编码基础
离散信道
➢单符号离散信道
X
X:(a1,a2,...,ar)
信道
P(y | x)
Y
Y:(b1,b2,...,bs)
例1 BSC信道
BSC(p)信道是实际中几乎所有重要的二进制脉冲传输系统的模型 p为交叉(crossover)概率等于解调器/检测器出现硬判决译码错 误的概率
信息论与编码基础
离散信道
➢单符号离散信道
•条件转移概率
P ( y |x ) P ( y b j|x a i) P ( b j|a i) P i(j i 1 ,2 ,.r .;.j ,1 ,2 ,.s .).,
•转移矩阵
•转移概率图
P11 P12 ... P1s
P
P21
P22
...
P2
s
)
a
1
i
|
b
j
)
由于条件引入获得的信息量
I(ai;bj
)
logP(ai |bj P(ai)
)
2）事I(Ia(件ia;bi;统jb)j)计==I独(0b立j;ai时) 3）可正、可负 4）I(ai;bj) ≤ I(ai)
练习：
令随性信机，变x息＝量1论x为表女与示性随编。机随码抽机取基变人量础群y中表的示随性机别抽，取x＝人绪0为是论否男
信息论与编码基础_教学课件
信息论与编码基础
离散信道
➢信道的分类
•根据信道转移概率的性质
无扰信道
有扰信道
无记忆信道
实际的通信信道几乎都是有扰信道
有记忆信道
•实信按际道信信中道道的一惯统般性计都，特是如有电性记缆忆信的道，中信的•根道电中感据的或信记电道忆容现、噪象无声来线的源信于道性物中质理电
波传播的恒衰落参现信象道等。卫星信道
XY
P(x)
P(xy)log P(xy)
XY
P(x)P(y)
P(y| x)
P(xy)log
XY
P(y)
信息论与编码基础
离散信道
1、非负性
I(X ;Y ) H (X ) H (X |Y ) XYP(xy)logP(Px()xP(y)y)
利用詹森不等式
I信(X源;Y) X加Y P (密x)y loP 信g (P x()道x P ()y y) 解密
信息论与编码基础
离散信道
一、信道疑义度与平均互信息
二、信道容量
•信道模型 •信道疑义度 •平均互信息及其性质
三、有噪信道编码定理
信息论与编码基础
离散信道
0≤H(X|Y)≤H(X)
先验熵
H (X ) XP (x )lo P (x g ) i r1P (a i)lo P (1 g a i)
若信道中存在干扰时 r
（2）若（x，y）的联合概率分布如表1－2所示，求 “已知抽取人为男性”，对“该人抽烟”提供的 信息量。
信息论与编码基础
本课小结
1、信道模型 BSC, BEC 2、信道疑义度、互信息
离散信道
信息论与编码基础
离散信道
一、信道疑义度与平均互信息
二、信道容量
三、有噪信道编码定理
信息论与编码基础
离散信道