等差数列中的最值问题
等差数列的前n项和的最值及应用
法二 同法一，求出公差d＝－2. 所以an＝25＋(n－1)×(－2)＝－2n＋27. 因为a1＝25>0， 又由因aann为＝＋1n＝－∈－2Nn2*＋（，2n7＋≥10），＋27≤0得nn≤ ≥11321212， . 所以当n＝13时，Sn有最大值，为S13＝169.
索引
法三 因为S8＝S18，所以a9＋a10＋…＋a18＝0. 由等差数列的性质得a13＋a14＝0. 因为a1>0，所以d<0. 所以a13>0，a14<0.所以当n＝13时，Sn有最大值. 由a13＋a14＝0，得a1＋12d＋a1＋13d＝0，又a1＝25， 解得d＝－2， 所以 S13＝13×25＋13×2 12×(－2)＝169， 所以 Sn 的最大值为 169.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
一、基础达标
1.已知数列{an}满足an＝26－2n，则使其前n项和Sn取最大值的n的值为( D )
A.11或12
B.12
C.13
D.12或13
解析 ∵an＝26－2n，∴an－an－1＝－2， ∴数列{an}为等差数列. 又 a1＝24，d＝－2， ∴Sn＝24n＋n（n2－1）×(－2)＝－n2＋25n＝－n－2252＋6425. ∵n∈N*，∴当 n＝12 或 13 时，Sn 最大.
索引
3.做一做 《张邱建算经》卷上第22题为：今有女善织，日益功疾，且从第2天 起，每天比前一天多织相同量的布，若第1天织5尺布，现在一月(按30天 16
计)共织390尺布，则每天比前一天多织___2_9____尺布(不作近似计算). 解析 由题意知，该女每天的织布尺数构成等差数列{an}，其中 a1＝5，S30＝390， 设其公差为 d，则 S30＝30×5＋30×2 29d＝390，解得 d＝1269.故该女子织布每天增 加1269尺.
等差数列求和求最值
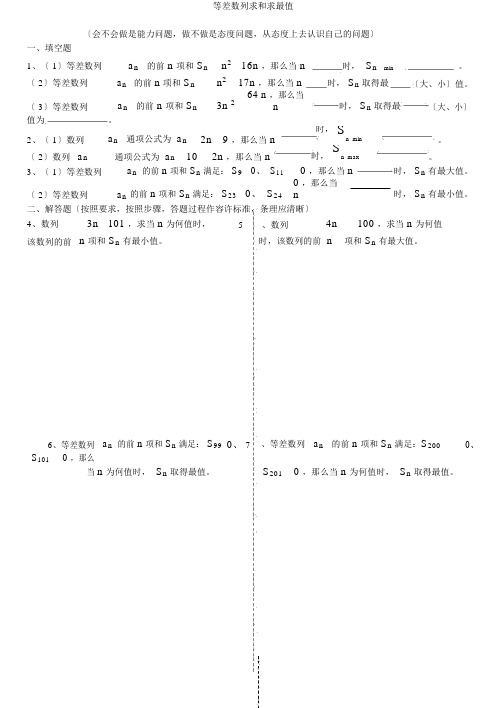
〔会不会做是能力问题，做不做是态度问题，从态度上去认识自己的问题〕一、填空题1、〔 1〕等差数列 a n 的前 n 项和 S n n 2 16n ，那么当 n 时， S nmin。
〔 2〕等差数列 a n 的前 n 项和 S nn 2 17n ，那么当 n时， S n 取得最〔大、小〕值。
〔 3〕等差数列 a n 的前 n 项和 S n3n 2 64 n ，那么当n时， S n 取得最〔大、小〕值为。
2、〔 1〕数列 a n 通项公式为 a n2n 9 ，那么当 n时， S n min 。
〔 2〕数列 a n 通项公式为 a n 102n ，那么当 n时，Sn max。
3、〔 1〕等差数列 a n 的前 n 项和 S n 满足： S 9 0、 S 110 ，那么当 n 时， S n 有最大值。
〔 2〕等差数列 a n 的前 n 项和 S n 满足： S 23 0、 S 240 ，那么当 n时， S n 有最小值。
二、解答题〔按照要求，按照步骤，答题过程作容许标准，条理应清晰〕4、数列3n 101 ，求当 n 为何值时，5、数列4n 100 ，求当 n 为何值该数列的前 n 项和 S n 有最小值。
时，该数列的前 n项和 S n 有最大值。
6、等差数列 a n 的前 n 项和 S n 满足： S 99 0、 7、等差数列 a n 的前 n 项和 S n 满足：S 200 0、S 101 0 ，那么当 n 为何值时， S n 取得最值。
S 201 0 ，那么当 n 为何值时， S n 取得最值。
8、数列a n的前 n 项和 S n n 27n ，〔1〕求9、数列a n的前 n 项和 S n2n 29n 1，a n，〔2〕求当n 为何值时，S n取得最值，并求出最〔 1〕求a n，〔 2〕求当n 为何值时，S n取得最值，值并求出最值。
10、数列a n的前n 项和 S n3n28n ，求11 、〔挑战题〕数列a n的通项 a n3n 11，a5 a6 a7a8a9a10的值。
等差数列中的最值问题
1.等差数列的通项公式： 等差数列的通项公式： 等差数列的通项公式
an=a1+(n-1)d
当d≠0，an=dn+a1-d是n的一次函数 ， 是 的一次函数 2.等差数列的前n项和公式 2.等差数列的前n项和公式： 等差数列的前 项和公式：
n(a1 + an ) Sn= 2
或 Sn=
n( n − 1) na1 + d 2
d 2 d n + (a1 − )n n的二次 当d≠0， Sn= ， 是 的二次 2 2
函数。 函数。
在等差数列{a 中 在等差数列 n}中
a1 > 0, d < 0, Sn有最
an ≥ 0 ) 值(填大或小 an+1 ≤ 0
an ≤ 0 a1 < 0, d > 0, Sn有最 值（填大或小） an+1 ≥ 0
在等差数列｛ 【 问题 2】 在等差数列｛ a n ｝ 中 ， a1 = 26 ， S9 =S18 , 求使 S n ＞０时 n 的最大值
变式训练 是等差数列， 若{an}是等差数列，a1>0,a2003+a2004>0,a2003a2004<0 是等差数列 求使前n项和 最大的自然数n。 项和S ①求使前 项和 n最大的自然数 。 求使前n项和 项和S 成立的最大自然数n。 ②求使前 项和 n>0成立的最大自然数 。 成立的最大自然数
作业
1.等差数列｛an｝的前 项和 n，且Sm=Sn，Sm+n=—— 等差数列｛ 的前n项和 项和S 等差数列 2．设等差数列 n}的前 项和为 n，已知 3=12，S12>0,S13<0. 的前n项和为 ．设等差数列{a 的前 项和为S 已知a ， (1)求公差 的取值范围 求公差d的取值范围 求公差 的取值范围; (2)指出 1，S2，…Sn中哪个值最大，并说明理由。 指出S 中哪个值最大，并说明理由。 指出
等差数列的最值问题
解析（1）设数列{ }的公差为d，则由2009 = 0得20091 +
= 0，
2
1
2009−
即1 + 1004 = 0，则 = −
1 ,所以1 + =
1 ,所以 = (1 +
1004
1004
2
2009−
) = ⋅
1 = 1 ⋅ (2009 − 2 ).因为1 < 0, ∈ ∗ ,所以当 = 1004或
由 S5＝S12 得 5a1＋10d＝12a1＋66d，
d＝－ a1<0.
8
1
－ a1
n（n－1）
n（n－1）
1
则 Sn ＝ na1 ＋
d ＝ na1 ＋
· 8 ＝ － a1(n2 － 17n) ＝ －
16
2
2
17
n－
1
2 289
a1
2 ＋
a1，因为 a1>0，n∈N*，所以当 n＝8 或 9 时，Sn 有最大值．
2
1004
2008
1005
= 1005时， 取得最小值，最小值为
1 .
2
1005−
1
1005−
2
（2）由（1）得 =
1 . 由 ≤ , 得
(2009 − ) ≤
1 .
1004
2008
1004
因为 1 < 0, 所以 2 − 2011 + 2010 ≤ 0, 即 ( − 1)( − 2010) ≤ 0 ，解得 1 ≤
≤ 2010 .故所求 的取值集合为 {|1 ≤ ≤ 2010, ∈ ∗ } .
高考数学复习等差数列的前n项和Sn的最值问题
10×9 15×14 解法 2 设公差为 d.因为 S10＝S15，所以 10a1＋ 2 d＝15a1＋ 2 d， nn－1 5 5 2 125 代入 a1＝20，得 d＝－3.所以 Sn＝na1＋ 2 d＝－6n ＋ 6 n＝ 12×11 5 2 －6(n －25n)， 所以当 n＝12 或 13 时， Sn 取得最大值为 12a1＋ 2 5 ×－3＝130.
S7<S8， 所以 S9<S8， 49＋21d<56＋28d， 7 即 解得－1<d<－8. 63＋36d<56＋28d，
即d
7 的取值范围为－1，－8 .
a11 5．在等差数列{an}中，a <－1，若它的前 n 项和 Sn 有最大值，则使 Sn 10 取得最小正数的 n＝
1 3 － － q∈ . 2 2，2 7
8．在等差数列{an}中，已知 a1＝20，前 n 项和为 Sn，且 S10＝S15，求当 n 取何值时，Sn 取得最大值，并求出它的最大值．
答案：当 n＝12 或 13 时，Sn 取得最大值为 130.
解法 1 因为 S10＝S15，所以 S15－S10＝0，即 a11＋a12＋a13＋a14＋a15＝0， 也即 5a13＝0，所以 a13＝0，即 a1>a2>…>a12>a13＝0>a14>a15>…， 13a1＋a13 13×20＋0 故当 n＝12 或 13 时，Sn 取得最大值为 ＝ ＝ 2 2 130.
微专题47
等差数列的前n项和Sn的最 值问题
2 4 1．已知等差数列{an}：5,47，37，…，当 n＝
7 或8
时，数列
{an}的前 n 项和 Sn 最大？
由一道题谈求解数列最值问题的方法
学考方略数列最值问题的综合性较强，常与不等式、函数、方程、数列等相结合.此类问题的难度较大，侧重于考查同学们的推理和综合分析能力.本文以一道题为例，谈一谈解答数列最值问题的方法.题目：在等差数列{}a n 中，a 1<0，S 9=S 12，则数列{}a n 的前几项和最小？该题看似简单，其实较为复杂.要求得数列和的最小值，我们需根据等差数列的性质、公式和已知关系式，推理出数列各项之间的规律，明确公差d 的取值范围，以便确定数列中的哪些项为负值、0、正值，那么所有负数项的和必然最小，再根据等差数列的前n 项和公式就能求得数列的和的最小值.有如下三种求解的方法.一、利用数列的单调性求解我们知道数列具有单调性，一般地，若a n >a n +1，则{}a n 是递减数列；若a n <a n +1，则{}a n 是递增数列.对于等差数列而言，若公差大于零则数列是递增数列，公差小于零则数列是等差数列.在解答等差数列问题时，我们可以根据数列的通项公式或者公差来判断数列的单调性，然后根据数列的单调性来求数列和的最值.对于本题，我们可以根据已知关系式和等差数列前n 项和公式S n =n (a 1+a n )2=na 1+n (n -1)2d 来确定公差d 的取值范围，从而判断出数列的单调性，再根据数列的单调性来求数列和的最小值.解：因为S 9=S 12，所以9a 1+9×82d =12a 1+12×112d ,即d =-110a1.由a 1<0知d >0，则数列{}a n 是递增数列，则ìíîïï1-110()n -1≥0，1-110n ≤0，解得10≤n ≤11，所以当n =10或n =11时，S n 的值最小，即数列{}a n 的前10或11项和最小.二、巧用等差中项的性质求解若a 、b 、c 成等差数列，则b 为a 、c 的等差中项.a 、b 、c 成等差数列的充分必要条件是b =a +c 2.在求解等差数列最值问题时，我们可以借助等差中项的性质来建立关系式，从而明确数列中的哪些项为负数，哪些项为正数，求得数列和的最值.解：因为S 9=S 12，根据数列的前n 项求和公式S n =(a 1+a n )2可得9(a 1+a 9)2=12(a 1+a 12)2，化简得a 10+a 11+a 12=3a 11=0，解得a 11=0，所以数列{}a n 前10或11项和最小.此解法主要运用了等差中项的性质，从而求得a 11=0，求得数列和的最小值.该解题思路巧妙，解题过程简捷.运用该方法解题，同学们需灵活运用等差中项的性质.三、借助函数思想求解数列是一种特殊的函数，不过其自变量为自然数.在解答数列最值问题时，我们可巧妙利用函数思想来解题，将等差数列的前n 项和看作关于n 的二次函数式，将等比数列的前n 项和看作关于n 的指数函数式，借助二次函数、指数函数的图象和性质来解题.对于本题，我们可以将等差数列的前n 项和看作关于n 的二次函数式，借助二次函数的单调性来求数列的最值.解：因为S 9=S 12，所以9a 1+9×82d =12a 1+12×112d ，即d =-110a1，因为S n =na 1+n ()n -12d =d 2n 2+æèöøa 1-d 2n ，所以S n =æèöø-120a 1∙n 2+æèöø2110a 1∙n =-a 120æèöøn -2122+44180a1，由二次函数的性质知，函数图象的开口向下，对称轴为n =212=10.5，所以当n =10或n =11时，S n 的值最小，即数列{}a n 的前10或11项和最小.借助函数思想，可将数列问题转化为函数问题，使问题快速得解.虽然数列最值问题较为复杂，但是同学们只要熟练运用数列的通项公式、前n 项和公式，并掌握一些求解数列最值问题的方法，如利用数列的单调性、数列中项的性质以及函数思想，就能顺利破解难题.（作者单位：山东省青岛市即墨区第二中学）50Copyright©博看网 . All Rights Reserved.。
求等差数列前n项和的最值问题的两种常用解法
求等差数列前n 项和的最值问题的两种常用解法【必备方法】1.函数法：利用等差数列前n 项和的函数表达式bn an S n +=2，通过配方或借助图象求二次函数最值的方法求解，一定注意n 是正整数。
2.邻项变号法：①0,01<>d a 时，满足⎩⎨⎧≤≥+001n n a a 的项数m 使得n S 取得最大值为m S ； ②当0,01><d a 时，满足⎩⎨⎧≥≤+001n n a a 的项数m 使得n S 取得最小值为m S . 【典例示范】例1、等差数列}{n a 前n 项和为n S ，已知1131,13S S a ==，当n S 最大时，n 的值是( )(A)5 (B)6 (C)7 (D)8解：方法一：由113S S =得01154=+++a a a ，根据等差数列性质可得087=+a a ，根据首项等于13可推知这个数列递减，从而得到0,087<>a a ，故n=7 时，n S 最大.方法二：由113S S =可得d a d a 55113311+=+，把131=a 代入得2-=d ，故n n n n n S n 14)1(132+-=--=，根据二次函数性质，当n=7时，n S 最大. 方法三：根据131=a ,113S S =，知这个数列的公差不等于零.由于113S S =说明这个数列的和先是单调递增的然后又单调递减.根据公差不为零的等差数列的前n 项和是关于n 的二次函数，以及二次函数图象的对称性，当113S S =时，只有72113=+=n 时，n S 取得最大值. 答案：C练习：1.已知在等差数列}{n a 中，311=a ，n S 是它的前n 项的和，2210S S =.（1）求n S ；（2）这个数列前多少项的和最大，并求出这个最大值. 解析：（1）∵102110a a a S ++= ，222122a a a S ++= ，又2210S S =， ∴0221211=++a a a ，则031212211=+=+d a a a ，又311=a ，2-=∴d ，∴21322)1(n n d n n na S n -=-+=。
等差数列前n项和最值问题
等差数列前n项和最值问题Company Document number：WUUT-WUUY-WBBGB-BWYTT-1982GT等差数列前n 项和的最值问题问题引入：已知数列{},n a 的前n 项和212n S n n =+,求这个数列的通项公式.数列是等差数列吗如果是,它的首项与公差分别是什么 解:当n>1时:1122n n n a s s n -=-==-当n=1时:211131122a s ==+⨯= 综上:122na n =-,其中:132a =,2d = 探究1:一般地,如果一个数列{}n a 的前n 项和为:2,n s pn qn r =++≠0,那么这个数列一定是等差数列吗如果是,它的首项和公差分别是什么结论:当r=0时为等差,当r ≠0时不是一、 应用二次函数图象求解最值 例1：等差数列{}n a 中， 1490,a S S >=，则n 的取值为多少时n S 最大分析：等差数列的前n 项和n S 是关于n 的二次函数，因此可从二次函数的图象的角度来求解。
解析：由条件1490,a S S >=可知，d<0，且211(1)()222n n n d dS na d n a n -=+=+-， 其图象是开口向下的抛物线，所以在对称轴处取得最大值，且对称轴为496.52n +==，而n N *∈，且介于6与7的中点，从而6n =或7n =时n S 最大。
1.已知等差数列{n a }中1a =13且3S =11S ,那么n 取何值时,n S 取最大值.解析：设公差为d ，由3S =11S 得：3×13+3×2d/2=11×13+11×10d/2 d= -2, n a =13-2(n-1), n a =15-2n,由⎩⎨⎧≤≥+0a 0a 1n n 即⎩⎨⎧≤+-≥-0)1n (2150n 215得：≤n ≤,所以n=7时,n S 取最大值.2.已知a n 是各项不为零的等差数列，其中a 1＞0，公差d ＜0，若S 10=0，求数列a n 前 5 项和取得最大值．结合二次函数的图象，得到二次函数图象的开口向下，根据图象关于对称轴对称的特点，得到函数在对称轴处取到最大值，，注意对称轴对应的自变量应该是整数或离对称轴最近的整数．a n 是各项不为零的等差数列，其中a 1＞0，公差d ＜0，S 10=0，根据二次函数的图象特点得到图象开口向下，且在n==5时，数列a n 前5项和取得最大值．二、转化为求二次函数求最值例2、在等差数列{n a }中, 4a ＝－14, 公差d ＝3, 求数列{n a }的前n 项和n S 的最小值 分析：利用条件转化为二次函数，通过配方写成顶点式易求解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
等差数列及其前n 项和（2）
——等差数列中的最值问题
数学组
一、教学目标
1、掌握等差数列的通项公式和前n 项和公式的形式和应用。
2、掌握常见题型的解法及常用思想方法。
3、掌握等差数列求最值问题的多种不同方法，并能对最值问题进行归纳总结。
二、教学重点和难点
重点：等差数列求最值问题的常用解法。
难点：通过例题的讲解引导学生对等差数列的最值问题进行归纳和总结，并理解何种形式会有最大值，何种形式会有最小值。
三、教学过程
1、复习旧知，回顾等差数列的常用公式：
（1）通项公式()11n a a n d =+-
（2）前n 项和公式()112
n n n S na d -=+=()12n n a a + （3）等差中项概念1
2()A a b =+
（4）等差数列的判定方法
定义法：1n n a a +-=常数（*n N ∈）⇔{}n a 为等差数列；
中项公式法：122n n n a a a ++=+（*n N ∈）⇔{}n a 为等差数列；
通项公式法：n a kn b =+（*n N ∈）⇔{}n a 为等差数列；
前n 项求和法：2n S pn qn =+（*n N ∈）⇔{}n a 为等差数列
（复习时主要以口述为主，必要的公式进行板书，主要让学生进行回顾，强调等差数列的通项公式和前n 项和公式的形式，即通项公式是关于n 的一次函数，前n 项和公式是关于n 的二次函数，且常数项为0，为后面课程的讲述埋好伏笔。
）
2、教授新课：
复习用书《高考总复习学案与测评》第87页，题型四：等差数列中的最值问题 例4、在等差数列{}n a 中，已知201=a ，前n 项和为n S ，且1510S S =，求当n 取何值时，n S 有最大值，并求出它的最大值。
分析：要求n 为何值时，n S 有最大值，可从n S 的形式入手思考，n S 是关于n 的二次函数，可以从函数的角度求出n S 的最大值。
解：（方法一）因为201=a ，且1510S S =可得
d a d a 2
14151529101011⨯+=⨯+
解得35-=d 所以243125)225(656125652)1(221+--=+-=-+=n n n d n n na S n 又因为*
∈N n ，所以比较1301212==S n 时，
1301313==S n 时，
因此，n n n S 1312时，或者==的最大值为130.
思考：在用n S 是关于n 的二次函数求最值时，如何避免复杂的计算，比如本题中的配方 引导学生讨论得到只要取离对称轴最近的整数处的和，即可得到最值，而对称轴可以由二次函数中的公式得到，这样可以避免复杂的计算，以便提高计算的准确度。
3、小组合作讨论
思考：为什么等差数列会存在最值，是不是所有的等差数列都有最值呢什么样的等差数列存在最大值，什么样的等差数列又存在最小值
通过观察数列、归纳特点并讨论可得两类数列存在最值，
（1） 若0,01<>d a ，数列有最大值
（2） 若0,01><d a ，数列有最小值
思考：那有没有更简单的方法来得到等差数列何时取到最值呢
由数列的增减情况可以得到只要找出何时出现正负转折项，在该项处即得到等差数列前n 项和的最值。
以0,01<>d a 的数列为例，若前7项为正，第8项开始为负，则前7项和为最大值。
练习：（方法二）学生用此方法求出例4中的最值，并与前一种方法进行比较。
4、归纳等差数列最值问题的求法
方法一、利用2n S pn qn =+是关于n 的二次函数，在离对称轴最近的整数处取得最值。
方法二、利用等差数列的单调性，求出正负转折项。
思考：本题还有没有什么特点能够使得我们很快得出哪一项开始出现正负转折 引导学生观察得出
（方法三）
因为1510S S =，所以01514131211=++++a a a a a
由等差数列的性质可以得出013=a
所以0,01412<>a a
所以，n n n S 1312时，或者==的最大值为130.
5、课内训练
复习用书《高考总复习学案与测评》第85页例4的举一反三题
已知数列{}n a 的前n 项和)(242*∈+-=N n n n S n ，（1）求{}n a 的通项公式；（2）当n 为
何值时，n S 达到最大最大值是多少
6、小结
等差数列前n 项和的两种常用解法，并能在具体题目中选择合适的方法进行求解。