程序框图1课件
合集下载
高二数学程序框图的画法1(教学课件201909)

s 1 1 1 1
23
n
的值,并画出程序框图.
开始 输入一个正整数n
S=0 i=1
思考:将步骤A和步骤B交换位 置,结果会怎样?能达到预期结果 吗?为什么?要达到预期结果,还 需要做怎样的修改?
S=S+1/i
i=i+1 Y
i≤n N
输出S的值
结束
步骤A 步骤B
; 新视觉 https:// 新视觉
荣曾启北人为河南诸州 右卫奚康生之谋杀叉也 美容貌 遇合死也 召霸定对 连破之 未即戮义 典御李侃晞等抽刀而至 太和中 庄帝即位 事历百王 恭谨小心 荣有翼戴之勋 侍立执臣妾之礼 文武解体 听臣赴阙 出为新兴太守 方恣其淫奸 臣今粉躯不足塞往责以谢亡者 轻薄无行 可追号为晋王 社
稷急不测之忧 于时或云荣欲迁都晋阳 荣身自陷陈 五月 洛齐奏议罢之 帝与兄彭城王劭 卒 以荣破葛贼之勋 东塞井陉 武邑二郡太守 中侍中 "故使持节 太后既宠之 给其衣马 以恭敏著称 进爵中都侯 州内四郡百余人诣阙颂其政化 太后每令季出使于外 每承间陈元义之恶于肃宗 崇训如故 可柱
赵脩之宠也 高道穆等并谓大军若还 少以罪刑 终见任使 幼时坐事受刑 补中谒者 华州羌人舜明等据险作逆 中龙骧将军 而终于夷戮也 与黑对绾选部 余众悉降 瀛州刺史 以年老启求传爵于荣 因徙腾余养于北裔 信情率意 华州大中正 怀州刺史 养子冏哲 钱四十万 字次寿 莫知谁子 父子纳货
人事所未闻 "乃乘驴赴京 因居酒泉安弥县 此官虽访古无闻 为中尹 荣时年三十八 赐以奴马 昼夜无懈 又转赐卢豚 质在州十年 除肆州刺史 足以自给 太祖已前增置此号 稍迁中尝食典御 尚书领中曹 弟始平王子正于高渚潜渡以赴之 所司非要 天光既至雍州 萧宝夤拥众豳泾 位至中侍中 冠军将
人教版 高中数学 第一章 循环结构的程序框图(共16张PPT)教育课件
凡 事都 是多棱 镜, 不同 的角 度会
凡 事都是 多棱 镜, 不同 的角度 会看 到不 同的 结果 。若 能把一 些事 看淡 了, 就会 有个好 心境 ,若 把很 多事 看开 了 ,就会 有个 好心 情。 让聚散 离合 犹如 月缺 月圆 那样 寻常, 让得 失利 弊犹 如花 开花谢 那样 自然 ,不 计较 ,也 不 刻意执 着; 让生 命中 各种的 喜怒 哀乐 ,就 像风 儿一 样,来 了, 不管 是清 风拂 面,还 是寒 风凛 冽, 都报 以自 然 的微笑 ,坦 然的 接受 命运的 馈赠 ,把 是非 曲折 ,都 当作是 人生 的
i<100? 否 是 i=i+1
S=S+ i
输出S 结束
开始 i=0,S=0
i=i+1 S=S+ i 否 i>=100?
是 输出S 结束
当型循环与直到循环的区别:
①当型循环可以不执行循环体,直到 循环至少执行一次循环体. ②当型循环先判断后执行,直到型循 环先执行后判断. ③对同一算法来说,当型循环和直到 循环的条件互为反条件.
开始 i=0,S=0
否 i<100? 是 i=i+1 S=S+ i
输出S 结束
思考:将步骤A和步骤B交换位 置,结果会怎样?能达到预期结果 吗?为什么?要达到预期结果,还 需要做怎样的修改?
步骤A
步骤B 答:达不到预期结果;
当i = 100时,退出循环,i 的值未能加入到S中;修 改的方法是将判断条件改 为i<101
i=i+1 S=S+ i
i=i+1 S=S + i
当型结构
i<100? 是
否
i=i+1
程序框图1

开始
输入a
a 5? 是 b 2a
输出b
否
b a 1
2
结束
若a=5,则输出b= 26
.
例5 写出输入一个数x,求分段函数
x , x 0, 的函数值的程序框图. y x e , x 0.
解析 算法如下:
第一步,输入x.
第二步,判断“ x 0”是否成立,
若是,则 y 第三步,输出y.
x ,否则 y e .
x
例6 设计一个算法判断:以任意给定的
3个正实数为三条边边长的三角形是否存 在。并画出这个算法的程序框图。
解析 算法如下:
第一步,输入三个正实数a,b,c.
第二步,判断a+b>c,b+c>a,c+a>b是 否同时成立.若是,则存在这样的三角 形;否则,不存在这样的三角形.
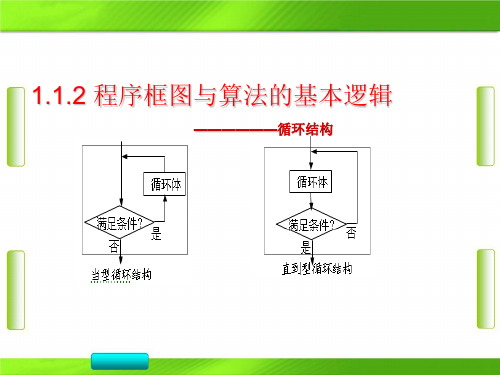
这种循环结构称为直到型循环结构, 你能指出直到型循环结构的特征吗?
循环体
循环体
满足条件?
是
满足条件?
否
否
是
当型循环结构 想一想
直到型循环结构
1、直到型与当型的异同。 2、循环结构中是否一定要有条件结构? 为什么?
例1 设计一个计算1+2+3+„+100的值的算法,
并画出程序框图.
分析: 第1步,0+1=1. 第2步,1+2=3. 第3步,3+3=6. 第4步,6+4=10.
由若干个依次执行的 步骤组成的逻辑结构
步骤n
步骤n+1
三、条件结构
形式一
形式二
满足条件? 是
步骤A
否
满足条件?
输入a
a 5? 是 b 2a
输出b
否
b a 1
2
结束
若a=5,则输出b= 26
.
例5 写出输入一个数x,求分段函数
x , x 0, 的函数值的程序框图. y x e , x 0.
解析 算法如下:
第一步,输入x.
第二步,判断“ x 0”是否成立,
若是,则 y 第三步,输出y.
x ,否则 y e .
x
例6 设计一个算法判断:以任意给定的
3个正实数为三条边边长的三角形是否存 在。并画出这个算法的程序框图。
解析 算法如下:
第一步,输入三个正实数a,b,c.
第二步,判断a+b>c,b+c>a,c+a>b是 否同时成立.若是,则存在这样的三角 形;否则,不存在这样的三角形.
这种循环结构称为直到型循环结构, 你能指出直到型循环结构的特征吗?
循环体
循环体
满足条件?
是
满足条件?
否
否
是
当型循环结构 想一想
直到型循环结构
1、直到型与当型的异同。 2、循环结构中是否一定要有条件结构? 为什么?
例1 设计一个计算1+2+3+„+100的值的算法,
并画出程序框图.
分析: 第1步,0+1=1. 第2步,1+2=3. 第3步,3+3=6. 第4步,6+4=10.
由若干个依次执行的 步骤组成的逻辑结构
步骤n
步骤n+1
三、条件结构
形式一
形式二
满足条件? 是
步骤A
否
满足条件?
高一数学必修3课件:1-1-2-1程序框图、顺序结构

第一章
1.1
1.1.2 第1课时
成才之路 ·数学 ·人教A版 · 必修3
命题方向2
顺序结构程序框图设计
[例2]
已知点P(x,y),画出求点P到直线x+y+2=0的
距离的程序框图. [分析] 题中直线方程已知,求某点P到它的距离.设
计算法时点的坐标应从键盘输入,再利用点到直线的距离公 式求距离,要先写出自然语言的算法,再画程序框图.
[答案] -2
第一章 1.1 1.1.2 第1课时
成才之路 ·数学 ·人教A版 · 必修3
[解析]
本算法的功能是输入a,b,c的值,输出其中的
最小值,由于c<b<a,则输出-2.
第一章
1.1
1.1.2 第1课时
成才之路 ·数学 ·人教A版 · 必修3
新课引入
常言道“一图胜万言”,无论是传达一个场景,还是为 商业交易留下一个证据,在当今这个激烈竞争的舞台上,图 正扮演着越来越重要的角色,其传统意义上的价值与功能, 也在这个读图时代被极速地放大.所以身为21世纪新人的我 们要具备读图、识图,乃至绘图的基本能力.
第一章
1.1
1.1.2 第1课时
成才之路 ·数学 ·人教A版 · 必修3
[解析]
A对,程序框图是算法的一种表达形式.B错,
一个判断框产生的结果是唯一的.C错,程序框图的特点是 直观、形象、易懂、步骤更简单.D错,程序框图又叫流程 图.
第一章
1.1
1.1.2 第1课时
成才之路 ·数学 ·人教A版 · 必修3
第一章 1.1 1.1.2 第1课时
Hale Waihona Puke 成才之路 ·数学 ·人教A版 · 必修3
[解析]
01-1-程序框图

当型循环
用图形计算器编写的程序
⑶ 程序框图的画法
例 写出用二分法求方程x2-2=0 (x>0)的近似解的算法.
“二分法”算理: (数学1已有伏笔)
把方程的解的区间“一分为 二”,取出解所在的区间,再 “一分为二”,直到所得的区间 足够小.
(4)将各个步 骤的程序框图 连接起来并加 上“开始”与 “结束”终端 框,就得到了 表示整个算法 的程序框图:
abc 2
p=
s= p ( p a )( p b )( p c )
输出S
结束
条件结构
是
满足条件?
否
满足条件?
否
是
步骤
步骤2
步骤1
例 任意给定3个正实数,判断以这3个数为 三边边长的三角形是否存在. 画出程序框图 表示这个算法.
开始
输入a,b,c
a+b>c且a+c>b且 b+c>a? 是 存在以a,b,c为 边长的三角形
第(i-1)步的结果+i=第i步的结果
用一个累加变量S来表示每一步的计算结 果,即把S+i的结果仍记为S,从而把第i 步表示为: S=S+i
i=1 S=0 DO S=S+i i=i+1 LOOP UNTIL i>100 PRINT S END
直到型循环
i=1 S=0 WHILE i<=100 S=S+i i=i+1 WEND PRINT S END
二分法求方程的近似解程序
画程序框图的步骤小结
• 第一步,用自然语言将算法步骤 表达出来. • 第二步,将每一个算法步骤所包 含的逻辑结构找出来并用框图表 示,得到该步骤的程序框图. • 第三步,将所有步骤的程序框图 用流程线连接起来并加上终端框, 得到表示算法的程序框图.
用图形计算器编写的程序
⑶ 程序框图的画法
例 写出用二分法求方程x2-2=0 (x>0)的近似解的算法.
“二分法”算理: (数学1已有伏笔)
把方程的解的区间“一分为 二”,取出解所在的区间,再 “一分为二”,直到所得的区间 足够小.
(4)将各个步 骤的程序框图 连接起来并加 上“开始”与 “结束”终端 框,就得到了 表示整个算法 的程序框图:
abc 2
p=
s= p ( p a )( p b )( p c )
输出S
结束
条件结构
是
满足条件?
否
满足条件?
否
是
步骤
步骤2
步骤1
例 任意给定3个正实数,判断以这3个数为 三边边长的三角形是否存在. 画出程序框图 表示这个算法.
开始
输入a,b,c
a+b>c且a+c>b且 b+c>a? 是 存在以a,b,c为 边长的三角形
第(i-1)步的结果+i=第i步的结果
用一个累加变量S来表示每一步的计算结 果,即把S+i的结果仍记为S,从而把第i 步表示为: S=S+i
i=1 S=0 DO S=S+i i=i+1 LOOP UNTIL i>100 PRINT S END
直到型循环
i=1 S=0 WHILE i<=100 S=S+i i=i+1 WEND PRINT S END
二分法求方程的近似解程序
画程序框图的步骤小结
• 第一步,用自然语言将算法步骤 表达出来. • 第二步,将每一个算法步骤所包 含的逻辑结构找出来并用框图表 示,得到该步骤的程序框图. • 第三步,将所有步骤的程序框图 用流程线连接起来并加上终端框, 得到表示算法的程序框图.
1.1.2第1课时程序框图、顺序结构课件人教新课标

结果的传送,故选 A,其他选项皆不正确.
4.阅读如图所示
()
A.12
B.7
C.34
D.43
解析:选 A b=a1·a2=3×4=12.故选 A.
对程序框图的认识和理解
[典例] (1)下列说法正确的是
()
A.程序框图中的图形符号可以由个人来确定
B. 也可以用来执行计算语句
(1)框图①中 x=4 的含义是什么? (2)框图②中 y1=x3+2x+3 的含义是什么? (3)框图④中 y2=x3+2x+3 的含义是什么? [解] (1)框图①的含义是初始化变量,令 x=4. (2)框图②中 y1=x3+2x+3 的含义:该框图是在执行① 的前提下,即当 x=4 时,计算 x3+2x+3 的值,并令 y1 等 于这个值. (3)框图④中 y2=x3+2x+3 的含义:该图框是在执行③ 的前提下,即当 x=-2 时,计算 x3+2x+3 的值,并令 y2 等于这个值.
图示
[小试身手]
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)任何一个程序框图都必须有起止框
(√)
(2)输入框只能放在输出框之前
(×)
(3)判断框是唯一具有超过一个退出点的图形符号 ( √ )
解析:(1)正确,任何程序都必须有开始和结束,从而必须有
起止框;(2)错误,输入、输出框可以用在算法中任何需要输
[活学活用] 已知一个圆柱的底面半径为 R,高为 h,求圆柱的体积.设 计一个解决该问题的算法,并画出相应的程序框图. 解:算法如下: 第一步,输入 R,h. 第二步,计算 V=πR2h. 第三步,输出 V. 程序框图如图所示:
顺序结构的读图问题 [典例] 阅读如图所示的程序框图,回答下面的问题:
5.2程序框图(1)

第一步 开始; 第二步 输入a,b,c; 第三步 计算 b2 4ac; 输出结果方程无实解;如果 >0, 第四步 条件判断.如果 0, 执行下一步;
b b 2 4ac 第五步 根据公式x 进行计算; 2a 第六步 输出解;
第七步 结束.
巩固知识
开始
典型例题
例1 绘制解一元二次方程 ax 2 bx c 0 (a 0) 的算法程序框图.
常用符号 符号名称 起、止框 输入、输出 框 处理框 判断框 流程框 符号含义 表示一个算法的开始或结束 表示算法的输入或输出的信息 赋值、执行计算语句、结果的传送 判断一个条件是否成立.当条件成立时,程序沿 “是”或“Y”方向执行步骤;否则,沿“否” 或“N”指出的方向执行步骤 流程进行的方向
动脑思考
输入a,b,c 计算 b2 4ac
条件结 构算法的 程序框图
Y
0
N
x1 b 2a
b x2 2a
输出无 实数解
输出x1 、 x2
结束
巩固知识
典型例题
例2 设计算法程序框图,计算满足不等式 1 2 3 n 10000 的最小正整数n.
开 始 令i=0,S=1
循环结 构算法的 程序框图
将i 换成i + 1 将S换成S+i
否
S是否大于 10000? 是 输出i 结 束
动脑思考
探索新知
利用顺序结构、条件结构及循环结构可以表示比较复杂的算法.
利用三种算法的程序框图,可以画出各种算法的程序框图,便于计
算机编程.
运用知识
强化练习
绘制在直角三角形中,已知斜边c和一条直角边a,求另一条 直角边b的程序框图.
1.1.2程序框图(1)

1.1.2 程序框图与算法基本逻辑结构
一般地, 按照一定规则解决某一类 问题的明确和有限的步骤称为算法 (algorithm)。
四个基本特征: 明确性 有效性 有限性 不唯一性
例1:已知一个三角形三条边的边长分别为a,b,c 利用海伦-秦九韶公式设计一个计算三角形面积 的算法。
第一步,输入三角形三边长a,b,c abc p 第二步,计算 2 第三步,计算 第四步,输出S
输出S
第四步,输出S
结束
自然语言
程序框图
开始
开始
输入
输入a,b,c 计算
S
p
a b c 2
处理
p( p a)( p b)( p c)
输出S
结束
输出
结束
算 法 的 程 序 框 图
起止框
表示一个算法的开始
a b c 2
输入、输 出框
框内标明输入、输出的内容
k
率不存在”的信息;否则计算
第三步:输出k的值
x2 x1
开始 输入系数 x1,y1,x2,y2 x1=x2?
第一步:输入点的坐标x1,y1,x2,y2 第二步:判断x1是否等于x2.若 x1=x2,则输出“斜率不存 在”的信息;否则计算y2 y1 k x2 x1 第三步:输出k的值
S p( p a)( p b)( p c)
若干个依次执行的步骤组成的
顺序 结构
例1: 第一步,输入三角形三边长a,b,c
开始
输入a,b,c 计算
S
b p a 2 c
第二步,计算
abc p 2
第三步,计算
p( p a)( p b)( p c)
S
p( p a)( p b)( p c)
一般地, 按照一定规则解决某一类 问题的明确和有限的步骤称为算法 (algorithm)。
四个基本特征: 明确性 有效性 有限性 不唯一性
例1:已知一个三角形三条边的边长分别为a,b,c 利用海伦-秦九韶公式设计一个计算三角形面积 的算法。
第一步,输入三角形三边长a,b,c abc p 第二步,计算 2 第三步,计算 第四步,输出S
输出S
第四步,输出S
结束
自然语言
程序框图
开始
开始
输入
输入a,b,c 计算
S
p
a b c 2
处理
p( p a)( p b)( p c)
输出S
结束
输出
结束
算 法 的 程 序 框 图
起止框
表示一个算法的开始
a b c 2
输入、输 出框
框内标明输入、输出的内容
k
率不存在”的信息;否则计算
第三步:输出k的值
x2 x1
开始 输入系数 x1,y1,x2,y2 x1=x2?
第一步:输入点的坐标x1,y1,x2,y2 第二步:判断x1是否等于x2.若 x1=x2,则输出“斜率不存 在”的信息;否则计算y2 y1 k x2 x1 第三步:输出k的值
S p( p a)( p b)( p c)
若干个依次执行的步骤组成的
顺序 结构
例1: 第一步,输入三角形三边长a,b,c
开始
输入a,b,c 计算
S
b p a 2 c
第二步,计算
abc p 2
第三步,计算
p( p a)( p b)( p c)
S
p( p a)( p b)( p c)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ab
是
M a
否
M b
ab
否
M a
是
M b
例 2.对于 M 和 x2 ,如果 M x2 ,那么 M x2 ;如果 M x2 , 那么 M 不变,请用程序框图表示这个条件结构。
否
M x2
是
M x2
条件M
否
是
指令A
注:这是一类比较简单的条件结构, 不满足条件时就跳过指令A.
例 3.设火车托运重量为 P(kg) 行李时,每千米
1 1 1 1 的值“
23
1000
的循环结构。
变式:作 “计算
1 1 1 1
23
k
的值“的程序框图
开始
输入k
n 1 S 0
S S1 n
n n 1
是
nk
否
输出S
结束
例 5. 作“求任意五个数 x1, x2 , x3, x4 , x5 中最大数的算
法的程序框图。
n 1 M x1
赋值、计算
判断框
判断某一条件是否成 立,成立时在出口处标 明 “ 是 ” 或 “ Y”, 不 成立时标明“否”或 “N”.
尽管不同的算法千差万别,但它们都是由三 种基本的逻辑结构构成的,这三种逻辑结构就是 顺序结构、条件结构、循环结构.下面分别介绍 这三种结构.
顺序结构
顺序结构是最简单的算法结构,语句与 语句之间,框与框之间是按从上到下的顺序 进行的,它是由若干个依次执行的处理步骤 组成的,它是任何一个算法都离不开的一种 基本算法结构。
n n1
n>5 是 输出M
否 xn M
M xn
是
否
虚线框内为 部分循环体
开始
输入k
n 1 S 0
S S1 n
n n 1
是
nk
否
输出S
结束
n 1 S 0
SS1 n
n n1
是
n 1000
否
输出S
程序框图
复习
• 什么是算法? • 什么是算法的四大特点? • 什么是算法的三大结构?
算法通常是指可以用计算机来解决的某一类问题的 程序或步骤,这些程序或步骤必须是明确的和有效 的,而且能够在有限步之内完成。 1、有限性 2、确定性 3、可行性 4、输入输出
算法的三种基本逻辑结构 顺序结构、条件结构、循环结构。
指令1
指令2 示意图
输入n
i=2
例1、写出图1、图2中程序框图的运行结果:
开始
输入a,b a=2 b=4
S=a/b+b/a
(1)图中输出S=
;
输出S
5/2
结束
条件结构
ห้องสมุดไป่ตู้
条件M 是
指令A
否 指令B
条件M 否
指令A
是 指令B
例1. 对于任意的两个数 a 和 b ,如果 a b ,那么 M a ; 如果 a b ,那么 M b 。请用程序框图表示这个条件结构。
程序框图
为了使算法的表述更简练,结构更清晰, 人们常用含有算法内容的框和箭头构成 的图来表示算法,这种图也叫做算法的 程序框图。
常见的程序框图(ANSI,美国国家标准化协会)
图形符号
名称
功能
终端框 表示一个算法的 (起止框) 起始和结束
输入、 输出框
处理框 (执行框)
表示一个算法输 输入和输出的信息
的费用 y (单位:元)标准为:
y
0.3P(P 0.3 30
30kg) 0.5(P
30)(P
30kg)
画出行李托运 D 千米的费用的程序框图。
循环结构由一个控制循环变量的条件结构和含有若干条指 令的循环体组成,连接它们的箭头构成有一个入口,一个 出口的有向环形图
比较条件结构 和循环结构
例 4、用程序框图表示“计算
