随机前沿模型(SFA)-原理解读
物流业要素配置效率及区域异质性——基于SFA模型的实证检验

分析了 2005-2018 年全国各地区劳动、资本、技术三大生产要素资源配置效率。结果表明,全国物流业要素配置
效率大体呈波动变化的下降态势。资本和劳动力要素配置效率差异格局明显,总体呈现出“东强西弱”的异质性
格局,需要针对性地提升各区域生产要素的配置和利用水平,实现物流业多样化发展。
关键词:劳动力要素配置;物流业;随机前沿模型;异质性;实证分析
的产出模式,当 ui,t>0 时表示为产出导向型生产非效率项。
考虑物流业完全竞争要素市场下生产要素的自由流
动,在供求双方均拥有完全信息交换需求以保证竞争不受
到阻碍与干扰的前提下,要素配置便达到最优状态。参考
Kim(1992)的研究,有如下结论:
生产函数:Y=f (x1、x2…xj )
(2)
利润函数:π=TR-c=p·f (x1、x2…xj )-∑ j wj xj
中图分类号:F252
文献标识码:A
文章编号:2095-9397(2021)14-0111-04
文章著录格式:何纪翔,马晓琳 . 物流业要素配置效率及区域异质性——基于 SFA 模型的实证检验 [J]. 商业经
济研究,2021(14):111-114
引言
资本、劳动力均是维持生产活动不可或缺的物质基 础,为产业经济建设和发展提供了有力支撑。一直以来, 我国物流业粗放式发展格局依赖于生产要素无序的高投 入和高消耗,在很大程度上造成了要素配置扭曲,引起了 各类生产要素过度消耗、效率低下等严重阻碍经济可持 续发展的问题。而物流业不仅是服务业的重要组成部分, 在新常态经济格局下,物流业还是促进资源融通、加速 生产、带动消费发展的重要行业,物流业的发展需要更 多要素投入,要素资源约束也会更多地体现在物流业发 展过程中,以物流业提质增效为关键的第三产业发展方 式转型的要求同样迫切。因此,基于要素配置效率角度, 合理分析物流业发展质量,是加速物流经济整体发展水平 的关键。从物流业业务量来看,2020 年第一季度全国快 递单量累计 125.3 亿件,同比增长 3.2%;从市场规模来看, 伴随着存量消费市场持续向线上转移,多样化的物流形 态不断发展,以往的社会物流体系不断派生出市域物流、 短途快速物流等新业态,特别是移动互联网催生社区新 零售的发展,在很大程度上使得物流市场日益发展完善。 在物流经济可持续快速发展背景下,劳动力要素的稳定投 入不可或缺,2020 年 4 月,中共中央、国务院关于构建 更加完善的要素市场化配置体制机制的意见中指出要引 导劳动力要素合理畅通有序流动,这在一定程度上对于提
中国工业企业生产效率随机前沿模型分析

若TEC>1,则存在前沿效率的进步。 (3)规模效率变化(SEC) 一个厂商可以通过变动他的运营规模 使得该厂商运营与生产的技术最优规模 (TOPS)处,以提高其生产效率。 一个厂商在 某个时期的规模效率可以表示为:
均来源于2000 年~2 0 0 8年的 《中国统计年 鉴》 和 《科技统计年鉴》 , 部分年份的数据来 源于各年各地区的统计年鉴。 (1)实际工业总产值(Y)。 本文采用实际 工业总产值作为产出。 处理方式如下:将 《中国统计年鉴》 中规模以上工业企业的各 年名义工业总产值,经过各年各地区工业 品出厂价格指数平减, 得到实际的工业总 产值。 内资工业部门的实际工业总产值由 规模以上工业企业和规模以上三资企业的 实际工业总产值相减得到。 (2)固定资产净值(K)。 对于固定资产净 值的处理采用永续盘存法(PIM),以1999年 的 固 定 资 产 净 值 为 基 期, 以 相 邻 两 年 的 固 定资产年末余值之差作为当年的新增固定 资产投资。 公 式 如 下:
表2
+∑
n =1
N
n
InX nit +
1 N N ∑∑ 2 n =1 j =1
nj
InX nit InX njt +
∑
n =1
N
tn
tInX nit + t t +
1 2
tt
t 2 + D1 + D2 + D3 + Vit − U it (11)
(1)内 资 工 业 企 业 的 估 计 结 果 分 析:我 们将内资工业部门的估计结果统计如表1 所示。 (2)对 于 显 著 性 和 假 设 检 验 的 说 明:由 表3.1,除了δ4、 δ7之外,所有系数均通过 了1%的t检验;而γ=0.999,并且显著,这说 明 生 产 对 于 前 沿 的 偏 离, 主 要 是 由 于 技 术 无效率所引起的。 对于是否存在无效性的
空间面板随机前沿模型及技术效率估计.doc

空间面板随机前沿模型及技术效率估计空间面板随机前沿模型及技术效率估计林佳显, 龙志和, 林光平 1 12 ( 1. 华南理工大学经济与贸易学院, 广东广州510006; 摘要: 随机前沿模型是测算技术效率的重要方法之一。
通常,模型假设生产单元之间彼此独立,然而在技术扩散过程中,空间外部性起着重要作用。
文章结合随机前沿模型理论与空间经济计量分析方法,构建空间面板随机前沿模型, 同时考虑空间滞后因变量和空间误差自相关,并逐步放松模型设定条件, 首先考虑技术效率时变,接着引入技术无效率项的异方差性,之后考虑观察数据中潜在的截面异质性,分别以引入随机截面特有项和设定随机系数的形式来表示截面中图分类号: F064. 1 ----------------------------------- 精选公文范文,管理类,工作总结类,工作计划类文档,感谢阅读下载---------------------------------------- ~ 1 ~文献标识码: A 文章编号: 100022154 ( 2010 ) 05 20071 20 、引言随机前沿模型( SFM ) 的理论最初 A igne r、Love ll 和Schm id t (ALS) ( 1977 ) [ 2 ] [ 1 ] , Meeu sen 和V an den B roeck (MB ) ( 1977 ) 提出, 并很快成为计量经济学中一个引人注目的分支,被广泛应用于效率测算和生[ 3 ] 产率分析尤其是在Jond row 等( JLM S) ( 1982 )指出各个生产单元的技术无效率可以通过条件分布[ u |i vi - ui ] 的期望 E [ ui | vi - ui ] 或模M ode [ ui | vi - ui ] 来估算以后。
随机前沿分析( SFA ) 始于对生产最优化的研究, 经过30 多年的发展, 其在理论研究与实践应用方面都得到了深入的发展, 已被尝试性地应用于生产经济学以外的领域, 如劳动经济学、公共经济学以及金融经济学等。
【国家自然科学基金】_随机前沿方法(sfa)_基金支持热词逐年推荐_【万方软件创新助手】_20140802
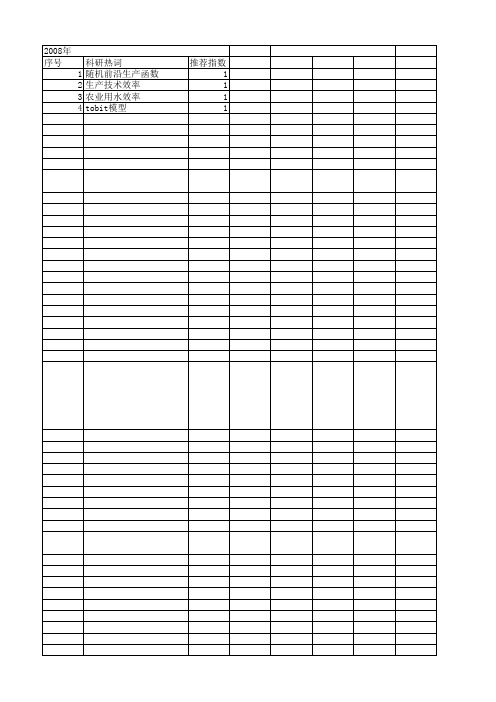
科研热词 随机前沿生产函数 生产技术效率 农业用水效率 tobit模型
推荐指数 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
科研热词 随机前沿分析 灌溉用水效率 sfa dea 面板数据 随机前沿生产函数 通径分析 跨国公司r&d投资 绩效 生产效率 玉米优势产区 玉米 溢出效应 投资效率 技术非效率模型 大股东控制 多层次/随机前沿分析 农户 全要素生产率 供应商 人力资源外包 主成分变量 c-d生产函数
推荐指数 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 随机前沿分析 技术效率 物流业 数据包络分析 全要素生产率 随机前沿方法 随机前沿主方程组方法 配置效率 能源消耗 股权结构 综合绩效 经济增长 空间相关性 空间收敛性 研究现状 研发技术效率 独立董事 影响因素 大型综合医院 复合残差项 地区差异 区域增长 全要素生产率变动分解 企业效率 代理成本 主成分分析 sfa
2014年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 高技术产业 随机前沿函数 环境因素 旅游业 医疗服务 医疗卫生服务效率 医疗卫生服务 全要素生产率 专利产业化效率 sfa方法 malmquist指数
推荐指数 1 1 1 1 1 1 1 1 1 1 1
2013年 科研热词 推荐指数 随机前沿方法 4 随机前沿分析 4 技术效率 4 高校校办产业 2 随机前沿分析(sfa) 2 效率 2 投资来源 2 成本函数 2 全要素生产率 2 fdi 2 高校知识创新链 1 高校 1 随机前沿分析方法(sfa) 1 随机前沿 1 绩效评价 1 统计分析 1 科技创新 1 碳排放 1 湖北省 1 数据包络分析 1 政产学研用 1 技术转移效率 1 房地产上市公司 1 战略性新兴产业 1 成本效率 1 成本一效益效率 1 成本-效益效率 1 影响因素 1 当地政府支持 1 外部运营环境 1 国防科技工业 1 商业银行 1 参数法 1 协同 1 医疗卫生 1 区域市场需求规模不确定性 1 创新效率 1 创意经济 1 农地城市流转效率 1 军民融合 1 公交线路 1 企业规模 1 人力资本 1 产权类型 1 产业集聚 1 产业竞争力 1 交通运输系统工程 1 专利转化效率 1 x效率 1 malmquist指数 1
基于SFA方法的中国智能制造业全要素生产率研究

基于SFA方法的中国智能制造业全要素生产率研究*申丹虹 崔张鑫内容摘要:本文基于随机前沿分析(SFA)和Malmquist法对我国2010—2018年的智能制造业①上市公司的全要素生产率进行了测算和分解,以探寻智能制造业的发展现状及存在的问题,从而找到提升路径。
结果表明:智能制造业目前还处于规模递减的状态,但是发展潜力很大。
智能制造业的全要素生产率年均增长为 5%,主要归因于技术水平的落后,说明智能与制造业的融合并没有消除“信息技术生产率悖论”的存在。
我国依然要加大对技术创新的投入并加强对高素质人才和管理人才的投入,推进要素的优化配置以及增加资本的投入从而促进制造业的高质量发展。
关键词:智能制造业;全要素生产率;Malmquist;随机前沿函数中图分类号:C812 文献标识码:A 文章编号:1004-7794(2021)01-0048-06DOI: 10.13778/ki.11-3705/c.2021.01.006一、引言和文献综述在互联网、大数据、云计算等技术不断发展的基础上,人工智能催生了一批新技术,引领着新一轮的科技革命和产业变革,各领域对人工智能的应用加速推进,在此背景下,人工智能和制造业的融合,可以为制造业的高质量发展提供新动能。
米晋宏等(2020)运用上市公司的数据实证研究分析了人工智能技术的应用对制造业产业结构的升级有促进作用[1]。
付文宇等(2020)通过2003—2018年30个省份的面板数据实证分析表明人工智能通过技术的创新和人才资本的积累效应促进了了制造业的升级[2]。
智能制造业是人工智能和制造业的深度融合。
目前,对于智能制造业全要素生产率的研究是热点话题。
葛金田(2019)提出生产率是衡量竞争力和经济可持续发展的重要影响因素,因而提高智能制造业全要素生产率极其重要[3]。
一些学者认为智能促进制造业全要素生产率的提升,刘亮等(2020)证伪了“信息技术生产率悖论”的存在,指出人工智能对中高技术行业生产率的提升效应强[4]。
随机前沿模型SFA原理解读

随机前沿模型(SFA )原理和软件实现一、SFA 原理在经济学中,常常需要估计生产函数或者成本函数。
生产函数f (x)的定义为:在给定投入x 情况下的最大产出。
但现实中的产商可能达不到最大产出的前沿,为了,假设产商i 的产量为:i i i y f (x ,)βξ= (1) 其中,β为待估参数;i ξ为产商i 的水平,满足i 01ξ<≤。
如果i =1ξ,则产商i 正好处于效率前沿。
同时,考虑生产函数还会受到随机冲击,故将方程(1)改写成:i v i i i y f (x ,)e βξ= (2) 其中,i v e 0>为随机冲击。
方程(2)意味着生产函数的前沿i v i f (x ,)e β是随机的,故此类模型称为“随机前沿模型”(stochastic frontier model )。
随机前沿模型最早由Aigner, Lovell and Schmidt(1977)提出,并在实证领域运用广泛,Kumbhakar and Lovell(2000)为该领域的研究写了一本著作,有兴趣的同学可以去参考。
假设o k 1i 1i ki f (x ,)e x x ββββ=(柯布道格拉斯生产函数,共有K 个投入品),则对方程(2)取对数可得:K i 0k ki i i k 1ln y =+ln x ln ββξν=++∑ (3)由于i 01ξ<≤,故i ln 0ξ≤。
定义i i u =-ln 0ξ≥,则方程3可以写成:Ki 0k ki i i k 1ln y =+ln x -u ββν=+∑ 其中,i u 0≥为“无效率”项,反映产商i 距离效率前沿面的距离。
混合扰动项i i i ενμ=-分布不对称,使用OLS 估计不能估计无效率项i u 。
为了估计无效率项i u ,必须对i i νμ、的分布作出假设,并进行更有效率的MLE (最大似然估计)估计。
一般,无效率项的分布假设有如下几种:(1) 半正态分布(2) 截断正态分布(3) 指数分布在一般的论文中,使用的最多的是半正态分布随机前沿模型可以很容易地用于估计成本函数,经过与生产函数的随机前沿模型类似的推导可得:Ki 0y i k ki i i k 1ln c =+lny ln P +u βββν=++∑其中,i c 为产商i 的成本,i y 为产出,ki P 为要素K 的价格,i u 为无效率项,i ν为成本函数的随机冲击。
【国家自然科学基金】_随机前沿分析(sfa)_基金支持热词逐年推荐_【万方软件创新助手】_20140801
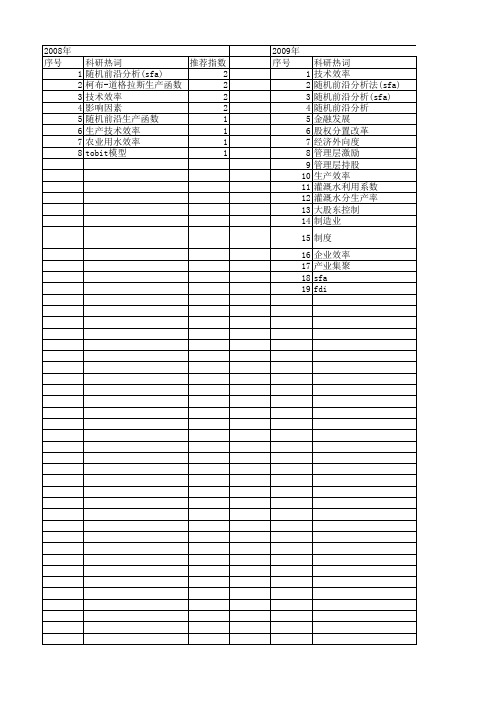
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74
协同 区域市场需求规模不确定性 创意经济 出口贸易 农户技术效率 农地城市流转效率 农业产业化 军民融合 公交线路 企业规模 人力资源效率 人力资本 产权类型 产业集聚 产业竞争力 交通运输系统工程 主成分分析 专利转化效率 不良贷款 三阶段dea模型 x效率 malmquist指数
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
科研热词 推荐指数 技术效率 8 随机前沿分析 7 随机前沿方法 4 随机前沿模型 3 随机前沿分析(sfa) 3 效率 3 影响因素 3 商业银行 3 sfa 3 高校校办产业 2 能源效率 2 投资来源 2 战略性新兴产业 2 成本效率 2 成本函数 2 创新效率 2 全要素生产率 2 fdi 2 高校知识创新链 1 高校 1 面板单位根 1 随机效应回归 1 随机性收敛 1 随机前沿生产函数 1 随机前沿分析方法(sfa) 1 长三角 1 自然因素 1 绿色经济 1 绩效评价 1 统计分析 1 空间差异 1 科技环境 1 科技创新 1 碳排放 1 知识溢出 1 滞后效应 1 湖北省 1 水资源利用效率 1 数据包络分析 1 政产学研用 1 技术转移效率 1 房地产上市公司 1 成本一效益效率 1 成本-效益效率 1 当地政府支持 1 外部运营环境 1 外资r&d 1 地区差异 1 国际比较 1 国防科技工业 1 国民健康 1 参数法 1
基于SFA模型的我国旅游业效率估计与区域差异性分析

基于SFA模型的我国旅游业效率估计与区域差异性分析内容摘要:本文以柯布-道格拉斯函数为基准,采用随机前沿方法(SFA)对我国省际旅游业的效率进行实证分析,结果显示:我国区域旅游业的发展正处于低效率不断向高效率转变的时期;区域旅游业效率存在较大差异,但这种差异正不断减小。
关键词:旅游业效率区域差异SFA引言及相关研究回顾随着经济的发展,我国旅游业有着惊人的进步:国际旅游外汇收入由1978年的2.6亿美元增长到2012年的500亿美元。
截至2012年底,全年国内旅游收入22706亿元,约占GDP的4.37%,同期增长了17.6%,国内出游人数达到29.6亿人次。
我国旅游业的快速发展为旅游目的地的相关产业发展提供了良好的发展市场。
虽然我国旅游业呈快速发展的态势,但是我国旅游产业的发展却呈现较强的区域异质性。
国外学者对于旅游效率的研究主要集中于可持续发展的方向,Blancas等(2010)利用随机前沿函数来评价西班牙旅游业的资源利用效率,他们认为西班牙应重视旅游资源的可持续发展原则,发展以保护生态为核心的绿色环保型旅游业。
国内也有很多学者对旅游业的效率进行评价,但是大部分学者都采用DEA 评价的方法对我国旅游业的效率进行估计,采用SFA对我国旅游业效率评价和区域差异性分析的学者较为鲜有。
刘长生(2012)选取张家界市为例,对旅游区服务的效率进行分析,认为环保交通低碳旅游服务效率呈显著性季节变化,且旅游业服务的效率较低。
也有少数学者采用其他方法对旅游业发展的区域差异性进行研究,如吴玉鸣(2013)采用地理加权回归的方法检验了我国省域旅游业的空间差异性,认为我国省域旅游产业具有显著的局部集群效应,且存在较强的空间自相关性。
本文利用随机前沿分析技术,对我国区域旅游业的效率进行实证分析,并分析其区域差异性。
模型构建与数据样本(一)模型设定在一般的实证分析中,对技术效率的测算主要有两种方法:一种是数据包络分析(DEA),一种是随机前沿分析(SFA)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机前沿模型(SFA )原理和软件实现
一、SFA 原理
在经济学中,常常需要估计生产函数或者成本函数。
生产函数f (x)的定义为:在给定投入x 情况下的最大产出。
但现实中的产商可能达不到最大产出的前沿,为了,假设产商i 的产量为:
i i i y f (x ,)βξ= (1)
其中,β为待估参数;i ξ为产商i 的水平,满足i 01ξ<≤。
如果i =1ξ,则产商i 正好处于效率前沿。
同时,考虑生产函数还会受到随机冲击,故将方程(1)改写成:
i v i i i y f (x ,)e βξ= (2)
其中,i v e 0>为随机冲击。
方程(2)意味着生产函数的前沿i v i f (x ,)e β是随机的,故此类模型称为“随机前沿模型”(stochastic frontier model )。
随机前沿模型最早由Aigner, Lovell and Schmidt(1977)提出,并在实证领域运用广泛,Kumbhakar and Lovell(2000)为该领域的研究写了一本著作,有兴趣的同学可以去参考。
假设o k
1i 1i ki f (x ,)e x x ββββ=L (柯布道格拉斯生产函数,共有K 个投入品),则对方程(2)取对数可得:
K i 0k ki i i k 1ln y =+ln x ln ββξν=++∑ (3)
由于i 01ξ<≤,故i ln 0ξ≤。
定义i i u =-ln 0ξ≥,则方程3可以写成:
K
i 0k ki i i k 1ln y =+ln x -u ββν=+∑ 其中,i u 0≥为“无效率”项,反映产商i 距离效率前沿面的距离。
混合扰动项
i i i ενμ=-分布不对称,
使用OLS 估计不能估计无效率项i u 。
为了估计无效率项i u ,必须对i i νμ、的分布作出假设,并进行更有效率的MLE (最大似然估计)估计。
一般,无效率项的分布假设有如下几种:
(1) 半正态分布
(2) 截断正态分布
(3) 指数分布
在一般的论文中,使用的最多的是半正态分布
随机前沿模型可以很容易地用于估计成本函数,经过与生产函数的随机前沿模型类似的推导可得:
K
i 0y i k ki i i k 1ln c =+lny ln P +u βββν=++∑
其中,i c 为产商i 的成本,i y 为产出,ki P 为要素K 的价格,i u 为无效率项,i ν为成本函数的随机冲击。
注意混合误差项的形式(符号)。
对于成本函数,i u =0意味着产商达到最低成本的效率前沿;
反之,如果i u 0>,则产商需付出更高的成本。
i u 是否存在的检验
使用随机前沿模型的前提是无效率项i u 存在,此假定可以通过检验
“220u 1u H : =0 vs H : >0σσ”来判断是否成立。
使用单边的广义似然比检验。
二、软件实现
Frontier4.1软件是由Tim Coelli 开发的一款专门用于完成随机前沿分析的软件,它可以用最大似然估计随机前沿成本模型和随机前沿生产模型,下面简单介绍一下该软件的使用方法,更加详细的说明可以参考英文指导《A Guide to FRONTIER Version 4.1: A Computer Program for Stochastic Frontier Production and Cost Function Estimation 》
Eg1.DTA 用于输入数据,是一个纯文本文件,数据文件的格式必须是3+K[+p]列。
第一列是评价体系的序号;
第二列是时期t ;
第三列是因变量;
第四列之后是K 个自变量;
[+p]仅当选择TE EFFECTS MODEL 模型输入。
EG1.INS 设置命令
1 1=ERROR COMPONENTS MODEL, 2=TE EFFECTS MODEL
选择模型
eg1.dta DATA FILE NAME
数据文件
eg1.out OUTPUT FILE NAME
结果存储文件
2 1=PRODUCTION FUNCTION, 2=COST FUNCTION
选择生产模型(1)还是成本模型(2)
n LOGGED DEPENDENT V ARIABLE (Y/N)
变量是不是已经进行了对数运算
25 NUMBER OF CROSS-SECTIONS
评价体系数目
1 NUMBER OF TIME PERIODS
时期数目
25 NUMBER OF OBSERV ATIONS IN TOTAL
总记录数目
2 NUMBER OF REGRESSOR V ARIABLES (Xs)
自变量个数
Y MU (Y/N) [OR DELTA0 (Y/N) IF USING TE EFFECTS MODEL]
假设U的分布。
Y表示截断分布,N表示半正态分布
n ETA (Y/N) [OR NUMBER OF TE EFFECTS REGRESSORS (Zs)]
y 表示时变模型,n表示非时变模型。
n STARTING V ALUES (Y/N)
选择n
其他设置保持不变。
