盖革米勒计数器 实验报告
仿真实验-G-M计数管特性研究

实验十五 G-M计数管特性的研究测量核辐射的仪器称为核辐射探测器,G-M计数管是盖革-米勒计数管的简称,它是结构简单而又经济实用的核辐射探测器。
核辐射探测器有多种类型,如按功能分有用作测量粒子数目的计数器型,能分辨粒子能量的能谱仪型,能显示粒子运动路径的径迹型等。
若按工作物质分,有气体,液体和固体等探测器。
本实验中测量用的G-M计数管属于气体计数器型的核辐射探测器,其工作物质是气体,其功能是记录射线粒子的数目,但不能区别粒子能量。
G-M计数管有易于加工,输出信号幅度大,配套仪器简单等优点,在放射性测量方面有广泛的应用,在核物理实验教学中更是不可缺少的探测器。
【实验目的】1. 掌握G-M计数管的结构,工作原理和使用方法。
2. 研究G-M计数管的主要特性。
3. 学习有关使用放射源的安全操作规则。
【实验原理】1.G-M计数管的结构和工作原理G-M计数管如图1所示,通常为一密封并抽真空的玻璃管,中央是一根细金属丝作为阳极,玻璃管内壁涂以导电材料薄膜或另装一金属圆筒作为阴极构成真空二极管。
同时充有一定量的惰性气体和少量猝灭气体,一般二者充气分压比例是9:1。
G-M计数管有很多类型,按结构形状区分有圆柱形和钟罩形等;按探测对象分类有β、γ或兼测βγ型计数管;按所充猝灭气体种类不同分,有卤素管,其猝灭气体为Br2,Cl2等,如果用乙醇或乙醚等碳氢化合物作为猝灭气体,称为有机计数管。
图1 G-M计数管当计数管的阳极和阴极之间加有适当的工作电压时,管内形成柱形对称电场。
如有带电粒子进入管内,由于粒子与管内惰性气体原子的电子之间的库仑作用,可使气体电离(或激发),形成正、负离子对(负离子即为电子),这种电离称为初级电离。
在电场作用下,正,负离子分别向各自相反的电级运动,但正离子向阴极运动的速度比电子向阳极运动的速度慢得多。
在电子向阳极运动过程中不断被电场加速,又会和原子碰撞而再次引起气体电离,称为次级电离。
由于不断的电离过程使电子数目急剧增加,形成自激雪崩放电现象。
试验1盖革—弥勒计数器的特性预习提要试验目的试验仪器

实验1 盖革—弥勒计数器的特性[ 预习提要 ]1.弄清实验原理及操作方法和注意事项。
2.坪曲线怎样进行测绘?测量中要注意什么问题?3.如何由坪曲线求得G-M计数管的性能参量和确定工作电压?4.设计各项实验数据记录表格。
[ 实验目的 ]1.了解盖革—弥勒计数器的结构、原理和主要性能参数的测定方法,了解核辐射探测常识。
2.熟悉放射性测量误差的表示方法及其与测量次数和时间之间的关系。
3.应用微机系统处理实验数据。
[ 实验仪器 ]盖革—弥勒计数管1支,长寿命放射源1个,铅室1个,FJ-367型通用闪烁探头1个,FH-408型自动定标器2台,长余辉示波器1台,微机及计算软件1套。
[ 实验基础知识 ]在原子核物理领域内的实验技术可分为三个方面:加速器技术、反应堆技术和探测技术。
它们构成一套完整的和物理实验技术。
加速器核反应堆是产生核辐射的工具,也就是粒子源。
探测技术则包括探测和研究这些核辐射的性质,以及它们与物质的相互作用等课题。
在我们做得和物理实验中,主要是掌握一些辐射探测技术。
近四十年来探测技术发展很快,就放射性计数测量的装置就有各式各样的很多,如盖革—弥勒计数器(简称G-M计数器),正比计数器,脉冲电离室,闪烁计数器,半导体探测器等等。
本实验要介绍和使用的G-M计数器是核辐射探测器中较简单的一种。
它本身只能用于测定辐射粒子的数目。
它是最早使用的核辐射探测器,近年来随着闪烁计数器和半导体探测器的发展,其重要性有所下降,但由于它设备简单,使用方便,仍广泛用于有关放射性测量的工作中。
阴管阳极a. 钟罩型 b. 长圆管形型图1-1-1 G-M计数管1. G-M 计数器的结构和工作原理G-M 计数器由G-M 计数管、高压电源和定标器构成。
G-M 计数管有各种不同的结构。
最常见的有钟罩形β计数管(图1-1-1a )和长圆管形γ计数管(图1-1-1b )两种。
他们都是由圆筒状的阴极和装在轴上的阳极丝密封在玻璃管内构成。
盖革一米勒计数管的特性及放射性衰变的统计规律

1.计数管在什么情况下出现连续放电? 出现连续放电时怎徉处理? 如何延长计数管的使用寿命?当电场强度大到一定程度时,由于放大后的次级离子数足够多,电离电荷所产生的电场抵消一部分外加电场,即所谓空间电荷效应,这时气体放大系数不是恒定的,而与原电离有关。
区域Ⅴ为G-M 区,进入该区后,离子倍增更加猛烈,空间电荷效应越来越强,此时电离电流强度不再与原电离有关,反映在曲线上是α和β两根曲线重合,并且随电压的变化较小。
工作在该区的气体探测器是G-M 计数管。
当工作电压超过2V 继续升高时,计数率将急剧上升,这时计数管已进入“连续放电区”。
计数管经过一次连续放电,就会使猝熄气体大量分解。
使用时,要小心避免发生连续放电。
升高电压时,应该特别注意其计数情况,如发现计数率剧增,要立刻降低电压!计数管每计数一次,就有部分猝熄气体分子被分解(每次约1010个),从而失去猝熄作用,所以G-M 计数管有一定的寿命。
在正常条件下,有机管约为891010次计数。
卤素气体分解后有可能重新复合,因此尽管含量少,但计数寿命可达9101010次计数。
G-M 计数管必须在一定温度范围内才能正常工作。
温度太低时,部分猝熄气体会凝聚,使猝熄作用减弱,坪长缩短直至完全丧失猝熄能力而连续放电。
一般有机管的工作温度约为0~40℃,卤素管约为-10~50℃。
2.G-M 计数管的计数与哪些因素有关? 能否用它来测量能量和区分射线种类?与坪曲线、分辨时间、探测效率和寿命等因素有关。
在一定的外加电压下,不论射线在计数管内打出多少正负离子对,最后形成的正离子鞘总是一样的。
因此,G-M 计数管不能区分不同种类,不同能量的粒子,只要射入的粒子引起电离,就可以被记录。
3.分辨时间的存在对计数有什么影响? 能否克服? 如何用示波器来测量分辨时间? 一般情况下,G-M 计数管的分辨时间在100μs ~400μs 之间。
由于分辨时间较长,故G-M 计数管不能进行快速计数。
盖革—弥勒计数器和核衰变的统计规律

分辨时间的测量
假设测得计数率m,分辨时间为τ,则单位时间内有mτ 时间要产生漏记。若实际的计数率为n,则单位时间内的 漏记数为nmτ
n-m=nmτ
修正后的计数率公式 :n=m/(1-mτ)
双源法测量分辨时间
• nA=mA/(1-ma τ) • nB=mB/(1-mB τ) • Nab=nA+nB=mAB/(1-mAB τ) • τ =(mA+mB-mAB)/2mAmB
fj :每个分组区间中实际观测到的次数 fj’:每个分组区间中按理论分布应有的出现次数
• 算出随机变数x2所取的值大于某个预定值x21- α的概率P(x2>x21- α), 令此概率为α
• 在检验时,先设定一个小概率α,称为显著性水平,一般设为0.10,可 从表中找到对应的x21- α
• 自由度v=r-s-1 • 若x2<x21- α,则小概率事件未发生,认为此组数据服从泊松分布
核衰变的统计规律
在t时间内平均衰变的原子核的数目:m=N(1-e-λt)
每个核在t时间内发生衰变的几率为1-e-λt,不发生衰变 的几率为e-λt
在t时间内,在N个原子核中有n个核发生衰变的几率为
p(n)=CNn(1-e-λt)n(e-λt)N-n
当N很大且λt<<1时,二项式分布简化为泊松分布
射粒子的数目
所产生的负离子在电场 加速下向阳极运动
负离子与气体分子发生 碰撞打出更多的次级电
子,引起了“雪崩放 电”,在阳极上便得到
一个负的电压脉冲
为了使一个辐射粒子 引起放电后只计一次 数,在计数管内加入 少量猝灭的气体,用 来猝灭正离子鞘和电 离产生的离子增殖。
电流I与计数率的关系
图(1)
盖革一米勒计数管的特性及放射性衰变的统计规律

佛山科学技术学院实 验 报告课程名称 近代物理实验 实验项目 盖革一米勒计数管的特性及放射性衰变的统计规律专业班级 10物师 姓名 李福潘 学号 2010284113 仪器组号指导教师 李斌老师 成绩 日期 2013年4月8日星期一 一.实验目的(1)了解盖革—米勒计数管的工作原理及特点;(2)学会如何测量其特性参数及确定管子的工作电压;(3)掌握测量物质吸收系数的方法,并验证核衰变的统计规律。
二 实验仪器实验装置包括G-M 计数管、计数管探头、自动定标器、铝吸收片和β放射源。
计数管探头是一个前置放大器,用于将计数管产生的脉冲进行放大。
自动定标器已集高、低压电源和定标器为一体,计数管所需高压便由自动定标器提供。
三.实验原理计数管可看成是一个电容,雪崩放电前加有高压,因而在两极上有一定量的电荷存在,放电后电子中和了阳极上一部分电荷,使阳极电位降低。
随着正离子向阴极运动,高压电源便通过电阻 R 向计数管充电,使阳极电位恢复,在阳极上就得到一个负的电压脉冲。
因此,一次雪崩放电就得到一个脉冲,即一个入射粒子入射只形成一个脉冲,脉冲幅度的大小由高压电源电压和电阻R 决定,与入射粒子的能量和带电量无关。
2、G-M 管的特性(1) 坪曲线。
在强度不变的放射源照射下,G-M 管的计数率n 随外加电压变化的曲线如图1所示。
由于该曲线存在一段随外加电压变化而变化较小的区间即坪区,因此把它叫做坪曲线。
坪曲线的主要参数有起始电压、坪长和坪斜。
起始电压即计数管开始放电时的外加电压,图中用0V 表示。
坪长即坪区的长度,图中为21V V 和之差。
坪斜即坪区的坡度,通常用坪区内电压每增加l00V 时计数率增长的百分比表示:42112211012n n T n n V V -=⨯+-()(V ) [单位:%/(l00V)], (1) 式中T 表示坪斜,1n ,2n 分别对应于1V 和2V 时的计数率。
实验报告内容:一.实验目的 二.实验仪器 (仪器名称,型号,参数,编号) 三.实验原理(原理文字叙述和公式,原理图) 四.实验步骤 五,实验数据和数据处理 六,实验结果 七,分析讨论(实验结果的误差来源和减小误差的方法,实验现象的分析,问题的讨论) 八,思考题坪曲线是衡量G-M 管性能的重要指标,在使用前必须进行测量,以鉴别计数管的质量并确定工作电压。
盖革米勒计数器实验报告

近代物理实验报告指导教师:得分:实验时间: 2009 年 10 月 22 日,第九周,周四,第 5-8 节实验者:班级材料0705 学号 200767025 姓名童凌炜同组者:班级材料0705 学号 2007670 姓名车宏龙实验地点:综合楼 507实验条件:室内温度℃,相对湿度 %,室内气压实验题目:盖革-米勒计数器实验仪器:(注明规格和型号)圆柱形γ计数管一支,自动定标器一台(带高压电源),示波器一台,137Cs放射源一枚。
实验目的:1.掌握盖革-米勒计数器的结构、原理、使用方法2.验证核衰变的统计规律,熟悉放射性测量误差的表示方法实验原理简述:1.计数管的构造与工作原理GM计数管有圆柱形和钟罩型两种,其共同结构为圆筒状的阴极和装在轴线上的阳极丝共同密封在玻璃管内而成。
管内通常充有约10kpa的惰性气体及相应的猝熄气体。
当带电粒子进入计数管的灵敏区域时,将引起管内气体的电离,电力产生的电子在电场加速下向阳极运动,一方面因电场加速获得能量,一方面又因与气体分子碰撞而损失能量。
在充有猝熄气体的计数管中,这些光子大部分将被猝熄气体所吸收,因而达不到阴极,但却会逐步沿铅丝极方向扩展并产生新的电子(光电作用),这些电子又会进一步产生雪崩式的放电。
当电子到达阳极的时候,因为正离子移动的很慢,基本上没有移动能力,从而形成了围绕着丝级的正离子鞘。
由于放电后电子中和了阳极上的一部分电荷, 使得阳极电位降低, 随着正粒子向着阳极运动, 高压电源便通过电阻R 向计数管充电, 使得阳极电位回复, 在阳极上变得到一个负的脉冲电压。
这个负的脉冲电压, 便起到了计数的显示作用。
2. 计数管的特性2.1 坪特性——包括起始电压、 坪长、 坪斜等 当射入计数管的粒子数目不变时, 改变计数管两级之间所加的高压值, 发现由定标器测得的计数率有变化, 如图所示的曲线。
在这个图中, V0称为起始电压, ΔV=V2-V1称为坪长, 在坪区内, 电压每升高1V 是, 计数率增加的百分数称为坪斜, 由公式表示为%100*)(12112V V n n n k l --=坪特性曲线反映了计数管的性能, 所以使用前必须对它进行测量。
盖革-弥勒计数管及核衰变的统计规律实验报告
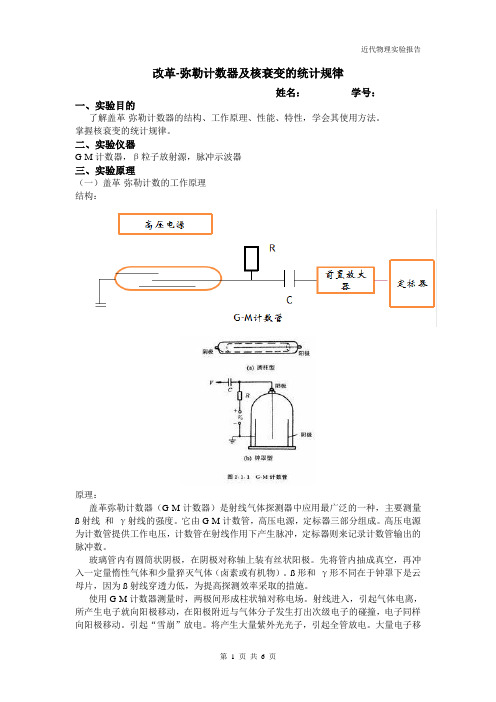
改革-弥勒计数器及核衰变的统计规律姓名:学号:一、实验目的了解盖革-弥勒计数器的结构、工作原理、性能、特性,学会其使用方法。
掌握核衰变的统计规律。
二、实验仪器G-M计数器,β粒子放射源,脉冲示波器三、实验原理(一)盖革-弥勒计数的工作原理结构:原理:盖革弥勒计数器(G-M计数器)是射线气体探测器中应用最广泛的一种,主要测量ß射线和γ射线的强度。
它由G-M计数管,高压电源,定标器三部分组成。
高压电源为计数管提供工作电压,计数管在射线作用下产生脉冲,定标器则来记录计数管输出的脉冲数。
玻璃管内有圆筒状阴极,在阴极对称轴上装有丝状阳极。
先将管内抽成真空,再冲入一定量惰性气体和少量猝灭气体(卤素或有机物)。
ß形和γ形不同在于钟罩下是云母片,因为ß射线穿透力低,为提高探测效率采取的措施。
使用G-M计数器测量时,两极间形成柱状轴对称电场。
射线进入,引起气体电离,所产生电子就向阳极移动,在阳极附近与气体分子发生打出次级电子的碰撞,电子同样向阳极移动。
引起“雪崩”放电。
将产生大量紫外光光子,引起全管放电。
大量电子移动到阳极被中和。
大量正离子由于质量大,移动缓慢,在阳极附近形成正离子鞘。
可将计数器看作电容器,使阳极得到一个负的脉冲。
电源高,波幅大:电阻高,脉冲宽。
(二)计数管的特性开始输出小,计数器示零,电压超过某一值时,定标器开始计数,此时电压Va 为阈电压。
随着脉冲幅度升高,计数率迅速增加,升到Vb 时,只要产生一个离子对,就能引起全管雪崩放电。
进一步升高,只能提高幅度,不能增加个数,直到Vc ,称为坪区。
Vc-Vb 为坪长度。
坪斜]%100[)(2212121每伏特⋅-⋅+-=V V n n n n ε,表示为电压升高1伏计数率的相对增加量。
(三)核衰变的统计规律及测量数据的处理 1、衰变规律:对大量核而言,其衰变遵从统计规律,有衰变定律-λλ0(t)e N =N其中t 表示时间,N0为t=0时刻的放射性核数,N(t)为t 时刻的放射性核数,λ称为衰变常数。
盖革弥勒计数器及核衰变的统计规律实验报告

盖革-弥勒计数器及核衰变的统计规律盖革-弥勒计数器是气体探测器的一种,用来测定射线强度,既单位时间的粒子个数。
近年来,随着闪烁探测器及半导体探测器的发展,其重要性有所下降,但由于它的设备简单,使用方便,在有关的放射性测量中仍在广泛使用。
一、实验目的掌握G-M计数器的工作基础,测定其有关特性,学会使用;以G-M计数器未测试设备,验证核衰变的统计规律;学会使用放射性测量结果的误差表示法,学会多次测量结果的误差计算及测试时间的选择。
二、实验原理1、G-M计数器原理:G-M计数器是利用射线使计数管内的工作气体电离,然后收集产生的电荷来记录射线的探测器。
玻璃管内有圆筒状阴极,在阴极对称轴上装有丝状阳极。
先将管内抽成真空,再充入一定量的惰性气体和少量猝灭气体(卤素或有机物)在G-M计数管两级加上电压,设其阳极半径为a,阴极半径为b,阳极与阴极间的电压为U,则沿着管径向位置为r处的电场强度为,可见随着r减小,电场强度增大,且阳极附近急剧增大。
2、脉冲原理(1)当射线进入G-M管中使得管中气体电离后,正离子和负离子在管内电场的作用下分别向阴极和阳极移动。
在阳极附近强大的电场作用下,电子获得强大的动能以至于将阳极附近的气体电离。
经过多次碰撞,殃及附近的电子急剧增多,形成了“雪崩电子”;在这些碰撞中会产生大量的紫外线光子,这些光子能进一步的产生第二波的“雪崩”效应,增加电子。
这个电子不断增加的过程称为气体放大。
(2)雪崩过程发生在殃及附近,加上电子的质量远远小于阳离子的质量,速度比阳离子快,因此电子很快被阳极吸收,在管内留下一个被大量阳离子构成的阳离子鞘包围着的阳极。
正离子鞘将随着电离的发生逐渐增厚,由于正离子鞘的作用,阳极附近的电场将随之减小,以致新电子无法增殖,即电场强度不足以引发雪崩效应,雪崩效应停止,正离子鞘停止生成,放电便终止了,伺候,正离子鞘在电场的作用下慢慢移向阴极,最后到达阴极被中和,阳极附近的电场也随之恢复,使得与G-M串联的电阻记录下一个电压脉冲。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
近代物理实验报告指导教师:得分:实验时间: 2009 年 10 月 22 日,第九周,周四,第 5-8 节实验者:班级材料0705 学号 200767025 姓名童凌炜同组者:班级材料0705 学号 2007670 姓名车宏龙实验地点:综合楼 507实验条件:室内温度℃,相对湿度 %,室内气压实验题目:盖革-米勒计数器实验仪器:(注明规格和型号)圆柱形γ计数管一支,自动定标器一台(带高压电源),示波器一台,137Cs放射源一枚。
实验目的:1.掌握盖革-米勒计数器的结构、原理、使用方法2.验证核衰变的统计规律,熟悉放射性测量误差的表示方法实验原理简述:1.计数管的构造与工作原理GM计数管有圆柱形和钟罩型两种,其共同结构为圆筒状的阴极和装在轴线上的阳极丝共同密封在玻璃管内而成。
管内通常充有约10kpa的惰性气体及相应的猝熄气体。
当带电粒子进入计数管的灵敏区域时,将引起管内气体的电离,电力产生的电子在电场加速下向阳极运动,一方面因电场加速获得能量,一方面又因与气体分子碰撞而损失能量。
在充有猝熄气体的计数管中,这些光子大部分将被猝熄气体所吸收,因而达不到阴极,但却会逐步沿铅丝极方向扩展并产生新的电子(光电作用),这些电子又会进一步产生雪崩式的放电。
当电子到达阳极的时候,因为正离子移动的很慢,基本上没有移动能力,从而形成了围绕着丝级的正离子鞘。
由于放电后电子中和了阳极上的一部分电荷, 使得阳极电位降低, 随着正粒子向着阳极运动, 高压电源便通过电阻R 向计数管充电, 使得阳极电位回复, 在阳极上变得到一个负的脉冲电压。
这个负的脉冲电压, 便起到了计数的显示作用。
2. 计数管的特性2.1 坪特性——包括起始电压、 坪长、 坪斜等 当射入计数管的粒子数目不变时, 改变计数管两级之间所加的高压值, 发现由定标器测得的计数率有变化, 如图所示的曲线。
在这个图中, V0称为起始电压, ΔV=V2-V1称为坪长, 在坪区内, 电压每升高1V 是, 计数率增加的百分数称为坪斜, 由公式表示为%100*)(12112V V n n n k l --=坪特性曲线反映了计数管的性能, 所以使用前必须对它进行测量。
2.2死时间, 回复时间与分辨时间将正离子鞘从r0移动到rc 这段不能输出脉冲的死寂时间称为死时间td , 而此后正离子鞘从rc 移动到阴极这段时间内, 阳极附近的电场逐步恢复到原来的大小, 这段所消耗的时间称为恢复时间tg 。
将从一个正常呗记录的脉冲之后, 到能产生第二个可触动定标器的脉冲这段时间τ, 叫做分辨时间。
即是说, 只有飞来的两个粒子的时间间隔大于这个分辨时间时, 才能够触发两个能够被识别的定标器脉冲。
由于分辨时间的存在, 有很多粒子将会被漏记, 影响测量值的准确度。
因而需要计数率修正公式进行修正, 修正公式如下τm mn -=22.3 计数管的本底计数管处于工作电压下, 在没有放射源时所测得的计数率叫本底。
在实际测量中需要在实测值中减去本底2.4计数管的探测效率探测效率是指当有一个粒子通过计数管的灵敏体积时, 引起一个输出脉冲的概率。
3. 核衰变的统计规律以及放射性测量的统计误差3.1 核衰变的统计规律放射性核衰变的统计性是指, 放射性元素的每一个核的衰变与否是相互独立的事件, 彼此无关。
每一个核什么时候衰变纯属偶然事件。
但是对于大量的放射性核来说, 实践证明其衰变规律遵从统计规律, 即)ex p(0t N N λ-=3.2 泊松分布与高斯分布 泊松分布: 若有N 0个未衰变的放射性原子核, 其寿命很长, 即λ很小, 单位时间内平均衰变数为n , 而且0N n <, 则可以认为在测量过程中0N n <近似不变。
显然, 考虑到一些可以简化和忽略的条件,在单位时间内有n 个核衰变, 其余核不衰变的概率为n N n N n n n n P --=0)1(!)()(0, 而P(n)同时可以表达为, 在满足以上假定的条件下, 进行多次测量时, 测量结果为n 的概率分布。
上式可以进一步简化为)ex p(!)()(n n n n P n-=高斯分布: 当n 比较大时, 使用泊松分布来计算, 会因为阶乘的存在而使得计算困难, 因而改用高斯分布来表达统计规律, 公式为)2ex p(21)(22σπσ∆-=∆P 3.3 标准误差的概率含义3.4 放射性测量中统计误差的表示 测量结果的表示式为NN ±相对标准误差为N N N 1±=±实验步骤简述:1.按照图连接电路,经检查无误后,接通电源使仪器预热将放射源置于合适的位置,并用铅砖屏蔽好。
将“高压细调”反时针调节至最低位置,打开“高压”开关,是定标器处于纪录状态。
缓缓提高电压,找出起始电压V0,然后每增加20V测量一次,每次1min,直到测完坪区为止,然后立即降下高压,保护计数管。
画出坪曲线,标出某几个点的标准误差。
由坪曲线求出坪长。
坪斜率,选择工作电压。
2.用示波器观测计数管的死时间与整个测量系统的分辨时间打开示波器电源,调整示波器有关旋钮,使屏上呈现2-1-4所示的波形,测出定标器输入时的阈值电压,以及td和τ值。
3.测量时间和测量次数对计数率标准误差的影响固定测量时间为5min,重复3次,分别算出每次测量的相对标准误差,在算出3次的平均计数率和相对标准误差。
固定测量时间为10min。
算出测量的相对标准误差,然后针对测量时间与测量次数对误差的影响进行讨论。
4.验证统计规律在没有放射源的情况下,利用本底验证泊松分布。
先对本底测量5min,根据所得的计数大小,选定一个测量时间,使每次测量的平均值在3~7之间,然后以这个选定的时间,重复测量300次以上。
并记录每个值出现的次数。
在同一坐标纸上做出泊松分布的实验曲线和理论曲线,并加以比较讨论。
原始数据、 数据处理及误差计算: 1. 坪特性的测量与计算测量的电压与计数数据如下:n 3140 3052 3308 3292 3477 3851 4172 4411 5408 6952作出坪特性曲线如下:可以看到, 起始电压为V0=0.9kV ,坪区从V5=0.94kV 开始, 从V11=1.06kV 结束 坪长为ΔV=V2-V1=1.06kV-0.94kV=0.12kV 对应的计数差为Δn=3052-2942=110可得, 坪斜为%031.0%100*)12.0(2942110)(1%100*)(12112==∆∆=--=kV V n n V V n n n k l2. 有源计数实验的计算处理有源计数实验的数据如下:计数次数A=3, 平均计数值为33.29606==∑ANi N 计数平均值的标准误差为341.99±=±=ANN σ 而通过无源计数得到的本底值为M=695, 本底值的标准误差为36.26±=±=M M σ 因而实际的计数值为33.2891169533.29606=-=-M N实际计数值标准误差为934.5300695300.333.29606'±=+±=+⋅±=t M t A N final σ最终的实际计数值表达为: N=28911 ± 5 (为符合测量实际, 数据结果仅保留到个位)3. 本底计数验证泊松分布本底验证的计数结果及出现次数见下页表格:Total counts=300将这些计数的分布结果表达为图像, 并且在同一坐标系上绘制标准的泊松分布图样作比较, 如下页图所示:可以看到, 实际测量的分布曲线虽然与理论值存在偏移, 但是形状上较好地保持了泊松分布的特征, 因而可以认为本底计数的验证是成功的。
思考题, 实验感想, 疑问与建议:1. 坪曲线如何测量? 如何由坪曲线选定工作电压坪曲线的测量方法如下:将放射源置于合适的位置, 并用铅砖屏蔽好。
将“高压细调”反时针调节至最低位置, 打开“高压”开关, 是定标器处于纪录状态。
缓缓提高电压, 找出起始电压V0, 然后每增加20V 测量一次, 每次1min , 每次测量后清零计数, 再次测量。
直到测完坪区为止(离开坪区时表现为计数值迅速上升), 然后立即降下高压, 保护计数管。
通过测得的数据可以看出坪区的始末电压V1和V2, 根据实验中所得, 工作电压选在坪区的1/3处, 即工作电压设置为(V2+V1)/3较为合适2. 什么是放射性核衰变的统计性?放射性核衰变的统计性是指, 放射性元素的每一个核的衰变与否是相互独立的事件, 彼此无关。
每一个核什么时候衰变纯属偶然事件。
但是对于大量的放射性核来说, 实践证明其衰变规律遵从统计规律, 即)ex p(0t N N λ-=3. 如何验证泊松分布?方法是在没有放射源的情况下, 利用本底验证泊松分布。
先对本底测量5min , 根据所得的计数大小, 选定一个测量时间, 使每次测量的平均值在3~7之间, 然后以这个选定的时间, 重复测量300次以上。
并记录每个值出现的次数, 之后将这个计数结果表达为泊松分布曲线, 并与该条件下的理想分布曲线进行比较。
4. “标准误差”的意义是什么?对于某一个实验, 多次重复进行, 得到的结果表示为σ±n 的话, 表示测量值落在这个范围内的概率是某一个实现约定的可信值(特定值, 如0.95)5. 对实验的一些改进与看法在实验中发现, 调节计数管高压的旋钮以及显示表的设计上存在缺陷, 一方面电压表的最小刻度过大, 不便于读数, 另一反面旋钮不方便细调。
建议改为数显与按钮调节式, 并且数显的精确位数要多, 以满足实验的要求。
原始记录及图表粘贴处:(见附页)。
