第一篇第一章薄膜光学的理论基础
合集下载
《薄膜光学基础》PPT课件
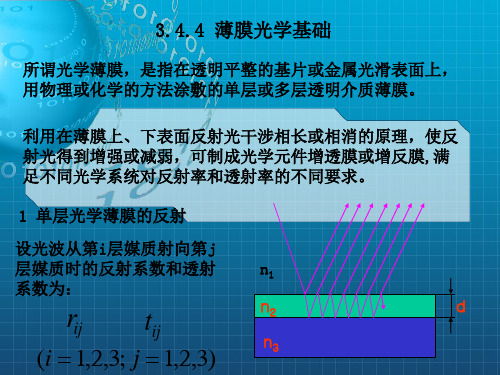
1 2
3
先考虑由基底g和膜层3
g
组成的单层膜系统。
由式(3-225)可得,此单层膜系统的反射系数:
r r23 r3g exp( j) 1 r23r3g exp( j)
由于是λ。/4膜系,所以:
r r23 r3g 1 r23r3g
1
再考虑由膜层2和反射系
2
数为 r 的等效膜层(3,g)
2
R1
nA nA
nI nI
式中
nI
nH2 nG
是镀第一层膜后的等效折射率。若在高折射率膜层上再镀一层
低折射率膜层,其反射率为
2
R2
nA nA
nII nII
式中
nII
nL2 nI
nL nH
2
nG
是镀双层膜后的等效折射率。依此类推,当膜层为偶数(2p)层 时, (HL)p膜系的等效折射率为
3
组成的“单层膜”系统。
g
这样,此“单层膜”系统的反射系数:
r r12 r 1 r12 r
最后得到双层膜系统的反射系数:
r r12 r23 r3g r12r23r3g 1 r12r23 r12r3g r23r3g
考虑到正入射的菲涅耳系数:
rij
ni ni
nj nj
令r=0,可得双层减反膜的材料折射率条件:
此时反射率最小,透过率最大:
Rm
r12 1
r23 r12r23
2
n22 n22
n1n3 n1n3
2
Rm
r12 1
r23 r12r23
2
n22 n22
n1n3 n1n3
2
当满足下面条件时,R=0,消反射:
薄膜光学5

薄 膜 光 学——基础理论
前一次课旳主要内容
光学薄膜在倾斜入射时旳体现 考虑到基片背面反射时旳情况 对称膜系旳等效折射率 矢量法 麦克劳德纳图解法简介 用麦克劳德纳图解法解释单、双层增透膜
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
经典膜系简介
❖增透膜 ❖分光膜 ❖反射膜 ❖滤光片 ❖特殊膜系
i n3 n1
in1
Y C / B n12 / n3
显然,在中心波优点旳反射率与单层膜相同。
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
1.2 双层增透膜
单 层 膜 、 λ/4-λ/4和 λ/2-λ/2型 双 层 增 透 膜 理 论 曲 线
5
4 3 2
% Reflectance
薄 膜 光 学——经典膜系
1.2 双层增透膜
上面讨论旳λ0/4- λ0/4 构造旳V形膜只能 在较窄旳光谱范围内有效地减反射,所以仅合适 于工作波段窄旳系统中应用.厚度为λ0/4- λ0/ 2型旳双层增透膜,在中心波长λ0两侧, 可望有 两个反射率极小值,反射率曲线呈W型,所以也 有把这种双层增膜称作为W型膜旳.对于中心波 长膜层和基片组合旳特征矩阵为
n1
Y n0
n2
n3
n0
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
1.2 双层增透膜
当折射率完全满足以上关系旳材料不能找到时,能够经 过厚度旳调整来到达,如图所示,n0、n3分别为入射介 质和基片旳折射率,n1和n2为折射率己拟定旳低折射率 和高折射率材料旳膜层,δ1、δ2便是待定旳膜层位相厚 度,用矢量法进行分析:
值为离开原点. 2. 矢量之间旳夹角仅决定于膜层旳光学厚度和所考察
前一次课旳主要内容
光学薄膜在倾斜入射时旳体现 考虑到基片背面反射时旳情况 对称膜系旳等效折射率 矢量法 麦克劳德纳图解法简介 用麦克劳德纳图解法解释单、双层增透膜
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
经典膜系简介
❖增透膜 ❖分光膜 ❖反射膜 ❖滤光片 ❖特殊膜系
i n3 n1
in1
Y C / B n12 / n3
显然,在中心波优点旳反射率与单层膜相同。
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
1.2 双层增透膜
单 层 膜 、 λ/4-λ/4和 λ/2-λ/2型 双 层 增 透 膜 理 论 曲 线
5
4 3 2
% Reflectance
薄 膜 光 学——经典膜系
1.2 双层增透膜
上面讨论旳λ0/4- λ0/4 构造旳V形膜只能 在较窄旳光谱范围内有效地减反射,所以仅合适 于工作波段窄旳系统中应用.厚度为λ0/4- λ0/ 2型旳双层增透膜,在中心波长λ0两侧, 可望有 两个反射率极小值,反射率曲线呈W型,所以也 有把这种双层增膜称作为W型膜旳.对于中心波 长膜层和基片组合旳特征矩阵为
n1
Y n0
n2
n3
n0
中国科学院长春光学精密机械与物理研究所
薄 膜 光 学——经典膜系
1.2 双层增透膜
当折射率完全满足以上关系旳材料不能找到时,能够经 过厚度旳调整来到达,如图所示,n0、n3分别为入射介 质和基片旳折射率,n1和n2为折射率己拟定旳低折射率 和高折射率材料旳膜层,δ1、δ2便是待定旳膜层位相厚 度,用矢量法进行分析:
值为离开原点. 2. 矢量之间旳夹角仅决定于膜层旳光学厚度和所考察
光学薄膜基础理论

n0 cos1 N1 cos0 n0 cos1 N1 cos0
可见rs、rp都是复数,rs rs eis 和rp rp ei p的
辐角是反射的位相变化,反射率由模的平方确定
波长为 546nm的 光入射到金 属Ag和Cu 上的情形
第二种介质为吸收时的情况
不管入射角如何,反射光的位相变化不 再是00或1800而是它们中间的某一角度, 同时s—分量和P—分量之间有一个不为0的 相对位相差, 因而当入射光为线偏振光在吸 收介质上反射后通常成为椭圆偏振光, 正 是基于这种认识,利用反射光的椭圆偏振 测量就可确定吸收介质的光学常数。
η2/Y。由于λ/2和λ/4的光学厚度的膜层组成的膜系比较简
单,所以膜系设计常常用指定波长1/4的倍数来表示,一般
只用两种或三种不同的膜料构造膜系, λ/4光学厚度的常用
缩写符号是H、M、L分别表示高、中、低折射率。
λ/2和λ/4的光学厚度
当膜层的光学厚度为λ/2时
cos
i sin
i
sin cos
sin0
ik1
可 见1为 复 数, 除0 1 0时 ,1不 再 为折 射 角 ;
当0
1
0时 ,rp
rs
n0 n1 ik1 n0 n1 ik
第二种介质为吸收时的情况
当0 0时情况要复杂的多
rs
rs
eis
n0 cos0 n0 cos0
N1 cos1 N1 cos1
rp
rp
ei p
负向行进的波位相因子应乘以ei
单层膜的反射
在膜层内E和H在边界a上的值为:
E1a
E1bei ,即k
E1a
1 2
Hb
1
光学薄膜原理 ppt课件

1.2E6~12000ev
由炽热物体、气体 放电或其它光源激 发分子或原子等微 观客体所产生的电
磁辐射
用高速电子流轰击原子中的内层 电子而产生的电磁辐射 放射性原子衰变发出的电磁辐射 或高能粒子碰撞产生的电磁辐射
光学薄膜基础理论
几个条件: ✓工作波段:光学 ✓薄膜厚度于考虑的波长在一个数量级 ✓薄膜的面积与波长相比可认为无限大 ✓薄膜材料各向均匀、同性 ✓薄膜材料为非铁磁性材料 ✓光穿过膜层而非沿着膜层在膜层内传播
20 0 1
c os 0 c os1
R r 2 (0 1 )2 0 1
T
N1 N0
t2
4N0 N1 (N0 N1)2
T
1 0
ts2
401 (0 1)2
s N cos
p N / cos
第三节 单层薄膜的传输矩阵
E12
1 2 E2
1
21
H2
E12
1 2
E2
1
21
H2
( e iδ1 = cosδ1+ i sinδ1, e -iδ1 = cos δ1 - i sin δ1 )
η: Amended admi. or effect. index
倾斜入射时反射系数和透射系数:
由切向连续
Ei 0 tan
Er 0 tan
Et 1 ta n
(1)
Hi 0 tan
Hr 0 tan
Ht 1 ta n
E i 0 0 tan
Er
0 0 tan
Et
1 1tan
(2)
切向反射系数: (1)×η1- (2): 切向透射系数:(1)×η0+(2):
N
c os
由炽热物体、气体 放电或其它光源激 发分子或原子等微 观客体所产生的电
磁辐射
用高速电子流轰击原子中的内层 电子而产生的电磁辐射 放射性原子衰变发出的电磁辐射 或高能粒子碰撞产生的电磁辐射
光学薄膜基础理论
几个条件: ✓工作波段:光学 ✓薄膜厚度于考虑的波长在一个数量级 ✓薄膜的面积与波长相比可认为无限大 ✓薄膜材料各向均匀、同性 ✓薄膜材料为非铁磁性材料 ✓光穿过膜层而非沿着膜层在膜层内传播
20 0 1
c os 0 c os1
R r 2 (0 1 )2 0 1
T
N1 N0
t2
4N0 N1 (N0 N1)2
T
1 0
ts2
401 (0 1)2
s N cos
p N / cos
第三节 单层薄膜的传输矩阵
E12
1 2 E2
1
21
H2
E12
1 2
E2
1
21
H2
( e iδ1 = cosδ1+ i sinδ1, e -iδ1 = cos δ1 - i sin δ1 )
η: Amended admi. or effect. index
倾斜入射时反射系数和透射系数:
由切向连续
Ei 0 tan
Er 0 tan
Et 1 ta n
(1)
Hi 0 tan
Hr 0 tan
Ht 1 ta n
E i 0 0 tan
Er
0 0 tan
Et
1 1tan
(2)
切向反射系数: (1)×η1- (2): 切向透射系数:(1)×η0+(2):
N
c os
第一篇-第一章 薄膜光学的理论基础.

式中
(1-3)
薄膜光学与薄膜技术基础
在求解具体的薄膜光学问题时,麦克斯 韦方程还涉及反映介质特性的关系,即电磁 场量之间关系的物质方程
D 0 r E B 0 H J E
(1-4)
- 12 e 淮 8 . 85 10 式中 0 (F/m)为真空介电常数, r - 7 m = 4 p? 10 为复相对介电常数; 0 (H/m)为
(1-5) 式中n表示介质的折射率,均匀介质取常数值。 (2)对于各向同性线性非均匀介质,介质 非导电 s = 0 , r 为实函数,则有 (1-6) r r 0 r r 0n2 r 非均匀介质折射率n随空间变量变化。
c r 0 r 0n2
(1-11)
a 称之为消 式中 n 称之为导电介质的折射率, 光系数。由式(1-11)可以看出,导电介质 的折射率和消光系数是光波频率的函数,所 以光波在导电介质中传播或在导电介质表面 反射和透射都存在色散。 (4)对于通常的光学介质,其特征表现为 在某一光频范围的辐射是透明的,比如玻璃
薄膜光学与薄膜技术基础
/ m
图 1-1
常用光学材料的透光范围
薄膜光学与薄膜技术基础
介质对光的吸收分为两类:一般吸收和 选择吸收。一般吸收与波长无关,吸收系数 很小;选择吸收与波长紧密相关,吸收系数 很大。选择吸收与构成介质的电偶极子有关, 反映了介质中原子结构的本质。 光学介质的折射率随波长而改变的现象 称之为介质的色散。色散与吸收密切相关, 根据经典振子模型,可以说明色散和吸收现 象。假设单原子中有Z个电子, f i 个电子对应 的振子固有圆频率和衰减系数分别为 w0i 和 gi , 则由振子的运动方程求解可得介质的相对介
薄膜光学与薄膜技术_第01篇-01-薄膜光学的理论基础

c r 0r 0n2
(1-5)
式中n表示介质的折射率,均匀介质取常数值。 (2)对于各向同性线性非均匀介质,介质
非导电 s = 0, r 为实函数,则有
r r 0r r 0n2 r (1-6)
非均匀介质折射率n随空间变量变化。
k = w me
(1-25)
则方程(1-22)和方程(1-23)就化为理想介 质中的复矢量波动方程。
薄膜光学与薄膜技术基础
波数 k 也称之为空间角频率。波数 k 与
波速 u 及角频率 w之间的关系为
k = w me = w = wn uc
(1-26)
式中
u= 1 = c me n
(1-27)
为光波在介质中的传播速度,c为真空中的光
界面上的自由电流面密度复振幅矢量。如果
把边界条件写成标量形式,有
ìïïíïïî
E%1t H%1t
= -
E%2t H%2t
=
J%s
(1-18)
式中 E%1t 、E%2t 和 、 H%1t H%2t 分别表示介质1和介质2分 界面上电场和磁场复振幅矢量的切向分量。J%s 为分界面上 p2 2 4 2 2
n
1 2
p2 1 4 2 2
(1-11)
式中 n 称之为导电介质的折射率,a 称之为消
光系数。由式(1-11)可以看出,导电介质
的折射率和消光系数是光波频率的函数,所
以光波在导电介质中传播或在导电介质表面
CsI
KI CsBr
BaF2
KBr
CaF2
KCI
SiO2
NaCI
NaF
0.8 100 200
第一篇-第一章 薄膜光学的理论基础解读

对于可见光波段是透明的,而半导体锗对于 波长大于2μm的红外波段是透明的,等等。 图1-1给出的是一些常用光学介质的透光范围。
氟化镁(MgF2) 氟化钙(CaF2) 氟化钡(BaF2) 石英(SiO2) 紫外石英(SiO2) 熔石英(SiO2) 玻璃(BK-7) 硅(Si) 锗(Ge) 硫化锌(ZnS) 砷化镓(GaAs) 硒化锌(ZnSe) 碲化镉(CdTe) 0.1 0.2 0.3 0.4 0.5 0.6 1.0 2.0 3.0 4.0 5.0 6.0 10.0
薄膜光学与薄膜技术基础
合导电体。麦克斯韦方程是描述一切宏观电 磁现象的普遍规律,因而,薄膜光学中描述 光传播特性的光波动方程可以由麦克斯韦方 程导出。 考虑时谐电磁场,空间任一点的电场强 度和磁场强度随时间作正弦或余弦变化,场 量随时间变化的因子取ejωt,则有
E(r; t ) Re E r e jt D(r; t ) Re D r e jt jt H r e H(r; t ) Re jt B ( r ; t ) Re B r e
式中
(1-3)
薄膜光学与薄膜技术基础
在求解具体的薄膜光学问题时,麦克斯 韦方程还涉及反映介质特性的关系,即电磁 场量之间关系的物质方程
D 0 r E B 0 H J E
(1-4)
- 12 e 淮 8 . 85 10 式中 0 (F/m)为真空介电常数, r - 7 m = 4 p? 10 为复相对介电常数; 0 (H/m)为
真空磁导率;σ为电导率。 式(1-2)和式(1-4)构成麦克斯韦方程 的限定形式,当 r 和 σ 给定之后,就可以针
薄膜光学与薄膜技术基础
薄膜光学技术-1第一章 薄膜光学特性计算基础

tp
2N 0co0s N0co1sN1co0s
1
s
Kcos0 cos1
p
其中,计算
r
和
s
t
时,公式中的
s
应代入 s ;
计算 rp和 t p时,公式中的应代入 p 。
显然,引入修正导纳的好处是菲涅耳公式的形式简化易记了。
第20页
2 单一界面的反射率和透射率
RIr Ii
EE00ri22
2
r201 01
求解依据:
E、H、k0 之间的右旋法则
电磁场的边界条件 在两种介质的分界面上没有面电荷和面电流的情 况下,电磁场量H和E的切向分量是连续的。
第15页
垂直入射
由切向分量连续:
H
i 0
N0
N1
E
i 0
k0
H1t
E
r 0
kE0 1t
k0
H
r 0
E0i E0r E1t
(1)
H0i H0r H1t
p N / cos 第22页
3 等效界面思想
将一个多界面的薄膜系统等效地看作一个单一界 面。等效界面两侧的介质分别是入射介质和等效介质。 入射介质的折射率仍旧是N0,等效介质具有等效光 学导纳。 因此,薄膜系统的反射率就是等效界面的反射率, 而等效界面的反射率计算公式是:
2
R 0 Y 0 Y
s Ncos
H
i 0
N0 N1
p 偏振
Ei0 0 Ei0 cos 0
1 H1t
H
r 0
0
E1t E1t cos1
E0r cos 0
H与界面平行
Htan H
E0r
EtanEcos
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
熔石英(SiO2)
玻璃(BK-7)
硅(Si)
硫化锌(ZnS)
锗(Ge)
砷化镓(GaAs)
硒4 0.5 0.6
1.0 2.0 3.0 4.0 5.0 6.0 10.0 / m
图 1-1 常用光学材料的透光范围
介质对光的吸收分为两类:一般吸收和
第一篇 薄膜光学理论基础
第一章 薄膜光学的电磁理论基础 曹建章
薄膜光学的理论基础是光的电磁理论,其 内容包括:光的干涉、偏振和吸收,平面电 磁波以及平面电磁波在介质表面的反射和透 射等。鉴于后续章节的需要,本章简要介绍 麦克斯韦方程、描述介质特性的物质方程、 平面电磁波的解形式以及光强和电磁波谱。 1.1 麦克斯韦方程
度和磁场强度随时间作正弦或余弦变化,场
量随时间变化的因子取ejωt,则有
E(r;
t
)
Re
E%
r
e
jt
D(r;t) Re D%r e jt
H
(r;
t
)
Re
H%
r
e
jt
B(r;
t
)
Re
B%r
e
jt
(1-1)
在无源区域,介质介电常数为 ,且介
质的电导率 0 ,则时谐形式的麦克斯韦方 程为
式(1-8)和式(1-10)联立求解,得到
n2
2
4
2 2 p2 2 4 2 2
n
1 2
p2 1 4 2 2
(1-11)
式中 n 称之为导电介质的折射率,a 称之为消
光系数。由式(1-11)可以看出,导电介质
的折射率和消光系数是光波频率的函数,所
以光波在导电介质中传播或在导电介质表面
(1-2)可导出金属材料的介电常数为
%c
0%r
0
N%2
0
1
2
2 p
j
1
(1-8)
式中 N%为复折射率,w为光波圆频率。 wp为
金属的等离子体频率,大小为
wp =
Ne2 = mee0
m0s c2 t
式中 c 表示真空中的光速。 令
%r r ji , N% n j
(1-9) (1-10)
反射和透射都存在色散。
(4)对于通常的光学介质,其特征表现为
在某一光频范围的辐射是透明的,比如玻璃
对于可见光波段是透明的,而半导体锗对于 波长大于2μm的红外波段是透明的,等等。 图1-1给出的是一些常用光学介质的透光范围。
氟化镁(MgF2) 氟化钙(CaF2)
氟化钡(BaF2)
石英(SiO2) 紫外石英(SiO2)
fi
n2 + 2 3e0me i w02i - w2
(1-15)
该式表明折射率取实数,对应于光学介质是
透明的,但折射率也与入射光频有关,属一
般吸收。一般吸收折射率随波长的增加而减
小,这种现象称为正常色散。
图1-2给出的是几种玻璃的折射率随波长变化 的曲线。
折射率 n
重火石玻璃
1.7
轻质火石玻璃
1.6
宏观上讲,光的电磁理论全面揭示了光 的主要性质,不仅适合各向同性介质,也适 合各向异性介质;不仅适用于均匀介质,也 适合非均匀介质;不仅适合吸收介质,也适
合导电体。麦克斯韦方程是描述一切宏观电 磁现象的普遍规律,因而,薄膜光学中描述 光传播特性的光波动方程可以由麦克斯韦方 程导出。
考虑时谐电磁场,空间任一点的电场强
为复相对介电常数;m0 = 4p ? 10- 7 (H/m)为
真空磁导率;σ为电导率。
式(1-2)和式(1-4)构成麦克斯韦方程 的限定形式,当 %r 和 σ 给定之后,就可以针
对具体问题进行求解。下面就薄膜光学中涉
及的介质参数作简单讨论。
(1)对于各向同性线性均匀介质,介质非
导电 s = 0,%r 取实常数,则式(1-3)简化为
选择吸收。一般吸收与波长无关,吸收系数 很小;选择吸收与波长紧密相关,吸收系数 很大。选择吸收与构成介质的电偶极子有关, 反映了介质中原子结构的本质。
光学介质的折射率随波长而改变的现象
称之为介质的色散。色散与吸收密切相关, 根据经典振子模型,可以说明色散和吸收现 象。假设单原子中有Z个电子, fi 个电子对应 的振子固有圆频率和衰减系数分别为 w0i和 gi , 则由振子的运动方程求解可得介质的相对介
以在光波交变电场的作用下,通过电子运动
方程的求解,可得金属材料的电导率为率
Ne2 s= t
me
(1-7)
式中 N 为单位体积的导电电子数,me 为电子
质量,- e 为电子电荷。t 称为弛豫时间,表
示在时间 t 内电流密度衰减到初始值的 1 / e 。
met - 1代表电子运动的阻尼系数。
在介质均匀的情况下,利用麦克斯韦方程
H% E%
j%cE% jB%
B%
0
D% 0
(1-2)
式中
%ec = e-
js w
(1-3)
为介质的等效复介电常数。
在求解具体的薄膜光学问题时,麦克斯
韦方程还涉及反映介质特性的关系,即电磁 场量之间关系的物质方程
D% B%
0%r E% 0H%
J% E%
(1-4)
式中 e0 淮8.85 10- 1(2 F/m)为真空介电常数, %r
%c r 0r 0n2
(1-5)
式中n表示介质的折射率,均匀介质取常数值。
(2)对于各向同性线性非均匀介质,介质
非导电 s = 0, %r 为实函数,则有
%r r 0r r 0n2 r (1-6)
非均匀介质折射率n随空间变量变化。
(3)金属材料对光的吸收体现在电导率s ? 0 在金属材料中,由于电子运动是自由的,所
石英晶体 硼硅冕玻璃
1.5
丙烯酸塑料 透明石英
1.4
0
200
400
600
800 1000
波长 λ (nm)
图 1-2 几种玻璃的折射率随波长的变化曲线
电常数为
å %er =
N%2 (w)=
1+
Ne2 e0me
i
fi w02i - w2 -
jgiw
(1-12)
式中 N% n j 为复折射率; N为介质单位体积 中的原子数,me 为电子质量, e 为电子电荷;
w为光波圆频率。式(1-12)是对一个原子
中的所有振子类型求和,显然有
å fi = Z
(1-13)
i
式(1-12)是由稀薄气体推导出来的,
对于稠密介质液体和固体,需要考虑偶极振
子间的相互作用,修正可得
å N%2 -
N%2 +
1= 2
Ne2 3e0me
i
fi w02i - w2 -
jgiw
(1-14)
当 w02i - w2 ? giw 时,即电偶极子的固有频率远 远大于入射光频时,则有
å n2 - 1 = Ne2
玻璃(BK-7)
硅(Si)
硫化锌(ZnS)
锗(Ge)
砷化镓(GaAs)
硒4 0.5 0.6
1.0 2.0 3.0 4.0 5.0 6.0 10.0 / m
图 1-1 常用光学材料的透光范围
介质对光的吸收分为两类:一般吸收和
第一篇 薄膜光学理论基础
第一章 薄膜光学的电磁理论基础 曹建章
薄膜光学的理论基础是光的电磁理论,其 内容包括:光的干涉、偏振和吸收,平面电 磁波以及平面电磁波在介质表面的反射和透 射等。鉴于后续章节的需要,本章简要介绍 麦克斯韦方程、描述介质特性的物质方程、 平面电磁波的解形式以及光强和电磁波谱。 1.1 麦克斯韦方程
度和磁场强度随时间作正弦或余弦变化,场
量随时间变化的因子取ejωt,则有
E(r;
t
)
Re
E%
r
e
jt
D(r;t) Re D%r e jt
H
(r;
t
)
Re
H%
r
e
jt
B(r;
t
)
Re
B%r
e
jt
(1-1)
在无源区域,介质介电常数为 ,且介
质的电导率 0 ,则时谐形式的麦克斯韦方 程为
式(1-8)和式(1-10)联立求解,得到
n2
2
4
2 2 p2 2 4 2 2
n
1 2
p2 1 4 2 2
(1-11)
式中 n 称之为导电介质的折射率,a 称之为消
光系数。由式(1-11)可以看出,导电介质
的折射率和消光系数是光波频率的函数,所
以光波在导电介质中传播或在导电介质表面
(1-2)可导出金属材料的介电常数为
%c
0%r
0
N%2
0
1
2
2 p
j
1
(1-8)
式中 N%为复折射率,w为光波圆频率。 wp为
金属的等离子体频率,大小为
wp =
Ne2 = mee0
m0s c2 t
式中 c 表示真空中的光速。 令
%r r ji , N% n j
(1-9) (1-10)
反射和透射都存在色散。
(4)对于通常的光学介质,其特征表现为
在某一光频范围的辐射是透明的,比如玻璃
对于可见光波段是透明的,而半导体锗对于 波长大于2μm的红外波段是透明的,等等。 图1-1给出的是一些常用光学介质的透光范围。
氟化镁(MgF2) 氟化钙(CaF2)
氟化钡(BaF2)
石英(SiO2) 紫外石英(SiO2)
fi
n2 + 2 3e0me i w02i - w2
(1-15)
该式表明折射率取实数,对应于光学介质是
透明的,但折射率也与入射光频有关,属一
般吸收。一般吸收折射率随波长的增加而减
小,这种现象称为正常色散。
图1-2给出的是几种玻璃的折射率随波长变化 的曲线。
折射率 n
重火石玻璃
1.7
轻质火石玻璃
1.6
宏观上讲,光的电磁理论全面揭示了光 的主要性质,不仅适合各向同性介质,也适 合各向异性介质;不仅适用于均匀介质,也 适合非均匀介质;不仅适合吸收介质,也适
合导电体。麦克斯韦方程是描述一切宏观电 磁现象的普遍规律,因而,薄膜光学中描述 光传播特性的光波动方程可以由麦克斯韦方 程导出。
考虑时谐电磁场,空间任一点的电场强
为复相对介电常数;m0 = 4p ? 10- 7 (H/m)为
真空磁导率;σ为电导率。
式(1-2)和式(1-4)构成麦克斯韦方程 的限定形式,当 %r 和 σ 给定之后,就可以针
对具体问题进行求解。下面就薄膜光学中涉
及的介质参数作简单讨论。
(1)对于各向同性线性均匀介质,介质非
导电 s = 0,%r 取实常数,则式(1-3)简化为
选择吸收。一般吸收与波长无关,吸收系数 很小;选择吸收与波长紧密相关,吸收系数 很大。选择吸收与构成介质的电偶极子有关, 反映了介质中原子结构的本质。
光学介质的折射率随波长而改变的现象
称之为介质的色散。色散与吸收密切相关, 根据经典振子模型,可以说明色散和吸收现 象。假设单原子中有Z个电子, fi 个电子对应 的振子固有圆频率和衰减系数分别为 w0i和 gi , 则由振子的运动方程求解可得介质的相对介
以在光波交变电场的作用下,通过电子运动
方程的求解,可得金属材料的电导率为率
Ne2 s= t
me
(1-7)
式中 N 为单位体积的导电电子数,me 为电子
质量,- e 为电子电荷。t 称为弛豫时间,表
示在时间 t 内电流密度衰减到初始值的 1 / e 。
met - 1代表电子运动的阻尼系数。
在介质均匀的情况下,利用麦克斯韦方程
H% E%
j%cE% jB%
B%
0
D% 0
(1-2)
式中
%ec = e-
js w
(1-3)
为介质的等效复介电常数。
在求解具体的薄膜光学问题时,麦克斯
韦方程还涉及反映介质特性的关系,即电磁 场量之间关系的物质方程
D% B%
0%r E% 0H%
J% E%
(1-4)
式中 e0 淮8.85 10- 1(2 F/m)为真空介电常数, %r
%c r 0r 0n2
(1-5)
式中n表示介质的折射率,均匀介质取常数值。
(2)对于各向同性线性非均匀介质,介质
非导电 s = 0, %r 为实函数,则有
%r r 0r r 0n2 r (1-6)
非均匀介质折射率n随空间变量变化。
(3)金属材料对光的吸收体现在电导率s ? 0 在金属材料中,由于电子运动是自由的,所
石英晶体 硼硅冕玻璃
1.5
丙烯酸塑料 透明石英
1.4
0
200
400
600
800 1000
波长 λ (nm)
图 1-2 几种玻璃的折射率随波长的变化曲线
电常数为
å %er =
N%2 (w)=
1+
Ne2 e0me
i
fi w02i - w2 -
jgiw
(1-12)
式中 N% n j 为复折射率; N为介质单位体积 中的原子数,me 为电子质量, e 为电子电荷;
w为光波圆频率。式(1-12)是对一个原子
中的所有振子类型求和,显然有
å fi = Z
(1-13)
i
式(1-12)是由稀薄气体推导出来的,
对于稠密介质液体和固体,需要考虑偶极振
子间的相互作用,修正可得
å N%2 -
N%2 +
1= 2
Ne2 3e0me
i
fi w02i - w2 -
jgiw
(1-14)
当 w02i - w2 ? giw 时,即电偶极子的固有频率远 远大于入射光频时,则有
å n2 - 1 = Ne2
