专题(八) 构造“三线合一”巧解题(选用)
利用三线合一解题

等腰三角形的顶角平分线、底边上的中线、底边上的高线相互重合.
1.等腰三角形的顶角平分线也是底边上的中线、底边上的高线.
∵ △ABC中,AB=AC,-∠---B--A---D--=---∠--C---A--D-
A
∴
AD⊥BC
BD=CD
------------- ----------------
只要证DB=DE即可
4
练习:如图3,△ABC中,AB=AC,BD⊥AC
Байду номын сангаас
交AC于D.
1
A
求证:∠DBC= ∠BAC.
2
D
B
C
5
当题目中出现等腰三角形和“三线” 之一时,直接得到其余两线的性质, 但表达要规范;
6
三线合一基本图形
7
∴
∠BAD=∠CAD BD=CD
------------- ----------------
1
三线合一的简单应用 (1)如图,已知AB=BC,D是AC的中点,
∠A=34°,则∠DBC= 56 度.
2
(3)如图,∠A=∠D=90°,AB=CD,AC与 BD相交于点F,E是BC的中点. 求证:∠BFE=∠CFE.
证明:∵∠1=∠2 (对顶角相等) ∠A=∠D=90° AB=CD
∴△ABF≌△DCF (AAS) ∴BF=CF ∴ △BCF是等腰三角形. 又 E是BC的中点, ∴EF是∠BFC的角平分线.
∴ ∠BFE=∠CFE. ( 三线合一 )
3
(4)已知,等边三角形ABC,D是AC的中 点,点E在BC的延长线上,且CE =CD。若 DM⊥BC,垂足为M,那么M是BE的中点, 请说明理由。
北师大版初二数学下册《活用“三线合一”巧解题》讲义

北师大版初二数学下册《活用“三线合一” 巧解题》讲义【名师点睛】等腰三角形〝顶角均分线、底边上的高、底边上的中线〞只需知道此中〝一线〞,就能够说明是其余〝两线〞。
运用等腰三角形〝三线合一〞的性质证明角相等、线段相等或垂直关系,能够减少证明全等的次数,简化解题过程。
[ 技巧 1]利用〝三线合一〞求角1.如图 ,房子的顶角∠ BAC=100°,过屋顶 A 的立柱 AD ⊥BC,屋椽 A B=AC ,求顶架上∠ B、∠ C、∠ BAD 、∠ CAD 的度数。
解答:∵△ ABC 中,AB=AC, ∠BAC=100°∴∠ B=∠C= 1°∠BAC)=1(180°°°2(180 -2- 100 )=40∵A B=AC,AD ⊥BC,∠BAC=100°∴AD 均分∠ BAC∴∠ BAD= ∠CAD=50.[ 技巧 2]利用〝三线合一〞求线段2.如图,在△ ABC 中,AB=AC ,AD=DB=BC ,DE⊥AB 于点 E,假定CD=4,且△ BDC 的周长为 24,求 AE 的长。
解答:∵A D=DB=BC ,CD=4,且△ BDC 的周长为 24∴A D=DB=BC=10∴A C=14∵A B=AC∴A B=14∵A D=DB ,DE⊥AB∴A E=BE= 1AB=7. 2[ 技巧 3]利用〝三线合一〞证全等3.:三角形 ABC 中,∠A=90°,AB=AC ,D 为 BC 的中点,如图, E, F 分别是 AB ,AC 上的点,且 BE=AF ,求证:△ DEF 为等腰直角三角形。
解答:证明:连结 AD∵A B=AC, ∠ A=90°,D 为 BC 中点∴AD=BC2=BD=CD且 AD 均分∠ BAC∴∠ BAD= ∠CAD=45 °在△ BDE 和△ ADF 中, BD=AD ,∠ B=∠DAF=45 °,BE=AF ∴△ BDE≌△ ADF∴D E=DF ,∠ BDE=∠ADF∵∠ BDE+ ∠ADE=90 °∴∠ ADF+ ∠ADE=90 °即:∠ EDF=90°∴△ EDF 为等腰直角三角形。
三线合一专题练习
三线合一专题练习
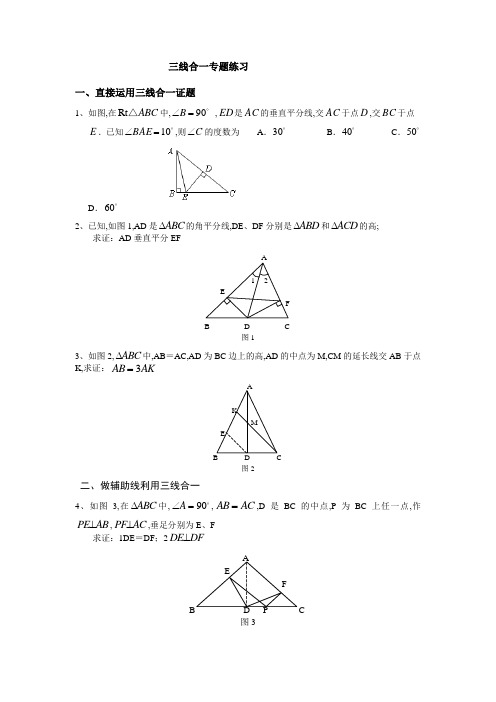
一、直接运用三线合一证题
1、如图,在Rt ABC △中,
90=∠B ,ED 是AC 的垂直平分线,交AC 于点D ,交BC 于点E .已知 10=∠BAE ,则C ∠的度数为 A . 30 B . 40 C . 50
D . 60
2、已知,如图1,AD 是∆ABC 的角平分线,DE 、DF 分别是∆ABD 和∆ACD 的高; 求证:AD 垂直平分EF
A
1 2
E
F
B D C
图1
3、如图2,∆ABC 中,AB =AC,AD 为BC 边上的高,AD 的中点为M,CM 的延长线交AB 于点K,求证:AB AK =3
A
K
M
E
图2
二、做辅助线利用三线合一
4、如图3,在∆ABC 中,∠=A 90
,AB AC =,D 是BC 的中点,P 为BC 上任一点,作PE AB ⊥,PF AC ⊥,垂足分别为E 、F
求证:1DE =DF ;2DE DF ⊥ A
E
F
B D P 图3
5、如图,在等腰梯形ABCD中,G为对角线交点,△ADG、△GBC为正三角形;F、E、H为AG、BG、DC的中点; 连接CE BF
1求证:△EFH为正三角形;
2若AD=2,BG=3,求S△EFH;
ACB ADB90 ,M、N分别为AB、CD的中点,求6、如图4,已知四边形ABCD中,∠=∠=
⊥
证:MN CD
C
N
D
A M B
图4
7、如图,已知在等边三角形ABC中,D是AC的中点,E为BC延长线上一点,且CE=CD,DM ⊥BC,垂足为M;求证:M是BE的中点;
A
D
1
B M
C E。
正多边形三线合一专项综合练习

正多边形三线合一专项综合练习本文档旨在提供正多边形三线合一综合练的相关内容。
以下是几个题例以供参考。
问题1:正三角形的三线合一问题假设有一个正三角形ABC,其中A、B、C分别代表三个角。
现在要求证明三角形内的三条特殊线段AA'、BB'、CC'共点于一个点O,即三线合一。
对于正三角形ABC来说,我们可以通过几何推导来证明三线合一的问题。
具体证明过程如下:1. 连接BC、AC、AB,得到线段AA'、BB'、CC';2. 在AB上任意取一点D,连接CD;3. 观察△ACD和△BCD,通过对角线法则和对边法则,可以得出△ACD与△BCD相似;4. 由于△ACD与△BCD相似,我们可以推导出DD'与BB'比例一致;5. 同理,可以推导出AA'与DD'比例一致;6. 因此,根据比例定理,我们可以得到AA'与BB'的延长线与CC'的交点为O,即证明了正三角形的三线合一问题。
问题2:正方形的三线合一问题假设有一个正方形ABCD,其中A、B、C、D分别代表四个角。
现在要求证明三线合一。
对于正方形ABCD来说,我们可以通过以下几个步骤来证明三线合一问题:1. 连接AC,得到线段AA';2. 连接BD,得到线段BB';3. 连接AD和BC,得到线段CC';4. 线段AA'、BB'的延长线与线段CC'的交点为O,即证明了正方形的三线合一问题。
问题3:正六边形的三线合一问题假设有一个正六边形ABCDEF,其中A、B、C、D、E、F分别代表六个角。
现在要求证明三线合一。
对于正六边形ABCDEF来说,我们可以通过以下几个步骤来证明三线合一问题:1. 连接CD和FA,得到线段AA';2. 连接CE和FB,得到线段BB';3. 连接CF和AE,得到线段CC';4. 线段AA'、BB'的延长线与线段CC'的交点为O,即证明了正六边形的三线合一问题。
【北师大版】初二八年级数学下册《活用“三线合一”巧解题》专题考点试卷(附答案)

专训3活用“三线合一”巧解题名师点金:等腰三角形“顶角平分线、底边上的高、底边上的中线”只要知道其中“一线”,就可以说明是其他“两线”.运用等腰三角形“三线合一”的性质证明角相等、线段相等或垂直关系,可减少证全等的次数,简化解题过程.利用“三线合一”求角1.如图,房屋顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋檐AB=AC.求顶架上的∠B,∠C,∠BAD,∠CAD的度数.(第1题)利用“三线合一”求线段2.如图,在△ABC中,AB=AC,AD=DB,DE⊥AB 于点E,若BC=10,且△BDC的周长为24,求AE的长.(第2题)3.如图,在△ABC中,∠A=90°,AB=AC,D为BC 的中点,E,F分别是AB,AC上的点,且BE=AF,求证:DE=DF.(第3题)利用“三线合一”证垂直4.如图,在△ABC中,AC=2AB,AD平分∠BAC,E 是AD上一点,且EA=EC.求证:EB⊥AB.(第4题)利用“三线合一”证线段的倍数关系(构造三线法)5.如图,在等腰直角三角形ABC中,AB=AC,∠BAC =90°,BF平分∠ABC,CD⊥BF交BF的延长线于点D.求证:BF=2CD.(第5题)利用“三线合一”证线段的和差关系(构造三线法)6.如图,在△ABC中,AD⊥BC于点D,且∠ABC=2∠C.求证:CD=AB+BD.(第6题)答案1.解:∵AB=AC,∠BAC=100°,AD⊥BC,∴∠B =∠C=40°,∠BAD=∠CAD=50°.2.解:∵△BDC的周长=BD+BC+CD=24,BC=10,∴BD+CD=14.∵AD=BD,∴AC=AD+CD=BD+CD=14. ∴AB=AC=14.∵AD=DB,DE⊥AB,∴AE=EB=12AB=7.3.证明:如图,连接AD.∵AB=AC,D为BC的中点,∴AD⊥BC.∴∠ADB=90°.∵AB=AC,∠BAC=90°,∴∠B=∠C=45°.在△ABD中,∠BAD=180°-∠B-∠ADB=45°,∴∠B=∠BAD.∴BD=AD.又∵BD=CD,∴AD=CD.∴∠DAC=∠C=45 °.∴∠B=∠DAF.又∵BE=AF,∴△BDE≌△ADF(SAS).∴DE=DF.(第3题4.证明:如图,过点E作EF⊥AC于F.∵AE=EC,∴AC =2AF.又∵AC=2AB,∴AF=AB.∵AD平分∠BAC,∴∠FAE=∠BAE.又∵AE=AE,∴△AEF≌△AEB(SAS).∴∠ABE=∠AFE=90°,即EB⊥AB.(第4题) 5.证明:如图,延长BA,CD交于点E.由BF平分∠ABC,CD⊥BD,BD=BD,易得△BDC≌△BDE.∴BC=BE.又∵BD⊥CE,∴CE=2CD.∵∠BAC=90°,∠BDC=90°,∠AFB=∠DFC,∴∠ABF=∠DCF.又∵AB=AC,∠BAF=∠CAE=90°,∴△ABF≌△ACE(ASA).∴BF=CE.∴BF=2CD.(第5题)6.证明:如图,以A为圆心,AB长为半径画弧交CD 于点E,连接AE,则AE=AB,所以∠AEB=∠ABC.因为AD⊥BC,所以AD是BE边上的中线,即DE=BD.又因为∠ABC=2∠C,所以∠AEB=2∠C.而∠AEB=∠CAE+∠C,所以∠CAE=∠C.所以CE=AE=AB.故CD=CE+DE=AB+BD.(第6题)。
1 活用“三线合一”解题的六种技巧

返回
技巧 2 利用“三线合一”求线段的长
2.如图,在△ABC中,AB=AC,AD=DB,DE⊥AB 于点E,若BC=10,且△BDC的周长为24,求AE 的长.
解:∵△BDC的周长=BD+BC+CD=24,BC=10,
∴BD+CD=14.
∵AD=BD,
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/172021/9/172021/9/172021/9/179/17/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月17日星期五2021/9/172021/9/172021/9/17 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/172021/9/172021/9/179/17/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/172021/9/17September 17, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/172021/9/172021/9/172021/9/17
第1章 三角形的证明
双休作业(一) 1 活用“三线合一”解题的六种技巧
1
2
3
4
5
6
技巧 1 利用“三线合一”求角
1.如图,房屋顶角∠BAC=100°,过屋顶A的立柱 AD⊥BC,垂足为D,AB=AC,求∠B,∠C, ∠BAD,∠CAD的度数.
解: ∵ AB = AC , ∠ BAC = 100° , AD⊥BC,
专题08 解题技巧专题:利用等腰三角形的'三线合一'作辅助线压轴题三种模型全攻略(原卷版)

专题08解题技巧专题:利用等腰三角形的'三线合一'作辅助线压轴题三种模型全攻略【考点导航】目录【典型例题】 (1)【类型一等腰三角形中底边有中点时,连中线】 (1)【类型二等腰三角形中底边无中点时,作高线】 (4)【类型三巧用“角平分线+垂线合一”构造等腰三角形】 (5)【典型例题】【类型一等腰三角形中底边有中点时,连中线】例题:已知,在ABC 中,90ACB ∠=︒,AC BC =,点M 是AB 的中点,作90DME ∠=︒,使得射线MD 与射线ME 分别交射线AC ,CB 于点D ,E .(1)如图1,当点D 在线段AC 上时,线段MD 与线段ME 的数量关系是___________;(2)如图2,当点D 在线段AC 的延长线上时,用等式表示线段CD ,CE 和BC 之间的数量关系并加以证明.【变式训练】1.在ABC 中,90A ∠=︒,AB AC =,点D 是边BC 的中点.(1)如图,若点E ,F 分别在边AB ,AC 上,DE DF ⊥,求证:BE AF =,并说明理由;(2)在(1)的条件下,AB AC a ==,求AE AF +的值.2.如图1,在Rt ABC △中,90C ∠=︒,AC BC =,点P 是斜边AB 的中点,点D ,E 分别在边,AC BC 上,连接,PD PE ,若PD PE ⊥.(1)求证:PD PE =;(2)若点D ,E 分别在边,AC CB 的延长线上,如图2,其他条件不变,(1)中的结论是否成立?并加以证明;(3)在(1)或(2)的条件下,PBE △是否能成为等腰三角形?若能,请直接写出PEB ∠的度数(不用说理);若不能,请说明理由.(1)若90EOF ∠=︒,两边分别交,AC BC 于E ,F 两点.【类型二等腰三角形中底边无中点时,作高线】例题:如图,已知点D 、E 在△ABC 的边BC 上,AB =AC ,AD =AE .(1)求证:BD =CE ;(2)若AD =BD =DE =CE ,求∠BAE 的度数.【变式训练】1.如图,ADB 与△BCA 均为等腰三角形,AD AB CB ==,且90ABC ∠=︒,E 为DB 延长线上一点,2DAB EAC ∠=∠.(1)若20∠=︒EAC ,求CBE ∠的度数;(2)求证:AE EC ⊥;(3)若BE a =,AE b =,CE c =,求ABC 的面积(用含a ,b ,c 的式子表示).(1)如图1,若ACD ∠与BAC ∠互余,则DCB ∠=__________(【类型三巧用“角平分线+垂线合一”构造等腰三角形】例题:如图,在ABC 中,AD 平分BAC ∠,E 是BC 的中点,过点E 作FG AD ⊥交AD 的延长线于H ,交AB 于F ,交AC 的延长线于G .求证:(1)AF AG =;(2)BF CG =.【变式训练】(1)【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP 平分MON ∠.点AC OP ⊥,垂足为C ,延长AC 交ON 于点B ,可根据证明AOC ≌△△点C 为AB 的中点).(2)【类比解答】如图2,在ABC 中,CD 平分ACB ∠,AE CD ⊥于E ,若63EAC ∠=︒,办法,可求得DAE ∠=.(3)【拓展延伸】如图3,ABC 中,AB AC =,90BAC ∠=︒,CD 平分ACB ∠,BE CD ⊥,垂足E 在CD 的延长线上,试探究BE 和CD 的数量关系,并证明你的结论.(4)【实际应用】如图4是一块肥沃的三角形土地,其中AC 边与灌渠相邻,李伯伯想在这块地中划出一块直角三角形土地进行水稻试验,故进行如下操作:①用量角器取ACB ∠的角平分线CD ;②过点A 作AD CD ⊥于D .已知13BC =,10AC =,ABC 面积为20,则划出的ACD 的面积是多少?请直接写出答案.2.【问题情境】利用角平分线构造全等三角形是常用的方法,如图1,OP 平分MON ∠,点A 为OM 上一点,过点A 作AC OP ⊥,垂足为C ,延长AC 交ON 于点B ,易证AOC ∆≌BOC ∆,则AC BC =.其分析过程如下:在AOC ∆和BOC ∆中,OP 平分MON AOC BOC∠⇒∠=∠90OC OC AC OP OCA OCB =⊥⇒∠=∠=︒,⇒AOC ∆≌BOC ∆(___________)在括号内填写全等判定方法字母简称AC BC ⇒=(___________)在括号内填写理由依据【问题探究】如图2,ABC ∆中,90AB AC BAC CD =∠=︒,,平分ACB BE CD ∠⊥,,垂足E 在CD 的延长线上.证明:2CD BE =;【拓展延伸】。
三线合一解题
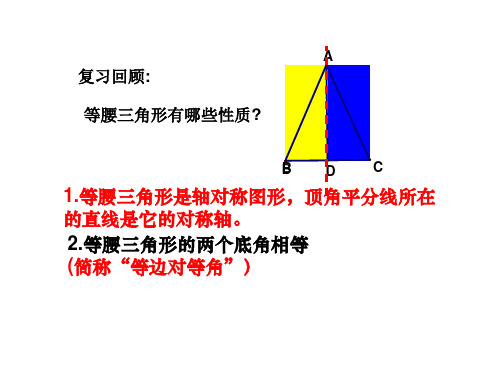
求证:CE=ED
A
C
D
B'
E
B
例3.已知:如图,在△ABC中,AB=AC, E在 AC上,D 在BA的延长线上,
AD=AE,连接DE.求证:DE⊥BC.
D
A
E
B
C
添加辅助线思路
图中AR这条线段的引出可以看成是: 1 .过A点作DE的平行线. 2 .过A点作BC的垂线. 3 . ∠BAC的角平分线. 4 . BC边的中线.
证明:∵∠1=∠2 (对顶角相等) ∠A=∠D=90° AB=CD
∴△ABF≌△DCF (AAS) ∴BF=CF ∴ △BCF是等腰三角形. 又 E是BC的中点, ∴EF是∠BFC的角平分线.
∴ ∠BFE=∠CFE. ( 三线合一 )
例1.已知AB′=AB,E为BB′的中点,
EC⊥AB′, ED ⊥AB.
A
复习回顾:
等腰三角形有哪些性质?
BD
C
1.等腰三角形是轴对称图形,顶角平分线所在
的直线是它的对称轴。
2.等腰三角形的两个底角相等
(简称“等边对等角”)
三线合一基本图形
等腰三角形三线合一性质
等腰三角形的顶角平分线、底边上的中线、底边上的高线相互重合.
1.等腰三角形的顶角平分线也是底边上的中线、底边上的高线.
这节课你有那些收获?
结束
∵ △ABC中,AB=AC,-∠---B--A---D--=---∠--C---A--D-
A
∴
AD⊥BC
BD=CD
------------- ----------------
2.等腰三角形底边上的中线也是的顶角平分线、 底边
上的高线.
∵ △ABC中,AB=AC,-----B--D---=---C--D-------
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方法技巧三: 遇有垂直时 , 将图形以垂线为轴翻折 , 构造 “ 三线合
一”.
6.如图,在△ABC中,AD⊥BC于点D,且∠ABC=2∠C.求证:CD=
AB+BD.
解:在DC上截取DE=BD,连接AE,∵BD=DE,AD⊥BC,∴AB= AE,∠B=∠AEB=∠EAC+∠C,又∵∠ABC=2∠C,∴∠EAC=∠C, ∴AE=EC,∴CD=CE+DE=AE+ED=AB+BD
求证:DE=DF.
解:连接 AD,∵AB=AC,D 是 BC 的中点,∴∠EAD=∠FAD, AE=AF, 在△AED 与△AFD 中∠EAD=∠FAD,∴△AED≌△AFD(SAS),∴ AD=AD, DE=DF
2 . 如 图 , 在 △ ABC 中 , AB = AC , D 是 BC 的 中 点 , 过 A 点 的 直 线
八年级上册人教版数学 第十二章
专题(八)
全等三角形
构造“三线合一”巧解题(选用)
等腰三角形“顶角平分线、底边上的高、底边上的中线”只要知道其中“一
线”,就可以说明是其他“两线”.运用等腰三角形“三线合一”的性质证明 角相等、线段相等或垂直关系,可减少证全等的次数,简化解题过程. 方法技巧一:有等腰三角形底边中点时,常作这底边上的中线,构造“三线 合一”图形. 1.如图,在△ABC中,AB=AC,D是BC的中点,E,F分别是AB,AC上 的点,且AE=AF.
5.如图,在△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD
上一点,且EA=EC.求证:EB⊥AB.
解:作EF⊥AC于点F,∵EA=EC,∴AF=FC,又∵AC=2AB,∴AF
= AB , 又∵ AD 平分∠ BAC , ∴∠ BAE =∠ FAE , ∴△ ABE≌△AFE ,
∴∠ABE=∠AFE=90°,∴EB⊥AB
解:(1)连接 AD,∵AB=AC,∴AD⊥BC,∠BAD=∠CAD,∠B= ∠C,∵∠BAC=90°,∴∠B=∠C=∠BAD=∠CAD=45°,∴AD= BE=AF, BD.在△BED 与△AFD 中,∠B=∠DAF,∴△BED≌△AFD(SAS),∴ BD=AD, DE=DF (2)∵△BED≌△AFD, ∴∠BDE=∠ADF, ∴∠BDE+∠EDA=∠EDA +∠ADF=90°,∴ED⊥DF
EF∥BC,且AE=AF.求证:DE=DF.
解:连接AD,∵AB=AC,D是BC的中点,∴AD⊥BC,∵EF∥BC,
∴AD⊥EF,又∵AE=AF,∴DE=DF
3.如图,在△ABC中,∠A=90°,AB=AC,D为BC的中点,E,F 分别是AB,AC上的点,且BE=AF,求证:(1)DE=DF;(,构造“三线合一”图形.
4.如图,点D,E分别在BA,AC的延长线上,且AB=AC,AD=AE.
求证:DE⊥BC.
解 : 作 AG⊥DE , ∵ AD = AE , ∴ ∠ DAG = ∠ EAG , 又 AB = AC ,
∴∠B=∠ACB,∵∠DAE=∠B+∠ACB=2∠B=2∠DAG,∴∠DAG =∠B,∴AG∥BC,∴DE⊥BC
