堆与堆排序
八大排序算法

八大排序算法排序有内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
我们这里说说八大排序就是内部排序。
基本思想:将一个记录插入到已排序好的有序表中,从而得到一个新,记录数增1的有序表。
即:先将序列的第1个记录看成是一个有序的子序列,然后从第2个记录逐个进行插入,直至整个序列有序为止。
要点:设立哨兵,作为临时存储和判断数组边界之用。
直接插入排序示例:如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。
所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
算法的实现:1.void print(int a[], int n ,int i){2. cout<<i <<":";3.for(int j= 0; j<8; j++){4. cout<<a[j] <<" ";5. }6. cout<<endl;7.}8.9.10.void InsertSort(int a[], int n)11.{12.for(int i= 1; i<n; i++){13.if(a[i] < a[i-1]){ //若第i个元素大于i-1元素,直接插入。
小于的话,移动有序表后插入14.int j= i-1;15.int x = a[i]; //复制为哨兵,即存储待排序元素16. a[i] = a[i-1]; //先后移一个元素17.while(x < a[j]){ //查找在有序表的插入位置18. a[j+1] = a[j];19. j--; //元素后移20. }21. a[j+1] = x; //插入到正确位置22. }23. print(a,n,i); //打印每趟排序的结果24. }25.26.}27.28.int main(){29.int a[8] = {3,1,5,7,2,4,9,6};30. InsertSort(a,8);31. print(a,8,8);32.}效率:时间复杂度:O(n^2).其他的插入排序有二分插入排序,2-路插入排序。
堆排序实例演示

91 47 24 16 85 36 53 30
小顶堆 :16,36,24,85,47,30,53,91
16 36 85 91 24
47 30 53
如果该序列是一个堆,则对应的这棵完全二叉树的特点是: 所有分支结点的值均不小于 (或不大于)其子女的值,即每棵 子树根结点的值是最大(或最小)的。 堆特点:堆顶元素是整个序列中最大(或最小)的元素。
仅需调整一次,
堆建成 。
2018/8/8
数据结构
7
第二个问题的背景: 输出堆顶元素后,将堆底元素送入堆顶(或将堆顶元素 与堆底元素交换),堆可能被破坏。 破坏的情况仅是根结点和其左右孩子之间可能不满足堆 的特性,而其左右子树仍然是局部的堆。
在这种情况下,将其R1 … Ri整理成堆。 (i=n-1..1)
2018/8/8
c.右子树不满 d.到了叶子结 足堆,继续调 点,调整结束, 整。 堆建成。
数据结构
6
85
30
53
53 47 85 91 30 36 16 85
47
24 91 36
53
16 30 91 24
47 36
16
24
堆调整结束。
R1 与 Rn-1 交换 , 堆被破坏。 对 R1 与 Rn-2 调整。
91,47,85,24,36,53,30,16是一个大顶堆。
数据结构 1
在完全二叉树上,双亲和左右孩子之间的编号就是i和2i、 2i+1的关系。因此一个序列可以和一棵完全二叉树对应起来, 用双亲其左、右孩子之间的关系可以直观的分析是否符合堆 的特性。
大顶堆:91,47,85,24,36,53,30,16
2018/8/8
数据结构
数字排序技巧

数字排序技巧数字在我们日常生活中无处不在,我们可以通过数字对事物进行分类、排序和比较。
在处理数字时,掌握一些排序技巧可以帮助我们更高效地处理数据和解决问题。
本文将介绍一些数字排序的技巧,帮助读者更好地理解数字排序的原理和应用。
一、冒泡排序冒泡排序是最常见也是最简单的排序算法之一。
其基本思想是通过不断比较相邻元素的大小,将较大的元素向后移动,较小的元素向前移动,从而实现对数组的排序。
具体步骤如下:1. 从数组的第一个元素开始,依次比较相邻元素的大小;2. 如果前一个元素大于后一个元素,则交换它们的位置;3. 重复以上步骤,直到没有需要交换的元素;4. 重复以上步骤,直到所有元素有序排列。
冒泡排序的时间复杂度为O(n^2),其中n为数组的长度。
虽然冒泡排序不适用于大规模数据的排序,但它对理解排序算法的基本原理非常有帮助。
二、选择排序选择排序也是一种简单直观的排序算法,它的基本思想是每一趟从待排序的元素中选出最小(或最大)的元素放在已排序的末尾。
具体步骤如下:1. 在未排序序列中找到最小(或最大)元素,存放到排序序列的起始位置;2. 从剩余未排序元素中继续寻找最小(或最大)元素,存放到已排序序列的末尾;3. 重复以上步骤,直到所有元素有序排列。
选择排序的时间复杂度也为O(n^2),但相较于冒泡排序,选择排序每一轮只需要进行一次交换,因此在实际应用中更加高效。
三、插入排序插入排序是一种稳定的排序算法,其基本思想是将待排序的元素插入到已排序序列的适当位置,形成有序的新序列。
具体步骤如下:1. 将第一个元素视为已排序序列,将第二个元素到最后一个元素视为待排序序列;2. 从待排序序列中取出一个元素,将其插入已排序序列的适当位置;3. 重复以上步骤,直到所有元素有序排列。
插入排序的时间复杂度同样为O(n^2),但在待排序序列已经基本有序或者规模较小的情况下,插入排序的性能较好。
四、快速排序快速排序是一种高效的排序算法,其基本思想是通过一趟排序将待排序序列分割成独立的两部分,其中一部分的元素均小于另一部分的元素,然后对这两部分分别进行快速排序,从而实现整个序列的有序排列。
C语言八大排序算法
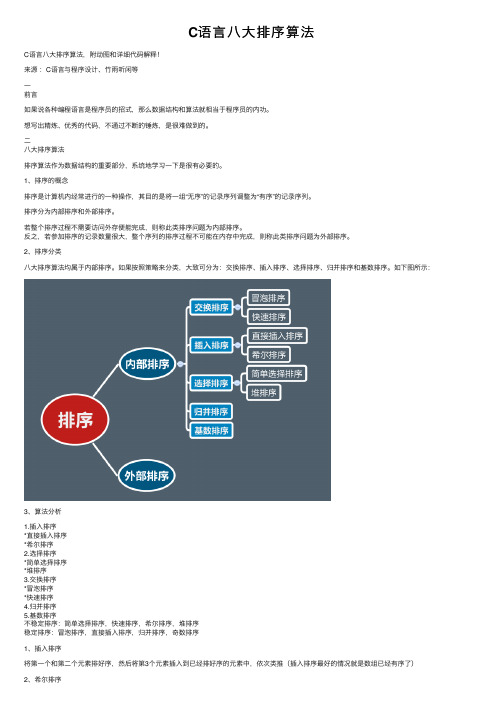
C语⾔⼋⼤排序算法C语⾔⼋⼤排序算法,附动图和详细代码解释!来源:C语⾔与程序设计、⽵⾬听闲等⼀前⾔如果说各种编程语⾔是程序员的招式,那么数据结构和算法就相当于程序员的内功。
想写出精炼、优秀的代码,不通过不断的锤炼,是很难做到的。
⼆⼋⼤排序算法排序算法作为数据结构的重要部分,系统地学习⼀下是很有必要的。
1、排序的概念排序是计算机内经常进⾏的⼀种操作,其⽬的是将⼀组“⽆序”的记录序列调整为“有序”的记录序列。
排序分为内部排序和外部排序。
若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。
反之,若参加排序的记录数量很⼤,整个序列的排序过程不可能在内存中完成,则称此类排序问题为外部排序。
2、排序分类⼋⼤排序算法均属于内部排序。
如果按照策略来分类,⼤致可分为:交换排序、插⼊排序、选择排序、归并排序和基数排序。
如下图所⽰:3、算法分析1.插⼊排序*直接插⼊排序*希尔排序2.选择排序*简单选择排序*堆排序3.交换排序*冒泡排序*快速排序4.归并排序5.基数排序不稳定排序:简单选择排序,快速排序,希尔排序,堆排序稳定排序:冒泡排序,直接插⼊排序,归并排序,奇数排序1、插⼊排序将第⼀个和第⼆个元素排好序,然后将第3个元素插⼊到已经排好序的元素中,依次类推(插⼊排序最好的情况就是数组已经有序了)因为插⼊排序每次只能操作⼀个元素,效率低。
元素个数N,取奇数k=N/2,将下标差值为k的数分为⼀组(⼀组元素个数看总元素个数决定),在组内构成有序序列,再取k=k/2,将下标差值为k的数分为⼀组,构成有序序列,直到k=1,然后再进⾏直接插⼊排序。
3、简单选择排序选出最⼩的数和第⼀个数交换,再在剩余的数中⼜选择最⼩的和第⼆个数交换,依次类推4、堆排序以升序排序为例,利⽤⼩根堆的性质(堆顶元素最⼩)不断输出最⼩元素,直到堆中没有元素1.构建⼩根堆2.输出堆顶元素3.将堆低元素放⼀个到堆顶,再重新构造成⼩根堆,再输出堆顶元素,以此类推5、冒泡排序改进1:如果某次冒泡不存在数据交换,则说明已经排序好了,可以直接退出排序改进2:头尾进⾏冒泡,每次把最⼤的沉底,最⼩的浮上去,两边往中间靠16、快速排序选择⼀个基准元素,⽐基准元素⼩的放基准元素的前⾯,⽐基准元素⼤的放基准元素的后⾯,这种动作叫分区,每次分区都把⼀个数列分成了两部分,每次分区都使得⼀个数字有序,然后将基准元素前⾯部分和后⾯部分继续分区,⼀直分区直到分区的区间中只有⼀个元素的时候,⼀个元素的序列肯定是有序的嘛,所以最后⼀个升序的序列就完成啦。
堆排序的原理

堆排序的原理
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是选择排序的一种,由于其在实现时只需要一个很小的辅助栈,因而也被称为“不占用额外空间的排序”。
堆排序的基本思想是,将待排序的序列构造成一个大(小)根堆,此时整个序列的最大值(最小值)就是堆顶的根节点。
将它移走(即与堆数组的末尾元素交换,此时末尾元素就是最大值(最小值)),然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素的次小值。
如此反复执行,便能得到一个有序序列了。
堆排序的时间复杂度为O(nlogn),空间复杂度为O(1)。
由于堆排序的时间复杂度与数据的初始状态无关,因此在实际应用中,堆排序的适用范围非常广泛。
- 1 -。
8种排序算法

J=2(38) [38 49] 65 97 76 13 27 49
J=3(65) [38 49 65] 97 76 13 27 49
J=4(97) [38 49 65 97] 76 13 27 49
J=5(76) [38 49 65 76 97] 13 27 49
2. 堆的定义: N个元素的序列K1,K2,K3,...,Kn.称为堆,当且仅当该序列满足特性:
Ki≤K2i Ki ≤K2i+1(1≤ I≤ [N/2])
堆实质上是满足如下性质的完全二叉树:树中任一非叶子结点的关键字均大于等于其孩子结点的关键字。例如序列10,15,56,25,30,70就是一个堆,它对应的完全二叉树如上图所示。这种堆中根结点(称为堆顶)的关键字最小,我们把它称为小根堆。反之,若完全二叉树中任一非叶子结点的关键字均大于等于其孩子的关键字,则称之为大根堆。
(6)基数排序
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序,最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以其是稳定的排序算法。
2. 排序过程:
【示例】:
初始关键字 [49 38 65 97 76 13 27 49]
第一趟排序后 13 [38 65 97 76 49 27 49]
第二趟排序后 13 27 [65 97 76 49 38 49]
第三趟排序后 13 27 38 [97 76 49 65 49]
其次,说一下稳定性的好处。排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。基数排序就是这样,先按低位排序,逐次按高位排序,低位相同的元素其顺序再高位也相同时是不会改变的。另外,如果排序算法稳定,对基于比较的排序算法而言,元素交换的次数可能会少一些(个人感觉,没有证实)。
堆排序算法复杂度分析及优化思路

堆排序算法复杂度分析及优化思路堆排序是一种高效的排序算法,它的核心思想是通过构建堆来实现排序过程。
在本文中,我们将对堆排序算法的时间复杂度进行分析,并提出一些优化思路。
一、堆排序算法简介堆排序是一种基于二叉堆的排序算法,它包括两个基本步骤:建堆和排序。
建堆的过程是将一个无序序列构建成一个堆,排序的过程是将堆顶元素和堆底元素交换,并将剩余元素重新构建成堆。
二、堆排序算法的时间复杂度分析1. 建堆的时间复杂度:建堆的过程包括从最后一个非叶子节点开始进行下沉操作,因此建堆的时间复杂度为O(n),其中n为待排序序列的长度。
2. 排序的时间复杂度:排序的过程包括将堆顶元素和堆底元素交换,并对剩余元素进行下沉操作。
每次交换后,堆的大小减少1,因此需要进行n-1次交换。
而每次交换和下沉的操作的时间复杂度都是O(logn),因此排序的时间复杂度为O(nlogn)。
综上所述,堆排序算法的时间复杂度为O(nlogn)。
三、堆排序算法的空间复杂度分析堆排序算法的空间复杂度主要取决于堆的建立过程中所使用的辅助空间。
在建堆的过程中,需要使用一个大小为n的辅助数组来存储待排序序列。
因此,堆排序算法的空间复杂度为O(n)。
四、堆排序的优化思路虽然堆排序算法的时间复杂度较好,但在实际应用中,我们可以通过以下几种方式来进一步提高算法的性能。
1. 优化建堆过程:建堆的过程中,我们可以对所有非叶子节点进行下沉操作,但实际上,只有前一半的非叶子节点需要下沉操作。
因此,在建堆过程中,我们可以只对前一半的非叶子节点进行下沉操作,减少了一些不必要的操作,提高了建堆的效率。
2. 优化排序过程:在排序的过程中,每一次交换堆顶元素和堆底元素后,需要重新进行下沉操作。
然而,每次下沉操作都需要遍历堆的高度,时间复杂度为O(logn)。
可以考虑采用堆化的方式,即将堆底元素移至堆顶后,直接对堆顶元素进行下沉操作,减少了遍历的次数,进而提高了排序的效率。
3. 优化空间复杂度:在实际应用中,我们可以使用原地排序的方式来优化空间复杂度。
nlogn时间复杂度的排序

nlogn时间复杂度的排序排序是计算机科学中的一个重要问题,对于大多数计算机程序,排序都是必不可少的。
排序算法的效率直接影响着程序的运行速度和资源占用。
在排序算法中,时间复杂度是一个重要的指标,它反映了算法的运行效率。
在本文中,我们将介绍一些时间复杂度为nlogn的排序算法。
一、归并排序归并排序是一种分治算法,它将一个大问题分解为若干个小问题,然后将小问题合并成一个大问题的解。
归并排序的过程可以分为两个阶段:分治和合并。
分治阶段:将待排序的序列分成两个子序列,分别对两个子序列进行递归排序。
合并阶段:将两个已经有序的子序列合并成一个有序的序列。
归并排序的时间复杂度为O(nlogn),空间复杂度为O(n)。
由于归并排序需要额外的空间来存储中间结果,因此空间复杂度比较高。
二、快速排序快速排序是一种基于分治思想的排序算法,它的核心思想是选取一个基准元素,将序列分成两个部分,一部分小于基准元素,一部分大于基准元素,然后对两个子序列进行递归排序。
快速排序的时间复杂度为O(nlogn),空间复杂度为O(logn)。
由于快速排序是一种原地排序算法,不需要额外的空间来存储中间结果,因此空间复杂度比较低。
但是,快速排序的最坏时间复杂度为O(n^2),当序列已经有序或者基准元素选取不当时,快速排序的性能会退化。
三、堆排序堆排序是一种基于堆的排序算法,它的核心思想是将序列构建成一个大根堆或小根堆,然后依次取出堆顶元素,将其放到已排序的序列中。
堆排序的时间复杂度为O(nlogn),空间复杂度为O(1)。
由于堆排序是一种原地排序算法,不需要额外的空间来存储中间结果,因此空间复杂度比较低。
四、基数排序基数排序是一种非比较排序算法,它的核心思想是将待排序的序列按照位数进行排序,从低位到高位依次排列。
基数排序可以使用桶排序或计数排序作为内部排序算法。
基数排序的时间复杂度为O(d(n+k)),其中d是最大位数,k是桶的数量。
当d比较小,k比较大时,基数排序的效率比较高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
if ( R[i].key > R[j].key ) { R[i] <-> R[j] ; // 将较小的孩子与根交换 - i = j ; j = 2*i ; // 上述交换可能使以该孩子结点为根的
子树不再为堆, 子树不再为堆,则需重新调整
} else break ; } }
将初始无序的R[1]到R[n]建成一个小根堆,可用以 到 建成一个小根堆, 将初始无序的 建成一个小根堆 下语句实现: 下语句实现: for ( i = n/2 ; i >= 1 ; i - - ) sift ( R , i , n ) ;
Heapsort
Fig. 27-9 A trace of heapsort (g – i)
Heapsort
时间复杂度分析
该方法创建堆的时间复杂度为O( n ) 证明过程请看教材341页
7.5.2 堆和堆排序
一、堆和堆排序的概念 二、堆的调整 三、建堆 ☞ 四、堆排序
Heapsort
Fig. 27-9 A trace of heapsort (a – c)
Heapsort
Fig. 27-9 A trace of heapsort (d – f)
{ int j ; j = 2*i ; while ( j <= m)
//若j<=m,R[2*i]是R[i]的左孩子 若 , 是 的左孩子
{ if ( j<m &&R[j].key> R[j+1].key)
比较左右孩子的大小, 为较小的孩子的下标 j ++ ; // 比较左右孩子的大小,使j为较小的孩子的下标
由于堆实质上是一个完全二叉树,那么我们可以 顺序存储一个堆。 顺序存储一个堆 下面以一个实例介绍建一个小根堆的过程。 例:有关键字为49,38,65,97,76,13,27, 例: 49的一组记录,将其按关键字调整为一个小根堆。
49 38 97 49 76 13 65 27
13 49 38 97 49 97 49 76 13 65 27 13 49 65
你能画出删除堆顶元素时相应数组的变化吗? 你能画出删除堆顶元素时相应数组的变化吗? 删除元素代码见课本204 删除元素代码见课本7.Fra bibliotek.2 堆和堆排序
一、堆和堆排序的概念 二、堆的调整 ☞ 三、建堆 四、堆排序
第一种方法:
把一个数组看成两部分,左边是堆,右边是还 没加入堆的元素,步骤如下: 1、数组里的第一个元素自然地是一个堆 2、然后从第二个元素开始,一个个地加入左 边的堆,当然,每加入一个元素就破坏了左边 元素堆的性质,得重新把它调整为堆
4 15 16 25 7 5 12 11 8 9
6 23 27 20
Example (end)
10 4 15 16 25 7 5 12 11 8 9 27 6 23 20
4 5 15 16 25 10 7 12 11 8 9 27 6 23 20
Analysis
We visualize the worst-case time of a downheap with a proxy path that goes first right and then repeatedly goes left until the bottom of the heap (this path may differ from the actual downheap path) Since each node is traversed by at most two proxy paths, the total number of nodes of the proxy paths is O(n) Thus, bottom-up heap construction runs in O(n) time Bottom-up heap construction is faster than n successive insertions and speeds up the first phase of heap-sort
删除元素
Fig. 27-5 The steps to remove the entry in the root of the maxheap of Fig. 27-3d
Removing the Root
Fig. 27-6 The steps that transform a semiheap into a heap without swaps.
Adding an Entry
Begin at next available position for a leaf Follow path from this leaf toward root until find correct position for new entry As this is done
Adding an Entry----代码见课本203
Algorithm for adding new entry to a heap
Algorithm add(newEntry) if (the array heap is full) Double the size of the array newIndex = index of next available array location parentIndex = newIndex/2 // index of parent of available location while (newEntry > heap[parentIndex]) { heap[newIndex] = heap[parentIndex] // move parent to available location // update indices newIndex = parentIndex parentIndex = newIndex/2 } // end while
6 7 8
0
1
2
3
4
5
49 65 13 27 97 13 38 27 49 76 65 49 49 49 13 97
筛选过程的算法描述为: sift (rectype R[ ] , int i , int m )
// 在数组 中将下标从 到m的元素序列调整为堆,即将以 在数组R中将下标从 中将下标从i到 的元素序列调整为堆 的元素序列调整为堆, R[i]为根的子树调整为堆;初次调整的是以序号 为根的子树调整为堆; 为根的子树调整为堆 初次调整的是以序号m/2的结点为根的 的结点为根的 子树; 子树;
自底向上地创建堆
16
15
4
12
6
7
23
20
25 16 15 4
5 12 6
11 7 23
27 20
Example (contd.)
25 16 15 4
5 12 6
11 9 23
27 20
15 16 25 5
4 12 11
6 9 27
23 20
Example (contd.)
7 15 16 25 5 4 12 11 6 9 27 8 23 20
Move entries from parent to child Makes room for new entry
Adding an Entry
Fig. 27-3 A revision of steps shown in Fig. 27-2 to avoid swaps.
Adding an Entry
堆与堆排序
软件学院 王建文
7.5.2 堆和堆排序
☞ 一、堆和堆排序的概念 二、堆的调整 三、建堆 四、堆排序
堆的定义: 个元素的序列{a 若n个元素的序列 1 a2 … an} 满足 个元素的序列 ai ≤ a2i ai ≤ a2i+1 或 ai ≥ a2i ai ≥ a2i+1
则分别称该序列{a 大根堆。 则分别称该序列 1 a2 … an}为小根堆 和大根堆。 为 从堆的定义可以看出, 从堆的定义可以看出,堆实质是满足如下性质的完 全二叉树: 全二叉树: 二叉树中任一非叶子结点均小于(大于) 二叉树中任一非叶子结点均小于(大于)它的孩子结点
Fig. 27-4 An array representation of the steps in Fig. 27-3 … continued →
Adding an Entry
Fig. 27-4 (ctd.) An array representation of the steps in Fig. 27-3.
堆排序 若在输出堆顶的最小值(最大值) 若在输出堆顶的最小值(最大值)后,使得剩余 n-1个元素的序列重又建成一个堆,则得到n个元素 个元素的序列重又建成一个堆,则得到 个元素 个元素的序列重又建成一个堆 的次小值(次大值) 如此反复, 的次小值(次大值)……如此反复,便能得到一个 如此反复 有序序列,这个过程称之为堆排序 堆排序。 有序序列,这个过程称之为堆排序。
首先, 调整从第n/2 n/2个元素开始 首先, 调整从第n/2个元素开始 将以该元素为根的二叉树调整为堆 然后,将以序号为n/2 n/2- 然后,将以序号为n/2-1的结点 为根的二叉树调整为堆; 为根的二叉树调整为堆; 27 49 再将以序号为n/2 n/2- 再将以序号为n/2-2的结点为根 的二叉树调整为堆; 的二叉树调整为堆; 再将以序号为n/2 n/2- 再将以序号为n/2-3的结点为根 的二叉树调整为堆; 的二叉树调整为堆;
显然: 单结点的二叉树是堆; 单结点的二叉树是堆;在完全二叉树中所有以叶子 结点(序号i 结点(序号 > n/2)为根的子树是堆。 )为根的子树是堆。 这样,我们只需依次将以序号为 , - , 这样,我们只需依次将以序号为n/2,n/2-1,……, 1的结点为根的子树均调整为堆即可。 的结点为根的子树均调整为堆即可。 的结点为根的子树均调整为堆即可 即:对应由n个元素组成的无序序列,“筛选” 即:对应由n个元素组成的无序序列,“筛选”只需 从第n/2个元素开始。 从第n/2个元素开始。
