(完整版)小学奥数数论问题余数问题练习题【五篇】
四年级常考的奥数题:余数问题

四年级常考的奥数题:余数问题四年级常考的奥数题:余数问题导语:任何一个人,都要必须养成自学的习惯,即使是今天在学校的学生,也要养成自学的习惯,因为迟早总要离开学校的!自学,就是一种独立学习,独立思考的能力。
行路,还是要靠行路人自己。
下面是小编为大家整理的:奥数题。
希望对大家有所帮助,欢迎阅读,仅供参考,更多相关的知识,请关注CNFLA学习网!小学奥数题【例一】所谓同余问题,就是给出“一个数除以几个不同的数”的余数,反求这个数,称作同余问题。
首先要对这几个不同的数的最小公倍数心中有数,下面以4、5、6为例,请记住它们的最小公倍数是60。
1、差同减差:用一个数除以几个不同的`数,得到的余数,与除数的差相同,此时反求的这个数,可以选除数的最小公倍数,减去这个相同的差数,称为:“差同减差”。
例:“一个数除以4余1,除以5余2,除以6余3”,因为4-1=5-2=6-3=3,所以取-3,表示为60n-3。
【60后面的“n”请见4、,下同】2、和同加和:用一个数除以几个不同的数,得到的余数,与除数的和相同,此时反求的这个数,可以选除数的最小公倍数,加上这个相同的和数,称为:“和同加和”。
例:“一个数除以4余3,除以5余2,除以6余1”,因为4+3=5+2=6+1=7,所以取+7,表示为60n+7。
3、余同取余:用一个数除以几个不同的数,得到的余数相同,此时反求的这个数,可以选除数的最小公倍数,加上这个相同的余数,称为:“余同取余”。
例:“一个数除以4余1,除以5余1,除以6余1”,因为余数都是1,所以取+1,表示为60n+1。
4、最小公倍加:所选取的数加上除数的最小公倍数的任意整数倍(即上面1、2、3中的60n)都满足条件,称为:“最小公倍加”,也称为:“公倍数作周期”。
小学奥数题【例二】基本概念:对任意自然数a、b、q、r,如果使得a÷b=q……r,且0余数的性质:①余数小于除数。
②若a、b除以c的余数相同,则c|a-b或c|b-a。
五年级奥数题及答案-求余数问题

五年级奥数题及答案-求余数问题
编者小语:奥数教学不能单纯是传授数学知识,更重要的是培养学生数学意识、数学思想、独立获得和运用数学知识的能力和良好的数学学习习惯的过程。
让学生具备在未来的工作中科学地提出数学问题、探索数学问题、创造性地解决数学问题的能力。
为大家准备了小学五年级奥数题,希望小编整理的五年级奥数题及参考答案:求余数问题,可以帮助到你们,助您快速通往高分之路!!
求余数:
求437×319×2010+2010被7除的余数。
解答:437≡3(mod7),319≡5(mod7),2010≡1(mod7)
由"同余性质"可知:
437×319×2010≡3×5×1(mod7)=15(mod7)≡1(mod7)
所以:437×319×2010+2010≡1+1(mod7)=2(mod7)
即:437×319×2010+2010被7除的余数是2.这道题主要考察了同余性质。
必须注意的是同余性质只能用在加、减、乘。
五年级奥数.数论.中国剩余定理及弃九法(B级).学生版

五年级奥数.数论.中国剩余定理及弃九法(B级).学⽣版⼀、中国剩余定理——中国古代趣题1) 趣题⼀中国数学名著《孙⼦算经》⾥有这样的问题:“今有物,不知其数,三三数之,剩⼆,五五数之,剩三,七七数之,剩⼆,问物⼏何?”答⽈:“⼆⼗三。
”此类问题我们可以称为“物不知其数”类型,⼜被称为“韩信点兵”。
韩信点兵⼜称为中国剩余定理,相传汉⾼祖刘邦问⼤将军韩信统御兵⼠多少,韩信答说,每3⼈⼀列余1⼈、5⼈⼀列余2⼈、7⼈⼀列余4⼈、13⼈⼀列余6⼈……。
刘邦茫然⽽不知其数。
我们先考虑下列的问题:假设兵不满⼀万,每5⼈⼀列、9⼈⼀列、13⼈⼀列、17⼈⼀列都剩3⼈,则兵有多少?⾸先我们先求5、9、13、17之最⼩公倍数9945(注:因为5、9、13、17为两两互质的整数,故其最⼩公倍数为这些数的积),然后再加3,得9948(⼈)。
孙⼦算经的作者及确实著作年代均不可考,不过根据考证,著作年代不会在晋朝之后,以这个考证来说上⾯这种问题的解法,中国⼈发现得⽐西⽅早,所以这个问题的推⼴及其解法,被称为中国剩余定理。
中国剩余定理(Chinese Remainder Theorem )在近代抽象代数学中占有⼀席⾮常重要的地位。
2) 趣题⼆我国明朝有位⼤数学家叫程⼤位,他在解答“物不知其数”问题(即:有物不知其数,三三数之剩⼆,五五数之剩三,七七数之剩⼆,问物⼏何?)时⽤四句诗概括出这类问题的优秀解法:“三⼈同⾏七⼗稀,五树梅花廿⼀枝,七⼦团圆正⽉半,除百零五便得知.”这⾸诗就是解答此类问题的⾦钥匙,它被世界各国称为“中国剩余定理”(Chinese Remainder Theorem ),是我国古代数学的⼀项辉煌成果.诗中的每⼀句话都表⽰⼀个步骤:三⼈同⾏七⼗稀,是说除以3所得的余数⽤70乘.五树梅花廿⼀枝,是说除以5所得的余数⽤21乘.七⼦团圆正⽉半,是说除以7所得的余数⽤15乘.除百零五便得知,是说把上⾯乘得的3个积加起来,减去105的倍数,减得差就是所求的数.此题的中国剩余定理的解法是:⽤70乘3除所得的余数,21乘5除所得的余数,15乘7除所得的余数,把这3个结果加起来,如果它⼤于105,则减去105,所得的差如果仍⽐105⼤,则继续减知识框架中国剩余定理及弃九法去105,最后所得的整数就是所求.也就是270321215233-=++=,233105128-=,12810523为什么70,21,15,105有此神奇效⽤?70,21,15,105是从何⽽来?先看70,21,15,105的性质:70被3除余1,被5,7整除,所以70a是⼀个被3除余a⽽被5与7整除的数;21是5除余1,被3与7整除的数,因此21b是被5除余b,被3与7整除的数;同理15c是被7除余c,被3、5整除的数,105是3,5,7的最⼩公倍数.也就是说,702115++是a b c被3除余a,被5除余b,被7除余c的数,这个数可能是解答,但不⼀定是最⼩的,因此还要减去它们的公倍数.了解了“剩余定理”的秘密后,对类似于上⾯的题⽬,我们都可以⽤中国剩余定理来解答.3)核⼼思想和⽅法对于这⼀类问题,我们有⼀套看似繁琐但是⼀旦掌握便可⼀通百通的⽅法,下⾯我们就以《孙⼦算经》中的问题为例,分析此⽅法:今有物,不知其数,三三数之,剩⼆,五五数之,剩三,七七数之,剩⼆,问物⼏何?题⽬中我们可以知道,⼀个⾃然数分别除以3,5,7后,得到三个余数分别为2,3,2.那么我们⾸先构造⼀个数字,使得这个数字除以3余1,并且还是5和7的公倍数。
小学奥数题库《数论》余数问题中国剩余定理3星题(含解析)全国通用版

数论-余数问题-中国剩余定理-3星题课程目标知识提要中国剩余定理•概述中国剩余定理即我们常说的“物不知数”,是利用同余式组来求解的一类问题。
A、一个数分别除以两个数余数相同的时候,将原数减去这个余数之后可以整除那两个数B、上述情况下的余数虽有不同,但与各自对应的除数的差相同,将原数加上这个差之后便可以整除C、其他情况下,凑出相同余数之后,运用第一种情况的方法.精选例题中国剩余定理1. 某个自然数除以2余1,除以3余2,除以4余1,除以5也余1,则这个数最小是.【答案】41【分析】这个自然数除以2、4、5都余1,[2,4,5]=20,所以这个数应满足1+20n,同时除以3余2,所以最小是41.2. 一个大于10的自然数,除以5余3,除以7余1,除以9余4,那么满足条件的自然数最小为.【答案】148【分析】观察发现三个数中前两个数的除数与余数的和都是5+3=7+1=8,这样我们可以把余数都处理成8,即一个数除以5余3相当于除以5余8,除以7余1相当于除以7余8,所以满足前两个条件的自然数为a=35m+8,下一步只需要a除以9余4,35÷9=3⋯8,只需8+8m除以9余4,只需8m除以9余5,最小的m=4,因此满足所有条件的最小自然数为8+35×4=148.3. 有一筐苹果,甲班分,每人3个还剩11个;乙班分,每人4个还剩10个;丙班分,每人5个还剩12个.那么这筐苹果至少个.【答案】62【分析】设有x个苹果.因为11除以3余2,所以x除以3余2;因为10除以4余2,所以x除以4余2;因为12除以5余2,所以x除以5余2.又因为x大于12,x=[3,4,5]+2=60+2=62(个).4. 小明心里想了一个正整数.并且求出了它分别被14和21除后所得的余数,已知这两个余数的和是33,则该整数被42除的余数是.【答案】41【分析】该整数除以14的余数不大于13,除以21余数不大于20,所以这两个余数的和不大于33,而由题有这两个余数的和恰好是33,所以该整数除以14余数是13,除以21余数是20.这个数加上1就是14和21的倍数,而[14,21]=42,所以这个数可以表示成42k−1的形式,被42除的余数是41.5. 一个大于2的数,除以3余1,除以5余3,除以7余5,问满足条件的最小自然数是.【答案】103.【分析】我们发现两个算式除数与余数的差都相等,所以把他们都处理成都缺2能被整除,这样得[3、5、7]−2=103.6. 某数除以11余8,除以13余10,除以17余12,那么这个数的最小可能值是.【答案】998【分析】观察到11−8=13−10=3,因此除以11余8,除以13余10的最小自然数为11×13−3=140,设某数为a,则a=143m−3m为非零自然数,只需143m−3除以17余12,而143÷17=8⋯7,只需(7m−3)÷17=n⋯12,即7m−15是17的倍数所以,m=7,所以a=143×7−3=998.7. 一个大于3的数,除以7余4,除以9余6,除以11余8,问满足条件的最小自然数是.【答案】690.【分析】我们发现两个算式除数与余数的差都相等,所以把他们都处理成都缺3能被整除,这样得[7、9、11]−3=690.8. 一个大于10的数,除以5余3,除以7余1,问满足条件的最小自然数为.【答案】43.【分析】根据总结,我们发现两个数的除数与余数的和都是5+3=7+1=8,这样我们可以把余数都处理成都余8,所以[5、7]=35,所以这个数就是35+8=43.9. 我国南宋数学家杨辉在其《续古摘奇算法》上记载了这样一个问题:“二数余一,五数余二,七数余三,九数余四,问本数.”用现代语言表述就是:“有一个数用2除余1,用5除余2,用7除余3,用9除余4,问这个数是多少?”请将满足条件的最小的自然数写在这里.【答案】157【分析】(解法一)先考虑除以5余2,除以7余3,除以9余4;用剩余定理得5×7×5+5×9×1+7×9×4=472[5,7,9]=315,故472±315k都符合除以5余2,除以7余3,除以9余4最小是472−315=157,且也符合除以2余1.(解法二)除以2余1的数有:1,3,5,7,9,11,13,15,17,⋯;除以5余2的数有:2,7,12,17⋯;除以7余3的数有:3,10,17⋯;所以满足“用2除余1,用5除余2,用7除余3”的数的形式为[2,5,7]n+17=70n+17(n为自然数)此时只需要找一个最小的n,满足除以9余4即可.当n=2时,满足除以9余4,所以满足条件的最小的自然数为70⋯2+17=15710. 一个数,除以11余7,除以13余9,除以19余15,问满足条件的最小自然数是.【答案】2713.【分析】我们发现两个算式除数与余数的差都相等,所以把他们都处理成都缺4能被整除,这样得[11、13、19]−4=2713.11. 智慧老人到小明的年级访问,小明说他们年级共一百多名同学,老人请同学们按三人一行排队,结果多出一人,按五人一行排队,结果多出二人,按七人一行排队,结果多出一人,老人说我知道你们年级人数应该是人.【答案】127【分析】根据条件,该数除以3余1,除以5余2,除以7余1,逐级满足法,令该数为a,则a÷3⋯⋯1 ①a÷5⋯⋯2 ②a÷7⋯⋯1 ③符合条件①的有1,4,7,10,13,16,⋯.同时满足①、②的最小值为7,以后a=7+15m均满足①、②;现在来看(7+15m)除以7余1,则15m除以7余1,则m最小取1,符合,最小的符合的数为a=22.以后每隔[3,5,7]=105即符合.由于该年级有100多名学生,为22+105= 127.12. 一个大于2000数,除以11余5,除以13余3,除以17余16,问满足条件的最小自然数为.【答案】2447.【分析】根据题意,我们发现三个算式中两个数的除数与余数的和都是11+5=13+3= 16,这样我们可以把余数都处理成都余16,所以[11、13、17]=2431,所以这个数就是2431+16=2447.13. 某个两位数是2的倍数,加1是3的倍数,加2是4的倍数,加3是5的倍数,那么这个两位数是.【答案】62【分析】由题可知,此数是一个2的倍数,并且除以3、4、5都余2的数,这样的数最小是2,因为这个数是两位数,2+[3、4、5]=62.14. 5年级3班同学上体育课,排成3行少1人,排成4行多3人,排成5行少1人,排成6排多5人,问上体育课的同学最少人.【答案】59.【分析】分析题意知,这个班的人数除以3余2,除以4余3,除以5余4,除以6余5,凑缺相同,这个班人数为[3、4、5、6]−1=59(人).15. 有一堆水果糖,如果按8块一份来分,最后剩下2块;如果按9块一份来分,最后剩3块;如果按10块一份来分,最后剩下4块.这堆糖至少有块.【答案】354【分析】这堆水果糖的总数被8除余2,被9除余3,被10除余4,如果增加6块就刚好是8、9、10的公倍数,又8、、9、10的最小公倍数是360.所以这堆水果糖至少有360−6=354(块).16. 一个大于100的数,除以9余3,除以11余1,问满足条件的最小自然数为.【答案】111.【分析】据题意,我们发现两个数的除数与余数的和都是9+3=11+1=12,这样我们可以把余数都处理成都余12,所以[9、11]=99,所以这个数就是99+12=111.17. 一个大于10的自然数,除以5余3,除以7余1,除以9余8,那么满足条件的自然数最小为.【答案】323【分析】根据总结,我们发现三个数中前两个数的除数与余数的和都是5+3=7+1=8这样我们可以把余数都处理成8,即一个数除以5余3相当于除以5余8,除以7余1相当于除以7余8,所以可以看成这个数除以5、7、9的余数都是8,那么它减去8之后是5、7、9的公倍数.而[5,7,9]=315所以这个数最小为315+8=323.18. 一个大于10的数,除以5余3,除以7余1,除以9余8,问满足条件的最小自然数为.【答案】323.【分析】根据总结,我们发现三个数中两个数的除数与余数的和都是5+3=7+1=8,这样我们可以把余数都处理成都余8,所以[5、7、9]=315,所以这个数就是315+8=323.19. 红星小学组织学生划船.若乘坐大船,除1条船坐6人外,其余每船均坐17人;若乘小船,则除1条船坐2人外,其余每船均坐10人.如果学生的人数超过100、不到200,那么学生共有人.【答案】142【分析】除1条船坐6人外,其余每船均坐17人,说明总人数可以表示成17m+6的形式;除1条船坐2人外,其余每船均坐10人,说明总人数可以表示成10n+2的形式;那么有17m+6=10n+2,化简得17m+4=10n,经分析m的个位只能是8.又学生的人数超过100、不到200,所以m=8,学生的人数是17×8+6=142.20. 一个自然数能被11整除,除以13余12;除以15余13;这个数最小为.【答案】1078.【分析】n除以15余13:最小为13,通式为13+15k1;n除以13余12:k1最小为6,则有13+15×6=103,通式为103+[15,13]k2=103+195k2.n除以11余0:k2最小为5,则有103+195×5=1078.21. —个自然数被3除余2,被5除余4,并且这个数大于100且小于125,那么这个数是.【答案】104或119【分析】被3除余2,被5除余4,求出3和5的最小公倍数15,估算15的哪一个倍数大于100小于125,经计算可知,105和120介于100到125之间,再用105和120分别减1即可,这个自然数是104或119.22. 在1到100这100个数中,被2,3,5除都有非零的余数,且余数彼此不等的数有个.【答案】6【分析】根据余数不能比除数大.一个数除以2,余数只能是1.而要求余数彼此不等,所以,这些数除以3,余数只能是2.满足以上两个条件的数为6的倍数少1.有:5、11、17、23、29、35、41、47、53、59、65、71、77、83、89、95.再满足被5除有余数,且余数不为1和2,(个位不能为5、1、7).符合条件的数只有:23、29、53、59、83、89,共6个数.23. 有一个自然数用7除余3,用9除余4,请按照从小到大的顺序,将满足条件的前两个自然数写在这里.【答案】31,94【分析】除以7余3的数有:3,10,17,24,31⋯;除以9余4的数有:4,13,22,31⋯;所以满足“除以7余3,除以9余4”的数的形式为[7,9]n+31=63n+31(n为自然数)按照从小到大的顺序,将满足条件的前两个自然数为31,94.24. 有一个整数,用它分别去除157、234和324,得到的三个余数之和是100,这个整数是多少?【答案】41【分析】详解:157、234和324的和是715,减去100的差是615.615是这个整数的倍数.而615的约数有1、3、5、15、41、123、205、615,验证只有41满足余数和是100.25. 有三个连续自然数,其中最小的能被15整除,中间的能被17整除,最大的能被19整除,请写出一组这样的三个连续自然数.【答案】2430,2431,2432.【分析】设三个连续自然数中最小的一个为n,则其余两个自然数分别为n+1,n+2.依题意可知:15∣n,17∣(n+1),19∣(n+2),根据整除的性质对这三个算式进行变换:15∣n 17∣(n +1)19∣(n +2)→→→15∣2n 17∣(2n +2)19∣(2n +4)→→→15∣(2n −15)17∣(2n −15)19∣(2n −15)}⇒[15,17,19]∣(2n −15)从上面可以发现 2n −15 应为 15、17、19 的公倍数.由于 [15,17,19]=4845,所以 2n −15=4845(2k −1)(因为 2n −15 是奇数),可得 n =4845k −2415.当 k =1 时 n =2430,n +1=2431,n +2=2432,所以其中的一组自然数为 2430、2431、2432.26. 一个大于 10 的数,除以 3 余 1,除以 5 余 2,除以 11 余 7,问满足条件的最小自然数是多少?【答案】 172【分析】 法一:仔细分析可以发现 3×2+1=5+2=7,所以这个数可以看成被 3、5、11 除余 7,由于 [3,5,11]=165,所以这个数最小是 165+7=172.法二:事实上,如果没有“大于 10”这个条件,7 即可符合条件,所以只需要在 7 的基础上加上 3、5、11 的最小公倍数,得到 172 即为所求的数.27. 一个三位数除以 5 余 2,除以 7 余 3.这个三位数最小是多少?【答案】 122【分析】 使用逐步满足条件法,满足第一个条件的数依次为 2、7、12、17,而 17 除以 7 余 3.那么同时满足两个条件的数最小是 17.然后依次为 52、87、122.最小的三位数是 122.28. 一个布袋中装有 5000 多个小球,如果 10 个一包,最后还剩 9 个,如果 9 个一包,最后还剩 8 个 ⋯⋯ 如果 5 个一包,最后还剩 4 个,那么如果 13 个一包,最后还剩多少个?【答案】 8 个【分析】 简答:布袋中的小球数除以 10 余 9,除以 9 余 8,除以 8 余 7⋅⋯,除以 5 余 4,[5,6,7,8,9,10]=[5,7,8,9]=5×7×8×9=2520,所以,布袋中球数是 2520−1+2520=5039,5039÷13 余 8.29. (1)—个三位数除以 4 余 2,除以 6 余 2,那么这个三位数最小是多少?(2)—个三位数除以 3 余 1,除以 4 余 2,除以 6 余 4,那么这个三位数最小是多少?(3)—个数除以 9 余 2,除以 12 余 5,那么这个数最小是多少?【答案】 (1)110;(2)106;(3)29【分析】简答:(1)[4,6]=12,14+12×8=110;(2)按“差同”计算;(3)按“差同”计算.30. 一个自然数除以8、9、11后分别余2、7、3,而所得的三个商的和是622,这个数是多少?【答案】1906.【分析】设这个数为x.x除以8余2:最小为2,通式为2+8k1;x除以9余7:k1最小为4,则有2+8×4=34,通式为34+[8,9]k2=34+72k2.x除以11余3:k2最小为4,则有34+72×4=322.则x=322+[8,9,11]n=322+792n.322+792n−28+322+792n−79+322+792n−311=622 40+99n+35+88n+29+72n=622259n=518n=2x=322+792×2=1906.31. 已知自然数A除以11余5,除以9余7,除以13余3,这个数最小是多少?【答案】1303【分析】本题属于“物不知数”问题,可以运用中国剩余定理,但需要先要找出11与9的公倍数中除以13余1的数、11与13的公倍数中除以9余1的数以及9与13的公倍数中除以11余1的数.比较麻烦.实际上,观察可知11+5=9+7=13+3=16,也就是说这个数减去16后是11、9、13的公倍数,那么这个数最小就是11、9、13的最小公倍数加上16,为11×9×13+16=1303.32. 今有一堆石子,三个三个数余1个,五个五个数余3个,七个七个数余5个,这堆石子最少有多少个?【答案】103【分析】三个三个、五个五个、七个七个的数都是差两个,那借来两个石子,现在的就可以被3、5和7除得开,最小是3×5×7=105,归还那两块,总计最少103个.借来还去的思想.33. 有一个自然数,用它分别去除61、90、130都有余数,3个余数的和是26,这3个余数中最大的一个是多少?【答案】11【分析】.简答:61、90和130的和减去26得到255,255的约数中验证得满足条件的只有17,所以这个自然数是17,所以余数中最大的是130除以17的余数1134. 已知两个连续的两位数除以5的余数之和是5,除以6的余数之和是5,除以7的余数之和是1.求这两个两位数.【答案】77和78【分析】两个连续的两位数除以5的余数之和是5,则可以判断出第一个数除以5余2.除以6的余数之和是5,则可以判断出第一个数除以6余2或余5.除以7的余数之和是1,则可以判断出第一个数除以7余0.满足第一、三两个条件的数有7、42、77,再考虑第二个条件,只有77满足.因此这两个数为77和78.35. 有一个自然数,用它分别去除63,90,130都有余数,3个余数的和是25.这3个余数中最大的一个是多少?【答案】20【分析】设这个除数为M,设它除63,90,130所得的余数依次为a,b,c,商依次为A,B,C.63÷M=A⋯⋯aa+b+c=25,则(63+90+130)−(a+b+c)=(A+B+C)×M,即283−25=258=(A+B+C)×M.所以M是258的约数.258=2×3×43显然当除数M为2、3、6时,3个余数的和最大为3×(2−1)=3,3×(3−1)=6,3×(6−1)=15所以均不满足.而当除数M为43×2,43×3,43×2×3时,它除63的余数均是63,所以也不满足.那么除数M只能是43,它除63,90,130的余数依次为20,4,1,余数的和为25,满足.显然这3个余数中最大的为20.36. 一个小于200的数,它除以11余8,除以13余10,这个数是几?【答案】140.【分析】分析题意,我们发现这两个算式除数与余数的差都等于11−8=13−10=3,观察发现这个数加上3后就能同时被11和13整除,所以[11、13]=143,所以这个数是143−3=140.37. 有一个整数,用它去除63,90,130所得到的3个余数之和是25,那么这3个余数中最大的一个是多少?【答案】20【分析】设这个数为x,由题意可得:① $\left\{\begin{gathered}63 \div x = a \cdots {r_1} \hfill \\90 \div x = b \cdots {r_2} \hfill \\130 \div x = c \cdots {r_3} \hfill \\\end{gathered} \right. \Rightarrow 63 + 90 + 130 - 25 =258$ 为x的倍数;②258=2×3×43③枚举验证⇒x=43.所以 $\left\{ \begin{gathered}63 \div 43 \cdots 20 \hfill \\90 \div 43 \cdots 4 \hfill \\130 \div 43 \cdots 1 \hfill \\\end{gathered} \right.$,显然这3个余数中最大的一个是20.38. (1)一个三位数除以6余2,除以8余2,那么这个三位数最小是多少?(2)—个数除以3余2,除以5余4,除以7余6,那么这个数最小是多少?(3)—个数除以6余2,除以11余1,那么这个数最小是多少?【答案】(1)122;(2)104;(3)5639. 有一个自然数,除以2余1,除以3余2,除以4余3,除以5余4,除以6余5,除以7余6,则这个数最小是.【答案】419.【分析】分析题意知,这个数加1就能被2,3,4,5,6,7整除,所以这个数为[2、3、4、5、6、7]−1=420−1=419.40. 一个数除以3余2,除以5余3,除以7余4,问这个数是多少?【答案】53【分析】如果用剩余定理相信大家会做了,接下来看逐步满足法.第一个条件,除以3余2,最小是2;先记下2.第二个条件,除以5余3,原来已经有了2,要保持满足第一个条件不变,那么在2的基础上增加3的倍数,这样除以3余2不会变.2+3n的形式.这个数要满足第二个条件,除以5余3.在2+3n中,2已经余2了,3n需要余1,所以n=2即可.这样满足前两个条件的最小的数是8.第三个条件,除以7余4.8+3×5n的形式.3×5n=15n除以7要余4−1=3,15除以7余1,所以n最小是3,这个数是8+45=53满足题意.41. 今有物不知其数,三三数之剩一,四四数之剩三,五五数之剩二,问物几何?【答案】7【分析】40×1+45×3+36×2=247,3×4×5=60,247÷60=4⋯⋯7,最少是7.42. 一个三位数除以4余3,除以6也余3.这个三位数最大是多少?【答案】999【分析】这是一道余同的问题.满足条件的数可以表示为[4,6]×n+3,其中n为自然数.要求满足条件的最大三位数,应令n为83,即[4,6]×83+3=999.43. 一个数被5除余3,被7除余4,被9除余5,这个数最小是几?【答案】158【分析】7和9的公倍数9和5的公倍数5和7的公倍数6345351269070135105180140225175210245280⋯⋯⋯在7和9的公倍数中,除以5余1的最小数是126;在5和9的公倍数中,除以7余1的最小数是225;在5和7的公倍数中,除以9余1的最小数是280;那么126×3+225×4+280×5=2678.[5,7,9]=315.所以,最小的数为2678−315×8=158.44. 四年级的同学,每9人一排多5人,每7人一排多1人,每5人一排多2人,问这个年级至少有多少人?【答案】302【分析】这个题相当于是一个数被9除余5,被7除余1,被5除余2,这个数最小是几.9、7、5三个数两两互质。
小学奥数题库《数论》余数问题带余除法5星题(含解析)全国通用版
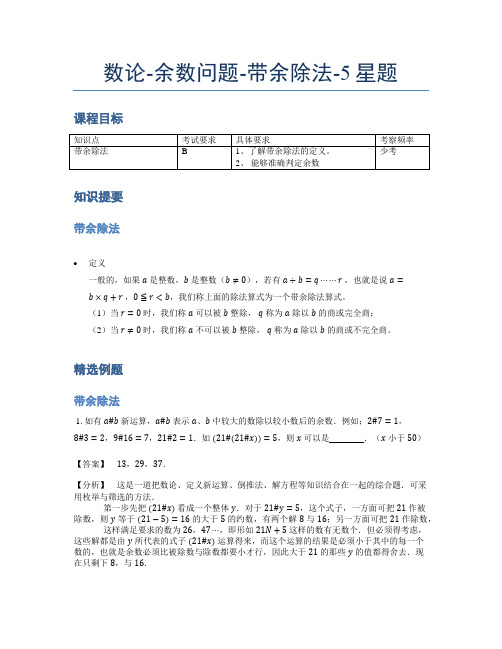
数论-余数问题-带余除法-5星题课程目标知识提要带余除法•定义一般的,如果a是整数,b是整数(b≠0),若有a÷b=q⋯⋯r,也就是说a=b×q+r,0≦r<b,我们称上面的除法算式为一个带余除法算式。
(1)当r=0时,我们称a可以被b整除,q称为a除以b的商或完全商;(2)当r≠0时,我们称a不可以被b整除,q称为a除以b的商或不完全商。
精选例题带余除法1. 如有a#b新运算,a#b表示a、b中较大的数除以较小数后的余数.例如;2#7=1,8#3=2,9#16=7,21#2=1.如(21#(21#x))=5,则x可以是.(x小于50)【答案】13,29,37.【分析】这是一道把数论、定义新运算、倒推法、解方程等知识结合在一起的综合题.可采用枚举与筛选的方法.第一步先把(21#x)看成一个整体y.对于21#y=5,这个式子,一方面可把21作被除数,则y等于(21−5)=16的大于5的约数,有两个解8与16;另一方面可把21作除数,这样满足要求的数为26,47⋯,即形如21N+5这样的数有无数个.但必须得考虑,这些解都是由y所代表的式子(21#x)运算得来,而这个运算的结果是必须小于其中的每一个数的,也就是余数必须比被除数与除数都要小才行,因此大于21的那些y的值都得舍去.现在只剩下8,与16.第二步求:(21#x)=8与(21#x)=16.对于(21#x)=8可分别解得,把21作被除数时:x=13,把21作除数时为:x=29,50,⋯形如21N+8的整数(N是正整数).对于(21#x)=16,把21作被除数无解,21作除数时同理可得:x=37,58⋯所有形如21N+16这样的整数.(N是正整数).所以符合条件的答案是13,29,37.2. 字母a,b,c,d,e,f,g分别代表1至7中的一个数字,若a+b+c=c+d+e=c+f+g,则c可取的值有个.【答案】3【分析】a+b+c=c+d+e=c+f+g,a+b+c+c+d+e+c+f+g=(a+b+c+d+e+f+g)+2c=(1+2+3+4+5+6+7)+2c=28+2c28+2c是3的倍数,28÷3⋯1,所以2c÷3⋯2,c=1或4或7都可满足;构造:当c=1时,(28+2)÷3=10,所以a+b=d+e=f+g=9,a=2,b=7,d=3,e=6,f=4,g=5;当c=4,(28+2×4)÷3=12,所以a+b=d+e=f+g=8,a=1,b=7,d=2,e=6,f=3,g=5;当c=7,(28+2×7)÷3=14,所以a+b=d+e=f+g=7,a=1,b=6,d=2,e=5,f=3,g=4.综上,共有3种情况.3. 1×3×5×⋯×1991的末三位数是多少?【答案】625【分析】首先,仅考虑后三位数字,所求的数目相当于1×3×5×⋯×991的平方再乘以993×995×997×999的末三位.而993×995×997×999=993×999×995×997=(993000−993)×(995000−995×3)=(993000−993)×(995000−2985),其末三位为7×15=105;然后来看前者.它是一个奇数的平方,设其为(5k)2(k为奇数),由于(5k)2=25k2=25+25(k2−1),而奇数的平方除以8余1,所以k2−1是8的倍数,则25(k2−1)是200的倍数,设25(k2−1)=200m,则(5k)2=25+25(k2−1)=25+200m,所以它与105的乘积(5k)2×105=(25+200m)×105=21000m+2625,所以不论m的值是多少,所求的末三位都是625.4. 如果某整数同时具备如下三条性质:(1)这个数与1的差是质数;(2)这个数除以2所得的商也是质数;(3)这个数除以9所得的余数是5.那么我们称这个整数为幸运数,求出所有的两位幸运数.【答案】14【分析】条件(1)也就是这个数与1的差是2或奇数,这个数只能是3或者是偶数,再根据条件(3),除以9余5,在两位的偶数中只有14,32,50,68,86,这五个数满足条件;其中86与50不符合(1),32与68不符合(2).三个条件都符合的只有14,所以这个数是14.5. 求证:可以找到一个各位数字都是4的自然数,它是1996的倍数.【答案】见解析.【分析】1996÷4=499,下面证明可以找到1个各位数字都是1的自然数,它是499的倍数.取500个数:1,11,111,⋯⋯,111⋯⋯1(500个1).用499去除这500个数,得到500个余数a1,a2,a3,⋯,a500.由于余数只能取0,1,2,⋯,498这499个值,所以根据抽屉原则,必有 2 个余数是相同的,这 2 个数的差就是 499 的倍数,差的前若干位是 1,后若干位是 0:11⋯100⋯0.又 499 和 10 是互质的,所以它的前若干位由 1 组成的自然数是 499 的倍数,将它乘以 4,就得到一个各位数字都是 4 的自然数,这是 1996 的倍数.6. 用 1、2、3、4、5 各一个可以组成 120 个五位数,你能否从这 120 个数里面找出 11 个数来,使得它们除以 11 的余数各不相同?如果五个数字是 1、3、4、6、8 呢?【答案】 不能;不能.【分析】 (1)不能.五位数有 3 个奇位数字和 2 个偶位数字,将 1、2、3、4、5 分到奇偶位有 C 52=10 种方法,那么形成的五位数最多只能产生 10 种除以 11 的余数,无法出现 11 种除以 11 的余数.(2)不能.与(1)同理.当然,想不到这个的同学一一枚举即可,(1)中很明显余数为 0 的是构造不出来的,此外,余数为 2、4、6 也无法构造出来.(2)中余数为 6、7、10 的是构造不出来的.7. 任意给定一个正整数 n ,一定可以将它乘以适当的整数,使得乘积是完全由 0 和 7 组成的数.【答案】 见解析.【分析】 考虑如下 n +1 个数:7,77,777,⋯⋯,77⋯7⏟n 位,77⋯7⏟n+1位,这 n +1 个数除以 n 的余数只能为 0,1,2,⋯⋯,n −1 中之一,共 n 种情况,根据抽屉原理,其中必有两个数除以 n 的余数相同,不妨设为 77⋯7⏟p 位和 77⋯7⏟q 位(p >q ),那么 77⋯7⏟p 位−77⋯7⏟q 位=77⋯7⏟(p−q)位00⋯0⏟q 位 是 n 的倍数,所以 n 乘以适当的整数,可以得到形式为 77⋯7⏟(p−q)位00⋯0⏟q 位的数,即由 0 和 7 组成的数.8. 两个不等的自然数 a 和 b ,较大的数除以较小的数,余数记为 a ⊙b ,比如 5⊙2=1,7⊙25=4,6⊙8=2.(1)求 1991⊙2000,(5⊙19)⊙19,(19⊙5)⊙5;(2)已知 11⊙x =2,而 x 小于 20,求 x ;(3)已知 (19⊙x)⊙19=5,而 x 小于 50,求 x .【答案】 (1)9;3;1;(2)x =3,9,13;(3)x =12,26,33,45.【分析】 (1)1991⊙2000=9;由5⊙19=4,得(5⊙19)⊙19=4⊙19=3;由19⊙5=4,得(19⊙5)⊙5=4⊙5=1.(2)我们不知道11和x哪个大(注意,x≠11),即哪个作除数,哪个作被除数,这样就要分两种情况讨论.①x<11,这时x除11余2,x整除11−2=9.又x⩾3(因为x应大于余数2),所以x=3或9.②x>11,这时11除x余2,这说明x是11的倍数加2,但x<20,所以x=11+2=13.因此(2)的解为x=3,9,13.(3)这个方程比(2)又要复杂一些,但我们可以用同样的方法来解.用y表示19⊙x,不管19作除数还是被除数,19⊙x都比19小,所以y应小于19.方程y⊙19=5,说明y除19余5,所以y整除19−5=14,由于y⩾6,所以y=7,14.当y=7时,分两种情况解19⊙x=7.①x<19,此时x除19余7,x整除19−7=12.由于x⩾8,所以x=12.②x>19,此时19除x余7,x是19的倍数加7,由于x<50,所以x=19+7= 26,x=19×2+7=45.当y=14时,分两种情况解19⊙x=14.①x<19,这时x除19余14,x整除19−14=5,但x大于14,这是不可能的.②x>19,此时19除x余14,这就表明x是19的倍数加14,因为x<50,所以x=19+14=33.总之,方程(19⊙x)⊙19=5有四个解,x=12,26,33,45.9. 箱子里面有两种珠子,一种每个19克,另一种每个17克,所有珠子的重量为2017克,求两种珠子的数量和所有可能的值.【答案】107,109,111,113,115,117【分析】设19克的珠子有a个,17克的珠子有b个,根据题意列方程得19a+17b=2017利用余数分析法解不定方程.由于2017÷19余3所以有17b÷19余3,解得b=8从而得出a=99,即19×99+17×8=2017,即找到一组解为{a=99b=8此时a+b=99+8=107,由于19和17互质,那么只需要将a顺次减少17,b顺次增大19即可得出其他解{a=82b=27{a=65b=46{a=48b=65{a=31b=84{a=14b=103对于a+b的和而言,共可算得6个答案,分别为:107,109,111,113,115,117.10. 一个自然数除以8得到的商加上这个数除以9的余数,其和是13.求所有满足条件的自然数.【答案】108,100,92,84,76,68,60,52,44.【分析】本题考査学生掌握带余除法及枚举筛选的综合能力.设所求的自然数为n,且设n除以8商x余r,n除以9商a余y,于是有n=8x+r=9a+y(其中x+y=13).又已知0⩽y⩽8,0⩽r⩽7,下面分类讨论:若y=0,则x=13,得8×13+r=9a,解出r=4,故n=8×13+4=108;若y=1,则x=12,得8×12+r=9a+1,解出r=4,故n=8×12+4=100;类似地,若y=2、3、4、5、6、7、8,则分别有x=11、10、9、8、7、6、5,解得r=4,故n=8×11+4=92;n=8×10+4=84;n=8×9+4=76;n=8×8+4=68;n=8×7+4=60;n=8×6+4=52;n=8×5+4=44.答:满足条件的然数共有9个:108、100、92、84、76、68、60、52、44.说明:本题也可以先确定r=4.由y=13−x代人可得8x+r=9a+(13−x),即9x−9a=13−r,于是13−r的差应是9的倍数,又0⩽r⩽7,故r=4.。
五年级奥数余数问题

五年级奥数余数问题一、题目。
1. 一个数除以3余2,除以5余3,除以7余2,求这个数最小是多少?解析:我们先列出除以3余2的数:2、5、8、11、14、17、20、23、26…再列出除以5余3的数:3、8、13、18、23、28…然后列出除以7余2的数:2、9、16、23、30…可以发现23同时满足这三个条件,所以这个数最小是23。
2. 有一个数,除以4余1,除以5余2,除以6余3,这个数最小是多少?解析:这个数加上3就能被4、5、6整除。
4、5、6的最小公倍数是4 = 2×2,5 = 5,6=2×3,最小公倍数LCM = 2×2×3×5 = 60。
所以这个数最小是60 3=57。
3. 一个数除以5余4,除以8余3,求这个数最小是多少?解析:设这个数为x。
根据除以5余4,可设x = 5a+4(a为整数)。
又因为除以8余3,所以5a + 4=8b+3(b为整数),即5a=8b 1。
通过试值法,当b = 2时,a = 3。
此时x=5×3 + 4=19,19除以8余3,所以这个数最小是19。
4. 一个数除以9余7,除以11余9,这个数最小是多少?解析:这个数加上2就能被9和11整除。
9和11互质,它们的最小公倍数是9×11 = 99。
所以这个数最小是99 2 = 97。
5. 某数除以7余1,除以8余2,除以9余3,求这个数最小是多少?解析:这个数加上6就能被7、8、9整除。
7、8、9的最小公倍数为7×8×9=504。
所以这个数最小是504 6 = 498。
6. 一个数除以3余1,除以5余2,除以7余3,这个数最小是多少?解析:中国剩余定理:先求5×7 = 35,35除以3余2,2×2 = 7,7除以3余1。
再求3×7=21,21除以5余1,1×2 = 2,2除以5余2。
然后求3×5 = 15,15除以7余1,1×3=3,3除以7余3。
小学奥数题及答案余数问题

小学奥数题及答案余数问题
小学奥数题及答案余数问题
1.应用题
用一根既细又直的竹竿测量游泳池的水深,把竹竿的一端插入水中(碰到池底)后,没浸湿的部分长120厘米,把竹竿掉过头来,再插入水中(也碰到池底),此时没浸湿的'部分长30厘米,问游泳池有多深?
解答:第二次浸湿的部分就是游泳池的深度,所以游泳池深为:120-30=90(厘米)
【小结】。
第一次浸湿的长度实际上也是游泳池的深度。
2.余数问题
人教版小学五年级奥数题及答案余数问题:一批图书,数量在20到30本之间,平均分给7个同学,结果剩余的图书每比个人分到的书多2本,那么这批图书有多少本?
解答:
【小结】先估算出每个人可能分到几本,再分情况依次考虑。
小学奥数数论问题余数问题练习题【五篇】

小学奥数数论问题余数问题练习题【五篇】分析:这个题没有告诉我们,这三个数除以这个数的余数分别是多少,但是因为所得的余数相同,根据性质2,我们能够得到:这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有1,2,7,14,所以这个数可能为2,7,14.2.已知三个数127,99和一个小于30的两位数a除以一个一位数b的余数都是3,求a和b的值.分析:127-3=124,99-3=96,则b是124和96的公约数.而(124,96)=4,所以b=4.那么a的可能取值是11,15,19,23,27.3.除以99,余数是______.分析:所求余数与19×100,即与1900除以99所得的余数相同,所以所求余数是19.4.求下列各式的余数:(1)2461×135×6047÷11(2)19992000÷7分析:(1)5;(2)1999÷7的余数是4,19992000 与42000除以7 的余数相同.然后再找规律,发现4 的各次方除以7的余数的排列规律是4,2,1,4,2,1......这么3个一循环,所以由2000÷3 余2 能够得到42000除以7 的余数是2,故19992000÷7的余数是2 .【第二篇】(小学数学奥林匹克初赛)有苹果,桔子各一筐,苹果有240个,桔子有313个,把这两筐水果分给一些小朋友,已知苹果等分到最后余2个不够分,桔子分到最后还余7个桔子不够再分,求最多有多少个小朋友参加分水果分析:此题是一道求除数的问题.原题就是说,已知一个数除240余2,除313余7,求这个数为多少,我们能够根据带余除法的性质把它转化成整除的情况,从而使问题简化,因为240被这个数除余2,意味着240-2=238恰被这个数整除,而313被这个数除余7,意味着这313—7=306恰为这个数的倍数,我们只需求238和306的公约数便可求出小朋友最多有多少个了.240—2=238(个) ,313—7=306(个) ,(238,306)=34(人) .【第三篇】有一个大于1的整数,除45,59,101所得的余数相同,求这个数.分析:这个题没有告诉我们,这三个数除以这个数的余数分别是多少,但是因为所得的余数相同,根据性质2,我们能够得到:这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有1,2,7,14,所以这个数可能为2,7,14.【第四篇】1.已知三个数127,99和一个小于30的两位数a除以一个一位数b的余数都是3,求a和b的值.分析:127-3=124,99-3=96,则b是124和96的公约数.而(124,96)=4,所以b=4.那么a的可能取值是11,15,19,23,27.2.除以99的余数是______.分析:所求余数与19×100,即与1900除以99所得的余数相同,所以所求余数是19.【第五篇】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学奥数数论问题余数问题练习题【五篇】
分析:这个题没有告诉我们,这三个数除以这个数的余数分别是多少,但是因为所得的余数相同,根据性质2,我们能够得到:这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.
101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有1,2,7,14,所以这个数可能为2,7,14.
2.已知三个数127,99和一个小于30的两位数a除以一个一位数b的余数都是3,求a和b的值.
分析:127-3=124,99-3=96,则b是124和96的公约数.而(124,96)=4,所以b=4.那么a的可能取值是11,15,19,23,27.
3.除以99,余数是______.
分析:所求余数与19×100,即与1900除以99所得的余数相同,所以所求余数是19.
4.求下列各式的余数:
(1)2461×135×6047÷11
(2)19992000÷7
分析:(1)5;(2)1999÷7的余数是4,19992000 与42000除以7 的余数相同.然后再找规律,发现4 的各次方除以7的余数的排列规律是4,2,1,4,2,1......这么3个一循环,所以由2000÷3 余2 能够得到42000除以7 的余数是2,故19992000÷7的余数是2 .
【第二篇】
(小学数学奥林匹克初赛)有苹果,桔子各一筐,苹果有240个,桔子有313个,把这两筐水果分给一些小朋友,已知苹果等分到最后余2个不够
分,桔子分到最后还余7个桔子不够再分,求最多有多少个小朋友参加
分水果
分析:此题是一道求除数的问题.原题就是说,已知一个数除240余2,除313余7,求这个数为多少,我们能够根据带余除法的性质把它转化成整除的情况,从而使问题简化,因为240被这个数除余2,意味着240-
2=238恰被这个数整除,而313被这个数除余7,意味着这313—7=306
恰为这个数的倍数,我们只需求238和306的公约数便可求出小朋友最多有多少个了.240—2=238(个) ,313—
7=306(个) ,(238,306)=34(人) .
【第三篇】
有一个大于1的整数,除45,59,101所得的余数相同,求这个数.
分析:这个题没有告诉我们,这三个数除以这个数的余数分别是多少,但是因为所得的余数相同,根据性质2,我们能够得到:这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.
101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有
1,2,7,14,所以这个数可能为2,7,14.
【第四篇】
1.已知三个数127,99和一个小于30的两位数a除以一个一位数b的
余数都是3,求a和b的值.
分析:127-3=124,99-3=96,则b是124和96的公约数.而(124,96)=4,所以b=4.那么a的可能取值是11,15,19,23,27.
2.除以99的余数是______.
分析:所求余数与19×100,即与1900除以99所得的余数相同,所以所求余数是19.
【第五篇】
19941994…1994(1994个1994)除以15的余数是______.
分析:法1:从简单情况入手找规律,发现1994÷15余
14,19941994÷15余4,199419941994÷15余9,
1994199419941994÷15余14,......,发现余数3个一循
环,1994÷3=664...2,19941994…1994(1994个1994)除以15的余数是4;法2:我们利用最后一个例题的结论能够发现199419941994能被3整除,那么19941994199400…0能被15整
除,1994÷3=664...2,19941994…1994(1994个1994)除以15的余数是4.。
