材料力学第9章 应力状态分析
材料力学第9章 强度理论
由于物体在外力作用下所发生的弹性变形既包括 物体的体积改变,也包括物体的形状改变,所以可推 断,弹性体内所积蓄的变形比能也应该分成两部分: 一部分是形状改变比能(畸变能) ,一部分是体积改 变比能 。 在复杂应力状态下,物体形状的改变及所积蓄的 形状改变比能是和三个主应力的差值有关;而物体体 积的改变及所积蓄的体积改变比能是和三个主应力的 代数和有关。
注意:图示应力状态实际上为弯扭组合加载对 应的应力状态,其相当应力如下:
r 3 2 4 2 [ ] 2 2 [ ] r 4 3
可记住,便于组合变形的强度校核。
例1 对于图示各单元体,试分别按第三强度理论及第四强度理论 求相当应力。
120 MPa 140 MPa
r4
1 2 2 2 [(0 120) ( 120 120) ( 120 0) ] 120MPa 2
140 MPa
(2)单元体(b)
σ1 140MPa
σ 2 110MPa
σ3 0
110 MPa
σr 3 σ1 σ 3 140MPa 1 2 2 2 σr 4 [30 110 ( 140) ] 128MPa 2
1u
1u
E
b
E
1 1 1 2 3 E
1u
1u
E
b
E
1 2 3 b
强度条件为: 1 2 3
b
n
[ ]
实验验证: a) 可解释大理石单压时的纵向裂缝; b) 脆性材料在双向拉伸-压缩应力状态下,且压应 力值超过拉应力值时,该理论与实验结果相符合。
σ1 94 .72MPa σ 3 5 .28MPa
材料力学应力状态分析

材料力学应力状态分析材料力学是研究物质内部力学性质和行为的学科,其中应力状态分析是材料力学中的重要内容之一。
应力状态分析是指对材料内部受力情况进行分析和研究,以揭示材料在外力作用下的应力分布规律和应力状态特征,为工程设计和材料选用提供依据。
本文将从应力状态的基本概念、分类和分析方法等方面展开讨论。
首先,我们来介绍一下应力状态的基本概念。
应力是指单位面积上的力,是描述物体内部受力情况的物理量。
在材料力学中,通常将应力分为正应力和剪应力两种基本类型。
正应力是指垂直于截面的应力,而剪应力是指平行于截面的应力。
在实际工程中,材料往往同时受到多种应力的作用,因此需要对应力状态进行综合分析。
其次,我们将对应力状态进行分类。
根据应力的作用方向和大小,可以将应力状态分为拉应力状态、压应力状态和剪应力状态三种基本类型。
拉应力状态是指材料内部受到拉力作用的状态,压应力状态是指材料内部受到压力作用的状态,而剪应力状态是指材料内部受到剪切力作用的状态。
这三种应力状态在工程实践中都具有重要的意义,需要我们进行深入的分析和研究。
接下来,我们将介绍应力状态分析的方法。
应力状态分析的方法有很多种,常用的有应力分析法、应变分析法和能量方法等。
应力分析法是通过应力分布的计算和分析来揭示应力状态的特征,应变分析法则是通过应变分布的计算和分析来揭示应力状态的特征,而能量方法则是通过能量原理和平衡条件来揭示应力状态的特征。
这些方法各有特点,可以根据具体情况选择合适的方法进行分析。
最后,我们需要注意的是,在进行应力状态分析时,需要考虑材料的本构关系、边界条件和载荷情况等因素,以确保分析结果的准确性和可靠性。
同时,还需要注意应力状态分析的结果对工程实践的指导意义,以便更好地指导工程设计和材料选用。
总之,材料力学应力状态分析是一个复杂而重要的课题,需要我们进行深入的研究和分析。
只有深入理解应力状态的特征和规律,才能更好地指导工程实践,为实际工程问题的解决提供科学依据。
《材料力学 第2版》_顾晓勤第09章第2节 二向应力状态分析
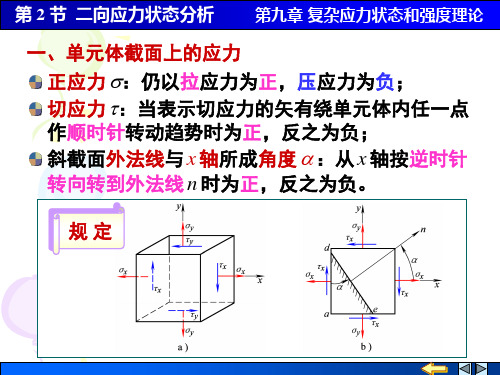
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
最大主应力和最小主应力的计算式
max m in
x
y
2
x
2
y
2
2 x
确定 max 和 min 所在平面的方法
1)若x>y,则所求的两个角度0 和 90º+0 中, 绝对值较小的一个确定max 所在的平面;
2)若x <y,则所求的两个角度0 和 90º+0 中, 绝对值较小的一个确定min 所在的平面;
2
及
2sin cos sin 2 对以上二式进行整理得到:
x
y
2
x
y
2
cos2
x
sin 2
x
y
2
sin 2
x
cos2
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
x
y
2
x
y
2
cos2
x
sin 2
x
y
2
sin 2
x
cos2
利用上述两式可以求得 de 斜截面上的正应力和切
设 de 斜截面面积为 dA,则 ae 面的面积为 dAsin , ad面的面积为 dAcos 。取 t 和 n 为参考轴,建立棱
柱体 ade 的受力平衡方程如下:
dA ( xdAcos ) sin ( xdAcos ) cos ( ydAsin ) cos ( ydAsin ) sin 0
y
2
2 x
105 MPa
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
0
1 2
arctan(
2 x x
材料力学:第九章 应力状态分析

τx
C
F
Me
d
C
(a)
·
σx
(b)
C
T
F
解:C点所在横截面上的正应力和切应力的分布规律如图 所示, 点所在横截面上的正应力和切应力的分布规律如图b所示 点所在横截面上的正应力和切应力的分布规律如图 所示, 其值为
FN 500 × 103 N σx = = = 63.7 × 106 Pa=63.7MPa π 2 A 0.1m ) ( 4
经整理后得到 )、(2) )、( (1) 由(1)、( )式,可以求出单 ) 元体各个截面上的应力。( 。(即 点 元体各个截面上的应力。(即a点 (2) 处各个方向上的应力) ) 处各个方向上的应力)
∑F = 0
t
τ =τ′
σ α = −τ sin 2α
τ α = τ cos 2α
定义:构件内一点处各个方向上的应力集合, 定义:构件内一点处各个方向上的应力集合,称为该点处的 应力状态。 应力状态。
F F
横截面上只有正应力,且 横截面上只有正应力, 均匀分布 计算公式: 计算公式:
m
σ
F
FN
FN σ= A
等直圆杆扭转时横截面上的应力: 等直圆杆扭转时横截面上的应力:
Me m Me
m
横截面上只有切应力,呈 横截面上只有切应力, 线性分布
T
o
τρ
τmax
T⋅ρ 计算公式: 计算公式: τρ = Ip
R
τ
T 16 M e τ= = WP πd3
为了研究a点处各个方向的应力,围绕a点取一个各边长均为无 为了研究 点处各个方向的应力,围绕 点取一个各边长均为无 点处各个方向的应力 限小的六面体(称为单元体)。 限小的六面体(称为单元体)。 径向截面
材料力学(单辉祖版)完整课后习题答案-9

第九章复杂应力状态强度问题题号页码9-4 (1)9-5 (3)9-8 (4)9-9 (5)9-10 (7)9-14 (8)9-16 (10)9-17 (11)9-18 (13)9-19 (14)9-22 (16)9-23 (16)9-24 (17)9-25 (18)9-26 (18)9-27 (20)9-28 (21)(也可通过左侧题号书签直接查找题目与解)9-4试比较图示正方形棱柱体在下列两种情况下的相当应力r3σ,弹性常数E和µ均为已知。
(a) 棱柱体轴向受压;(b) 棱柱体在刚性方模中轴向受压。
题9-4图(a)解:对于棱柱体轴向受压的情况(见题图a),三个主应力依次为0,===σσσ−σ132由此可得第三强度理论的相当应力为σσσσ=−=31r3 (a)(b)解:对于棱柱体在刚性方模中轴向受压的情况(见题图b ),可先取受力微体及坐标如图9-4所示,然后计算其应力。
图9-4由图9-4可得σσy −=根据刚性方模的约束条件,有 0)]([1=+−=z y x x σσµσE ε即)(z y x σσµσ+=注意到x z σσ=故有 σµµσσz x −−==1三个主应力依次为 σσσµµσσ−=−−==3211,由此可得其相当应力为 σµµσσσ−−=−=12131r3 (b)比较:按照第三强度理论,(a)与(b)两种情况相当应力的比值为µµσσr b a 211)r3()r3(−−==1>r ,这表明加刚性方模后对棱柱体的强度有利。
9-5 图示外伸梁,承受载荷F = 130 kN 作用,许用应力[σ]=170 MPa 。
试校核梁的强度。
如危险点处于复杂应力状态,采用第三强度理论校核强度。
题9-5图解:1.内力分析由题图可知,+B 截面为危险截面,剪力与弯矩均为最大,其值分别为 m N 1080.7m 600.0N 10130 kN 130432S ⋅×=××====Fl M F F ,2.几何量计算34324max ,)(343)(343545433m 1090.2]m )0137.0140.0(0085.0211023.2[2m 1023.2)m 20137.0140.0(0137.0122.0m 1005.5m 140.01007.7m 1007.712)0137.02280.0()0085.0122.0(12280.0122.0[−−−−−−×=−××+×==×=−××=×=×=×=×−×−−×=z a z b z z z S S S W I 式中的足标b ,系指翼缘与腹板的交界点,足标a 系指上翼缘顶边中点。
应力状态分析和强度理论

03
弹性极限
材料在弹性范围内所能承受的最大应力状态,当超过这一极限时,材料会发生弹性变形。
01
屈服点
当物体受到一定的外力作用时,其内部应力状态会发生变化,当达到某一特定应力状态时,材料会发生屈服现象。
02
强度极限
材料所能承受的最大应力状态,当超过这一极限时,材料会发生断裂。
应力状态对材料强度的影响
形状改变比能准则
04
弹塑性材料的强度分析
屈服条件
屈服条件是描述材料在受力过程中开始进入屈服(即非弹性变形)的应力状态,是材料强度分析的重要依据。
根据不同的材料特性,存在多种屈服条件,如Mohr-Coulomb、Drucker-Prager等。
屈服条件通常以等式或不等式的形式表示,用于确定材料在复杂应力状态下的响应。
最大剪切应力准则
总结词
该准则以形状改变比能作为失效判据,当形状改变比能超过某一极限值时发生失效。
详细描述
形状改变比能准则基于材料在受力过程中吸收能量的能力。当材料在受力过程中吸收的能量超过某一极限值时,材料会发生屈服和塑性变形,导致失效。该准则适用于韧性材料的失效分析,尤其适用于复杂应力状态的失效判断。
高分子材料的强度分析
01
高分子材料的强度分析是工程应用中不可或缺的一环,主要涉及到对高分子材料在不同应力状态下的力学性能进行评估。
02
高分子材料的强度分析通常采用实验方法来获取材料的应力-应变曲线,并根据曲线确定材料的屈服极限、抗拉强度等力学性能指标。
03
高分子材料的强度分析还需要考虑温度、湿度等环境因素的影响,因为高分子材料对环境因素比较敏感。
02
强度理论
总结词
该理论认为最大拉应力是导致材料破坏的主要因素。
材料力学-应力状态与应变状态分析

s2 引起 1 s 2 E 2 s 2 E 3 s 2 E
s3 引起 1 s 3 E 2 s 3 E 3 s 3 E
小变形 i i i i i 1,2,3
1
1 E
s1
(s 2
s 3 )
广
2
1 E
s 2
(s 3
s1 )
义 虎 克 定
3
1 E
s 3
(s 1
s 2)
t T = 1 πD3 (1-a4) 16
1
=
1 E
[s1-
(s2+s3)]
=
1+
E
t
T=8.38 kN·m
二、体积应变
单元体边长:dx、dy、dz
体积:V0 = dx·dy·dz
dy
dx → dx +△dx = dx + 1dx = (1 + 1) dx
dy → dy +△dy = dy + 2dy = (1 + 2) dy
体积的绝对增量:△V = V-V0 = V0 (1+ 2+ 3)
单位体积增量:
V V0
1 2
3
体积应变 体积的相对增量
1 2
E
(s1
s2
s
3)
讨论:
V V0
1 2
E
(s1 s 2
s 3)
⒈ 若 s1 + s2 + s3>0,
则 >0 →△V >0,即体积增大;
若 s1 + s2 + s3<0,
s2
s3 dsz 1
dx
dz → dz +△dz = dz + 3dz = (1 + 3) dz
材料力学第9章 压杆稳定(土木)

2.1922年冬天下大雪,美国华盛 . 年冬天下大雪, 年冬天下大雪 顿尼克尔卜克尔剧院由于屋顶结 构中的一根压杆超载失稳,造成 构中的一根压杆超载失稳, 一根压杆超载失稳 剧院倒塌, 余人。 剧院倒塌,死98人,伤100余人。 人 余人
3.2000年10月25日 . 年 月 日 上午10时 分 上午 时30分,在南京 电视台演播中心演播厅 屋顶的浇筑混凝土施工 顶的浇筑混凝土施工 中,因脚手架失稳,造 脚手架失稳, 成演播厅屋顶模板倒塌, 成演播厅屋顶模板倒塌, 死5人,伤35人。 人 人
欧拉公式与精确解曲线 精确解曲线
F =1.152F 时,
cr
δ ≈ 0.3l
理想受压直杆 非理想受压直杆
y
适用条件: 适用条件: •理想压杆(轴线为直线,压力与 理想压杆(轴线为直线, 理想压杆 轴线重合,材料均匀) 轴线重合,材料均匀) •线弹性,小变形 线弹性, 线弹性 •两端为铰支座 两端为铰支座
hb3 Iz = = 32cm 4 12
µl
iz =
Iz 32 = = 1.155cm A 4× 6
x
h
µ z = 0.5,
0.5 × 2 λz = = = 86.6 −2 iz 1.155 ×10
A3钢的λs= 61.6, λs<λ< λp,属于中 钢的 , 长压杆稳定问题。 长压杆稳定问题。 由表9-2查得 由表 查得: 查得
挠曲线的近似微分方程 挠曲线的近似微分方程
d w M =− dx EI
2
2
d w Fw =− 2 dx EI
引入记号
2
F w′′ + w = 0 EI
F k = EI
2
w′′ + k w = 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
方位角α, 对应于应力圆上为2 α
a τy σy τx e σα σx a ταf
n
c
τ
a
B 2a
τσx x x o C
角, 自起始半径旋转, 且与α转向 一致;
A 单元体上A、B面夹角α, σ 应力圆上弧长AB的圆心角
b
σyτy d
为2 α角, 且转向一致。
3、主应力、主平面与主单元体
t
图解法
tadA (t xdAcosa ) cosa (s xdAcosa )sina (t ydAsina )sina (s ydAsina) cosa 0
关系式
t x =t
(负号已包含在指向中);
y
sin
2a
2 sin a
cosa;
cos2 a 1 cos 2a ; sin2 a 1 cos 2a
t
图解法
注意A1、A2点
σx
σ( 2,0)
A2 B2
σ τ E(
2a
Dα1,σ( xα,)τ x )
2a
数值 方位
τy τx
o
σ a C B1 A1 σ
( 1,0) 主点法
s1 = sx s y
s2
2
s
(
x
s
2
y
)2
t
2 x
tan
2a0
2t x sx s
y
(σy ,Dτ2y) σy
K
s1的方位
作D1K⊥σ轴, 交圆与K点, 则A2K方向
2
2
sa、ta
计算公式
sa
ta
sx sx
sy
2
s y
2
s x s y cos2a
2
sin2a t xcos2a
t
xsin2a
3、讨论:
e
τx σx a
σα a τα
n
b
f
sa
sx
sy
2
sx
s y
2
cos2a
t xsin2a
ta
sx
s y
2
sin2a
t xcos2a
στyy t
s a 90
sx
到smax和tmax
s a s cos2a
ta
s 2
sin2a
F
FN
paσα
FN
α τα
一点处的应力状态:受力构件内一点处不同方位上应力的集合。
2、全面进行强度计算的需要
σmax
τmin
①只存在s:
s
≤
m ax
s
轴向拉压、梁截面上下边缘 z
τmax
②只存在t: t m ax ≤ t
自由扭转、梁截面中性轴处
τy σy c
τσx x σyτy d
x
二、应力圆 1、应力圆的绘制
t
σx
试作图示单元体的应力圆
D1σ( x ,τ x )
圆心:( s x s y ,0)
2
半径:(s
x
s
2
y
)2
t
2 x
o
B2 C B1
σ
τy τx
证明:
OC= OB1 OB2 = s x s y
2
2
2
2
CD1= CB1 B1D1
A2 B2
σ τ E(
2a
Dα1,σ( xα,)τ x )
2a
数值
s1 = sx s y
s2
2
s
(
x
s
2
y
)2
t
2 x
方位 A1点如何得到?
τy τx
o
C
σ B1 A1 σ
( 1 ,0)
以CD1点为起始半径, 顺时针旋转2α0
(σy ,Dτ2y)
至CA1即可。
σy
y
a τy σy τx e σα
b
σyτy d
已知s x、s y、t x、a,求sa、ta
e
τx σx a
σα a τα
n
b
f
στyy t
y
t xdAcosa n
s xdAcosa a
sa dA a t ydAsin a
a
s
a ydAsin a
ta dA t
x
解: Fn 0
sadA (t xdAcosa )sina (s xdAcosa ) cosa (t ydAsina ) cosa (s ydAsina)sina 0
sx
sy
2
sx
s y
2
cos2a
t xsin2a
sa
c
a
EF=CEsin(2a0 +2a)
σx a ταf τσx x x
bLeabharlann σyτy d=CD1cos2a0sin2a CD1sin2a0cos2a
sx
s
2
y
sin2a
t xcos2a
ta
2、应力圆求斜截面上的应力 试求图示单元体α截面上的应力
t
CB1 OB1 OC
=s
x
s
x
s
2
y
=sx sy
2
(σy ,Dτ2y) σy
y
a τy σy c
B1D1 t x
τx
该圆即为方程
CD1=
s
(
x
s
2
y
)2
t
2 x
σx
b
(sa
sx
sy
2
)2
t
2 a
s
(
x
s y
2
)2
t
2所表示的圆。
x
τσx x x σyτy d
2、应力圆求斜截面上的应力 试求图示单元体α截面上的应力
t
σx
σ τ E(
2a
Dα1,σ( xα,)τ x )
1、作单元体的应力圆
2、以CD1为起始半径, 按α的旋转方 向旋转2α, 得到E点。
B2
o
C F B1
σ E点的坐标即为:(sa,ta)
τy τx
(σy ,Dτ2y) σy
y
a τy σy c n τx e σα a
σx a ταf τσx x x
注意A1、A2点
τy τx
σx
σ( 2,0)
A2 B2 o
(σy ,Dτ2y) σy
σ τ E(
2a
Dα1,σ( xα,)τ x )
2a
σ C B1 A1 σ
( 1 ,0)
y
数值
s1 OA1=OC CA1
=sx sy
2
s
(
x
s
2
y
)2
t
2 x
s2 OA2 =OC CA2
=sx sy
2
s
sa
sx
sy
2
sx
s y
2
cos2a
t xsin2a
e
τx σx a
σα a τα
n
ta
sx
s y
2
sin2a
t xcos2a
s a、t a 均以2a 为参变量
b
f
στyy t
sa
sx
sy
2
sx
s y
2
cos2a
t xsin2a
ta
s
x
s
2
y
sin2a
t xcos2a
德国 1895年提出
(s a
sx
sy
2
)2
t
2 a
s
(
x
s y
2
)2
t
2 x
圆的方程
s a、 t a 在 s
t 直角坐标系内的轨迹是以(s
x
s
2
y
, 0)为 圆 心 ,
(s
x
2
s
y
)2
t
2为半径的圆,此圆称为应力圆,或莫尔圆。
x
二、应力圆 1、应力圆的绘制 试作图示单元体的应力圆
t
σx
D1σ( x ,τ x )
τy τx
①: 建立σ-τ坐标系
ttzyyz tzx
txz tzx sz tzy
ttyyxz
sz txz
txy
sx
x
z
sy
三、主平面、主应力与主单元体
σy σz
主平面:切应力为零的截面(t =0)。
主应力:主平面上的正应力。
σx
σx
主单元体:三对相互垂直的平面均为主平面的单元体。σz σy
可以证明, 通过一点处的各不同方位的截面中, 一
txz tzx sz tzy
ttyyxz
sz txz
txy
应力张量的第一、第二和第三不变量。
sx x I1 s x s y +s z
z
sy
I2
sxs y
s ysz -szsx
t
2 xy
t
2 yz
t
2 zx
s x t xy t xz I3 t yx s y t yz
t zx t zy s z
二、应力圆
dy dz
单元体的特点: dx dy dz 0
A
①单元体各个面上的应力是均匀分布的;
②两个平行面上的应力大小相等。
dx
(一个面的两侧)
y sy
只要知道单元体三对相互平行面上的应力, 其它任意截面上的应力均可用截面法求出, 因此可用单元体三个互相垂直平面上的应 力来表示一点的应力状态。
