第1章 热力学基础3热力学函数关系
合集下载
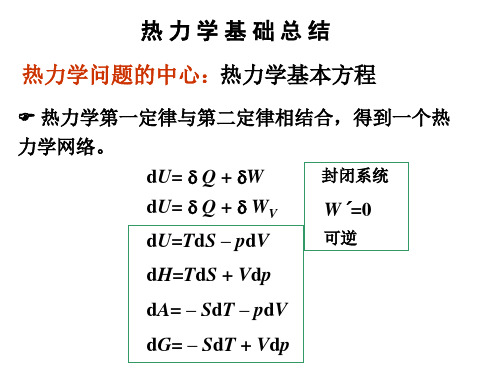
热力学函数的基本关系式

dU = TdS- pdV
(1-108)
dH = TdS + Vdp
(1-109)
dA = -SdT- pdV
(1-110)
dG = -SdT + Vdp
(1-111)
式(1-108),(1-109),(1-110),(1-111)称为热力学基本方程
dU = TdS- pdV dH = TdS + Vdp dA = -SdT- pdV dG = -SdT + Vdp
常用的是式(1-120)及式(1-121),这两等式右边的变化率是可以由 实验直接测定的,而左边则不能。可用等式右边的变化率代替左
4.热力学状态方程
由dU=TdS-pdV
定温下, dUT=TdST-pdVT
等式两边除以dVT 即
dUT T dST p
dVT
dVT
由麦克斯韦方程 于是
U T S p V T V T S p V T T V
式(1-116)及 (1-117)叫吉布斯 - 亥姆霍茨方程。
(1-117)
G-H方程常用的形式为:
即
(G / T )
T p
H T2
加△
(1-116)
Gibbs自由能随压力的变化
因
(эG/эP)T,n=V
(э△G/эP)T,n=△V 此即G---V关系式
只要知道△V--p关系式,在定温下P1的△G1就可求算出P2的△G2。
在定压下从T1到 T2积分得: (△G)2/ T2- (△G)1/ T1=- =∫T1 T2 △H/T2dT 若知△H--T关系以及T1时的△G1就可求算T2时的△G2 而: △H= △H T0+∫ T0 T △CpdT △H T0是T0时的焓变。
热 力 学 基 础 总 结
(CB)
;
(
A nB
)T
,v,nc
(CB)
;
(
G nB
)T
,V
,nc
; (CB)
(
U nB
)
S ,V
,nc
V
(CB)
;
( nB
)T , p,nc
H
(CB)
;
( nB
) S , p,nc
; (CB)
A ( nB )T , p,nc (CB) ;
解: 偏摩尔量:
; ; ; H
( nB )T , p,nc (CB)
• 热力学量变换法(变量变换法)就是将不能用实 验直接测量的量转换为用实验量或状态方程表 示的关系的基本方法。
变量变换法
从研究工作需要来看:
变量变换法是在学科发展中形成的科学方法。 通常在研究工作中会提出许多科学命题,为 寻求解决问题的思路或设计实验,总要想法 进行命题的转换,以利用已有信息或通过实 验进行分析,其间变量变换就是一个有效的 方法,今以实例说明。
解:在水的正常沸点时 1= 2;
在温度为 373.15K 及 202 650 Pa 下
因为 所以
故
(
Gm* p
)T
Vm
>0
3> 1
4> 2
4> 3> 2= 1。
4> 3。
计算题
1 一定量纯理想气体由同一始态,分别经绝热可逆 膨胀至(T2,p2, V2)和经绝热不可逆膨胀至(T2',p2',V2')
=
nCV,m dT T
p dV T V
dG= – SdT + Vdp dGT= Vdp
变量变换法
热力学函数的基本关系式

dG = -SdT + Vdp
S p
T
V T
p
麦克斯韦关系式 :表示的是系统在同一状态的两种
变化率数值相等。 9
二阶混合偏导数
T p V S S V 麦氏方程记忆法:
T p
S
V S
p
① 对角乘积永远是pV,TS;
② 等式两边分母与外角标互换;
S p
T
V T
4
由四个热力学基本方程,分别加上相应的条件,可得到
8个派生公式:
dU = TdS- pdV
U S
V
T
U V
S
p
dH = TdS + Vdp
T V H
S p
H p S
dA = -SdT- pdV
A T
V
S
A V
T
p
dG = -SdT + Vdp
G T
P
S
G P
则
U T p p
V T T V
11
练习:由热力学基本方程出发证明,
H p
T
T
V T
p
V
证明:
dH=TdS+Vdp
定温下,等式两边除以dp
H p
T
T
S p
T
V
由麦克斯韦方程
S p
T
V T
p
返回
H p
T
T
V T
p
V
12
U T p p V T T V
S T p
T
T
定容
S CV T V T
S T V
15
T
V
5
2. 吉布斯 - 亥姆霍茨方程
热力学函数间的关系

则T = 1000 K, rG1000 = 61900 Jmol-1>0
计算结果说明,在给定条件下,298K时,合成氨反应可 以进行;而在1000K时,反应不能自发进行
再见!
H
U
TS
G
TS F
H U pV pV U H pV
G H TS F pV pV F U TS G pV
T1
T
T2 T1
H T2
dT
(1) 若温度变化范围不大,△H可近似为不随温度变化的常数
G T
T 2
G T
T 1
H
1 T2
1 T1
四、G与温度的关系—吉布斯-亥姆霍兹公式
25℃,反应 2SO3(g) 2SO2(g) O2(g)
rGm (298K) 1.400 10 5 J mol1 r Hm 1.966 105 J mol1
H T2
吉布斯-亥姆赫兹公式
G T
T
H T2
P
四、G与温度的关系—吉布斯-亥姆霍兹公式
吉布斯-亥姆赫兹方程式
Байду номын сангаас
G T
T
H T2
P
(微分形式)
应用:在等压下若已知反应在T1的rGm(T1),则可求得该反 应在T2时的rGm(T2)。
积分形式
T2 d ( G )
M 和N也是 x,y 的函数
二阶导数
M
2Z
( y )x xy ,
N
2Z
( x )y xy
所以
M N ( y )x ( x )y
三、Maxwell 关系式
热力学函数是状态函数,数学上具有全微分性质,将上述
关系式用到四个基本公式中, 就得到Maxwell关系式:
计算结果说明,在给定条件下,298K时,合成氨反应可 以进行;而在1000K时,反应不能自发进行
再见!
H
U
TS
G
TS F
H U pV pV U H pV
G H TS F pV pV F U TS G pV
T1
T
T2 T1
H T2
dT
(1) 若温度变化范围不大,△H可近似为不随温度变化的常数
G T
T 2
G T
T 1
H
1 T2
1 T1
四、G与温度的关系—吉布斯-亥姆霍兹公式
25℃,反应 2SO3(g) 2SO2(g) O2(g)
rGm (298K) 1.400 10 5 J mol1 r Hm 1.966 105 J mol1
H T2
吉布斯-亥姆赫兹公式
G T
T
H T2
P
四、G与温度的关系—吉布斯-亥姆霍兹公式
吉布斯-亥姆赫兹方程式
Байду номын сангаас
G T
T
H T2
P
(微分形式)
应用:在等压下若已知反应在T1的rGm(T1),则可求得该反 应在T2时的rGm(T2)。
积分形式
T2 d ( G )
M 和N也是 x,y 的函数
二阶导数
M
2Z
( y )x xy ,
N
2Z
( x )y xy
所以
M N ( y )x ( x )y
三、Maxwell 关系式
热力学函数是状态函数,数学上具有全微分性质,将上述
关系式用到四个基本公式中, 就得到Maxwell关系式:
1-3热力学定律复习

热力学定律知识概要
•化学热力学的理论基础是热力学第一定律和热力学第二定律.
•在气液固三种聚集状态中, 气体最容易用分子模型进行研究. 一,气体的pVT关系
理想气体 理想气体状态方程: pV = nRT 真实气体 范德华方程 二,热力学第一定律 • 热力学第一定律本质是能量守恒. U = Q + W • 基本概念和术语
数据包括标准热容、标准相变焓、标准生成焓和标准燃烧焓 等.
8
二 热力学第一定律--系统与环境,过程与途径
系统
所研究的 物质对象
敞开系统 封闭系统 隔离系统
物质进出 能量得失
√
√
√
系统的宏观性质: • 广延性质 n, V, U, H, S, G, A, …, 有空间上的加和性.
• 强度性质 T, p, Vm , Um , , …, 无空间上的加和性.
理想气体:在任何温度/ 压力下均服从理想气体状态方程的气体. 两个特征: (1)分子本身必定不占有体积; (2)分子间无相互作用.
3
一 气体的 p V T 关系—理想气体
分压力pB: 无论是理想气体还是真实气体, 混合气中任一组分B的 摩尔分数yB与总压力p 的乘积定义为该组分的分压力:
pB = yB p
功的符号: 系统得功, W > 0 ;系统作功, W <0 .
体积功的一般计算式:
W
V2 V1
pambdV
热(Q): 因系统与环境间未达到热平衡而传递的能量. 热的符号: 系统吸热, Q > 0 ;系统放热, Q < 0. 热的类型: 物质变温过程的热; 相变热; 化学反应热等.
• 故功和热不是系统性质, 不是状态函数!
•化学热力学的理论基础是热力学第一定律和热力学第二定律.
•在气液固三种聚集状态中, 气体最容易用分子模型进行研究. 一,气体的pVT关系
理想气体 理想气体状态方程: pV = nRT 真实气体 范德华方程 二,热力学第一定律 • 热力学第一定律本质是能量守恒. U = Q + W • 基本概念和术语
数据包括标准热容、标准相变焓、标准生成焓和标准燃烧焓 等.
8
二 热力学第一定律--系统与环境,过程与途径
系统
所研究的 物质对象
敞开系统 封闭系统 隔离系统
物质进出 能量得失
√
√
√
系统的宏观性质: • 广延性质 n, V, U, H, S, G, A, …, 有空间上的加和性.
• 强度性质 T, p, Vm , Um , , …, 无空间上的加和性.
理想气体:在任何温度/ 压力下均服从理想气体状态方程的气体. 两个特征: (1)分子本身必定不占有体积; (2)分子间无相互作用.
3
一 气体的 p V T 关系—理想气体
分压力pB: 无论是理想气体还是真实气体, 混合气中任一组分B的 摩尔分数yB与总压力p 的乘积定义为该组分的分压力:
pB = yB p
功的符号: 系统得功, W > 0 ;系统作功, W <0 .
体积功的一般计算式:
W
V2 V1
pambdV
热(Q): 因系统与环境间未达到热平衡而传递的能量. 热的符号: 系统吸热, Q > 0 ;系统放热, Q < 0. 热的类型: 物质变温过程的热; 相变热; 化学反应热等.
• 故功和热不是系统性质, 不是状态函数!
第一章热力学第一定律

20
4.热力学平衡 热力学平衡态:指外界条件不变时,体系内 部性质均匀且不随时间变化的状态
1) 热平衡:无绝缘壁时,体系内各部分, 体系与环境之间温度相等 2)力学平衡:无刚性壁时,体系内各部分, 体系与环境之间力相等 3)相平衡:体系各相物质组成、数量不变
4)化学平衡:化学反应不引起物质组成或 浓度随时间的变化
18
2)几种重要的过程: a)等温过程:T 始 =T 终 =T 环 b)等压过程:P 始 =P 终 =P 环
c)等容过程:V 始 =V 终
d)等温等压过程:a,b 二者都具备
e)绝热过程:体系与环境之间没有热量传 递,只有功的传递 f)循环过程:体系由一始态出发,经一系列 变化过程又回到原来的状态
b. 人造金刚石: C(石墨)→C(金刚石) 由热力学知道 P>15000P° 时,才有可能; 今天已实现了这个转变(60000P°,1000℃, 催化剂)
二. 热力学研究方法的特点和局限性
3
1. 热力学方法的特点
研究大量粒子的宏观体系的宏观性质之间的 关系及变化规律,
不考虑微观粒子的微观结构
不涉及反应的速度和机理
4
2. 优点和局限性
1)热力学只研究体系的始终态 根据始终态的性质而得到可靠的结果;不 考虑变化中的细节;不考虑物质内部的结构 因素
2)不考虑时间因素
3)不考虑粒子的个别行为
5
热力学常用术语 1、体系与环境
体系(System) 简单而言,体系即研究之对象 。也就是为了研究问题的方便 ,我们常常用一个真实或想象 的界面把一部分物质或空间与 其余分开,这种被划定的研究 对象称为体系,亦称为物系或 环境( 系统。surroundings) 与体系密切相关、影响所 及的那部分物质或空间称为环 境。
4.热力学平衡 热力学平衡态:指外界条件不变时,体系内 部性质均匀且不随时间变化的状态
1) 热平衡:无绝缘壁时,体系内各部分, 体系与环境之间温度相等 2)力学平衡:无刚性壁时,体系内各部分, 体系与环境之间力相等 3)相平衡:体系各相物质组成、数量不变
4)化学平衡:化学反应不引起物质组成或 浓度随时间的变化
18
2)几种重要的过程: a)等温过程:T 始 =T 终 =T 环 b)等压过程:P 始 =P 终 =P 环
c)等容过程:V 始 =V 终
d)等温等压过程:a,b 二者都具备
e)绝热过程:体系与环境之间没有热量传 递,只有功的传递 f)循环过程:体系由一始态出发,经一系列 变化过程又回到原来的状态
b. 人造金刚石: C(石墨)→C(金刚石) 由热力学知道 P>15000P° 时,才有可能; 今天已实现了这个转变(60000P°,1000℃, 催化剂)
二. 热力学研究方法的特点和局限性
3
1. 热力学方法的特点
研究大量粒子的宏观体系的宏观性质之间的 关系及变化规律,
不考虑微观粒子的微观结构
不涉及反应的速度和机理
4
2. 优点和局限性
1)热力学只研究体系的始终态 根据始终态的性质而得到可靠的结果;不 考虑变化中的细节;不考虑物质内部的结构 因素
2)不考虑时间因素
3)不考虑粒子的个别行为
5
热力学常用术语 1、体系与环境
体系(System) 简单而言,体系即研究之对象 。也就是为了研究问题的方便 ,我们常常用一个真实或想象 的界面把一部分物质或空间与 其余分开,这种被划定的研究 对象称为体系,亦称为物系或 环境( 系统。surroundings) 与体系密切相关、影响所 及的那部分物质或空间称为环 境。
热力学基础

冰-水的相变潜热为335kJ·kg-1,而水的显热吸收 仅为4kJ·kg-1·K-1。储存相同的热量,潜热储热设 备所需的设备体积比显热储热小得多。潜热储能是 一种重要的储能方式。
如LiF的熔点为848℃,相变潜热为1300kJ·kg-1; LiH的熔点为688℃,相变潜热高达2840kJ·kg-1。
量、物质交换
(2)体系的性质与状态函数
经典热力学中把系统在任何瞬时所处的宏观物理状 况称为系统的状态,而把用来描述系统所处状态的物理 量,即系统的宏观性质称为状态参数(状态函数),又 称为热力学变量。
体系状态确定后,各性质就有完全确定的值,即性 质与(热力学平衡)状态间存在单值对应关系,性质之 中只有几个是独立的。
前言
热力学-研究各种形式的能相互转化规律 以及与此转化有关的物质性质间相互关系的科学。
热力学一般从两个方面来讨论物质进行的变 化: (1)物质的性质按指定要求发生变化时(各种 物理变化和化学变化过程),必须与外界交换多 少各种形式的能(热、功和其他形式能量之间的 相互转换及其转换过程中所遵循的规律)?
热力学是材料科学的重要基础,是理解材 料制备加工(如金属渗碳、熔化-凝固、陶瓷烧 成、聚合物合成)、相的平衡与转变、元素在 不同相之间的分布以及金属的腐蚀、氧化、材 料表面与界面性质、结构上的物理和化学有序 性以及各类晶体缺陷的形成等一系列重要现象 的的钥匙,而动力学研究有助于了解这些现象 的发展历程,深入揭示材料中的组织形成规律。
内能为状态函数,用符号U表示。它的绝对值
尚无法测定,只能求出变化值。 对于组成与质量确定的体系而言,
U f (T ,V )
§1. 2 热力学第一定律
1.2.1 表达式
• 热力学第一定律的实质就是能量守恒原理。热力学 第一定律适用于任何系统的任何过程。
如LiF的熔点为848℃,相变潜热为1300kJ·kg-1; LiH的熔点为688℃,相变潜热高达2840kJ·kg-1。
量、物质交换
(2)体系的性质与状态函数
经典热力学中把系统在任何瞬时所处的宏观物理状 况称为系统的状态,而把用来描述系统所处状态的物理 量,即系统的宏观性质称为状态参数(状态函数),又 称为热力学变量。
体系状态确定后,各性质就有完全确定的值,即性 质与(热力学平衡)状态间存在单值对应关系,性质之 中只有几个是独立的。
前言
热力学-研究各种形式的能相互转化规律 以及与此转化有关的物质性质间相互关系的科学。
热力学一般从两个方面来讨论物质进行的变 化: (1)物质的性质按指定要求发生变化时(各种 物理变化和化学变化过程),必须与外界交换多 少各种形式的能(热、功和其他形式能量之间的 相互转换及其转换过程中所遵循的规律)?
热力学是材料科学的重要基础,是理解材 料制备加工(如金属渗碳、熔化-凝固、陶瓷烧 成、聚合物合成)、相的平衡与转变、元素在 不同相之间的分布以及金属的腐蚀、氧化、材 料表面与界面性质、结构上的物理和化学有序 性以及各类晶体缺陷的形成等一系列重要现象 的的钥匙,而动力学研究有助于了解这些现象 的发展历程,深入揭示材料中的组织形成规律。
内能为状态函数,用符号U表示。它的绝对值
尚无法测定,只能求出变化值。 对于组成与质量确定的体系而言,
U f (T ,V )
§1. 2 热力学第一定律
1.2.1 表达式
• 热力学第一定律的实质就是能量守恒原理。热力学 第一定律适用于任何系统的任何过程。
热力学统计物理第一章讲解

T
p
知道物态方程,可以导出体胀系数和等温压缩系数(见习题);
反过来,知道体胀系数和等温压缩系数,可以导出物态方程, (见习题)。
4. 物态方程举例
(1)理想气体的物态方程:
(2)实际气体
范氏方程(Van der Waals Equation):
(
p
an2 V2
)(V
nb)
nRT
昂尼斯方程
等压过程: W pV
§1.2 热力学第一定律
一、热力学第一定律提出的实验根据 实验根据是焦耳热功当量实验(见书P25图1.9和图1.10)
无论经历何种过程,使水温升高同样的温度,做 的功一样多。表明:绝热过程中外界对系统做功与方 式(或过程)无关。
二、内能的定义
宏观定义:内能U是一个态函数(状态量),它满足:
•热力学第二定律的开尔文表述( 1851): 不可能从单一热源吸热使之完全变成有用功而不引 起其它变化。
开氏表述指明功变热的过程是不可逆的。
开尔文(W. Thomson,1824-1907),原名汤姆 孙,英国物理学家,热力学的奠基人之一。1851 年表述了热力学第二定律。他在热力学、电磁学、 波动和涡流等方面卓有贡献,1892年被授予开尔 文爵士称号。他在1848年引入并在1854年修改的 温标称为开尔文温标。为了纪念他,国际单位制 中的温度的单位用“开尔文”命名。
N d AB NA d B
dt
dt
安培定律给出了磁介质中的磁场强度H 为:
H l NI
dW
NA
dB dt
l N
H
dt
AlH dB
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
U T T (S ,V ) S V
f ( p, V, T ) = 0
U p p( S , V ) V S
联立上两式,消去S,得状态方程:
再由定义:
H = U + pV = U + V (∂U/∂V )S = H ( S, V )
A = U – TS = U – S (∂U/∂S )V = A ( S, V ) G = H – TS = H – V (∂U/∂V )S = G ( S, V ) 热容CV也可用V,S 的函数表示:
U U S CV ( )V ( )V ( )V T S T U U ( )V ( )V S S CV ( S ,V ) T U ( )V ( ( )V )V S S S
对非理想气体,如服从 pV = nRT + nbp 的气体的等温过程
S
p2
p1
V p2 ( ) p dp nRT ln T p1
3 热容与 p、V 的关系
H H ( )T { ( ) p} { ( )T } p p T T p
C p
V { (V T ( ) p )} T T 2 V V V ( )p T( 2 )p ( )p T T T
H G V p p S T
(12-5)
(12-6)
(12-7)
A G S T V T p
式(12-7)不难得到等温过程中ΔG = ∫Vdp 。
(12-8)
这四组关系式可对系统的变化作定性讨论和定量计算。如从
F F Z ( )Y ( )Y ( )Y X Z X F F F Z ( )Y ( ) Z ( ) X ( )Y X X Z X
F = F ( X, Z (X,Y ) )
1 热力学状态方程 由dU = TdS - pdV 定温下, dUT = TdST - pdVT 等式两边除以dVT 即
2. 7. 2 麦克斯韦关系式
若Z=f (x,y),且Z有连续的二阶偏微商,则必有
Z Z x y x y y x y x
把以上结论应用于热力学基本方程有 dU=TdS-pdV dS=0 dV=0
T,
p1=100kPa
S1
p2
p1
S p dp T
ΔS2 =0
S S 3 dp p2 p T
p1
B(真实气体) 1mol T, p2→0
B(理想气体) 1mol T, p2→0
ΔS = ΔS1 + ΔS2 + ΔS3
(12-11)
S V p T p T
(12-12)
上面四个关系式称为麦克斯韦关系式 ,各式表示系统在同 一状态的两种变化率数值相等。因此应用于某种场合等式右左可 以代换。常用的是式(12-11)及式(12-12) ,这两等式右边的变 化率是可以由实验直接测定的,而左边则不能。可用等式右边的
变化率代替左边的变化率。
例1 试求标准摩尔熵中对气体的修正值。 解:气体的标准摩尔熵是温度为T,压力为p⊝ 下且具有理想气 体行为的摩尔熵 Smy(B,相态,T ) ,而在T、p⊝下的真实气体
的摩尔熵为 Sm (B,相态,T ) ,二者之差即为修正值ΔS 。
B(真实气体) 1mol ΔS B(理想气体) 1mol T, p1=100kPa
(12-22)
式(12-21)及 (12-22)称为吉布斯 - 亥姆霍兹方程。
1. 12. 4 小结——热力学函数关系图 将四个能函数U、H、A、G 和四个共轭函数 p、V 、T 、S 排成一个图形。
-S
H
U
V
A
四边形的每个边都是由能函数和它对
应的特性变量组成。十字交叉线将两组 共轭函数连接。
对理想气体,V‒T(∂ V/∂ T )p=V – T×nR /p = 0,节流膨胀后, 系统的温度不变。
2
熵与 p, V, T 的关系 由基本方程 dH=TdS +Vdp ,在定压下同除以dT 得:
H S ( )p T( )p T T Cp S (12-15) ( )p T T CV S ( )V (12-16) T T S S dS ( ) p dT ( ) T dp 设 S = S ( p, T ),则有 T p Cp V (12-17) dS dT ( ) p dp T T CV p (12-18) dT ( )V dV 同理 S = S ( V, T ) dS T T
则δWr=-pdV,δQr =T d S,将此关系式代入热力学第一定 律的表达式dU =δQr+δWr中,有
dU =T d S -pdV
(12-1)
由定义式可导出等价的另三个关系式:对 H = U + pV 两边微分 dH = dU +pdV +Vdp =T d S -pdV + pdV +Vdp
由麦克斯韦关系式得
S1
p2
p1
p2 S Vm p dp p1 T dp p T
(真实气体) (理想气体)
p1 V S m S 3 dp dp p2 p p2 T p T p1
dH = T d S +Vdp
同理: dA = -S d T - pdV dG = -S d T + Vdp 这四个关系式称为热力学基本方程。其使用条件是: 没有非体积功的均相组成不变的封闭系统。
(12-2)
(12-3) (12-4)
在这四个关系式中, U = f ( V, S ) = U ( V, S ),由全微分的性质, 得 U
p1
1. 12. 3 特性函数 对可由两个独立变量描述的均相组成不变的封闭系统,若两 个独立变量的选择适当,则可从一个已知的以这两个独立变量 为变量的状态函数的解析表达式,得到系统的全部信息。这个 热力学状态函数就称为特性函数,这两个独立变量就称为相应 特性函数的特性变量。
如 U = U ( V, S ) 是以 V, S 为特性变量的特性函数。
上两式是计算单纯 p, V, T 的熵变的基本公式。
V dS dT ( ) p dp T T
恒压 恒温
Cp
dS
对理想气体:
Cp T
T2
dT
Cp
V dS ( ) p dp T
T2 S dT nCp ,m ln T1 T T1 p2 p2 V S ( ) p dp nRT ln p1 T p1
(TS G ) T2
(12-21)
1 (G / T ) T T p
H (G / T ) T T 2
H (G / T ) T T 2
同理,有
(12-21)
U ( A / T ) T T 2
(12-13)
同理,由dH=TdS+Vdp,并用麦克斯韦方程
H p
V T T V p T
(12-14)
式(12-13), (12-14 )称为热力学状态方程。由此式不难计算单纯 p,V,T 变化时的ΔU 和ΔH。 U = f ( T, V )
因热容恒大于零, μJ-T = (∂T / ∂p)H 的值取决于V ‒ T (∂ V/∂ T )p的
正负,若气体的物态方程已知,则不难得出。 V ‒ T (∂ V/∂ T )p < 0, μJ-T > 0,p↓,T ↓ ;
V ‒ T (∂ V/∂ T )p > 0, μJ-T < 0, p↓,T ↑ 。
U ( )S p V
V一定时对S 微分
U ( )V T S
S 一定时对V 微分 (12-9)
p T ( )V = ( ) S S V
同理可得另三个关系式: T V p S p S
(12-10)
S p V T T V
可以证明: H = H ( p, S ), A = A ( T, V ),G = G ( T, p ) 都 是特性函数。
1. 12. 4 其它重要的关系式 热力学函数关系的推导证明过程中,常用到下面三个数学公式: f ( X, Y, Z ) = 0
▲倒易关系
▲循环关系
▲复合函数 导数关系
X 1 ( )Z Y Y ( )Z X X Y Z ( ) Z ( ) X ( ) Y 1 Y Z X
dU T dST T p dVT dVT
U S T p V T V T
由麦克斯韦方程
S p V T T V
U p T p V T T V
1.12 热力学函数关系式
热力学函数之间的关系如下 H = U + pV U H pV A
A = U – TS
TS
pV
G=H–TS TS G 其中U、H、A、G与能量的量纲 相同,单位是J;称为能函数。 p、V 和T、S总是成对出现,称为共轭函数。乘积的单位是J。 1. 12. 1 热力学基本方程
在封闭系统中发生一微小可逆变化,若过程的δWr ′=0,
p1
V [V T ( ) p ]dp T
(12-16)
例:试讨论节流膨胀后系统的温度变化。 在节流过程中,ΔH = 0, μJ-T = (∂T / ∂p)H,利用循环关系,得
T ( )H p
H V ( )T V T( )p p T H Cp ( )p T
