82AHP决策分析方法应用实例
AHP方法简介与应用举例

也是被比较元素指标,而表格中得数字就是用1-9比例标度进行判断后得数
值。如表2:
表2
判断矩阵
上层指标N 受支配指标a1 受支配指标a2 受支配指标a3
受支配指标a1 1 相应倒数 相应倒数
受支配指标a2 判断值 1 相应倒数
受支配指标a3 判断值 判断值 1
权重 排序值 排序值 排序值
决策者只需做n*(n-1)/2个判断,比如表2,含有三个被比较指标,则可进行3*(31)/2=3次判断。
第八页,共17页。
第一步 建立层次分析模型
C6 研究周期 C5 C4
C3
C2
C1
合理选择科研课题A
科研成果贡献B1
人才培养B2
经
科
优
济
学
势
价
意
发
值
义
挥
待选课题1
待选课题2
课题可行性B3
难
财
易
政
程
支
度
持
待选课题3
第九页,共17页。
第二步 进行两两比较判断
相对于总目标“合理选择科研课题”,各选择准则相对比较 可以建立如下判断矩阵:
表5-1
标度 1 3 5 7 9 2,4,6,8 倒数
1-9比例标度(最常用)
含义 两个元素同样重要 前者比后者稍微重要 前者比后者明显重要 前者比后者强烈重要 前者比后者极端重要 相邻判断的中间值 反过来比的值
第五页,共17页。
关于第二步-续
所谓判断矩阵就是指建立一个表格,它的第一行是被比较元素指标,第一列
第三页,共17页。
这些元素又按其属 性分成若干组,形 成不同层次。同一 层次的元素作为准 则对下一层次的某 些元素起支配作用, 同时它又受上一层 次元素的支配。这 些层次大体上可以 分为3类:目标层、 准则层和方案层。
层次分析法(AHP)实例介绍 [

层次分析法(AHP)简介Analytical Hierarchy Process层次分析法(AHP)简介⏹美国运筹学家Thomas Saaty⏹70年代末提出⏹定性与定量相结合⏹多目标(Multi-attribute)决策方法AHP Analytical Hierarchy ProcessAHP=Analytical Hierarchy ProcessLean-Six SigmaAHP在我国80年代以后的应用概况•AHP的出现与应用为了测定对象系统的属性,并将这些属性变为客观的定量的计为了测定对象系统的属性并将这些属性变为客观的定量的计值或者主观效用的行为,即对目标系统进行评价,故先后出现了很多不同的评价分析方法,包括专家评价法、经济分析法以及运筹学和其他数学方法。
AHP法属于应用数学方法的一类在实践中筹学和其他数学方法法属于应用数学方法的类在实践中得到广泛应用。
•AHP在我国的研究与应用年代以来,我国的很多领域都先后使用了AHP进行评价与决80年代以来我国的很多领域都先后使用了策。
Lean-Six Sigma一、自然界油资1989石油资源1989环境污染治理方案二、科学技术1988军械系统软科学成果评定1989产业科技水平1989地区科技综合实力1989专科项目的邻选和评价1989科技规划决策1989中科院青年研究基金评审1989农业科技成果评定Lean-Six Sigma三、教育评估教学质1988评估教学质量1989后勤院校教学质量1989大学生综合素质1989毕业生质量1989高校基金分配四、人工制造系统1981987武器系统1987反坦克导弹武器系统方案1989柔性结构系统设计1989择优水利工程开发方案综合评价1989采矿方法可行方案综合评价Lean-Six Sigma五、人和社会系统1987领导能力考评1988专业技术人员评价1989人事管理制度制定1989开放实验室(中科院)1989科协和学会(中国科协)1989工业企业经济效益1989中小企业经济效益1989青海省南州畜牧业发展状况评价Lean-Six SigmaAHP分析基本过程⏹把复杂问题分解成各个组成元素⏹按支配关系将这些元素分组﹑分层(方案层,准则层)按支配关系将这些元素分组分层(方案层准则层)⏹通过两两比较方式判断各层次中诸元素的重要性⏹综合这些判断计算单准则排序和层次总排序⏹确定诸元素在决策中的权重Lean-Six SigmaAHP法(层次分析法)最优化设施布局目标层方案一1.空间利用率方案二方案层•确定各准则的权重2.物流强度3.搬运距离准则层4.扩充弹性1 1/5 1/7 1/3比较矩阵权重0.0571.空间利用率(1)物流强度() 5 1 1/337 3 1 53 1/3 1/510.2630.55801222.物流强度(5)3.搬运距离(7)4Lean-Six Sigma0.1224.扩充弹性(3)•一致性检验算得CI= 0.04查表得RI=0.90 CR=0.04/0.90=0.044 < 0.1通过一致性检验•水平分值方案比较矩阵0857012501670250 1 61/6 11 1/77 11 1/55 11 1/33 1比较矩阵扩充弹性搬运距离物流强度空间利用率准则方案一水平分值0.8570.1430.1250.8750.1670.8330.2500.750水平分值方案方案二•综合分值0057综合分值扩充弹性搬运距离物流强度空间利用率准则01430875083307500.3610.8570.1250.1670.250方案一0.1220.5580.2630.057权重Lean-Six Sigma0.6390.1430.8750.8330.750方案二方案二最优解读案例目标寻求最佳的方案⏹目标:寻求最佳的方案⏹对象:方案一,方案二⏹主要考虑四个方面的问题✓空间利用率✓物流强度✓搬运距离✓扩充弹性Lean-Six Sigma解读案例布局优选方案目标层空间利物流搬运扩充准则层用率强度距离弹性方案一方案方案二方案层Lean-Six Sigma准则层元素重要性分析空间利物流搬运扩充用率强度距离弹性间利用率空间利用率物流强度搬运距离扩充弹性Lean-Six SigmaLean-Six Sigma判断矩阵构成空间利用率的重要性是物流强度的1/5空间利用率物流强度搬运距离扩充弹性空间利用率 1 1/5 1/7 1/3物流强度 5 1 1/3 37315搬运距离A 7 3 1 53 1/3 1/5 1扩充弹性Lean-Six SigmamLean-Six Sigmaj =1Lean-Six Sigmamw i =Lean-Six Sigma对于本例1 1/5 1/7 1/35 1 1/3 30.2630.057 1.0990.230TAW7 3 1 53 1/3 1/5 10.1220.558=0.4922.355Temp =¼(0.230/0.057+1.099/0.263+2.355/0.558+0.492/0.122)=4.1168=4.1168-4/(4-1)=0.0389CI 4.11684/(41)0.0389查表得RI=0.90 CR=0.04/0.90=0.044 < 0.1通过一致性检验Lean-Six Sigma通过致性检验方案层对于准则的重要性类似的得出•类似的得出2个方案对不同基准的比较矩阵1611/711/51 1/3空间利用率物流强度搬运距离扩充弹性重要方案一 1 61/6 11 1/77 11 1/55 13 1性矩阵方案二0.85701430.12508750.16708330.2500750权方案一0.1430.8750.8330.750重方案二Lean-Six Sigma结果计算•最后一步计算每个方案的优劣最后步计算每个方案的优劣方案一得分=0.057*0.25+0.263*0.167+0.558*0.125+0.122*0.857=0.361方案二得分=0.057*0.75+0.263*0.833+0.558*0.875+0.122*0.143=0.639Lean-Six Sigma案例:物流系统供货商选择的评价与决策⏹研究背景及目的⏹建模及分析过程⏹结论研究背景及目的•货物采购是物流系统一项独立并且重要的功能,供货商的工作情况对物流企业生产率、产品质量及竞争力有很大影工作情况对物流企业生产率产品质量及竞争力有很大影响,因此选择合适的供货商尤为重要。
AHP法在案例中评价应用

AHP方法在“企业科研课题的选择”评价中的应用陈作灿(工业工程1班 200941108118)摘要:本文介绍了AHP法的基本原理及操作步骤,并利用此方法对企业科研课题的选择进行了评估。
首先明确企业在选择科研课题时应该考虑的因素,然后按照AHP法的四个步骤对企业可选的5个科研课题进行评估,最后得出结论。
关键词:AHP法,基本原理,操作步骤,企业科研课题的选择。
1 问题的提出对于一个企业单位,企业科研课题的选择是组织管理的首要任务。
课题选择合适与否直接关系到企业的盈利与发展方向。
因而它是一项关键性的技术决策和管理决策。
选题必须考虑到贡献大小、人才培养、可行性和今后发展影响4个准则,与这4个准则相联系的主要因素又有:实用价值、企业优势、研究周期、经费支持。
如今企业考虑的选题方案有:设计开发新产品、研发新型生产模式、设备管理系统研究、信息管理系统研究、物流管理系统研究。
目前企业需要根据以上要考虑的因素对5个方案进行选择。
2 评价方法2.1 AHP法简介层次分析法是由美国匹兹堡大学教授T.L.Saaty在70年代中期提出的。
它的基本思想是把一个复杂的问题分解为各个组成因素,并将这些因素按支配关系分组,从而形成一个有序的递阶层次结构。
通过两两比较的方式确定层次中诸因素的相对重要性,然后综合人的判断以确定决策诸因素相对重要性的总排序。
层次分析法的出现给决策者解决那些难以定量描述的决策问题带来了极大的方便,从而使它的应用几乎涉及任何科学领域。
2.2 AHP操作步骤步骤1分析系统中各因素之间的关系,建立系统的递阶层次结构模型;步骤2对同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较判断矩阵,进行层次单排序和一致性检验;步骤3由判断矩阵计算被比较元素对该准则的相对权重;步骤4计算各层元素对系统目标的合成权重,并进行层次总排序和一致性检验。
3 企业科研课题的选择评价应用案例3.1 建立评价指标体系结构3.2 构造判断矩阵第二层中的4个准则对目标层的判断矩阵如下第三层中的4个子准则对准则层B 1的判断矩阵如下第三层中的4个子准则对准则层B2的判断矩阵如下第三层中的4个子准则对准则层B3的判断矩阵如下第三层中的4个子准则对准则层B4的判断矩阵如下第四层中的5个方案对子准则层C1的判断矩阵如下第四层中的5个方案对子准则层C 2的判断矩阵如下第四层中的5个方案对子准则层C 3的判断矩阵如下第四层中的5个方案对子准则层C 4的判断矩阵如下3.3 计算单层次判断矩阵特征值和特征向量并进行一致性检验采用AHP 软件计算,通过计算可得到判断矩阵X 的特征向量和特征根以及进行一致性检验,实验过程如下:(需附截图)表1 判断矩阵A -B 的特征向量和特征根以及进行一致性检验表3 判断矩阵B2-C的特征向量和特征根以及进行一致性检验表4 判断矩阵B3-C的特征向量和特征根以及进行一致性检验表5 判断矩阵B4-C的特征向量和特征根以及进行一致性检验表7 判断矩阵C2-P的特征向量和特征根以及进行一致性检验表8 判断矩阵C3-P的特征向量和特征根以及进行一致性检验表9 判断矩阵C4-P的特征向量和特征根以及进行一致性检验实验结果如下:(1) A-B层判断矩阵特征向量为:(0.467,0.095,0.160,0.278)T,最大特征根为:4.031,一致性检验通过;(2) B1-C层判断矩阵特征向量为:(0.530,0.277,0.115,0.078)T,最大特征根为:4.049,一致性检验通过;(3) B2-C层判断矩阵特征向量为:(0.278,0.467,0.160,0.095)T,最大特征根为:4.031,一致性检验通过;(4) B3-C层判断矩阵特征向量为:(0.088,0.157,0.483,0.272)T,最大特征根为:4.015,一致性检验通过;(5) B4-C层判断矩阵特征向量为:(0.222,0.576,0.125,0.076)T,最大特征根为:4.034,一致性检验通过;(6) C1-P层判断矩阵特征向量为:(0.383,0.203,0.088,0.123,0.203)T,最大特征根为:5.052,一致性检验通过;(7) C2-P层判断矩阵特征向量为:(0.387,0.212,0.069,0.119,0.212)T,最大特征根为:5.017,一致性检验通过;(8) C3-P层判断矩阵特征向量为:(0.097,0.284,0.053,0.383,0.183)T,最大特征根为:5.082,一致性检验通过;(9) C4-P层判断矩阵特征向量为:(0.430,0.236,0.073,0.152,0.109)T,最大特征根为:5.067,一致性检验通过;3.4 层次总排序及一致性检验企业科研课题的选择层次总排序计算如表10所示。
AHP应用实例
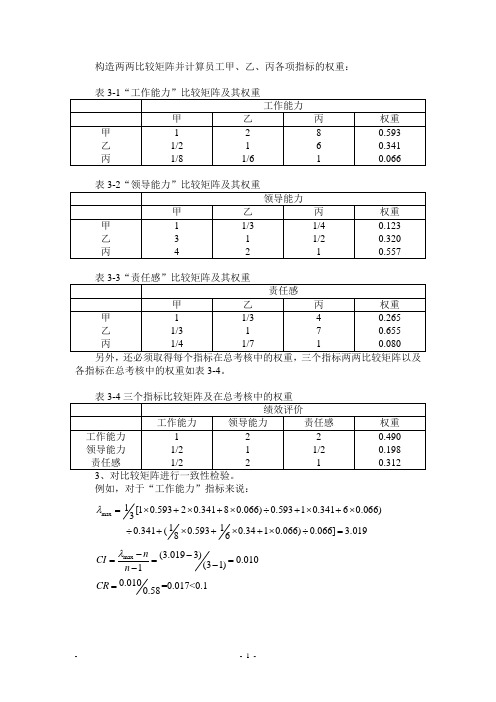
构造两两比较矩阵并计算员工甲、乙、丙各项指标的权重:各指标在总考核中的权重如表3-4。
例如,对于“工作能力”指标来说:max 1[10.59320.34180.066)0.59310.34160.066)3110.341(0.5930.3410.066)0.066] 3.01986λ=⨯+⨯+⨯÷+⨯+⨯÷+⨯+⨯+⨯÷=max (3.0193)0.010(31)1nCI n λ--===--0.0100.58CR ==0.017<0.1所以,“工作能力”比较矩阵满足一致性要求,其相应求得的权重有效。
同样,“领导能力”、“责任感”“绩效评价”两两比较矩阵都满足一致性要求,求得的权重也有效。
4、利用权数求出被考核对象的总排序。
三外指标的权重甲的总得分为0.490⨯0.593+0.198⨯0.123+0.312⨯0.25=0.398乙的总得分为0.490⨯0.341+0.198⨯0.320+0.312⨯0.655=0.435 丙的总得分为0.490⨯0.066+0.198⨯0.557+0.312⨯0.080=0.167 结果分析:由以上分析可知,员工甲、乙、丙中,乙的绩效考核得分最高,其次是甲、丙。
如果把总得分分别乘以考核人数,结果会更直观。
不仅如此,我们也可以从各项指标权重发现一些有价值的信息,如A的工作能力最强,领导能力一般;丙的工作能力最差,但其领导能力非常强。
如果领导能知人善用,发挥各人所长,将会起到事半功倍的效果。
采用AHP方法确定权重系数,可以提高权重的准确性,通过对结果逻辑性、合理性进行辨别的筛选,可以提高权重的可靠性。
同时,整个工作过程可以通过编制计算机程序完成,易于实现,这种绩效考核的方法对于激励员工,提高员工的素质有着非常重要的作用。
下面再通过一个具体实例说明层次分析的应用例2设某高新企业需要对某部门6名职工进行绩效考核与6项指标126,,...,F F F (政策、方针贯彻落实,服从工作安排,工作主动性,相关文件的上传下达,廉洁自律,精神风貌)现对考核对象进行综合评估,即要找出一线性函数112266...y w x w x w x =+++,其中,y 作为综合线性评价值,(1,2,...,6)i w i =为对应于指标(1,2,...,6)i F i =的权系数,(1,2,...,6)i x i =为待测的指标值,根据综合线性评价值,推断此考核对象的优秀、合格与否。
ahp层次分析法案例

ahp层次分析法案例AHP层次分析法是一种决策分析方法,适用于解决复杂的决策问题。
以下是一个AHP层次分析法的案例,用于决策一个公司在新市场中选择合适的产品。
某公司考虑进入新市场,希望选择一个适合的产品。
为了做出最佳决策,他们使用AHP层次分析法,按照以下步骤进行分析:1. 首先,确定决策层次结构。
公司将决策分为三个层次:目标层、准则层和备选方案层。
目标层是公司的终极目标,准则层是实现目标所需的因素,备选方案层是可以选择的不同产品。
2. 其次,制定判断矩阵。
为了做出决策,公司需要以对比方式,对准则和备选方案进行比较。
他们使用一个判断矩阵,将每个准则和备选方案两两对比,来确定它们的重要性或优劣。
假设公司选择了三个准则:市场需求、竞争力和技术实施。
他们对每个准则进行两两对比,并使用1-9的标度,表示相对重要性。
例如,市场需求对竞争力的重要性可能被评价为5,而竞争力对技术实施的重要性可能被评价为3。
3. 确定权重向量。
根据判断矩阵,公司计算每个准则的权重。
通过对矩阵的每一列进行平均化,可以计算出每个准则的权重向量。
例如,如果市场需求对竞争力的重要性为5,竞争力对技术实施的重要性为3,则市场需求的权重为5/(5+3)=0.625,竞争力的权重为3/(5+3)=0.375。
4. 计算一致性检查。
公司通过计算一致性指标(CI)和一致性比率(CR)来确定判断矩阵的一致性。
如果CI小于0.10,且CR小于0.10,则认为判断矩阵是一致的。
5. 最后,比较备选方案。
根据判断矩阵和准则的权重,公司可以计算每个备选方案的总权重。
备选方案的总权重越高,表示其相对于其他备选方案的优势越大。
根据AHP层次分析法,公司能够比较不同产品在新市场中的优势,并根据准则的权重,做出最佳选择。
通过AHP层次分析法的应用,公司能够对于复杂的决策问题进行系统化、结构化的分析,以更有根据地做出决策,提高决策的准确性和可靠性。
同时,该方法还能帮助公司更好地理解和分析决策过程中的关键因素和限制条件,以及它们之间的相互关系,从而更好地促进决策的质量和效益。
层次分析法分析(AHP)及实例教程

设定评价标准
根据问题背景和目标,设定合理的评价标准,如 成本、效益、风险等。
识别关键因素和指标
关键因素识别
分析影响决策目标的关键因素,如市 场需求、技术水平、资源条件等。
指标选取
针对每个关键因素,选取具体的评价 指标,如市场份额、创新能力、资源 利用率等。
构建递阶层次结构图
目标层
准则层
将决策目标作为最高层, 表示解决问题的总体目标。
层次分析法分析 (AHP)及实例教程
目录
• 层次分析法(AHP)概述 • 构建层次结构模型 • 构造判断矩阵与权重计算 • 实例教程:以某企业投资决策为例 • AHP优缺点及改进方向 • 总结与展望
01
层次分析法(AHP)概述
AHP定义与发展历程
定义
层次分析法(Analytic Hierarchy Process,简称AHP)是一种定性与定量相结合的、系统化、 层次化的分析方法。它通过将复杂问题分解为若干层次和因素,对各因素进行两两比较,构造 判断矩阵,进而计算各因素的权重,为决策问题提供定量依据。
对计算得到的权重进行一致性检 验,确保结果的合理性和准确性。
一致性检验与调整策略
一致性检验方法
通过计算一致性指标CI和随机一 致性指标RI,判断判断矩阵的一 致性。
调整策略
当判断矩阵不满足一致性要求时, 需要对判断矩阵进行调整,包括 调整元素值、重新构造判断矩阵 等方法,直至满足一致性要求。
注意事项
针对缺点提出改进措施
1 2
提高数据质量和数量
通过改进数据采集和处理方法,提高数据的质量 和数量,减少数据不准确和不完整对决策结果的 影响。
引入客观标准
在构建判断矩阵时,可以引入客观标准和量化指 标,减少主观判断对决策结果的影响。
层次分析法AHP、ANP与熵值法(带例子和软件操作说明)

i n max
i2
上述结论告诉我们,当判断矩阵不能保证具有完全 一致性时,相应判断矩阵的特征根也将发生变化, 这样就可以用判断矩阵特征根的变化来检验判断的 一致性程度。因此,在层次分析法中引入判断矩阵 最大特征根以外的其余特征根的负平均值,作为度 量判断矩阵偏离一致性的指标,即用:
123456789
0.00 0.00 0.58 0.90 1.12 1.24 1.32 1.41 1.45
当阶数大于2时,判断矩阵的一致性指标CI与同阶平均 随机一致性指标RI之比称为随机一致性比率CR,当 CR=CI/RI<0.10时,可以认为判断矩阵具有满意的一 致性,否则需要调整判断矩阵。
0.491 0.232
W 0.092 , max 5.126, CI 0.032, RI 1.12, CR 0.028
0.138 0.046
对于判断矩阵B2,其计算结果为:
0.550
W
0.564 0.118
,
max
CI max n
n 1
检查决策者思维的一致性。CI值越大,表明判断矩 阵偏离完全一致性的程度越大;CI值越小(接近于 0),表明判断矩阵的一致性越好。
当判断矩阵具有完全一致性时,CI=0; 当判断矩阵具有满意一致性时,需引入判断矩阵的平均
随机一致性指标RI值。对于1-9阶判断矩阵,RI值如下:
C2
0.232
C3
0.092
C4
0.138
C5
0.046
B2 0.637
0 0.055 0.564 0.118 0.263
B3 0.258 0.406 0.406 0.094 0.094
AHP决策分析方法及其应用

5
AHP决策分析法,是一种将决策者对复杂问
题的决策思维过程模型化、数量化的过程。通过
这种方法,可以将复杂问题分解为若干层次和若 干因素,在各因素之间进行简单的比较和计算, 就可以得出不同方案重要性程度的权重,从而为 决策方案的选择提供依据。
AHP决策分析法,是解决复杂的非结构化的
地理决策问题的重要方法。
主讲: 殷红春
博士 新浪微博@北洋1895
13
判断矩阵 A 中的元素具有下述性质
(i)aij 0
1 (ii)aij a ji
(iii)aii 1
但是,决策者在做估计的时候,有可能造成判断 的不一致性
aik akj aij
怎么会出现这种情况?
这时,A为正互反非一致性矩阵,怎么办?
n是判断矩阵B的特征值,且为最大特征值 W 是 B 的对应于特征值n的特征向量。
主讲: 殷红春 博士 新浪微博@北洋1895
9
上述事实告诉我们,如果有一组物体,需要知道它
们的重量,而又没有衡器,那么就可以通过两两比
较它们的相互重量,得出每一对物体重量比的判断,
从而构成判断矩阵;然后通过求解判断矩阵的最大 特征值λmax和它所对应的特征向量,就可以得出这 一组物体的相对重量。
AW=λ
max
W
T
由此得到的特征向量W= (w1, w2, …,wn) 对应评价单元的权重向量。
就作为
λmax和W的计算一般采用幂法、和法和方根法
主讲: 殷红春
博士 新浪微博@北洋1895
15
如何检验判断矩阵A是否在一致性允许的范围之内呢?
生活中的苦恼
丈夫和妻子的选择总会有不一致的地方,怎么
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(一)层次结构模型
总目标A 使甘肃省两西地区稳定解决温饱,彻
底脱贫致富,改变落后面貌。 战略目标
包括: O1 —— 改善生态环境,力争达到良性 循环; O2 —— 发展大农业生产; O3 —— 积极发展第二、三产业。
发展战略
包括:
C1 —— 移民; C2 —— 建设河西商品粮基地; C3 —— 建设中部自给粮基地; C4 —— 种树种草,大力发展林牧业; C5 —— 扩大经济作物种植面积,发展名优 农副生产基地;
(4)O3—C判断矩阵及层次单排序结果 λ=2,CI=RI=0
(5)发展战略的层次总排序结果 CI=0.059,RI=1.022,CR=0.058<0.10
(6) C1—S判断矩阵及层次单排序结果 λ=4.259,CI=0.086,RI=0.9,CR=0.096<0.10
(7)C2—S判断矩阵及层次单排序结果
S7 —— 饲料严重不足; S8 —— 人口自然增长率高。 方针措施
包括:
P1 —— 国家投入专项基金; P2 —— 省财政设立农业专项开发资金; P3 ——当地对资源实行有偿使用,以便 积累资金;
P4 —— 向国际金融机构申请贷款;
P5 —— 采取联合开发的方式,弥补 资金、技术力量的不足;
④ 计算各方针措施P1,P2,……,P19 对每个制约因素的相对权重(层次单排 序),并用各制约因素的组合权重对措施 的相应权重加权后相加,计算各方针措施 的组合权重(层次总排序),它们表示各 方针措施对实现总目标重要程度。
权重越大越重要,因此在实现总目标 的过程中,应该首先考虑实施那些权重较 大的措施。
(13)S1—P判断矩阵及层次单排序结果 λ=6.394,CI=0.079,RI=1.24,CR=0.064<0.10
O3
C1
C2
C3
C4
C5
C6
S1
S2
S3
S4
S5
S6
S7
S8
P1 P2 P3 P4 P5 P6 P7 P8 P9 P10 P11 P12 P13 P14 P15 P16 P17 P18 P19
图8.2.1 甘肃省两西地区扶贫开发战略决策分析层次结构模型
(二)模型计算
① 计算3个战略目标O1,O2,O3的相对 权重(既是层次单排序,也是层次总排序), 它们表示各战略目标对实现总目标的重要程
C6 —— 充分利用当地资源,发展多样化产 业。
制约因素
有:
S1 —— 资金不足; S2 —— 水资源不足; S3 —— 有效灌溉面积不足; S4 —— 技术力量缺乏(包括农业技术人员、工程技 术人员、科研人员、教员等);
S5 —— 交通运输条件差; S6 —— 自然条件恶劣,自然灾害频繁,水土 流失严重;
第2节 AHP决策分析方法应用实例
➢甘肃省两西地区扶贫开发战略决策定量分析 ➢兰州市主导产业选择的决策分析 ➢晋陕蒙三角地区综合开发治理战略决策分析
一、甘肃省两西地区扶贫开发 战略决策定量分析
甘肃省两西地区,旱区。
其中,中部地区,属黄土高原西部半 干旱区,资源贫乏,生态环境脆弱,植被 稀少,水土流失严重,自然灾害频繁,人 口严重超载,经济、文化落后,是一个集 中连片的区域性贫困地区。
计算结果: (1) A—O判断矩阵及单/总层次排序结果
λ=3.018,CI=0.009,RI=0.58, CR=0.015<0.10
(2)O1—C判断矩阵及层次单排序结果 λ=5.179,CI=0.045,RI=1.12,CR=0.040<0.10
(3) O2—C判断矩阵及层单排序结果 λ=6.524,CI=0.105,RI=1.24,CR=0.085<0.10
λ=4.145,CI=0.048,RI=0.9,CR=0.047<0.10
(8) C3—S判断矩阵及层次单排序结果 λ=6.290,CI=0.058,RI=1.24,CR=0.047<0.10
(9)C4—S判断矩阵及层次单排序结果 λ=5.338,CI=0.084,RI=1.12,CR=0.075<0.10
P6 —— 实施高扬程引黄提灌工程;
P7 —— 积极修建河西蓄水工程;
P8 —— 开采地下水资源;
P9 —— 发展节水农业,提高水资源 利用率;
P10 —— 开垦荒地; P11 —— 建设基本农田;
P12 —— 努力提高粮食单产; P13 —— 退耕还林、还牧; P14 ——开展科技培训、提高劳动者科技 素质;
河西走廊地区,地处西北干旱区,降水 稀少,水资源紧缺,荒漠面积广阔,沙漠化 严重,人口稀少;然而,丰富的光热资源、 发源于祁连山冰川的灌溉水源以及成片的宜 农荒地孕育了历史悠久绿洲农业,独特的自 然风光(如,七一冰川等)和丝绸古道上的 历史文化遗产(如,敦煌莫高窟等)是国内 外著名的旅游景点,我国著名的镍都——金 昌市与钢铁工业基地之一——嘉峪关市也位 于本区。
P15 —— 建立健全科技服务网络; P16 ——兴办集体企业,壮大集体经济实 力;
P17 —— 改善公路运输条件,兴建公路; P18 —— 修建铁路,提高铁路运输能力; P19 —— 抓紧抓好计划生育工作。 根据上述各因素及其之间的相互关系,可
以建立如图8.2.1所示的决策层次结构模型。
A
O1
O2
度。
② 计算每一个发展战略C1,C2,……, C6对每个战略目标的相对权重(层次单排 序),并用O1,O2,O3的权重对发展战略的 相应权重加权后相加,计算各发展战略的组
合权重(层次总排序),它们表示各发展战略 对实现总目标的重要程度。
③ 计算每个制约因素S1,S2,……,S8 对每个发展战略的相对权重(层次单排序), 并用发展战略C1,C2,……,C6的组合权重 对制约因素的相应权重加权后相加,计算各 制约因素的组合权重(层次总排序),它们表 示各制约因素对实现总目标的制约程度。
(10)C5—S判断矩阵及层次单排序结果 λ=5.314,CI=0.078,RI=1.12,CR=0.07<0.10
(11)C6—S判断矩阵及层次单排序结果 λ=3.01,CI=0.005,RI=0.58,CR=0.009<0.10
(12)制约因素的层次总排序结果 CI=0.063,RI=0.956,CR=0.066<0.10
