量子力学_习题2
量子力学课后习题答案

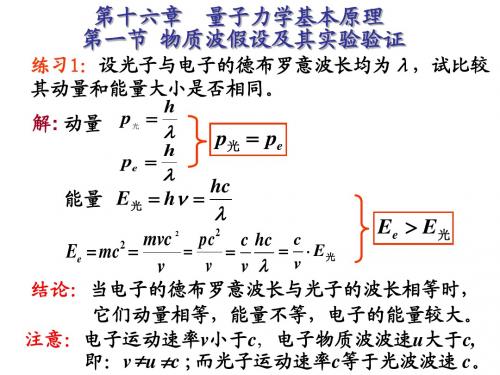
量子力学习题及解答第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv e chv d kThv v v 11833-⋅=πρ, (1)以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThc λλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ 把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
高等量子力学-习题及答案 ch02

第二章量子力学测量问题一、从不同角度,量子测量有不同分类,常见的分类有哪些。
(1)一般测量、投影测量和POVM;(2)直接测量和间接测量;(3)完全测量与不完全测量。
二、理想测量的三个基本要求是什么。
(1)当t=0,即探测体和被测系统相互作用之前,探测体制备在量子态ρp,同时量子客体制备在ρ0态。
(2)使用仪器测量之前,量子客体和探测体在t=0时开始相互作用,在t=τ>0时结束作用。
(3)此方法的第三步是,一个经典仪器及在探测体上的测量可以用冯·诺依曼投影假设的理想测量描述。
三、什么叫标准量子极限,标准量子极限可以逾越吗?其中,叫作标准量子极限。
标准量子极限可以逾越吗?答案是肯定的。
在得到这个极限时用了不确定关系,但是二者是不相同的。
标准量子极限的具体数值依赖于量子态,与如何测量有关,而不确定关系是底线。
那么,在遵守不确定性原理的前提下如何使测量精度超越标准量子极限呢?目前有两种思路:一种是以牺牲共轭量一方为代价,去求得另一方的超精度测量,这即是压缩态的思想;另一种就是量子非破坏性测量(QuantumNon-DemolitionMeasurement,QND测量)。
四、什么是量子Zeno效应,在对量子系统进行连续测量时,测量设备一般以两种不同的方式反作用于量子系统,请简单描述。
量子Zeno效应是纯量子测量效应。
理论和实验都已经表明,频繁的测量能阻止不稳定量子系统的衰变或跃迁。
极端而言,连续进行的量子测量将使不稳定的量子系统稳定地保持在其初态上,这种不稳定初态的存活概率在连续测量下将成为百分之百,这就是量子Zeno 效应。
这种在古代哲学中提到的“飞矢不动”的佯谬,在量子系统中真的可以实现。
在对量子系统进行连续测量时,测量设备一般以两种不同的方式反作用于量子系统。
其一,它可以影响被测量的可观测值的期望值的演化。
这被称为“动力学反作用”,这种影响是可以预测的。
其二,测量设备以随机的方式扰动这个可观测量,增加它们的不确定性,从而造成对期.望值的随机偏离。
量子力学(二)习题参考答案

2µ (U1 − E ) h2 2µ E h2
ψ 2 '' ( x) + k 2ψ 2 ( x ) = 0, k =
西华师大物理与电子信息学院
4
四川省精品课程——量子力学补充习题参考答案
ψ 3'' ( x) − β 2ψ 3 ( x) = 0, β =
其解分别为:
2µ (U 2 − E ) h2
ψ 1 ( x) = A1eα x + B1e −α x ψ 2 ( x) = C sin(kx + δ ) ψ 3 ( x ) = A2e β x + B2 e− β x
2
2
⑤
而透射系数
⑥
2) 、当 E<U0 时,有ψ 2 '' ( x ) − k3 2ψ 2 ( x ) = 0 , k3 = 其解为:ψ 2 ( x ) = Ce
− k3 x
+ De k3 x = Ce − k3 x (ψ 2 有限条件)
⑦
以下可以重复前面的求解过程。 不过, 为了简单我们亦可以在前面得到的结果⑤中做代 换 k2 =i k3 ,得到
由(18)式, (16) 、 (17)变成 或由 (19) 式, (16) 、 (17) 变成
(20)或(21)式就是讲义上习题 2.7 的结果。 a) 将 δ = 0 代入ψ 2 ( x) 中有:ψ 2 ( x) = C sin kx 由连续性条件:ψ 2 ( a) = ψ 3 ( a ) → C sin( ka ) = B2 e − β a
ψ m (ϕ ) =
除了 m=0 的态之外, E m 圴是二重简并的。 5、梯形式——— U ( x ) =
0, x < 0 U 0 , x > 0
量子力学2

量子力学基础
德布罗意假设:实物粒子具有波粒二象性 .
E h
p
h
2
E mc h h 德布罗意公式 h h p mv 1)若 v c 则 m m0 注意
若
v c 则 m m0
2)宏观物体的德布罗意波长小到实验难以测 量的程度,因此宏观物体仅表现出粒子性 .
理学院 黄玉
d sin k , k 1,2,3,
K=1 得 =16.5nm
德布罗意物质波理论 电子的德布罗意波长:
h p
量子力学基础
h 2meU
16.7 nm
理论值与实验结果符合的非常好!!
2 G .P .汤姆孙电子衍射实验 ( 1927年 ) 电子束透过多晶铝箔的衍射
mn 1.67 10
慢中子的德布罗意波长
理学院 黄玉
3 2 kT 3.85 10 eV 2 27
kg
24 1
p 2mn 4.5410 kg m s
h 0.146nm p
德布罗意物质波理论 11.5 德布罗意波的统计解释
量子力学基础
经典粒子 不被分割的整体,有确定位置和运动轨道 ; 经典的波 某种实际的物理量的空间分布作周期性的变 化,波具有相干叠加性 . 二象性 要求将波和粒子两种对立的属性统一到同一 物体上 . 1926 年玻恩提出 德布罗意波是概率波 . 统计解释:在某处德布罗意波的强度是与粒子在 该处邻近出现的概率成正比的 . 概率概念的哲学意义:在已知给定条件下,不 可能精确地预知结果,只能预言某些可能的结果的 概率 . 理学院 黄玉
结果表明:原子中电子速度的不确定量与速度本身的大 小可比,甚至还大。微观粒子的波粒二象性可用不确定 关系具体说明。
大学物理 第16章量子力学基本原理-例题及练习题
∴ n = 2,6,10...... 时概率密度最大
nhπ 6 × 10 = =1时 (3) n=1时: E = =1 2mL L
2 2 2 2 2 −38
A 例题3 例题3 设粒子沿 x 方向运动,其波函数为 ψ ( x ) = 方向运动, 1 + ix
( n = 1,2,3,...)
E n=4
p2 E = 2m p= nπh nh 2 mE = = a 2a
n=3 n=2 n=1
h 2a λ= = p n
二者是一致的。 二者是一致的。
( n = 1, 2, 3,...)
o a
x
例题2 粒子质量为m, 在宽度为L的一维无限 的一维无限深势 例题2 P516例1:粒子质量为m, 在宽度为 的一维无限深势 中运动,试求( 粒子在0 阱中运动,试求(1)粒子在0≤x≤L/4区间出现的概率。并 ≤ / 区间出现的概率。 求粒子处于n=1 状态的概率。 在哪些量子态上, 求粒子处于 1和n=∞状态的概率。(2)在哪些量子态上, 状态的概率 (2)在哪些量子态上 L/4处的概率密度最大?(3)求n=1时粒子的能量 补充 。 /4处的概率密度最大 (3)求 =1时粒子的能量(补充 处的概率密度最大? =1时粒子的能量 补充)。 2 nπ x 由题得: 解:(1) 由题得: 概率密度 |ψ | = sin
2 2 2 2 0
2
2
2
2
0
0
k
0
2
2
2 k
0
k
k
k
0
h ∴λ = = p
hc 2E m c + E
2 k 0
量子力学习题及答案

(7)代入(6)
csin2kk22a?dcos2k2a??kccos2k2a?
k21
kdsin2k2a
1
利用(4)、(5),得
k1k2kasin2k2a?acos2k2a??acos2k2a?2kdsin2k2a
1
a[(
k1k2k?2k)sin2k2a?2cos2k2a]?0
1?a?0
?
2
2?
??4
??0?e?4(b?x)对于区域Ⅰ,u(x)??,粒子不可能到达此区域,故?1(x)?0
而. ????2? (u0?e)
2
0?
2
?2?①
??2? (u1?e)
3
???
2
?3?0 ②
??2?e4
???
2
?
4
?0
对于束缚态来说,有?u?e?0
∴ ????k21?2?0 k22? (u0?e)
因此k1x
??1?ae ?
3
?fe
?k
1x
由波函数的连续性,有
?1(0)??2(0),?a?d(4)
?1?(0)???2
(0),?k1a?k2c (5)??(2a)??1a
3?(2a),?k2ccos2k2a?k2dsin2k2a??k?2k2
1fe(6)
?1a
2(2a)??3(2a),?csin2k2a?dcos2k2a?fe
1???k1?1?1?2?(u0?e)?????2??k22?2?0 (2) k22?2?e?2
束缚态0<e<u0 ??
??3??k2
1?3?0 (3)?1x
1?ae
?k?be
?k1x
量子力学
第二章 波函数与薛定谔方程(2)一、填空题1、一维谐振子处于其能量本征态n ψ,则其动能的平均值为__________;势能的平均值为___________________。
2、一维线性谐振子的量子数取n 的波函数为ψn (x ),其定态薛定谔方程为 ,与ψn (x )相对应的能量为 。
3、一般来说,把无限远处为零的波函数所描写的状态称为 ,体系能量最低的态称为 。
4、线性谐振子的x x dx d H αμωμ++-=22222212ˆ ,α为实数,则其能n E = 。
5、粒子处在a x ≤≤0的一维无限深势阱中,第一激发态的能量为 ,第一激发态的波函数为 。
6、基态是指 的状态,一维线性谐振子的基态波函数为 。
7、一维线性谐振子的第一激发态的能量为 、第一激发态的波函数为 。
8、t =0时体系的状态为()()()x x x 300,ψψψ+=,其中()x n ψ为一维线性谐振子的定态波函数,则()=t x ,ψ 。
9、 称为隧道效应。
答案:粒子在能量小于势垒高度时仍能贯穿势垒的现象10、 的状态称为束缚态,其能量一般为 谱。
10、处于第3激发态的线性谐振子的经典禁区为 。
二、选择题1、在一维无限深势阱U x x ax a (),,=<∞≥⎧⎨⎩022中运动的质量为μ的粒子的能级为A.πμ22224 n a B.πμ22228 n a C.πμ222216 n a D.πμ222232 n a. 2、在一维无限深势阱U x x a x a (),,=<∞≥⎧⎨⎩0中运动的质量为μ的粒子处于基态,其位置几率分布最大处是A.x =0B.x a =C.x a =-D.x a =2 3、线性谐振子的能级为A.,...)3,2,1(,21=⎪⎭⎫ ⎝⎛+n n ω . B.(),....)2,1,0(,1=+n n ω .C.,...)2,1,0(,21=⎪⎭⎫ ⎝⎛+n n ω . D.(),(,,,...)n n +=1123 ω 4、线性谐振子的能量本征方程是A.2222221[]22d x E dx μωψψμ-+= . B.[]--= 22222212μμωψψd dx x E . C.[] 22222212μμωψψd dx x E -=-. D.2222221[]22d x E dx μωψψμ+=- 5、线性谐振子的第一激发态的波函数为ψαα()exp()x N x x =-122122,其位置几率分布最大处为A.x =0B.x =±μωC.x =μωD.x =±μω.6、一维无限深势阱中,粒子任意两个相邻能级之间的间隔 A.和势阱宽度成正比 B.和势阱宽度成反比 C.和粒子质量成正比 D.随量子数n 增大而增大7、一维谐振子处于01A B ψϕϕ=+,其中A 、B 为实常数,n ϕ为谐振子的第n 个归一化本征函数,则A.122=+B AB.1)(2=+B AC.1=+B AD.B A =8、对于一维方势垒的穿透问题,关于粒子的运动,正确的是 A. 粒子在势垒中有确定的轨迹; B.粒子在势垒中有负的动能;C.粒子以一定的几率穿过势垒; D 粒子不能穿过势垒。
《量子力学》(专升本)练习题
《量子力学》练习题一一、基本概念及简答1. 简述2|(,)|x t ψ的物理意义及其实验基础。
2.简述迭加原理。
若nnnc ψψ=∑,^nnnf Fψψ=,n c 的物理意义是什么?3.三维空间中运动的粒子,其波函数的方位角(ϕ)部分 ()ϕΦ=ϕ3cos ,求zL ˆ的平均值。
4.设^^F F +=,^^G G+=A.若^^[]0,F G =,是否^F 的本征态一定是^G 的本征态,举例说明。
B.若^^[]0,F G ≠,^^,G F 是否就一定无共同本征态,举例。
C.若^^[],iC F G =,C 是常数,^^,G F 是否能有共同本征态,证明你的结论。
5、判定^x p x及^x p i 是否厄迷算符。
6、^^^[,]0G C F =≠,^^F F+=,^^G G+=,试问^F ,^G 是否必然没有共同本征态,举例说明7、已知 ,ˆˆ,B C 为厄米算符,ˆˆˆAiBC ≡也为厄米算符的条件是什么? 8、能否把,,x y z σσσ看作自旋角动量算符的矩阵表示?9、哪个实验证实了电子具有自旋,怎样证实的;为什么不能把电子自旋看成电子的机械转动? 10、对于全同性粒子说来要满足那些基本方程?全同粒子的交换算符是可以对易的吗?它们能否有共同的本征态?11. 波函数的导数是否一定要连续?举例说明。
12. 如果ˆˆAA +=,ˆˆBB +=且ˆˆˆˆ,C i A B C +⎡⎤==⎣⎦,ˆˆ,,Aa a a Bb b b == a b 和都是束缚态,则ˆˆ0.a Ca b C b == 13.什么是量子力学中的守恒量?其主要特征是什么?什么定态?定态主要特征是什么?14.已知ˆˆ[,]1αβ=,求证 1ˆˆˆˆˆn n n n αββαβ--= 15.已知 ,ˆˆ,B C 为厄米算符,则ˆˆˆAiBC ≡也为厄米算符的条件是什么? 16.若一个算符与角动量算符J ˆ的两个分量对易,则其必与J ˆ 的另一个分量对易;17.设 22,0,1,0,2x V m x x ω∞≤⎧⎪=⎨>⎪⎩当当 且已知以一维线性谐振子的能量本征值n E ,本征函数()n x ψ,及()n x ψ的宇称为()1n-。
量子力学_参考答案
∫ x cos axdx = a
2
cos ax +
x sin ax a
(7 x cos axdx =
∫
2x x2 2 cos ax + ( − ) sin ax ) a a3 a2 x c ax 2 + c + ln( a x + ax 2 + c ) 2 2 a
(a > 0)
(8)
∫
ax 2 + c dx = x c −a ax 2 + c + arcsin( x) 2 c 2 −a
在边界上,波函数应满足连续性条件,即
ψ ( x) x = − a / 2 = 0 ψ ( x) x = + a / 2 = 0
将通解代入有
− A sin
ka ka + B cos = 0 2 2 ka ka A sin + B cos = 0 2 2
由此可得
ka =0 2 ka B cos = 0 2 A sin
n = 1,3,5,L n = 2,4,6,L
mπ ⎧ ⎪ B cos b x, Ym ( y ) = ⎨ mπ ⎪ B′ sin x, b ⎩ lπ ⎧ ⎪ C cos c x, Z l ( x) = ⎨ lπ ⎪C ′ sin x, c ⎩
由波函数的连续性可知在边界上
X (− a / 2) = X (a / 2) = 0 Y (−b / 2) = Y (b / 2) = 0 Z (−c / 2) = Z (c / 2) = 0
由方程和边界条件可得
nπ ⎧ ⎪ A cos a x, X n ( x) = ⎨ nπ ⎪ A′ sin x, a ⎩
7
量子力学习题2
量子力学习题2一、选择1. 氢原子的能级为A.- 2222e n s μ.B.-μ22222e n s .C.242ne sμ -. D. -μe n s 4222 . 2. 在球坐标系下,氢原子体系在不同球壳内找到电子的几率为 A.r r R nl )(2. B.22)(r r R nl . C.rdr r R nl )(2. D.dr r r R nl 22)(. 3. 在球坐标系下,氢原子体系在不同方向上找到电子的几率为A.),(ϕθlm Y .B. 2),(ϕθlm Y . C. Ωd Y lm ),(ϕθ. D. Ωd Y lm 2),(ϕθ.4. 波函数ψ和φ是平方可积函数, 则力学量算符 F为厄密算符的定义是 A.ψφτφψτ*** F d Fd =⎰⎰. B.ψφτφψτ** ( )F d F d =⎰⎰. C.( ) **F d F d ψφτψφτ=⎰⎰. D. ***F d F d ψφτψφτ=⎰⎰.5. F和 G 是厄密算符,则 A. F G 必为厄密算符. B. F GG F-必为厄密算符. C.i F G G F ( )+必为厄密算符. D. i F G G F ( )-必为厄密算符.6. 已知算符 x x=和 p i xx =- ∂∂,则 A. x 和 p x 都是厄密算符. B. xp x 必是厄密算符.C. x p p x x x +必是厄密算符.D. x p p x x x-必是厄密算符. 7. 自由粒子的运动用平面波描写,则其能量的简并度为A.1.B. 2.C. 3.D. 4.8. 二维自由粒子波函数的归一化常数为(归到δ函数)A.1212/()/π .B.12/()π .C.1232/()/π . D.122/()π 9. 角动量Z 分量的归一化本征函数为A.12πϕe x p ()i m . B.)exp(21r k i ⋅π. C.12πϕe x p ()im . D.)exp(21r k i⋅π.10. 波函数)exp()(cos )1(),(ϕθϕθim P N Y m l lm m lm -=A. 是 L 2的本征函数,不是 L z 的本征函数.B.不是 L 2的本征函数,是 L z的本征函数.C 是 L 2、 L z 的共同本征函数. D. 即不是 L 2的本征函数,也不是 L z的本征函数. 11. 若不考虑电子的自旋,氢原子能级n=3的简并度为 A. 3. B. 6. C. 9. D. 12. 12. 氢原子能级的特点是A.相邻两能级间距随量子数的增大而增大.B.能级的绝对值随量子数的增大而增大.C.能级随量子数的增大而减小.D.相邻两能级间距随量子数的增大而减小.13. 对于氢原子体系,其径向几率分布函数为W r d r R r d r 323222()=,则其几率分布最大处对应于Bohr 原子模型中的圆轨道半径是 A.a 0. B. 40a . C. 90a . D. 160a .14. 设体系处于ψ=--123231102111RY RY 状态,则该体系的能量取值及取值几率分别为A.E E 321434,;,.B.E E 321232,;,-.C.E E 321232,;,. D.E E 323414,;,.15. 接14题,该体系的角动量的取值及相应几率分别为A.21 , .B. ,1.C.212 ,. D.212 ,. 16. 接14题,该体系的角动量Z 分量的取值及相应几率分别为A.01434,;,- .B. 01434,;, .C.01232,;, -.D. 01232,;,-- .17. 接14题,该体系的角动量Z 分量的平均值为A.14 .B. -14 .C. 34 .D. -34 .18. 接14题,该体系的能量的平均值为A.-μe s 4218 .B.-3128842μe s .C.-2925642μe s .D.-177242μe s.19. 体系处于ψ=C k xc o s 状态,则体系的动量取值为 A. k k ,-. B. k . C. - k . D.12k . 20. 接上题,体系的动量取值几率分别为A. 1,0.B. 1/2,1/2.C. 1/4,3/4/ .D. 1/3,2/3. 21. 接19题, 体系的动量平均值为A.0.B.k . C. - k . D. 12k . 22.一振子处于ψψψ=+c c 1133态中,则该振子能量取值分别为A.3252 ωω,.B. 1252 ωω,.C. 3272 ωω,.D. 1252 ωω,.23. 接上题,该振子的能量取值E E 13,的几率分别为 A.2321,c c . B.232121c c c +,232123c c c +. C.23211c c c +,23213c c c +. D. 31,c c .24. 接22题,该振子的能量平均值为A. ω 232123215321c c c c ++.B. 5 ω.C. 92 ω.D. ω 232123217321c c c c ++. 25. 对易关系[ ,()]p f x x等于(f x ()为x 的任意函数) A.i f x '().B.i f x ().C.-i f x '(). D.-i f x (). 26. 对易关系[ ,e x p ()]p i y y等于 A.)exp(iy . B. i i y e x p (). C.- e x p ()i y . D.-i i y e x p (). 27.对易关系[, ]x px 等于 A.i . B. -i . C. . D. - .28. 对易关系[, ]L yx 等于 A.i z . B. z . C.-i z . D.- z. 29. 对易关系[, ]L zy 等于 A.-i x . B. i x . C. x . D.- x. 30. 对易关系[, ]L zz 等于 A.i x. B. i y . C. i . D. 0. 31. 对易关系[, ]x py 等于 A. . B. 0. C. i . D. - .32. 对易关系[ , ]pp y z 等于 A.0. B. i x. C. i p x . D. p x . 33. 对易关系[ , ]L L x z等于 A.i L y . B. -i L y . C. L y . D. - L y . 34. 对易关系[ , ]L L z y等于A.i L x .B. -i L x .C. L x .D. - L x. 35. 对易关系[ , ]L L x2等于 A. L x. B. i L x . C. i L L z y ( )+. D. 0. 36. 对易关系[ , ]L L z 2等于A. L z. B. i L z . C. i L L x y ( )+. D. 0. 37. 对易关系[, ]L px y 等于 A.i L z . B. -i L z. C. i p z . D. -i p z . 38. 对易关系[ , ]p L z x等于 A.-i p y . B. i p y . C.-i L y . D. i L y . 39. 对易关系[ , ]L p zy 等于 A.-i p x . B. i p x . C. -i L x . D. i L x . 40. 对易式[ , ]L x y 等于A.0.B. -i z .C. i z. D. 1. 41. 对易式[ , ]F Fm n 等于(m,n 为任意正整数) A. F m n +. B. F m n -. C. 0. D. F. 42. 对易式[ , ]FG 等于 A. F G . B. G F . C. F G G F -. D. F GG F+. 43. .对易式[ ,]Fc 等于(c 为任意常数) A.cF. B. 0. C. c . D. F ˆ. 44. 算符 F 和 G 的对易关系为[ , ] F G i k=,则 F 、 G 的测不准关系是 A.( )( )∆∆F G k 2224≥. B. ( )( )∆∆F G k 2224≥. C. ( )( )∆∆F G k 2224≥. D. ( )( )∆∆F G k 2224≥.45. 已知[ , ]x p i x= ,则 x 和 p x 的测不准关系是 A.( )( )∆∆x p x222≥ . B. ( )( )∆∆x p 2224≥ . C. ( )( )∆∆x p x 222≥ . D. ( )( )∆∆x p x 2224≥ . 46. 算符 L x 和 L y 的对易关系为[ , ] L L i L x y z = ,则 L x、 L y 的测不准关系是 A.( )( ) ∆∆L L L x yz 22224≥ . B.( )( ) ∆∆L L L x y 22224≥ . C.( )( ) ∆∆F G L z 22224≥ . D.( )( ) ∆∆F GL 22224≥ . 47. 电子在库仑场中运动的能量本征方程是A.[]-∇+= 2222μψψz e r E s. B. []-∇+= 22222μψψz e r E s . C.[]-∇-= 2222μψψz e r E s. D.[]-∇-= 22222μψψz e rE s . 48. 在一维无限深势阱Ux x a x x a (),,,=<<∞≤≥⎧⎨⎩00中运动的质量μ为的粒子,其状态为 ψππ=42aa x a xs i n c o s ,则在此态中体系能量的可测值为 A.22222229,2a a μπμπ , B. πμπμ2222222 a a , , C.323222222πμπμ a a ,, D.524222222πμπμ a a , . 49. 接上题,能量可测值E 1、E 3出现的几率分别为 A. 1/4,3/4. B. 3/4,1/4. C.1/2, 1/2. D. 0,1.50. 接48题,能量的平均值为A.52222πμ a ,B.2222πμ a ,C.72222πμ a ,D.5222πμ a .51. 如果力学量算符 F 和 G 满足对易关系[ , ]FG =0, 则A. F和 G 一定存在共同本征函数,且在任何态中它们所代表的力学量可同时具有确定值. B. F和 G 一定存在共同本征函数,且在它们的本征态中它们所代表的力学量可同时具有确定值.C. F和 G 不一定存在共同本征函数,且在任何态中它们所代表的力学量不可能同时具有确定值.D. F和 G 不一定存在共同本征函数,但总有那样态存在使得它们所代表的力学量可同时具有确定值.52. 氢原子的能量本征函数ψθϕθϕn l mn ll mr R r Y (,,)()(,)= A.只是体系能量算符、角动量平方算符的本征函数,不是角动量Z 分量算符的本征函数. B.只是体系能量算符、角动量Z 分量算符的本征函数,不是角动量平方算符的本征函数. C.只是体系能量算符的本征函数,不是角动量平方算符、角动量Z 分量算符的本征函数. D.是体系能量算符、角动量平方算符、角动量Z 分量算符的共同本征函数. 二、综合1. 证明厄密算符的本征值为实数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 ( )有限 由波函数的有限性有 3 ( )有限
1 1
A0 E 0
因此
1 Be k x
1
3 Fe k x
1
1 ( a ) 2 ( a ), Be k a C sin k2 a D cos k2 a
( a ) 2 ( a ), k1 Be k a k2C cos k2 a k2 D sin k 2 a 由波函数 1 连续性有 ( a ) ( a ), C sin k a D cos k a Fe k a 2 3 2 2
量子力学
Quantum Mechanics
习题解答
量子力学
Quantum Mechanics
第二章 波函数和薛定谔方程
2.1 证明在定态中,几率流与时间无关。
在定态下,一切力学量的本征值和相对分布是不随时间改变的 定态的波函数代入薛定谔方程中,可以将坐标与时间变量分离, 从而将波函数写成坐标的函数与时间因子的乘积
k2 cos k2 aC k2 sin k2 aD k1e k1a F 0
e k1a k1e k1a 0 0 cos k 2 a cos k 2 a e
可见 J 与 t 无关。
2.2 由下列定态波函数计算几率流密度:
(1) 1 1 ikr e r ( 2 ) 2 1 ikr e r
从所得结果说明 1 表示向外传播的球面波, 2 表示向内(即向原点) 传播的球面波。
解:J1和J2只有r分量 在球坐标中
r0 1 1 e e r r r sin
2
2
③
由于(1)、(3)方程中,由于 U ( x) ,要等式成立,必须
1( x ) 0
3( x ) 0
即粒子不能运动到势阱以外的地方去。 方程(2)可变为 令
k2 2mE 2
d 2 2 ( x ) 2mE 2 2( x ) 0 2 dx
,得
d 2 2 ( x ) 2 k 2( x ) 0 2 dx
n ( x a ), A sin a n 0, xa x a
归一化常数是
A
1 a
证: 由归一化,得
1 n
2 a 2 a 1 n n 2 dx A sin ( x a )dx A [ 1 cos ( x a )]dx a a a 2 a a 2 2
i i 1 ikr 1 ikr 1 ikr 1 ikr * * ( 1 ) J1 ( 1 1 1 1 ) [ e ( e ) e ( e )]r0 2m 2m r r r r r r i 1 1 1 1 1 1 k k [ ( 2 ik ) ( 2 ik )]r0 r r 2 0 3 2m r r r r r r mr mr
d2 ( x ) U( x ) ( x ) E ( x ) 2 2 dx
2
③
比较①、③式可知, ( x)和 ( x) 都是描写在同一势场作用下的 粒子状态波函数。由于它们描写的是同一个状态,因此 ( x)和 ( x) 之间只能相差一个常数
方程①、③可相互进行空间反演 ( x x) 得其对方
所以当势场满足 U ( x) U ( x) 时,粒子定态波函数具有确定的宇称。
2.7 一粒子在一维势阱中
U 0 0, U( x ) 0,
x a x a
运动,求束缚态( 0 E U0 )的能级所满足的方程。
解:粒子所满足的薛定谔方程为
d2 ( x ) U( x ) ( x ) E ( x ) 2 2 dx
a
( n 1, 2, 3,
a
)
由归一化条件
由
( x ) dx 1
2
得
得 A
A
2 a
2
0
n sin xdx 1 a
2
a
b
m n a sin x sin xdx mn a a 2
2( x )
2 n sin x a a
2( x )
因为 ka n k
⑦ ⑧ ⑨ 各方程 解为
2 k2 Ⅱ: 2 2 0
1 Ae k x Be k x 2 C sin k2 x D cos k 2 x
1 1
k 3 0 Ⅲ: 3
2 1
3 Ee k x Fe k x
1 1
1 Ae k x Bek x, 2 C sink2 x Dcos k2 x, 3 Ee k x Fe k x
1
( 10 ) ( 11 ) ( 12 ) ( 13 )
( a ) 3 ( a ), k2C cos k2 a k2 D sin k2 a k1 Fe k a 2
1
整理(10)-(13)式,并合并的关于系数B, C, D, F的方程组
e k1a B 0 0 sin k2 aC sin k2 aC cos k2 aD cos k2 aD 0 0 0 0 k1e k1a B k2 cos k2 aC k2 sin k2 a D 0 e k1a F
2
2 n sin x a a
En
2mE
2
得量子化的E
2
2 2
2ma
n2
( n 1,2,3,
)
对应于En 的归一化的定态波函数为
2 n i En t sin xe , 0 xa n ( x,t ) a a 0, x a, x a
2.4. 证明(2.6-14)式,即一维无限深势阱的波函数
2
a x
整理后得
Ⅰ: Ⅱ: Ⅲ: 令
k12
2
1
2 ( U0 E )
2
1 0
④
⑤ ⑥
2
3
2 E
2
2 0
3 0
2 (U 0 E )
2 2 k2
2 (U 0 E )
2 E
2
则
2 k1 1 0 Ⅰ: 1
A A 2 x 2 a 2
n A 2 a n 2 2 cos ( x a )dx A a sin ( x a ) A a a a 2 n a a
a
a
∴ 归一化常数
A
1 a
2.5 求一维谐振子处在激发态
1 ( x ) 2 xe 2 2
( x ) c ( x )
( x ) c ( x )
④乘 ⑤,得 可见, c 2 1
④ ⑤
( x ) ( x ) c 2 ( x ) ( x )
c 1
( x ) 具有偶宇称, ( x ) 具有奇宇称,
当 c 1 时, ( x ) ( x ) 当 c -1 时, ( x ) ( x )
2
在各区域的具体形式为
Ⅰ:
x0 d2 ( x ) U( x ) 1 ( x ) E 1 ( x ) 2m dx 2 1
2
① ②
Ⅱ: 0 x a
Ⅲ:
xa
d2 2 ( x ) E 2 ( x ) 2 2m dx
d2 3 ( x ) U( x ) 3 ( x ) E 3 ( x ) 2 2m dx
2
按势能 U ( x) 的形式分区域的具体形式为
d2 Ⅰ: ( x ) U0 1 ( x ) E 1 ( x ) 2 dx 2 1
2
x a
a x a
①
② ③
d2 2 ( x ) E 2 ( x ) Ⅱ: 2 2 dx
2 d Ⅲ: 3 ( x ) U0 3 ( x ) E 3 ( x ) 2 2 dx 2
证:在一维势场中运动的粒子的定态薛定谔方程为
d2 ( x ) U( x ) ( x ) E ( x ) 2 2 dx
2
①
将式中的 x以( x) 代换,得
d2 ( x ) U( x ) ( x ) E ( x ) 2 2 dx
2
②
利用
U ( x) U ( x) ,得
2 2
x
时几率最大的位置。
( x ) ( x ) 4 x 2 e 解: 1 1 2 2 3 2 x x e
2 2
2 2 2 2
x
2 2 d 1 ( x ) 2 3 [ 2 x 2 2 x 3 ]e x dx
令 d1 ( x) 0 ,得
[(1 5 2 x 2 2 4 x 4 )]e
2 2
x
d 21 ( x ) dx 2
x
1 2
4 3 1 2 0 e
可见
x
1
是所求几率最大的位置。
2.6
在一维势场中运动的粒子,势能对原点对称:
U ( x) U ( x) ,证明粒子的定态波函数具有确定的宇称。
其解为
2 ( x ) A sinkx B cos kx
2 ( 0 ) 1( 0 )
④
⑤
由波函数连续性条件,得
2 ( a ) 3( a )
确定系数A,B得
B0
⑥
A sin ka 0
A sin ka 0
A 0 sin ka 0 ka n n 2 ( x ) A sin x
