第五章 多相平衡
合集下载
第五章 多相平衡-2003版
关系：K = S – R - R’
组分数=物种数-独立化学平衡数-独立浓度关系数 例：NH4HCO3 (s) 部分分解，建立如下反应平衡： NH4HCO3 (s) = NH3(g) + H2O(g) + CO2 (g) 有 x(NH3) = x(H2O) = x(CO2 ) 则 R′= 2 K = S – R - R’ = 4 – 1 - 2 = 1
对大多数物质来说， H m 0, Vm 0;
L S L S
即：T升高，P增大。 但对水来说： H m 0, Vm 0;
L S L S
即：P增大，T降低。
定量计算：
假定相变焓和摩尔相变体积为常数。
fus H m dT dP fusVm T
p2 p1
F =K– Φ + 2
吉布斯相律
f=自由度，K=独立组分数，Φ=相数
一定条件下，f=K-Φ+1（凝固相系统或指定一个变量）
如果考虑电场、磁场，则f=K-Φ+n
或者这样推导：
S个物种，Φ个相，S个物种在每一相中均存在。
总变量数=SΦ+2
限制条件：每一相摩尔分数之和等于1，共Φ个 每一相化学势相等，共S（ Φ-1)个
但这些变量之间不是独立的 每种物质在各相中的化学势相等：
μ A α = μ A β = .... = μ A Φ ............................... μ S α = μ S β = .... = μ S Φ
共有 K （Φ-1）个 等式。
独立变量数f=变量数-限制条件
f ( K 1) 2 K ( 1) K 2
系统的自由度是一定范围内独立可变的, 若不指定它们则系统的状态就不能确定.
物理化学课件第五章 多相平衡
d ln p sub H m 2 dT RT
当温度变化不大时，subHm可看作常数
p2 sub H m 定积分: ln p1 R
1 1 T T 2 1
C-C方程
山东理工大学
25
三、固－液平衡 dp
dT
fus H m T fusVm
-----Clapeyron方程
克拉贝龙方程 克劳修斯-克拉贝龙方程
Trouton规则
山东理工大学
19
克拉贝龙方程 设某物质在一定T，p时达两相平衡： T, p平衡 相()
G=0
相()
dG()
T+dT, p+dp 平衡 所以dG()=dG()
相()
G=0
dG()
相()
当n=1mol时，即dGm()=dGm()
上式两边分别代入基本公式 dGm= – SmdT + Vmdp
山东理工大学
20
得 –Sm()dT + Vm()dp = –Sm()dT + Vm()dp
移项: [Vm()－Vm()]dp =[Sm()–Sm()]dT 整理为: dp /dT=Sm/ Vm 对于可逆相变Sm=Hm(可逆相变焓)/T
第五章 多相平衡
克 相 克 律 方 程
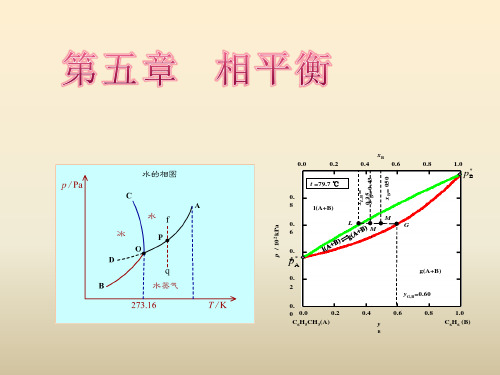
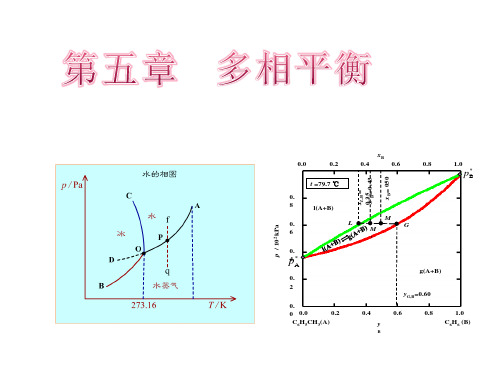
水 的 相 图
二 组 分 系 统
完 全 互 溶 双 液 系 统
部 分 互 溶 双 液 系 统
完 全 不 互 溶 双 液 系 统
低 共 熔 混 合 物
有 化 合 物 的 固 液 系 统
三 角 坐 标 图 表 示 法
习 题 课
引 言
相平衡是热力学在化学领域中的重要应用之一 研究多相系统的平衡在化学、化工的科研和生产 中有重要的意义，例如：溶解、蒸馏、重结晶、萃取、
第五章多相离子平衡.
(2) 浓度必须用体积物质的量浓度,严格说应是活度
（3）多相离子平衡系统中，必须有未溶解的固相存 o K 在,否则离子积不等于 sp 。
二、溶度积与溶解度的关系
（The Relationship of Solubility Product and Solubility）
1.溶解度 定义：在一定的温度下达到溶解平衡时，一定量 的溶剂中含有溶质的质量，定量地表明了物质的溶解性. 一般用每100克溶剂中溶解溶质的质量来表示 也可用每升溶剂中溶质的摩尔数来表示。 由于难溶电解质的溶解度很小，所以虽然是饱和溶液， 但此饱和溶液很稀，则 溶液 水 1 可以把摩尔溶解度 换算成g / 100g H2O. 2．溶解度so (mol·dm3)与 K sp 的换算
一般式：
AgCl(s):
o Ksp
An Bm (s)
nA (aq) mB (aq)
o Ksp
m
n
o mn Ksp (nS0 )n (mS0 )m nn mm S0
2 s0
Mg(OH)2(s):
s0 (2s0 ) 4
2
3 s0
例 1：已知25℃时，AgCl的溶解度为1.92103 g·dm3， 试求该温度下AgCl的溶度积。 3
BaSO 4 (s) Ba 2+ + SO 24
组成，pH改变、配合物生成等有关。 *难溶电解质的简单水合离子的浓度与其摩尔溶解度往 往不是等同的。 例如Ag3PO4的溶解度为s0: [PO3 ] s0 4
s0 [PO ] [HPO ] [H 2 PO ] [H3PO4 ] [PO ]{1
3 4 2 4 4 3 4
目的要求: 通过分析和计算掌握溶度积原理及 其应用，以及多重平衡问题。
物理化学第五章 多相平衡
f ( K 1) 2 K ( 1) K 2
F = K – Φ + 2 吉布斯相律
f=自由度，K=独立组分数，Φ=相数
一定条件下，f=K-Φ+1（凝固相系统或指定一个变量）
如果考虑电场、磁场，则f=K-Φ+n
例1 (1) 仅由 NH4Cl(s) 部分分解，建立如下反应平衡： NH4Cl (s) =NH3(g)+HCl(g) (2) 由任意量的 NH4Cl (s) 、NH3(g)、HCl(g) 建立如下反应 平衡： NH4Cl (s) =NH3(g)+HCl(g) 试求(1) 、(2)两种情况下，系统的 组分数 K=？自由度数f =? 解： (1) K = S - R - R´= 3 - 1 - 1=1 f = K - Φ + 2= 1 - 2 + 2 = 1 (2) K = S - R - R´= 3 - 1 - 0 =2 f =K-Φ+2= 2-2+2=2
xB 0.0 0.2 t =79.7 ℃ 0. 8 p / 102 kPa 0. 6 0. 4 p* 0. 2 yG,B=0.60 0. 0.2 0 0.0 C6H5CH3(A) 0.4 y
B
0.4 xL,B= 0.35 0.43 x' = xB= 050
0.6
0.8
1.0
* pB
l(A+B) L M ' M G
K=S-R=3-1=2
要注意独立二字：
C ( s) H 2O( g ) CO( g ) H 2 ( g ) C (s) C O2 (g) 2 C O(g) C O (g) H2O (g) C O2 ( g) H2 (g) (1) (2) (3)
第五章多相平衡
例5.1 Na2CO3与H2O可形成下列化合物：Na2CO3· 2O(s) ; H Na2CO3· 2O(s)； Na2CO3· 2O(s)； Na2CO3· 2O(s) 5H 7H 10H 求：（1）pθ下，与Na2CO3水溶液及冰共存的含水盐最多 有几种？ （2）30℃时，与H2O(g)平衡共存的含水盐最多有几种？ 解： 分析：C=2，含水盐多一种，则多一相，含水盐种 数最多时，其Ф最大。 （2）30℃，f' =C－ Ф +1，C =2，Ф max=C+1=2+1=3 三相中，一相为H2O(g)，另两相为Na2CO3· 2O(s)， nH 故含水盐最多可有2种。
H m T
Clapeyron(克拉贝龙)方程
讨论：（1）Clapeyron方程 适用于纯物质的 dp H m dT T Vm 任意两相平衡系统，反映了两相平衡时系统 的压力随温度的变化关系。 （2）液-气平衡或固-气平衡： β相——气相，α相——液相 或固相。 视为理想气体 RT △Vm = Vm(g)－Vm(l,s)≈ Vm(g)
2
CO + C =？R=？ S=5
2 1 2
H2O
CO 2
②
③
O2
①+②=③，故
C = S－ R － R'
（2）例：起始，容器内只有PCl5(g)，平衡时：C=？ 平衡时 S=3，R =1 c(PCl3) = c(Cl2)，R' =1 C =3-1-1=1 NaCl Na+ + Cl－ PCl5(g)
80kPa 40680J mol 1 (T2 373K) ln , 1 1 100 kPa 8.314J K mol T2 373K
第五章 多相平衡(含答案)
第五章相平衡一、选择题1、下列体系中哪一个是均相体系：( )(A)水雾和水蒸气混合在一起； (B)乳状液(C)水和被水饱和的空气 (D)两种不同的金属形成的固熔体2、克拉佩龙方程表明：( )(A)两相平衡时的平衡压力随温度而变化的变化率(B)任意状态下压力随温度的变化率(C)它适用于任何物质的两相平衡(D)以上说法都不对3、压力升高时，单组分体系的熔点将如何变化：（）(A) 升高(B) 降低(C) 不变(D) 不一定４、对于下列平衡系统：①高温下水被分解；②同①，同时通入一些H2(g) 和O2(g)；③H2 和O2同时溶于水中，其组元数K和自由度数f的值完全正确的是：（）(A) ①K = 1，f= 1 ②K = 2，f= 2 ③K = 3，f = 3 ；(B) ①K = 2，f= 2 ②K = 3，f= 3 ③K = 1，f = 1(C) ①K = 3，f= 3 ②K = 1，f= 1 ③K = 2，f = 2(D) ①K = 1，f= 2 ②K = 2，f= 3 ③K = 3，f = 3５、水可形成H2SO4·H2O(s)、H2SO4·2H2O(s)、H2SO4·4H2O(s)三种水合物,问在 101325 Pa 的压力下，能与硫酸水溶液及冰平衡共存的硫酸水合物最多可有多少种? ( )(A) 3 种(B) 2 种(C) 1 种(D) 不可能有硫酸水合物与之平衡共存６、298 K 时，蔗糖水溶液与纯水达渗透平衡时，整个体系的组分数、相数、自由度为：（）(A) C= 2，φ= 2，f*= 1 (B) C= 2，φ = 2，f*= 2 (C) C= 2，φ= 1，f*= 2 (D) C= 2，φ = 1，f*= 3７、如右图所示，当水处在三相点平衡时，若系统发生绝热膨胀，水的相态将如何变化？ ( )(A)气相、固相消失，全部变成液态；(B)气相、液相消失，全部变成固态；(C)液相消失，固相、气相共存；(D)固相消失，液相、气相共存8、对简单低共熔体系，在最低共熔点，当温度继续下降时，体系存在( )(A)一相 (B)二相 (C)一相或二相 (D)三相9、已知纯A和纯B的饱和蒸气压p A*<p B*，且A和B所组成的体系具有最高恒沸点。
第五章 多相平衡答案
（2）C = = 2, P = 3, F = = 1. （3）C = = 1, P = 2, F = 1.
（4）C = 2, P = 2, F == 2.
（5）C = 3, P = 2, F = 2.
5.2 试指出下述系统的自由度数、如 f ≠ 0,则指出变量是什么？ （1） 在标准压力下，水与水蒸气平衡 （2） 水与水蒸气平衡 （3） 在标准压力下，I2 在水中和 CCl4 中分配已达平衡，无 I2(S)存在 （4）NH3、H2、N2 三种气体已达平衡 解：（1）f＝0 体系为无变量体系 （2）f = 1 体系为单变量体系，变量是温度或压力中的任一个 （3）f = 2 体系为双组分变量，变量为温度和 I2 在水或 CCl4 中的任一个浓度。 （4）f = 3 体系为多变量体系，变量为温度、压力和某种物质浓度。 5.3 今把一批装有注射液的安培放入高压消毒锅内加热消毒，若用 151.99 kPa 的水 蒸气进行加热，问锅内的温度有多少度？（已知 ΔvapHm = 40.67 kJ/mol）
xB(l) =0.88 , yB=0.50 n(l) GK 0.8 − 0.50 n(g) = KL = 0.88 − 0.8 n(g)+n(l)=5 mol 解得：n(l)= 4.0mol；n(g)=1.0 mol
(2) t1=200 ℃时，处于液相；t3 =600 ℃时，处于气相。
5.16 水-异丁醇系统液相部分互溶。在 101.325 kPa 下， 系统的共沸点为 89.7 。气C (G)、液(L1)、液(L2)三相平衡时
（5）欲将甲醇水溶液完全分离，要采取什么步骤？ 解： （1）如图(a)所示，K 点代表的总组成 x(CH3OH)=0.33 时，系统为气、液两相平衡,
L 点为平衡液相, x(CH3OH)=0.15，G 点为平衡气相，y(CH3OH)=0.52； （2）由图(b)可知，馏出液组成 yB,1=0.52，残液组成 xB,1=0.15。经过简单蒸馏，馏
物化课件第五章-相平衡)
(4)C=3, Φ =2， f = 3– 2 + 1 = 2 (T以及I2在任一相
中的浓度)
§5.4 单组分系统的相平衡
1、Clapeyron方程 2、Clausius-Clapeyron方程
液-气平衡 固-气平衡 固-液平衡 3、单组分系统相律——水的相图
第五章 多相平衡
返回目录 退出
单组分系统的相律
若将CaCO3(s)单独放在一密闭容器中，达平衡后C=？
容器内有CaCO3(s)+CaO(s)+CO2(g)。 S=3，R=1，R’=0，C=3– 1– 0=2。 因CaO(s)和CO2(g)在两相中，没有浓度关系。
注意：系统确定后，其组分数是确定的，物种数有一定随 意性，可以随人们考虑问题的出发点不同而不同。
=RT/p (设气体为理想气体)
整理为:
vapH m RT 2
dp pdT
d ln p dT
Clausius---
Clapeyron方程
积分:
d ln p
vapH m RT 2
dT
适用于液气或固气 两相平衡
第五章 多相平衡
返回目录 退出
若温度变化不大时，vapHm为常数 d ln p
பைடு நூலகம்
第五章 多相平衡
第五章 多相平衡
返回目录 退出
例 NaCl-H2O系统
NaCl，H2O: S=2, R=0, R’=0, C=2 NaCl不饱和水溶液 S=3： Na+, Cl－, H2O, R=0, R’=1: [Na+]=[Cl－], 所以 C= 3– 1=2 NaCl饱和水溶液，有NaCl(s)存在
S=4：NaCl(s), Na+, Cl－, H2O, R=1: NaCl(s) = Na++ Cl－,
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Na2CO3H2O, Na2CO37H2O, Na2CO310H2O (1)p下,与Na2CO3(aq)和冰共存的含水盐最多有几种？ (2)30℃时，可与水蒸气共存的含水盐最多有几种？ 解：系统由Na2CO3和H2O构成, k=2 若S=5, 但存在三个平衡关系: R=3, Na2CO3+xH2O = Na2CO3.xH2O k=2
上一内容
下一内容
回主目录
返回
2013-7-31
§5.1 相律（Phase rule）
一、基本概念
1. 相
2.物种数S和组分数k ； 3. 自由度数f
二、相律：f = K – Φ + 2
上一内容 下一内容 回主目录 返回
2013-7-31
一、基本概念
1.相
定义：相（phase）是指体系内部物理和化学性 质完全均匀的部分称为相。 特点： 1）相与相之间在指定条件下 有明显的界面，在界面上宏观 性质的改变是飞跃式的。 2）体系可以是单相和多相， 相的总数称为相数，用 表 示。
回主目录
返回
2013-7-31
无化学反应体系：组分数 = 物种数（S） 有化学反应（R）体系：组分数 ≠ 物种数 如 ★ ★ H2(g)， O2(g)， H2O(g) 常温、常压下， K = 3 2000℃、常压下，2H2(g)+ O2(g) == H2和O2浓度比为2：1混合
2H2O(g)
上一内容
上一内容 下一内容 回主目录 返回
2013-7-31
基本要求
◆ 理解相律的意义、推导，掌握其应用;
◆ 掌握单组分系统、二组分气-液平衡系统和
二组分凝聚系统典型相图的分析和应用; ◆ 掌握用杠杆规则进行分析与计算; ◆ 了解由实验数据绘制简单相图的方法;
上一内容
下一内容
回主目录
返回
2013-7-31
上一内容 下一内容 回主目录 返回
2013-7-31
2 多相体系平衡的一般条件
四个平衡条件： (1)热平衡条件：设体系有Ф 个相，达到平衡时， 各相具有相同温度. T = T =……= T (2)压力平衡条件：达到平衡时各相的压力相等
P = P =……= P
(3)相平衡条件：任一物质B在各相中的化学势相等， 相变达到平衡. B = B =……=B (4) 化学平衡条件：化学变化达到平衡
2013-7-31
例2
系统中有C(s), H2O(g), CO2(g), CO(g), H2(g)共存，k=？ 答：系统中有反应： (1) C(s)+H2O(g) CO(g)+H2(g) (2) C(s)+CO2(g) 2CO(g) (3) CO(g)+H2O(g) CO2(g)+H2(g) 其中S=5， 独立化学平衡数 R3=2, k=5– 2=3 注意：系统确定后，其组分数是确定的，物种数有一 定随意性。
电中性 [Na+]+[H+]=[Cl－]+[OH－], K=6– 2–2=2
上一内容
下一内容
回主目录
返回
2013-7-31
例4 固体NaCl, KCl, NaNO3, KNO3与H2O达平衡
解：NaCl, KCl, NaNO3, KNO3, H2O : S=5, NaCl+ KNO3 = NaNO3+KCl R=1, R’=0, K= 4 或 Na+ Cl-, K+ , NO3-, H2O : S=5 电中性 [Na+]+[K+]=[Cl－]+[NO3－], R’=1 K= 5– 1= 4 或 饱和水溶液，有固体存在 NaCl, KCl, NaNO3, KNO3, Na+, Cl－, K+ , NO3-, H2O : S= 9, R=4: NaCl(s) Na++ Cl－,…… R’=1:电中性 [Na+]+[K+]=[Cl－]+[NO3－], K=9– 4 –1= 4
上一内容 下一内容 回主目录 返回
2013-7-31
例1
NH4Cl的分解，开始只有NH4Cl
NH4Cl(s)=NH3(g) + HCl(g)
k= S – R– R’ S=3 R =1 Kp= P(NH3) × P(HCl) R´=1 P(NH3)=P(HCl) k=1
上一内容 下一内容 回主目录 返回
上一内容 下一内容 回主目录 返回
2013-7-31
4.自由度（degrees of freedom）
自由度（degrees of freedom）:确定平衡体系的状 态所必须的独立变量的数目称为自由度，用字母 f 表示。强度变量通常是: T, P, c 等。 例： ① 一杯水和一桶水：
T, p, f=2，状态相同，不用确定系统的大小；
上一内容 下一内容 回主目录 返回
2013-7-31
系统确定后，其组分数是确定的
NaCl(s), Na+, Cl－, H2O ,H+ , OH－:
S=6, R=2:
NaCl(s) Na++ Cl－, H2O H+ + OH－,
R’=2: [Na+]=[Cl－], [H+]=[OH－],
② H2O(l)-H2O(g)共存系统： f=1, T,p中只有一个独立变量因 p=f(T) 。 ③NaCl(sln)：T, p, c, f=3 ④ NaCl(饱和)： T, p, f=2（浓度确定c=f(T)）
上一内容 下一内容 回主目录 返回
2013-7-31
二、 相律的推导
相律（phase rule）
上一内容 下一内容 回主目录 返回
2013-7-31
例
指出含有 CaCO3(s) 、CaO(s) 、CO2(g)的体系 与CO2(g)和N2(g)的混合物达渗透平衡时的物种数、 组分数、相数和自由度数。 答: S = 4 , R = 1, R′ = 0
CaCO3(s) = CaO(s) + CO2(g)
上一内容 下一内容 回主目录 返回
2013-7-31
例3 NaCl-H2O系统
NaCl，H2O: S=2, R=0, R’=0, K=2 NaCl不饱和水溶液 Na+, Cl－, H2O : S=3, R=0, R’=1: [Na+]=[Cl－], K= 3– 1=2 NaCl饱和水溶液，有NaCl(s)存在 NaCl(s), Na+, Cl－, H2O : S=4, R=1: NaCl(s) Na++ Cl－, R’=1: [Na+]=[Cl－], K= 4 – 1– 1=2
根据相平衡条件，每个组分在各相中的化学
势相等： i() = i() = … i(Φ) 共有(Φ–1)个等式，k个组分则共有k(Φ–1)个等式
f = Φ(K–1) + 2 – K(Φ–1) = k – Φ + 2
上一内容 下一内容 回主目录 返回
2013-7-31
几点说明
1. 推导过程假设S种物质存在于Φ相的每一 相中，若实际情况不符合仍可适用。 *2. f=K- Φ +n ( T, P, 电场………)
引 言
相平衡是热力学在 化学领域中的重要应用 之一。研究多相体系的 平衡在化学、化工的科 研和生产中有重要的意 义，例如：溶解、蒸馏、 重结晶、萃取、提纯及 金相分析等方面都要用 到相平衡的知识。
上一内容 下一内容 回主目录 返回
2013-7-31
引 言
相图（phase diagram） 表达多相体系的状态如何随 温度、压力、组成等强度性质变化而变化的图形，称 为相图。
上一内容 下一内容 回主目录 返回
2013-7-31
1) 指定p, f = 2 – + 1= 3 – , f = 0, = 3
最多为3,与Na2CO3(aq)和冰(s)与共存的
盐只有一种。 2) 指定30℃, f = 3 – , f = 0, = 3 最多为3， 与水蒸气共存的含水盐最多有2种
B B 0 B
回主目录
上一内容
下一内容
返回
2013-7-31
3. 物种数S和组分数k
物种数S：系统中所含化学物质的数量。
如：水和水蒸气, S=1
组分数k：能够表示系统组成的独立物质数。 k= S – R– R’ R： 独立的化学平衡数 R’：独立的浓度关系数
上一内容
下一内容
பைடு நூலகம்
1 2 k
上一内容
c1() c2() ck()
…… …… …… ……
返回
Φ
c1() c2() ck()
下一内容
c1(Φ) c2(Φ) ck(Φ)
2013-7-31
回主目录
推导：
每一相中有(k–1)个浓度，共有Φ个相，必须
指定Φ(k–1)个浓度.
f = Φ ( k–1) + 2
上一内容 下一内容 回主目录 返回
2013-7-31
例 说明下列平衡系统的自由度数 f =？
1)25℃，py下,与NaCl(aq)和NaCl(s)平衡共存 2)I2(s)与I2(g)平衡共存 3)开始时用任意量的HCl(g)和NH3(g)组成系统， 反应 HCl(g)+NH3(g) NH4Cl(s) 达平衡 解：1) K=2, Φ =2, 指定25℃，py, f=2–2+0=0 （饱和浓度为定值） 2) K=1, Φ =2, f = 1– 2 + 2 = 1 (p or T) 3) K=2, Φ =2(g,s),f = 2 – 2 + 2 = 2 (T, p或T，某气体浓度)
上一内容
下一内容
回主目录
返回
2013-7-31
§5.1 相律（Phase rule）
一、基本概念
1. 相
2.物种数S和组分数k ； 3. 自由度数f
二、相律：f = K – Φ + 2
上一内容 下一内容 回主目录 返回
2013-7-31
一、基本概念
1.相
定义：相（phase）是指体系内部物理和化学性 质完全均匀的部分称为相。 特点： 1）相与相之间在指定条件下 有明显的界面，在界面上宏观 性质的改变是飞跃式的。 2）体系可以是单相和多相， 相的总数称为相数，用 表 示。
回主目录
返回
2013-7-31
无化学反应体系：组分数 = 物种数（S） 有化学反应（R）体系：组分数 ≠ 物种数 如 ★ ★ H2(g)， O2(g)， H2O(g) 常温、常压下， K = 3 2000℃、常压下，2H2(g)+ O2(g) == H2和O2浓度比为2：1混合
2H2O(g)
上一内容
上一内容 下一内容 回主目录 返回
2013-7-31
基本要求
◆ 理解相律的意义、推导，掌握其应用;
◆ 掌握单组分系统、二组分气-液平衡系统和
二组分凝聚系统典型相图的分析和应用; ◆ 掌握用杠杆规则进行分析与计算; ◆ 了解由实验数据绘制简单相图的方法;
上一内容
下一内容
回主目录
返回
2013-7-31
上一内容 下一内容 回主目录 返回
2013-7-31
2 多相体系平衡的一般条件
四个平衡条件： (1)热平衡条件：设体系有Ф 个相，达到平衡时， 各相具有相同温度. T = T =……= T (2)压力平衡条件：达到平衡时各相的压力相等
P = P =……= P
(3)相平衡条件：任一物质B在各相中的化学势相等， 相变达到平衡. B = B =……=B (4) 化学平衡条件：化学变化达到平衡
2013-7-31
例2
系统中有C(s), H2O(g), CO2(g), CO(g), H2(g)共存，k=？ 答：系统中有反应： (1) C(s)+H2O(g) CO(g)+H2(g) (2) C(s)+CO2(g) 2CO(g) (3) CO(g)+H2O(g) CO2(g)+H2(g) 其中S=5， 独立化学平衡数 R3=2, k=5– 2=3 注意：系统确定后，其组分数是确定的，物种数有一 定随意性。
电中性 [Na+]+[H+]=[Cl－]+[OH－], K=6– 2–2=2
上一内容
下一内容
回主目录
返回
2013-7-31
例4 固体NaCl, KCl, NaNO3, KNO3与H2O达平衡
解：NaCl, KCl, NaNO3, KNO3, H2O : S=5, NaCl+ KNO3 = NaNO3+KCl R=1, R’=0, K= 4 或 Na+ Cl-, K+ , NO3-, H2O : S=5 电中性 [Na+]+[K+]=[Cl－]+[NO3－], R’=1 K= 5– 1= 4 或 饱和水溶液，有固体存在 NaCl, KCl, NaNO3, KNO3, Na+, Cl－, K+ , NO3-, H2O : S= 9, R=4: NaCl(s) Na++ Cl－,…… R’=1:电中性 [Na+]+[K+]=[Cl－]+[NO3－], K=9– 4 –1= 4
上一内容 下一内容 回主目录 返回
2013-7-31
例1
NH4Cl的分解，开始只有NH4Cl
NH4Cl(s)=NH3(g) + HCl(g)
k= S – R– R’ S=3 R =1 Kp= P(NH3) × P(HCl) R´=1 P(NH3)=P(HCl) k=1
上一内容 下一内容 回主目录 返回
上一内容 下一内容 回主目录 返回
2013-7-31
4.自由度（degrees of freedom）
自由度（degrees of freedom）:确定平衡体系的状 态所必须的独立变量的数目称为自由度，用字母 f 表示。强度变量通常是: T, P, c 等。 例： ① 一杯水和一桶水：
T, p, f=2，状态相同，不用确定系统的大小；
上一内容 下一内容 回主目录 返回
2013-7-31
系统确定后，其组分数是确定的
NaCl(s), Na+, Cl－, H2O ,H+ , OH－:
S=6, R=2:
NaCl(s) Na++ Cl－, H2O H+ + OH－,
R’=2: [Na+]=[Cl－], [H+]=[OH－],
② H2O(l)-H2O(g)共存系统： f=1, T,p中只有一个独立变量因 p=f(T) 。 ③NaCl(sln)：T, p, c, f=3 ④ NaCl(饱和)： T, p, f=2（浓度确定c=f(T)）
上一内容 下一内容 回主目录 返回
2013-7-31
二、 相律的推导
相律（phase rule）
上一内容 下一内容 回主目录 返回
2013-7-31
例
指出含有 CaCO3(s) 、CaO(s) 、CO2(g)的体系 与CO2(g)和N2(g)的混合物达渗透平衡时的物种数、 组分数、相数和自由度数。 答: S = 4 , R = 1, R′ = 0
CaCO3(s) = CaO(s) + CO2(g)
上一内容 下一内容 回主目录 返回
2013-7-31
例3 NaCl-H2O系统
NaCl，H2O: S=2, R=0, R’=0, K=2 NaCl不饱和水溶液 Na+, Cl－, H2O : S=3, R=0, R’=1: [Na+]=[Cl－], K= 3– 1=2 NaCl饱和水溶液，有NaCl(s)存在 NaCl(s), Na+, Cl－, H2O : S=4, R=1: NaCl(s) Na++ Cl－, R’=1: [Na+]=[Cl－], K= 4 – 1– 1=2
根据相平衡条件，每个组分在各相中的化学
势相等： i() = i() = … i(Φ) 共有(Φ–1)个等式，k个组分则共有k(Φ–1)个等式
f = Φ(K–1) + 2 – K(Φ–1) = k – Φ + 2
上一内容 下一内容 回主目录 返回
2013-7-31
几点说明
1. 推导过程假设S种物质存在于Φ相的每一 相中，若实际情况不符合仍可适用。 *2. f=K- Φ +n ( T, P, 电场………)
引 言
相平衡是热力学在 化学领域中的重要应用 之一。研究多相体系的 平衡在化学、化工的科 研和生产中有重要的意 义，例如：溶解、蒸馏、 重结晶、萃取、提纯及 金相分析等方面都要用 到相平衡的知识。
上一内容 下一内容 回主目录 返回
2013-7-31
引 言
相图（phase diagram） 表达多相体系的状态如何随 温度、压力、组成等强度性质变化而变化的图形，称 为相图。
上一内容 下一内容 回主目录 返回
2013-7-31
1) 指定p, f = 2 – + 1= 3 – , f = 0, = 3
最多为3,与Na2CO3(aq)和冰(s)与共存的
盐只有一种。 2) 指定30℃, f = 3 – , f = 0, = 3 最多为3， 与水蒸气共存的含水盐最多有2种
B B 0 B
回主目录
上一内容
下一内容
返回
2013-7-31
3. 物种数S和组分数k
物种数S：系统中所含化学物质的数量。
如：水和水蒸气, S=1
组分数k：能够表示系统组成的独立物质数。 k= S – R– R’ R： 独立的化学平衡数 R’：独立的浓度关系数
上一内容
下一内容
பைடு நூலகம்
1 2 k
上一内容
c1() c2() ck()
…… …… …… ……
返回
Φ
c1() c2() ck()
下一内容
c1(Φ) c2(Φ) ck(Φ)
2013-7-31
回主目录
推导：
每一相中有(k–1)个浓度，共有Φ个相，必须
指定Φ(k–1)个浓度.
f = Φ ( k–1) + 2
上一内容 下一内容 回主目录 返回
2013-7-31
例 说明下列平衡系统的自由度数 f =？
1)25℃，py下,与NaCl(aq)和NaCl(s)平衡共存 2)I2(s)与I2(g)平衡共存 3)开始时用任意量的HCl(g)和NH3(g)组成系统， 反应 HCl(g)+NH3(g) NH4Cl(s) 达平衡 解：1) K=2, Φ =2, 指定25℃，py, f=2–2+0=0 （饱和浓度为定值） 2) K=1, Φ =2, f = 1– 2 + 2 = 1 (p or T) 3) K=2, Φ =2(g,s),f = 2 – 2 + 2 = 2 (T, p或T，某气体浓度)