岩体强度破坏判断准则PPT课件
岩石破坏准则

2.1岩石破坏强度准则岩石的破坏主要与外荷载的作用方式、温度及湿度有关。
一般在低温、低围压及高应变率的条件下,岩石表现为脆性破坏,而在高温、高围压、低应变率作用下,岩石则表现为塑性或者塑性流动。
对于较完整的岩石来说,其破坏形式可以分为:1)脆性破坏;3)延性破坏。
图2-1给出了不同应力状态下岩石破裂前应变值、破坏形态示意图和典型的应力-应变曲线示意图。
图2-1岩石破坏形态示意图从图2-1中可以看出岩石破裂种类繁多、岩石破坏过程中的应力、变形、裂纹产生和扩展极为复杂,很难用一种模型进行描述,很多学者针对不同岩石破坏特征提出多种不同岩石的强度破坏准则。
本节主要对已有的岩石强度破坏准则进行总结,找出它们各自的优缺点。
2.1.1最大正应力强度理论最大正应力强度理论也称朗肯理论,该理论是1857年提出的。
它假定挡土墙背垂直、光滑,其后土体表面水平并无限延伸,这时土体内的任意水平面和墙的背面均为主平面(在这两个平面上的剪应力为零),作用在该平面上的法向应力即为主应力。
朗肯根据墙后主体处于极限平衡状态,应用极限平衡条件,推导出了主动土压力和被动土压力计算公式。
考察挡土墙后主体表面下深度z 处的微小单元体的应力状态变化过程。
当挡土墙在土压力的作用下向远离土体的方向位移时,作用在微分土体上的竖向应力sz 保持不变,而水平向应力sx 逐渐减小,直至达到土体处于极限平衡状态。
土体处于极限平衡状态时的最大主应力为s1=gz ,而最小主应力s3即为主动土压力强度pa 。
根据,当主体中某点处于极限平衡状态时,大主应力1σ和小主应力3σ之间应满足以下关系式:粘性土:213...2tan tan 454522c ϕϕσσ⎛⎫⎛⎫︒︒=-++ ⎪ ⎪⎝⎭⎝⎭(1)无粘性土231.tan 452ϕσσ⎛⎫︒=- ⎪⎝⎭(2)该理论认为材料破坏取决于绝对值最大的正应力。
因此,作用于岩石的三个正应力中,只要有一个主应力达到岩石的单轴抗压强度或岩石的单轴抗拉强度,岩石便被破坏。
岩石力学优秀课件

极限应力圆与抗剪强度(shear strength )直线相切的两 点D1 、D1' 表示岩石内将出现一组共轭剪切破坏裂面的临界状态。
从图中可以看出,这一组剪切破裂面上的剪应力并非是 最大剪应力(maximum shear stress )。
f 0 f n
上式中: | f |:岩石剪切面的抗剪强度(shear strength );
0 :岩石固有剪切强度(inherent shear strength ),它与粘聚力
C相当;
f n :剪切面上的摩擦阻力; n :剪切面上的正应力;
f :岩石内摩擦系数 f = tg 。
取、 为直角坐标系的横轴、纵轴,则上式为一直线
t
t
2
tg 1 c 3 2 t
这是双曲线型包络线形式下的剪切强度曲线方程。
第三节 软弱面或各向异性岩层 的破坏准则及稳定条件
岩石的破坏包括破裂(failure )和摩擦滑动(slide )两 种情况。
破裂是完整岩石中发生破坏的唯一机制。破裂的条件可以由 库 仑 准 则 给 出 。 倘 若 岩 石 中 预 先 就 存 在 着 软 弱 面 ( plane of weakness ),比如存在着断层,情况就变了,这时岩石发生破 坏的机制可能是沿断层面的摩擦滑动,也可能是穿过断层面的破 裂。究竟发生哪一种类型的破坏,要视岩石内部哪种情况首先满 足库仑准则。
图5-2 共扼剪裂面与主应力关系 图5-3 剪裂面上应力与主应力关系
三、库伦一纳维尔破坏准则的第二种表示方法
库伦一纳维尔破坏准则也可采用主应力 1 、 3 来表示,剪裂
最新岩体强度破坏判断准则专业知识讲座
仿。文档如有不当之处,请联系本人或网站删除。
屈服条件的研究历史-2(续上)
π平面
Mises (1913)
– Mises指出Tresca试验结果在π平面上得到六个 点,六个点之间的连线是直线?曲线?还是圆? Mises采用了圆形,并为金属材料试验所证实。
DruckJ e2 r a1 6 n[ d P( 1 r ag2 e)r2 (1(952 2) 3 )2 (31 )2 ] C
岩石破坏有两种基本类型:
1. 脆性破坏(格里菲斯强度理论 ),它的特点是岩 石达到破坏时不产生明显的变形,岩石的脆性 破坏是由于应力条件下岩石中裂隙的产生和发 展的结果;
2. 塑性破坏(莫尔—库仑强度理论),破坏时会产 生明显的塑性变形而不呈现明显的破坏面。塑 性破坏通常是在塑性流动状态下发生的,这是 由于组成物质颗粒间相互滑移所致。
Mises & Tresca这两种屈服条件都主要适用
于金属材料,对于岩土类介质材料一般不能很 好适用,因为岩土类材料的屈服与体积变形或 静水应力状态有关。
文档来第2源章于岩网石络的物,理文力学档性所质提供的信息仅供参考之用,不能作为科学依据,请勿模 仿。文档如有不当之处,请联系本人或网站删除。
1. 莫尔-库仑准则
库仑(C.A. Coulomb)1773年提出内摩擦准则,常称为库仑强度理论。
破坏机理:(基本思想)材料属压剪破坏,剪切破坏力的一部分用来克 服与正应力无关的粘聚力,使材料颗粒间脱离联系;另一部分剪切破坏力 用来克服与正应力成正比的摩擦力,使面内错动而最终破坏。
P
上盒
A
S
下盒
T
文档来第2源章于岩网石络的物,理文力学档性所质提供的信息仅供参考之用,不能作为科学依据,请勿模 仿。文档如有不当之处,请联系本人或网站删除。
5岩石强度与破坏 课件 [兼容模式]
![5岩石强度与破坏 课件 [兼容模式]](https://img.taocdn.com/s3/m/30b0ce5cf7ec4afe04a1df80.png)
a)直接法
试验时将这种试件两端固定在拉力机上,然后对试样施加 轴向拉力,直至试件破坏,试件的抗拉强度为:
t
P A
关键技术:①试件和夹具之间的连接;②加力P与试件同心 缺点:试样制备困难,它不易与拉力机固定,且在试样断裂 处附近往往有应力集中,同时难免在试件两端面有弯矩
B)劈裂法(巴西法),对称径向压裂法
一、莫尔判据
莫尔认为:材料在极限状态下,剪切面上的剪应力就达 到了随法向应力和材料性质而定的极限值时,发生破坏。 也就是说,当材料中一点可能滑动面上的剪应力超过该 面上的剪切强度时,该点就产生破坏,而滑动面的剪切 强度τ又是作用于该面上法向应力σ的函数。
f ( )
8
一、莫尔判据
1、抛物线型
C)点荷载试验法
是上世纪发展起来的一种简便的现场试验方法 试件:任何形状,尺寸大致5cm,不做任何加工 试验:在直接带到现场的点荷载仪上,加载劈裂 破坏。
t 2 p / Dt
式中 式中: t——试验中心的最大拉应力,抗拉强度 p ——试验中破坏时的压力 D ——试件的直径 t ——试件的厚度
三、剪切强度
1.定义:在剪切荷载作用下,岩块抵抗剪切破坏的最大剪
岩石名称 页岩 砂岩 砾岩 灰岩 千枚岩、 片岩
应力,称为剪切强度
2.类型:
1)抗剪断强度:指试件在 定的法向应力作用下,沿预定 1)抗剪断强度:指试件在一定的法向应力作用下,沿预定 剪切面剪断时的最大剪应力 2)抗切强度:指试件上的法向应力为零时,沿预定剪切面 剪断时的最大剪应力 3)摩擦强度:指试件在一定的法向应力作用下,沿已有破 裂面(层面、节理等)再次剪切破坏时的 最大剪应力。
2 n( t )
n是待定系数
3.2岩石破坏理论强度准则

五、岩石的破坏准则对岩石试样的室内及现场试验,可获得岩石试样的强度指标,但对复杂应力状态下的天然岩体,又是如何判断其破坏呢?因此,就必须建立判断岩石破坏的准则(或称强度理论)。
岩石的应力、应变增长到一定程度,岩石将发生破坏。
用来表征岩石破坏条件的函数称为岩石的破坏准则。
岩石在外力作用下常常处于复杂的应力状态,许多试验指出,岩石的强度及其在荷载作用下的性状与岩石的应力状态有着很大的关系。
在单向应力状态下表现出脆性的岩石,在三向应力状态下具有延性性质,同时它的强度极限也大大提高了。
许多部门和学者从不同角度提出不同的破坏准则,目前岩石破坏准则主要有:最大正应力理论最大正应变理论最大剪应力理论(H.Tresca)八面体应力理论莫尔理论及库伦准则格里菲思理论(Griffith)伦特堡理论(Lundborg)经验破坏准则1、最大正应力理论这是较早的一种理论,该理论认为岩石的破坏只取决于绝对值最大的正应力。
即岩石内的三个主应力中只要有一个达到单轴抗压或抗拉强度时,材料就破坏。
适用条件:单向应力状态。
对复杂应力状态不适用。
写成解析式:破坏2、最大正应变理论该理论认为岩石的破坏取决于最大正应变,即岩石内任一方向的正应变达到单向压缩或拉伸时的破坏数值时,岩石就发生破坏。
则破坏准则为式中ε——岩石内发生的最大应变值;maxε——单向拉、压时极限应变值;u这一破坏准则的解析式为(由广义虎克定律)R —R t或R c推出:实验指出,该理论与脆性材料实验值大致符合,对塑性材料不适用。
3、最大剪应力理论(H.Tresca)该理论认为岩石材料的破坏取决于最大剪应力,即当最大剪应力达到单向压缩或拉伸时的危险值时,材料达到破坏极限状态。
其破坏准则为:在复杂应力状态下,最大剪应力231 max σστ-=单位拉伸或压缩时,最大剪应力的危险值则有 R ≥-31σσ或写成 {}{}{}0)][)][)][221222232231=------R R R σσσσσσ这个理论适用于塑性岩石,不适用于脆性岩石。
岩石力学第三章岩石的力学特性及强度准则精品PPT课件

C-粘聚力
-内摩擦角
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
密度是试验指标,只有通过试验才能得到具体数值,而 孔隙度和孔隙比是计算指标。
(二)岩石的水理性质
1.吸水性:在常压条件下,岩石浸人水中充分吸 水,被吸收的水质量与干燥岩石质量之比为吸 水率—岩石的容水性(已介绍)
2.透水性:是指岩石容许水透过的能力,用渗透 系数表示(已介绍)
3.软化性:岩石浸水后强度降低的性能称软化性。 软化性用软化系数表示,它是指岩石饱和状态 下与天然风干状态下单轴抗压强度之比。
岩石名称 泥岩 泥灰岩 石灰岩 片 麻岩
石英片岩、角闪片岩 云母片岩、 绿泥石片岩 千枚岩 硅质板岩 泥质板岩 石英岩
软化系数 0.40~0.60 0.44~0.54 0.70~0.94 0.75~0.97 0.44~0.84
0.53~0.69 0.67~0.96 0.75~0.79 0.39~0.52 0.94~0.96
研究生课程:石油工程岩石力学 第三章:岩石的力学特性及强度准则
第一节:岩石的力学性质
岩浆岩、沉积岩和变质岩是岩石的成因 分类,它主要讨论岩石的结构、构造和 矿物成分等地质特性。
对于工程技术人员,更应关注的是直接 用于工程设计的岩石工程性质:岩石的 物理性质、水理性质和力学性质。
一、岩石的工程性质
常 见 岩 石 的 软 化 系 数
岩石名称 花岗岩 闪长岩 辉绿岩 流纹岩 安山岩
最新岩石的强度理论及破坏判据ppt课件

σ1 σ
莫尔包络线的具体表达式,可根据试验结果用拟合法求得。
包络线形式有:斜直线型、二次抛物线型、双曲线型等。
斜直线型与库仑准则基本一致,库仑准则是莫尔准则的一个特例。
这里主要介绍二次抛物线和双曲线型的判据表达式。
1、二次抛物线型
τ
岩性较坚硬至较弱的岩石。
2nt
2
τ=
n(σ
+σt
)
M(σ ,τ)
1
1 f2 1f 3 f2 1f 2 c
P β
3 1
1
1 2
c
1
1 2
c
0
σc / 2
σc
σ1
-σt
A
S
图7-8 σ1-σ3坐标系中的库仑准则的完整强度曲线
在此库仑准则条件下,岩石可能发生以下四种方式的破坏。
(1)当 0 0 1 1 1 12 2 时c c ,3 3 岩 石 属tt单轴拉伸破裂;
c
2c ctg 1sin
A
σ1
D
Φc O σ3 B
L
σ1 σ
1 坐标3 中库仑准则的强度曲
线,如图 6-7所示,极限应力条
件下剪切面上正应力 和剪力
用主应力可表示为:
σ1
1 tan2 c
arc( tan2 θ)
σc
121 3121 3cos2
121
3
sin2
O
σ3
图7-7 σ1-σ3坐标系的库仑准则
f
上式在 坐标系中为一条对称于 轴的 曲线,它可通过试
验方法求得,即由对应于各种应力状态(单轴拉伸、单轴压缩 及三轴压缩)下的破坏莫尔应力圆包络线,即各破坏莫尔圆的 外公切线(图7-9) ,称为莫尔强度包络线给定。
岩体强度和力学参数.ppt

mb , S, a
--岩体力学参数
GSI根据岩体所处的地质环境、岩体结构特性和表面特性来确 定。但以往在岩体结构的描述或岩体结构的形态描述中缺乏 定量化, 难以准确确定岩体的 GSI 值。为使其描述定量化 , 引入岩体质量 RMR 分级法定量确定岩体质量等级。根据 Z. T. Bieniawski研究认为 , 修正后的 RMR 指标值与 GSI 值 具有等效关系, 确定修正后的 RMR 指标值, 即得出 GSI值。 RMR 分级方法是采用多因素得分, 然后求其代数和 (RMR 值 ) 来评价岩体质量。参与评分的 6 因素 : 岩石单轴抗压强度 ; 岩石质量指标 RQD; 节理间距; 节理性状; 地下水状态; 节 理产状与巷道轴线的关系。在 1989年的修正版中, 不但对评 分标准进行了修正 , 而且对第 4项因素进行了详细分解 , 即 节理性状包括 : 节理长度 ; 间隙 ; 粗糙度 ; 充填物性质和 厚度; 风化程度。 实际应用中应在现场工程地质调查的基 础上, 进行岩体质量指标 RMR 的分析与评价 , 需结合矿区 实际, 在确定优势结构面组后 , 再根据结构面产状与巷道轴 线的关系来确定岩体 RMR 分级节理方向的修正值, 得出岩体 RMR 评分值 , 确定岩体质量等级。( 参 考 盛 佳 和 李 向 东 基 于 Hoek- Brown强度准则的岩体力学参数确定方法)
岩体强度估算的经验办法
基于岩体弹性波传播速度的经验公式 1)1970 年,日本 Ikeda 提出岩体单轴抗压强度与岩体纵波波速 2 及岩石纵波波速的关系 m
m i , V , , V cm p ci P -- 分别为岩体和岩石的单轴抗压强度与纵波波
cm V p Vi ci p
GSI指标定量化第二种确定方法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
oct
1 3
1 2 2 2 3 2 3 1 2
第2章 岩石的物理力学性质
屈服条件的研究历史
Coulumb (1773)
– 把土及岩石看成摩擦材料。
f c n tan
Tresca (1864)
– 作了一系列的挤压实验,发现金属材料在屈
2 2
R2
2 3
R2
0
最大正应变理论
max
≤
u
R E
最大剪应力理论
max ≤ u
[(1 3 )2 R2 ] [( 3 2 )2 R2 ] [( 2 1)2 R2 ] 0
八面体剪应力理论
oct ≤ S
最大应变能理论
第2章 岩石的物理力学性质
屈服条件的研究历史-4(续上)
Roscoe and Burland(1968) – 修正了子弹头形屈服面,改为椭球形屈服 面,并编入剑桥大学CRISP有限元软件, 风行欧美,成为软粘土弹塑性模型的经典 作品。
Mises & Tresca这两种屈服条件都主要适用
于金属材料,对于岩土类介质材料一般不能很 好适用,因为岩土类材料的屈服与体积变形或 静水应力状态有关。
服时,可以看到有很细的痕纹;而这些痕纹
的方向接近于最大剪应力方向。
max
1
3
2
J2 cos 0,
π
π
θσ
6
6
第2章 岩石的物理力学性质
屈服条件的研究历史-2(续上)
π平面
Mises (1913)
– Mises指出Tresca试验结果在π平面上得到六个 点,六个点之间的连线是直线?曲线?还是圆? Mises采用了圆形,并为金属材料试验所证实。
ij=
x xy xz yx y yz
zx zy z
x xz
ij = zx z
求导得到:
莫尔应力圆的表达式:
第2章 岩石的物理力学性质
+zx z
1
x
-xz
大主应力: 1 R r
σz按顺时针方向旋转α
小主应力: 3 R r
-+ --
第2章 岩石的物理力学性质
库仑公式 f c tan
c 粘聚力 内摩擦角
P A
S T
f : 抗剪强度
tg: 摩擦强度-正比于压力
c: 粘聚强度-与所受压力无关
固定滑裂面 一般应力状态如何判断是否破坏?
借助于莫尔圆
第2章 岩石的物理力学性质
极限平衡应力状态:
有一对面上的应力状态达到 = f
第2章 岩石的物理力学性质
1. 莫尔-库仑准则 库仑(C.A. Coulomb)1773年提出内摩擦准则,常称为库仑强度理论。 破坏机理:(基本思想)材料属压剪破坏,剪切破坏力的一部分用来克服 与正应力无关的粘聚力,使材料颗粒间脱离联系;另一部分剪切破坏力用 来克服与正应力成正比的摩擦力,使面内错动而最终破坏。
高等岩石力学
第七讲:岩体强度破坏判断准则
目前,人们根据岩石的不同破坏 机理,已经建立了多种强度判据。强度理 论是指人们认为在某种应力或组合应力的 作用下,岩石就会破坏,从而建立了相应 的判据。
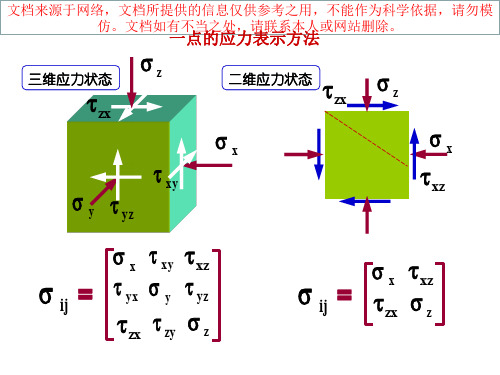
一点的应力表示方法
三维应力状态
z
zx
xy y yz
二维应力状态 zx
x
z
x
xz
σx按顺时针方向旋转α
+zx
O
-xz
r
3 x
R
2
z 1
圆心: R x z
2
半径:
r
x
2
z
2
2 xz
莫尔圆:代表一个单元的应力状态;圆周 上一点代表一个面上的两个应力与
第2章 岩石的物理力学性质
岩石破坏有两种基本类型:
1. 脆性破坏(格里菲斯强度理论 ),它的特点是岩 石达到破坏时不产生明显的变形,岩石的脆性 破坏是由于应力条件下岩石中裂隙的产生和发 展的结果;
滑动摩擦
N
T
T= N
滑动摩擦
第2章 岩石的物理力学性质
摩擦强度 tg
咬合摩擦引起的剪胀
滑动摩擦
咬合摩擦引起的剪胀
第2章 岩石的物理力学性质
摩擦强度 tg
颗粒的破碎与重排列
N T
颗粒破碎与重排列 滑动摩擦
咬合摩擦引起的剪胀
第2章 岩石的物理力学性质
凝聚强度 c
粘聚强度机理 静电引力(库仑力) 范德华力 颗粒间胶结 假粘聚力(毛细力等)
强度包线: 所有达到极限平衡状态的莫尔园的公切线。
f
第2章 岩石的物理力学性质
•强度包线以内:任何一个面
f
上的一对应力与 都没有达
到破坏包线,不破坏;
•与破坏包线相切:有一个面 上的应力达到破坏;
2. 塑性破坏(莫尔—库仑强度理论),破坏时会产 生明显的塑性变形而不呈现明显的破坏面。塑 性破坏通常是在塑性流动状态下发生的,这是 由于组成物质颗粒间相互滑移所致。
经典的强度理论:
应力理论 应变理论 能量理论
第2章 岩石的物理力学性质
最大正应力理论
2 1
R2
第2章 岩石的物理力学性质
屈服条件的研究历史-3(续上)
Drucker(1957年) – 指出岩土材料在静水压力下可以屈服,历史 上的屈服面在主应力空间是开口的,不符合 岩土材料特性,应加帽子,俗称“帽子模 型”。
Rscoe(1958-1963年) – 针对剑桥软土进行三轴及压缩试验,在e-p-q 空间中获得临界状态线,在p-q平面上得出子 弹形屈服曲线,获得了“帽子模型”的实验 证实及函数表达。
P
上盒
A
下盒
S T
第2章 岩石的物理力学性质
c tan
c 粘聚力 内摩擦角
σ = 300KPa
σ = 200KPa
σ = 100KPa ε
f : 抗剪强度
tg: 摩擦强度-正比于压力
c: 粘聚强度-与所受压力无关
第2章 岩石的物理力学性质
摩擦强度 tg
D–rucDkreurcJka2enrd和P16r[aP(grea1rge(r1首925)22先) (把 2不 考3 )2虑 (σ23影 响1)2的] CCoulomb屈服准 则与不考虑静水压力p影响的Mises屈服准则联系 在一起,提出了广义的Mises模型,后被称为D-P模 型。
