实验4-异方差性的检验和修正(更新至20131015)
实验四异方差性的检验与处理

实验四异方差性的检验与处理集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]实验四 异方差性的检验及处理(2学时)一、实验目的(1)、掌握异方差检验的基本方法; (2)、掌握异方差的处理方法。
二、实验学时:2学时 三、实验要求(1)掌握用MATLAB 软件实现异方差的检验和处理; (2)掌握异方差的检验和处理的基本步骤。
四、实验原理1、异方差检验的常用方法(1) 用X-Y 的散点图进行判断(2). 22ˆ(,)(,)e x e y 或的图形 ,),x )i i y i i ((e 或(e 的图形)(3) 等级相关系数法(又称Spearman 检验)是一种应用较广的方法,既可以用于大样本,也可与小样本。
检验的三个步骤 ① ˆt t y y=-i e②|i x i i 将e 取绝对值,并把|e 和按递增或递减次序排序,计算Spearman 系数rs ,其中:21ni i d =∑s 26r =1-n(n -1)③ 做等级相关系数的显着性检验。
n>8时,/2(2),t t n α>-反之,若||i i e x 说明与之间存在系统关系,异方差问题存在。
(4) 帕克(Park)检验帕克检验常用的函数形式:若在统计上是显着的,表明存在异方差性。
2、异方差性的处理方法: 加权最小二乘法 如果在检验过程中已经知道:222()()()i i i ji u Var u E u f x σσ===则将原模型变形为:121(i i p pi iy x x uf xβββ=+⋅++⋅+在该模型中:即满足同方差性。
于是可以用OLS估计其参数,得到关于参数12,,,pβββ的无偏、有效估计量。
五、实验举例例101i i iy x u=++若用线性模型,研究不同收入家庭的消费情况,试问原数据有无异方差性如果存在异方差性,应如何处理解:(一)编写程序如下:(1)等级相关系数法(详见文件)%%%%%%%%%%%%%%% 用等级相关系数法来检验异方差性 %%%%%%%%[data,head]=xlsread('');x=data(:,1); %提取第一列数据,即可支配收入xy=data(:,2); %提取第二列数据,即居民消费支出yplot(x,y,'k.'); % 画x和y的散点图xlabel('可支配收入x(千元)') % 对x轴加标签ylabel('居民消费支出y(千元)') % 对y轴加标签%%%%%%%% 调用regres函数进行一元线性回归 %%%%%%%%%%%%xdata=[ones(size(x,1),1),x]; %在x矩阵最左边加一列1,为线性回归做准备[b,bint,r,rint,s]=regress(y,xdata);yhat=xdata*b; %计算估计值y% 定义元胞数组,以元胞数组形式显示系数的估计值和估计值的95%置信区间head1={'系数的估计值','估计值的95%置信下限','估计值的95%置信上限'};[head1;num2cell([b,bint])]% 定义元胞数组,以元胞数组形式显示y的真实值,y的估计值,残差和残差的95%置信区间head2={'y的真实值','y的估计值','残差','残差的95%置信下限','残差的95%置信上限'};[head2;num2cell([y,yhat,r,rint])]% 定义元胞数组,以元胞数组形式显示判定系数,F统计量的观测值,检验的P值和误差方差的估计值head3={'判定系数','F统计量的观测值','检验的P值','误差方差的估计值'};[head3;num2cell(s)]%%%%%%%%%%%%% 残差分析 %%%%%%%%%%%%%%%%%%figure;rcoplot(r,rint) % 按顺序画出各组观测值对应的残差和残差的置信区间%%% 画估计值yhat与残差r的散点图figure;plot(yhat,r,'k.') % 画散点图xlabel('估计值yhat') % 对x轴加标签ylabel('残差r') % 对y轴加标签%%%%%%%%%%%% 调用corr函数计算皮尔曼等级相关系数res=abs(r); % 对残差r取绝对值[rs,p]=corr(x,res,'type','spearman')disp('其中rs为皮尔曼等级相关系数,p为p值');(2)帕克(park)检验法(详见文件)%%%%%%%%%%%%%%% 用帕克(park)检验法来检验异方差性 %%%%%%%[data,head]=xlsread(''); %导入数据x=data(:,1);y=data(:,2);%%%%%% 调用regstats函数进行一元线性回归,linear表带有常数项的线性模型,r表残差ST=regstats(y,x,'linear',{'yhat','r','standres'});scatter(x,.^2) % 画x与残差平方的散点图xlabel('可支配收入(x)') % 对x轴加标签ylabel('残差的平方') %对y轴加标签%%%%%%% 对原数据x和残差平方r^2取对数,并对log(x)和log(r^2)进行一元线性回归ST1=regstats(log(.^2),log(x),'linear',{'r','beta','tstat','fstat'})% 输出参数的估计值% 输出回归系数t检验的P值% 输出回归模型显着性检验的P值(3)加权最小二乘法(详见文件)%%%%%%%%%%% 调用robustfit函数作稳健回归 %%%%%%%%%%%%[data,head]=xlsread(''); % 导入数据x=data(:,1);y=data(:,2);% 调用robustfit函数作稳健回归,返回系数的估计值b和相关统计量stats[b,stats]=robustfit(x,y) %调用函数作稳健回归% 输出模型检验的P值%%% 绘制残差和权重的散点图 %%%%%%%plot,,'o') %绘制残差和权重的散点图xlabel('残差')ylabel('权重'(二)实验结果与分析:第一步::用OLS方法估计参数,并保留残差(1)散点图图可支配收入(x)居民消费支出(y)散点图因每个可支配收入x的值,都有5个居民消费收入y与之对应,所以上述散点图呈现此形状。
实验四异方差的检验

LOGO
w1=1/e
表一
themegallery
LOGO
w2=1/e^2
表二
themegallery
LOGO
3、分析
由表一的估计结果如下
Y i 374.89340.737423X i
(211.4532 ) (0.039238)
t = (1.772938) (18.7937)
R20.982523 R 2 =0.999889 F=989.2625
themegallery
LOGO
themegallery
LOGO
2、构造子样本区间,建立回归模型。
本题中样本容量n=20,删除中间的 1/4(20/4=5)的观测值,因为余下的观测 值要平分样本容量n1=n2=8.
LOGO
实验四
下表列出了某年中国部分省市城镇居民每 个家庭平均全年可支配收入X与消费性支出Y的 统计数据
themegallery
LOGO
themegallery
LOGO
(1)使用最小二乘法建立消费性支出与 可支配收入的线性模型;
(2)检验模型是否存在异方差; (3)如果存在异方差,是采用适当的方
themegallery
LOGO
(2)再点击 “view→Representations”,得到居 民人均消费支出与可支配收入的线性模型:
themegallery
LOGO
themegallery
LOGO
由表知参数估计线 性方程为:
Y i 2 7 2 .3 6 3 5 0 .7 5 5 1 2 5 X i
themegallery
LOGO
themegallery
异方差性的检验及处理方法

异方差性的检验及处理方法异方差性是指随着自变量变化,因变量的方差不保持恒定,即方差存在不均匀的变化趋势。
在统计分析中,如果忽视了异方差性,可能会导致误差的不准确估计,从而影响对因变量的显著性检验和参数估计结果的准确性。
为了避免异方差性给统计分析带来的影响,需要进行异方差性的检验和处理。
下面将介绍几种常用的异方差性检验及处理方法。
一、异方差性的检验方法:1.绘制残差图:绘制因变量的残差(观测值与拟合值之差)与自变量的散点图,观察残差是否随着自变量的变化而存在明显的模式。
如果残差图呈现出锥形或漏斗形状,则表明存在异方差性。
2.帕金森检验:帕金森检验是一种常用的检验异方差性的方法。
该方法的原理是通过对残差进行变换,判断变换后的残差是否与自变量相关。
3. 布罗斯-佩根检验(Breusch-Pagan test):布罗斯-佩根检验是一种常用的检验异方差性的方法。
该方法的原理是通过计算残差与自变量的相关系数,进而判断是否存在异方差性。
4. 品尼曼检验(Leve ne’s test):品尼曼检验是一种非参数的检验方法,可以用于检验不同组别的方差是否存在显著差异。
二、异方差性的处理方法:1.变量转换:通过对因变量和自变量进行变换,可以使数据满足异方差性的假设。
比如可以对因变量进行对数转换或平方根转换,对自变量进行标准化处理等。
2.使用加权最小二乘法(WLS):加权最小二乘法是一种可以处理异方差性的回归分析方法。
该方法的原理是通过对残差进行加权,使得残差的方差与自变量无关。
3.使用广义最小二乘法(GLS):广义最小二乘法是一种可以处理异方差性的回归分析方法。
该方法的原理是通过对残差进行加权,使得残差的方差可以通过自变量的一个线性组合来估计。
4.进行异方差性的鲁棒估计:鲁棒估计是一种对异常值和异方差性具有较好鲁棒性的估计方法。
通过使用鲁棒估计,可以减少异方差性对参数估计的影响。
综上所述,异方差性是统计分析中需要重视的问题。
实验四异方差性13金数2班201330110203何健华教材
图3.6
图3.7
可以看出,估计的参数与普通最小二乘法的结果相同,只是由于参数的标准差得到了修正,从而使得t检验值与普通最小二乘法的结果不同。
回归结果显示,Y变化的98.3%都可以由X的变化来解释,说明模型的拟合度较高。X在5%的显著性水平下显著,同样的F统计量的临界值为 ,说明在5%显著水平下模型的线性关系显著成立。
二、检验模型的异方差性
(1)图示检验法
生成残差平方序列。在得到图1.2中结果后,在工作文件中点击Object\Generate Series…,在弹出的窗口中,在主窗口键入命令如下e2=resid^2,得到残差平方和序列e2,如图2.1。
图1.1
设定并估计多元线性回归模型:
-----------(1-1)
点击主界面菜单Quick\Estimate Equation,在弹出的对话框中输入Y C X,点击确定即可得到回归结果,如图1.2。
图1.2
根据图1.2中的数据,得到模型(1-1)的估计结果为
-----------(1-1-1)
(1.705713)(32.3869)
上 海
11718.01
8868.19
青 海
5169.96
4185.18
新 疆
5644.86
4422.93
1、使用普通最小二乘法建立居民人均消费支出与可支配收入的线性模型;
2、检验模型是否存在异方差性;
3、如果存在异方差性,试采用适当的方法估计模型参数。
一、建立和对象,录入变量消费性支出Y、城镇居民家庭平均全年可支配收入X。如图1.1。
湖 北
5524.54
4644.5
内蒙古
5129.05
3927.75
异方差性的检验和补救
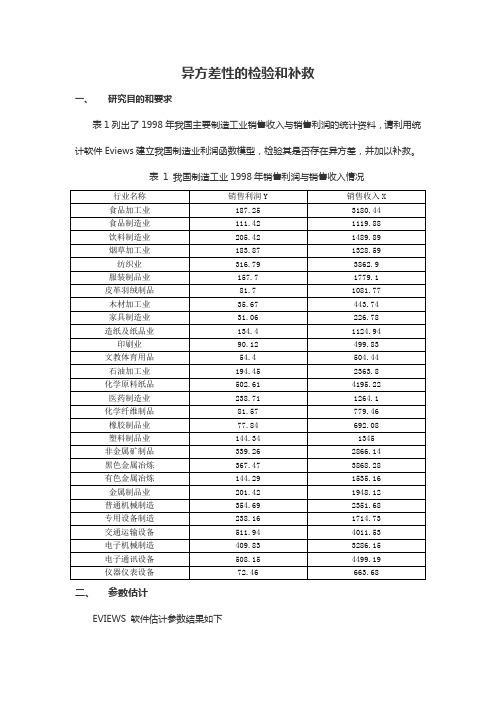
异方差性的检验和补救一、研究目的和要求表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型,检验其是否存在异方差,并加以补救。
表1 我国制造工业1998年销售利润与销售收入情况二、参数估计EVIEWS 软件估计参数结果如下Dependent Variable: Y Method: Least Squares Date: 06/01/16 Time: 20:16 Sample: 1 28Included observations: 28Variable Coefficient Std. Error t-Statistic Prob. C 12.03349 19.51809 0.616530 0.5429 X0.1043940.008442 12.366580.0000R-squared 0.854694 Mean dependent var 213.4639 Adjusted R-squared 0.849105 S.D. dependent var 146.4905 S.E. of regression 56.90455 Akaike info criterion 10.98938 Sum squared resid 84191.34 Schwarz criterion 11.08453 Log likelihood -151.8513 Hannan-Quinn criter. 11.01847 F-statistic 152.9322 Durbin-Watson stat 1.212781 Prob(F-statistic)0.000000用规范的形式将参数估计和检验结果写下2ˆ12.033490.104394(19.51809)(0.008442) =(0.616530) (12.36658)0.854694152.9322iY X t R F =+ = =三、 检验模型的异方差(一) 图形法 1. 相关关系图X YX Y 相关关系图2. 残差图形生成残差平方序列22e resid ,做2e 与解释变量 X 的散点图如下。
实验四异方差问题及其修正
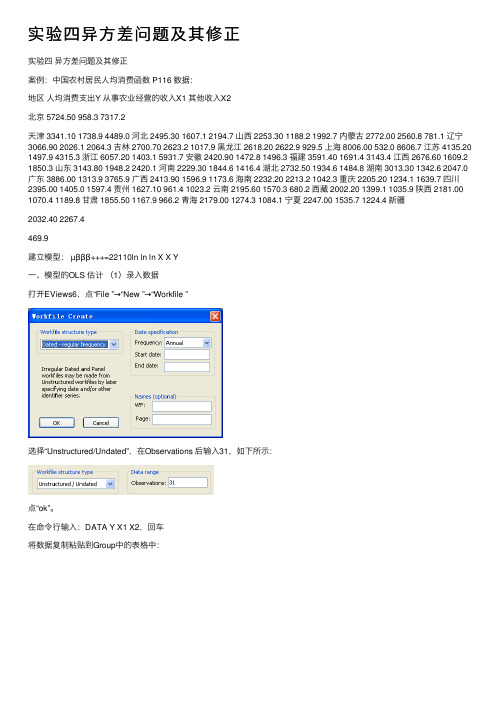
实验四异⽅差问题及其修正实验四异⽅差问题及其修正案例:中国农村居民⼈均消费函数 P116 数据:地区⼈均消费⽀出Y 从事农业经营的收⼊X1 其他收⼊X2北京 5724.50 958.3 7317.2天津 3341.10 1738.9 4489.0 河北 2495.30 1607.1 2194.7 ⼭西 2253.30 1188.2 1992.7 内蒙古 2772.00 2560.8 781.1 辽宁3066.90 2026.1 2064.3 吉林 2700.70 2623.2 1017.9 ⿊龙江 2618.20 2622.9 929.5 上海 8006.00 532.0 8606.7 江苏 4135.20 1497.9 4315.3 浙江 6057.20 1403.1 5931.7 安徽 2420.90 1472.8 1496.3 福建 3591.40 1691.4 3143.4 江西 2676.60 1609.2 1850.3 ⼭东 3143.80 1948.2 2420.1 河南 2229.30 1844.6 1416.4 湖北 2732.50 1934.6 1484.8 湖南 3013.30 1342.6 2047.0⼴东 3886.00 1313.9 3765.9 ⼴西 2413.90 1596.9 1173.6 海南 2232.20 2213.2 1042.3 重庆 2205.20 1234.1 1639.7 四川2395.00 1405.0 1597.4 贵州 1627.10 961.4 1023.2 云南 2195.60 1570.3 680.2 西藏 2002.20 1399.1 1035.9 陕西 2181.00 1070.4 1189.8 ⽢肃 1855.50 1167.9 966.2 青海 2179.00 1274.3 1084.1 宁夏 2247.00 1535.7 1224.4 新疆2032.40 2267.4469.9建⽴模型: µβββ+++=22110ln ln ln X X Y⼀、模型的OLS 估计(1)录⼊数据打开EViews6,点“File ”→“New ”→“Workfile ”选择“Unstructured/Undated”,在Observations 后输⼊31,如下所⽰:点“ok”。
异方差进行检验和补救

实验报告课程名称:实验项目名称:单方程线性回归模型中异方差的检验与补救院(系):专业班级:姓名:学号:实验地点:实验日期:年月日实验目的:掌握利用EViews软件对模型中存在的异方差进行检验和补救。
实验内容:根据我国2000年部分地区城镇居民每个家庭平均全年可支配收入X与消费支出Y 的统计数据,通过建立双变量线性回归模型分析人均可支配收入对人均消费支出的线性影响,并讨论异方差的检验与修正过程。
1、异方差的检验1)图示法2)Park检验3)Glejser检验4)Goldfeld-Quandt检验5)White检验2、异方差的补救1)加权最小二乘法(WLS)2)对数变换实验方法、步骤和结果:一、建立工作文件并完成数据输入1、File---new---workfile2、Quick---Empty Group ----paste3、将ser01重命名为x,ser01重命名为y二、写模型的估计方程Quick---Estimate Equation---y c x,得到在不考虑异方差且其他假定都成立的情况下的估计结果,如下图所示:三、异方差的检验找y的估计值在估计结果中点击forcast 将其重命名为yf生成残差序列:在估计窗口中点击proc---make residual series将resid01重命名为res,并保存(一)图示法(对异方差粗略的判定)1.用x-y的散点图进行判断,看是否存在明显的散点扩大、缩小或是复杂性的变动趋势X y ----open----as GroupView---graph ----scatter-----simple scatter2、用y的估计值与残差平方的散点图进行判断,看是否存在一条斜率为零的直线Quick---graph----scatter—写入方程yf res^2图形显示斜率不为零,所以可知模型存在异方差3、任一解释变量x与残差平方的散点图进行判断,看是否存在一条斜率为零的直线Quick—graph—scatter写入方程x res^2图形显示斜率不为零,所以可知模型存在异方差由以上三种图示法可知,模型存在异方差(二)帕克(Park)检验(将图示法公式化)Quick—Estimate Equation---log(res^2) c log(x)由估计结果可知:log(x)=3.703235 P=0.020622<0.05,所以拒绝原假设,模型具有统计显著性,即模型具有异方差。
异方差性的检验和修正
甘肃
4916.25
4126.47
上 海 11718.01
8868.19
青海
5169.96
4185.73
江 苏 6800.23
5323.18
新疆
5644.86
4422.93
1、做 Y 关于 X 的散点图以及回归分析 将数据通过 excel 录入到 eviews 中,对解释变量与被解释变量做散点图,选择解 释变量作为 group 打开,在数据表“ group”中点击 view/graph/scatter/simple scatter,出现以上数据的散点图,如下图所示:
图的结果显示,X 前的参数在 5%的显著性水平下不为零,同时,F 检验也表明方程的线性 关系在 5%的显著性水平下成立。 其次,采用异方差稳健标准误法修正原 OLS 的标准差,得到下图所示的估计结果:
任然可以看出,变量 x 对应参数修正后的标准差比 ols 估计的结果有所增大,这表明原模型 OLS 估计结果低估了 X 的标准差。
上海
11718.01
8868.19
青海
5169.96
4185.73
北京
10349.69
8493.49
内蒙古
5129.05
3927.75
广东
9761.57
8016.91
陕西
5124.24
4276.67
浙江
9279.16
7020.22
甘肃
4916.25
4126.47
天津
8140.5
6121.04
黑龙江
4912.88
计量经济学实验四——异方差的检验和修正
实验目的:学习建立回归模型,并进行异方差检验和对模型进行修正 实验内容:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下图 2.3.7,确认并“ok” ,得样本回归估计结果,见图 2.3.8。
5
图 2.3.7
图 2.3.8 再将子样本 14~21 进行 OLS 估计,求得如下结果。
6
图 2.3.9 下面求 F 统计量值。基于图 2.3.8 和图 2.3.9 中残差平方和的数据,即 Sum squared resid 的值。由图 2.3.8 计算得到的残差平方和为 e12i 144958.9 ,由
在 运 用 WLS 法 估 计 过 程 中 , 我 们 分 别 选 用 了 权 数
w1t 1/ X t , w2i 1/ X t2 , w3i 1/ X t 。权数的生成过程如下,由图 2.3.4,在对话框中
的 Enter equation 处 , 按 如 下 格 式 分 别 键 入 : w1 1/ X ; w2 1/ X ^ 2 ;
6304 911 934 1297 1085 1616 1021 1375 1212 1132 4064
339.9 508.5 438.6 620.1 149.8 346.7 488.4 82.9 88.9 402.4
827 1530 1589 2403 866 1223 1361 536 594 1471
图 2.3.6 构造子样本区间,建立回归模型。在本例中,样本容量 n 21 ,删除中间 1/4 的观测值,即大约 5 个观测值,余下部分平分得两个样本区间:1—8 和 14—21, 它们的样本个数均是 8 个,即 n1 n2 8 。 分别对两个样本区间:1—8 和 14—21 回归。Quick/Estimate Equation,进入 Equation Specification 窗口,键入“y c x” , ,并定义 sample 为 1 8,如
heteroskedasticity(no cross terms or cross terms) ,进入 White 检验。 根据 White 检验中辅助函数的构造,最后一项为变量的交叉乘积项,因为本例 为一元函数,故无交叉乘积项,因此应选 no cross terms,则辅助函数为
t2 0 1 xt 2 xt2 vt
9
图 2.3.12
图 2.3.13
10
图 2.3.13 的估计结果如下
ˆ 368.6203 2.952837 X Y i i
(84.1683) t (4.3796) (0.8227) (3.5893)
(2.3.4)
R 2 0.9387, R 2 0.9354, F 12.88288, df 19
图 2.3.2
2
点击主界面菜单 Quick\Estimate Equation,在弹出的对话框中输入 y c x, 点确定即可得到回归结果(图 2.3.3)。
图 2.3.3 估计结果为:
ˆ 562.9074 5.372828 X Y i i
( 291.5462) (0.644239) t (-1.930646) (8.339811) R 2 0.785438, R 2 0.774145, F 69.55245, df 19
2 图 2.3.9 计算得到的残差平方和为 e2 i 735844.7 ,根据 Goldfeld-Quanadt 检
验,F 统计量为
F
e e
2 2i 2 1i
735844.7 5.0762 144958.9
(2.3.2)
判断:在 0.05 下,在式 2.3.1 中分子、分母的自由度均为 6,查 F 分布 表得临界值为 F0.05 (6,6) 4.28 ,因为 F 5.0762 F0.05 (6,6) 4.28 ,所以拒绝原假设, 表明模型确实存在异方差。 (3)White 检验 由 图 2.3.3 估 计 结 果 , 按 路 径 view/Residual tests/white
(2.3.1)
3. 检验模型的异方差
本例用的是四川省 2000 年各地市州的医疗机构数和人口数,由于地区之间 存在的不同人口数,因此,对各种医疗机构的设置数量会存在不同的需求,这 种差异使得模型很容易产生异方差,从而影响模型的估计和运用。为此,必须 对该模型是否存在异方差进行检验。 (1)图形法 由路径:Quick/Estimate Equation,进入 Equation Specification 窗口, 键入“y c x” ,确认并“ok” ,得样本回归估计结果,见图 2.3.3。
图 2.3.5
4
判断。由图 2.3.5 可以看出,残差平方 ei2 对解释变量 X i 的散点图主要分布 在图形中的下三角部分,大致看出残差平方 ei2 随 X i 的变动呈增大的趋势,因此, 模型很可能存在异方差。但是否确实存在异方差还应通过更进一步的检验。 (2)Goldfeld-Quanadt 检验 对变量取值排序(按递增或递减) 。直接在工作文件窗口中按 Proc\Sort Current Page…,在弹出的对话框中输入 X 即可(默认项是 Ascending(升序))。 本例选升序排序,这时变量 Y 与 X 将以 X 按升序排序(如图 2.3.6)。
生成残差平方序列。在得到图 2.3.2 估计结果后,直接在工作文件窗口中
3
按 Genr,在弹出的窗口中, 在主窗口键入命令如下 e2 resid ^ 2 (用 e2 来表示残 差平方序列 ei2 ),得到残差平方序列 e2 (如图 2.3.4)
图 2.3.4 绘制 et2 对 X t 的散点图。方法 1:按住 Ctrl 键,同时选择变量 X 与 e2 (注意 选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴)以 组对象方式打开,进入数据列表,再按路径 view\Graph\Scatter\Simple Scatter, 可得散点图,见图 2.3.5。方法 2:点击 Eviews 主窗口 Quick\Graph\Scatter。
所以拒绝原假设,接受备择假设,表明模型存在异方差。 根据 White 统计量所对应 p 值的分析: 给定显著性水平 0.05 ,因为 Probabilit y (White) 0.000119 0.05 ,所 以拒绝原假设,表明模型存在异方差。
图 2.3.10
8
4.异方差性的修正
实验 4 异方差性
在现实经济活动中,最小二乘法的基本假定并非都能满足,本案例将讨论 随机误差违背基本假定的一个方面——异方差性。本案例将介绍:异方差模型 的图形法检验、Goldfeld-Quanadt 检验与 White 检验;异方差模型的 WLS 法修 正。
表 1 四川省 2000 年各地区医疗机构数与人口数
括号中数据为 t 统计量值。 可以看出运用加权小二乘法消除了异方差性后,参数的 t 检验均显著,可决 系数大幅提高, F 检验也显著,并说明人口数量每增加 1 万人,平均说来将增 加 2.953 个卫生医疗机构,而不是引子中得出的增加 5.3735 个医疗机构。虽然 这个模型可能还存在某些其他需要进一步解决的问题,但这一估计结果或许比 引子中的结论更为接近真实情况。
11
w3 1/ sqr ( X ) ,经估计检验发现用权数 w2t 的效果最好。下面仅给出用权数 w2t 的
结果。 在工作文件窗口中点 Quick\Estimate Equation,在弹出的对话框中输 入y c x
图 2.3.11 然后在图 2.3.11 中点 Options 选项,选中 Weighted LS/TLS 复选框,在 Weight 框中输入 w2,即可得到加权最小二乘法的结果。
地区 成都 自贡 攀枝 花 泸州 德阳 绵阳 广元 遂宁 内江 乐山 南充
人口数(万人)
医疗机构数(个)
地区 眉山 宜宾 广安 达州 雅安 巴中 资阳 阿坝 甘孜 凉山
人口数(万人) 医疗机构数(个)
1013.3 315 103 463.7 379.3 518.4 302.6 371 419.9 345.9 709.2
7
( 2.3.3) 经估计出现 White 检验结果,见图 2.3.10。 根据 White 统计量的分析: 从图 2.3.10 可以看出,nR2 18.0748 , 由 White 检验知, 在 0.05 下, 查 2
2 分布表,得临界值 0.05 (2) 5.9915 (在式 2.3.3 式中只有两项含有解释变量,故 2 自由度为 2) , 比较计算的 2 统计量与临界值, 因为 nR2 18.0748 0.05 (2) 5.9915 ,
1.建立 Workfile 和对象,录入变量人口数 X .1。
图 2.3.1
2.参数估计 按住 ctrl 键,同时选中序列 X 和序列 Y ,点右键,在所出现的右键菜单中, 选择 open\as Group 弹出一对话框,点击其上的“确定” ,可生成并打开一个群 对象 (图 2.3.1) 。 在群对象窗口工具栏中点击 view\Graph\Scatter\Simple Scatter, 可得 X 与 Y 的简单散点图(图 2.3.2),可以看出 X 与 Y 是带有截距的近似线性关 系。
