计量经济学及其应用:第6章
计量经济学讲义第六讲(共十讲)

第六讲 多重共线一、 FWL 定理及其应用考虑模型:112233i i i i i y a b x b x b x ε=++++ (1)假如我们只关注1ˆb,则通过如下步骤可以获得之。
第1步:把1x 对其他解释变量进行回归(请注意,截距所对应的解释变量为1),即有: 101223ˆˆˆˆi i i ix x x v βββ=+++ (2)第2步:把y 也对(2)中的解释变量进行回归,即有:01223ˆˆˆˆi i i i y x x w ϕϕϕ=+++ (3)第3步:把ˆw 对ˆv 进行回归(不含截距,当然你可以包含截距,但你会发现,截距的估计结果是零,这是因为ˆw 与ˆv 其均值都为零),即有模型:ˆˆi i i ve w η=+ (4) 则有:2ˆˆˆˆi i iw v v η=∑∑,可以验证,1ˆˆb η=,且残差ˆi e 等于初始的残差ˆi ε。
此即著名的FWL 定理(Frisch-Waugh-Lovell theorem )。
关于FWL 定理的一个简单证明见附录1。
思考题:利用关于“偏导数”的直觉,你能够理解1ˆˆb η=吗? 考察2ˆˆˆˆi i iw v v η=∑∑,把01223ˆˆˆˆi i i i y x x w ϕϕϕ=---代入,现在分子是:2012230123ˆˆˆˆ()ˆˆˆˆˆˆˆˆˆi i i i i i i ii i i v x i i y x x y v x v v v wv ϕϕϕϕϕϕ------∑∑∑==∑∑∑应该注意到,在进行第一步回归时,OLS 法保证了203ˆˆˆi i i i i v x x vv ===∑∑∑ 因此,22ˆˆˆˆˆˆi i i i i iw v y v v v η==∑∑∑∑ 显然,如果把y 对ˆv 直接进行无截距回归:*ˆiiiy v ης=+ (5)我们也可以得到:*122ˆˆˆˆˆˆˆi i i i i i y v w v b v vηη====∑∑∑∑。
计量经济学复习知识点重点难点

计量经济学复习知识点重点难点计量经济学知识点第一章导论1、计量经济学的研究步骤:模型设定、估计参数、模型检验、模型应用。
2、计量经济学是统计学、经济学和数学的结合。
3、计量经济学作为经济学的一门独立学科被正式确立的标志:1930年12月国际计量经济学会的成立。
4、计量经济学是经济学的一个分支学科。
第二章简单线性回归模型1、在总体回归函数中引进随机扰动项的原因:①作为未知影响因素的代表;②作为无法取得数据的已知因素的代表;③作为众多细小影响因素的综合代表;④模型的设定误差;⑤变量的观测误差;⑥经济现象的内在随机性。
2、简单线性回归模型的基本假定:①零均值假定;②同方差假定;③随机扰动项和解释变量不相关假定;④无自相关假定;⑤正态性假定。
3、OLS回归线的性质:①样本回归线通过样本均值;②估计值的均值等于实际值的均值;③剩余项ei的均值为零;④被解释变量的估计值与剩余项不相关;⑤解释变量与剩余项不相关。
4、参数估计量的评价标准:无偏性、有效性、一致性。
5、OLS估计量的统计特征:线性特性、无偏性、有效性。
6、可决系数R2的特点:①可决系数是非负的统计量;②可决系数的取值范围为[0,1];③可决系数是样本观测值的函数,可决系数是随抽样而变动的随机变量。
第三章多元线性回归模型1、多元线性回归模型的古典假定:①零均值假定;②同方差和无自相关假定;③随机扰动项和解释变量不相关假定;④无多重共线性假定;⑤正态性假定。
2、估计多元线性回归模型参数的方法:最小二乘估计、极大似然估计、矩估计、广义矩估计。
3、参数最小二乘估计的性质:线性性质、无偏性、有效性。
4、可决系数必定非负,但是根据公式计算的修正的可决系数可能为负值,这时规定为0。
5、可决系数只是对模型拟合优度的度量,可决系数越大,只是说明列入模型中的解释变量对被解释变量的联合影响程度越大,并非说明模型中各个解释变量对被解释变量的影响程度也大。
6、当R2=0时,F=0;当R2越大时,F值也越大;当R2=1时,F→∞。
计量经济学第六章-PPT课件

若模型有三个未知数,将数据三等分,分别求出 每部分的和,代入方程,得到三个方程,解方程 组可获得三个参数的估计值 10
模型的参数估计(续1)
参数的非线性最小二乘估计(第五章)
非线性模型可利用NLS进行参数的精确估计
首先,用param命令对参数赋初值 其次,输入方程,对模型进行估计
11
考虑选择指数曲线模型
2000000
1500000
1000000
500000
0 72 74 76 78 80 Y 82 84 YF 86 88 90 92
9
模型的参数估计
参数的最小二乘估计
常用的各类趋势模型参数估计仍常用OLS 其中,自变量为时间t
参数的三和值法(第五章)
若选用有增长上限的曲线趋势模型,当增长 上限事先不能确定时,可采用三和值法 基本思想
1961-1981年我国搪瓷面盆销售量数据如下 根据其变化,试以Gompertz曲线作为预测模型
由于增长上限L事先无法得知,参数估计可用NLS 在精确估计前,选择三和值法获得参数的初值 模型取对数转换成修正指数曲线 t ˆ y log L b log a log t
计算各段和值 根据参数计算公式计算参数值
产品市场生命周期
进入期 成长期 成熟期 衰退期
20
产品生命周期分析(续1)
f(t)
饱和点
进 成长期 入 期
成熟期 后 期 前 期
衰退期
t
21
产品生命周期分析(续2)
产品市场生命周期的各个阶段与某些趋势 模型存在大致的对应关系
最新计量经济学第六章习题答案讲课教案

3解:(1)样本回归方程为998792.00170.1226.793261-176283.0454750.12^t r X Y t,(2)残差图(3)DW 统计量的值734726.0DW(4)BG LM 自相关检验辅助回归式估计结果是t t t tX e e 000420.0060923.0638831.01因为84.3998223.7,84.31205.0LM ,所以LM 检验量也说明样本回归方程的误差项存在一阶正自相关。
首先估计自相关系数^,得632637.02734726.0121^DW 对原变量做广义差分变换。
令1t 632637.0t t Y Y GDY ,1t 632637.0t t X X GDX 以年1994~1975,,t t GDX GDY 为样本再次回归,得tGDX GDY 173740.0391490.0t 回归方程拟合的效果仍然比较好,651914.1DW 对于给定05.0,查表得,。
43.1,24.1U L d d 因为75.243.11651914.1DW ,依据判别规则,误差项已消除自相关。
由391490.0^*0,得06568.1632637.01/391490.01/^^*0^0则原模型的广义最小二乘估计结果是t X Y 173470.006568.1^t 。
4解:(1)样本回归方程为tGDP Y 694454.0674.2816^t(2)残差图(3)3397.0DW(4)BG LM 自相关检验辅助回归式估计结果是t t t tGDP e e 029062.07871.334985257.01因为84.309615.30,84.31205.0LM ,所以LM 检验量也说明样本回归方程的误差项存在一阶正自相关。
首先估计自相关系数^,得83015.023397.0121^DW对原变量做广义差分变换。
令1t 83015.0t t Y Y GDY ,183015.0t t tGDGDP GDP GDGDP ,以年1994~1975,,t t GDGDP GDY 为样本再次回归,得。
计量经济学重点知识整理

计量经济学重点知识整理1一般性定义计量经济学是以经济理论和经济数据的事实为依据,运用数学和统计学的方法,通过建立数学模型来研究经济数量关系和规律的一门经济学科。
研究的主体〔动身点、回宿、核心〕:经济现象及数量变化规律研究的工具〔手段〕:模型数学和统计方法必须明确:方法手段要服从研究对象的实质特征〔与数学不同〕,方法是为经济咨询题效劳2注重:计量经济研究的三个方面理论:即讲明所研究对象经济行为的经济理论——计量经济研究的根底数据:对所研究对象经济行为瞧测所得到的信息——计量经济研究的原料或依据方法:模型的方法与估量、检验、分析的方法——计量经济研究的工具与手段三者缺一不可3计量经济学的学科类型●理论计量经济学研究经济计量的理论和方法●应用计量经济学:应用计量经济方法研究某些领域的具体经济咨询题4区不:●经济理论重在定性分析,并不对经济关系提供数量上的具体度量●计量经济学对经济关系要作出定量的估量,对经济理论提出经验的内容5计量经济学与经济统计学的关系联系:●经济统计侧重于对社会经济现象的描述性计量●经济统计提供的数据是计量经济学据以估量参数、验证经济理论的全然依据●经济现象不能作实验,只能被动地瞧测客瞧经济现象变动的既成事实,只能依靠于经济统计数据6计量经济学与数理统计学的关系联系:●数理统计学是计量经济学的方法论根底区不:●数理统计学是在标准假定条件下抽象地研究一般的随机变量的统计规律性;●计量经济学是从经济模型动身,研究模型参数的估量和推断,参数有特定的经济意义,标准假定条件经常不能满足,需要建立一些专门的经济计量方法3、计量经济学的特点:计量经济学的一个重要特点是:它自身并没有固定的经济理论,而是依据其它经济理论,应用计量经济方法将这些理论数量化。
4、计量经济学什么缘故是一门单独的学科计量经济学是经济理论、数理经济、经济统计与数理统计的混合物。
1、经济理论所作的陈述或假讲大多数是定性性质的,计量经济学对大多数经济理论给予经验内容。
最全计量经济学课件(所有章节打包)

GNP 10201.4 11954.5 14922.3 16917.8 18598.4 21662.5 26651.9 34560.5 46670 57494.9 66850.5 73142.7 76967.2
80579.36 88189.6
截面数据(cross-section data)
• 在某一时刻所观察到的一组个体的数据。 • 这类数据反应个体在分布或者结构上的差
1998 2011.31 1336.38 4256.01 1486.08 1192.29 3881.73 1557.78 2798.89 3688.20
1999 2174.46 1450.06 4569.19 1506.78 1268.20 4171.69 1660.91 2897.41 4034.96
• 费瑞希:“对经济的数量研究有好几个 方面,其中任何一个就其本身来说都不 应该和经济计量学混为一谈。因此,经 济计量学与经济统计学绝不是一样的。 它也不等于我们所说的一般经济理论, 即使这种理论中有很大部分具有确定的 数量特征,也不应该把经济计量学的意 义与在经济学中应用数学看成是一样的。
一、什么是计量经济学
计量经济学构成要素
经济理论 模型
计量经济模型
数据 精炼的数据
数理统计理论 计量经济理论
采用计量经济技术并使用精练数据估计计量经济模型 应用
结构分析
经济预测
政策评价
计算机
三大要素
• 经济理论 • 数据 • 统计推断 • 经济理论、数据和统计理论这三者对于真
正了解现代经济生活中的数量关系都是必 要的,但本身并非是充分条件。三者结合 起来就是力量,这种结合便构成了计量经 济学。
• 经济数据是计量经济分析的材料。 • 经济数据是经济规律的信息载体。
计量经济学及其应用

an1
an
2
anm
1、 方 阵 当m n时, 称A 为n阶 方 阵, 即
a11 a12 a1n
A a21
a22
a2
n
an1 an2
ann
在 方 阵A 中,
当i
j时,a
称 为A 的 对 角 线 元 素,
计量经济学方法
计量分析一般步骤
• 通过理论分析建立理论假设
• 在理论假设基础上构建计量经济学模型
• 收集样本数据
• 估计计量经济学模型的参数
• 模型的检验
构建计量经济学模型
计量经济学模型
选择变量
确定变量之间关系 拟定代估参数理论值
变量
被解释变量
解释变量
b
b
RJCi 0 1PGDPi i
被检验的假设称为原假设,原假设的对立 假设称为备择假设。
假设检验的思路是:假设定原假设为真, 在此条件下计算已知样本出现的概率,如果是 小概率(即小于5%),就违背了小概率原理 (小概率事件在一次试验中几乎不应该出现), 这从统计上说明原假设为真是错误的,因此拒 绝原假设,否则接受原假设。
2、假设检验的一般步骤:统计量以小概率取值
绪论
通过本章我们要知道
• 什么是计量经济学 • 为什么要学习计量经济学 • 如何学习计量经济学 • 计量经济学方法
什么是计量经济学?
• 计量经济学是一门用于验证和测度的学 科
• 运用数学、统计学、和经济理论对经济 现象进行定量分析的社会学科
• 对客观经济数据得出的理论结果验证
安徽财经大学计量经济学 第六章练习题及参考解答
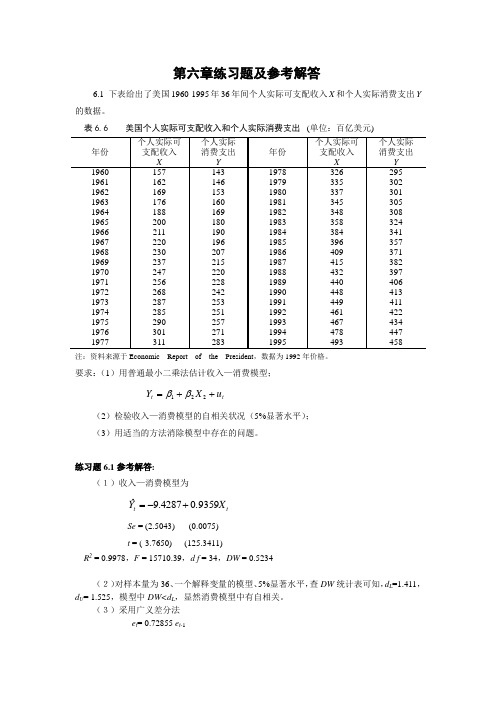
第六章练习题及参考解答6.1 下表给出了美国1960-1995年36年间个人实际可支配收入X 和个人实际消费支出Y 的数据。
表6.6 美国个人实际可支配收入和个人实际消费支出 (单位:百亿美元)注:资料来源于Economic Report of the President ,数据为1992年价格。
要求:(1)用普通最小二乘法估计收入—消费模型;t t u X Y ++=221ββ(2)检验收入—消费模型的自相关状况(5%显著水平); (3)用适当的方法消除模型中存在的问题。
练习题6.1参考解答:(1)收入—消费模型为 tt X Y 0.93594287.9ˆ+-=Se = (2.5043) (0.0075)t = (-3.7650) (125.3411)R 2 = 0.9978,F = 15710.39,d f = 34,DW = 0.5234(2)对样本量为36、一个解释变量的模型、5%显著水平,查DW 统计表可知,d L =1.411,d U = 1.525,模型中DW<d L ,显然消费模型中有自相关。
(3)采用广义差分法e t = 0.72855 e t-1**9484.07831.3ˆtt X Y +-=)8710.1(=Se (0.0189)t = (-2.0220) (50.1682)R 2 = 0.9871 F = 2516.848 d f = 33 DW = 2.0972查5%显著水平的DW 统计表可知d L = 1.402,d U = 1.519,模型中DW = 2.0972> d U ,说明广义差分模型中已无自相关。
同时,可决系数R 2、t 、F 统计量均达到理想水平。
9366137285501783131...ˆ=--=β最终的消费模型为 Y t = 13.9366+0.9484 X t6.2 在研究生产中劳动所占份额的问题时,古扎拉蒂采用如下模型模型1 t t u t Y ++=10αα模型2 t t u t t Y +++=2210ααα其中,Y 为劳动投入,t 为时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注意:Goldfeld-Quant检验法无法识别复杂的 异方差!
3、帕克检验法(Park test)
• 思路:把图示法进行量化,给出 e 关于 X i 的具体函数形式,然后检验这种结构是否显著 • 具体步骤: (1)建立被解释变量Y对所有解释变量X的回归 方程,然后计算残差 (2)建立辅助模型 ei2 2 xi ei ,或改写成 对数形式 ln(ei2 ) ln 2 ln xi i (6-7) (3)可以将上述函数形式改写为
(2)假设 i2 与 X 2 成比例 即 变换得
E(ui2 ) i2 2 X i2
(6-17)
Yi Xi i 1 ( ) ( ) 0 1 Xi Xi Xi Xi
Yi i 1 * 令 Yi , X i , ui ; Xi Xi Xi
*
则
Var ( i ) 2 Var (ui ) ( X i )2
• 步骤 2 (1)先对该模型进行OLS回归,得到 ei , (2)如下辅助回归: 2 2 2 ei =0 1 X1i 2 X 2i 3 X1i 4 X 2i 5 X1i X 2i+ui
(6-10)
2 2 R nR (3)计算统计量 ,其中n为样本容量, 为 辅助回归的可决系数。 在同方差假设下, (k为解释变量个 nR2 2 (k ) 数) 如果算得的统计量 nR 2 超过选定显著性水平下 的 2 临界值,则认为原线性回归模型中存在 2 2 异方差性。如果 nR 不超过 ,则认为原模型 中不存在异方差性,即在辅助回归中 1 2 3 4 5 0 。
按照第1章讲述的数据录入方法,将数据录入EViews, 在工作文件窗口中按先后顺序,选中PCON,REG, PRICE,点右键Open/as Equation,点击“OK”;或在 主菜单下,选择Quick/Estimate equation,键入“PCON REG PRICE c”,点击“OK”,便得到以下的结果。
F
2 e 2i 2 e 1i
3866128 20.08 192511.5
在5%的显著水平下,查分子和分母自由度均为17的F 分布表得 F0.05 2.48 。由于 F F0.05 ,所以拒绝原假设, 认为模型存在异方差性。 同理,可以对变量REG影响异方差的主要因素,进行 Goldfeld-Quant异方差检验。
顺序由小到大排列; (2)将其中间的 c n / 4个观察值除去,将 余下的 n c 个观测值划分为容量相等的前后 两个子样本; (3)每个子样本的个数为 (n c) / 2 ,将两个 子样本分别进行回归; (4)分别计算两个子样本回归方程的残差平方 2 和 e12i 和 e2 i 。
Yi 0 1 X i i
(1)已知 Var (i ) E(ui2 ) i2 ,则
i
Yi 0 (
*
(6-11)
1
i
* 0
) 1 (
i
Xi
)(
*
i
ui
)
(6-12) (6-13)
即 此时
Yi 1 X i ui
ui )2 E (ui2 )
6.4如何消除异方差
1、加权最小二乘法WLS • 适用于随机干扰项的方差 i2 已知的情况 • 思路:对较小的 i2 赋予较大的权重;对较大 的 i2 赋予较小的权重,对原模型进行加权, 使其成为一个不存在异方差性的新模型,然后 采用普通最小二乘法进行估计。
• 具体步骤 以一元回归模型为例
X i 表示人均年收 Yi 表示人均食品支出, 其中, 入。在其他条件不变的情况下,随着收入水平 X i 的提高,随机干扰项的方差也会发生变动。 普通最小二乘法失效。
6.1什么是异方差性
• 异方差性:经典线性回归模型的基本假设之一 随机干扰项的同方差性不成立,即至少有一 个 i ,使得 Var i i2 2 ,模型即存在异 方差性(heteroskedasticity)。 • 类型: 1、单调递增:以截面资料研究居民家庭的储蓄行 为,建立储蓄函数 Yi 0 1 X i i 2、单调递减:边错边改的学习模型 3、复杂型:以截面数据为样本建立居民消费函数
图6-3 e2和REG散点图
从图6-3可以看出,散点图的点主要分布在左下角,大 致可以看出,残差平方 ei2 随REG增大似乎呈现变大的趋 2 势。用同样的方法,可以发现 ei 随PRICE的增大也随之 增大。因此,我们可以认为模型很可能存在异方差性。但 这只是一种直观的判断,模型是否真的存在异方差性,还 需用其他方法进一步检验。
第 6章
异方差性
通过本章我们要知道
• • • • • 6.1什么是异方差性 6.2异方差性会产生什么后果 6.3异方差性的诊断 6.4如何消除异方差性 6.5案例分析
引子
• 在以截面数据研究家庭人均年收入与人均食品 支出之间关系的时候,假定两者为线性关系, 有如下模型: Yi 0 1 X i i
2 i
ln(e ) ln xi i 对此模型应用OLS法,得出 和 的估计值
2 i
(4) 对 进行 t 检验。如果 不显著,则说明 2 ei 实际上与 X i 无关,即不存在异方差性。反 之,则表明存在异方差性。 4、Glesjer检验法(Glesjer test) • 思路:通过建立 ei与X i 的关系,对新模型 进行估计。 • 步骤: (1)建立被解释变量Y 对所有解释变量的回归 方程,然后计算残差;
*
Var (ui* ) E (ui* )2 E (
i
i2
i2 2 1 (6-14) i
(2)用OLS法对(6-13)进行回归
说明:由于随机干扰项的方差 i2 通常是未知的 ,因此在实际运用中,常常采用残差的绝对值 的倒数 1/ ei 作为权重进行加权最小二乘法。
2、模型变换法 2 (1)假设 i 与 X i 成比例 即
1/ ei
6.5 CASE(P93)
油价和机动车注册数对汽油消耗量的影响研究
1. 建立模型如下:
PCONi 0 1REGi 2 PRICEi i
其中: PCON表示第i个州的汽油消耗量(单位:100万BTU); REG表示第i个州的机动车注册数(单位:千辆) ; PRICE表示第i个州的汽油价格(单位:美分/加仑)。 注:相关数据详见教材相关内容
(2) Goldfeld-Quant检验 首先,对解释变量进行排序。在工作文件下,点击 Procs/Sort Series,将出现如图6-4的对话框。
左图中,Ascending表示 升序排列,Descending 表示降序排列。在空白 处键入需要排序的变量 名就可以实现排序。本 例中,需要对解释变量 进行排序,因此,在空 白处键入“price”,并 按升序排列,点击“OK” 后就实现了对应解释变 量的排序。
图6-4 排序对话框
构造子样本区间,建立子回归模型。在本例中样本容 量为50,删去中间的1/4的观察值,大约12个,余下部分 分为两个子样本区间:1-19和32-50,其样本容量都是18 ,即 n1 n2 18 。在输出回归结果的界面下,点击 Estimate,将Sample里面的“1 50”改为“1 19”,点 击“OK”就得到如下的结果。
Ci 0 1 X i i
6.2异方差的后果
• 异方差的产生原因 1、模型中缺少某些解释变量 2、测量误差 3、异常值的出现 4、采用截面数据时,不同样本点上解释变量以 外的其他因素差异较大
• 异方差产生的后果 1、参数估计量非有效(但仍为线性无偏的)
2、t检验和F检验失效(一般会低估存在的异方 差,从而夸大参数的显著性) 3、模型预测失效
• 检验思路: (1)由于同方差的方差之比趋近于1,递增型 异方差的方差之比大于1,而递减型异方差的 方差之比小于1。 (2)因此可将样本分为两个部分,再对这两 个部分的子样本分别进行回归,然后用两个部 分子样本残差平方和之比构造一个 F 统计量 进行异方差检验。
具体步骤
(1)将n对观察值 Xi ,Yi 按解释变量 X i 的大小
表6-3 第一个子样本的回归结果
再次点击Estimate,将Sample里面的“1 19”改为“32 50”,点击“OK”就得到第二个子样本的回归结果。
表6-4 第二个子样本的回归结果
计算F统计量。从上述两表中的sum squared residual 便可获得两个子样本的残差平方和的值。第一个子样本的 2 2 e 中 1i 3866128 ,第二个子样本的中 e2i 192511.5 。 因此,Goldfeld-Quant检验的F统计量为
变换得
E(u ) X i
2 i 2 i
Yi Xi ui 1 0 1 Xi Xi Xi Xi
(6-15)
此时
ui Var (ui ) 1 2 Var X i 2 (6-16) X Xi Xi)将 e 为被解释变量,将原模型的某一解释 变量 x j 作为解释变量,建立如下方程:
2 i
ei f X ji vi
常用的函数形式有:
ei X ji vi ei X ji vi 1 ei vi X ji ei 1 vi X ji
6.3异方差的诊断
1、图示法 在无异方差性的假定下作回归分析,作出 X e2 散点图,观察其是否呈现任何系统性的样式。
2 图 6-1 X e 散点图的假象样式
2、 Goldfeld-Quant检验法
适用的情况是: (1) 样本容量较大,观测值的数目一般不低于 参数个数的两倍; (2) 除了同方差假定之外,古典线性回归模型 的其它假定是满足的; 2 2 2 X (3)异方差的类型是单调型,即有 i 。 i
